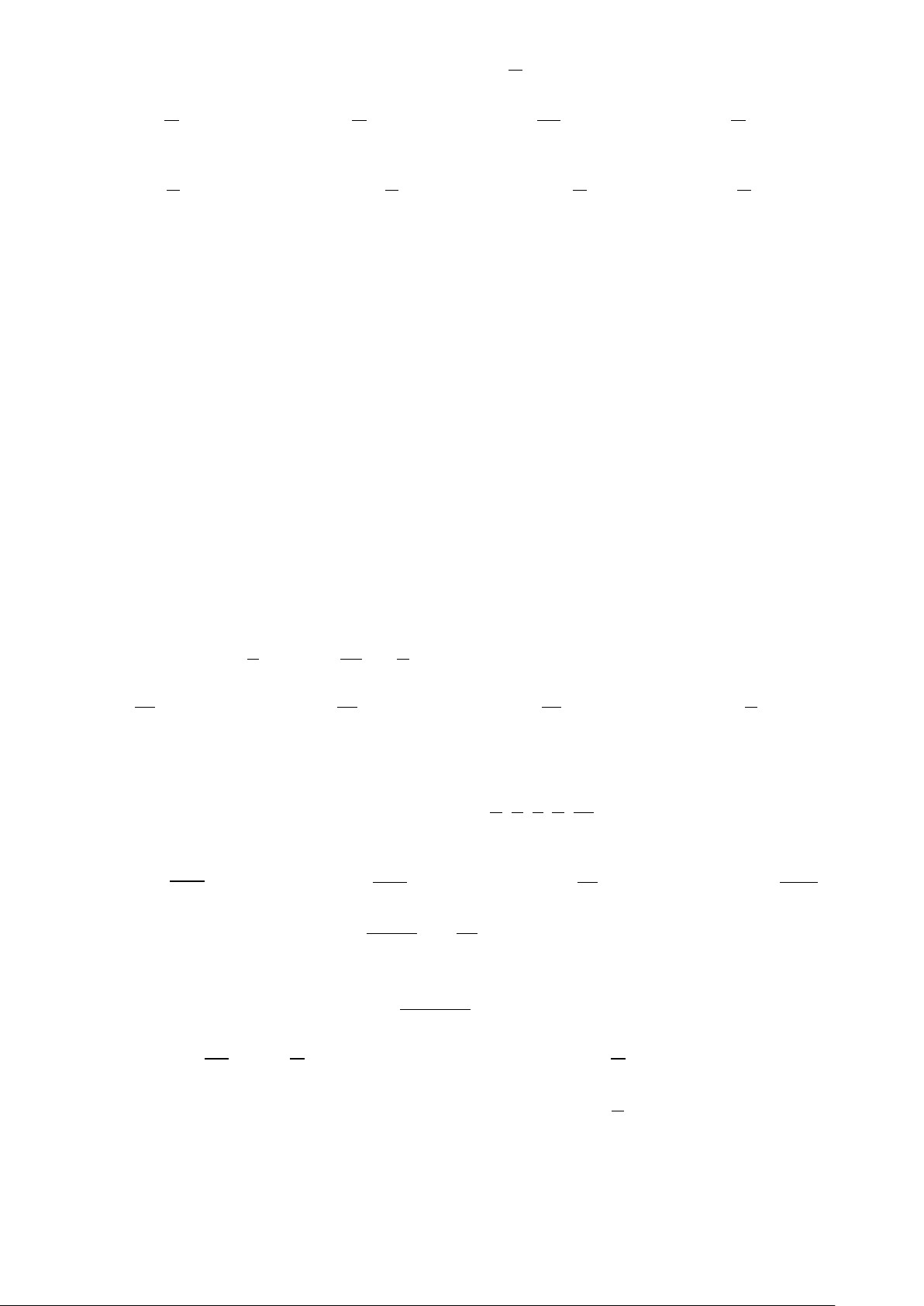




Preview text:
SỞ GDĐT THÁI BÌNH
ĐỀ KIỂM TRA GIỮA HỌC KÌ I NĂM HỌC 2023 - 2024
TRƯỜNG THPT NGUYỄN TRÃI MÔN: TOÁN 11
Thời gian làm bài: 90 phút, không kể thời gian giao đề.
(Đề gồm 04 trang) Mã đề: 111
Họ, tên thí sinh: ..........................................................................
Số báo danh: ...............................................................................
A. PHẦN TRẮC NGHIỆM (7 điểm)
Câu 1. Cho hình chóp S.ABCD . Gọi I, J lần lượt là trung điểm của AB và BC . Giao tuyến của hai
mặt phẳng (SAC) và (SIJ ) là một đường thẳng song song với:
A. đường thẳng AD .
B. đường thẳng AB .
C. đường thẳng AC . D. đường thẳng BD .
Câu 2. Đường cong trong hình vẽ là đồ thị của hàm số nào dưới đây?
A. y = cos x .
B. y = cot x .
C. y = tan x .
D. y = sin x .
Câu 3. Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M ; N lần lượt là trung điểm của AD
và BC . Giao tuyến của (SMN ) và (SAC) là:
A. SK ( K là trung điểm của AB ).
B. SF ( F là trung điểm của CD ). C. SD .
D. SO (O là tâm của hình bình hành ABCD ). π
Câu 4. Tất cả các nghiệm của phương trình sin x + = 1 là: 6 5π π A. x =
+ k2π (k ∈).
B. x = + kπ (k ∈). 6 3 π π
C. x = + k2π (k ∈).
D. x = − + k2π (k ∈). 3 6
Câu 5. Cho hình chóp S.ABCD có đáy là hình bình hành tâm O . Các điểm M , N, P lần lượt là trung điểm của ,
SA SC và OD ; SO cắt MN tại điểm I . Giao điểm SB và mặt phẳng (MNP) là:
A. Giao điểm của PN với SB
B. Giao điểm của MN với SB .
C. Giao điểm của PI với SB .
D. Giao điểm của DI với SB .
Câu 6. Trong các khẳng định sau, khẳng định định nào đúng?
A. sin (a −b) = sin a cosb − cos asin b .
B. sin (a −b) = sin asinb − cosa cosb .
C. sin (a −b) = sin acosb + cos asinb .
D. sin (a −b) = cos acosb −sin asinb .
Câu 7. Cho tứ diện ABCD . I và J theo thứ tự là trung điểm của AD và AC . G là trọng tâm tam giác
BCD . Giao tuyến của hai mặt phẳng (GIJ ) và (BCD) là đường thẳng.
A. Qua J và song song với BD .
B. Qua G và song song với BC .
C. Qua I và song song với AB .
D. Qua G và song song với CD .
Câu 8. Cho tứ diện đều ABCD có các cạnh đều bằng a . Gọi G là trọng tâm tam giác ABC , M là trung
điểm của cạnh CD . Diện tích thiết diện của tứ diện khi cắt bởi mặt phẳng ( AMG)(tính theo a ) bằng: 2 2 2 2
A. a 11 .
B. a 11 .
C. a 11 . D. a 11 . 16 8 32 2 1
Câu 9. Tìm tất cả các nghiệm của phương trình π sin x + = sinx . 3 A. π π π π
x = + kπ (k ∈) .B. x = − + k2π (k ∈) .C. 5 x =
+ k2π (k ∈) .D. x = + k2π (k ∈) . 3 6 6 3
Câu 10. Nghiệm của phương trình cos x 0 là: A. x
k, k .
B. x k,k .
C. x k,k .
D. x k2,k . 6 6 2 3
Câu 11. Cho hình chóp S.ABCD có đáy là hình thang ABCD ( //
AD BC). Gọi M là trung điểm .
CD Giao tuyến của hai mặt phẳng (MSB) và (SAC) là:
A. SI ( I là giao điểm của AC và BM ).
B. SO (O là giao điểm của AC và BD ).
C. SJ ( J là giao điểm của AM và BD ).
D. SP ( P là giao điểm của AB và CD ).
Câu 12. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB và AC . Đường thẳng MN
song song với mặt phẳng:
A. ( ABC) .
B. ( ACD) ;
C. (BCD); D. ( ABD) ;
Câu 13. Cho hình chóp S.ABCD có đáy là hình bình hành. Các điểm I, J lần lượt là trọng tâm các tam
giác và SAB và SAD . Gọi M là trung điểm CD . Chọn mệnh đề đúng trong các mệnh đề sau:
A. IJ //(SBM ) ;
B. IJ //(SCD);
C. IJ //(SBD);
D. IJ //(SBC) .
Câu 14. Cho tứ diện ABCD . Gọi M , N lần lượt là trung điểm của AB, AC ; E là điểm trên cạnh CD sao
cho 2EC = ED . Khi đó, thiết diện tạo bởi (MNE) và tứ diện ABCD là hình gì?
A. Hình chữ nhật.
B. Hình thang có đáy lớn là MN .
C. Hình thang có đáy bé là MN . D. Hình bình hành. Câu 15. Cho 3 cos a = . Tính 3
cos a .cos a . 4 2 2 A. 23 . B. 23 . C. 7 . D. 7 . 16 8 16 8
Câu 16. Dãy số (u , n
∀ ∈ * được gọi là dãy số tăng khi: n ) A. u > B. u < C. u ≥ D. u ≤ + u n n. + u n n. + u n n. + u n n. 1 1 1 1
Câu 17. Cho dãy số (u n∈ n ) ,
* có 5 số hạng đầu là 1 1 3 1 5 ; ; ; ;
;...Số hạng tổng quát của dãy số (un ) 2 2 8 4 32 là: A. 1 u = . B. n 1 n n = . n u − = . C. u = . D. u n +1 n 2n n 2n n n + 2 3n +1 7
Câu 18. Cho dāy số (u , biết u = . Số
là số hạng thứ mấy của dāy số? n ) n 5n −1 11 A. 10. B. 11. C. 9. D. 8 .
Câu 19. Tập xác định x D của hàm số 3cos y = . 2sin x −1 A. 5π π π D \ k2π ; k2π ,k = + + ∈ .
B. D = \ + k2π,k ∈ . 6 6 6
C. D = . D. 1 D \ = . 2 2
Câu 20. Tất cả nghiệm của phương trình x = ( o cos2
cos x + 60 ) là: A. o o
x = 60 + k360 ,k ∈ . B. 0 o x = 20 − + 120 k ,k ∈. C. o o
x = 60 + k360 và o o x = 20 −
+ k360 ,k ∈. D. o o
x = 60 + k360 và o o x = 20 − + 120 k ,k ∈.
Câu 21. Cho đường thẳng a song song với mặt phẳng (α ) . Nếu mặt phẳng (β ) chứa a và cắt (α )
theo giao tuyến b thì b và a là hai đường thẳng:
A. trùng nhau. B. cắt nhau. C. chéo nhau.
D. song song với nhau.
Câu 22. Dãy số nào dưới đây là dãy số tăng? 1 1 1 1 1 1 A. 2, 4, 3 B. , , . C. 3, 3, 3 D. , , . 4 3 2 2 3 4
Câu 23. Rút gọn biểu thức cos a − cos5a P =
( với sin 4a + sin 2a ≠ 0 ) ta được: sin 4a + sin 2a
A. P = 2cos a .
B. P = 2sin a . C. P = 2 tan . a D. P = 2cot . a
Câu 24. Rút gọn biểu thức
sin a + sin 3a + sin 5a A = .
cos a + cos3a + cos5a
A. tan3a .
B. cos3a .
C. 1− tan 3a . D. sin 3a .
Câu 25. Nghiệm của phương trình tan x = 1 − là: A. π π
x = + k2π (k ∈) . B. x = − + kπ (k ∈) . 4 4 C. π π
x = + k2π (k ∈ 5 ) . D. x = ±
+ k2π (k ∈) . 3 6
Câu 26. Giá trị của m để phương trình cos 2x −(2m + )
1 sin x − m −1 = 0 có nghiệm trên khoảng (0;π ) là m∈[ ;
a b) thì a + b là: A. 1. B. 2 . C. 1 − . D. 0 .
Câu 27. Cho dãy số (u n∈ n n ) , * biết u = . Tính u . n n +1 5 A. 1 u = . B. 5 u = . C. 1 u = . D. 16 u = . 5 5 5 6 5 6 5 25
Câu 28. Đẳng thức nào sau đây là đúng? π 3 1 π 1 3 A. cos a + = sin a − cos a . B. cos a + = sin a − cos a . 3 2 2 3 2 2 π 1 3 C. π 1 cos a + = cos a + . D. cos a + = cos a − sin a . 3 2 3 2 2
Câu 29. Phương trình (x + °) 1 cos
30 = có các nghiệm là: 2 π x = + k360°
A. x = k360° 6 . B. .
x = −60° + k360° π
x = − + k360° 2
C. x = 30° + k2π x = ° + k ° . D. 30 360 .
x = −90° + k2π
x = −90° + k360° Mã đề 101 Trang 3/4
Câu 30. Nghiệm của phương trình 3 sin x + cos x = 2 là: π π
A. x = + kπ ,k ∈ . B. x = + k2π,k ∈ . 3 2 π π
C. x = + k2π,k ∈ . D. x = + k2π,k ∈ . 6 3
Câu 31. Giá trị của biểu thức cos5x + cos3x I = , biết 1 tan x = là:
sin 5x − sin 3x 3 A. I = 3 − . B. 1 I = − . C. 1 I = . D. I = 3 . 3 3 Câu 32. Biết 4 π π cosα = − và 3 < α < . Giá trị sin 2α bằng: 5 2 2 A. 24 − − . B. 8. C. 2 . D. 24 − . 25 25 5 5
Câu 33. Cho α là góc lượng giác, trong các khẳng định sau khẳng định nào đúng?
A. sin(π −α) = cosα.
B. sin(π −α) = −sinα.
C. sin(π −α) = sinα.
D. sin(π −α) = −cosα.
Câu 34. Giá trị lớn nhất (M), giá trị nhỏ nhất (m) của hàm số: y = 3sin x + 4cos x +1 là:
A. M = 6;m = 4 − .
B. M = 8;m = 6 − .
C. M = 6;m = 2 − .
D. M = 5;m = 5 − . 5
Câu 35. Cho góc α thỏa mãn sinα + cosα = . Giá trị của P = sinα.cosα là: 4 1 9 9 9
A. P = . B. P = . C. P = . D. P = . 8 8 16 32
II. PHẦN TỰ LUẬN (3 điểm).
Bài 1. Giải phương trình lượng giác sau:
a) sin2x + cos x = 0 . π π b) cos 3x + − sin − 3x = 3 6 3 4 3π π
Bài 2. a) Cho góc α thỏa mãn cosα = − và π < α < . Tính tan α − . 5 2 4 n + a
b) Cho dãy số (u có u = n∈ N u n ( *). Tìm n )
a để dãy số ( n ) là dãy giảm. n +1
Bài 3. Cho hình chóp SABC . Gọi M , N, E lần lượt là trung điểm của AC , BC , SB . Gọi H , K lần
lượt là trọng tâm của các tam giác SAC và SBC .
a) Chứng minh HK //(SAB).
b) Chứng minh HK song song với giao tuyến của hai mặt phẳng (MNE) và (SAB) .
------ HẾT ------ 4
Đề\câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 000
C A C B A A A A C B A C A C A C D A C A A B D A 111
C D D C C A D A A C A C C C C A C C A D D B B A 112
A C B B D C B A C A A B D A C C B C A D A B A A 113
A A C B A A C D A A D B D A B A C C D D D C B C 114
C B C A B B C B B C D B A C D A A D D C A D D B
25 26 27 28 29 30 31 32 33 34 35 D C C C B D B A B D A B C B D D D D A C A D A D D D D A B B D A D B B B C C A B B C D B B A C A C B C A B A C
Document Outline
- MÃ 111
- ĐÁP ÁN
- Sheet1




