



Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA GIỮA HỌC KỲ I THÀNH PHỐ HỒ CHÍ MINH NĂM HỌC 2023- 2024
TRƯỜNG THPT PHONG PHÚ
Môn Toán – Khối 11
Thời gian làm bài: 60 phút (không kể thời gian phát đề) ĐỀ CHÍNH THỨC
Họ và tên học sinh: ............................................................... …..Số báo danh: …………… …… 3
Câu 1. (3 điểm) Cho sin a = với 0 a . 4 2
a) Tính các giá trị lượng giác còn lại của góc a . b) Tính cos 2a .
Câu 2. (3,0 điểm) Giải các phương trình lượng giác cơ bản sau: 1 a) cos x = ; 2 b) tan 2x = 1 . x c) ( x + ) 4 2 sin 3 o c s
− sin x(1+ cos x) −3cos x −1 = 0. 2 x
Câu 3: ( 1 điểm) Tìm tập giá trị của hàm số sau: y = 2cos − + 8 10 3
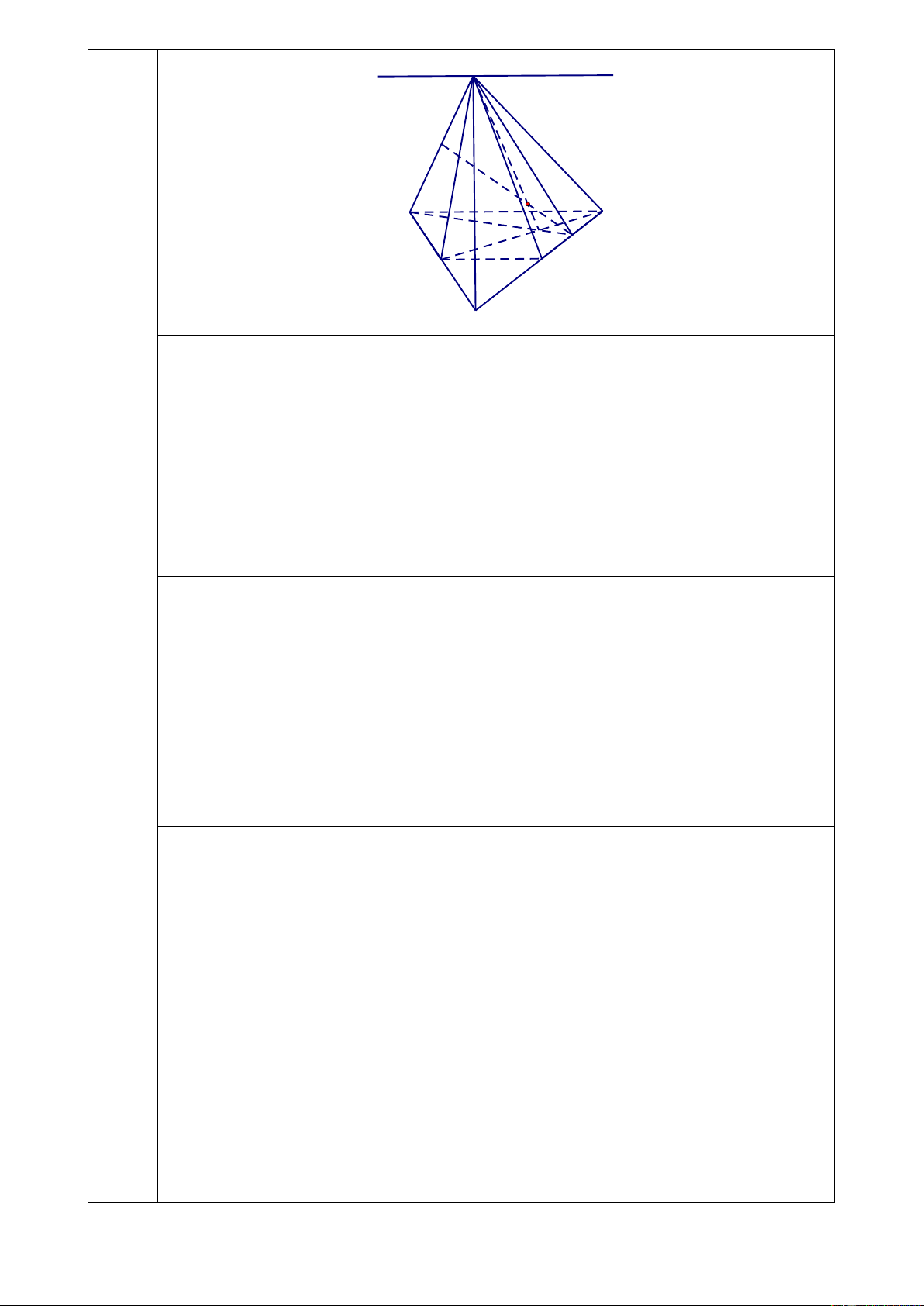
Câu 4. (3 điểm) Cho hình chóp S.ABCD có đáy là hình thang ABCD , đáy lớn AB . Gọi M , N
lần lượt là trung điểm của các cạnh S , A BC .
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC ) .
b) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD) .
c) Tìm giao điểm I của đường thẳng MN và mặt phẳng (SBD).
------------- Hết ------------- Trang 1/ 1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐÁP ÁN VÀ THANG ĐIỂM CHI TIẾT THÀNH PHỐ HỒ CHÍ MINH
ĐỀ KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT PHONG PHÚ NĂM HỌC 2023- 2024
Môn Toán – Khối 11 ĐỀ CHÍNH THỨC
Thời gian làm bài: 60 phút (không kể thời gian phát đề) Câu Đáp án Thang điểm Cho 3 π
sin a = với 0 < a < . 4 2
a) Tính các giá trị lượng giác còn lại của góc a . 2 2 2 3 7
cos a =1− sin a =1− = 4 16 0,5 7 ⇒ cos a = ± 4 0,25 1 0,25 Vì π 0 < a < nên 7 cos a = (3 đ) 2 4 sin a 3 7 tan a = = cos a 7 0,5 cos a 7 cot a = = 0,5 sin a 3
b) Tính cos2a . 1,0 2 1
cos 2a =1− 2sin a = − 8
Giải các phương trình lượng giác sau: a) 1 cos x = 2 0,5 π ⇔ cos x = cos . 3 2 π x = + k2π (3 đ) 3 0,5 ⇔ k ∈ π x = − + k2 π 3 b) tan 2x =1 π ⇔ tan 2x = tan 0,25 4 π ⇔ 2x = + kπ 0,25 4 π π
⇔ x = + k ,k ∈ . 0,5 8 2 c) ( + ) 4 2 sin 3 os x x c
− sin x(1+ cos x) − 3cos x −1 = 0. 2 ⇔ 2(sin + 3) 4 x 2 x 2 cos − 2sin cos − 6cos x x x + 2 = 0 2 2 2 ⇔ (sin + 3) 4 x 2 cos − cos x x (sin x +3)+1= 0 2 2 2 cos x (sin 3) 2 cos x x 1 ⇔ + − +1 = 0 2 2 1 ⇔ − (sin x + 3) 2 sin x +1 = 0 4 3 2
⇔ sin x + 3sin x − 4 = 0 ⇔ (sin x − ) 1 (sin x + 2)2 = 0 0,25 sin x =1 0,25 ⇔ sin x = 2 − (vn) 0,25 π
⇔ x = + k2π (k ∈ 0,25 ) 2
Tìm tập giá trị của hàm số sau: 2cos x π y = − + 8 10 3 1 cos x π − ≤ − ≤ 1 10 3 0,25 3 x π (1 đ) ⇔ 2 − ≤ 2cos − ≤ 2 10 3 0,25 6 2cos x π ⇔ ≤ − + 8 ≤ 10 ⇔ 6 ≤ y ≤10 10 3 0,25 Vậy T = [6;10] 0,25 4
Cho hình chóp S.ABCD có đáy là hình thang ABCD , đáy lớn AB . Gọi M , N
(3đ) lần lượt là trung điểm của các cạnh S , A BC . S x M I A B O N D C E
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC).
S ∈(SAD) ∩(SBC) 0,25
Trong mặt phẳng ( ABCD) , gọi E = AD ∩ BC
E ∈ AD ⊂ (SAD) 0,5
⇒ E ∈(SAD) ∩(SBC) E ∈ BC ⊂ (SBC)
⇒ (SAD) ∩(SBC) = SE 0,25
b) Tìm giao tuyến của hai mặt phẳng (SAB) và (SCD).
S ∈(SAB) ∩(SCD) 0,25
Trong mặt phẳng ( ABCD) , ta có AB / /CD AB ⊂ (SAB) 0,5 CD ⊂ (SCD)
⇒ (SAB) ∩(SCD) = Sx / / AB / /CD 0,25
c) Tìm giao điểm I của đường thẳng MN và mặt phẳng (SBD).
MN ⊂ (SAN ) 0,25
S ∈(SAN ) ∩(SBD)
Trong mặt phẳng ( ABCD) , gọi O = AN ∩ BD O ∈ AN ⊂ (SAN ) ⇒
⇒ O ∈(SAN ) ∩(SBD) O ∈ BD ⊂ (SBD) 0,5
⇒ (SAN ) ∩(SBD) = SO
Trong mặt phẳng (SAN ) , I = MN ∩ SO I ∈ MN ⇒ I ∈ SO ⊂ (SBD)
⇒ MN ∩(SBD) = I 0,25
(Học sinh giải theo cách khác đúng vẫn được điểm tối đa)
Document Outline
- thptphongphutoan11dechinhthucghkinh-2023-2024_1112023102536
- toan11thptphongphudapandechinhthucktgkhkinh-23-24_1112023102536




