-
Thông tin
-
Quiz
Đề giữa học kỳ 1 Toán 12 năm 2023 – 2024 trường THPT Nguyễn Du – TP HCM
Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra giữa học kỳ 1 môn Toán 12 năm học 2023 – 2024 trường THPT Nguyễn Du, quận 10, thành phố Hồ Chí Minh; đề thi gồm 04 trang, hình thức trắc nghiệm với 25 câu, thời gian làm bài 45 phút; đề thi có đáp án mã đề 101 – 102 – 103 – 104.Mời bạn đọc đón xem.
Chủ đề: Đề thi Toán 12 1.2 K tài liệu
Môn: Toán 12 3.8 K tài liệu
Thông tin:
Tác giả:
Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT NGUYỄN DU NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn:TOÁN 12
(Đề thi có 4 trang) Thời gian: 45 phút
Học sinh nhớ ghi tên và tô số báo danh, mã đề vào bảng trả lời bên dưới Mã đề thi: 101 HỌ VÀ TÊN Lớp:
Câu 1. Hình lập phương có bao nhiêu mặt phẳng đối xứng? TRƯỜNG: ĐIỂM KỲ THI: A 12. B 8. C 9. D 6. MÔN THI:
Câu 2. Cho khối lập phương có cạnh bằng 6. Thể THỜI GIAN:
tích của khối lập phương đã cho bằng SỐ BÁO DANH MÃ ĐỀ A B C D A 36. B 18. C 72. D 216. 0 0 0 0 0 0 0 0 0 0 1 A B C D 1 1 1 1 1 1 1 1 1 1 2 A B C D
Câu 3. Hàm số nào sau đây đồng biến trên ĐỀ R? 2 2 2 2 2 2 2 2 2 2 3 MÃ A B C D
A y = x3 + x2 − x − 1. À 3 3 3 3 3 3 3 3 3 3 V 4 A B C D x + 1 4 4 4 4 4 4 4 4 4 4 ANH 5 A B C D B y = . D 5 5 5 5 5 5 5 5 5 5 O 6 A B C D x − 1 BÁ 6 6 6 6 6 6 6 6 6 6 7 A B C D
C y = x3 − x2 + 2x − 1. SỐ 7 7 7 7 7 7 7 7 7 7 8 A B C D KÍN D y = x4 − 2x2 + 3. 8 8 8 8 8 8 8 8 8 8 9 TÔ A B C D 9 9 9 9 9 9 9 9 9 9 10 A B C D
Câu 4. Hàm số nào sau đây có hai điểm cực đại và A B C D A B C D 11 một điểm cực tiểu? A B C D 21 A B C D 12 A B C D 22 A B C D
A y = −x4 − 2x2 − 1.
B y = −x4 + 2x2 − 1. 13 A B C D 23 A B C D C y = x4 + 2x2 − 1. D y = x4 − 2x2 − 1. 14 A B C D 24 A B C D 15 A B C D 25 A B C D 3x − 1 16
Câu 5. Cho hàm số y = . Gọi M , m lần lượt A B C D x − 3 17 A B C D
là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn 18 A B C D 19
[−40; 2]. Giá trị của M + m bằng A B C D 20 94 14 14 94 A B C D A − . B . C − . D . 43 3 3 43
Câu 6. Cho hàm số y = f(x) có bảng x −∞ −1 0 1 +∞
biến thiên như hình vẽ bên. Hàm số y = f (x) y0 + 0 − − 0 +
nghịch biến trên khoảng nào trong các khoảng +∞ +∞ + sau đây? y A (−1; 1). B (0; +∞). −∞ −∞ C (−1; 0). D (−∞; −1).
Câu 7. Cho hàm số y = f(x) có lim f(x) = 0 và lim f(x) = +∞. Mệnh đề nào dưới đây là đúng? x→+∞ x→+∞
A Đồ thị hàm số y = f (x) có hai tiệm cận ngang.
B Đồ thị hàm số y = f (x) có một tiệm cận ngang là trục hoành.
C Đồ thị hàm số y = f (x) có một tiệm cận đứng là đường thẳng y = 0.
D Đồ thị hàm số y = f (x) không có tiệm cận ngang. 2017x + 2018
Câu 8. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số y = . x + 2 A x = −2. B y = −2. C x = 2017. D y = 2017.
Trang 1/4 − Mã đề 101
Câu 9. Cho hình chóp S.ABC có A0, B0 lần lượt là trung điểm của SA, SB. Gọi V1, V2 lần lượt là thể tích V
của khối chóp S.A0B0C và S.ABC. Tỉ số 1 bằng V2 1 1 1 1 A . B . C . D . 3 2 8 4 √
Câu 10. Cho khối chóp S.ABC có SA vuông góc (ABC) và đáy là tam giác đều cạnh a 17, góc giữa
(SBC) và mặt đáy (ABC) bằng 60◦. Thể tích V của khối chóp S.ABC là √ √ √ √ 17 51 17 51 51 51 17 51 A a3. B a3. C a3. D a3. 16 8 8 4
Câu 11. Cho hàm số y = f(x) xác định, liên tục trên x −∞ 0 1 +∞
R và có bảng biến thiên cho bởi hình bên. Mệnh đề nào sau đây đúng? f 0(x) + 0 − 0 +
A Hàm số có giá trị cực tiểu bằng 1. 5 +∞ +
B Hàm số có giá trị cực đại bằng −1. f (x)
C Hàm số có giá trị cực đại bằng 0. −∞ −1
D Hàm số có giá trị cực đại bằng 5. √
Câu 12. Cho lăng trụ đứng ABC.A1B1C1 có đáy là tam giác vuông cân tại B, BC = a 14, biết góc giữa
A1C và đáy bằng 45◦. Thể tích của khối lăng trụ đã cho bằng √ √ √ 14 7 7 7 √ A 7 7a3. B a3. C a3. D 14 7a3. 3 2
Câu 13. Điểm nào dưới đây thuộc đồ thị của hàm số y = x3 − x + 1? A Điểm M (1; 1). B Điểm Q (1; 3). C Điểm P (1; 2). D Điểm N (1; 0).
Câu 14. Điểm cực tiểu của hàm số y = −x4 + 5x2 − 2 là A y = −2. B y = 0. C x = 0. D x = −2.
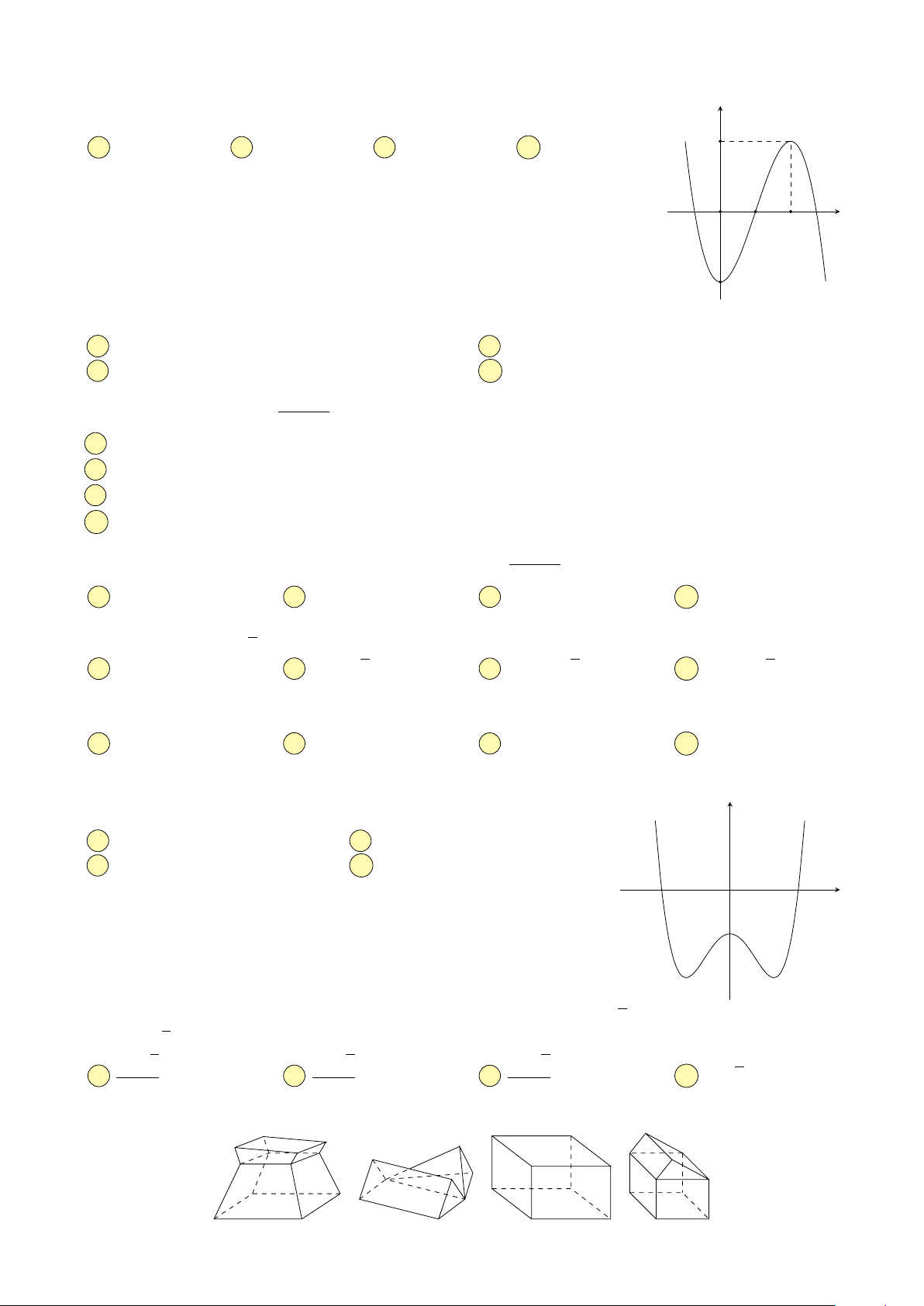
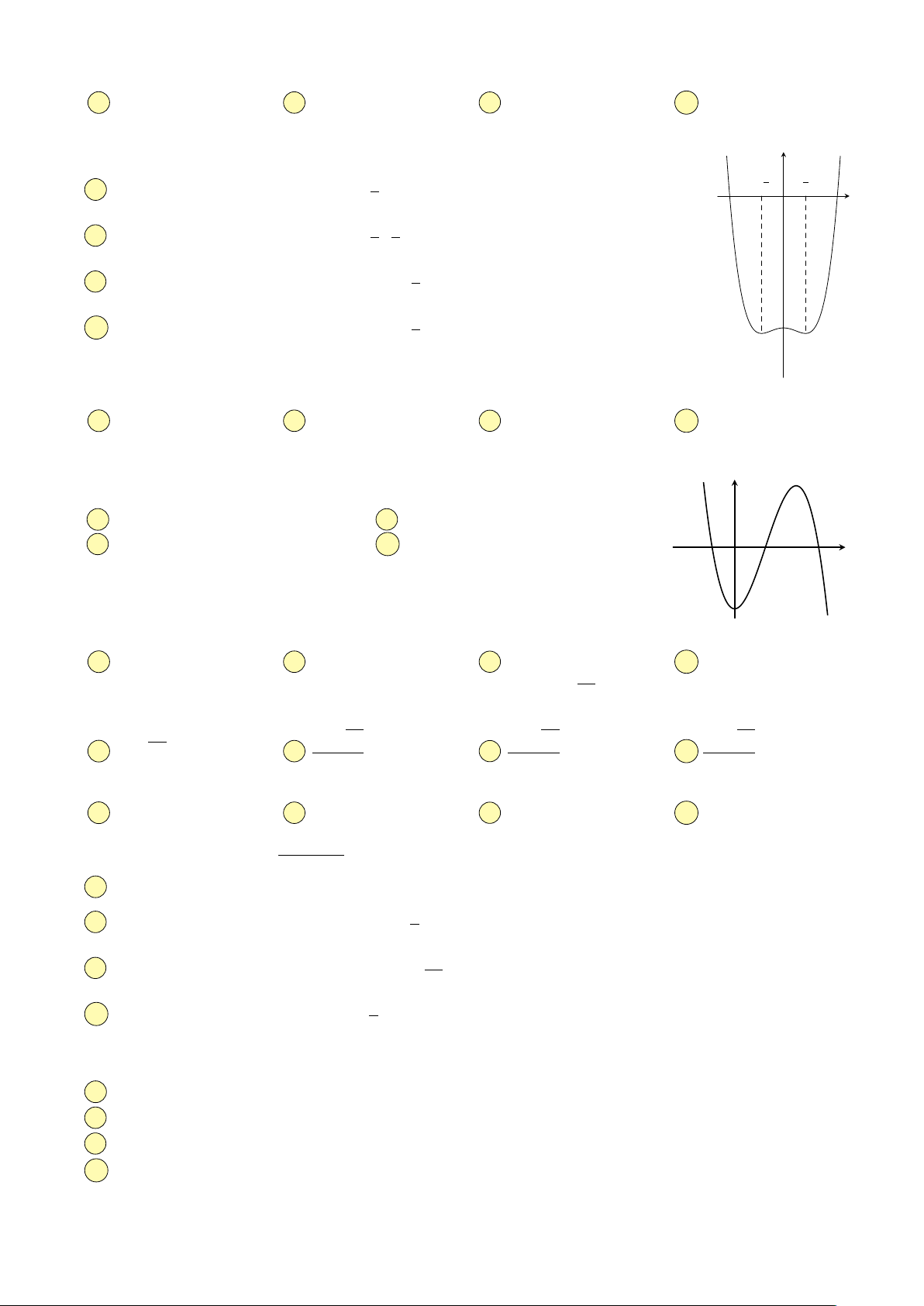
Câu 15. Đồ thị hình bên là đồ thị của hàm số nào dưới đây? y A y = x4 − x2 − 1.
B y = −x4 − 3x2 − 1.
C y = −x4 + 2x2 − 1. D y = x4 + x2 − 1. x O √
Câu 16. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a 10, SA vuông góc với đáy ABCD √
và bằng a 7. Thể tích V của khối chóp S.ABCD là √ √ √ 20 7 5 7 √ 10 7 A a3. B a3. C 10 7a3. D a3. 3 3 3
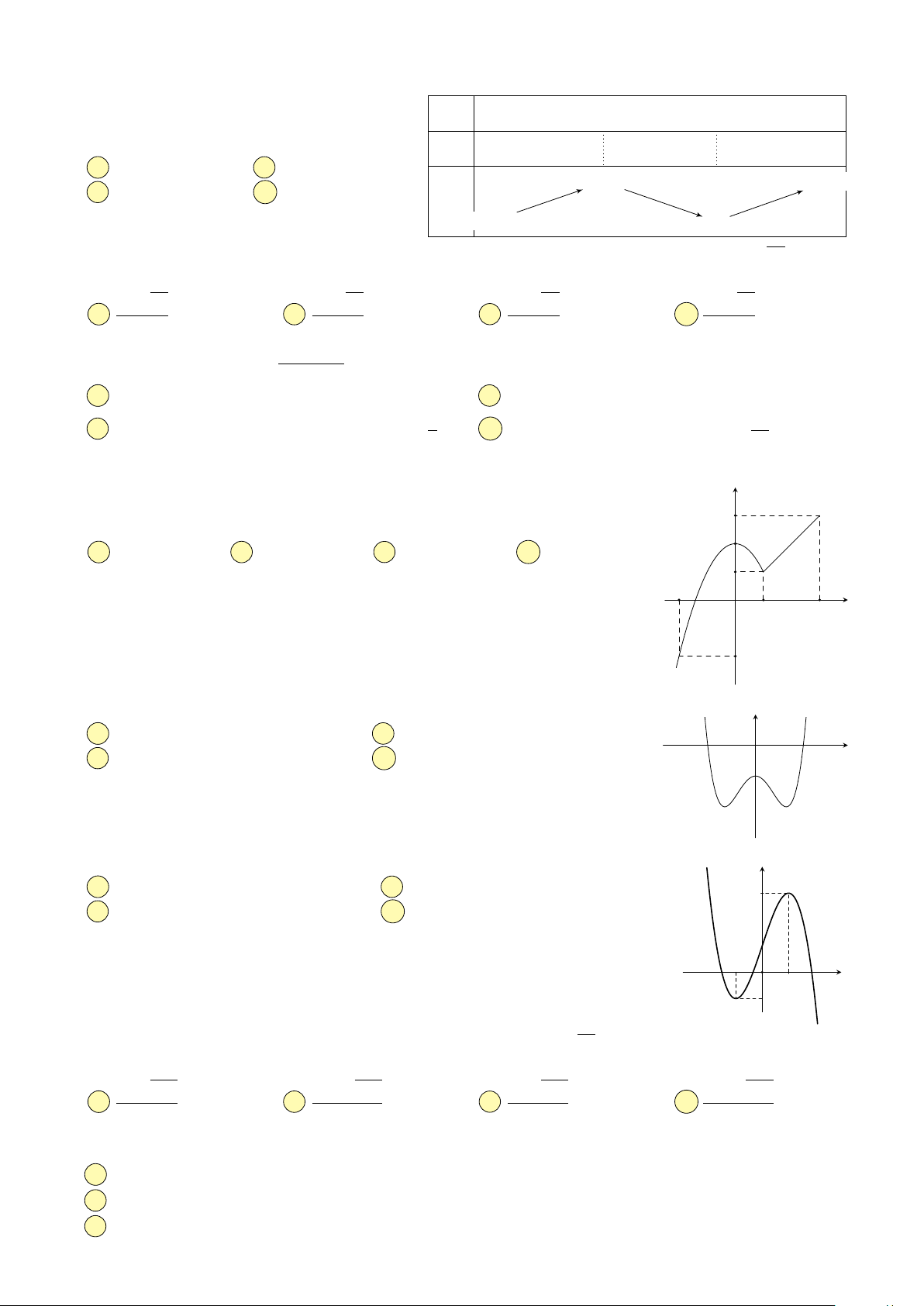
Câu 17. Hình nào dưới đây không phải là hình đa diện? Hình 1 Hình 2 Hình 3 Hình 4 A Hình 4. B Hình 3. C Hình 1. D Hình 2.
Trang 2/4 − Mã đề 101
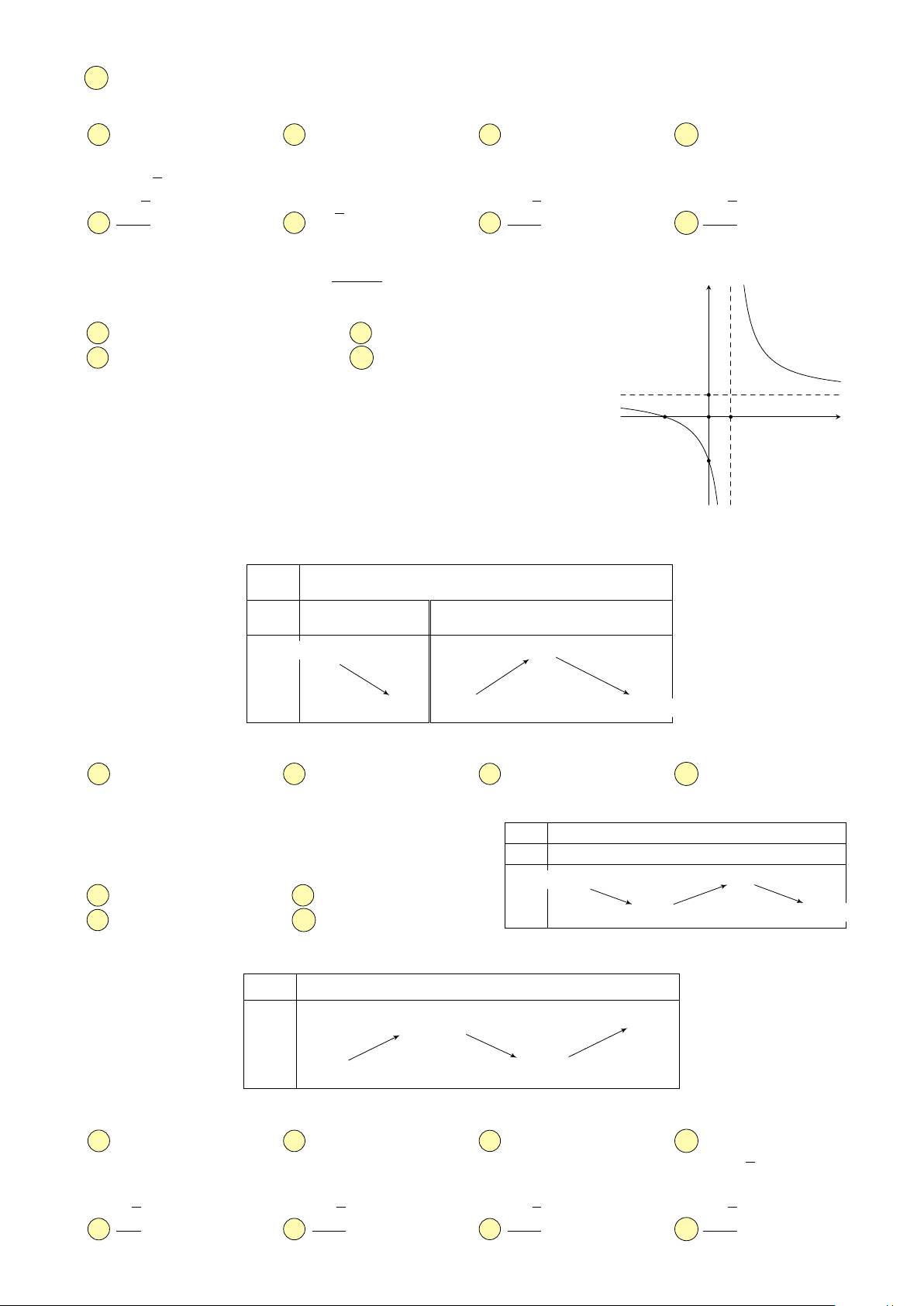
Câu 18. Cho hàm số y = f(x) có đạo hàm trên R, thỏa mãn f(−1) = f(3) = 0 y
và đồ thị hàm số y = f 0(x) có dạng như hình bên. Hàm số y = (f (x))2 đồng biến 3
trên khoảng nào trong các khoảng sau A (4; 6). B (0; 4). C (1; 2). D (−2; 1). −1 O x 1 3 −3 3x + 1
Câu 19. Cho hàm số f(x) =
. Trong các mệnh đề sau mệnh đề nào đúng? −x + 1
A f (x) đồng biến trên (−∞; 1) và (1; +∞).
B f (x) nghịch biến trên (−∞; 1) và (1; +∞).
C f (x) đồng biến trên R.
D f (x) nghịch biến trên R.
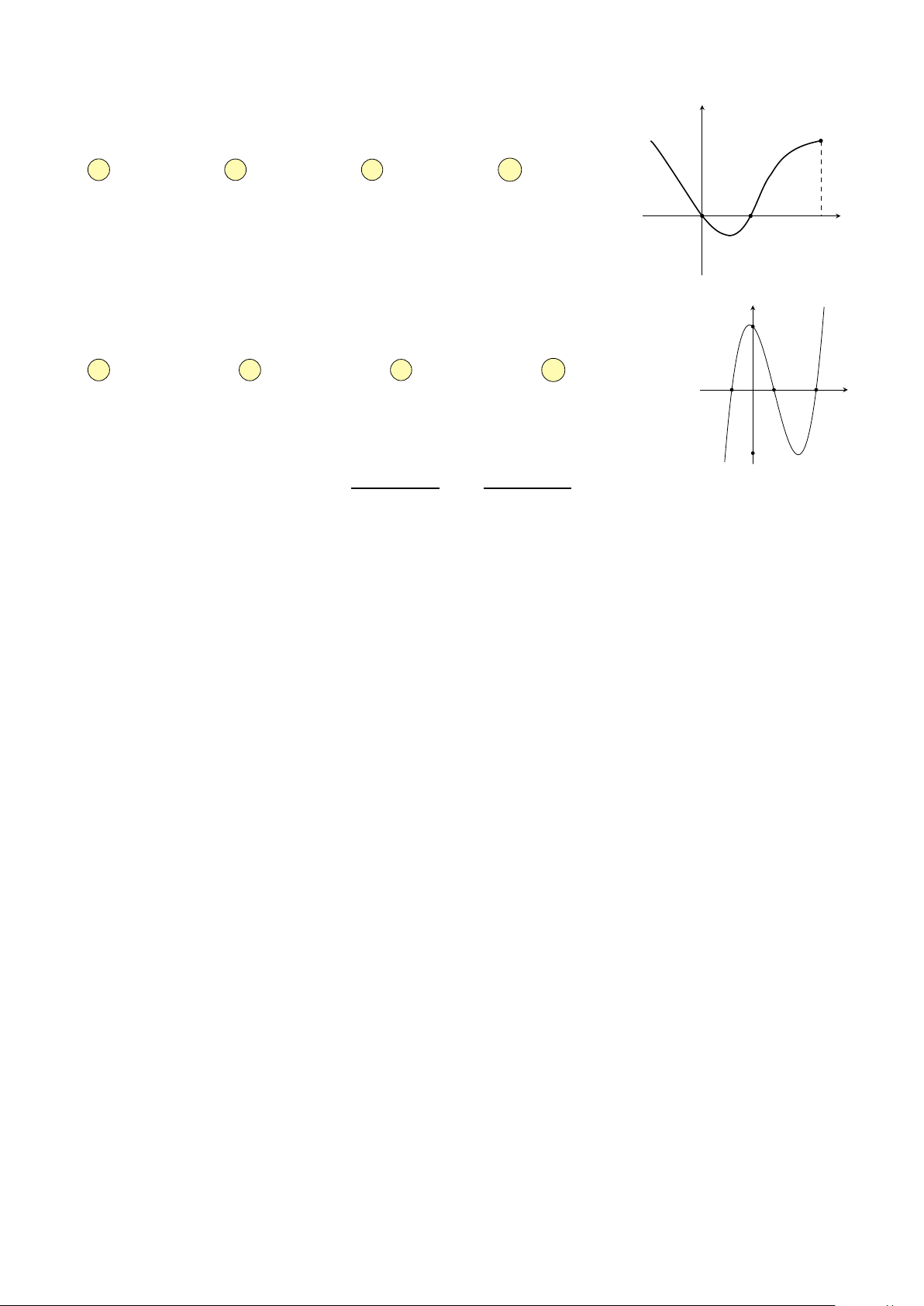
Câu 20. Cho hàm số f(x) liên tục trên đoạn [−2; 3] và có đồ thị như y
hình bên. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số đã 4
cho trên đoạn [−2; 3]. Giá trị của M − m bằng A 4. B 3. C 2. D 1. 3 2 1 x −2 2 3 √
Câu 21. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a 5, góc giữa cạnh bên và mặt đáy bằng
60◦. Thể tích V của khối chóp S.ABCD là √ √ √ 40 30 10 30 20 30 √ A a3. B a3. C a3. D 20 30a3. 3 3 3
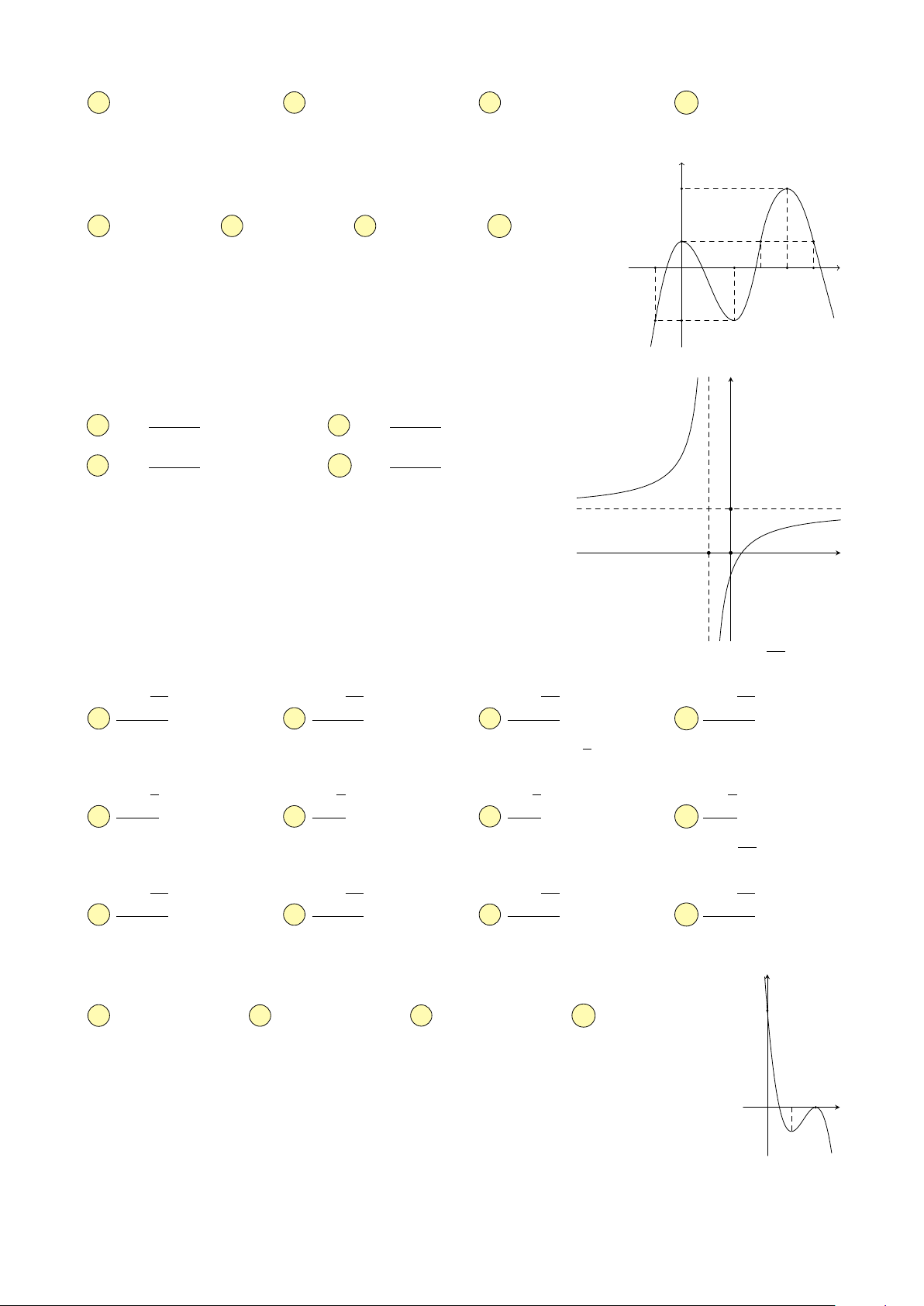
Câu 22. Đường cong trong hình bên là đồ thị của hàm số nào? y A y = x4 − 2x2. B y = x3 − x2. 2 C y = −x3 + 3x. D y = x3 − 3x. 1 −1 x O −2 ax + b
Câu 23. Cho đồ thị hàm số y =
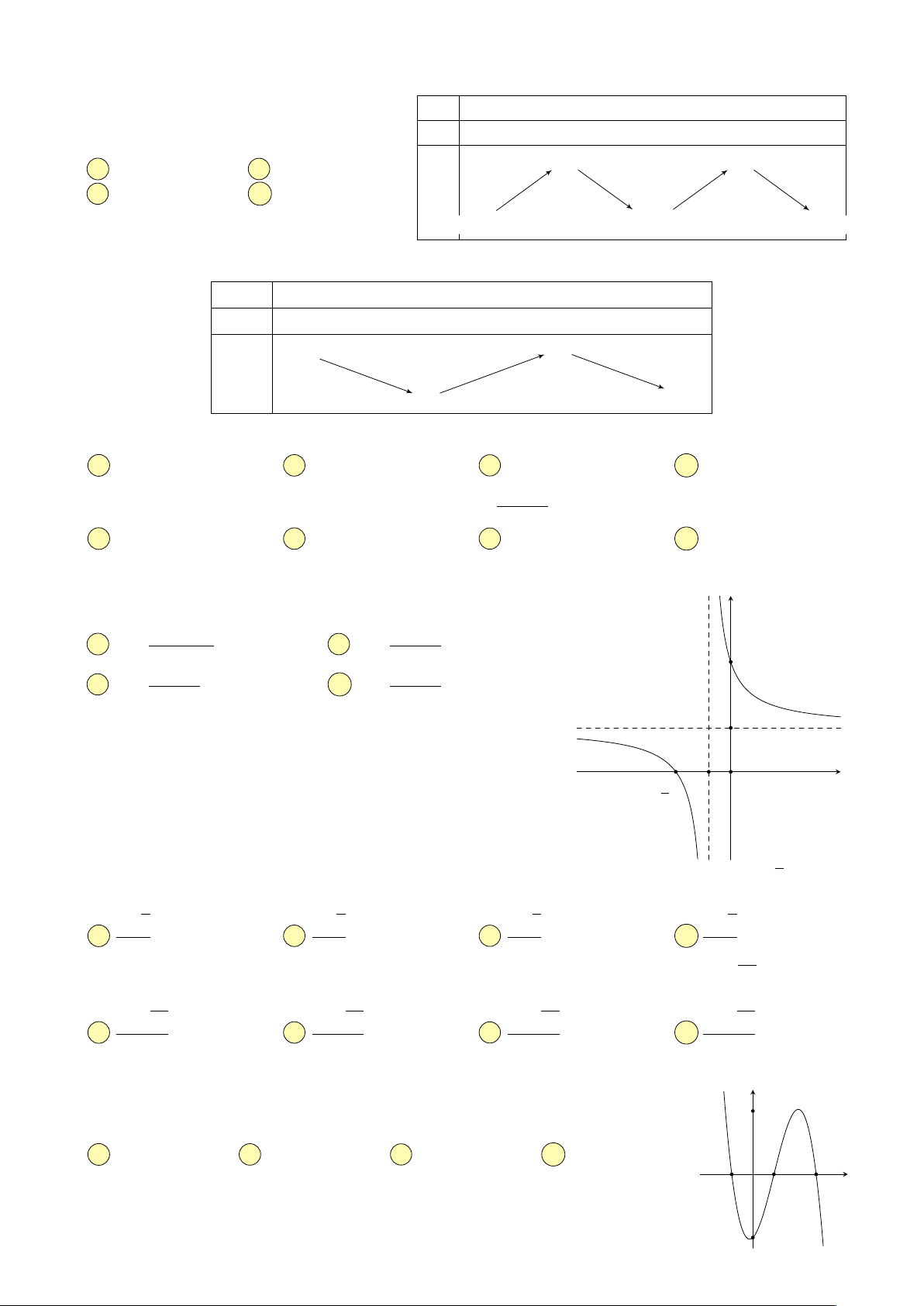
như hình vẽ. Tìm khẳng định y x + 1 đúng A 0 < a < b. B a < b < 0. C 0 < b < a. D b < 0 < a. 1 x −1 O
Trang 3/4 − Mã đề 101
Câu 24. Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn [−2; −2] và đồ y
thị hàm số y = f 0(x) như hình vẽ bên. Khi đó hàm số y = f (x) đạt giá trị lớn
nhất trên đoạn [−2; 2] tại điểm x0 nào dưới đây ? y = f 0(x) A x0 = 2. B x0 = 1. C x0 = −1. D x0 = −2. 2 O x −2 −1 1
Câu 25. Cho hàm số f(x) có bảng biến thiên như hình bên dưới. x −∞ −3 3 +∞ f (− ( 3) +∞ + f (x) −∞ f (3)
Hàm số y = f (4 − x2) + 2023 có bao nhiêu điểm cực đại? A 2. B 3. C 4. D 5. HẾT
Trang 4/4 − Mã đề 101
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT NGUYỄN DU NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn:TOÁN 12
(Đề thi có 4 trang) Thời gian: 45 phút
Học sinh nhớ ghi tên và tô số báo danh, mã đề vào bảng trả lời bên dưới Mã đề thi: 102 HỌ VÀ TÊN Lớp:
Câu 1. Số đường tiệm cận đứng của đồ thị của hàm x − 1 TRƯỜNG: ĐIỂM số y = là x KỲ THI: A 3. B 2. C 0. D 1. MÔN THI: THỜI GIAN:
Câu 2. Số mặt phẳng đối xứng của tứ diện đều là SỐ BÁO DANH MÃ ĐỀ A B C D A 12. B 9. C 4. D 6. 0 0 0 0 0 0 0 0 0 0 1 A B C D
Câu 3. Thể tích của khối lăng trụ có diện tích đáy B 1 1 1 1 1 1 1 1 1 1 2 A B C D ĐỀ 2 2 2 2 2 2 2 2 2 2 3 và chiều cao h là MÃ A B C D À 1 4 3 3 3 3 3 3 3 3 3 3 V 4 A B C D A Bh . B Bh. C Bh . D 3Bh . 4 4 4 4 4 4 4 4 4 4 ANH 5 A B C D 3 3 D 5 5 5 5 5 5 5 5 5 5 O 6 A B C D BÁ
Câu 4. Cho hình chóp S.ABC. Trên các cạnh SA, 6 6 6 6 6 6 6 6 6 6 7 A B C D SỐ 7 7 7 7 7 7 7 7 7 7 8 A B C D
SB, SC lần lượt lấy ba điểm A0, B0, C0 sao cho SA = KÍN 8 8 8 8 8 8 8 8 8 8 9 TÔ A B C D
2SA0, SB = 3SB0 và SC = 4SC0. Gọi V 0 và V lần 9 9 9 9 9 9 9 9 9 9 10 A B C D
lượt là thể tích của khối chóp S.A0B0C0 và S.ABC. Khi A B C D A B C D V 0 11 A B C D 21 A B C D đó tỉ số bằng bao nhiêu? 12 A B C D 22 A B C D V 13 1 1 1 1 A B C D 23 A B C D A . B . C . D . 14 A B C D 24 A B C D 12 24 6 9 15 A B C D 25 A B C D
Câu 5. Cho hàm số f(x) = x3 − 3x2 − 9x + 10. Gọi 16 A B C D 17
M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của A B C D 18 A B C D
hàm số trên đoạn [1; 50]. Giá trị của M + m bằng 19 A B C D A 117043. B 117059. 20 A B C D C −18. D −19.
Câu 6. Cho hàm số y = f(x) có lim f(x) = 1 và lim f(x) = −1. Khẳng định nào sau đây là đúng? x→+∞ x→−∞
A Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
B Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 1 và y = −1.
C Đồ thị hàm số đã cho không có tiệm cận ngang.
D Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 1 và x = −1.
Câu 7. Cho hàm số y = f(x) liên tục trên x −∞ −1 2 4 +∞
R và có bảng xét dấu như hình bên.
Hàm số y = f (x) có bao nhiêu điểm cực trị? f 0(x) + 0 − 0 − 0 + A 1. B 3. C 2. D 0.
Trang 1/4 − Mã đề 102
Câu 8. Cho hàm số y = f(x) có đồ thị như hình vẽ. y
Hàm số y = f (x) đồng biến trên khoảng nào dưới đây? A (−2; 2). B (−∞; 0). C (2; +∞). D (0; 2). 2 O x 1 2 −2
Câu 9. Cho hàm số y = x3 − 3x2 − 1. Mệnh đề nào sau đây đúng?
A Hàm số nghịch biến trên khoảng (−∞; 0).
B Hàm số nghịch biến trên khoảng (1; +∞).
C Hàm số nghịch biến trên khoảng (0; 1).
D Hàm số đồng biến trên khoảng (1; 2). 3x + 1
Câu 10. Cho hàm số y =
. Mệnh đề nào dưới đây đúng? x − 1
A Hàm số luôn luôn nghịch biến trên R \ {1}.
B Hàm số nghịch biến trên các khoảng (−∞; 1) và (1; +∞).
C Hàm số luôn luôn đồng biến trên R \ {1}.
D Hàm số đồng biến trên các khoảng (−∞; 1) và (1; +∞). 2x + 1
Câu 11. Tìm tọa độ tâm đối xứng của đồ thị hàm số y = . x − 1 A (−1; 2). B (1; 2). C (1; −2). D (2; 1). 1
Câu 12. Hàm số y = x4 − 3x2 − 3 đạt cực đại tại 2 √ √ √ A x = 0. B x = 3. C x = ± 3. D x = − 3.
Câu 13. Biết hàm số y = f(x) có y = f0(x) = −(x − 1)2. Hàm số y = f(x) có bao nhiêu điểm cực trị? A 3. B 2. C 0. D 1.
Câu 14. Đồ thị của hàm số nào dưới đây có dạng như đường cong như y hình bên A y = x4 − 2x2 − 1.
B y = −x3 − 3x2 − 1. C y = x3 − 3x2 − 1.
D y = −x4 + 2x2 − 1. x O √
Câu 15. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh a 5, SA vuông góc với đáy ABCD √
và bằng 2a 3. Thể tích V của khối chóp S.ABCD là √ √ √ 10 3 80 3 40 3 √ A a3. B a3. C a3. D 10 3a3. 3 3 3
Câu 16. Cho các hình vẽ sau Hình a Hình b Hình c Hình d
Trang 2/4 − Mã đề 102
Hỏi trong bốn hình trên có bao nhiêu hình đa diện? A 4. B 1. C 2. D 3.
Câu 17. Cho hàm số f(x) liên tục trên đoạn [−1; 5] và có đồ thị như y
hình vẽ bên. Gọi M, m lần lượt là giá trị lớn nhất, nhỏ nhất của hàm số trên 3
đoạn [−1; 5]. Khi đó M − m bằng A 1. B 5. C 6. D 4. 1 −1 2 x 4 5 −2
Câu 18. Đồ thị hình bên là của hàm số nào trong bốn hàm số y được cho dưới đây? 2x + 1 2x − 1 A y = . B y = . x − 1 x + 1 1 − 2x 1 − 2x C y = . D y = . x + 1 x − 1 2 x −1 O √
Câu 19. Cho khối chóp S.ABC có SA vuông góc (ABC) và đáy là tam giác đều cạnh a 13, góc giữa
(SBC) và mặt đáy (ABC) bằng 60◦. Thể tích V của khối chóp S.ABC là √ √ √ √ 39 39 39 39 13 39 39 39 A a3. B a3. C a3. D a3. 16 32 8 8 √
Câu 20. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a 3, góc giữa cạnh bên và mặt đáy bằng
60◦. Thể tích V của khối chóp S.ABCD là √ √ √ √ 12 2 9 2 3 2 6 2 A a3. B a3. C a3. D a3. 5 2 2 5√
Câu 21. Cho lăng trụ đứng ABC.A1B1C1 có đáy là tam giác vuông cân tại B, BC = a 19, biết góc giữa
A1B và đáy bằng 45◦. Thể tích của khối lăng trụ đã cho bằng √ √ √ √ 95 19 95 19 19 19 19 19 A a3. B a3. C a3. D a3. 8 4 6 2
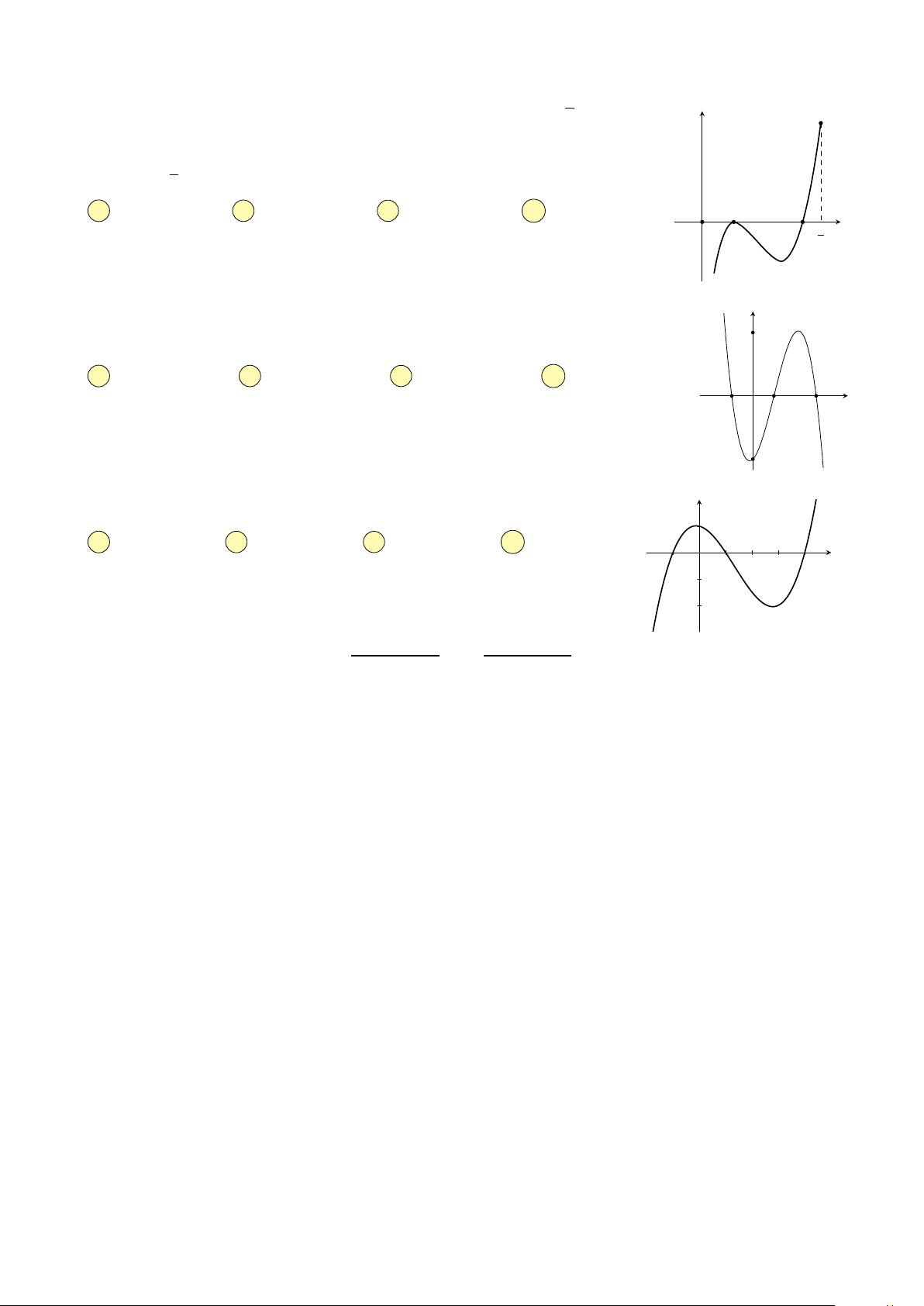
Câu 22. Cho đồ thị hàm số y = −2x3 + bx2 + cx + d như hình vẽ bên. Tổng b + c + d y bằng A 5. B 1. C 7. D 3. 4 1 2 x O
Trang 3/4 − Mã đề 102 7
Câu 23. Cho hàm số y = f(x) có đạo hàm liên tục trên đoạn 0; và đồ thị y 2
hàm số y = f 0(x) như hình vẽ bên. Khi đó hàm số y = f (x) đạt giá trị nhỏ nhất 7 trên đoạn 0; tại điểm x y = f 0(x) 0 nào dưới đây ? 2 A x 1 3 0 = 3. B x0 = 2. C x0 = 0. D x0 = 1. O 7 x 2
Câu 24. Cho hàm số y = f(x) có đạo hàm trên R, thỏa mãn f(−1) = f(3) = 0 y
và đồ thị hàm số y = f 0(x) có dạng như hình bên. Hàm số y = (f (x))2 nghịch biến 3
trên khoảng nào trong các khoảng sau A (1; 2). B (−2; 1). C (0; 4). D (−2; 2). −1 O x 1 3 −3
Câu 25. Cho hàm số y = f(x). Hàm số y = f0(x) có đồ thị như hình vẽ y
bên. Hàm số y = f (x2) + 2023 có bao nhiêu điểm cực đại? A 4. B 5. C 2. D 3. −1 1 x O 4 HẾT
Trang 4/4 − Mã đề 102
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT NGUYỄN DU NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn:TOÁN 12
(Đề thi có 4 trang) Thời gian: 45 phút
Học sinh nhớ ghi tên và tô số báo danh, mã đề vào bảng trả lời bên dưới Mã đề thi: 103
Câu 1. Thể tích khối lập phương có cạnh 2a bằng A a3. B 6a3. C 8a3. D 2a3. HỌ VÀ TÊN Lớp:
Câu 2. Phương trình đường tiệm cận ngang và tiệm TRƯỜNG: ĐIỂM 3x + 2 KỲ THI:
cận đứng của đồ thị hàm số y = là x − 1 MÔN THI: A y = 1, x = 3. B y = −2, x = 1. THỜI GIAN: SỐ BÁO DANH MÃ ĐỀ C y = 3, x = 1. D y = 3, x = −1. A B C D Câu 3. 0 0 0 0 0 0 0 0 0 0 1 A B C D
Hàm số nào dưới đây có 3 điểm cực trị? 1 1 1 1 1 1 1 1 1 1 2 A B C D ĐỀ A y = x3 + 4. 2 2 2 2 2 2 2 2 2 2 3 MÃ A B C D À
B y = −x4 + 3x2 − 1. 3 3 3 3 3 3 3 3 3 3 V 4 A B C D 4 4 4 4 4 4 4 4 4 4 ANH 5 A B C D C y = 2x4 + x2 + 2. D 5 5 5 5 5 5 5 5 5 5 O 6 A B C D BÁ
D y = x3 + 3x2 + 3x − 2. 6 6 6 6 6 6 6 6 6 6 7 A B C D SỐ 7 7 7 7 7 7 7 7 7 7 8 A B C D KÍN
Câu 4. Cho hình chóp S.ABC có A0, B0 lần lượt là 8 8 8 8 8 8 8 8 8 8 9 TÔ A B C D
trung điểm của SA, SB. Gọi V 9 9 9 9 9 9 9 9 9 9 10 A B C D
1, V2 lần lượt là thể tích A B C D A B C D V
của khối chóp S.A0B0C và S.ABC. Tỉ số 1 bằng 11 A B C D 21 A B C D V2 12 A B C D 22 A B C D 1 1 1 1 13 A . B . C . D . A B C D 23 A B C D 4 3 2 8 14 A B C D 24 A B C D 15 A B C D 25 A B C D
Câu 5. Hình lập phương có bao nhiêu mặt phẳng 16 A B C D đối xứng? 17 A B C D 18 A 12. B 8. C 9. D 6. A B C D 19 A B C D 2x − 6 20 A B C D
Câu 6. Tâm đối xứng của đồ thị hàm số y = x + 2 là điểm A I(−3; 2). B I(2; −2). C I(3; −2). D I(−2; 2).
Câu 7. Hình nào dưới đây không phải là hình đa diện? Hình 1 Hình 2 Hình 3 Hình 4 A Hình 4. B Hình 1. C Hình 2. D Hình 3.
Câu 8. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = x3 − 3x2 − 9x + 4 trên
đoạn [−24; 24]. Giá trị của M + m bằng A 11861. B −15323. C −14. D −3448.
Trang 1/4 − Mã đề 103
Câu 9. Cho hàm số y = f(x) có bảng biến x −∞ 2 3 +∞
thiên như hình bên. Hàm số đạt cực tiểu tại điểm y0 + 0 − 0 + A x = 3. B x = −5. −5 − +∞ + C x = 2. D x = 1. y −∞ 1 √
Câu 10. Cho khối chóp S.ABC có SA vuông góc (ABC) và đáy là tam giác đều cạnh a 19, góc giữa
(SBC) và mặt đáy (ABC) bằng 60◦. Thể tích V của khối chóp S.ABC là √ √ √ √ 19 57 57 57 19 57 19 57 A a3. B a3. C a3. D a3. 16 8 4 8 −3x − 1
Câu 11. Cho hàm số y =
. Khẳng định nào sau đây là đúng? −9x − 6
A Hàm số nghịch biến trên R.
B Hàm số đồng biến trên R. 2 25
C Hàm số nghịch biến trên khoảng −∞; − .
D Hàm số đồng biến trên khoảng ; +∞ . 3 3
Câu 12. Cho hàm số f(x) liên tục trên đoạn [−2; 3] và có đồ thị như hình vẽ. y
Gọi M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đã cho trên 3
[−2; 3]. Giá trị M + m bằng 2 A 1. B 4. C 2. D 5. 1 x −2 O 1 3 −2
Câu 13. Đồ thị hình vẽ bên là đồ thị của hàm số nào dưới đây? y A y = −x4 + x2 − 1. B y = x4 + x2 − 1. C y = x4 − x2 − 1.
D y = −x4 − x2 − 1. x O
Câu 14. Đường cong ở hình vẽ bên là của đồ thị hàm số nào dưới đây? y A y = x3 − 3x + 1. B y = −x3 + 3x − 1. 3 C y = −x3 + 3x + 1. D y = x3 − 3x2 + 1. −1 O x 1 −1 √
Câu 15. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a 19, góc giữa cạnh bên và mặt đáy bằng
60◦. Thể tích V của khối chóp S.ABCD là √ √ √ √ 19 114 133 114 19 114 133 114 A a3. B a3. C a3. D a3. 6 18 2 36
Câu 16. Cho hàm số y = f(x) có lim f(x) = 2 và lim f(x) = −2. Khẳng định nào sau đây đúng? x→+∞ x→−∞
A Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng x = 2 và x = −2.
B Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng y = 2 và y = −2.
C Đồ thị hàm số đã cho có đúng một tiệm cận ngang.
Trang 2/4 − Mã đề 103
D Đồ thị hàm số đã cho không có tiệm cận ngang.
Câu 17. Hàm số y = x4 − 2x2 nghịch biến trên khoảng nào sau đây? A (−1; 1). B (0; 1). C (1; +∞). D (−1; 0).
Câu 18. Cho khối chóp S.ABCD có đáy ABCD là hình vuông cạnh 2a, SA vuông góc với đáy ABCD √
và bằng a 3. Thể tích V của khối chóp S.ABCD là √ √ √ 4 3 √ 8 3 4 3 A a3. B 4 3a3. C a3. D a3. 3 9 9 ax − b
Câu 19. Cho đồ thị hàm số y =
như hình vẽ bên. Tìm khẳng y x − 1 định đúng A b < 0 < a. B a < b < 0. C a < 0, b < 0. D 0 < b < a. 1 x −2 O 1 −2
Câu 20. Cho hàm số f(x) xác định trên R \ {0}, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau x −∞ 0 1 +∞ y0 − + 0 − +∞ + 2 y −1 −∞ −∞
Hàm số đã cho có bao nhiêu điểm cực trị? A 3. B 2. C 1. D 0.
Câu 21. Cho hàm số y = f(x) có bảng biến thiên như x −∞ 0 2 +∞
hình bên. Hàm số y = f (x) đồng biến trên khoảng nào y0 − 0 + 0 − trong các khoảng sau? +∞ + 2 A (0; 3). B (2; +∞). y −6 − −∞ C (0; 2). D (−∞; 0).
Câu 22. Cho hàm số f(x) có bảng biến thiên như hình bên dưới. x −∞ −3 3 +∞ f (− ( 3) +∞ + f (x) −∞ f (3)
Hàm số y = f (4 − x2) + 2023 có bao nhiêu điểm cực tiểu? A 5. B 3. C 4. D 2. √
Câu 23. Cho lăng trụ đứng ABC.A1B1C1 có đáy là tam giác vuông cân tại B, BC = a 2, biết góc giữa
A1C và đáy bằng 30◦. Thể tích của khối lăng trụ đã cho bằng √ √ √ √ 3 4 3 2 3 2 3 A a3. B a3. C a3. D a3. 3 3 9 3
Trang 3/4 − Mã đề 103
Câu 24. Cho hàm số y = f(x) có đạo hàm liên tục trên [0; 5] và đồ thị y
hàm số y = f 0(x) như hình vẽ bên. Khi đó hàm số y = f (x) đạt giá trị nhỏ
nhất trên đoạn [0; 5] tại điểm x0 nào dưới đây ? A x0 = 1. B x0 = 2. C x0 = 5. D x0 = 0. y = f 0(x) O 2 x 5
Câu 25. Cho hàm số y = f(x) có đạo hàm trên R, thỏa mãn f(−1) = f(3) = 0 y
và đồ thị hàm số y = f 0(x) có dạng như hình bên. Hàm số y = (f (x))2 đồng biến 3
trên khoảng nào trong các khoảng sau A (0; 4). B (1; 2). C (−2; 1). D (4; 6). −1 O x 1 3 −3 HẾT
Trang 4/4 − Mã đề 103
SỞ GIÁO DỤC VÀ ĐÀO TẠO
THÀNH PHỐ HỒ CHÍ MINH
KIỂM TRA GIỮA HỌC KỲ I
TRƯỜNG THPT NGUYỄN DU NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn:TOÁN 12
(Đề thi có 4 trang) Thời gian: 45 phút
Học sinh nhớ ghi tên và tô số báo danh, mã đề vào bảng trả lời bên dưới Mã đề thi: 104 3x − 1
Câu 1. Cho hàm số y = . Gọi M , m lần lượt x − 3
là giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên đoạn
[−40; 2]. Giá trị của M + m bằng HỌ VÀ TÊN Lớp: 14 94 94 14 A . B . C − . D − . TRƯỜNG: ĐIỂM 3 43 43 3 KỲ THI: MÔN THI:
Câu 2. Điểm nào dưới đây thuộc đồ thị của hàm số THỜI GIAN: y = 2 + 3x2 − x3 SỐ BÁO DANH MÃ ĐỀ A I(2; 3). B I(0; 1). A B C D C I(−1; 5). D I(1; 4). 0 0 0 0 0 0 0 0 0 0 1 A B C D 1 1 1 1 1 1 1 1 1 1 2 A B C D ĐỀ 2 2 2 2 2 2 2 2 2 2 3 MÃ A B C D À Câu 3. 3 3 3 3 3 3 3 3 3 3 V 4 A B C D Cho hàm số f (x) y 4 4 4 4 4 4 4 4 4 4 ANH 5 A B C D
liên tục trên đoạn [−1; 3] D 3 5 5 5 5 5 5 5 5 5 5 O 6 A B C D
và có đồ thị như hình vẽ. BÁ 6 6 6 6 6 6 6 6 6 6 7 A B C D SỐ
Gọi M và m lần lượt là 7 7 7 7 7 7 7 7 7 7 8 A B C D KÍN 1 8 8 8 8 8 8 8 8 8 8 9
giá trị lớn nhất, giá trị nhỏ TÔ A B C D 9 9 9 9 9 9 9 9 9 9 10 A B C D
nhất của hàm số đã cho 2 A B C D A B C D x
trên [−1; 3]. Giá trị M − m −1O 3 11 A B C D 21 A B C D 12 bằng A B C D 22 A B C D −2 13 A B C D 23 A B C D A 0. B 4. 14 A B C D 24 A B C D C 5. D 1. 15 A B C D 25 A B C D 16 A B C D
Câu 4. Cho khối chóp S.ABCD có đáy ABCD là 17 A B C D
hình vuông cạnh 3a, SA vuông góc với đáy ABCD và 18 √ A B C D 3 19 bằng 2a
. Thể tích V của khối chóp S.ABCD là A B C D √ √ 20 A B C D A 8 3a3. B 18 3a3. √ √ C 6 3a3. D 4 3a3.
Câu 5. Số mặt phẳng đối xứng của tứ diện đều là A 9. B 4. C 12. D 6.
Câu 6. Cho hình chóp S.ABC. Trên các cạnh SA, SB, SC lần lượt lấy ba điểm A0, B0, C0 sao cho
SA = 2SA0, SB = 3SB0 và SC = 4SC0. Gọi V 0 và V lần lượt là thể tích của khối chóp S.A0B0C0 và V 0 S.ABC. Khi đó tỉ số bằng bao nhiêu? V 1 1 1 1 A . B . C . D . 12 9 6 24
Câu 7. Cho các hình vẽ sau Hình a Hình b Hình c Hình d
Trang 1/4 − Mã đề 104
Hỏi trong bốn hình trên có bao nhiêu hình đa diện? A 1. B 3. C 4. D 2.
Câu 8. Cho hàm số có đồ thị như hình bên. Khẳng định nào sau đây là đúng? y 1 1 1 −
A Hàm số đồng biến trên khoảng − ; 0 . 2 2 2 x O 1 1
B Hàm số đồng biến trên khoảng − ; . 2 2 3
C Hàm số đồng biến trên khoảng −∞; − . 2 1
D Hàm số đồng biến trên khoảng −∞; − . 2
Câu 9. Cho khối lập phương có thể tích bằng 343 (đvtt). Hỏi cạnh của hình lập phương bằng A 8. B 5. C 6. D 7.
Câu 10. Đồ thị của hàm số nào dưới đây có dạng như đường cong trong hình y bên? A y = x3 − 3x2 − 2.
B y = −x3 + 3x2 − 2. C y = x4 − 2x2 − 2.
D y = −x4 + 2x2 − 2. x O
Câu 11. Đồ thị hàm số nào sau đây có 3 điểm cực trị? A y = x4 − 2x2 − 1. B y = x4 + 2x2 − 1.
C y = −x4 − 2x2 − 1. D y = 2x4 + 4x2 + 1. √
Câu 12. Cho khối chóp tứ giác đều S.ABCD có cạnh đáy bằng a 14, góc giữa cạnh bên và mặt đáy bằng
60◦. Thể tích V của khối chóp S.ABCD là √ √ √ √ 14 21 28 21 14 21 A 14 21a3. B a3. C a3. D a3. 9 9 3
Câu 13. Hàm số y = x3 − 3x2 + 3x − 4 có bao nhiêu cực trị? A 0. B 1. C 2. D 3. −7x − 6
Câu 14. Cho hàm số y =
. Khẳng định nào sau đây là sai? 2 − 3x
A Hàm số nghịch biến trên R. 2
B Hàm số nghịch biến trên khoảng −∞; . 3 13
C Hàm số nghịch biến trên khoảng −∞; − . 3 2
D Hàm số nghịch biến trên khoảng ; +∞ . 3
Câu 15. Cho hàm số y = f(x) có lim f(x) = −∞ và lim f(x) = 2. Mệnh đề nào sau đây đúng? x→3+ x→3−
A Đường thẳng y = 2 là tiệm cận ngang của đồ thị hàm số y = f (x).
B Đường thẳng x = 3 không phải là tiệm cận của đồ thị hàm số y = f (x).
C Đường thẳng x = 3 là tiệm cận đứng của đồ thị hàm số y = f (x).
D Đồ thị hàm số y = f (x) không có tiệm cận đứng.
Trang 2/4 − Mã đề 104
Câu 16. Cho hàm số y = f(x) có bảng x −∞ −2 0 2 +∞
biến thiên như sau. Hàm số y = f (x) đồng y0 + 0 − 0 + 0 −
biến trên khoảng nào dưới đây? 3 3 A (−∞; −2). B (−2; 0). C (0; +∞). D (−∞; 3). y −∞ −1 − −∞
Câu 17. Cho hàm số y = f(x) có bảng biến thiên như hình vẽ sau x −∞ 0 2 +∞ y0 − 0 + 0 − +∞ + 5 y 1 −∞
Hàm số y = f (x) đạt cực tiểu tại điểm nào trong các điểm sau? A x = 5. B x = 0. C x = 1. D x = 2. 2x − 1
Câu 18. Tìm số đường tiệm cận của đồ thị hàm số y = . x2 + 1 A 1. B 0. C 2. D 3.
Câu 19. Đồ thị hình bên là của hàm số nào trong bốn hàm số y được cho dưới đây? −2x + 5 2x + 1 A y = . B y = . −x − 1 x + 1 2x + 3 2x + 5 5 C y = . D y = . x + 1 x + 1 2 x 5 −1 O − 2 √
Câu 20. Cho khối chóp S.ABC có SA vuông góc (ABC) và đáy là tam giác đều cạnh a 6, góc giữa
(SBC) và mặt đáy (ABC) bằng 30◦. Thể tích V của khối chóp S.ABC là √ √ √ √ 9 2 9 2 9 2 3 2 A a3. B a3. C a3. D a3. 40 4 20 4√
Câu 21. Cho lăng trụ đứng ABC.A1B1C1 có đáy là tam giác vuông cân tại B, BC = a 13, biết góc giữa
A1B và đáy bằng 30◦. Thể tích của khối lăng trụ đã cho bằng √ √ √ √ 13 39 65 39 13 39 65 39 A a3. B a3. C a3. D a3. 6 24 18 12
Câu 22. Cho hàm số y = f(x) có đạo hàm trên R, thỏa mãn f(−1) = f(3) = 0 y
và đồ thị hàm số y = f 0(x) có dạng như hình bên. Hàm số y = (f (x))2 nghịch biến 3
trên khoảng nào trong các khoảng sau A (1; 2). B (−2; 1). C (0; 4). D (−2; 2). −1 O x 1 3 −3
Trang 3/4 − Mã đề 104
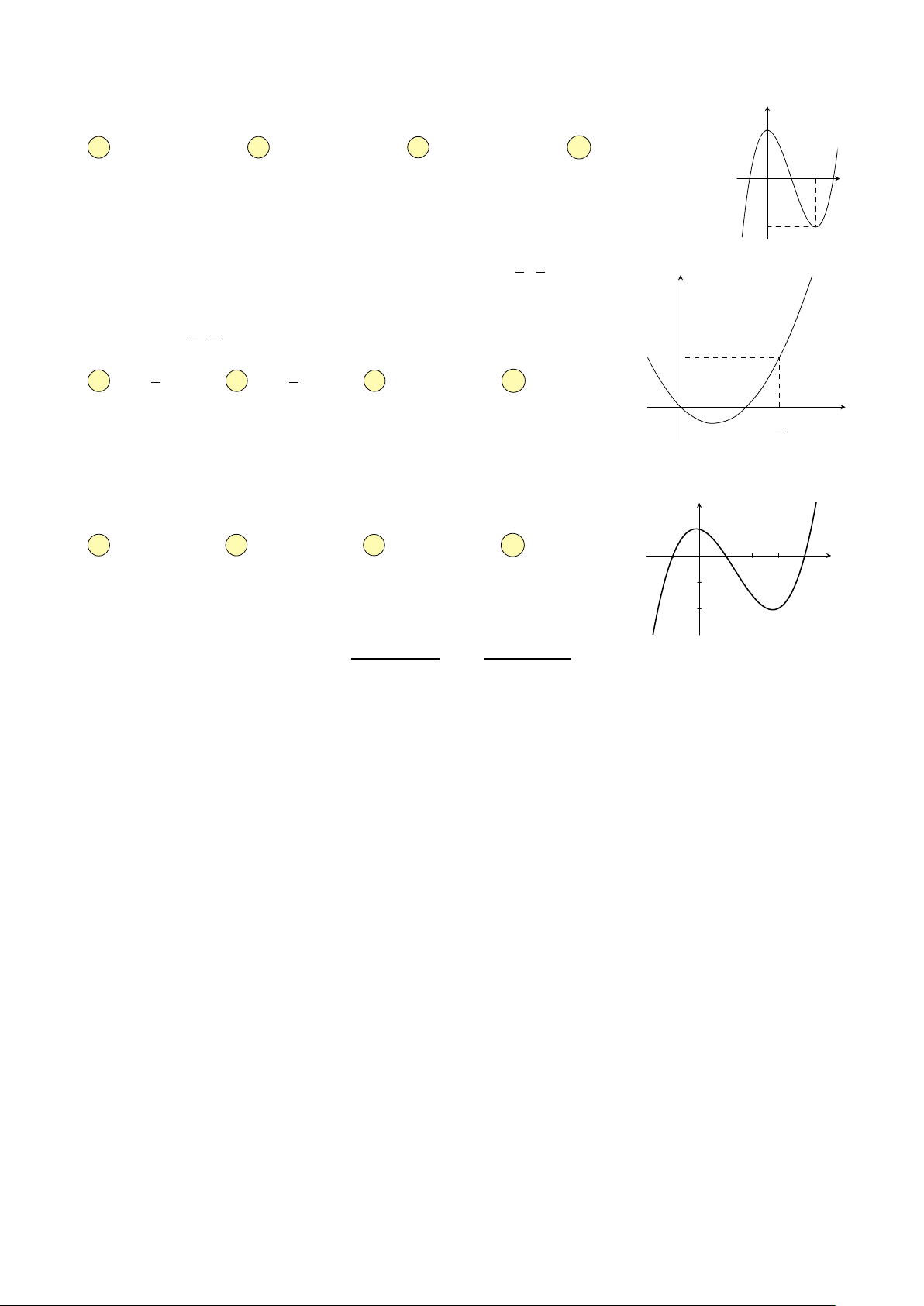
Câu 23. Cho đồ thị hàm số y = ax3 − 3x2 + cx + d như hình vẽ bên. Tổng a + c + d y bằng 2 A 3. B −3. C 0. D 2. 2 x O 1 −2 1 3
Câu 24. Cho hàm số y = f(x) có đạo hàm liên tục trên ; và đồ thị y 2 2
hàm số y = f 0(x) như hình vẽ bên. Khi đó hàm số y = f (x) đạt giá trị nhỏ y = f 0(x) 1 3 nhất trên đoạn ;
tại điểm x0 nào dưới đây ? 2 2 3 1 A x = . B x = . C x = 1. D x = 0. 2 2 x O 1 3 2
Câu 25. Cho hàm số y = f(x). Hàm số y = f0(x) có đồ thị như hình vẽ y
bên. Hàm số y = f (x2) + 2023 có bao nhiêu điểm cực tiểu? A 5. B 4. C 3. D 2. −1 1 x O 4 HẾT
Trang 4/4 − Mã đề 104 HỌ VÀ TÊN Lớp: TRƯỜNG: ĐIỂM KỲ THI: MÔN THI: THỜI GIAN: SỐ BÁO DANH MÃ ĐỀ A B C D 0 0 0 0 0 0 0 0 0 0 1 A B C D 1 1 1 1 1 1 1 1 1 1 2 A B C D ĐỀ 2 2 2 2 2 2 2 2 2 2 3 MÃ A B C D À 3 3 3 3 3 3 3 3 3 3 V 4 A B C D 4 4 4 4 4 4 4 4 4 4 ANH 5 A B C D D 5 5 5 5 5 5 5 5 5 5 O 6 A B C D BÁ 6 6 6 6 6 6 6 6 6 6 7 A B C D SỐ 7 7 7 7 7 7 7 7 7 7 8 A B C D KÍN 8 8 8 8 8 8 8 8 8 8 9 TÔ A B C D 9 9 9 9 9 9 9 9 9 9 10 A B C D A B C D A B C D 11 A B C D 21 A B C D 12 A B C D 22 A B C D 13 A B C D 23 A B C D 14 A B C D 24 A B C D 15 A B C D 25 A B C D 16 A B C D 17 A B C D 18 A B C D 19 A B C D 20 A B C D HỌ VÀ TÊN Lớp: TRƯỜNG: ĐIỂM KỲ THI: MÔN THI: THỜI GIAN: SỐ BÁO DANH MÃ ĐỀ A B C D 0 0 0 0 0 0 0 0 0 0 1 A B C D 1 1 1 1 1 1 1 1 1 1 2 A B C D ĐỀ 2 2 2 2 2 2 2 2 2 2 3 MÃ A B C D À 3 3 3 3 3 3 3 3 3 3 V 4 A B C D 4 4 4 4 4 4 4 4 4 4 ANH 5 A B C D D 5 5 5 5 5 5 5 5 5 5 O 6 A B C D BÁ 6 6 6 6 6 6 6 6 6 6 7 A B C D SỐ 7 7 7 7 7 7 7 7 7 7 8 A B C D KÍN 8 8 8 8 8 8 8 8 8 8 9 TÔ A B C D 9 9 9 9 9 9 9 9 9 9 10 A B C D A B C D A B C D 11 A B C D 21 A B C D 12 A B C D 22 A B C D 13 A B C D 23 A B C D 14 A B C D 24 A B C D 15 A B C D 25 A B C D 16 A B C D 17 A B C D 18 A B C D 19 A B C D 20 A B C D HỌ VÀ TÊN Lớp: TRƯỜNG: ĐIỂM KỲ THI: MÔN THI: THỜI GIAN: SỐ BÁO DANH MÃ ĐỀ A B C D 0 0 0 0 0 0 0 0 0 0 1 A B C D 1 1 1 1 1 1 1 1 1 1 2 A B C D ĐỀ 2 2 2 2 2 2 2 2 2 2 3 MÃ A B C D À 3 3 3 3 3 3 3 3 3 3 V 4 A B C D 4 4 4 4 4 4 4 4 4 4 ANH 5 A B C D D 5 5 5 5 5 5 5 5 5 5 O 6 A B C D BÁ 6 6 6 6 6 6 6 6 6 6 7 A B C D SỐ 7 7 7 7 7 7 7 7 7 7 8 A B C D KÍN 8 8 8 8 8 8 8 8 8 8 9 TÔ A B C D 9 9 9 9 9 9 9 9 9 9 10 A B C D A B C D A B C D 11 A B C D 21 A B C D 12 A B C D 22 A B C D 13 A B C D 23 A B C D 14 A B C D 24 A B C D 15 A B C D 25 A B C D 16 A B C D 17 A B C D 18 A B C D 19 A B C D 20 A B C D HỌ VÀ TÊN Lớp: TRƯỜNG: ĐIỂM KỲ THI: MÔN THI: THỜI GIAN: SỐ BÁO DANH MÃ ĐỀ A B C D 0 0 0 0 0 0 0 0 0 0 1 A B C D 1 1 1 1 1 1 1 1 1 1 2 A B C D ĐỀ 2 2 2 2 2 2 2 2 2 2 3 MÃ A B C D À 3 3 3 3 3 3 3 3 3 3 V 4 A B C D 4 4 4 4 4 4 4 4 4 4 ANH 5 A B C D D 5 5 5 5 5 5 5 5 5 5 O 6 A B C D BÁ 6 6 6 6 6 6 6 6 6 6 7 A B C D SỐ 7 7 7 7 7 7 7 7 7 7 8 A B C D KÍN 8 8 8 8 8 8 8 8 8 8 9 TÔ A B C D 9 9 9 9 9 9 9 9 9 9 10 A B C D A B C D A B C D 11 A B C D 21 A B C D 12 A B C D 22 A B C D 13 A B C D 23 A B C D 14 A B C D 24 A B C D 15 A B C D 25 A B C D 16 A B C D 17 A B C D 18 A B C D 19 A B C D 20 A B C D
Document Outline
- ghkik12_2410202316151
- 101_2410202316151
- 102_2410202316151
- 103_2410202316151
- 104_2410202316151