Đề giữa học kỳ 1 Toán 9 năm 2024 – 2025 phòng GD&ĐT Xuân Trường – Nam Định

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG GIỮA HỌC KỲ I HUYỆN XUÂN TRƯỜNG Năm học 2024 - 2025 ******* Môn: Toán lớp 9
Thời gian làm bài: 120 phút ( Không kể thời gian giao đề)
Họ và tên thí sinh: ............................................ Số báo danh: ……………………..
Giám thị: ......................................................................................................................................
Phần I. Trắc nghiệm (3,0 điểm)
1. Trắc nghiệm 4 phương án lựa chọn (2,0 điểm) Từ câu 1 đến câu 8, hãy chọn phương
án trả lời đúng và viết chữ cái đứng trước phương án đó vào bài làm.
Câu 1. Phương trình nào sau đây là phương trình bậc nhất hai ẩn? 1
A. x  0y  2 . B. 3x  y( y  2)  1. C. 0x  0y  3. D.  2y  3. x  x  y  1
Câu 2. Biết hệ phương trình  có nghiệm  ;
x y . Kết quả của phép tính x  y 2x  3y  7 bằng A. 5. B. 2. C. 3. D. 4.
Câu 3. Hệ phương trình nào sau đây có vô số nghiệm? 3x  y  7 4x  3y  2 6x  3y  9 x  3y  5 A.  . B.  . C.  . D.  . x  5y  10 5x  y  7 2x  y  3 3x  y  2
Câu 4. Điều kiện xác định của phương trình 5 x x  5   là 2 2 2 x  5 x 2 x  50 2 x  10 x
A. x  5. B. x  5, x  0 và x  5. C. x  5  và x  5. D. x  5  .
Câu 5. Giá trị các hệ số x, y trong phản ứng hóa học đã được cân bằng 3Fe  xO  yFe O là 2 3 4 A. x  1, y  2. B. x  2, y  1.
C. x  4, y  3. D. x  3, y  4.
Câu 6. Nghiệm của phương trình (x  1)(x  2)  0 là: A. x  1 và x  2
 . B. x  1 và x  2. C. x  1. D. x  1 và x  2. Câu 7. Cho 0
0    90 , khi đó ta có A . sin  cos. B.    0 cot
cos 90   . C. cot  tan. D.    0 sin cos 90  .
Câu 8. Cho tam giác MNP vuông tại M , có  0 N  60 ; MN  9c . m Khi đó 1 A . NP 18c . m B. NP  6 3c . m C. NP  c . m D. NP  9 3c . m 2
2. Trắc nghiệm đúng sai (1,0 điểm)
Trong mỗi ý a), b), c), d), ở câu 9 học sinh chỉ trả lời đúng hoặc sai và ghi chữ “Đúng” hoặc
“Sai” đó vào bài làm.
Câu 9. Cho tam giác ABC vuông ở A có độ dài các cạnh AC  6c ; m BC  12cm . a) AB cot C  . AC b) B  30. 3 c) cosB  . 2 d) 2 2 sin B  cos C 1.
Phần II: Tự luận (7,0 điểm)
Bài 1 (1,75 điểm) Giải các phương trình và bất phương trình sau: a) x x   2 3 1  x 1  0 ; 2 1 2 x  3x b)   ; 2 x  3 3  x x  9 x  2 2x 1 c)  x  1. 3 2
Bài 2 (1,25 điểm) Giải bài toán sau bằng cách lập hệ phương trình:
Hai vòi nước cùng chảy vào bể nước cạn thì sau 2 giờ đầy bể. Nếu mở vòi thứ nhất trong 1
45 phút rồi khóa lại và mở tiếp vòi thứ hai trong nửa giờ nữa thì chảy được bể. Hỏi nếu mở 3
chảy riêng từng vòi thì sau bao lâu chảy đầy bể? Bài 3 (3,0 điểm) 1.
Một bạn muốn tính khoảng cách giữa hai địa điểm A, B
ở hai bên hồ nước. Biết rằng các khoảng cách từ một
điểm C đến điểm A và đến điểm B là CA = 90 m, CB = 150 m và  0 ACB  120 (hình vē bên). a) Tính AH. b) Tính AB giúp bạn.
2. Cho tam giác ABC vuông tại B biết AB  2c , m AC  4cm . a) Tính 
BAC và độ dài cạnh BC .
b) Trên cạnh BC lấy điểm H . Từ C kẻ đường thẳng vuông góc với đường thẳng AH tại K , cắt tia AB tại .
D Gọi I là giao điểm của DH và AC . Viết tỉ số lượng giác cos  BDH và chứng minh D . B DA  DH.DI .
c) Chứng minh DK  DH.sin  DBK. Bài 4 (1,0 điểm)
a) Giải phương trình: x  2 2  x  2 x   2 3 5 3  4x  0.
b) Cho ba số dương x, y, z thỏa mãn 2 2 2 x  y  z . 1  1 1  Chứng minh  2 2 y  z  2  506x   2025 2  2 2  x  y z  -----Hết-----
PHÒNG GIÁO DỤC ĐÀO TẠO
HƯỚNG DẪN CHẤM BÀI KHẢO SÁT CHẤT LƯỢNG HUYỆN XUÂN TRƯỜNG
GIỮA HỌC KỲ I NĂM HỌC 2024 - 2025 ---***--- MÔN TOÁN LỚP 9
Thời gian làm bài: 120 phút I. Hướng dẫn chung:
1) Hướng dẫn chấm chỉ trình bày một cách giải với các ý cơ bản học sinh phải trình bày, nếu học
sinh giải theo cách khác mà đúng và đủ các bước thì cho điểm tương đương..
2) Bài hình (tự luận) bắt buộc phải vẽ đúng hình thì mới chấm điểm, nếu hình vẽ sai ở phần nào thì
không cho điểm phần lời giải liên quan đến hình của phần đó.
3) Điểm toàn bài là tổng điểm của các ý, các câu, tính đến 0,25 điểm và không làm tròn.
II. Đáp án và thang điểm:
Phần I:Trắc nghiệm (3,0 điểm)
Phần 1. Câu trắc nghiệm nhiều phương án lựa chọn: Mỗi câu trả lời đúng được 0,25 điểm. Câu 1 2 3 4 5 6 7 8 Đáp án A C C B B D D A
Phần 2. Câu trắc nghiệm đúng sai: 9a 9b 9c 9d Sai Đúng Đúng Sai
Chọn chính xác 1 ý được 0,1 điểm.
Chọn chính xác 2 ý được 0,25 điểm.
Chọn chính xác 3 ý được 0,5 điểm.
Chọn chính xác 4 ý được 1 điểm.
Phần II.Tự luận (7,0 điểm) Bài Nội dung Điểm 1 a) x x   2 3 1  x 1  0 ; 2  b) 1 2 x 3   ; 2 x  3 3  x x  9 x  2 2x 1 c)  x  1. 3 2 a x  x   2 3 1  x 1  0 (0.5đ)  x   1 4x   1  0 0,25
x 1  0 hoặc 4x  1  0 1 0,25 x  1 hoặc x   . 4 1
Vậy phương trình đã cho có hai nghiệm là x  1 ; x   4 b 2 1 2 x  3x (0,75đ)   ; 2 x  3 3  x 0,25 x  9
ĐKXĐ: x  3 và x  3 2 1 2 x  3x 0,25   x  3 3  x x 3x  3 x 3 2x  3 2 x  3x   
x  3x  3 x  3x  3 x  3x   3 x   x  x2 3 2 6  x 3  
x  3x  3 x   3 x  3 0,25 x   x2 3 3  x 3 x2 3  0 x (  3) x (  3)  0 0,25 x  3 (thỏa mãn ĐKXĐ)
x   3 thỏa mãn ĐKXĐ)
Vậy phương trình đã cho có hai nghiệm là: x  3 và x   3 c x  2 2x 1  x  1 (0,5đ) 3 2
2 x  2 6x 6 32x   1 0,25    6 6 6 6
2x  4  6x  6x  3  6 1  0x  5  1 0,25 x  2 1
Vậy nghiệm của bất phương trình là x  . 2 2
Hai vòi nước cùng chảy vào bể nước cạn thì sau 2 giờ đầy bể. Nếu mở vòi thứ nhất (1,25đ) 1
trong 45 phút rồi khóa lại và mở tiếp vòi thứ hai trong nửa giờ nữa thì chảy được 3
bể. Hỏi nếu mở chảy riêng từng vòi thì sau bao lâu chảy đầy bể? 3 Đổi 45 phút = giờ 4
Gọi thời gian vòi vòi thứ nhất chảy riêng đầy bể là: x (giờ)
Thời gian thời gian vòi vòi thứ hai chảy riêng đầy bể là: y (giờ) ( điều kiện x  2; y  2 ) 0,25 1
Trong 1 giờ, vòi vòi thứ nhất chảy được (phần bể) x 1
Trong 1 giờ, vòi vòi thứ hai chảy được (phần bể) y 1
Vì trong 1 giờ cả hai vòi chảy được (phần bể) 2 1 1 1 Nên ta có:   (1) 0,25 x y 2
Nếu mở vòi thứ nhất trong 45 phút rồi khóa lại và mở vòi thứ hai trong nửa giờ thì 1
cả hai vòi chảy được bể 3 3 1 1 1 1
Nên ta có phương trình : .  .  (2) 4 x 2 y 3 0,25 1 1 1   x y 2 Từ  
1 và 2 ta có hệ phương trình  3 1 1 1 1  .  .   4 x 2 y 3 0,25
Giải hệ phương trình ta tìm được x  3; y  6
x  3; y  6 (thỏa mãn điều kiện của ẩn) 0,25 Kết luận….. 3.1
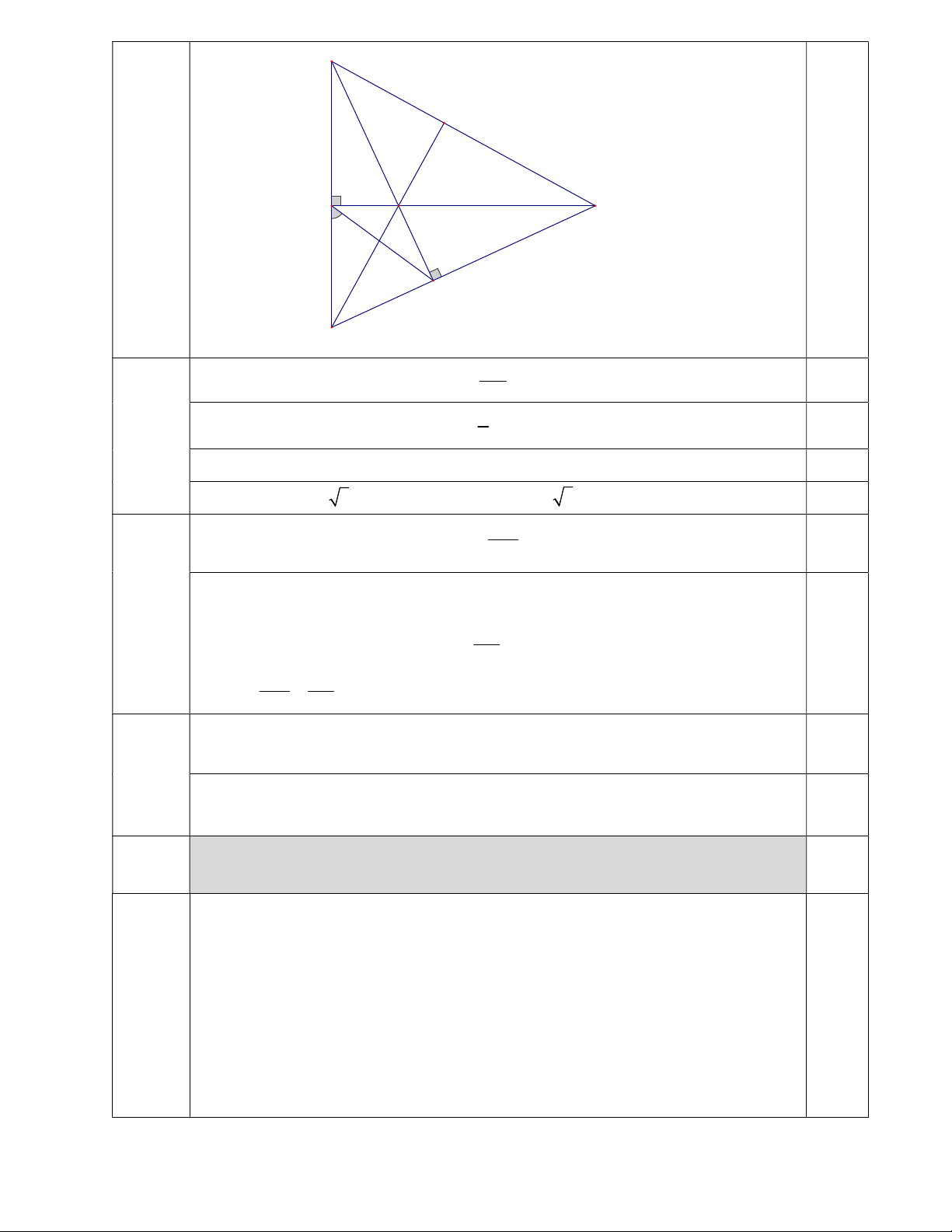
Một bạn muốn tính khoảng cách giữa hai địa điểm A, B ở hai bên hồ nước.
(1,0đ) Biết rằng các khoảng cách từ một điểm C đến A và đến B là CA = 90 m, CB = 150 m và  0 ACB  120 (hình vē bên). a) Tính AH. b) Tính AB giúp bạn. Ta có:  ACB   0
ACH  180 ( hai góc kề bù) Suy ra :  0 ACH  60
Xét ACH vuông tại H có 0,25 AH  AC.sin 
ACH (hệ thức về cạnh và góc) 0 AH  90.sin 60  45 3(m) 0,25
Xét ACH vuông tại H có CH  AC c  0 . osACH  90. o c s60  45( )
m (hệ thức về cạnh và góc) 0,25 BH  BC  CH  195( ) m
Xét ABH vuông tại H theo định lý Pythagore ta có 2 2 2 AB  BH  AH 2 AB  44100 AB  210( ) m 0,25 Vậy AB  210(m) 3.2
Cho tam giác ABC vuông tại B biết AB  2c , m AC  4cm . a) Tính 
BAC và độ dài cạnh BC .
b) Trên cạnh BC lấy điểm H . Từ C kẻ đường thẳng vuông góc với AH tại K , cắt tia AB tại .
D Gọi I là giao điểm của DH và AC . Viết tỉ số lượng giác cos  BDH và chứng minh D . B DA  DH.DI . DK  DH.sin  c) Chứng minh DBK. A I B H C K D a Xét AB A
 BC vuông tại B có cos  BAC  (định nghĩa TSLG) (1,0đ) AC 0,25 2 cos  BAC    0 BAC  60 4 0,25 Lại có BC  AC.sin 
BAC (hệ thức cạnh và góc) 0,25 0
BC  4.sin 60  2 3cm . Vậy  0 BAC  60 ; BC  2 3c . m 0,25 b BD 
(0,5đ) Xét BHD vuông tại B có cos  BDH (định nghĩa TSLG) DH 0,25
ADC có AK,CB là hai đường cao cắt nhau tại H
nên H là trực tâm của ADC , do đó DH  AC tại I DI 0,25
Xét ADI vuông tại I có cos  ADI  DA DB DI Suy ra:  , do đó: D . B DA  DH.DI DH DA c
Tương tự ta có DK.DC  DH.DI nên D . B DA  DK.DC (0,5đ) Lại có 
ADC chung nên DBK ∽DC ( A . c g.c)   DBK   DCA 0,25
Xét DHK vuông tại K có DK  DH.sin  DHK Lại có  DCA   DHK (cùng phụ với  IDC )  DK  DH.sin  DBK 0,25 4 2 Giải phương trình:  2 x    x 2 x   2 3 5 3  4x  0. (1.0đ) a x  2 2  x 2 x   2 3 5 3  4x  0. (0,5đ) x  2 2  x 2 x    x 2 x   2 3 3 4 3  4x  0   x  2 2  x  2 x     x     2 x   2 3 3 4 3  4x   0 
 2x   2x   x x 2 3 3 4 x  3  x  0  2x   x 2 3 x  3  4x  0
 2x  x 3x 1(x 3)  0 0,25 Suy ra 2
x  x  3  0 hoặc  x  
1  0 hoặc  x  3  0 *  x   1  0 x  1  *  x  3  0 x  3  2 0,25  1  11  1  11 * 2 2 x  x  3  x  x    x    0      4  4  2  4 Nên phương trình 2
x  x  3  0 vô nghiệm
Vậy phương trình có 2 nghiệm: x  1 và x  3. b Cho ba số dương , x y, z thỏa mãn 2 2 2 x  y  z . (0,5đ) 1  1 1  Chứng minh  2 2 y  z  2  506x   2025 2  2 2  x  y z  Ta có a  b2  a  b   a  b2 1 1 4 0 , 0  4ab    . a b a  b
Áp dụng BĐT trên ta được 1     2 2 2 y  z 2024x 0,25 y  z  2 2 1 1 y z 4 2 2 2 2  506x    506x .   2  2 2  2 2 2 x  y z  x y  z 2 2 2 x y  z 2 2 2 2 y  z x 2023x 0,25     2  2023  2025 (vì 2 2 2 x  y  z ) 2 2 2 2 2 x y  z y  z
Dấu “=” xảy ra khi và chỉ khi x  2y  2z 1  1 1  Vậy  2 2 y  z  2  506x   2025 2  2 2  x  y z 
Xem thêm: ĐỀ THI GIỮA HK1 TOÁN 9
https://thcs.toanmath.com/de-thi-giua-hk1-toan-9
Document Outline

• TOAN 9
• HDC MON TOAN 9
• XEM THEM - GIUA KY 1 - TOAN 9