Đề giữa kì 2 Toán 11 năm 2024 – 2025 trường THPT Thanh Miện 2 – Hải Dương có đáp án

Đề giữa kì 2 Toán 11 năm 2024 – 2025 trường THPT Thanh Miện 2 – Hải Dương có đáp án. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 21 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem

Chủ đề:

Đề giữa HK2 Toán 11 233 tài liệu

Môn:

Toán 11 3.3 K tài liệu

Thông tin:
19 trang 1 tuần trước
Tác giả:
Student
Kim Ngân Lê
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề giữa kì 2 Toán 11 năm 2024 – 2025 trường THPT Thanh Miện 2 – Hải Dương có đáp án

Đề giữa kì 2 Toán 11 năm 2024 – 2025 trường THPT Thanh Miện 2 – Hải Dương có đáp án. Tài liệu được sưu tầm và biên soạn dưới dạng PDF gồm 21 trang giúp em củng cố kiến thức, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem

6 3 lượt tải Tải xuống

Chủ đề: Đề giữa HK2 Toán 11 233 tài liệu

Môn: Toán 11 3.3 K tài liệu

Thông tin:

19 trang 1 tuần trước

Tác giả:

Profile Kim Ngân Lê
Mã đề 101 Trang 1/4
SỞ GD&ĐT HẢI DƯƠNG
TRƯỜNG THPT THANH MIỆN 2
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
Môn: TOÁN 11; Năm học 2024-2025
Thời gian làm bài: 90 phút không kể giao đề
Họ và tên:
............................................................................
S
ố báo danh: ....... Mã đề 101
PHẦN I. Trắc nghiệm nhiều lựa chọn
Từ câu 1 đến câu 12, học sinh chỉ được chọn 1 trong 4 phương án A, B, C, D. Mỗi câu
trả lời đúng học sinh được 0,25 điểm.
Câu 1. Trong không gian, cho đường thẳng
d
và điểm
O
. Qua
O
có bao nhiêu đường
thẳng vuông góc với đường thẳng
d
?
A. 2. B. 3. C. vô số. D. 1.
Câu 2. Cho hai biến cố
A
và
B
. Biến cố "
hoặc
B
xảy ra" được gọi là:
A. Biến cố hợp của
A
và
.B
B. Biến cố xung khắc của
A
và
.
B
C. Biến cố đối của
.A
D. Biến cố giao của
và
.
B
Câu 3. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi,
SA
vuông góc với đáy. Biểu
thức nào sau đây đúng:
A.
CD SD⊥
. B.
BD SC
⊥
. C.
AC SB⊥
. D.
BC SB
⊥
.
Câu 4. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
,
SO
vuông góc với
mặt phẳng đáy. Góc giữa đường thẳng
SD
và
(
)
ABCD
là
A.
SOA
. B.
SDA
. C.
SDO
. D.
SOD
.
Câu 5. Cho hình lập phương
.ABCD A B C D
′′′′
. Đường thẳng
AB
vuông góc với đường
thẳng nào sau đây:
A.
CD
. B.
AC
. C.
BD
. D.
A'D'
.
Câu 6. Với
a
và
b
là các số thực dương. Biểu thức
( )
2
log
a
ab
bằng
A.
1 2 log
a
b+
. B.
2 log
a
b−
. C.
2 log
a
b+
. D.
2 log
a
b
.
Câu 7. Nghiệm của phương trình
( )
3
log 2 1 2x −=
là
A.
5x =
. B.
3x =
. C.
7
2
x =
. D.
9
2
x =
.
Mã đề 101 Trang 2/4
Câu 8. Cho hình chóp
.S ABCD
(tham khảo hình vẽ), biết
( )
SA ABCD⊥
. Hình chiếu vuông
góc của đường thẳng
SC
lên mặt phẳng
( )
ABCD
là
A.
SA
. B.
AC
. C.
BC
. D.
SC
.
Câu 9. Cho
a
là số thực dương khác
1
. Tính
3
log
a
Ia=
A.
0I =
. B.
3I = −
. C.
3I =
. D.
1
3
I =
.
Câu 10. Nếu hai biến cố
A
và
B
xung khắc thì xác suất của biến cố
( )
PA B∪
bằng
A.
( ) ( )
.PAPB
B.
( ) ( )
1 PA PB−−
C.
( ) ( ) ( ) ( )
.PAPB PA PB−−
D.
( )
( )
PA PB
+
Câu 11. Tìm tập nghiệm
S
của phương trình
2
2
55
xx−
=
.
A.
1
1;
2
S

= −


. B.
{ }
0; 2S =
. C.
1
0;
2
S

=


. D.
S = ∅
.
Câu 12. Cho
0
a >
,
m
,
n∈
. Khẳng định nào sau đây đúng?
A.
( ) ()
mn nm
aa=
. B.
m
nm
n
a
a
a
−
=
.
C.
m n mn
aaa
+
+=
. D.
.
m n mn
aa a
−
=
.
PHẦN II. Trắc nghiệm đúng/sai
Từ câu 1 đến câu 2, mỗi ý a, b, c, d học sinh chỉ được chọn Đ/S. Điểm tối đa mỗi câu là 1
điểm
Câu 1. Một hộp đựng 4 viên bi màu xanh, 3 viên bi màu đỏ và 2 viên bi màu vàng. Chọn
ngẫu nhiên 2 viên bi từ hộp trên. Gọi A là biến cố: "Chọn được 2 viên bi màu xanh"
B
là
biến cố "Chọn được 2 viên bi màu đỏ",
C
là biến cố "Chọn được 2 viên bi màu vàng" .
Khi đó:
a)
1
()
8
PB =
b)
1
()
7
PA=
c) Xác suất để chọn được 2 viên bi cùng màu bằng
5
18
d)
1
()
36
PC =
A
B
D
S
C
Mã đề 101 Trang 3/4
Câu 2. Cho hình lập phương
111 1
.ABCD A B C D
cạnh
a
. Xét tính đúng sai của các khẳng
định sau
a)
( )
1 11
AB BCD A⊥
b) Gọi
α
là góc giữa
1
AC
và mp
( )
11
A BCD
thì
2
tan
3
α
=
c)
( )
1
AA ABCD⊥
d)
1
AB CC⊥
PHẦN III. Trắc nghiệm trả lời ngắn
Từ câu 1 đến câu 4, học sinh chỉ trả lời đáp số. Mỗi câu trả lời đúng được 0,5 điểm
Câu 1. Ba người cùng bắn vào bia Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng
đích lần lượt là ; ; . Xác suất để có đúng người bắn trúng đích bằng:…
Câu 2. Cho biểu thức
5
4
Px=
, với
0x >
. Ta biến đổi
m
n
Px=
. Tính tổng m+n =….
Câu 3. Một lớp học 40 học sinh gồm có 15 học sinh nam giỏi Toán và 8 học sinh nữ giỏi
Lí. Chọn ngẫu nhiên một học sinh. Hãy tính xác suất để chọn được một nam sinh giỏi
Toán hay một nữ sinh giỏi Lý.
Câu 4. Cho
2
log 5a =
,
3
log 5b =
. Biết
24
3
log 250
ab nb
a qb
+
=
+
với
,nq∈
. Tính giá trị biểu
thức
3A nq=
.
PHẦN IV. T ự luận
Học sinh trình bày chi tiết bài làm vào tờ giấy thi. Điểm tối đa mỗi câu là 0,5 điểm
ĐỀ LẺ
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số
2
22
log
aam
yx
− +−
=
đồng biến trên
( )
0; +∞
với mọi số thực
a
.
1
0,8
0, 6
0,5
2
Mã đề 101 Trang 4/4
Câu 2. Giải phương trình
9 5.3 6 0
xx
− +=
Câu 3. Một hộp có
5
bút bi mực xanh và
6
bút bi mực đỏ có kích thước và khối lượng như
nhau. Lấy bút ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một bút bi, ghi lại
màu mực và bỏ lại bút bi đó vào trong hộp. Tính xác suất của biến cố lần thứ nhất lấy được bút
bi mực màu xanh hoặc lần thứ hai lấy được bút bi mực màu đỏ
Câu 4. Trong đợt thi kiểm tra giữa học kỳ 2 vừa qua, đề thi môn Toán Khối 12 làm theo cấu trúc
mới của dạng đề minh họa thi TN 2025. Đề thi có 3 phần: PHẦN I-Câu trắc nghiệm nhiều
phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một
phương án, trả lời đúng mỗi câu được 0,25 điểm. PHẦN II-Câu trắc nghiệm đúng sai. Thí sinh
trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Trong
mỗi câu: Trả lời đúng một ý được 0,1 điểm, trả lời đúng hai ý được 0,25 điểm, trả lời đúng ba ý
được 0,5 điểm, trả lời đúng cả bốn ý được 1 điểm và PHẦN III-Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6, mỗi câu trả lời đúng được 0,5 điểm. Bạn Bình tham gia thi và
đã chắc chắn làm được 8 điểm, chỉ còn hai câu là Câu 3 và Câu 4 ở PHẦN II bạn không hiểu nên
bạn chọn ngẫu nhiên đúng hoặc sai tất cả các ý của hai câu này. Tính xác suất để bài thi của bạn
Bình đạt trên 9 điểm.
Câu 5. Cho hình vuông
ABCD
, gọi
,HK
lần lượt là trung điểm các cạnh
,AB AD
. Trên đường
thẳng vuông góc với mặt phẳng
( )
ABCD
tại
H
lấy một điểm
S
khác
H
. Chứng minh rằng
CK
vuông góc SD.
Câu 6. Cho hình chóp
.S ABC
có:
( )
, 2, 45 ,SA ABC SB BC a BSC ASB⊥ == =°=α
.
ABC∆
vuông tại
B
. Xác định
sin α
để góc nhị diện
[ ]
, , 45A SC B = °
.
------------ Hết ------------
Thí sinh không được sử dụng tài liệu, Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:……….………...….………Số báo danh………………………
Mã đề 102 Trang 1/4
SỞ GD&ĐT HẢI DƯƠNG
TRƯỜNG THPT THANH MIỆN 2
ĐỀ CHÍNH THỨC
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
Môn: TOÁN 11; Năm học 2024-2025
Thời gian làm bài: 90 phút không kể giao đề
Họ và tên: ............................................................................
Số báo danh: .......
Mã đề 102
PHẦN I. Trắc nghiệm nhiều lựa chọn
Từ câu 1 đến câu 12, học sinh chỉ được chọn 1 trong 4 phương án A, B, C, D. Mỗi câu
trả lời đúng học sinh được 0,25 điểm.
Câu 1. Với
a
và
b
là các số thực dương. Biểu thức
( )
2
log
a
ab
bằng
A.
2 log
a
b+
. B.
2 log
a
b
. C.
1 2 log
a
b+
. D.
2 log
a
b−
.
Câu 2. Nghiệm của phương trình
( )
3
log 2 1 2x −=
là
A.
7
2
x =
. B.
5x =
. C.
9
2
x =
. D.
3x =
.
Câu 3. Cho hình lập phương
.ABCD A B C D
′′′′
. Đường thẳng
AB
vuông góc với đường thẳng nào
sau đây:
A.
A'D'
. B.
BD
. C.
CD
. D.
AC
.
Câu 4. Cho
0a >
,
m
,
n∈
. Khẳng định nào sau đây đúng?
A.
m n mn
aaa
+
+=
. B.
m
nm
n
a
a
a
−
=
. C.
.
m n mn
aa a
−
=
. D.
( ) ()
mn nm
aa=
.
Câu 5. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi,
SA
vuông góc với đáy. Biểu thức
nào sau đây đúng:
A.
BC SB⊥
. B.
CD SD⊥
. C.
BD SC⊥
. D.
AC SB⊥
.
Câu 6. Cho hình chóp
.S ABCD
(tham khảo hình vẽ), biết
( )
SA ABCD⊥
. Hình chiếu vuông góc
của đường thẳng
SC
lên mặt phẳng
( )
ABCD
là
A.
AC
. B.
SC
. C.
SA
. D.
BC
.
A
B
D
S
C
Mã đề 102 Trang 2/4
Câu 7. Cho
a
là số thực dương khác
1
. Tính
3
log
a
Ia=
A.
3I = −
. B.
1
3
I
=
. C.
3I =
. D.
0I =
.
Câu 8. Nếu hai biến cố
A
và
B
xung khắc thì xác suất của biến cố
( )
PA B∪
bằng
A.
(
)
( )
.
PAPB
B.
(
)
( )
(
) ( )
.
PAPB PA PB
−−
C.
( ) ( )
PA PB+
D.
( ) ( )
1 PA PB−−
Câu 9. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
,
SO
vuông góc với mặt
phẳng đáy. Góc giữa đường thẳng
SD
và
( )
ABCD
là
A.
SDA
. B.
SOD
. C.
SOA
. D.
SDO
.
Câu 10. Trong không gian, cho đường thẳng
d
và điểm
O
. Qua
O
có bao nhiêu đường thẳng
vuông góc với đường thẳng
d
?
A. vô số. B. 2. C. 3. D. 1.
Câu 11. Tìm tập nghiệm
S
của phương trình
2
2
55
xx−
=
.
A.
S = ∅
. B.
1
0;
2
S

=


. C.
1
1;
2
S

= −


. D.
{ }
0; 2S =
.
Câu 12. Cho hai biến cố
A
và
B
. Biến cố "
A
hoặc
B
xảy ra" được gọi là:
A. Biến cố xung khắc của
A
và
.B
B. Biến cố giao của
A
và
.B
C. Biến cố hợp của
A
và
.B
D. Biến cố đối của
.A
PHẦN II. Trắc nghiệm đúng/sai
Từ câu 1 đến câu 2, mỗi ý a, b, c, d học sinh chỉ được chọn Đ/S. Điểm tối đa mỗi câu là 1
điểm
Câu 1. Cho hình lập phương
111 1
.
ABCD A B C D
cạnh
a
. Xét tính đúng sai của các khẳng định sau:
a)
( )
1 11
AB BCD A⊥
b)
( )
1
AA ABCD⊥
c)
1
AB CC⊥
d) Gọi
α
là góc giữa
1
AC
và mp
( )
11
A BCD
thì
2
tan
3
α
=
Câu 2. Một hộp đựng 4 viên bi màu xanh, 3 viên bi màu đỏ và 2 viên bi màu vàng. Chọn ngẫu
nhiên 2 viên bi từ hộp trên. Gọi A là biến cố: "Chọn được 2 viên bi màu xanh"
B
là biến cố
"Chọn được 2 viên bi màu đỏ",
C
là biến cố "Chọn được 2 viên bi màu vàng" . Khi đó:
Mã đề 102 Trang 3/4
a) Xác suất để chọn được 2 viên bi cùng màu bằng
5
18
b)
1
()
36
PC =
c)
1
()
7
PA=
d)
1
()
8
PB =
PHẦN III. Trắc nghiệm trả lời ngắn
Từ câu 1 đến câu 4, học sinh chỉ trả lời đáp số. Mỗi câu trả lời đúng được 0,5 điểm
Câu 1. Một lớp học 40 học sinh gồm có 15 học sinh nam giỏi Toán và 8 học sinh nữ giỏi Lí.
Chọn ngẫu nhiên một học sinh. Hãy tính xác suất để chọn được một nam sinh giỏi Toán hay một
nữ sinh giỏi Lý
Câu 2. Ba người cùng bắn vào bia Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần
lượt là ; ; . Xác suất để có đúng người bắn trúng đích bằng:……..
Câu 3. Cho
2
log 5a =
,
3
log 5b =
. Biết
24
3
log 250
ab nb
a qb
+
=
+
với
,nq∈
. Tính giá trị biểu thức
3A nq=
.
Câu 4. Cho biểu thức
5
4
Px=
, với
0x >
. Ta biến đổi
m
n
Px=
Tính tổng m+n =……
PHẦN IV. T ự luận
Học sinh trình bày chi tiết bài làm vào tờ giấy thi. Điểm tối đa mỗi câu là 0,5 điểm
ĐỀ CHẴN
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số
2
23
log
aam
yx
− +−
=
đồng biến trên
( )
0; +∞
với mọi số thực
a
.
Câu 2. Giải phương trình
4 3.2 2 0
xx
− +=
Câu 3. Một hộp có 4 bút bi mực xanh và 5 bút bi mực đỏ có kích thước và khối lượng như nhau.
Lấy bút ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một bút bi, ghi lại màu mực
và bỏ lại bút bi đó vào trong hộp. Tính xác suất của biến cố lần thứ nhất lấy được bút bi mực
màu xanh và lần thứ hai lấy được bút bi mực màu đỏ
Câu 4. Trong đợt thi kiểm tra giữa học kỳ 2 vừa qua, đề thi môn Toán Khối 12 làm theo cấu trúc
mới của dạng đề minh họa thi TN 2025. Đề thi có 3 phần: PHẦN I-Câu trắc nghiệm nhiều
phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một
phương án, trả lời đúng mỗi câu được 0,25 điểm. PHẦN II-Câu trắc nghiệm đúng sai. Thí sinh
trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Trong
mỗi câu: Trả lời đúng một ý được 0,1 điểm, trả lời đúng hai ý được 0,25 điểm, trả lời đúng ba ý
được 0,5 điểm, trả lời đúng cả bốn ý được 1 điểm và PHẦN III-Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6, mỗi câu trả lời đúng được 0,5 điểm. Bạn Bình tham gia thi và
đã chắc chắn làm được 8 điểm, còn hai câu là Câu 3 và Câu 4 ở PHẦN II bạn không hiểu nên bạn
chọn ngẫu nhiên đúng hoặc sai tất cả các ý của hai câu này. Tính xác suất để bài thi của bạn Bình
đạt đúng 9 điểm.
Câu 5. Cho hình vuông
ABCD
, gọi
,HM
lần lượt là trung điểm các cạnh
,AB BC
. Trên đường
thẳng vuông góc với mặt phẳng
( )
ABCD
tại
H
lấy một điểm
S
khác
H
. Chứng minh rằng
AM
vuông góc SD.
1
0,8
0, 6
0,5
2
Mã đề 102 Trang 4/4
Câu 6. Cho hình chóp
.S ABC
có:
( )
, 2, 45 ,SA ABC SB BC a BSC ASB⊥ == =°=α
.
ABC
∆
vuông tại
B
. Xác định
sin α
để góc nhị diện
[ ]
, , 30A SC B = °
.
------------ Hết ------------
Thí sinh không được sử dụng tài liệu, Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:……….………...….………Số báo danh………………………
PHẦN I PHẦN II PHẦN III
12 2 2
Đề\câu 101 102 103 104
1 C A C B
2 A B B B
3 B A B B
4 C D B C
5 D C D A
6 C A B D
7 A B A C
8 B C D A
9 D D C B
10 D A A C
11 A C C B
12 A C D B
1 SSDD DDDS DDDS SDDD
2 DSDD DDSS SDSD DDSS
1 0,46 0.58 0,46 0.58
2 9 0,46 9 0,46
3 0.58 9 0.58 9
4 9 9 9 9
ĐÁP ÁN CHẤM TRẮC NGHIỆM TOÁN 11. THANG ĐIỂM 7
KIỂM TRA GIỮA KÌ 2
TOÁN 11
PHẦN I
Câu 1. Cho
0a >
,
m
,
n ∈
. Khẳng định nào sau đây đúng?
A.
m n mn
aaa
+
+=
. B.
.
m n mn
aa a
−
=
. C.
( ) ()
mn nm
aa=
. D.
m
nm
n
a
a
a
−
=
.
Câu 2: Cho
a
là số thực dương khác
1
. Tính
3
log
a
Ia=
A.
1
3
I =
. B.
3I =
. C.
0I =
. D.
3I = −
.
Câu 3. Với
a
và
b
là các số thực dương. Biểu thức
( )
2
log
a
ab
bằng
A.
2 log
a
b−
. B.
2 log
a
b
+
. C.
1 2 log
a
b+
. D.
2 log
a
b
.
Câu 4. Nghiệm của phương trình
(
)
3
log 2 1 2
x −=
là
A.
3x =
. B.
5
x
=
. C.
9
2
x =
. D.
7
2
x =
.
Câu 5. Tìm tập nghiệm
S
của phương trình
2
2
55
xx−
=
.
A.
1
0;
2
S

=


. B.
{ }
0; 2S =
. C.
1
1;
2
S

= −


. D.
S = ∅
.
Câu 6. Nếu hai biến cố
A
và
B
xung khắc thì xác suất của biến cố
( )
PA B∪
bằng
A.
( ) ( )
1 PA PB−−
B.
( ) ( )
.PA PB
C.
(
) ( )
(
) (
)
.PAPB PA PB
−−
D.
( ) ( )
PA PB+
Câu 7: Cho hai biến cố
A
và
B
. Biến cố "
A
hoặc
B
xảy ra" được gọi là:
A. Biến cố giao của
A
và
.B
B. Biến cố đối của
.A
C. Biến cố hợp của
A
và
.B
D. Biến cố xung khắc của
A
và
.B
Câu 8: Cho hình lập phương
.ABCD A B C D
′′′′
. Đường thẳng
AB
vuông góc với đường thẳng nào sau
đây:
A.
CD
. B.
A'D'
. C.
AC
. D.
BD
.
Câu 9: Trong không gian, cho đường thẳng
d
và điểm
O
. Qua
O
có bao nhiêu đường thẳng vuông
góc với đường thẳng
d
?
A. 3. B. vô số. C. 1. D. 2.
Câu 10: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình thoi,
SA
vuông góc với đáy. Biểu thức nào
sau đây đúng:
A.
BC SB⊥
. B.
AC SB
⊥
. C.
BD SC⊥
. D.
CD SD⊥
.
Câu 11: Cho hình chóp
.S ABCD
(tham khảo hình vẽ), biết
(
)
SA ABCD⊥
. Hình chiếu vuông góc
của đường thẳng
SC
lên mặt phẳng
( )
ABCD
là
A.
AC
. B.
SA
. C.
BC
. D.
SC
.
Câu 12: Cho hình chóp
.S ABCD
có đáy
ABCD
là hình vuông tâm
O
,
SO
vuông góc với mặt
phẳng đáy. Góc giữa đường thẳng
SD
và
(
)
ABCD
là
A.
SDA
. B.
SDO
. C.
SOD
. D.
SOA
.
PHẦN II
Câu 1. Một hộp đựng 4 viên bi màu xanh, 3 viên bi màu đỏ và 2 viên bi màu vàng. Chọn ngẫu nhiên 2
viên bi từ hộp trên. Gọi A là biến cố: "Chọn được 2 viên bi màu xanh"
B
là biến cố "Chọn được 2
viên bi màu đỏ",
C
là biến cố "Chọn được 2 viên bi màu vàng" . Khi đó:
a)
1
()
7
PA
=
b)
1
()
8
PB =
c)
1
()
36
PC =
d) Xác suất để chọn được 2 viên bi cùng màu bằng
5
18
Câu 2: Cho hình lập phương
111 1
.
ABCD A B C D
cạnh
a
. Xét tính đúng sai của các khẳng định sau:
a)
1
AB CC⊥
A
B
D
S
C
b)
( )
1
AA ABCD⊥
c)
( )
1 11
AB BCD A⊥
d) Gọi
α
là góc giữa
1
AC
và mp
( )
11
A BCD
thì
2
tan
3
α
=
PHẦN III
Câu 1. Cho biểu thức
5
4
Px=
, với
0x >
. Ta biến đổi
m
n
Px=
Tính tổng m+n =
A. 9
Câu 2. Cho
2
log 5a =
,
3
log 5b =
. Biết
24
3
log 250
ab nb
a qb
+
=
+
với
,nq∈
. Tính giá trị biểu thức
3A nq=
.
B. 9
Câu 3. Một lớp học 40 học sinh gồm có 15 học sinh nam giỏi Toán và 8 học sinh nữ giỏi Lí. Chọn
ngẫu nhiên một học sinh. Hãy tính xác suất để chọn được một nam sinh giỏi toán hay một nữ sinh giỏi
Lí
A. 0.58
Câu 4. Ba người cùng bắn vào bia Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt
là ; ; . Xác suất để có đúng người bắn trúng đích bằng:
A. 0,46
TỰ LUẬN
ĐỀ LẺ
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số
2
22
log
aam
yx
− +−
=
đồng biến trên
( )
0; +∞
với
mọi số thực
a
.
Lời giải
Để hàm số đã cho đồng biến trên
( )
0; +∞
với mọi số thực
a
thì
2
22 1aa m− +− >
,
a∀∈
.
Suy ra
2
2 1,ma a a< − + ∀∈
.
Đặt
( ) ( )
2
2
2 1 1 0,fa a a a a= − += − ≥ ∀∈
.
Do đó ycbt
0m⇔<
.
Vậy
0m <
thỏa mãn đề bài.
Câu 2. Giải phương trình
9 5.3 6 0
xx
− +=
Ta có
9 5.3 6 0
xx
− +=
( )
2
3 5.3 6 0
x
x
⇔ − +=
( )
( )
2
3 5.3 6 0
xx
⇔ − += ∗
Đặt
30
x
t = >
.
Khi đó:
( )
∗
2
5 60tt⇔ − +=
( )
( )
2
3
t
t
=
⇔
=
32
33
x
x
t
t
= =
⇔
= =
3
log 2
1
x
x
=
⇔
=
Vậy nghiệm của phương trình là
3
1; lo g 2xx= =
.
1
0,8
0, 6
0,5
2
Câu 3. Một hộp có
5
bút bi mực xanh và
6
bút bi mực đỏ có kích thước và khối lượng như nhau.
Lấy bút ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một bút bi, ghi lại màu
mực và bỏ lại bút bi đó vào trong hộp. Tính xác suất của biến cố lần thứ nhất lấy được bút
bi mực màu xanh hoặc lần thứ hai lấy được bút bi mực màu đỏ
Lời giải
:A
“ Lần thứ nhất lấy được bút bi mực màu xanh ”.
:B
“Lần thứ hai lấy được bút bi mực màu đỏ”.
Biến cố lần thứ nhất lấy được bút bi mực màu xanh hoặc lần thứ hai lấy được bút bi mực
màu đỏ là
AB∪
( )
5
11
PA
=
( )
6
11
PB=
Hai biến cố
A
và
B
độc lập nên
( ) ( ) ( )
5 6 30
..
11 11 121
∩= = =PA B PAPB
.
Ta có:
( ) ( ) ( ) ( )
∪= + − ∩PA B PA PB PA B
5 6 30 91
11 11 121 121
=+− =
.
Câu 4. Trong đợt thi kiểm tra giữa học kỳ 2 vừa qua, đề thi môn Toán Khối 12 làm theo cấu trúc mới
của dạng đề minh họa thi TN 2025. Đề thi có 3 phần: PHẦN I-Câu trắc nghiệm nhiều
phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một
phương án, trả lời đúng mỗi câu được 0,25 điểm. PHẦN II-Câu trắc nghiệm đúng sai. Thí
sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc
sai. Trong mỗi câu: Trả lời đúng một ý được 0,1 điểm, trả lời đúng hai ý được 0,25 điểm, trả
lời đúng ba ý được 0,5 điểm, trả lời đúng cả bốn ý được 1 điểm và PHẦN III-Câu trắc
nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6, mỗi câu trả lời đúng được 0,5 điểm.
Bạn Bình tham gia thi và đã chắc chắn làm được 8 điểm, chỉ còn hai câu là Câu 3 và Câu 4 ở
PHẦN II bạn không hiểu nên bạn chọn ngẫu nhiên đúng hoặc sai tất cả các ý của hai câu
này. Tính xác suất để bài thi của bạn Bình đạt trên 9 điểm.
Lời giải
Ta có bài thi của Bình đạt trên 9 điểm khi bạn làm đúng cả 1 trong 2 câu và câu còn lại phải
có điểm.
TH1: Bình làm đúng cả câu 3 và câu 4 có điểm thì xác suất là
44
1
1 1 15
.1
2 2 256
p

 
= −=

 

 

.
TH2: Bình làm đúng cả câu 4 và câu 3 có điểm thì xác suất là
44
2
1 1 15
.1
2 2 256
p

 
= −=

 

 

.
Xác suất làm đúng hết cả hai câu là
44
3
11 1
.
2 2 256
p

= =


.
Khi đó xác suất để Bình đạt trên 9 điểm là
123
15 1 29
2.
256 256 256
pp p p=+−= − =
.
Câu 5. Cho hình vuông
ABCD
, gọi
,HK
lần lượt là trung điểm các cạnh
,AB AD
. Trên đường
thẳng vuông góc với mặt phẳng
( )
ABCD
tại
H
lấy một điểm
S
khác
H
. Chứng minh rằng
CK
vuông góc SD.
Lời giải
Trong mặt phẳng
( )
ABCD
, gọi
I
là giao điểm của
CK
và
DH
.
Ta có
00
90 90HAD KDC AHD DKC IDK DKC KID∆=∆⇒ = ⇒+ =⇒=
hay
CK DH⊥
Mặt khác, vì
(
)
SH ABCD
⊥
mà
(
)
CK ABCD⊂
nên
SH CK⊥
Do đó
( )
CK SHD⊥
mà
( )
SD SHD⊂
Suy ra
CK SD⊥
.
Câu 6. Cho hình chóp
.S ABC
có:
( )
, 2, 45 ,SA ABC SB BC a BSC ASB⊥ == =°=α
.
ABC∆
vuông tại
B
. Xác định
sin α
để góc nhị diện
[ ]
, , 45
A SC B = °
.
Lời giải
Vì
2, 45SB BC a BSC= = = °
nên
SBC∆
vuông cân tại
B
. Gọi
J
là trung điểm của
SC
.
Khi đó
(
)
1
BJ SC⊥
. Kẻ
( )
,
BK AC K AC⊥∈
.
Ta có:
( )
( )
2
BK AC
BK SAC BK SC
BK SA
⊥
⇒ ⊥ ⇒⊥
⊥
và
BK KJ⊥
.
Từ
( )
1
và
(
)
2
suy ra:
( ) ( )
3SC BJK SC KJ
⊥ ⇒⊥
.
Từ
( )
1
và
( )
3
suy ra góc nhị diện
[ ]
,,A SC B BJK
= = β
.
Trong
BJK∆
vuông tại
K
ta có
sin
BK
BJ
β=
.
Lại có:
222
1 1 11
,
2
BJ SC a
BK BA BC
= = = +
(
ABC∆
vuông tại
B
),
.sin 2.sinAB SB a= α= α
.
2
2 22 2 22
2
1 1 1 1 sin 2 sin
2 sin 2 2 sin
1 sin
a
BK
BK a a a
+α α
⇒ = + = ⇒=
αα
+α
2
2 sin
sin
1 sin
BK
BJ
α
⇒ β= =
+α
.
45β= °
thì
2
2
2
2
2 2 sin 2 sin 1 1 3
sin sin sin
2 2 1 sin 4 3 3
1 sin
αα
β= ⇒ = ⇔ = ⇔ α= ⇒ α=
+α
+α
.
ĐỀ CHẴN
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số
2
23
log
aam
yx
− +−
=
đồng biến trên
( )
0; +∞
với
mọi số thực
a
.
Lời giải
Để hàm số đã cho đồng biến trên
( )
0; +∞
với mọi số thực
a
thì
2
23 1aa m− +− >
,
a∀∈
.
Suy ra
2
2 2,ma a a< − + ∀∈
.
Đặt
( ) ( )
2
2
2 2 1 1 0,fa a a a a= − + = − +≥ ∀∈
.
Do đó ycbt
1m⇔<
.
Vậy
1m <
thỏa mãn đề bài.
Câu 2. Giải phương trình
4 3.2 2 0
xx
− +=
Ta có
4 3.3 2 0
xx
− +=
( )
2
2 3.2 2 0
x
x
⇔ − +=
( )
( )
2
2 3.2 2 0,
xx
⇔ − += ∗
Đặt
20
x
t = >
.
Phương trình
( )
∗
trở thành
2
3 20tt
− +=
Giải phương trình (*) ta tìm được
( ) ( )
2/ ; 1/t tm t tm= =
Với
2t
=
suy ra x =1
Với
1t =
suy ra x =0
Vậy nghiệm của phương trình là
1; 0xx= =
.
Câu 3. Một hộp có 4 bút bi mực xanh và 5 bút bi mực đỏ có kích thước và khối lượng như nhau. Lấy
bút ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một bút bi, ghi lại màu
mực và bỏ lại bút bi đó vào trong hộp. Tính xác suất của biến cố lần thứ nhất lấy được bút
bi mực màu xanh và lần thứ hai lấy được bút bi mực màu đỏ
Lời giải
:A
“ Lần thứ nhất lấy được bút bi mực màu xanh ”.
:B
“Lần thứ hai lấy được bút bi mực màu đỏ”.
Biến cố lần thứ nhất lấy được bút bi mực màu xanh và lần thứ hai lấy được bút bi mực màu
đỏ là
AB∩
(
)
4
9
PA=
(
)
5
9
PB=
Hai biến cố
A
và
B
độc lập nên
( ) ( ) ( )
4 5 20
..
9 9 81
PA B PAPB∩= = =
.
Câu 4. Trong đợt thi kiểm tra giữa học kỳ 2 vừa qua, đề thi môn Toán Khối 12 làm theo cấu trúc mới
của dạng đề minh họa thi TN 2025. Đề thi có 3 phần: PHẦN I-Câu trắc nghiệm nhiều
phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một
phương án, trả lời đúng mỗi câu được 0,25 điểm. PHẦN II-Câu trắc nghiệm đúng sai. Thí
sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc
sai. Trong mỗi câu: Trả lời đúng một ý được 0,1 điểm, trả lời đúng hai ý được 0,25 điểm, trả
lời đúng ba ý được 0,5 điểm, trả lời đúng cả bốn ý được 1 điểm và PHẦN III-Câu trắc
nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6, mỗi câu trả lời đúng được 0,5 điểm.
Bạn Bình tham gia thi và đã chắc chắn làm được 8 điểm, còn hai câu là Câu 3 và Câu 4 ở
PHẦN II bạn không hiểu nên bạn chọn ngẫu nhiên đúng hoặc sai tất cả các ý của hai câu
này. Tính xác suất để bài thi của bạn Bình đạt đúng 9 điểm.
Lời giải
Ta có bài thi của Bình đạt đúng 9 điểm khi bạn làm đúng cả 4 ý của câu 3 thì câu 4 sai hết,
hoặc làm đúng cả 4 ý của câu 4 thì câu 3 sai hết, hoặc trong 2 câu hoặc mỗi câu chỉ sai 1 ý.
TH1: Bình làm đúng cả câu 3 và câu 4 sai hết thì xác suất là
44
1
11 1
.
2 2 256
p

= =


.
TH2: Bình làm đúng cả câu 4 và câu 3 sai hết thì xác suất là
44
2
11 1
.
2 2 256
p

= =


TH3: Trong 2 câu, mỗi câu Bình sai 1 ý thì xác suất là
3
11 1
.
4 4 16
p

= =


.
Khi đó xác suất để Bình đạt đúng 9 điểm là
123
9
128
pp p p=++=
.
Câu 5. Cho hình vuông
ABCD
, gọi
,HM
lần lượt là trung điểm các cạnh
,AB BC
. Trên đường
thẳng vuông góc với mặt phẳng
( )
ABCD
tại
H
lấy một điểm
S
khác
H
. Chứng minh rằng
AM
vuông góc SD.
Lời giải
Trong mặt phẳng
( )
ABCD
, gọi
I
là giao điểm của
AM
và
DH
.
Ta có
HAD MBA AHD BMA∆=∆⇒ =
suy ra
00
90 90DHA HAI HIA+=⇒=
hay
AM DH⊥
Mặt khác, vì
( )
SH ABCD⊥
mà
( )
AM ABCD⊂
nên
SH AM⊥
Do đó
( )
AM SHD⊥
mà
( )
SD SHD⊂
Suy ra
AM SD⊥
.
Câu 6. Cho hình chóp
.S ABC
có:
( )
, 2, 45 ,SA ABC SB BC a BSC ASB⊥ == =°=α
.
ABC∆
vuông tại
B
. Xác định
sin α
để góc nhị diện
[ ]
, , 30A SC B = °
.
I
M
H
C
A
D
B
S
Lời giải
Vì
2, 45SB BC a BSC= = = °
nên
SBC∆
vuông cân tại
B
. Gọi
J
là trung điểm của
SC
.
Khi đó
(
)
1
BJ SC⊥
. Kẻ
( )
,BK AC K AC⊥∈
.
Ta có:
( ) ( )
2
BK AC
BK SAC BK SC
BK SA
⊥
⇒ ⊥ ⇒⊥
⊥
và
BK KJ⊥
.
Từ
( )
1
và
( )
2
suy ra:
( ) ( )
3SC BJK SC KJ⊥ ⇒⊥
.
Từ
( )
1
và
( )
3
suy ra góc nhị diện
[ ]
,,A SC B BJK= = β
.
Trong
BJK∆
vuông tại
K
ta có
sin
BK
BJ
β=
.
Lại có:
222
1 1 11
,
2
BJ SC a
BK BA BC
= = = +
(
ABC∆
vuông tại
B
),
.sin 2.sinAB SB a
= α= α
.
2
2 22 2 22
2
1 1 1 1 sin 2 sin
2 sin 2 2 sin
1 sin
a
BK
BK a a a
+α α
⇒ = + = ⇒=
αα
+α
2
2 sin
sin
1 sin
BK
BJ
α
⇒ β= =
+α
.
45β= °
thì
2
2
2
2
1 2 sin 1 2sin 1 1 7
sin sin sin
2 2 1 sin 4 7 7
1 sin
αα
β= ⇒ = ⇔ = ⇔ α= ⇒ α=
+α
+α
.
Xem thêm: ĐỀ THI GIỮA HK2 TOÁN 11
https://toanmath.com/de-thi-giua-hk2-toan-11
| 1/19

Tài liệu khác của Toán 11

Preview text:

SỞ GD&ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
TRƯỜNG THPT THANH MIỆN 2
Môn: TOÁN 11; Năm học 2024-2025
Thời gian làm bài: 90 phút không kể giao đề ĐỀ CHÍNH THỨC Họ và tên:
............................................................................ Số báo danh: ....... Mã đề 101
PHẦN I. Trắc nghiệm nhiều lựa chọn
Từ câu 1 đến câu 12, học sinh chỉ được chọn 1 trong 4 phương án A, B, C, D. Mỗi câu
trả lời đúng học sinh được 0,25 điểm.
Câu 1. Trong không gian, cho đường thẳng d và điểm O . Qua O có bao nhiêu đường
thẳng vuông góc với đường thẳng d ? A. 2. B. 3. C. vô số. D. 1.
Câu 2. Cho hai biến cố A và B . Biến cố " A hoặc B xảy ra" được gọi là:
A. Biến cố hợp của A và . B
B. Biến cố xung khắc của A và . B
C. Biến cố đối của . A
D. Biến cố giao của A và . B
Câu 3. Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA vuông góc với đáy. Biểu
thức nào sau đây đúng:
A. CD ⊥ SD .
B. BD ⊥ SC . C. AC ⊥ SB . D. BC ⊥ SB .
Câu 4. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SO vuông góc với
mặt phẳng đáy. Góc giữa đường thẳng SD và ( ABCD) là A. SOA . B. SDA . C. SDO . D. SOD .
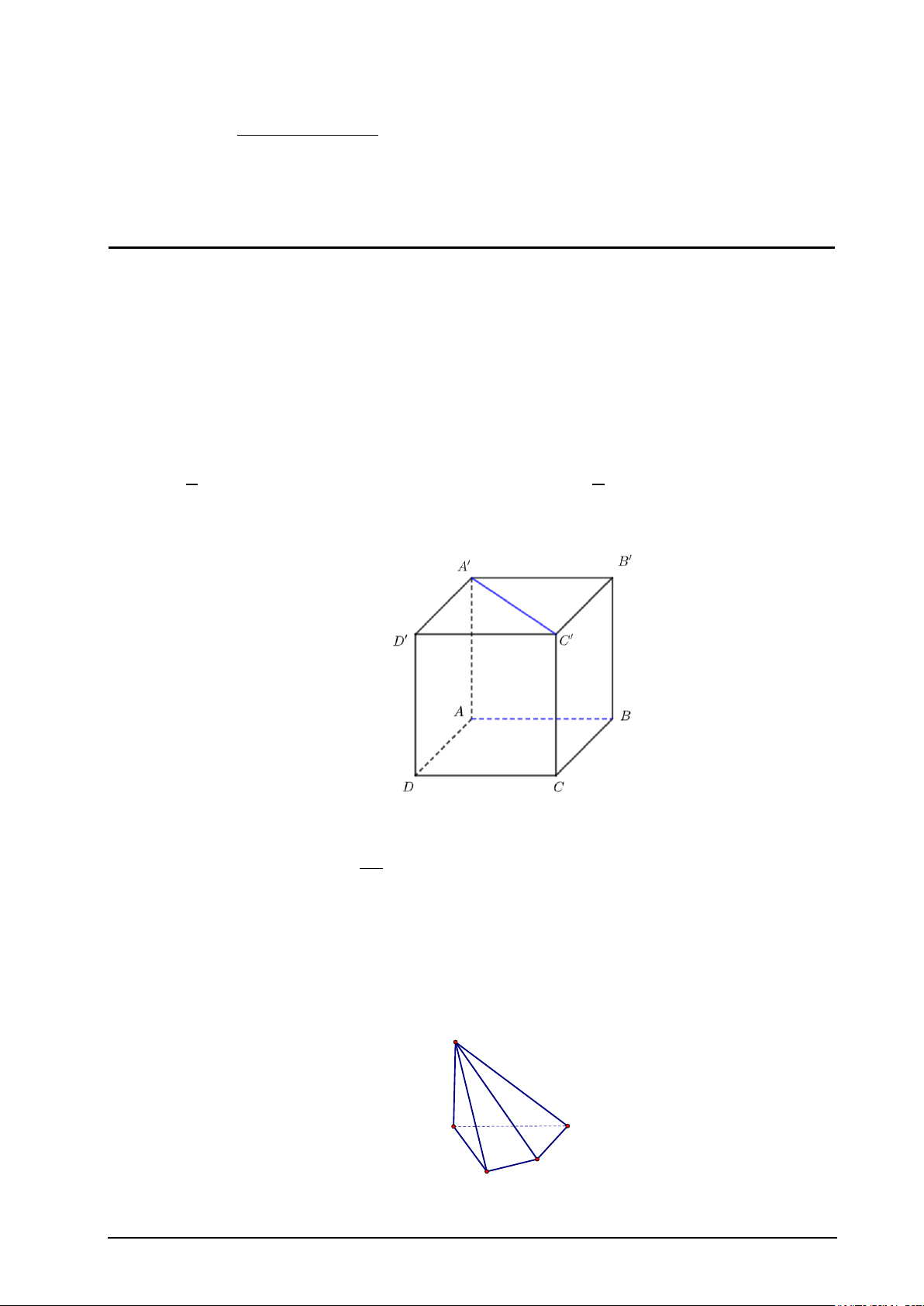
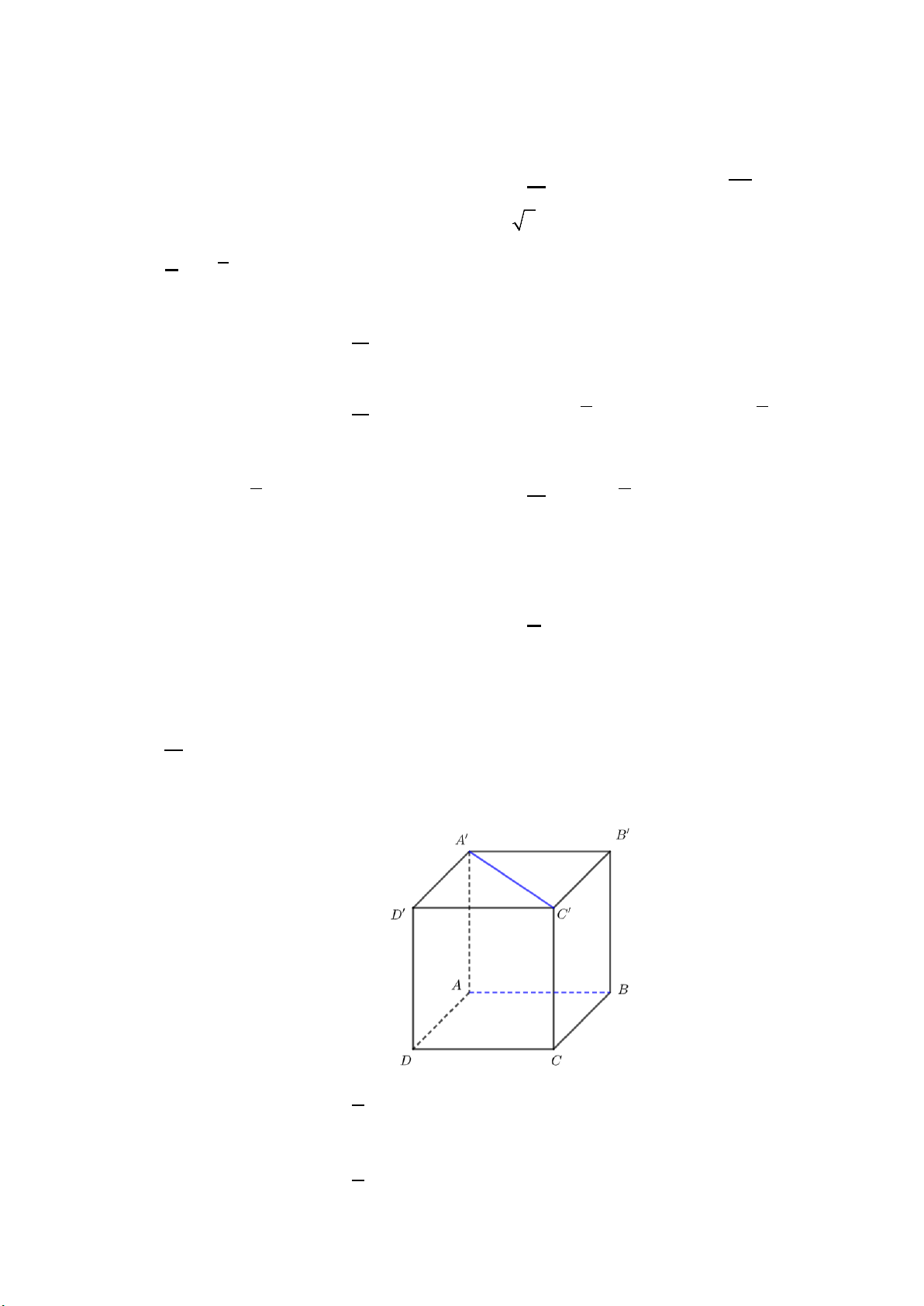
Câu 5. Cho hình lập phương ABC . D A′B C ′ D
′ ′ . Đường thẳng AB vuông góc với đường thẳng nào sau đây: A. CD . B. AC . C. BD . D. A'D'.
Câu 6. Với a và b là các số thực dương. Biểu thức ( 2 log a b bằng a )
A. 1+ 2log b .
B. 2 − log b .
C. 2 + log b. D. 2log b . a a a a
Câu 7. Nghiệm của phương trình log 2x −1 = 2 là 3 ( )
A. x = 5.
B. x = 3. C. 7 x = . D. 9 x = . 2 2 Mã đề 101 Trang 1/4
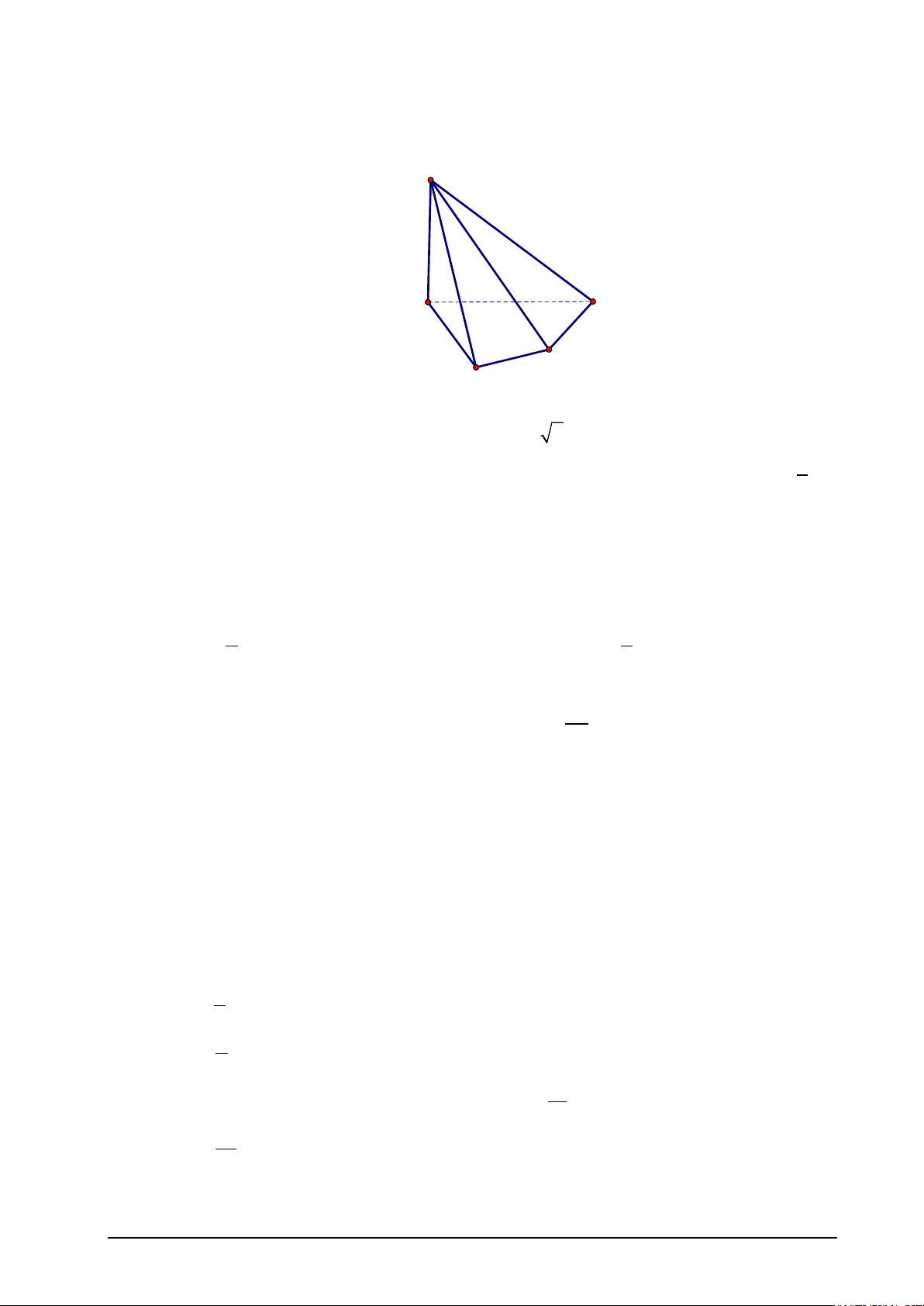
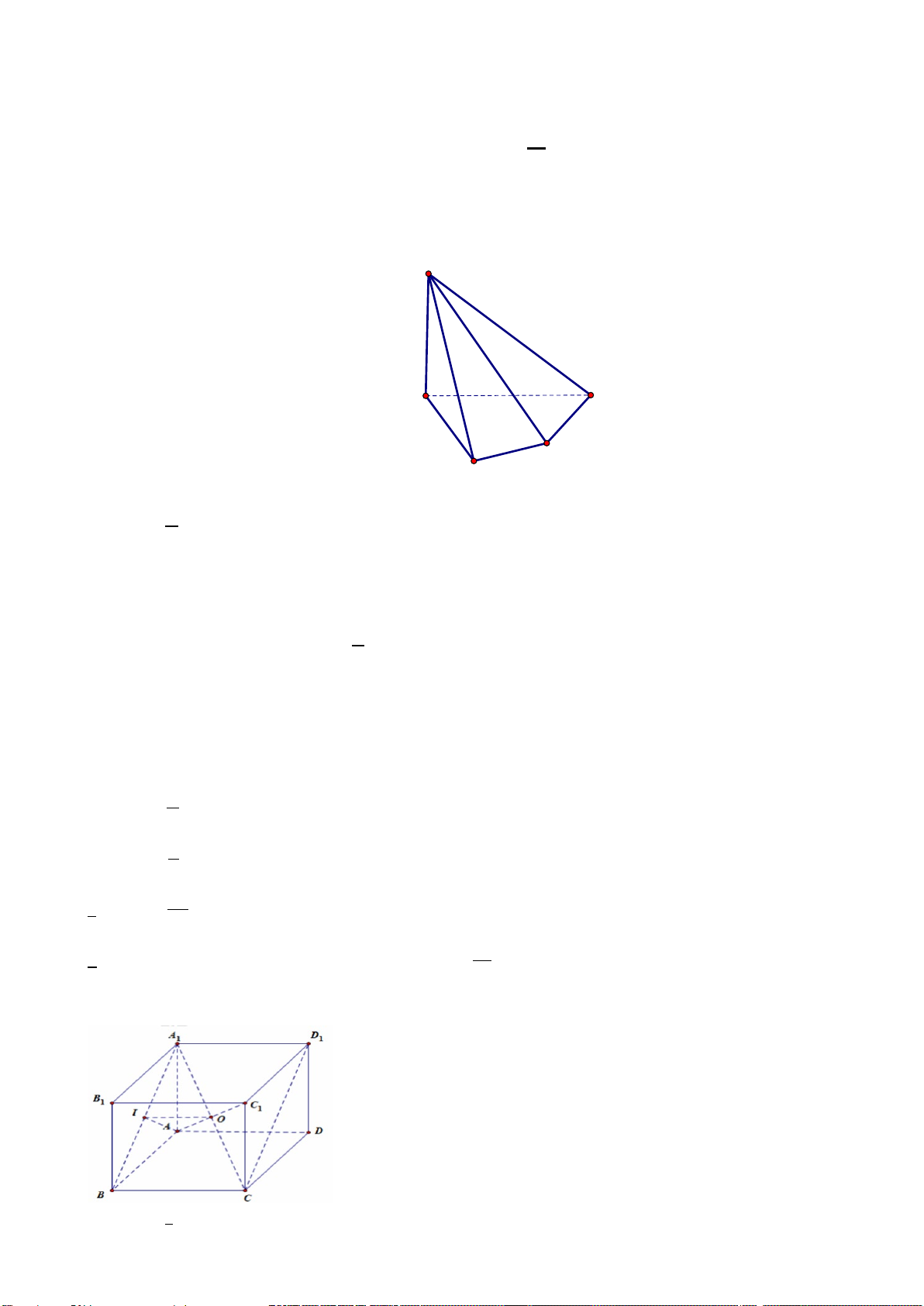
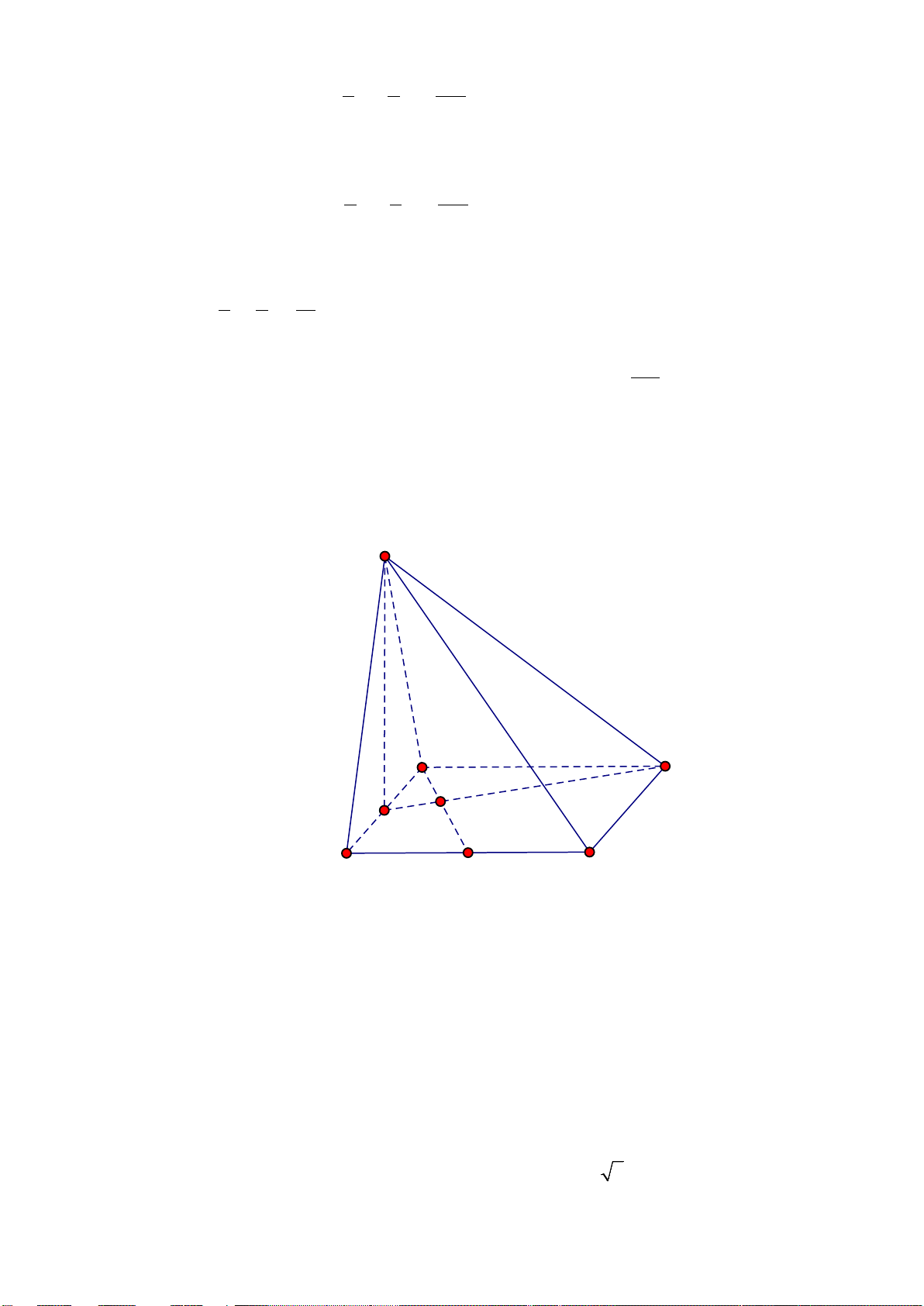
Câu 8. Cho hình chóp S.ABCD (tham khảo hình vẽ), biết SA ⊥ ( ABCD) . Hình chiếu vuông
góc của đường thẳng SC lên mặt phẳng ( ABCD) là S A D C B A. SA. B. AC . C. BC . D. SC .
Câu 9. Cho a là số thực dương khác 1. Tính 3
I = log a a
A. I = 0. B. I = 3 − .
C. I = 3. D. 1 I = . 3
Câu 10. Nếu hai biến cố A và B xung khắc thì xác suất của biến cố P( A∪ B) bằng
A. P( A).P(B)
B. 1− P( A) − P(B)
C. P( A).P(B) − P( A) − P(B)
D. P( A) + P(B)
Câu 11. Tìm tập nghiệm S của phương trình 2 2 5 x −x = 5. A.  1 S 1;  =   − . B. S = {0; } 2 . C. 1 S  = 0; . D. S = ∅ . 2     2
Câu 12. Cho a > 0 , m , n∈ . Khẳng định nào sau đây đúng? m
A. ( m)n = ( n)m a a . B. a n−m = a . n a C. m n m n a a a + + = . D. m. n m n a a a − = .
PHẦN II. Trắc nghiệm đúng/sai
Từ câu 1 đến câu 2, mỗi ý a, b, c, d học sinh chỉ được chọn Đ/S. Điểm tối đa mỗi câu là 1 điểm
Câu 1. Một hộp đựng 4 viên bi màu xanh, 3 viên bi màu đỏ và 2 viên bi màu vàng. Chọn
ngẫu nhiên 2 viên bi từ hộp trên. Gọi A là biến cố: "Chọn được 2 viên bi màu xanh" B là
biến cố "Chọn được 2 viên bi màu đỏ", C là biến cố "Chọn được 2 viên bi màu vàng" . Khi đó: a) 1 P(B) = 8 b) 1 P( ) A = 7
c) Xác suất để chọn được 2 viên bi cùng màu bằng 5 18 d) 1 P(C) = 36 Mã đề 101 Trang 2/4
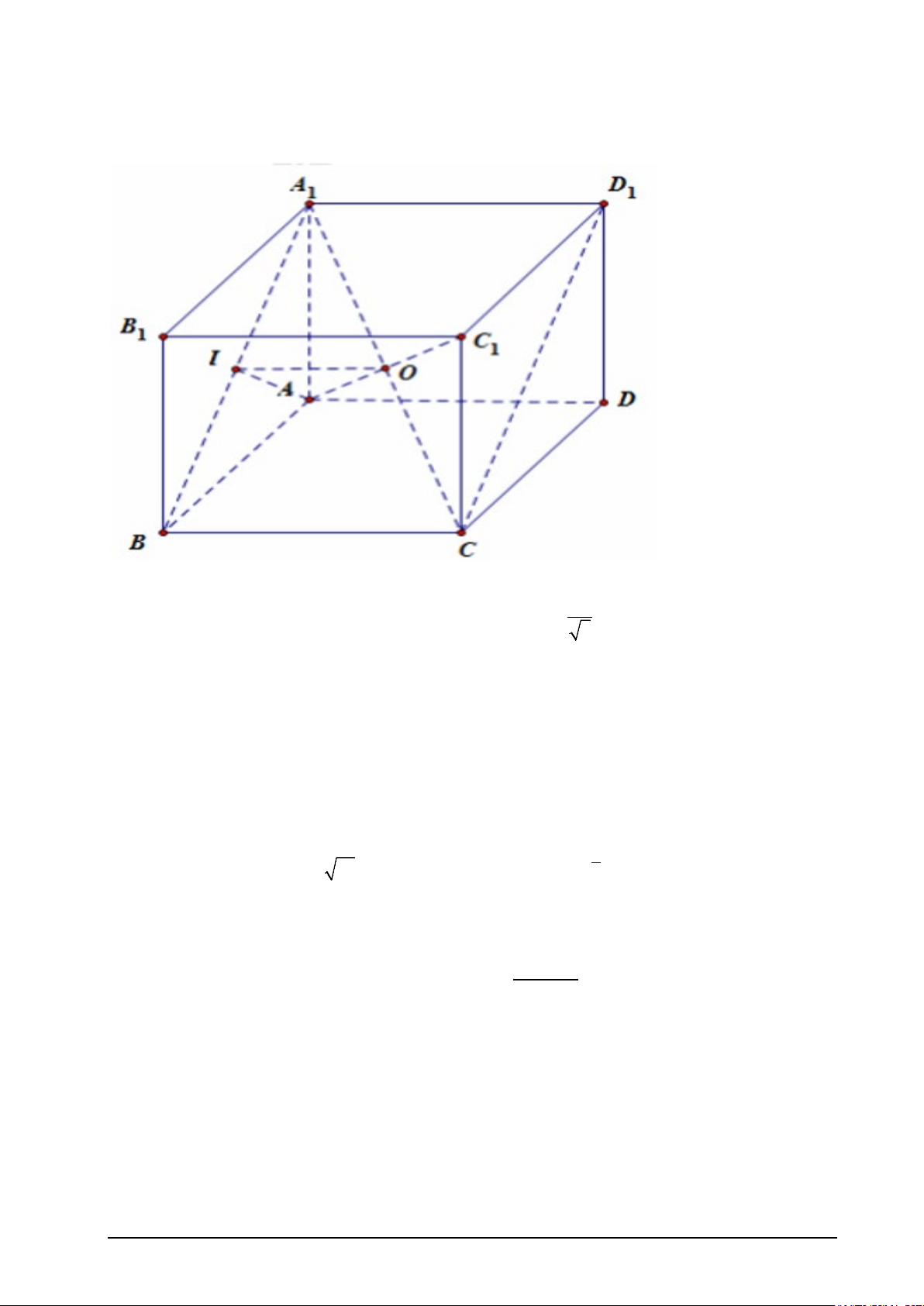
Câu 2. Cho hình lập phương ABC . D A B C D cạnh 1 1 1 1
a . Xét tính đúng sai của các khẳng định sau
a) AB ⊥ BCD A 1 ( 1 1 )
b) Gọi α là góc giữa AC và mp( A BCD thì 2 tanα = 1 1 ) 1 3
c) AA ⊥ ABCD 1 ( )
d) AB ⊥ CC 1
PHẦN III. Trắc nghiệm trả lời ngắn
Từ câu 1 đến câu 4, học sinh chỉ trả lời đáp số. Mỗi câu trả lời đúng được 0,5 điểm
Câu 1. Ba người cùng bắn vào 1 bia Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng
đích lần lượt là 0,8; 0,6 ;0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:… m
Câu 2. Cho biểu thức 4 5
P = x , với x > 0 . Ta biến đổi n
P = x . Tính tổng m+n =….
Câu 3. Một lớp học 40 học sinh gồm có 15 học sinh nam giỏi Toán và 8 học sinh nữ giỏi
Lí. Chọn ngẫu nhiên một học sinh. Hãy tính xác suất để chọn được một nam sinh giỏi
Toán hay một nữ sinh giỏi Lý. Câu 4. Cho 3 +
a = log 5, b = log 5. Biết log 250 ab nb = với , n q ∈ 2 3 24  . Tính giá trị biểu a + qb
thức A = 3nq . PHẦN IV. Tự luận
Học sinh trình bày chi tiết bài làm vào tờ giấy thi. Điểm tối đa mỗi câu là 0,5 điểm ĐỀ LẺ
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số y = log
x đồng biến trên 2
a −2a+2−m
(0;+∞) với mọi số thực a . Mã đề 101 Trang 3/4
Câu 2. Giải phương trình 9x 5.3x − + 6 = 0
Câu 3. Một hộp có 5 bút bi mực xanh và 6 bút bi mực đỏ có kích thước và khối lượng như
nhau. Lấy bút ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một bút bi, ghi lại
màu mực và bỏ lại bút bi đó vào trong hộp. Tính xác suất của biến cố lần thứ nhất lấy được bút
bi mực màu xanh hoặc lần thứ hai lấy được bút bi mực màu đỏ
Câu 4. Trong đợt thi kiểm tra giữa học kỳ 2 vừa qua, đề thi môn Toán Khối 12 làm theo cấu trúc
mới của dạng đề minh họa thi TN 2025. Đề thi có 3 phần: PHẦN I-Câu trắc nghiệm nhiều
phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một
phương án, trả lời đúng mỗi câu được 0,25 điểm. PHẦN II-Câu trắc nghiệm đúng sai. Thí sinh
trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Trong
mỗi câu: Trả lời đúng một ý được 0,1 điểm, trả lời đúng hai ý được 0,25 điểm, trả lời đúng ba ý
được 0,5 điểm, trả lời đúng cả bốn ý được 1 điểm và PHẦN III-Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6, mỗi câu trả lời đúng được 0,5 điểm. Bạn Bình tham gia thi và
đã chắc chắn làm được 8 điểm, chỉ còn hai câu là Câu 3 và Câu 4 ở PHẦN II bạn không hiểu nên
bạn chọn ngẫu nhiên đúng hoặc sai tất cả các ý của hai câu này. Tính xác suất để bài thi của bạn Bình đạt trên 9 điểm.
Câu 5. Cho hình vuông ABCD , gọi H, K lần lượt là trung điểm các cạnh AB, AD . Trên đường
thẳng vuông góc với mặt phẳng ( ABCD) tại H lấy một điểm S khác H . Chứng minh rằng CK vuông góc SD.
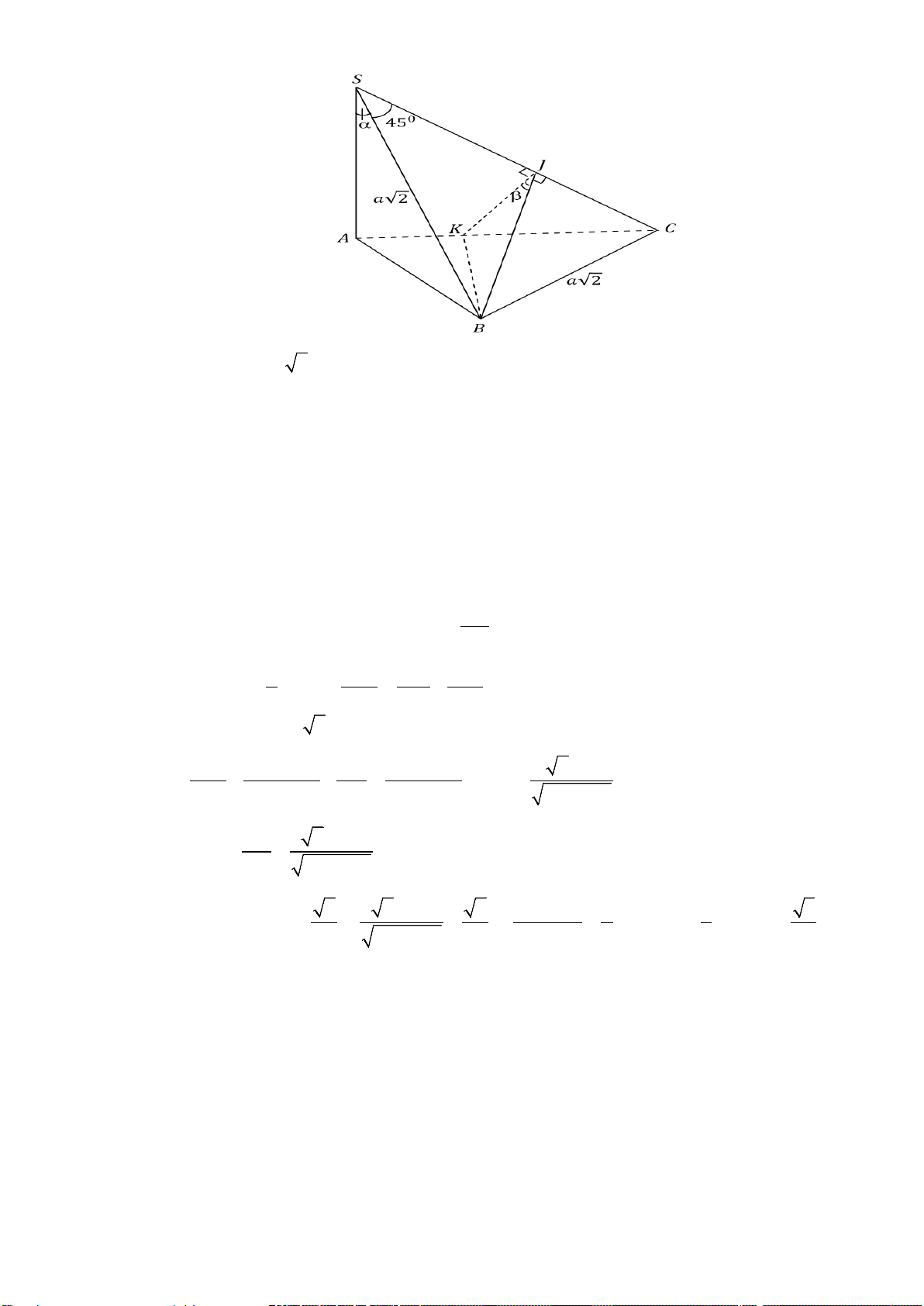
Câu 6. Cho hình chóp S.ABC có: SA ⊥ ( ABC),SB = BC = a 2, BSC = 45 ,° ASB = α . A ∆ BC
vuông tại B . Xác định sin α để góc nhị diện [ ,
A SC, B] = 45° .
------------ Hết ------------
Thí sinh không được sử dụng tài liệu, Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:……….………. .….………Số báo danh……………………… Mã đề 101 Trang 4/4
SỞ GD&ĐT HẢI DƯƠNG
ĐỀ KIỂM TRA GIỮA HỌC KÌ II
TRƯỜNG THPT THANH MIỆN 2
Môn: TOÁN 11; Năm học 2024-2025
Thời gian làm bài: 90 phút không kể giao đề ĐỀ CHÍNH THỨC
Họ và tên: ............................................................................ Số báo danh: ....... Mã đề 102
PHẦN I. Trắc nghiệm nhiều lựa chọn
Từ câu 1 đến câu 12, học sinh chỉ được chọn 1 trong 4 phương án A, B, C, D. Mỗi câu
trả lời đúng học sinh được 0,25 điểm.
Câu 1. Với a và b là các số thực dương. Biểu thức ( 2 log a b bằng a ) A. 2 + log b . b . + b . − b . a
B. 2loga
C. 1 2loga D. 2 loga
Câu 2. Nghiệm của phương trình log 2x −1 = 2 3 ( ) là A. 7 x = .
B. x = 5. C. 9 x = . D. x = 3. 2 2
Câu 3. Cho hình lập phương ABC . D A′B C ′ D
′ ′ . Đường thẳng AB vuông góc với đường thẳng nào sau đây: A. A'D'. B. BD . C. CD . D. AC .
Câu 4. Cho a > 0 , m , n∈ . Khẳng định nào sau đây đúng? m A. m n m n a a a + + = . B. a n−m = a . C. m. n m n a a a − =
. D. ( m)n = ( n)m a a . n a
Câu 5. Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA vuông góc với đáy. Biểu thức nào sau đây đúng:
A. BC ⊥ SB .
B. CD ⊥ SD .
C. BD ⊥ SC . D. AC ⊥ SB .
Câu 6. Cho hình chóp S.ABCD (tham khảo hình vẽ), biết SA ⊥ ( ABCD) . Hình chiếu vuông góc
của đường thẳng SC lên mặt phẳng ( ABCD) là S A D C B A. AC . B. SC . C. SA. D. BC . Mã đề 102 Trang 1/4
Câu 7. Cho a là số thực dương khác 1. Tính 3
I = log a a A. I = 3 − . B. 1 I = .
C. I = 3 . D. I = 0. 3
Câu 8. Nếu hai biến cố A và B xung khắc thì xác suất của biến cố P( A∪ B) bằng
A. P( A).P(B)
B. P( A).P(B) − P( A) − P(B)
C. P( A) + P(B)
D. 1− P( A) − P(B)
Câu 9. Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SO vuông góc với mặt
phẳng đáy. Góc giữa đường thẳng SD và ( ABCD) là A. SDA . B. SOD . C. SOA . D. SDO .
Câu 10. Trong không gian, cho đường thẳng d và điểm O . Qua O có bao nhiêu đường thẳng
vuông góc với đường thẳng d ? A. vô số. B. 2. C. 3. D. 1.
Câu 11. Tìm tập nghiệm S của phương trình 2 2 5 x −x = 5.
A. S = ∅ . B. 1 S 0;  =    . C. 1 S = 1;  − . D. S = {0; } 2 . 2     2
Câu 12. Cho hai biến cố A và B . Biến cố " A hoặc B xảy ra" được gọi là:
A. Biến cố xung khắc của A và . B
B. Biến cố giao của A và . B
C. Biến cố hợp của A và . B
D. Biến cố đối của . A
PHẦN II. Trắc nghiệm đúng/sai
Từ câu 1 đến câu 2, mỗi ý a, b, c, d học sinh chỉ được chọn Đ/S. Điểm tối đa mỗi câu là 1 điểm
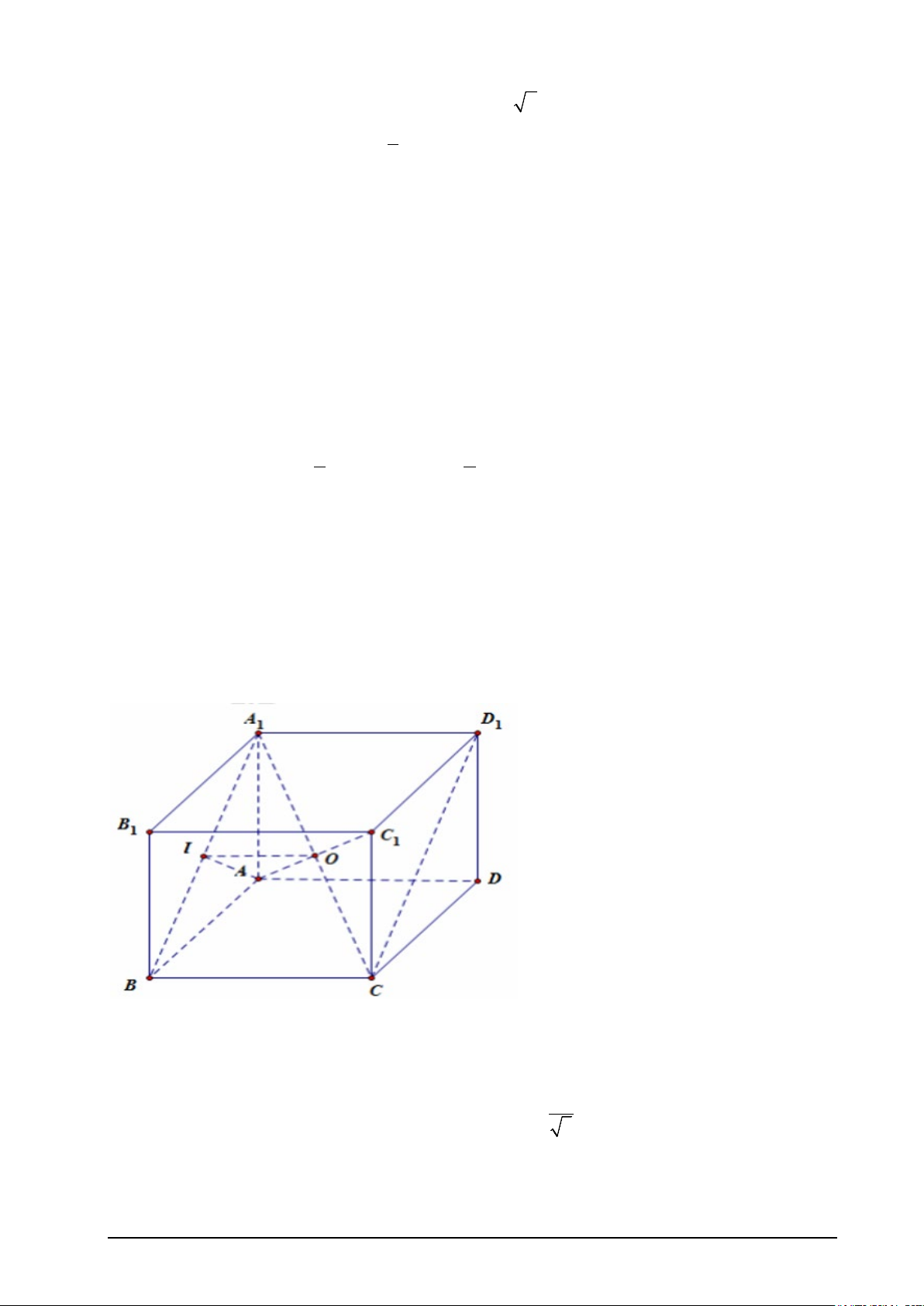
Câu 1. Cho hình lập phương ABC . D A B C D
1 1 1 1 cạnh a . Xét tính đúng sai của các khẳng định sau:
a) AB ⊥ BCD A 1 ( 1 1 )
b) AA ⊥ ABCD 1 ( )
c) AB ⊥ CC1 d) 2
Gọi α là góc giữa AC tanα = 1 và mp ( A BCD 1 1 ) thì 3
Câu 2. Một hộp đựng 4 viên bi màu xanh, 3 viên bi màu đỏ và 2 viên bi màu vàng. Chọn ngẫu
nhiên 2 viên bi từ hộp trên. Gọi A là biến cố: "Chọn được 2 viên bi màu xanh" B là biến cố
"Chọn được 2 viên bi màu đỏ", C là biến cố "Chọn được 2 viên bi màu vàng" . Khi đó: Mã đề 102 Trang 2/4
a) Xác suất để chọn được 2 viên bi cùng màu bằng 5 18 b) 1 P(C) = 36 c) 1 P( ) A = 7 d) 1 P(B) = 8
PHẦN III. Trắc nghiệm trả lời ngắn
Từ câu 1 đến câu 4, học sinh chỉ trả lời đáp số. Mỗi câu trả lời đúng được 0,5 điểm
Câu 1. Một lớp học 40 học sinh gồm có 15 học sinh nam giỏi Toán và 8 học sinh nữ giỏi Lí.
Chọn ngẫu nhiên một học sinh. Hãy tính xác suất để chọn được một nam sinh giỏi Toán hay một nữ sinh giỏi Lý
Câu 2. Ba người cùng bắn vào 1 bia Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần
lượt là 0,8; 0,6 ;0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:…….. Câu 3. Cho 3 +
a = log 5, b = log 5. Biết log 250 ab nb = với , n q ∈ 2 3 24
 . Tính giá trị biểu thức a + qb A = 3nq . m
Câu 4. Cho biểu thức 4 5
P = x , với x > 0 . Ta biến đổi n
P = x Tính tổng m+n =…… PHẦN IV. Tự luận
Học sinh trình bày chi tiết bài làm vào tờ giấy thi. Điểm tối đa mỗi câu là 0,5 điểm ĐỀ CHẴN
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số y = log
x đồng biến trên 2
a −2a+3−m
(0;+∞) với mọi số thực a .
Câu 2. Giải phương trình 4x 3.2x − + 2 = 0
Câu 3. Một hộp có 4 bút bi mực xanh và 5 bút bi mực đỏ có kích thước và khối lượng như nhau.
Lấy bút ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một bút bi, ghi lại màu mực
và bỏ lại bút bi đó vào trong hộp. Tính xác suất của biến cố lần thứ nhất lấy được bút bi mực
màu xanh và lần thứ hai lấy được bút bi mực màu đỏ
Câu 4. Trong đợt thi kiểm tra giữa học kỳ 2 vừa qua, đề thi môn Toán Khối 12 làm theo cấu trúc
mới của dạng đề minh họa thi TN 2025. Đề thi có 3 phần: PHẦN I-Câu trắc nghiệm nhiều
phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một
phương án, trả lời đúng mỗi câu được 0,25 điểm. PHẦN II-Câu trắc nghiệm đúng sai. Thí sinh
trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc sai. Trong
mỗi câu: Trả lời đúng một ý được 0,1 điểm, trả lời đúng hai ý được 0,25 điểm, trả lời đúng ba ý
được 0,5 điểm, trả lời đúng cả bốn ý được 1 điểm và PHẦN III-Câu trắc nghiệm trả lời ngắn.
Thí sinh trả lời từ câu 1 đến câu 6, mỗi câu trả lời đúng được 0,5 điểm. Bạn Bình tham gia thi và
đã chắc chắn làm được 8 điểm, còn hai câu là Câu 3 và Câu 4 ở PHẦN II bạn không hiểu nên bạn
chọn ngẫu nhiên đúng hoặc sai tất cả các ý của hai câu này. Tính xác suất để bài thi của bạn Bình đạt đúng 9 điểm.
Câu 5. Cho hình vuông ABCD , gọi H, M lần lượt là trung điểm các cạnh AB, BC . Trên đường
thẳng vuông góc với mặt phẳng ( ABCD) tại H lấy một điểm S khác H . Chứng minh rằng AM vuông góc SD. Mã đề 102 Trang 3/4
Câu 6. Cho hình chóp S.ABC có: SA ⊥ ( ABC),SB = BC = a 2, BSC = 45 ,° ASB = α . A ∆ BC
vuông tại B . Xác định sin α để góc nhị diện [ ,
A SC, B] = 30°.
------------ Hết ------------
Thí sinh không được sử dụng tài liệu, Cán bộ coi thi không giải thích gì thêm
Họ và tên thí sinh:……….………. .….………Số báo danh……………………… Mã đề 102 Trang 4/4
ĐÁP ÁN CHẤM TRẮC NGHIỆM TOÁN 11. THANG ĐIỂM 7 PHẦN I PHẦN II PHẦN III 12 2 2 Đề\câu 101 102 103 104 1 C A C B 2 A B B B 3 B A B B 4 C D B C 5 D C D A 6 C A B D 7 A B A C 8 B C D A 9 D D C B 10 D A A C 11 A C C B 12 A C D B 1 SSDD DDDS DDDS SDDD 2 DSDD DDSS SDSD DDSS 1 0,46 0.58 0,46 0.58 2 9 0,46 9 0,46 3 0.58 9 0.58 9 4 9 9 9 9
KIỂM TRA GIỮA KÌ 2 TOÁN 11 PHẦN I
Câu 1. Cho a > 0 , m , n∈ . Khẳng định nào sau đây đúng? m A. m n m n a a a + + = . B. m. n m n a a a − = .
C. ( m)n = ( n)m a a . D. a n−m = a . n a
Câu 2: Cho a là số thực dương khác 1. Tính 3
I = log a a A. 1 I = . B. I = 3 . C. I = 0. D. I = 3 − . 3
Câu 3. Với a và b là các số thực dương. Biểu thức ( 2 log a b bằng a )
A. 2 − log b . + b . + b . b . a B. 2 loga C. 1 2loga D. 2loga
Câu 4. Nghiệm của phương trình log 2x −1 = 2 là 3 ( ) A. x = 3. B. x = 5. C. 9 x = . D. 7 x = . 2 2
Câu 5. Tìm tập nghiệm S của phương trình 2 2 5 x −x = 5. A. 1 S 0;  =    . B. S = {0; } 2 . C. 1 S = 1;  − . D. S = ∅ . 2     2
Câu 6. Nếu hai biến cố A và B xung khắc thì xác suất của biến cố P( A∪ B) bằng
A. 1− P( A) − P(B)
B. P( A).P(B)
C. P( A).P(B) − P( A) − P(B)
D. P( A) + P(B)
Câu 7: Cho hai biến cố A và B . Biến cố " A hoặc B xảy ra" được gọi là:
A. Biến cố giao của A và . B
B. Biến cố đối của . A
C. Biến cố hợp của A và . B
D. Biến cố xung khắc của A và . B
Câu 8: Cho hình lập phương ABC . D A′B C ′ D
′ ′ . Đường thẳng AB vuông góc với đường thẳng nào sau đây: A. CD . B. A'D'. C. AC . D. BD .
Câu 9: Trong không gian, cho đường thẳng d và điểm O . Qua O có bao nhiêu đường thẳng vuông
góc với đường thẳng d ? A. 3. B. vô số. C. 1. D. 2.
Câu 10: Cho hình chóp S.ABCD có đáy ABCD là hình thoi, SA vuông góc với đáy. Biểu thức nào sau đây đúng:
A. BC ⊥ SB .
B. AC ⊥ SB .
C. BD ⊥ SC .
D. CD ⊥ SD .
Câu 11: Cho hình chóp S.ABCD (tham khảo hình vẽ), biết SA ⊥ ( ABCD) . Hình chiếu vuông góc
của đường thẳng SC lên mặt phẳng ( ABCD) là S A D C B A. AC . B. SA. C. BC . D. SC .
Câu 12: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SO vuông góc với mặt
phẳng đáy. Góc giữa đường thẳng SD và ( ABCD) là A. SDA . B. SDO . C. SOD . D. SOA . PHẦN II
Câu 1. Một hộp đựng 4 viên bi màu xanh, 3 viên bi màu đỏ và 2 viên bi màu vàng. Chọn ngẫu nhiên 2
viên bi từ hộp trên. Gọi A là biến cố: "Chọn được 2 viên bi màu xanh" B là biến cố "Chọn được 2
viên bi màu đỏ", C là biến cố "Chọn được 2 viên bi màu vàng" . Khi đó: a) 1 P( ) A = 7 b) 1 P(B) = 8 c) 1 P(C) = 36
d) Xác suất để chọn được 2 viên bi cùng màu bằng 5 18
Câu 2: Cho hình lập phương ABC . D A B C D
1 1 1 1 cạnh a . Xét tính đúng sai của các khẳng định sau: a) AB ⊥ CC1 b) AA ⊥ ABCD 1 ( )
c) AB ⊥ BCD A 1 ( 1 1 ) 2
d) Gọi α là góc giữa AC tanα = 1 và mp ( A BCD thì 1 1 ) 3 PHẦN III m
Câu 1. Cho biểu thức 4 5
P = x , với x > 0 . Ta biến đổi n
P = x Tính tổng m+n = A. 9 Câu 2. Cho 3 +
a = log 5, b = log 5. Biết log 250 ab nb = với , n q ∈ 2 3 24
 . Tính giá trị biểu thức a + qb A = 3nq . B. 9
Câu 3. Một lớp học 40 học sinh gồm có 15 học sinh nam giỏi Toán và 8 học sinh nữ giỏi Lí. Chọn
ngẫu nhiên một học sinh. Hãy tính xác suất để chọn được một nam sinh giỏi toán hay một nữ sinh giỏi Lí A. 0.58
Câu 4. Ba người cùng bắn vào 1 bia Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt
là 0,8; 0,6 ;0,5. Xác suất để có đúng 2 người bắn trúng đích bằng: A. 0,46 TỰ LUẬN ĐỀ LẺ
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số y = log
x đồng biến trên (0;+∞) với 2
a −2a+2−m mọi số thực a . Lời giải
Để hàm số đã cho đồng biến trên (0;+∞) với mọi số thực a thì 2
a − 2a + 2 − m >1 , a ∀ ∈  . Suy ra 2
m < a − 2a +1, a ∀ ∈  . Đặt f (a) 2
= a − 2a +1 = (a − )2 1 ≥ 0, a ∀ ∈  .
Do đó ycbt ⇔ m < 0 .
Vậy m < 0 thỏa mãn đề bài.
Câu 2. Giải phương trình 9x 5.3x − + 6 = 0 Ta có 9x 5.3x − + 6 = 0 ( 23)x 5.3x ⇔ − + 6 = 0 ( x)2 3 5.3x ⇔ − + 6 = 0 (∗) Đặt 3x t = > 0 . t = 2() t = 3x = 2 x = log 2 Khi đó: (∗) 2
⇔ t − 5t + 6 = 0 ⇔  ⇔  3 ⇔  t = 3  () t = 3x = 3 x = 1
Vậy nghiệm của phương trình là x =1; x = log 2 3 .
Câu 3. Một hộp có 5 bút bi mực xanh và 6 bút bi mực đỏ có kích thước và khối lượng như nhau.
Lấy bút ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một bút bi, ghi lại màu
mực và bỏ lại bút bi đó vào trong hộp. Tính xác suất của biến cố lần thứ nhất lấy được bút
bi mực màu xanh hoặc lần thứ hai lấy được bút bi mực màu đỏ Lời giải
A: “ Lần thứ nhất lấy được bút bi mực màu xanh ”.
B : “Lần thứ hai lấy được bút bi mực màu đỏ”.
Biến cố lần thứ nhất lấy được bút bi mực màu xanh hoặc lần thứ hai lấy được bút bi mực
màu đỏ là A∪ B P( A) 5 = 11 P(B) 6 = 11
Hai biến cố A và B độc lập nên P( A∩ B) = P( A) P(B) 5 6 30 . = . = . 11 11 121 5 6 30 91
Ta có: P( A∪ B) = P( A) + P(B) − P( A∩ B) = + − = . 11 11 121 121
Câu 4. Trong đợt thi kiểm tra giữa học kỳ 2 vừa qua, đề thi môn Toán Khối 12 làm theo cấu trúc mới
của dạng đề minh họa thi TN 2025. Đề thi có 3 phần: PHẦN I-Câu trắc nghiệm nhiều
phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một
phương án, trả lời đúng mỗi câu được 0,25 điểm. PHẦN II-Câu trắc nghiệm đúng sai. Thí
sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc
sai. Trong mỗi câu: Trả lời đúng một ý được 0,1 điểm, trả lời đúng hai ý được 0,25 điểm, trả
lời đúng ba ý được 0,5 điểm, trả lời đúng cả bốn ý được 1 điểm và PHẦN III-Câu trắc
nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6, mỗi câu trả lời đúng được 0,5 điểm.
Bạn Bình tham gia thi và đã chắc chắn làm được 8 điểm, chỉ còn hai câu là Câu 3 và Câu 4 ở
PHẦN II bạn không hiểu nên bạn chọn ngẫu nhiên đúng hoặc sai tất cả các ý của hai câu
này. Tính xác suất để bài thi của bạn Bình đạt trên 9 điểm. Lời giải
Ta có bài thi của Bình đạt trên 9 điểm khi bạn làm đúng cả 1 trong 2 câu và câu còn lại phải có điểm.
TH1: Bình làm đúng cả câu 3 và câu 4 có điểm thì xác suất là 4 4    1   1  15
p =   .1−   = . 1 2  2      256  
TH2: Bình làm đúng cả câu 4 và câu 3 có điểm thì xác suất là 4 4    1   1  15
p =   .1−   = . 2 2  2      256   4 4
Xác suất làm đúng hết cả hai câu là 1  1  1 p   =   . = . 3 2  2     256 15 1 29
Khi đó xác suất để Bình đạt trên 9 điểm là p = p + p − p = 2. − = 1 2 3 . 256 256 256
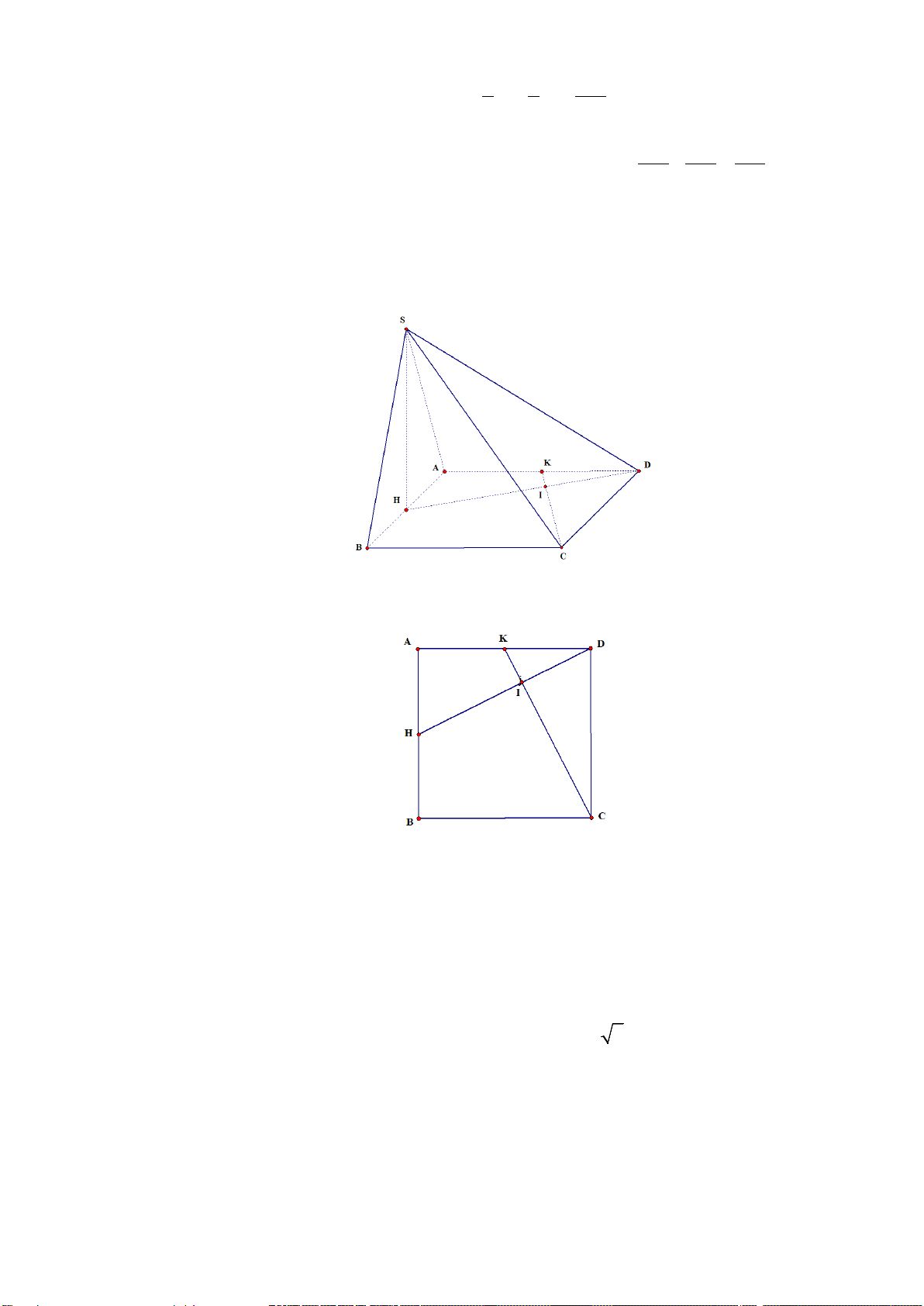
Câu 5. Cho hình vuông ABCD , gọi H, K lần lượt là trung điểm các cạnh AB, AD . Trên đường
thẳng vuông góc với mặt phẳng ( ABCD) tại H lấy một điểm S khác H . Chứng minh rằng
CK vuông góc SD. Lời giải
Trong mặt phẳng ( ABCD) , gọi I là giao điểm của CK và DH . Ta có ∆ = ∆ ⇒  =  ⇒  +  0 = ⇒  0 HAD KDC AHD DKC IDK DKC 90
KID = 90 hay CK ⊥ DH
Mặt khác, vì SH ⊥ ( ABCD) mà CK ⊂ ( ABCD) nên SH ⊥ CK
Do đó CK ⊥ (SHD) mà SD ⊂ (SHD)
Suy ra CK ⊥ SD .
Câu 6. Cho hình chóp S.ABC có: SA ⊥ ( ABC),SB = BC = a 2, BSC = 45 ,° ASB = α . A ∆ BC
vuông tại B . Xác định sin α để góc nhị diện [ ,
A SC, B] = 45° . Lời giải
Vì SB = BC = a 2,
BSC = 45° nên S
∆ BC vuông cân tại B . Gọi J là trung điểm của SC .
Khi đó BJ ⊥ SC ( )
1 . Kẻ BK ⊥ AC , (K ∈ AC) . BK ⊥ AC Ta có: 
⇒ BK ⊥ (SAC) ⇒ BK ⊥ SC (2) và BK ⊥ KJ . BK ⊥ SA Từ ( )
1 và (2) suy ra: SC ⊥ (BJK ) ⇒ SC ⊥ KJ (3). Từ ( )
1 và (3) suy ra góc nhị diện [ , A SC, B] = BJK = β. Trong B
∆ JK vuông tại K ta có sin BK β = . BJ Lại có: 1 1 1 1
BJ = SC = a, = + ( A
∆ BC vuông tại B ), 2 2 2 2 BK BA BC AB = S .
B sin α = a 2.sin α . 2 1 1 1 1+ sin α a 2 sin BK α ⇒ = + = ⇒ = 2 2 2 2 2 2 2 BK 2a sin α 2a 2a sin α 1+ sin α BK 2 sin sin α ⇒ β = = . 2 BJ 1+ sin α 2 2 2 sin α 2 sin α 1 1 3 β = 45° thì 2 sinβ = ⇒ = ⇔ = ⇔ sin α = ⇒ sin α = . 2 2 2 1+ sin α 2 1+ sin α 4 3 3 ĐỀ CHẴN
Câu 1. Tìm tất cả các giá trị của tham số m để hàm số y = log
x đồng biến trên (0;+∞) với 2
a −2a+3−m mọi số thực a . Lời giải
Để hàm số đã cho đồng biến trên (0;+∞) với mọi số thực a thì 2
a − 2a + 3− m >1 , a ∀ ∈  . Suy ra 2
m < a − 2a + 2, a ∀ ∈  . Đặt f (a) 2
= a − 2a + 2 = (a − )2 1 +1≥ 0, a ∀ ∈  .
Do đó ycbt ⇔ m <1.
Vậy m <1 thỏa mãn đề bài.
Câu 2. Giải phương trình 4x 3.2x − + 2 = 0 Ta có 4x 3.3x − + 2 = 0 ( 22)x 3.2x ⇔ − + 2 = 0 ( x)2 2 3.2x ⇔ − + 2 = 0, (∗) Đặt 2x t = > 0.
Phương trình (∗) trở thành 2t −3t + 2 = 0
Giải phương trình (*) ta tìm được t = 2(t / m); t =1(t / m)
Với t = 2 suy ra x =1 Với t =1 suy ra x =0
Vậy nghiệm của phương trình là x =1; x = 0 .
Câu 3. Một hộp có 4 bút bi mực xanh và 5 bút bi mực đỏ có kích thước và khối lượng như nhau. Lấy
bút ngẫu nhiên hai lần liên tiếp, trong đó mỗi lần lấy ngẫu nhiên một bút bi, ghi lại màu
mực và bỏ lại bút bi đó vào trong hộp. Tính xác suất của biến cố lần thứ nhất lấy được bút
bi mực màu xanh và lần thứ hai lấy được bút bi mực màu đỏ Lời giải
A: “ Lần thứ nhất lấy được bút bi mực màu xanh ”.
B : “Lần thứ hai lấy được bút bi mực màu đỏ”.
Biến cố lần thứ nhất lấy được bút bi mực màu xanh và lần thứ hai lấy được bút bi mực màu
đỏ là A∩ B P( A) 4 = 9 P(B) 5 = 9
Hai biến cố A và B độc lập nên P( A∩ B) = P( A) P(B) 4 5 20 . = . = . 9 9 81
Câu 4. Trong đợt thi kiểm tra giữa học kỳ 2 vừa qua, đề thi môn Toán Khối 12 làm theo cấu trúc mới
của dạng đề minh họa thi TN 2025. Đề thi có 3 phần: PHẦN I-Câu trắc nghiệm nhiều
phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12, mỗi câu hỏi thí sinh chỉ chọn một
phương án, trả lời đúng mỗi câu được 0,25 điểm. PHẦN II-Câu trắc nghiệm đúng sai. Thí
sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a), b), c), d) ở mỗi câu, thí sinh chọn đúng hoặc
sai. Trong mỗi câu: Trả lời đúng một ý được 0,1 điểm, trả lời đúng hai ý được 0,25 điểm, trả
lời đúng ba ý được 0,5 điểm, trả lời đúng cả bốn ý được 1 điểm và PHẦN III-Câu trắc
nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6, mỗi câu trả lời đúng được 0,5 điểm.
Bạn Bình tham gia thi và đã chắc chắn làm được 8 điểm, còn hai câu là Câu 3 và Câu 4 ở
PHẦN II bạn không hiểu nên bạn chọn ngẫu nhiên đúng hoặc sai tất cả các ý của hai câu
này. Tính xác suất để bài thi của bạn Bình đạt đúng 9 điểm. Lời giải
Ta có bài thi của Bình đạt đúng 9 điểm khi bạn làm đúng cả 4 ý của câu 3 thì câu 4 sai hết,
hoặc làm đúng cả 4 ý của câu 4 thì câu 3 sai hết, hoặc trong 2 câu hoặc mỗi câu chỉ sai 1 ý.
TH1: Bình làm đúng cả câu 3 và câu 4 sai hết thì xác suất là 4 4 1  1  1 p   =   . = . 1 2  2     256
TH2: Bình làm đúng cả câu 4 và câu 3 sai hết thì xác suất là 4 4 1  1  1 p   =   . = 2 2  2     256
TH3: Trong 2 câu, mỗi câu Bình sai 1 ý thì xác suất là 1  1  1 p   =  . = . 3 4  4      16 9
Khi đó xác suất để Bình đạt đúng 9 điểm là p = p + p + p = 1 2 3 . 128
Câu 5. Cho hình vuông ABCD , gọi H, M lần lượt là trung điểm các cạnh AB, BC . Trên đường
thẳng vuông góc với mặt phẳng ( ABCD) tại H lấy một điểm S khác H . Chứng minh rằng
AM vuông góc SD. Lời giải S A D I H B M C
Trong mặt phẳng ( ABCD) , gọi I là giao điểm của AM và DH . Ta có ∆ = ∆ ⇒  =  HAD MBA
AHD BMA suy ra  +  0 = ⇒  0 DHA HAI 90 HIA = 90 hay AM ⊥ DH
Mặt khác, vì SH ⊥ ( ABCD) mà AM ⊂ ( ABCD) nên SH ⊥ AM
Do đó AM ⊥ (SHD) mà SD ⊂ (SHD)
Suy ra AM ⊥ SD .
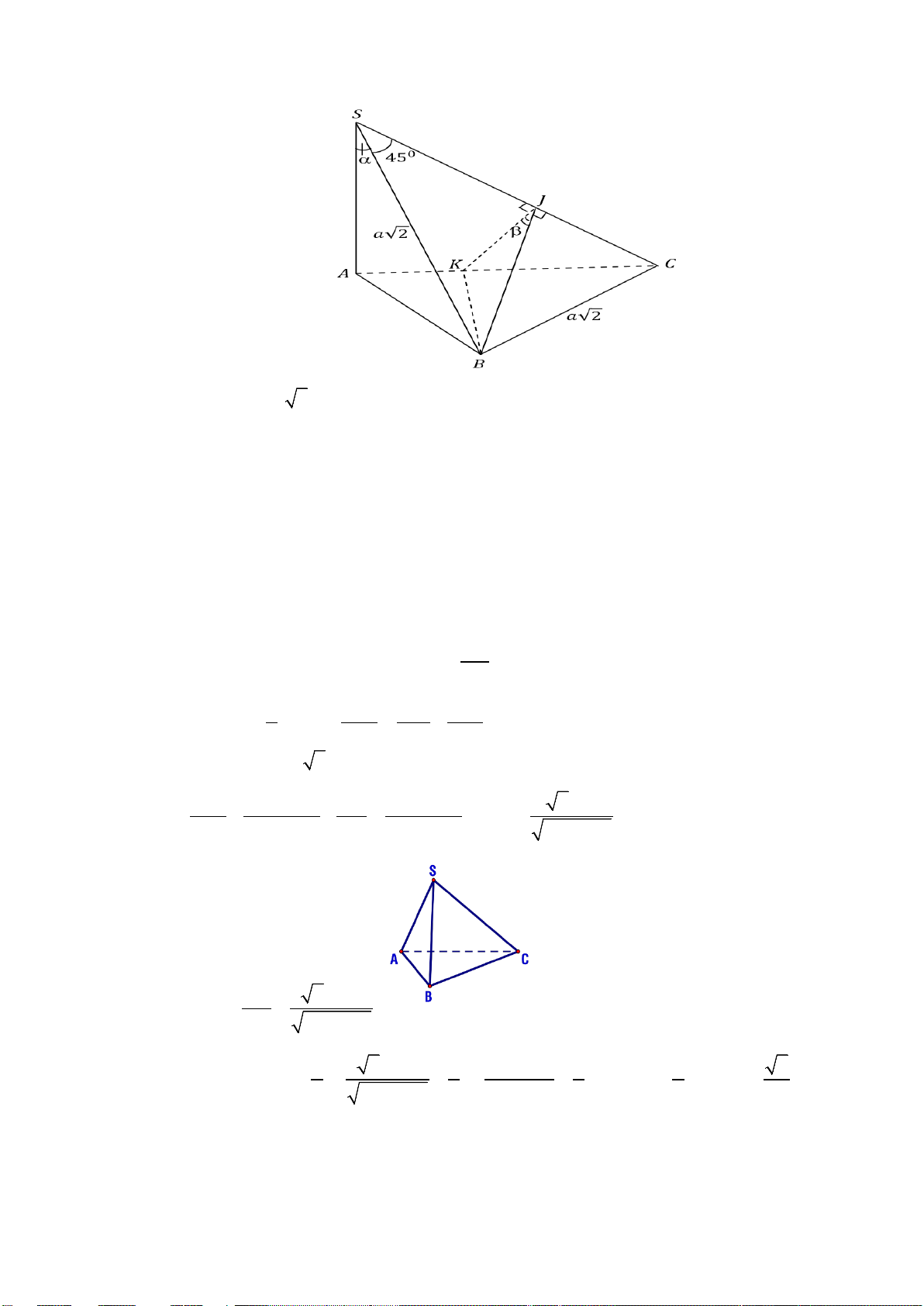
Câu 6. Cho hình chóp S.ABC có: SA ⊥ ( ABC),SB = BC = a 2, BSC = 45 ,° ASB = α . A ∆ BC
vuông tại B . Xác định sin α để góc nhị diện [ ,
A SC, B] = 30°. Lời giải
Vì SB = BC = a 2,
BSC = 45° nên S
∆ BC vuông cân tại B . Gọi J là trung điểm của SC .
Khi đó BJ ⊥ SC ( )
1 . Kẻ BK ⊥ AC , (K ∈ AC) . BK ⊥ AC Ta có: 
⇒ BK ⊥ (SAC) ⇒ BK ⊥ SC (2) và BK ⊥ KJ . BK ⊥ SA Từ ( )
1 và (2) suy ra: SC ⊥ (BJK ) ⇒ SC ⊥ KJ (3). Từ ( )
1 và (3) suy ra góc nhị diện [ , A SC, B] = BJK = β. Trong B
∆ JK vuông tại K ta có sin BK β = . BJ Lại có: 1 1 1 1
BJ = SC = a, = + ( A
∆ BC vuông tại B ), 2 2 2 2 BK BA BC AB = S .
B sin α = a 2.sin α . 2 1 1 1 1+ sin α a 2 sin BK α ⇒ = + = ⇒ = 2 2 2 2 2 2 2 BK 2a sin α 2a 2a sin α 1+ sin α BK 2 sin sin α ⇒ β = = . 2 BJ 1+ sin α 2 1 2 sin α 1 2sin α 1 1 7 β = 45° thì 2 sinβ = ⇒ = ⇔ = ⇔ sin α = ⇒ sin α = . 2 2 2 1+ sin α 2 1+ sin α 4 7 7
Xem thêm: ĐỀ THI GIỮA HK2 TOÁN 11
https://toanmath.com/de-thi-giua-hk2-toan-11
Document Outline

  • Ma_de_101
  • Ma_de_102
  • ĐÁP ÁN CHẤM TOÁN 11 - GK2
    • Sheet1
  • KIỂM TRA GIỮA KÌ 2 - TOÁN 11
    • a)
    • b)
    • c)
  • GK2 - 11