





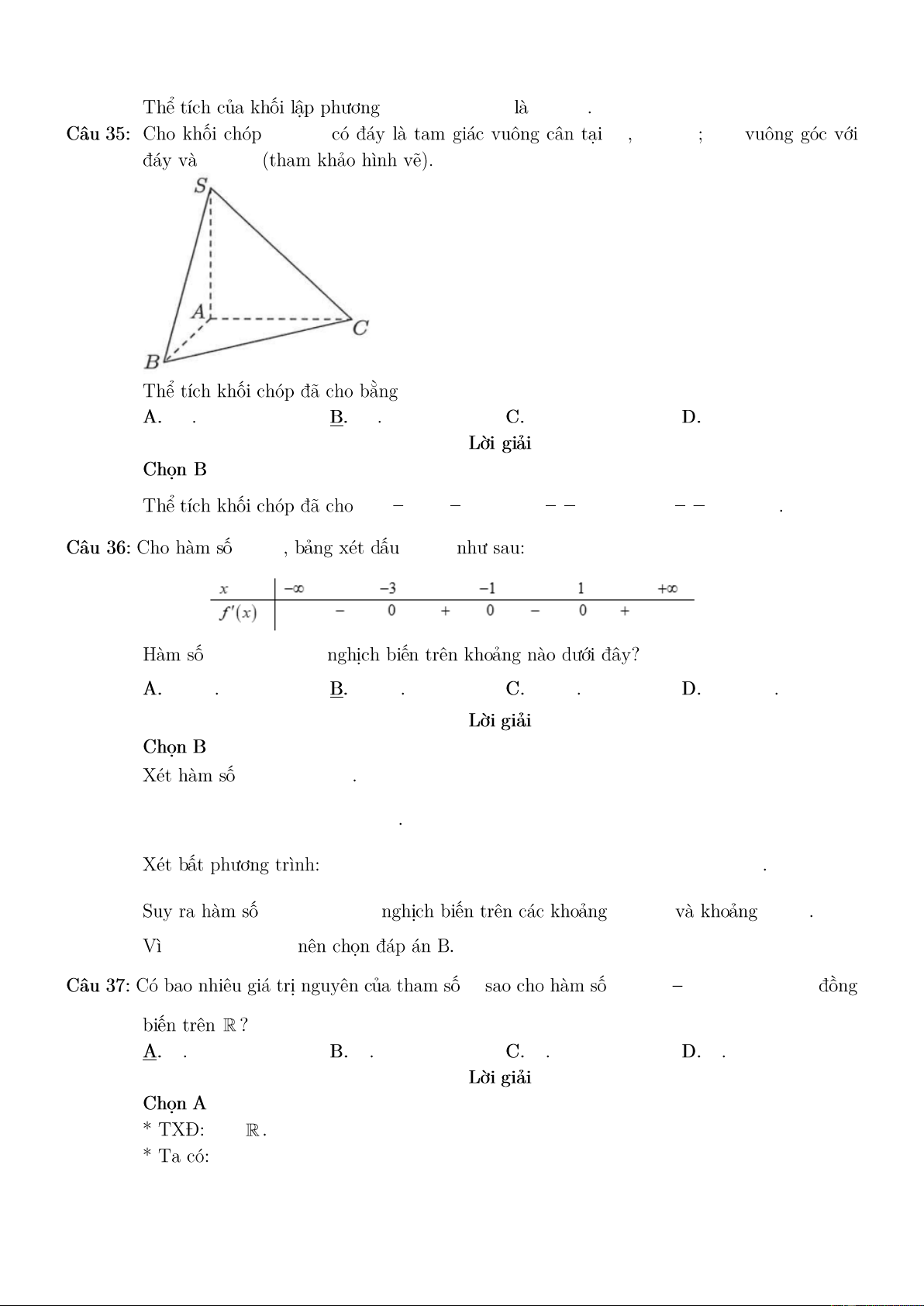




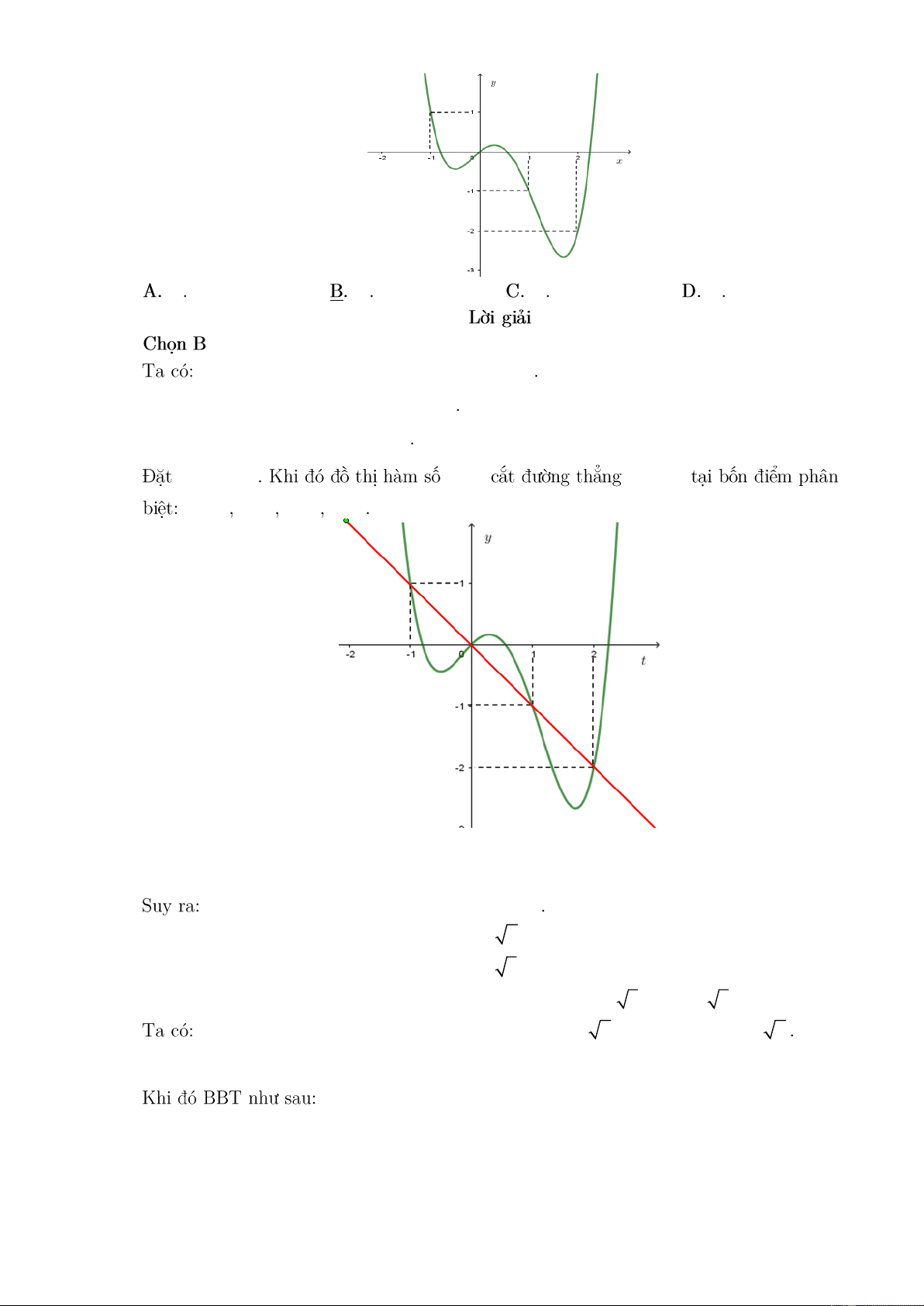
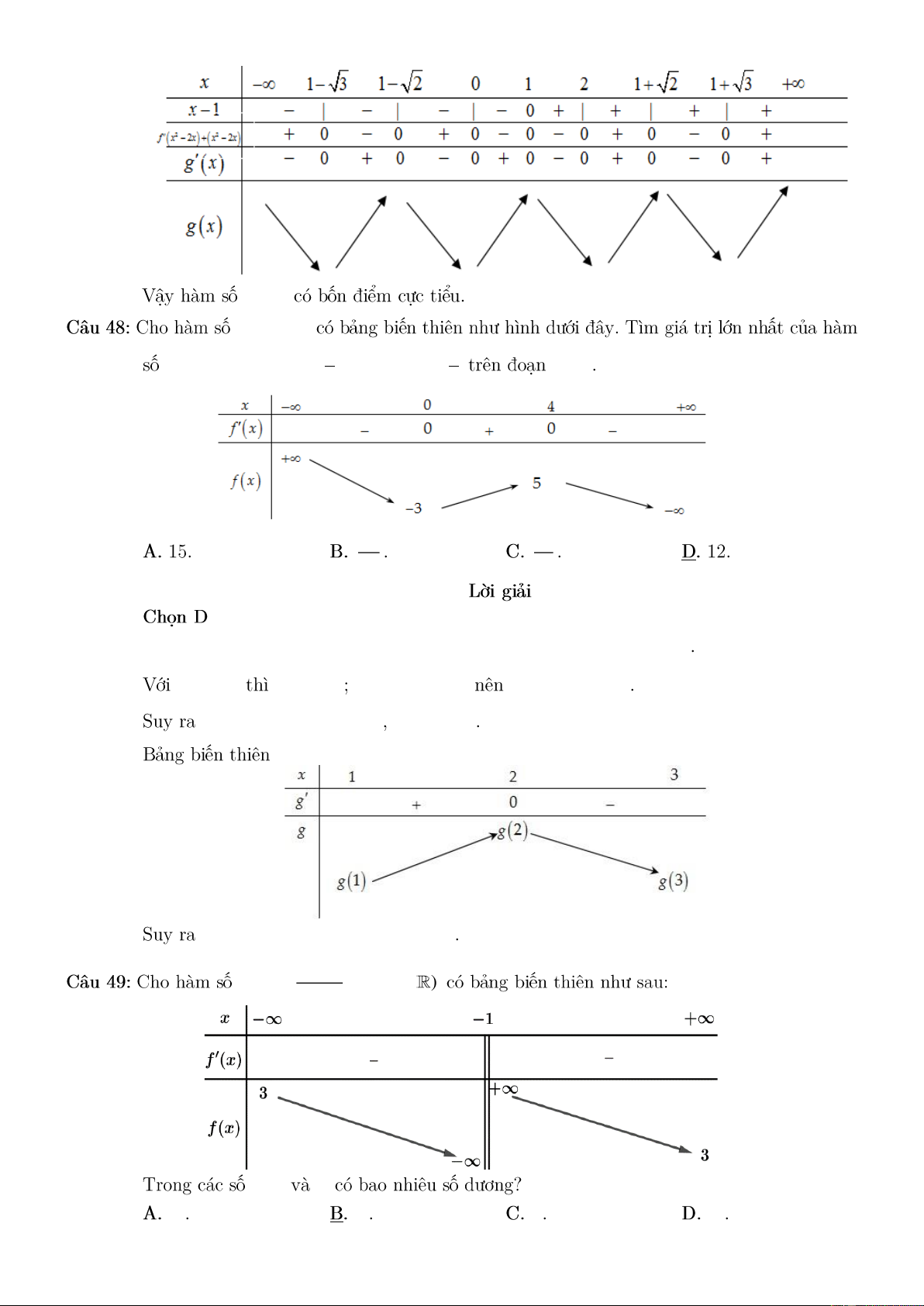

Preview text:
x − 4 2
y = x − x 3 y = x − 1 x y = 3 y = x + x x + 2 3 2
y = x + x y = 3x +1 0 x y = ( x) (2;+) (0;+) ( ;0 − ) ( 1 − ;2) f ( x) 0 x (2;+) (2;+) y = f (x) (0;+) (1;+) ( 1 − ;0) (0 ) ;1
y = f ( x) 1 (1;3) (3 ) ;1 ( 1 − ;− ) 1 (1;− )1
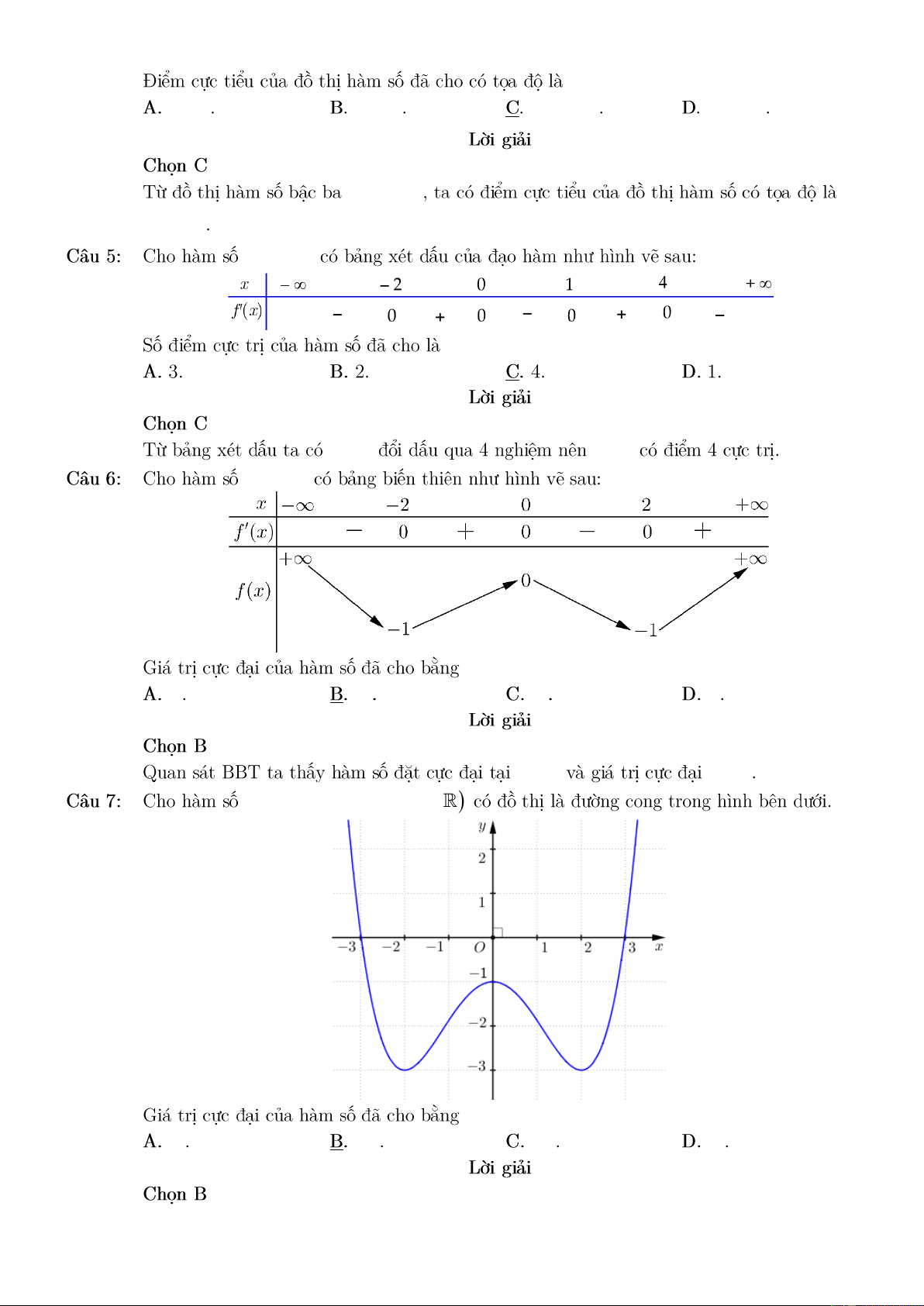
y = f ( x) ( 1 − ;− ) 1 y = f (x) f ( x) f (x) y = f (x) 3 0 2 1 x = 0 y = 0 4 2
y = ax + bx + c (a, , b c ) 0 1 − 3 − 2 2 x = 0 f (0) = 1 − f ( x) 3 = x −3x 3 − ; 3 18 18 − 2 − 2 f ( x) 2 = 3x −3 = − − f ( x) x 1 3; 3 = 0 x =1 3 − ; 3 f ( 3 − ) = 1
− 8; f (3) =18; f (− ) 1 = 2; f ( ) 1 = 2 −
min f ( x) = f ( 3 − ) = 1 − 8 3 − ; 3
y = f ( x) M m 1 − ; 3 M − m
M = max y = 3 m = min y = 2 − [ 1 − ;3] [ 1 − ;3] M − m = 5 3x −1 y = x−2 1 x = x = 2 − x = 3 x = 2 2 3x −1 lim = x = x→2 x − 2 2
y = f ( x) 3 x = 1 − x = 3 − x = 1 x = 3 lim y = − lim y = + + − x 1 → x 1 → x = 1 4x −1 y = x+1 y = 4 − y = 1 y = 4 y = 1 − 4x −1 lim y = lim = 4 y = x→ x→ x + 4 1 4 2
y = −x + 2x 3 2
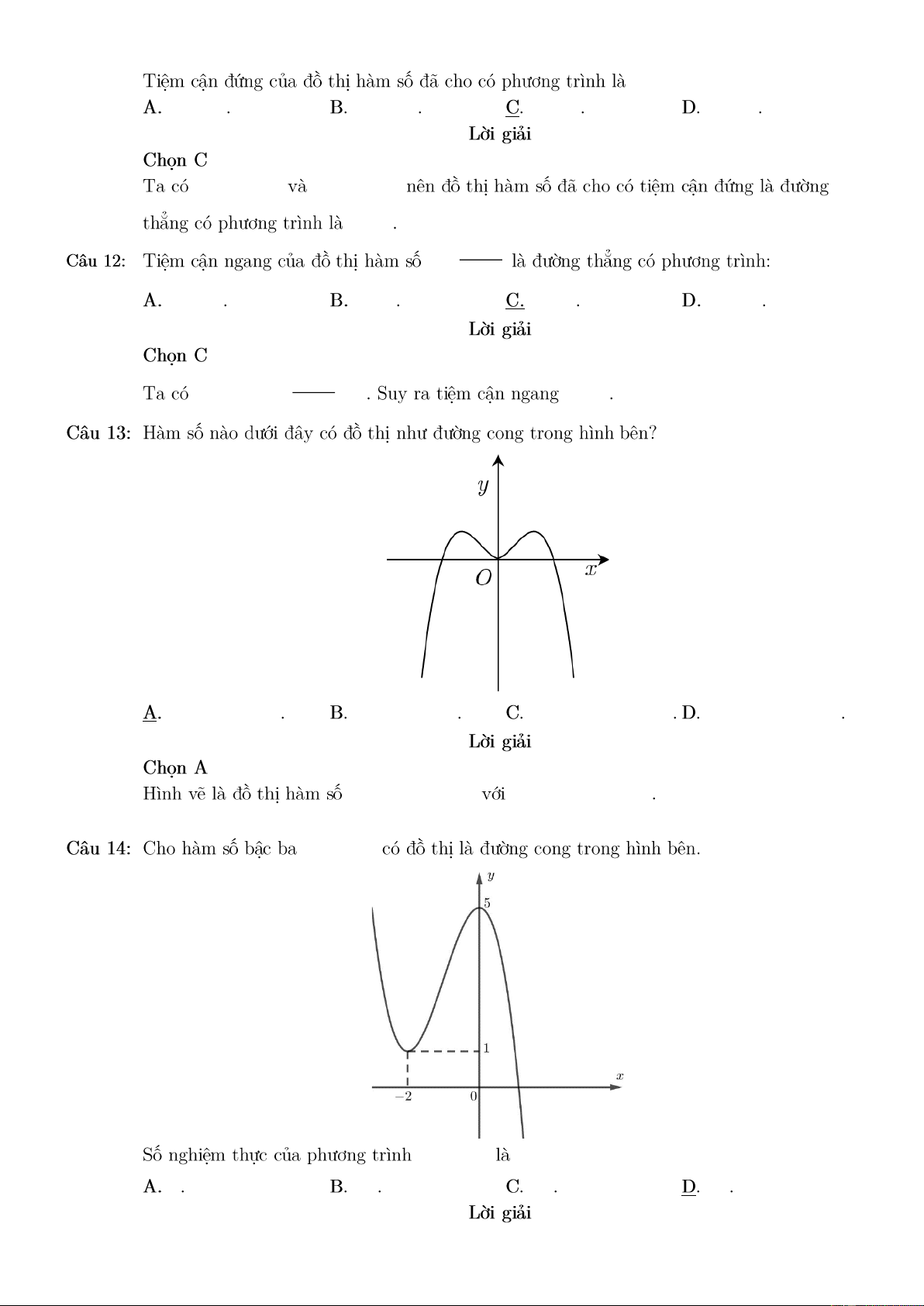
y = x − 3x 3 2
y = −x + 3x +1 4 2
y = x − 2x +1 4 2
y = ax + bx + c
a 0, b 0, c = 0
y = f ( x) f ( x) = 2 1 0 2 3 4
y = f ( x) y = 2 f ( x) = 2 6 10 12 11 4; 3 4; 3 4 3 3; 3 4 6 4 4; 3 8 12 6 3; 4 6 12 8 5; 3 20 30 12 3; 5 12 30 20 h B V = 1 Bh V = 1 Bh V = Bh V = 1 Bh 3 6 2 h B V = 1 Bh 3 S.ABCD 4 ABCD 3 7 5 4 12 5 1 1 V = . . h S = .4.3 = 4 S .ABCD 3 ABCD 3 3a 3 27a 3 3a 3 9a 3 a 3 3
V = (3a) = 27a 2; 4; 6 16 12 48 8 2.4.6 = 48. 4 2
y = x − 2x ( ) ;1 − ( 1 − ;0) (− ; − ) 1 (1;+) 3
y = 4x − 4x x = 0 3
y = 0 4x − 4x = 0 x = 1 x = 1 − 4 2
y = x − 2x (− ; − ) 1 (0 ) ;1
y = f ( x)
y = f ( x) ( 2 − ;0) (− ; 2 − ) (0;2) (0;+) ( 2 − ;0) (2;+) 4 2
y = ax + bx + c (a, , b c ) 6 x = 1 x = 1 − x = 2 − x = 0 f ( x) f ( x) 4 1 2 3 f ( x) x = 1 − x = 1 f ( x) x = 1 − x = 1 M 4 2
y = x − 2x + 3 0; 3 M = 9 M = 8 3 M = 1 M = 6 3
y = x − x = x ( 2 4 4 4 x − ) 1 x = 0 y = 0 x ( 2 4 x − ) 1 = 0 x = 1 x = 1 − (l) y (0) = 3 y ( ) 1 = 2 y ( 3) = 6 4 2
y = x − 2x + 3 0; 3 M = y ( 3) = 6 M , m f ( x) 4 2 = x − 2x + 3 0;2 M + m 11 14 5 13 D = f ( x) 3 = 4x − 4x 7 x = 0 0;2 f ( x) 3
= 0 4x − 4x = 0 x = 1 − 0;2 x =1 0;2 f (0) = 3; f ( ) 1 = 2; f (2) =11 M =11 M + m = 13 m = 2
y = f ( x) 4 1 3 2
lim y = 2 y = 2 x→−
lim y = 5 y = 5 x→+
lim y = + x = 1 − x 1 → 3 x + 9 − 3 y = 2 x + x 3 2 0 1 D = 9 − ;+) \0;− 1 x + 9 − 3 x + 9 − 3 lim y = lim = + lim y = lim = − + + − − x ( → − ) 1 x→(− ) 2 1 x + x x ( → − ) 1 x ( → − ) 2 1 x + x x = 1 − x + 9 − 3 x 1 1 lim y = lim = lim = lim = + + 2 + + x→0 x→0 x + x x→ ( 2 0
x + x)( x + 9 + 3) x→0 ( x + ) 1 ( x + 9 + 3) 6 x + 9 − 3 x 1 1 lim y = lim = lim = lim = − − 2 − − x→0 x→0 x + x x→ ( 2 0
x + x)( x + 9 + 3) x→0 ( x + ) 1 ( x + 9 + 3) 6 x = 0 1 8 x − 4 2
y = x − 3x + 3 2 y = 2
y = x − 4x +1 3
y = x − 3x − 5 x −1 −x + 5 y = x −1 y = x −2 x , x x + x 1 2 1 2 2 3 1 − 1 −x + 5 x = 1 − 2
= x −1 x − 2x − 3 = 0 x − 2 x = 3 x + x = 2 1 2 3
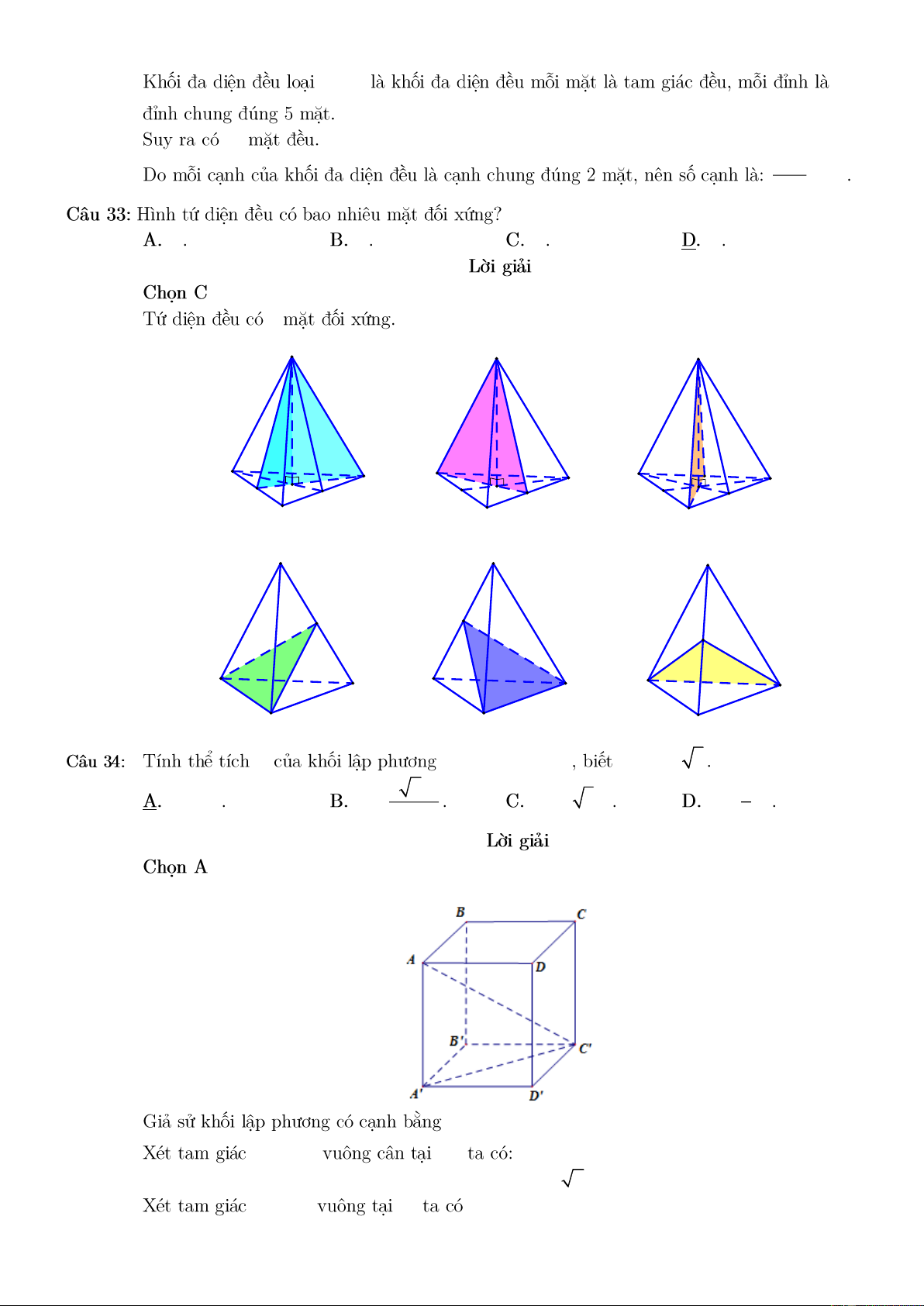
y = ax + 3x + d (a,d ) a 0, d 0 a 0, d 0 a 0; d 0 a 0; d 0 + a 0 d 0 3; 5 35 30 15 20 9 3; 5 20 20.3 = 30 2 3 9 4 6 6 A A A D C D D C C H H H B B B A A A D D D C C C B B B V ABC . D A B C D AC = a 3 3 3 6a 1 3 V = a V = 3 V = 3 3a 3 V = a 4 3 ; x ( x 0) A' B 'C ' B ' 2 2 2
A'C ' = A' B ' + B 'C ' 2 2 2
= x + x = 2x A'C ' = x 2 A' AC ' A' 10 2 2 2
AC ' = A' A + A'C ' 2 2 2
3a = x + 2x x = a ABC . D A B C D 3 V = a S.ABC A AB = 2 SA SA = 3 12 2 6. 4. 1 1 1 1 1 1 V = . B h = S .SA = . A .
B AC.SA = . .2.2.3 = 2 3 3 ABC 3 2 3 2 f ( x) f ( x)
y = f (5 − 2x) (2;3) (0;2) (3;5) (5;+)
y = f (5 − 2x) y = f (5 − 2x) = 2 − f (5−2x) − − − y
f ( − x) 3 5 2x 1 3 x 4 0 5 2 0 5 − 2x 1 x 2
y = f (5 − 2x) ( ;2 − ) (3;4) (0;2) (− ; 2) 1 m f ( x) 3 2
= x + mx + 4x + 3 3 5 4 3 2 D = f ( x) 2 = x + 2mx + 4 11 f ( x) 2 0; x
= m − 4 0 2 − m 2 m m 2 − ; 1 − ;0;1; 2 3 2
y = −x + 3x + 5 A B S OAB O S = 10 9 S = S = 5 S = 10 3 x = 0 2 y ' = 3 − x + 6x 2 y ' = 0 3
− x + 6x = 0 x = 2 ( A 0;5), B(2;9) 2 2
AB = (2;4) AB = 2 + 4 = 20 AB y = 2x + 5 OAB S = 5 1 m 3 2 2 y =
x − mx + (m − 4)x + 3 x = 3 3 m = 1 m = 1 − m = 5 m = 7 − 2 2
y = x − 2mx + (m − 4) y = 2x − 2m 1 y = 3 2 2 y =
x − mx + (m − 4)x + 3 x = (3) 0 3 3 y ( 3) 0 m =1(L) 2 2 9
− 6m + m − 4 = 0
m − 6m + 5 = 0
m = 5(TM ) 6 − 2m 0) m 3 m 3 1 3 2 2 y =
x + m x − 2m + 2m − 9, m S 3 m 0; 3 3 m S = (− ; − 3 1;+) S = ( 3 − ; ) 1 S = (− ; 3 − )(1;+) S = 3 − ; 1 2 2
y ' = x + m , x y ' 0, x 2
max y = y(3) = m + 2m 0; 3 2
m + 2m 3 m 3 − ; 1 m 2 − 021;202 1 x +1 y = 2 x − mx + 4 4033 4034 2017 2016 12 lim y = 0 y = 0 x→ 2
x − mx + 4 = 0 1 − m 4 − 2 m −16 0 m 4 1 + m + 4 0 m 5 − m 2 − 021;202 1 m 4033 f ( x) 3 2
= ax + bx + cx + d (a, , b c, d ) a, , b c, d
lim f ( x) = + a 0 x→+ x = 0 y = d = 1 0 x = − f ( x) 2
= 3ax + 2bx + c f ( x) 2 = 0 x =0 − b
f (0) = 0 c = 2 0 = 2
− b = 3a 0 3a a, , b d
y = f ( x)
f ( f ( x)) = 0 12 10 8 4 13
f (x) = a(a − ) 1 ( ) 1 = − f (
f ( x) b ( 1 b 0) (2)
f ( x)) = 0 f (x) = c(0 c )1 (3)
f (x) = d (d )1 (4) ( )1 (2) 4 (3) 4 (4)
f ( f ( x)) = 0 S.ABCD ABCD AB = a AD = a 3 SA (SBC) 60 V S.ABCD 3 a 3 a 3 V = V = 3 V = a 3 V = 3a 3 3 S a 60 B A a 3 D C 2 S = 3a ABC
(𝑆𝐵𝐶) ∩ (𝐴𝐵𝐶𝐷) = 𝐵𝐶
{𝐵𝐶 ⊥ 𝑆𝐵 ⊂ (𝑆𝐵𝐶) ⇒ ((𝑆𝐵𝐶), (𝐴𝐵
̂ 𝐶𝐷)) = (𝑆𝐵; 𝐴𝐵 ̂ ) = 𝑆𝐵𝐴 ̂
𝐵𝐶 ⊥ 𝐴𝐵 ⊂ (𝐴𝐵𝐶𝐷) 𝑆𝐵𝐴 ̂ = 60𝑜 𝑆𝐴 𝑆𝐴𝐵 tan60𝑜 =
⇒ 𝑆𝐴 = 𝐴𝐵. tan60𝑜 = 𝑎√3 𝐴𝐵 1 1
𝑉𝑆.𝐴𝐵𝐶𝐷 = 𝑆 𝑎2√3. 𝑎√3 = 𝑎3
3 𝐴𝐵𝐶𝐷. 𝑆𝐴 = 3 ABC .
D A' B 'C ' D ' BD = 4a (A'BD) (ABCD) 30o 14 16 3 16 3 3 a 3 48 3a 3 a 3 16 3a 9 3 O BD A ' AB = A ' AD
A' B = A' D A ' BD (
A' BD) ( ABCD) = BD
A'O ⊥ BD ((A B
D),( ABCD)) = A O A = 30 . 30o AO ⊥ BD A A A A A A A A a A O A A tan 30o = = = = 2 3
A' A = 2a tan 30 = AO AC BD 2a 3 2 2 ABCD
BD = AB 2 AB = 2a 2. 16 3 2 a V = A' . A AB ( a )2 2 3 . 2 2 3 a 3 3 x + m m f ( x) 4 = 2x+m+3 (0 ) ;1 1 5 4 3 m + 3 2m +12 D = \ − f ( x) = 2 (2x + m + 3)2 (0 ) ;1 y ' 0, x (0 ) ;1 2m +12 0 m 6 − m + 3 − 1 m 5 − m 5 − m ( 6 − ;− 5 −3; +) 2 m + 3 m 3 − m 3 − − 0 2 m 5 − ; 3 − ; 2 − ;− 1
y = f ( x)
y = f ( x)
g ( x) = f ( x − x) 4 x 2 3 2 2 +
− 2x + 2x + 2022 2 15 3 4 5 6
g( x) = ( x − ) f ( 2 x − x) 3 2 2 2 2
+ 2x − 6x + 4x
= (x − ) f ( 2
x − x) + ( x − )( 2 2 1 2 2 1 x − 2x)
= (x − ) f ( 2 x − x) + ( 2 2 1 2 x − 2x) 2
t = x − 2x f (t ) y = t − t = 1
− t = 0 t =1 t = 2 x =1 x =1 2 x − 2x = 1 − x =1 g ( x) 2
= 0 x − 2x = 0 x = 0 x = 2 2 x − 2x =1 x =1 2 2 x − 2x = 2 x =1 3 2
x − 2x 2
x 1− 3 x 1+ 3 f ( 2
x − 2x) −( 2 x − 2x) 2
0 x − 2x 1 1
− 2 x 0 2 x 1+ 2 2 x − 2x 1 − VN 16 g ( x)
y = f ( x)
g ( x) = f ( 1 1 2 4x − x ) 3 2
+ x − 3x + 8x + 1; 3 3 3 25 19 3 3
g( x) = ( − x) f ( 2 x − x ) 2 4 2 4
+ x − 6x + 8 = ( − x) f ( 2 2 2
4x − x ) + 4 − x x 1; 3 f ( 2 4x − x ) 4 − x 0 2
3 4x − x 4 0 f ( 2 2
4x − x ) + 4 − x 0 x 1; 3
max g ( x) = g (2) = f (4) + 7 = 12 1; 3 ax + 4 f (x) = (a, , b c ) bx + c a, b c 2 3 1 0 17 x = 1 − y = 3 c − 0 (1) b a 0 (2) b
ac − 4b 0 (3) − .
a c 0 ac 0 (3) 4
− b 0 b 0.
c 0, a 0, b 0. S.ABC ABC 1 A ( 6 15 SBC ) B (SCA) C 4 10 ( 30 SAB) S ABC 20 V . S.ABC 1 1 1 1 36 48 12 24 M , N , P H
AC, BC, AB 1 3 h 3
SH = h V = . . h = S . ABC 3 4 12 2S 6V h 3 30 SAB AP = = 2S = = = AB d ( S.ABC h SAB C;(SAB)) : 10 2 20 HM = 2 , h HN = h 2 2
PH = SP − SH = 3h 1 S = S + S + S = HP + HM + 3 3 HN 3h = h = ABC HAB HAC HBC ( ) 2 4 12 3 3 1 V = . = S .ABC 12 12 48 18




