Đề giữa kỳ 1 Toán 12 năm 2024 – 2025 trường THPT Huỳnh Thúc Kháng – Quảng Nam

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra giữa học kỳ 1 môn Toán 12 chương trình GDPT 2018 năm học 2024 – 2025 trường THPT Huỳnh Thúc Kháng, tỉnh Quảng Nam. Đề thi gồm 28 câu trắc nghiệm 04 phương án lựa chọn + 02 câu trắc nghiệm đúng hoặc sai + 03 câu trắc nghiệm trả lời ngắn, thời gian làm bài 90 phút. Đề thi có đáp án chi tiết và hướng dẫn chấm điểm mã đề 102 104 106 108 101 103 105 107. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

Chủ đề:

Đề giữa HK1 Toán 12 100 tài liệu

Môn:

Toán 12 3.8 K tài liệu

Thông tin:
16 trang 4 tháng trước
Tác giả:
L
Lê Phương
docx.com.vn

Bình luận

Vui lòng đăng nhập hoặc đăng ký để gửi bình luận.

Đề giữa kỳ 1 Toán 12 năm 2024 – 2025 trường THPT Huỳnh Thúc Kháng – Quảng Nam

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề kiểm tra giữa học kỳ 1 môn Toán 12 chương trình GDPT 2018 năm học 2024 – 2025 trường THPT Huỳnh Thúc Kháng, tỉnh Quảng Nam. Đề thi gồm 28 câu trắc nghiệm 04 phương án lựa chọn + 02 câu trắc nghiệm đúng hoặc sai + 03 câu trắc nghiệm trả lời ngắn, thời gian làm bài 90 phút. Đề thi có đáp án chi tiết và hướng dẫn chấm điểm mã đề 102 104 106 108 101 103 105 107. Mời các bạn cùng tham khảo chi tiết bài viết dưới đây nhé.

35 18 lượt tải Tải xuống

Chủ đề: Đề giữa HK1 Toán 12 100 tài liệu

Môn: Toán 12 3.8 K tài liệu

Thông tin:

16 trang 4 tháng trước

Tác giả:

Profile Lê Phương
Mã đề 101/1
ĐỀ CHÍNH THỨC
TRƯỜNG THPT QUẾ SƠN
TỔ: TOÁN-TIN.
(Đề gồm có 04 trang)
KIỂM TRA GIỮA KỲ I- NĂM HỌC 2024-2025
Môn: TOÁN – Lớp 12.
Thời gian làm bài: 90 phút
(Không kể thời gian giao đề)
MÃ ĐỀ 101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số
y f x
có bảng xét dấu của đạo hàm
'( )fx
như sau
x

2
1

'( )fx
0
+
0
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A.
;2
. B.
1; 
. C.
2;1
. D.
2; 
.
Câu 2. Cho hàm số
()y f x
có đồ thị như hình vẽ.
1
O
2
2
x
y
Hàm số đã cho nghịch biến trên khoảng nào dưới đây
A.
;1
. B.
2;
. C.
1;2
. D.
0;2
.
Câu 3. Cho hàm số
y f x
có bảng biến thiên như sau
x

2
1

'( )fx
0
+
0
()fx

3
2

Hàm số
y f x
đạt cực đại tại điểm
A.
2x 
. B.
1x
. C.
3x
. D.
2x
.
Câu 4. Cho hàm số
()y f x
có đồ thị như hình vẽ.
Cực tiểu của hàm số bằng
A.
1
. B.
4
. C.
0
. D.
2
.
Mã đề 101/2
Câu 5. Điểm cực tiểu của đồ thị hàm số
32
34y x x
là
A.
0x
. B.
4y 
. C.
(0; 4)M
. D.
(2;0)N
.
Câu 6. Cho hàm số
fx
liên tục trên
1;5
và có đồ thị trên đoạn
1;5
như hình vẽ bên
dưới. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
fx
trên đoạn
1;5
. Tính T = M + m.
A.
1T 
. B.
4T
. C.
1T
. D.
2T
.
Câu 7. Giá trị nhỏ nhất của hàm số
3
21f x x x
trên đoạn
2;4
bằng
A.
38
. B.
14 7
. C.
20
. D.
34
.
Câu 8. Tiệm cận đứng của đồ thị hàm số
22
1
x
y
x
là đường thẳng
A.
1x 
. B.
2x
. C.
2y
. D.
1y 
.
Câu 9. Tiệm cận ngang của đồ thị hàm số
5
2
1
y
x

là đường thẳng
A.
2y
. B.
5y
. C.
1x 
. D.
1x
.
Câu 10. Điểm nào sau đây là tâm đối xứng của đồ thị hàm số
32
1
x
y
x
?
A.
(1;3).I
B.
( 1;3).J
C.
(3;2)H
D.
(1; 3).K
Câu 11. Hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
25
.
1
x
y
x
B.
.
1
x
y
x
C.
2
.
1
x
y
x
D.
2
.
1
x
y
x
2
2
1
1
O
x
y
Câu 12. Hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
2
1
.
1
xx
y
x
B.
2
1
.
1
xx
y
x
C.
2
21
.
1
xx
y
x
D.
2
21
.
1
xx
y
x
Mã đề 101/3
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a, b, c, d ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số
3
3f x x x
. Các mệnh đề sau đúng hay sai?
a)
2
' 3 3f x x
.
b) Hàm số đồng biến trên
1;1
.
c) Hàm số đạt cực tiểu tại
1
1x 
và đạt cực đại tại
2
1x
.
d) Giá trị nhỏ nhất của hàm số
fx
trên đoạn [0;2] bằng
1f
.
Câu 2. Cho hàm số
2
1
x
y
x
có đồ thị là (C). Các mệnh đề sau đúng hay sai?
a) Đồ thị (C) của hàm số có đường tiệm cận ngang là đường thẳng
1x 
.
b) Hàm số đồng biến trên từng khoảng xác định của nó.
c) Tâm đối xứng của (C) nằm trên đường thẳng
: 4 3 0xy
.
d) Hàm số có 2 điểm cực trị.
Câu 3. Cho hàm số
2
22
1
xx
y
x

. Các mệnh đề sau đúng hay sai?
a) Hàm số đạt cực đại tại
0x
.
b) Đồ thị hàm số có 2 đường tiệm cận.
c) Hàm số đạt giá trị nhỏ nhất tại
2x
d) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho bằng
45
.
Câu 4. Cho hàm số
y f x
có đạo hàm liên tục trên . Hàm số
'y f x
có đồ thị như
hình sau:
Các mệnh đề sau đúng hay sai?
a) Hàm số
y f x
có hai cực trị.
b) Hàm số
y f x
đồng biến trên khoảng
;0
.
c)
1 2 4 .f f f
d) Trên đoạn
1;4
, giá trị lớn nhất của hàm số
y f x
là
1.f
Mã đề 101/4
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho hàm số
2
21
2
xx
y
x

. Tiệm cận xiên của đồ thị hàm số có phương trình
y ax b
.
Tính giá trị biểu thức T =
52ab
.
Câu 2. Biết đồ thị hàm số
32
y x bx c
có một điểm cực trị
2; 3M
. Tính
3.y
Câu 3. Ông An có một hàng rào thép dài
100
m và muốn rào cánh đồng thành một thửa ruộng
hình chữ nhật tiếp giáp với một con sông thẳng. Ông không cần rào cho phía giáp con sông. Biết
rằng ông An đã rào được thửa ruộng có diện tích lớn nhất là
2
()am
. Giá trị của a là bao nhiêu?
Câu 4. Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất
x
đơn vị hàng hóa nào đó của
một nhà máy là
23
( ) 16000 500 1,6 0,004C x x x x
và
( ) 1700 7p x x
là hàm cầu. Nhà máy
cần đặt phương án sản xuất bao nhiêu sản phẩm để lợi nhuận là lớn nhất.
Câu 5. Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2 lít.
Lượng vật liệu dùng để sản xuất chiếc hộp là nhỏ nhất khi chiều cao của chiếc hộp bằng
*
3
( ), ( , , 10)
a
cm a b N b
b

. Tính
2T a b
.
Câu 6. Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích
3
1000cm
.
Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,5 nghìn đồng/
2
cm
, trong khi mặt
xung quanh của bình được làm bằng vật liệu có giá 0,8 nghìn đồng/
2
cm
. Biết rằng chi phí thấp
nhất để sản xuất mỗi chiếc bình là a (nghìn đồng) (Kết quả làm tròn đến hàng đơn vị). Giá trị a
bằng bao nhiêu?
-----Hết-----
Mã đề 102/1
ĐỀ CHÍNH THỨC
TRƯỜNG THPT QUẾ SƠN
TỔ: TOÁN-TIN.
(Đề gồm có 04 trang)
KIỂM TRA GIỮA KỲ I- NĂM HỌC 2024-2025
Môn: TOÁN – Lớp 12.
Thời gian làm bài: 90 phút
(Không kể thời gian giao đề)
MÃ ĐỀ 102
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số
y f x
có bảng xét dấu của đạo hàm
'( )fx
như sau
x

1
3

'( )fx
+
0
0
+
Hàm số đã cho nghịch biến trên khoảng nào dưới đây
A.
;1
. B.
1;3
. C.
1; 
. D.
3; 
.
Câu 2. Cho hàm số
()y f x
có đồ thị như hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào dưới đây
A.
;1
. B.
1;2
. C.
4;2
. D.
0;2
.
Câu 3. Cho hàm số
y f x
có bảng biến thiên như sau
x

2
1

'( )fx
0
+
0
()fx

3
1

Hàm số
y f x
đạt cực tiểu tại điểm
A.
2x 
. B.
1x
. C.
3x
. D.
1x 
.
Câu 4. Cho hàm số
()y f x
có đồ thị như hình vẽ.
Cực đại của hàm số bằng
A.
1
. B.
4
. C.
1
. D.
2
.
Mã đề 102/2
Câu 5. Điểm cực đại của đồ thị hàm số
32
34y x x
là
A.
2x
. B.
0x
. C.
(0; 4)M
. D.
(2;0)N
.
Câu 6. Cho hàm số
fx
liên tục trên
1;5
và có đồ thị trên đoạn
1;5
như hình vẽ bên
dưới. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
fx
trên đoạn
1;5
. Tính T = M
m.
A.
5T
. B.
1T
. C.
3T
. D.
2T
.
Câu 7. Giá trị lớn nhất của hàm số
3
( ) 21f x x x
trên đoạn
2;5
bằng
A.
38
. B.
20
. C.
14 7
. D.
34
.
Câu 8. Tiệm cận ngang của đồ thị hàm số
22
1
x
y
x
là đường thẳng
A.
1x 
. B.
2x
. C.
2y
. D.
1y 
.
Câu 9. Tiệm cận đứng của đồ thị hàm số
2
25
2
xx
y
x

là đường thẳng
A.
1y
. B.
2x
. C.
2x 
. D.
1y 
.
Câu 10. Điểm nào sau đây là tâm đối xứng của đồ thị hàm số
52
1
x
y
x
?
A.
(1;5).I
B.
(1; 5).K
C.
(5; 2)H
D.
( 1;5).J
Câu 11. Hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
25
.
1
x
y
x
B.
.
1
x
y
x
C.
2
.
1
x
y
x
D.
3
.
1
x
y
x
O
1
1
x
y
Câu 12. Hình vẽ bên là đồ thị của hàm số nào sau đây?
A.
2
1
1
xx
y
x

. B.
2
22
1
xx
y
x

.
C.
23
1
x
y
x
. D.
2
22
1
xx
y
x

.
Mã đề 102/3
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a, b, c, d ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số
32
35f x x x
. Các mệnh đề sau đúng hay sai?
a)
2
' 3 6f x x x
.
b) Hàm số nghịch biến trên
(0;2)
.
c) Hàm số đạt cực tiểu tại
1
2x
và đạt cực đại tại
2
0x
.
d) Giá trị nhỏ nhất của hàm số
fx
trên đoạn [1;3] bằng
2f
.
Câu 2. Cho hàm số
53
2
x
y
x
có đồ thị là (C). Các mệnh đề sau đúng hay sai?
a) Đồ thị (C) của hàm số có đường tiệm cận ngang là đường thẳng
5y
.
b) Hàm số đồng biến trên từng khoảng xác định của nó.
c) Tâm đối xứng của (C) nằm trên đường thẳng
: 2 4 0xy
.
d) Hàm số không có cực trị.
Câu 3. Cho hàm số
2
4
1
xx
y
x

. Các mệnh đề sau đúng hay sai?
a) Hàm số đạt cực đại tại
3x
.
b) Đồ thị hàm số có 2 đường tiệm cận.
c) Hàm số đạt giá trị lớn nhất tại
1x 
d) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho bằng
45
.
Câu 4. Cho hàm số
y f x
có đạo hàm liên tục trên . Hàm số
'y f x
có đồ thị như
hình sau:
Các mệnh đề sau đúng hay sai?
a) Hàm số
y f x
có một điểm cực đại.
b) Hàm số
y f x
nghịch biến trên khoảng
0;1
.
c)
1 0 1 .f f f
d) Trên đoạn
4;1
, giá trị nhỏ nhất của hàm số
y f x
là
1.f
Mã đề 102/4
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6.
Câu 1. Cho hàm số
2
21
2
xx
y
x

. Tiệm cận xiên của đồ thị hàm số có phương trình
y ax b
.
Tính giá trị biểu thức T =
52ab
.
Câu 2. Biết đồ thị hàm số
32
y x bx c
có một điểm cực trị
2; 3M
. Tính
5.y
Câu 3. Ông Bình có một hàng rào thép dài
120
m và muốn rào cánh đồng thành một thửa ruộng
hình chữ nhật tiếp giáp với một con sông thẳng. Ông không cần rào cho phía giáp con sông. Biết
rằng ông Bình đã rào được thửa ruộng có diện tích lớn nhất là
2
()am
. Giá trị của a là bao nhiêu?
Câu 4. Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất
x
đơn vị hàng hóa nào đó của
một nhà máy là
23
( ) 17000 300 3,6 0,004C x x x x
và
( ) 1500 9p x x
là hàm cầu. Nhà máy
cần đặt phương án sản xuất bao nhiêu sản phẩm để lợi nhuận là lớn nhất.
Câu 5. Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 3 lít.
Lượng vật liệu dùng để sản xuất chiếc hộp là nhỏ nhất khi chiều cao của chiếc hộp bằng
*
3
( ), ( , , 10)
a
cm a b N b
b

. Tính
3T a b
.
Câu 6. Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích
3
1000cm
.
Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,8 nghìn đồng/
2
cm
, trong khi mặt
xung quanh của bình được làm bằng vật liệu có giá 0,6 nghìn đồng/
2
cm
. Biết rằng chi phí thấp
nhất để sản xuất mỗi chiếc bình là a (nghìn đồng) (Kết quả làm tròn đến hàng đơn vị). Giá trị a
bằng bao nhiêu?
-----Hết-----
TRƯỜNG THPT QUẾ SƠN
TỔ TOÁN-TIN
ĐÁP ÁN KIỂM TRA GIỮA HỌC KỲ 1 NĂM HỌC 2024-2025
MÔN TOÁN LỚP 12
Phần I (3 điểm): Gồm 12 câu mỗi câu đúng được 0, 25.
Phần II (4 điểm): Gồm 04 câu mỗi câu đúng cả 4 ý được 1,0.
Phần III(3 điểm): Gồm 06 câu mỗi câu đúng được 0,5.
ĐÁP ÁN ĐỀ 101
Phần I
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
C
D
B
B
C
C
B
A
A
D
C
A
Phần II:
Câu 1
Đúng
Sai
Câu 2
Đúng
Sai
Câu 3
Đúng
Sai
Câu 4
Đúng
Sai
a)
X
a)
X
a)
X
a)
X
b)
X
b)
X
b)
X
b)
X
c)
X
c)
X
c)
X
c)
X
d)
X
d)
X
d)
X
d)
X
Phần III:
Câu
Đáp số
1
1
6
2
–
4
7
3
1
2
5
4
1
0
0
5
2
8
6
5
4
6
ĐÁP ÁN ĐỀ 102
Phần I:
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
B
D
A
D
D
A
C
D
C
B
B
B
Phần II:
Câu 1
Đúng
Sai
Câu 2
Đúng
Sai
Câu 3
Đúng
Sai
Câu 4
Đúng
Sai
a)
X
a)
X
a)
X
a)
X
b)
X
b)
X
b)
X
b)
X
c)
X
c)
X
c)
X
c)
X
d)
X
d)
X
d)
X
d)
X
Phần III:
Câu
Đáp số
1
2
0
2
–
5
1
3
1
8
0
4
1
0
0
5
4
8
6
4
7
9
ĐÁP ÁN ĐỀ 103
Phần I:
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
C
B
A
B
A
A
D
A
B
B
B
D
Phần II:
Câu 1
Đúng
Sai
Câu 2
Đúng
Sai
Câu 3
Đúng
Sai
Câu 4
Đúng
Sai
a)
X
a)
X
a)
X
a)
X
b)
X
b)
X
b)
X
b)
X
c)
X
c)
X
c)
X
c)
X
d)
X
d)
X
d)
X
d)
X
Phần III:
Câu
Đáp số
1
–
4
7
2
1
6
3
1
2
5
4
1
0
0
5
2
8
6
5
4
6
ĐÁP ÁN ĐỀ 104
Phần I:
Câu
1
2
3
4
5
6
7
8
9
10
11
12
Đáp án
D
C
D
A
B
D
B
A
A
A
D
C
Phần II:
Câu 1
Đúng
Sai
Câu 2
Đúng
Sai
Câu 3
Đúng
Sai
Câu 4
Đúng
Sai
a)
X
a)
X
a)
X
a)
X
b)
X
b)
X
b)
X
b)
X
c)
X
c)
X
c)
X
c)
X
d)
X
d)
X
d)
X
d)
X
Phần III:
Câu
Đáp số
1
–
5
1
2
2
0
3
1
8
0
4
1
0
0
5
4
8
6
4
7
9
Hướng dẫn đáp số phần III
Đề 101 và 103:
1) Tìm được
: 2 3 5.2 2( 3) 16TCX y x T
2) Theo đề ta suy ra
32
'(2) 0 3
37
(2) 3 7
yb
y x x
yc




32
( 3) ( 3) 3( 3) 7 47y
3) Diện tích thửa ruộng lớn nhất khi chiều rộng x = 25 (m), y = 50(m) suy ra S = 1250 (m
2
).
4) Doanh thu của nhà máy
2
( ) . ( ) 1700 7R x x p x x x
Lợi thuận thu được:
2 2 3
( ) ( ) ( ) 1700 7 (16000 500 1,6 0,004 )P x R x C x x x x x x
=
23
16000 1200 5,4 0,004x x x
Suy ra
2
'( ) 1200 10,8 0,012P x x x
,
'( ) 0 100( 0)P x x do
Lập BB của P(x) ta được mức sản xuất để tối ưu hóa lợi nhuận là 100 đơn vị hàng hóa.
5) 2 lít = 2000cm
3
.
Gọi
( cm)x
là cạnh đáy của chiếc hộp.
Khi đó, ta có chiều cao của chiếc hộp là
2
2000
( cm)
x
.
Suy ra, tổng diện tích bề mặt của chiếc hộp là
22
2
2000 8000
2 4 2 , 0.S x x x x
xx
Ta có:
3
3
22
8000 4 8000
4 ; 0 10 2
x
S x S x
xx

.
Lập bảng biến thiên, ta có kết quả lượng vật liệu dùng để sản xuất là nhỏ nhất (tức là tổng
diện tích bề mặt hộp nhỏ nhất) khi cạnh đáy của hộp là
3
10 2 cm
và chiều cao của hộp là
3
20
cm
4
.
20 2.4 28T
.
6) Gọi bán kính đáy của bình là
( , 0)x cm x
, chiều cao của bình là
( , 0)h cm h
Có
2
. 1000( )x h cm
Suy ra chiều cao của bình là h:
2
1000
( )cm
x
Chi phí để sản xuất một chiếc bình là: C(x) =
2
2
1000
1,5.2 0,8.2. . .xx
x

2
1600
3 x
x

Để chi phí sản xuất mồi chiếc bình là thấp nhất thì C(x) là nhỏ nhất.
3
2
1600 800
'( ) 6 ; '( ) 0
3
C x x C x x
x
Lập BBT C(x), ta được C(x) đạt GTNN xấp xỉ 546 nghìn đồng khi
3
800
3
x
(nghìn đồng)
Đề 102 và 104:
1) Tìm được
: 2 5 5.2 2( 5) 20TCX y x T
2) Theo đề ta suy ra
32
'( 2) 0 3
31
( 2) 3 1
yb
y x x
yc



32
( 5) ( 5) 3( 5) 1 51y
3) Diện tích thửa ruộng lớn nhất khi chiều rộng x = 30 (m), y = 60(m) suy ra S = 1800 (m
2
).
4) Doanh thu của nhà máy
2
( ) . ( ) 1500 9R x x p x x x
Lợi thuận thu được:
2 2 3
( ) ( ) ( ) 1500 9 (17000 300 3,6 0,004 )P x R x C x x x x x x
=
23
17000 1200 5,4 0,004x x x
Suy ra
2
'( ) 1200 10,8 0,012P x x x
,
'( ) 0 100( 0)P x x do
Lập BB của P(x) ta được mức sản xuất để tối ưu hóa lợi nhuận là 100 đơn vị hàng hóa.
5) 3 lít = 3000cm
3
.
Gọi
( cm)x
là cạnh đáy của chiếc hộp.
Khi đó, ta có chiều cao của chiếc hộp là
2
3000
( cm)
x
.
Suy ra, tổng diện tích bề mặt của chiếc hộp là
22
2
3000 12000
2 4 2 , 0.S x x x x
xx
Ta có:
3
3
22
12000 4 12000
4 ; 0 10 3
x
S x S x
xx

.
Lập bảng biến thiên, ta có kết quả lượng vật liệu dùng để sản xuất là nhỏ nhất (tức là tổng
diện tích bề mặt hộp nhỏ nhất) khi cạnh đáy của hộp là
3
10 3 cm
và chiều cao của hộp là
3
30
cm
9
.
30 2.9 48T
.
6) Gọi bán kính đáy của bình là
( , 0)x cm x
, chiều cao của bình là
( , 0)h cm h
Có
2
. 1000( )x h cm
Suy ra chiều cao của bình là h:
2
1000
( )cm
x
Chi phí để sản xuất một chiếc bình là: C(x) =
2
2
1000
1,8.2 0,6.2. . .xx
x

2
1200
3,6 x
x

Để chi phí sản xuất mồi chiếc bình là thấp nhất thì C(x) là nhỏ nhất.
3
2
1200 500
'( ) 7,2 ; '( ) 0
3
C x x C x x
x
Lập BBT C(x), ta được C(x) đạt GTNN xấp xỉ 479 nghìn đồng khi
3
500
3
x
(nghìn đồng).
Trường THPT Quế Sơn
Tổ Toán-Tin
MA TRẬN +ĐẶC TẢ ĐỀ KIỂM TRA GIỮA KỲ I NĂM HỌC 2024-2025
MÔN: TOÁN 12 . Thời gian làm bài: 90 phút .
STT
Chươn
g/
Chủ đề
Nội dung
Mức độ kiểm tra, đánh giá
Tư duy và lập luận Toán
học (TD)
Giải quyết vấn đề Toán
học (GQ)
Mô hình hóa Toán học
(MH)
Điểm
Biết
Hiểu
Vận
dụng
Biết
Hiểu
Vận
dụng
Biết
Hiểu
Vận
dụng
1
Ứng
dụng
đạo
hàm để
khảo
sát và
vẽ đồ
thị
hàm số
Tính đơn
điệu, cực
trị của hàm
số
(6 tiết)
Nhận biết:
– Nhận biết được tính đồng
biến, nghịch biến của một hàm
số trên một khoảng dựa vào
dấu của đạo hàm cấp một của
nó.
– Nhận biết được tính đơn
điệu, điểm cực trị, giá trị cực trị
của hàm số thông qua bảng
biến thiên hoặc thông qua hình
ảnh hình học của đồ thị hàm số.
Câu 1
TD1.2
Câu 2.
TD1.2
Câu 3
TD 1.1
Câu
1a-ĐS
TD 1.1
Câu
1b-ĐS
TD 1.1
Câu
1c-ĐS
TD 1.1
Câu
2b-ĐS
TD 1.2
Câu
2d-ĐS
TD 1.2
Câu 4
TD 1.2
4,0
Thông hiểu:
-Thể hiện được tính đồng biến,
nghịch biến của hàm số trong
bảng biến thiên của hàm số
- Xác định cực trị của hàm số.
Câu 5
TD1.1
Câu
3a-ĐS
TD 1.1
Câu
3d-ĐS
TD 1.3
Câu
4a-ĐS
TD 1.3
Câu
4b-ĐS
TD 1.3
Câu 1
TLN
GQ
2.1
Giá trị lớn
nhất, giá
trị nhỏ
nhất của
hàm số
(3 tiết)
Nhận biết:
Nhận biết được giá trị lớn
nhất, giá trị nhỏ nhất của hàm
số trên một tập xác định cho
trước.
Thông hiểu:
Xác định được giá trị lớn nhất,
giá trị nhỏ nhất của hàm số bằng
đạo hàm trong những trường hợp
đơn giản.
Câu
1d-ĐS
TD 1.1
Câu
3c-ĐS
TD 1.3
Câu
4d-ĐS
TD 1.3
Câu 6
GQ2.1
Câu 7
GQ2.1
1,25
Khảo sát và
vẽ đồ thị
của hàm số
(4 tiết + 5
tiết +1 tiết)
Nhận biết:
– Nhận biết được hình ảnh
hình học của đường tiệm cận
ngang, đường tiệm cận đứng,
đường tiệm cận xiên của đồ thị
hàm số.
– Nhận biết được tính đối
xứng (trục đối xứng, tâm đối
Câu 8
TD 1.2
Câu 9
TD 1.3
Câu
2a-ĐS
xứng) của đồ thị các hàm số.
Thông hiểu
– Mô tả được sơ đồ tổng quát
để khảo sát hàm số (tìm tập xác
định, xét chiều biến thiên, tìm
cực trị, tìm tiệm cận, lập bảng
biến thiên, vẽ đồ thị).
Vận dụng:
Khảo sát được (tập xác định,
chiều biến thiên, cực trị, tiệm
cận, bảng biến thiên) và vẽ đồ
thị của các hàm số:
y=ax
3
+bx
2
+cx+d (a
0);
( 0, 0)
ax b
y c ad bc
cx d
;
2
( . 0, 0).
ax bx c e
y px q a m e
mx n mx n


TD 1.2
Câu 10
TD 1.3
Câu 11
TD 1.2
Câu 12
TD 1.1
Câu
3b-ĐS
TD 1.1
Câu
2c-ĐS
TD 1.2
Câu
4c-ĐS
TD 1.3
Câu 2
TLN
GQ 3.1
2,75
Ứng dụng
đạo hàm
để giải
quyết một
số vấn đề
liên quan
đến thực
tiễn
(4 tiết + 1
tiết)
Vận dụng
Vận dụng được đạo hàm và
khảo sát hàm số để giải quyết
một số vấn đề liên quan đến
thực tiễn.
Câu 6
TLN
GQ2.1
Câu 3
TLN
MH 3.1
Câu 4
TLN
MH 3.1
Câu 5
TLN
MH 3.1
2,0
Tổng
9TN
+7ĐS
1TN
+7ĐS
2ĐS
2TN
+1TL
N
+2TLN
3TLN
10,0
40%
20%
5%
10%
10%
15%
| 1/16

Tài liệu khác của Toán 12

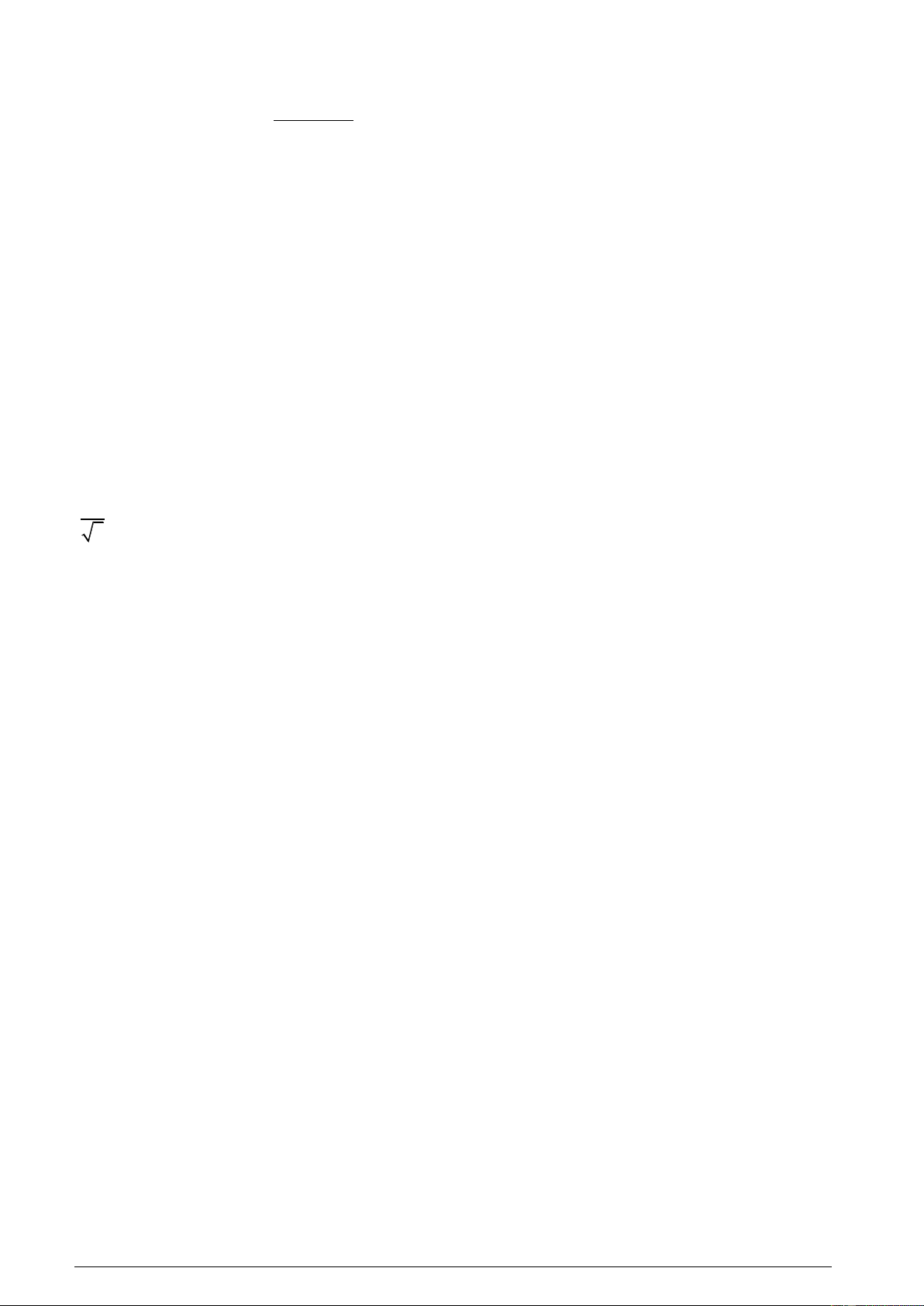
Preview text:

TRƯỜNG THPT QUẾ SƠN
KIỂM TRA GIỮA KỲ I- NĂM HỌC 2024-2025 TỔ: TOÁN-TIN.
Môn: TOÁN – Lớp 12.
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC
(Không kể thời gian giao đề)
(Đề gồm có 04 trang) MÃ ĐỀ 101
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y f x có bảng xét dấu của đạo hàm f '(x) như sau x  2  1 
f '(x)  0 + 0 
Hàm số đã cho đồng biến trên khoảng nào dưới đây A.  ;  2  .
B. 1; . C.  2   ;1 . D.  2;   .
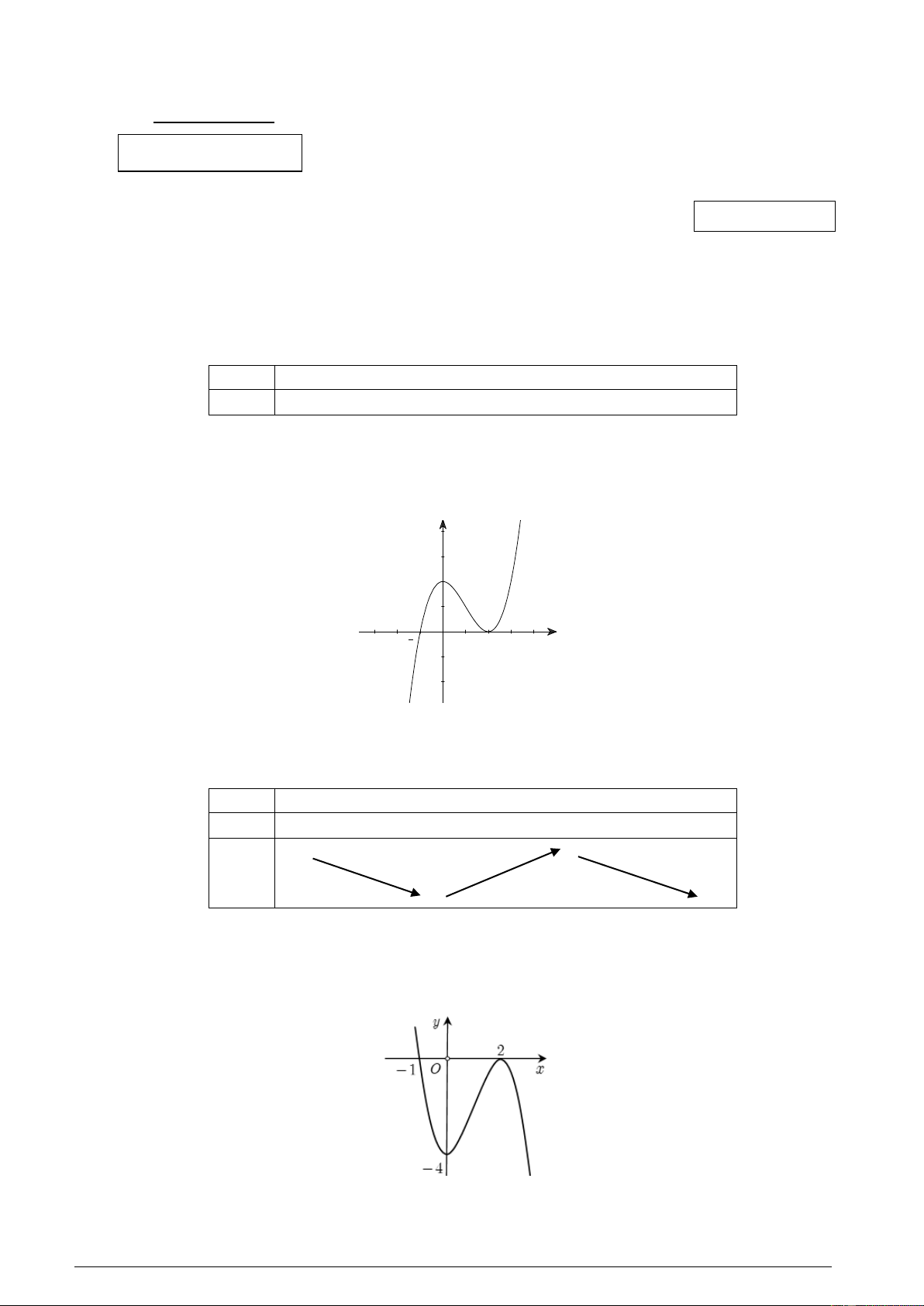
Câu 2. Cho hàm số y f (x) có đồ thị như hình vẽ. y 2 1 O 2 x
Hàm số đã cho nghịch biến trên khoảng nào dưới đây A.  ;    1 .
B. 2;  . C.  1  ;2 . D. 0; 2 .
Câu 3. Cho hàm số y f x có bảng biến thiên như sau x  2  1 
f '(x)  0 + 0   3 f (x) 2  
Hàm số y f x đạt cực đại tại điểm A. x  2  .
B. x 1.
C. x  3. D. x  2 .
Câu 4. Cho hàm số y f (x) có đồ thị như hình vẽ.
Cực tiểu của hàm số bằng A. 1. B. 4  . C. 0 . D. 2 . Mã đề 101/1
Câu 5. Điểm cực tiểu của đồ thị hàm số 3 2
y  x  3x  4 là
A. x  0 .
B. y  4 .
C. M (0; 4) . D. N (2;0) .
Câu 6. Cho hàm số f x liên tục trên  1  ; 
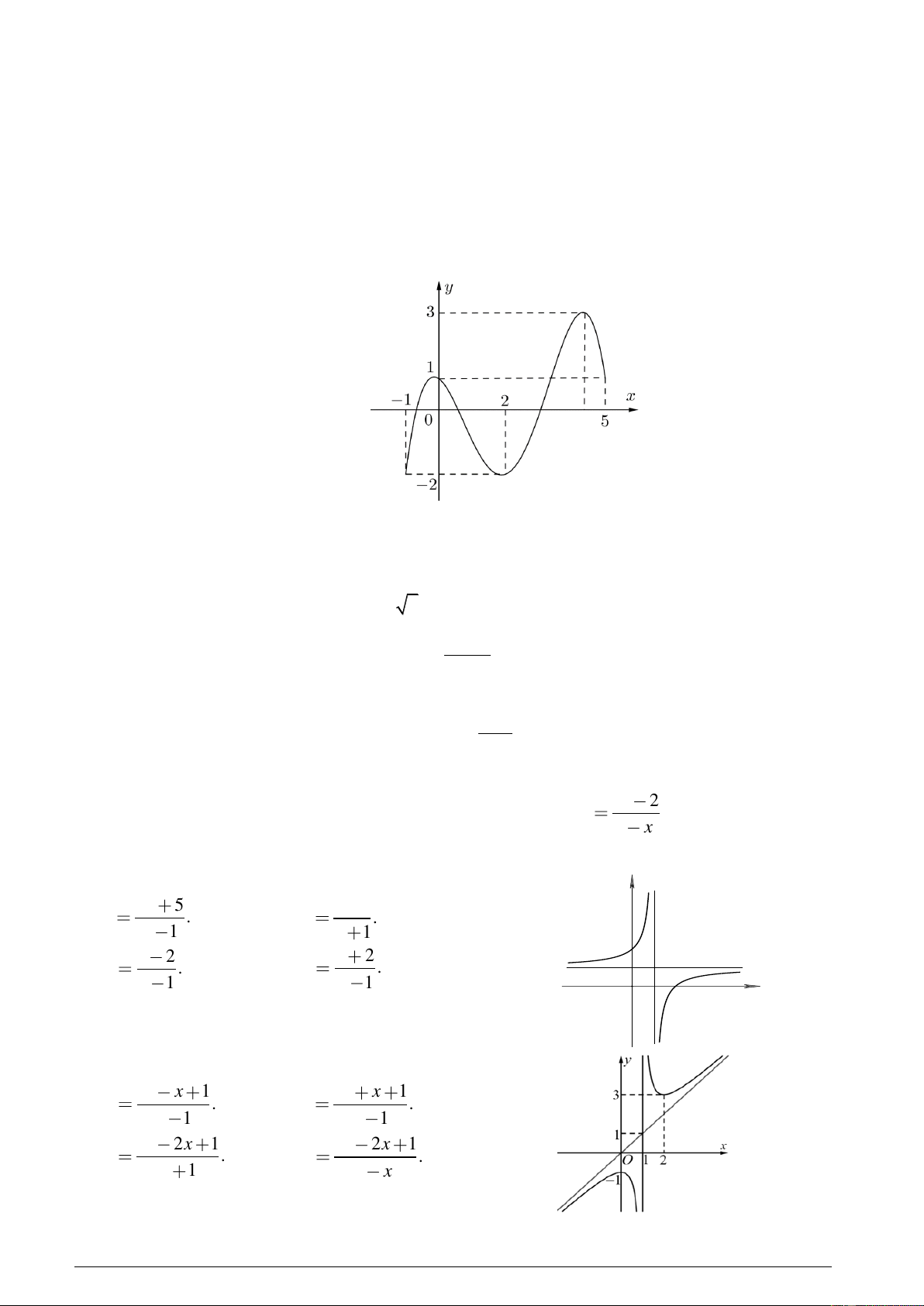
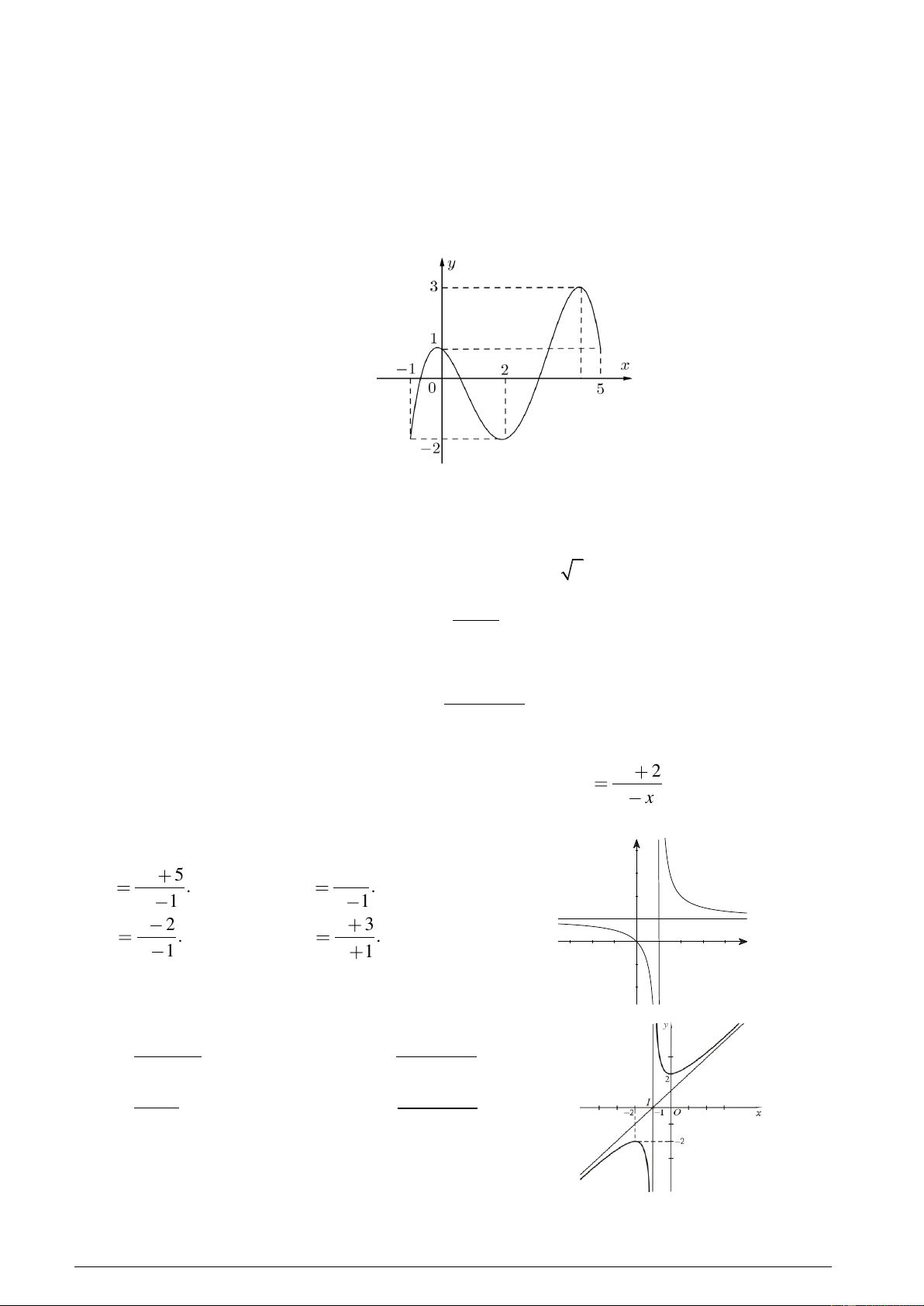
5 và có đồ thị trên đoạn  1  ;  5 như hình vẽ bên
dưới. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên đoạn  1  ;  5 . Tính T = M + m. A. T  1  .
B. T  4 .
C. T  1.
D. T  2 .
Câu 7. Giá trị nhỏ nhất của hàm số f x 3
x  21x trên đoạn 2;4 bằng A. 38  . B. 1  4 7 . C. 20  . D. 34  . x
Câu 8. Tiệm cận đứng của đồ thị hàm số 2 2 y  là đường thẳng x 1 A. x  1  .
B. x  2 .
C. y  2 . D. y  1.
Câu 9. Tiệm cận ngang của đồ thị hàm số 5 y  2  là đường thẳng x 1
A. y  2 .
B. y  5 . C. x  1  . D. x 1. x
Câu 10. Điểm nào sau đây là tâm đối xứng của đồ thị hàm số 3 2 y ? 1 x
A. I (1;3). B. J ( 1  ;3).
C. H (3; 2) D. K (1; 3).
Câu 11. Hình vẽ bên là đồ thị của hàm số nào sau đây? y 2x 5 x A. y . B. y . x 1 x 1 2 x 2 x 2 C. y . D. y . 1 x 1 x 1 O 1 2 x
Câu 12. Hình vẽ bên là đồ thị của hàm số nào sau đây? 2 x x 1 2 x x 1 A. y . B. y . x 1 x 1 2 x 2x 1 2 x 2x 1 C. y . D. y . x 1 1 x Mã đề 101/2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a, b, c, d ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số f x 3
x  3x . Các mệnh đề sau đúng hay sai? a) f x 2 '  3x 3 .
b) Hàm số đồng biến trên  1  ;  1 .
c) Hàm số đạt cực tiểu tại x  1
 và đạt cực đại tại x 1. 1 2
d) Giá trị nhỏ nhất của hàm số f x trên đoạn [0;2] bằng f   1 .  x Câu 2. Cho hàm số 2
y x  có đồ thị là (C). Các mệnh đề sau đúng hay sai? 1
a) Đồ thị (C) của hàm số có đường tiệm cận ngang là đường thẳng x  1  .
b) Hàm số đồng biến trên từng khoảng xác định của nó.
c) Tâm đối xứng của (C) nằm trên đường thẳng  : x  4y  3  0 .
d) Hàm số có 2 điểm cực trị. 2 x  2x  2
Câu 3. Cho hàm số y x
. Các mệnh đề sau đúng hay sai? 1
a) Hàm số đạt cực đại tại x  0 .
b) Đồ thị hàm số có 2 đường tiệm cận.
c) Hàm số đạt giá trị nhỏ nhất tại x  2
d) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho bằng 4 5 .
Câu 4. Cho hàm số y f x có đạo hàm liên tục trên
. Hàm số y f 'x có đồ thị như hình sau:
Các mệnh đề sau đúng hay sai?
a) Hàm số y f x có hai cực trị.
b) Hàm số y f x đồng biến trên khoảng  ;  0. c) f  
1  f 2  f 4. d) Trên đoạn  1
 ;4, giá trị lớn nhất của hàm số y f x là f   1 . Mã đề 101/3
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. 2 2x x 1
Câu 1. Cho hàm số y
. Tiệm cận xiên của đồ thị hàm số có phương trình y ax b . x  2
Tính giá trị biểu thức T = 5a  2b .
Câu 2. Biết đồ thị hàm số 3 2
y x bx c có một điểm cực trị M 2; 3. Tính y  3  .
Câu 3. Ông An có một hàng rào thép dài 100m và muốn rào cánh đồng thành một thửa ruộng
hình chữ nhật tiếp giáp với một con sông thẳng. Ông không cần rào cho phía giáp con sông. Biết
rằng ông An đã rào được thửa ruộng có diện tích lớn nhất là 2
a(m ) . Giá trị của a là bao nhiêu?
Câu 4. Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất x đơn vị hàng hóa nào đó của một nhà máy là 2 3
C(x)  16000  500x 1, 6x  0, 004x và p(x)  1700  7x là hàm cầu. Nhà máy
cần đặt phương án sản xuất bao nhiêu sản phẩm để lợi nhuận là lớn nhất.
Câu 5. Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 2 lít.
Lượng vật liệu dùng để sản xuất chiếc hộp là nhỏ nhất khi chiều cao của chiếc hộp bằng a *
(cm), (a, b N , b  10) . Tính T a  2b . 3 b
Câu 6. Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 3 1000cm .
Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,5 nghìn đồng/ 2 cm , trong khi mặt
xung quanh của bình được làm bằng vật liệu có giá 0,8 nghìn đồng/ 2
cm . Biết rằng chi phí thấp
nhất để sản xuất mỗi chiếc bình là a (nghìn đồng) (Kết quả làm tròn đến hàng đơn vị). Giá trị a bằng bao nhiêu? -----Hết----- Mã đề 101/4 TRƯỜNG THPT QUẾ SƠN
KIỂM TRA GIỮA KỲ I- NĂM HỌC 2024-2025 TỔ: TOÁN-TIN.
Môn: TOÁN – Lớp 12.
Thời gian làm bài: 90 phút ĐỀ CHÍNH THỨC
(Không kể thời gian giao đề)
(Đề gồm có 04 trang) MÃ ĐỀ 102
PHẦN I. Câu trắc nghiệm nhiều phương án lựa chọn. Thí sinh trả lời từ câu 1 đến câu 12. Mỗi câu
hỏi thí sinh chỉ chọn một phương án.
Câu 1. Cho hàm số y f x có bảng xét dấu của đạo hàm f '(x) như sau x  1 3 
f '(x) + 0  0 +
Hàm số đã cho nghịch biến trên khoảng nào dưới đây A.  ;    1 . B.  1  ;3. C.  1  ;. D. 3; .
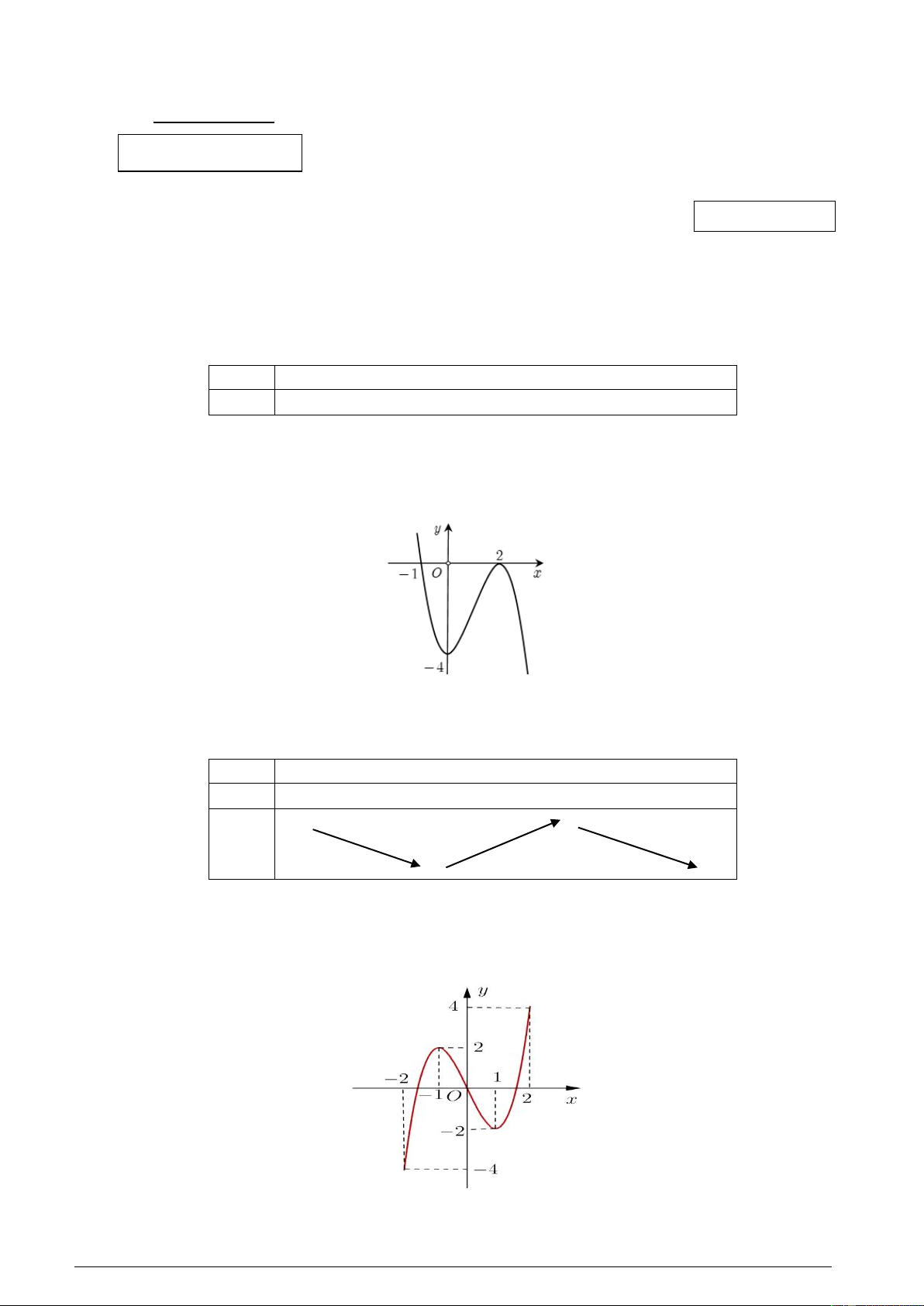
Câu 2. Cho hàm số y f (x) có đồ thị như hình vẽ.
Hàm số đã cho đồng biến trên khoảng nào dưới đây A.  ;    1 . B.  1  ;2 . C.  4  ;2 . D. 0; 2 .
Câu 3. Cho hàm số y f x có bảng biến thiên như sau x  2  1 
f '(x)  0 + 0   3 f (x) 1 
Hàm số y f x đạt cực tiểu tại điểm A. x  2  .
B. x 1.
C. x  3. D. x  1  .
Câu 4. Cho hàm số y f (x) có đồ thị như hình vẽ.
Cực đại của hàm số bằng A. 1. B. 4 . C. 1. D. 2 . Mã đề 102/1
Câu 5. Điểm cực đại của đồ thị hàm số 3 2
y  x  3x  4 là
A. x  2 .
B. x  0 .
C. M (0; 4) . D. N (2;0) .
Câu 6. Cho hàm số f x liên tục trên  1  ; 
5 và có đồ thị trên đoạn  1  ;  5 như hình vẽ bên
dưới. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số f x trên đoạn  1  ;  5 . Tính T = M  m.
A. T  5 .
B. T  1.
C. T  3.
D. T  2 .
Câu 7. Giá trị lớn nhất của hàm số 3
f (x)  x  21x trên đoạn 2;5 bằng A. 38 . B. 20  . C. 14 7 . D. 34 . x
Câu 8. Tiệm cận ngang của đồ thị hàm số 2 2 y  là đường thẳng x 1 A. x  1  .
B. x  2 .
C. y  2 . D. y  1. 2 x  2x  5
Câu 9. Tiệm cận đứng của đồ thị hàm số y  là đường thẳng x  2
A. y  1.
B. x  2 . C. x  2  . D. y  1. x
Câu 10. Điểm nào sau đây là tâm đối xứng của đồ thị hàm số 5 2 y ? 1 x
A. I (1;5). B. K (1; 5  ). C. H (5; 2  ) D. J ( 1  ;5).
Câu 11. Hình vẽ bên là đồ thị của hàm số nào sau đây? y 2x 5 x A. y . B. y . x 1 x 1 1 x 2 x 3 C. y . D. y . x 1 x 1 O 1 x
Câu 12. Hình vẽ bên là đồ thị của hàm số nào sau đây? 2 x x 1 2 x  2x  2 A. y  . B. y  . x 1 x 1 2x  3 2 x  2x  2 C. y  . D. y  . x 1 x 1 Mã đề 102/2
PHẦN II. Câu trắc nghiệm đúng sai. Thí sinh trả lời từ câu 1 đến câu 4. Trong mỗi ý a, b, c, d ở mỗi
câu, thí sinh chọn đúng hoặc sai.
Câu 1. Cho hàm số f x 3 2
 x  3x 5. Các mệnh đề sau đúng hay sai? a) f x 2 '  3  x  6x .
b) Hàm số nghịch biến trên (0; 2) .
c) Hàm số đạt cực tiểu tại x  2 và đạt cực đại tại x  0 . 1 2
d) Giá trị nhỏ nhất của hàm số f x trên đoạn [1;3] bằng f 2 .  x Câu 2. Cho hàm số 5 3
y x  có đồ thị là (C). Các mệnh đề sau đúng hay sai? 2
a) Đồ thị (C) của hàm số có đường tiệm cận ngang là đường thẳng y  5 .
b) Hàm số đồng biến trên từng khoảng xác định của nó.
c) Tâm đối xứng của (C) nằm trên đường thẳng  : x  2y  4  0 .
d) Hàm số không có cực trị. 2 x x  4
Câu 3. Cho hàm số y x
. Các mệnh đề sau đúng hay sai? 1
a) Hàm số đạt cực đại tại x  3.
b) Đồ thị hàm số có 2 đường tiệm cận.
c) Hàm số đạt giá trị lớn nhất tại x  1 
d) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho bằng 4 5 .
Câu 4. Cho hàm số y f x có đạo hàm liên tục trên
. Hàm số y f 'x có đồ thị như hình sau:
Các mệnh đề sau đúng hay sai?
a) Hàm số y f x có một điểm cực đại.
b) Hàm số y f x nghịch biến trên khoảng 0  ;1 . c) f  
1  f 0  f   1 . d) Trên đoạn  4  
;1 , giá trị nhỏ nhất của hàm số y f x là f   1 . Mã đề 102/3
PHẦN III. Câu trắc nghiệm trả lời ngắn. Thí sinh trả lời từ câu 1 đến câu 6. 2 2x x 1
Câu 1. Cho hàm số y
. Tiệm cận xiên của đồ thị hàm số có phương trình y ax b . x  2
Tính giá trị biểu thức T = 5a  2b .
Câu 2. Biết đồ thị hàm số 3 2
y x bx c có một điểm cực trị M  2
 ; 3 . Tính y 5  .
Câu 3. Ông Bình có một hàng rào thép dài 120m và muốn rào cánh đồng thành một thửa ruộng
hình chữ nhật tiếp giáp với một con sông thẳng. Ông không cần rào cho phía giáp con sông. Biết
rằng ông Bình đã rào được thửa ruộng có diện tích lớn nhất là 2
a(m ) . Giá trị của a là bao nhiêu?
Câu 4. Giả sử chi phí (tính bằng trăm nghìn đồng) để sản xuất x đơn vị hàng hóa nào đó của một nhà máy là 2 3
C(x)  17000  300x  3, 6x  0, 004x và p(x)  1500  9x là hàm cầu. Nhà máy
cần đặt phương án sản xuất bao nhiêu sản phẩm để lợi nhuận là lớn nhất.
Câu 5. Một chiếc hộp dạng hình hộp chữ nhật có đáy là hình vuông và có thể tích là 3 lít.
Lượng vật liệu dùng để sản xuất chiếc hộp là nhỏ nhất khi chiều cao của chiếc hộp bằng a *
(cm), (a, b N , b  10) . Tính T a  3b . 3 b
Câu 6. Một nhà sản xuất cần làm ra những chiếc bình có dạng hình trụ với dung tích 3 1000cm .
Mặt trên và mặt dưới của bình được làm bằng vật liệu có giá 1,8 nghìn đồng/ 2 cm , trong khi mặt
xung quanh của bình được làm bằng vật liệu có giá 0,6 nghìn đồng/ 2
cm . Biết rằng chi phí thấp
nhất để sản xuất mỗi chiếc bình là a (nghìn đồng) (Kết quả làm tròn đến hàng đơn vị). Giá trị a bằng bao nhiêu? -----Hết----- Mã đề 102/4 TRƯỜNG THPT QUẾ SƠN TỔ TOÁN-TIN
ĐÁP ÁN KIỂM TRA GIỮA HỌC KỲ 1 NĂM HỌC 2024-2025 MÔN TOÁN LỚP 12
Phần I (3 điểm): Gồm 12 câu mỗi câu đúng được 0, 25.
Phần II (4 điểm): Gồm 04 câu mỗi câu đúng cả 4 ý được 1,0.
Phần III(3 điểm): Gồm 06 câu mỗi câu đúng được 0,5. ĐÁP ÁN ĐỀ 101 Phần I Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C D B B C C B A A D C A Phần II: Câu 1 Đúng Sai Câu 2
Đúng Sai Câu 3 Đúng Sai Câu 4 Đúng Sai a) X a) X a) X a) X b) X b) X b) X b) X c) X c) X c) X c) X d) X d) X d) X d) X Phần III: Câu Đáp số 1 1 6 2 – 4 7 3 1 2 5 0 4 1 0 0 5 2 8 6 5 4 6 ĐÁP ÁN ĐỀ 102 Phần I: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án B D A D D A C D C B B B Phần II: Câu 1 Đúng Sai Câu 2
Đúng Sai Câu 3 Đúng Sai Câu 4 Đúng Sai a) X a) X a) X a) X b) X b) X b) X b) X c) X c) X c) X c) X d) X d) X d) X d) X Phần III: Câu Đáp số 1 2 0 2 – 5 1 3 1 8 0 0 4 1 0 0 5 4 8 6 4 7 9 ĐÁP ÁN ĐỀ 103 Phần I: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C B A B A A D A B B B D Phần II: Câu 1 Đúng Sai Câu 2
Đúng Sai Câu 3 Đúng Sai Câu 4 Đúng Sai a) X a) X a) X a) X b) X b) X b) X b) X c) X c) X c) X c) X d) X d) X d) X d) X Phần III: Câu Đáp số 1 – 4 7 2 1 6 3 1 2 5 0 4 1 0 0 5 2 8 6 5 4 6 ĐÁP ÁN ĐỀ 104 Phần I: Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án D C D A B D B A A A D C Phần II: Câu 1 Đúng Sai Câu 2
Đúng Sai Câu 3 Đúng Sai Câu 4 Đúng Sai a) X a) X a) X a) X b) X b) X b) X b) X c) X c) X c) X c) X d) X d) X d) X d) X Phần III: Câu Đáp số 1 – 5 1 2 2 0 3 1 8 0 0 4 1 0 0 5 4 8 6 4 7 9
Hướng dẫn đáp số phần III Đề 101 và 103:
1) Tìm được TCX : y  2x  3  T  5.2  2( 3  ) 16 y '(2)  0 b   3  2) Theo đề ta suy ra 3 2   
y x  3x  7 3 2  y( 3  )  ( 3  )  3( 3  )  7  4  7 y(2)  3 c  7
3) Diện tích thửa ruộng lớn nhất khi chiều rộng x = 25 (m), y = 50(m) suy ra S = 1250 (m2). 4) Doanh thu của nhà máy 2 R(x)  .
x p(x)  1700x  7x Lợi thuận thu được: 2 2 3
P(x)  R(x)  C(x)  1700x  7x  (16000  500x 1, 6x  0, 004x ) = 2 3 1
 6000 1200x  5,4x  0,004x Suy ra 2
P '(x)  1200 10,8x  0, 012x , P '(x)  0  x  100(do  0)
Lập BB của P(x) ta được mức sản xuất để tối ưu hóa lợi nhuận là 100 đơn vị hàng hóa. 5) 2 lít = 2000cm3.
Gọi x( cm) là cạnh đáy của chiếc hộp. Khi đó, ta có chiề 2000 u cao của chiếc hộp là ( cm) . 2 x 2000 8000
Suy ra, tổng diện tích bề mặt của chiếc hộp là 2 2
S  2x  4x   2x  , x  0. 2 x x 3 8000 4x  8000 Ta có: 3 S  4x  
; S  0  x  10 2 . 2 2 x x
Lập bảng biến thiên, ta có kết quả lượng vật liệu dùng để sản xuất là nhỏ nhất (tức là tổng
diện tích bề mặt hộp nhỏ nhất) khi cạnh đáy của hộp là 3
10 2 cm và chiều cao của hộp là
20 cm . T  202.4 28. 3 4
6) Gọi bán kính đáy của bình là x (cm, x  0) , chiều cao của bình là h (cm, h  0) 1000 Có 2
x .h 1000(c )
m Suy ra chiều cao của bình là h: (cm) 2  x 1000 Chi phí để 2
sản xuất một chiếc bình là: C(x) =1, 5.2 x  0,8.2. . . x 2  x 1600 2  3 x x
Để chi phí sản xuất mồi chiếc bình là thấp nhất thì C(x) là nhỏ nhất. 1600 800 3
C '(x)  6 x
; C '(x)  0  x  2 x 3 800
Lập BBT C(x), ta được C(x) đạt GTNN xấp xỉ 546 nghìn đồng khi 3 x  (nghìn đồng) 3 Đề 102 và 104:
1) Tìm được TCX : y  2x  5  T  5.2  2( 5  )  20 y '( 2)   0 b   3 2) Theo đề ta suy ra 3 2   
y x  3x 1 3 2  y( 5  )  ( 5  )  3( 5  ) 1  5  1 y( 2)   3 c  1 
3) Diện tích thửa ruộng lớn nhất khi chiều rộng x = 30 (m), y = 60(m) suy ra S = 1800 (m2). 4) Doanh thu của nhà máy 2 R(x)  .
x p(x)  1500x  9x Lợi thuận thu được: 2 2 3
P(x)  R(x)  C(x)  1500x  9x  (17000  300x  3, 6x  0, 004x ) = 2 3 1
 7000 1200x  5,4x  0,004x Suy ra 2
P '(x)  1200 10,8x  0, 012x , P '(x)  0  x  100(do  0)
Lập BB của P(x) ta được mức sản xuất để tối ưu hóa lợi nhuận là 100 đơn vị hàng hóa. 5) 3 lít = 3000cm3.
Gọi x( cm) là cạnh đáy của chiếc hộp. 3000
Khi đó, ta có chiều cao của chiếc hộp là ( cm) . 2 x 3000 12000
Suy ra, tổng diện tích bề mặt của chiếc hộp là 2 2
S  2x  4x   2x  , x  0. 2 x x 3 12000 4x 12000 Ta có: 3 S  4x  
; S  0  x  10 3 . 2 2 x x
Lập bảng biến thiên, ta có kết quả lượng vật liệu dùng để sản xuất là nhỏ nhất (tức là tổng
diện tích bề mặt hộp nhỏ nhất) khi cạnh đáy của hộp là 3
10 3 cm và chiều cao của hộp là
30 cm. T 302.9 48. 3 9
6) Gọi bán kính đáy của bình là x (cm, x  0) , chiều cao của bình là h (cm, h  0) 1000 Có 2
x .h 1000(c )
m Suy ra chiều cao của bình là h: (cm) 2  x 1000 Chi phí để 2
sản xuất một chiếc bình là: C(x) =1,8.2 x  0, 6.2. . . x 2  x 1200 2  3,6 x x
Để chi phí sản xuất mồi chiếc bình là thấp nhất thì C(x) là nhỏ nhất. 1200 500 3
C '(x)  7, 2 x
; C '(x)  0  x  2 x 3 500
Lập BBT C(x), ta được C(x) đạt GTNN xấp xỉ 479 nghìn đồng khi 3 x  (nghìn đồng). 3
Trường THPT Quế Sơn Tổ Toán-Tin
MA TRẬN +ĐẶC TẢ ĐỀ KIỂM TRA GIỮA KỲ I NĂM HỌC 2024-2025
MÔN: TOÁN 12 . Thời gian làm bài: 90 phút .
Tư duy và lập luận Toán
Giải quyết vấn đề Toán
Mô hình hóa Toán học Chươn Điểm học (TD) học (GQ) (MH) STT g/ Nội dung
Mức độ kiểm tra, đánh giá Chủ đề Biết Hiểu Vận Biết Hiểu Vận Biết Hiểu Vận dụng dụng dụng Nhận biết: Câu 1
– Nhận biết được tính đồng TD1.2
biến, nghịch biến của một hàm Câu 2.
số trên một khoảng dựa vào TD1.2
dấu của đạo hàm cấp một của Câu 3 nó. TD 1.1 – Câu
Nhận biết được tính đơn 1a-ĐS Ứng
điệu, điểm cực trị, giá trị cực trị TD 1.1 dụng
của hàm số thông qua bảng Câu đạo Tính đơn
biến thiên hoặc thông qua hình 1b-ĐS
hàm để điệu, cực
ảnh hình học của đồ thị hàm số. TD 1.1 1 khảo
trị của hàm Câu 4,0 sát và số 1c-ĐS
vẽ đồ (6 tiết) TD 1.1 thị Câu hàm số 2b-ĐS TD 1.2 Câu 2d-ĐS TD 1.2 Câu 4 TD 1.2 Câu 5 Câu 1 Thông hiểu: TD1.1 TLN
-Thể hiện được tính đồng biến, GQ
nghịch biến của hàm số trong Câu 2.1 bảng 3a-ĐS
biến thiên của hàm số TD 1.1
- Xác định cực trị của hàm số. Câu 3d-ĐS TD 1.3 Câu 4a-ĐS TD 1.3 Câu 4b-ĐS TD 1.3 Nhận biết: Câu
Nhận biết được giá trị lớn 1d-ĐS
nhất, giá trị nhỏ nhất của hàm TD 1.1
Giá trị lớn
số trên một tập xác định cho nhất, giá trước. trị nhỏ nhất của Thông hiểu: 1,25 hàm số
Xác định được giá trị lớn nhất, Câu Câu 6 (3 tiết)
giá trị nhỏ nhất của hàm số bằng 3c-ĐS GQ2.1
đạo hàm trong những trường hợp TD 1.3 Câu 7 đơn giản. Câu GQ2.1 4d-ĐS TD 1.3 Nhận biết: – Khảo sát và
Nhận biết được hình ảnh
vẽ đồ thị
hình học của đường tiệm cận của hàm số Câu 8
ngang, đường tiệm cận đứng, (4 tiết + 5
đường tiệm cận xiên của đồ thị TD 1.2
tiết +1 tiết) Câu 9 hàm số. TD 1.3
– Nhận biết được tính đối Câu
xứng (trục đối xứng, tâm đối 2a-ĐS
xứng) của đồ thị các hàm số. TD 1.2 2,75 Câu 10 TD 1.3 Câu 11 TD 1.2 Câu 12 TD 1.1 Thông hiểu Câu
– Mô tả được sơ đồ tổng quát 3b-ĐS
để khảo sát hàm số (tìm tập xác TD 1.1
định, xét chiều biến thiên, tìm
cực trị, tìm tiệm cận, lập bảng
biến thiên, vẽ đồ thị). Vận dụng: Câu
Khảo sát được (tập xác định, 2c-ĐS Câu 2
chiều biến thiên, cực trị, tiệm TD 1.2 TLN
cận, bảng biến thiên) và vẽ đồ Câu GQ 3.1 thị của các hàm số: 4c-ĐS
y=ax3+bx2+cx+d (a  0); TD 1.3 ax b y
(c  0, ad bc  0) cx d ; 2
ax bx c e y   pxq ( .
a m  0, e  0). mx n mx n Ứng dụng đạo hàm Câu 3 để giải TLN quyết một Vận dụng MH 3.1
số vấn đề
Vận dụng được đạo hàm và Câu 6 Câu 4
khảo sát hàm số để giải quyết TLN TLN 2,0 liên quan đến thực
một số vấn đề liên quan đến GQ2.1 MH 3.1 tiễn thực tiễn. Câu 5 (4 tiết + 1 TLN tiết) MH 3.1 9TN 1TN 2ĐS 2TN +7ĐS +7ĐS +1TL +2TLN 3TLN 10,0 Tổng N 40% 20% 5% 10% 10% 15%
Document Outline

  • DE-101_Toan-12_GK1_24-25
  • DE-102_Toan-12_GK1_24-25
  • Dap-an-Toan-12_GK1_24-25
  • 1-MA-TRAN-DAC-TA-Toan-12-GK1_24-25