Đề giữa kỳ 2 Toán 10 năm 2022 – 2023 trường THPT Nguyễn Thị Minh Khai – TP HCM

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra giữa học kỳ 2 môn Toán 10 năm học 2022 – 2023 trường THPT Nguyễn Thị Minh Khai, thành phố Hồ Chí Minh; thời gian học sinh làm bài thi là 60 phút, mời bạn đọc đón xem

28 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 10

Môn: Toán 10

Thông tin:

3 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
Họ tên học sinh: …………………………………………………… SBD: …………………………
Bài 1: (2,0 điểm) Giải các phương trình
a)
2
2 10 3 2 .
x x x
(1,0 điểm)
b)
2
2 2 3 8.
x x x
(1,0 điểm)
Bài 2: (1,0 điểm) Sau khi được ném lên, độ cao y
(mét) của một quả bóng so với mặt đất sau x (giây)
được cho bởi hàm số 𝑦(𝑥) = −0,02𝑥
+ 0,4𝑥. Hỏi
quả bóng đạt độ cao lớn hơn 1,5 (mét) so với mặt đất
trong thời gian khoảng bao lâu?
Bài 3: (2,0 điểm) Cho biểu thức
2
( ) 1 2 1 3 3
f x m x m x m
. Tìm tất cả giá trị của tham số
m
sao cho
( ) 0; .
f x x
Bài 4: (3,0 điểm) Trong mặt phẳng
Oxy
, cho
ABC
với
, .
1; 2 , 2;0 7; 5
A B C
a) Chứng minh
ABC
vuông tại A. (1,5 điểm)
b) Tìm tọa độ điểm
D
sao cho tứ giác ABCD là hình bình hành. (1,5 điểm)
Bài 5: (2,0 điểm) Trong mặt phẳng
Oxy
, cho đường thẳng
: 2 2023 0
x y
và hai điểm
,
2;5
P
5;1 .
Q
a) Viết phương trình đường thẳng
1
d
đi qua điểm P và song song với đường thẳng
. (1,0 điểm)
b) Viết phương trình đường thẳng
2
d
đi qua điểm P và cách điểm Q một khoảng bằng 3. (1,0 điểm)
HẾT
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
Năm học: 2022 – 2023
Môn TOÁN – Khối: 10
Thời gian: 60 phút
(Không kể thời gian phát đề)
Đ
ề
2
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 2 (Toán 10)
Bài 1
:
Giải phương trình
2đ
Câu 1a:
.
2
2 10 3 = 2
x x x
1đ
2
2
2 10 3 2
Pt x x x
0.25x4
2
6 7 0
x x
1 hay 7
x x
Thử lại: Pt có nghiệm là
1.
x
Câu 1b:
.
2
2 2 = 3 8
x x x
1đ
Pt
2
2 2 3 8
x x x
0.25x4
2
5 6 0
x x
2 hay = 3
x x
Thử lại: Pt có nghiệm là x = 3.
Bài 2:
Sau khi được ném lên, độ cao y (mét) của một quả bóng so với mặt đất sau x
(giây) được cho bởi hàm số
𝒚
(
𝒙
)
=
−
𝟎
,
𝟎𝟐
𝒙
𝟐
+
𝟎
,
𝟒
𝒙
. Hỏi quả bóng đạt độ cao lớn hơn
1,5 (mét) so với mặt đất trong thời gian khoảng bao lâu?
1đ
Ycbt
2
0,02 0,4 1,5
x x
2
0,02 0,4 1,5 0
x x
5 < x < 15.
Thời gian cần tìm là khoảng 10 (giây).
0.25x4
Bài 3:
2
( ) 1 2 1 3 3 0; .
f x m x m x m x
2đ
1
m
:
3
( ) 4 6 0 .
2
f x x x
(không thỏa ycbt)
0.25x2
1:
m
2
2
1 0
1
( ) 0;
1 1 3 3 0 2 2 4 0
m
m
f x x
m m m m m
0.25x6
1
2 1
m
m m
2.
m
Bài 4:
ABC
với
.
,
1; 2 , 2;0 7; 5
A B C
3đ
Câu 4a: Chứng minh
ABC
vuông tại A.
1,5đ
1; 2
AB
;
6; 3
AC
.
0.25x2
. 1.6 2.( 3) 0
AB AC
AB AC
.
0.25x3
ABC
vuông tại A.
0.25
Câu 4b: Tìm tọa độ điểm
D
sao cho tứ giác ABCD là hình bình hành. 1,5đ
Ycbt
AD BC

1 7 2
2 5 0
D
D
x
y
. Vậy
6; 7 .
D
0.5x3
Bài 5:
: 2 2023 0
x y
,
2; 5 , 5;1
P Q
.
2đ
Câu 5a: Phương trình
1
d
qua P và song song
.
1đ
1
: 2 0
d x y m
với
2023
m
.
0.25
1
2; 5 2 2.5 0 8
P d m m
(nhận).
0.25x2
Vậy
1
: 2 8 0.
d x y
0.25
Câu 5b: Phương trình
2
d
qua P và cách điểm Q một khoảng bằng 3.
1đ
Phương trình
2
d
có dạng:
2 5 0 2 5 0
a x b y ax by a b
(a
2
+ b
2
> 0).
0.25
2
, 3
d Q d
2 2
5 2 5
3
a b a b
a b
2 2
3 4 3
a b a b
0 hay 7 24
b b a
.
0.25
+ Với
0
b
, chọn
1
a
nên
2
: 2 0.
d x
+ Với
7 24
b a
, chọn
7 24
a b
nên
2
:7 24 134 0.
d x y
0.25x2
HẾT
D
A
B
C
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Đề 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI Năm học: 2022 – 2023 Môn TOÁN – Khối: 10 Thời gian: 60 phút
(Không kể thời gian phát đề)
Họ tên học sinh: …………………………………………………… SBD: …………………………
Bài 1: (2,0 điểm) Giải các phương trình a) 2 2x 10x  3  2  . x (1,0 điểm) b) 2
x  2x  2  3x  8. (1,0 điểm)
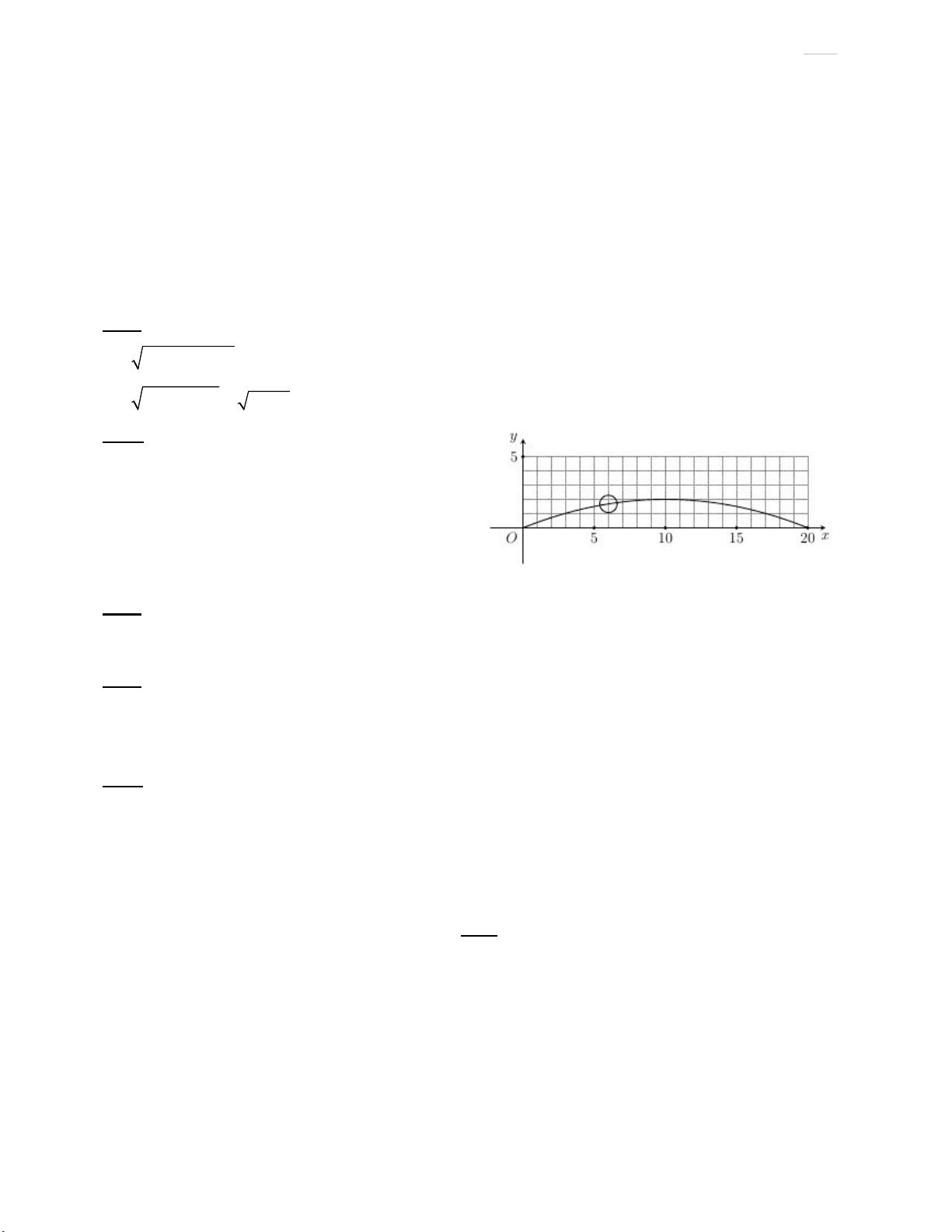
Bài 2: (1,0 điểm) Sau khi được ném lên, độ cao y
(mét) của một quả bóng so với mặt đất sau x (giây)
được cho bởi hàm số 𝑦(𝑥) = −0,02𝑥 + 0,4𝑥. Hỏi
quả bóng đạt độ cao lớn hơn 1,5 (mét) so với mặt đất
trong thời gian khoảng bao lâu?
Bài 3: (2,0 điểm) Cho biểu thức f x  m   2 ( )
1 x  2 m 1 x  3m  3 . Tìm tất cả giá trị của tham số m
sao cho f (x)  0; x  . 
Bài 4: (3,0 điểm) Trong mặt phẳng Oxy , cho ABC với A1;  2, B 2;0,C 7;  5.
a) Chứng minh ABC vuông tại A. (1,5 điểm)
b) Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. (1,5 điểm)
Bài 5: (2,0 điểm) Trong mặt phẳng Oxy , cho đường thẳng  : x  2y  2023  0 và hai điểm P 2;5, Q 5;  1 .
a) Viết phương trình đường thẳng d đi qua điểm P và song song với đường thẳng  . (1,0 điểm) 1 
b) Viết phương trình đường thẳng d đi qua điểm P và cách điểm Q một khoảng bằng 3. (1,0 điểm) 2  HẾT
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 2 (Toán 10)
Bài 1: Giải phương trình 2đ Câu 1a: 2 2 x  10x  3 = 2  x. 1đ 2
Pt  2x 10x  3  2  x2 2  x  6x  7  0 0.25x4  x  1 hay x  7
Thử lại: Pt có nghiệm là x  1. Câu 1b: 2 x  2x  2 = 3x  8. 1đ Pt  2 x  2x  2  3x  8  2 x  5x  6  0 0.25x4  x  2 hay x = 3
Thử lại: Pt có nghiệm là x = 3.
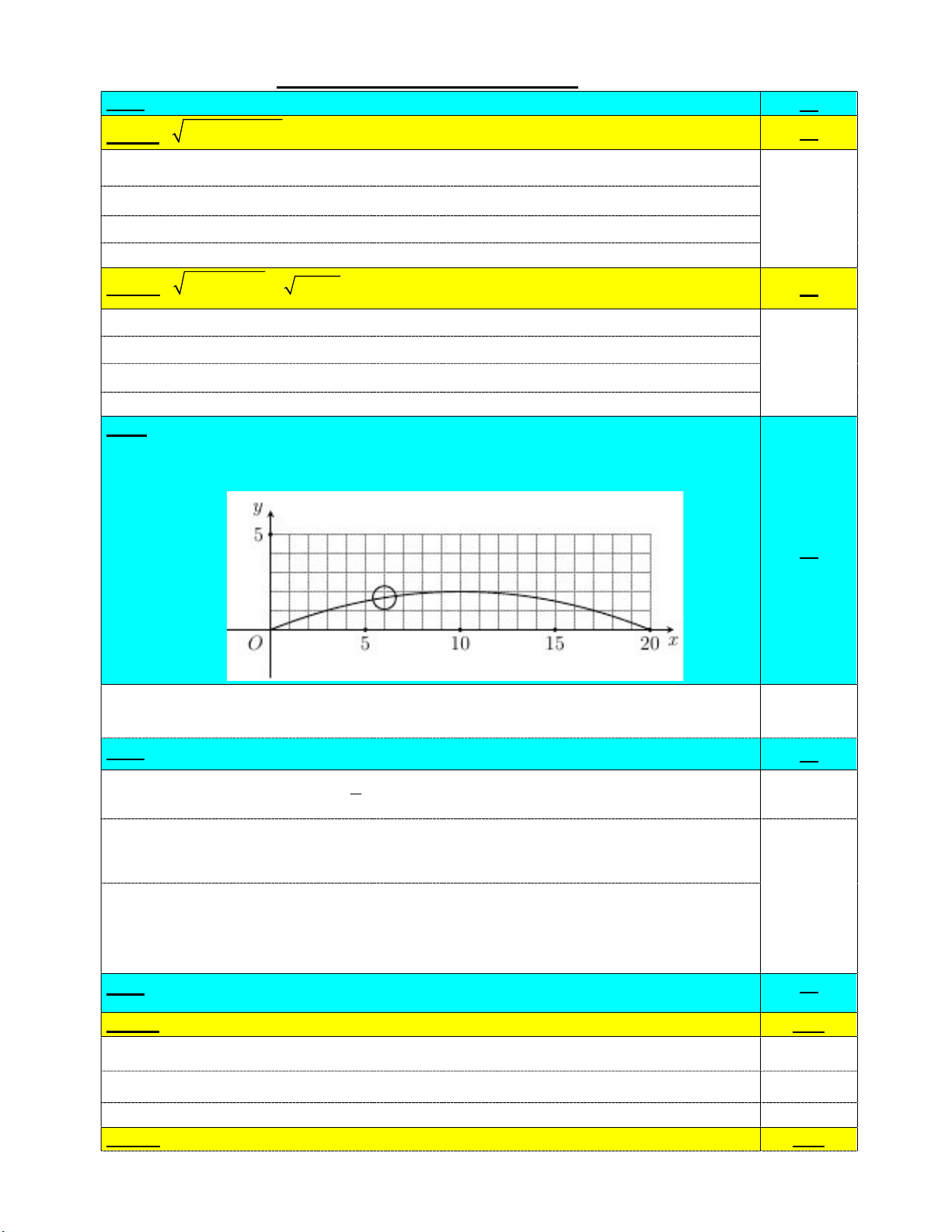
Bài 2: Sau khi được ném lên, độ cao y (mét) của một quả bóng so với mặt đất sau x
(giây) được cho bởi hàm số 𝒚(𝒙) = −𝟎, 𝟎𝟐𝒙𝟐 + 𝟎, 𝟒𝒙. Hỏi quả bóng đạt độ cao lớn hơn
1,5 (mét) so với mặt đất trong thời gian khoảng bao lâu? 1đ Ycbt  2 0,02x  0,4x 1,5  2
0, 02x  0, 4x 1,5  0  5 < x < 15. 0.25x4
Thời gian cần tìm là khoảng 10 (giây). Bài 3: f x  m   2 ( )
1 x  2 m  1 x  3m  3  0;x  . 2đ 3
 m  1 : f ( x)  4x  6  0  x  . (không thỏa ycbt) 2 0.25x2  m 1  0   m  1    m  1: f (x)  0; x          m   2 1  m   1 3m  3 2  0  2  m  2m  4  0 0.25x6  m  1     m  2  . m   2   m 1 Bài 4: 3đ
ABC với A1; 2 , B 2;0 ,C 7; 5.
Câu 4a: Chứng minh ABC vuông tại A. 1,5đ  
AB  1; 2; AC  6;  3 . 0.25x2    
AB . AC  1.6  2.(3)  0  AB  AC . 0.25x3  ABC vuông tại A. 0.25
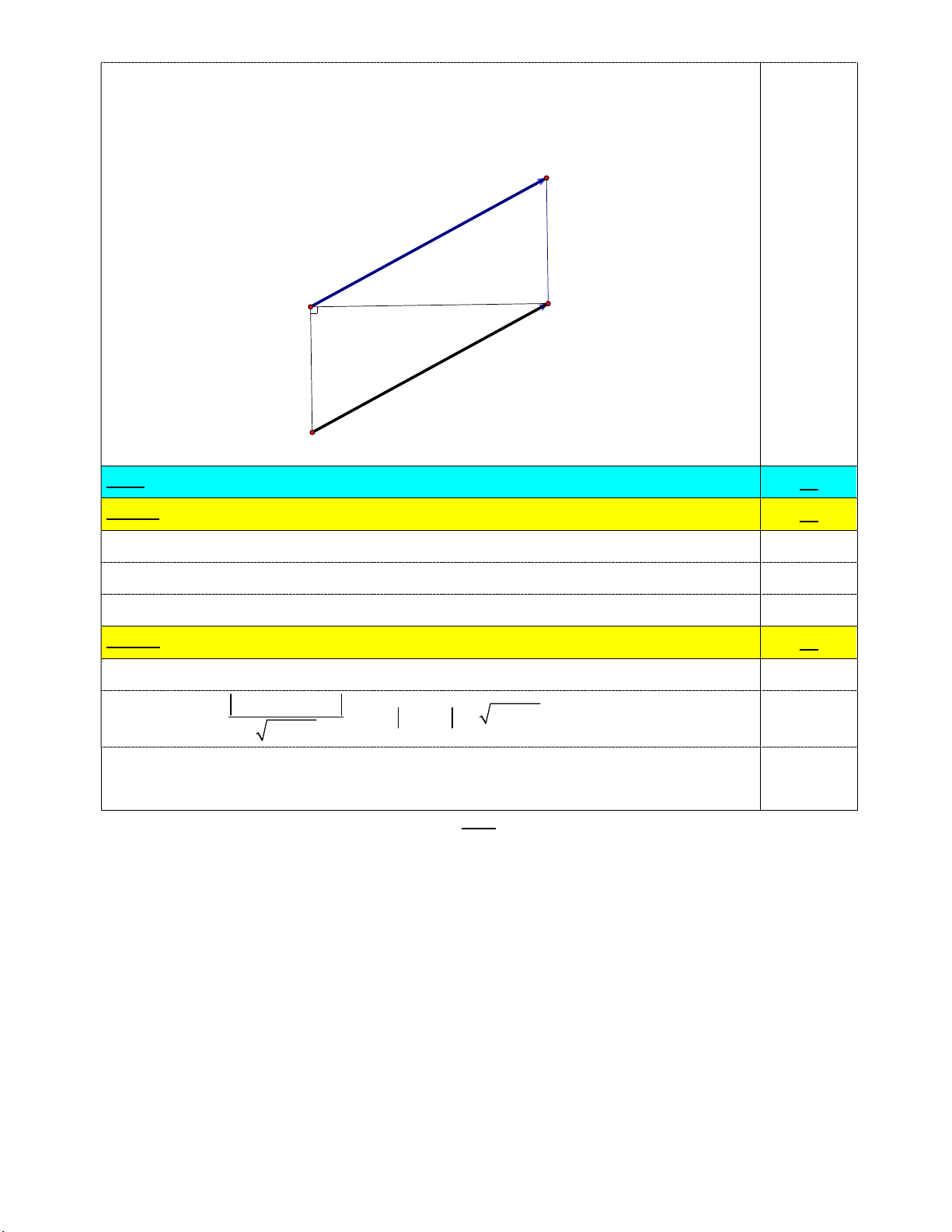
Câu 4b: Tìm tọa độ điểm D sao cho tứ giác ABCD là hình bình hành. 1,5đ   x 1  7  2 Ycbt  AD  BC D   . Vậy D 6;  7. y  2  5   0  D D 0.5x3 A C B
Bài 5:   : x  2 y  2023  0 , P 2; 5 , Q 5;1 . 2đ
Câu 5a: Phương trình d qua P và song song  . 1  1đ
d : x  2y  m  0 với m  2023. 1  0.25
P 2; 5  d  2  2.5  m  0  m  8 (nhận). 0.25x2 1 
Vậy d : x  2 y  8  0. 0.25 1 
Câu 5b: Phương trình d qua P và cách điểm Q một khoảng bằng 3. 2  1đ
Phương trình d có dạng: a  x  2  b y  5  0  ax  by  2a  5b  0 (a2 + b2 > 0). 0.25 2  5a  b  2a  5b d Q , d  3   3 2 2
 3a  4b  3 a  b  b  0 hay 7b  24a . 2  2 2 a  b 0.25
+ Với b  0 , chọn a 1 nên d : x  2  0. 2  0.25x2
+ Với 7b  24a , chọn a  7  b  24 nên d :7 x  24 y  134  0. 2  HẾT