Đề giữa kỳ 2 Toán 10 năm 2022 – 2023 trường THPT Thị xã Quảng Trị

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 10 đề kiểm tra giữa học kỳ 2 môn Toán 10 năm học 2022 – 2023 trường THPT Thị xã Quảng Trị, tỉnh Quảng Trị; thời gian làm bài 90 phút, mời bạn đọc đón xem

27 14 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 10

Môn: Toán 10

Thông tin:

19 trang 6 tháng trước

Tác giả:

Profile Thanh Tâm
Trang 1/3 - Mã đề 101
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II – NĂM HỌC 2022 - 2023
MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút; (Đề có 25 câu)
Họ và tên : ............................................................... Số báo danh : ...................
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1: Cho hàm số bậc hai
( )
y fx
=
có đồ thị như hình vẽ.
Tìm giá trị lớn nhất của hàm số
( )
.y fx=
A.
4.
B.
2.
C.
3.
D.
Câu 2: Tìm trục đối xứng của parabol có đồ thị được cho như hình vẽ bên
A.
3
y
=
. B.
3x =
. C.
2y
=
. D.
2x =
.
Câu 3: Xác định hệ số a của tam thức bậc hai
(
)
2
2 5 6.fx x x= ++
A.
6.a =
B.
2
2.ax=
C.
2.
a =
D.
5.a =
Câu 4:
Trong mặt phẳng
Oxy
, đường thẳng
:2 3 0d xy++=
vuông góc với đường thẳng nào dưới
đây?
A.
1
: 2 1 0.xy
∆ − +=
B.
4
: 2 3 0.xy∆ ++=
C.
3
: 2 1 0.xy∆ + +=
. D.
2
: 2 1 0.xy∆ − +=
.
Câu 5:
Điểm nào dưới đây nằm trên đường thẳng
:2 1 0?xy∆ + +=
A.
(1; 2).C
B.
(1; 3) .
A −
C.
(1; 2) .D −
D.
( 1; 3).B
−−
Câu 6: Với
x
thuộc tập hợp nào sau đây thì tam thức
2
() 3 2fx x x=++
luôn dương?
A.
( 2; 1).−−
B.
.
C.
( ; 2).−∞ −
D.
( 2; ).− +∞
Câu 7: Tìm tọa độ đỉnh
I
của parabol
2
y ax bx c= ++
có đồ thị như hình vẽ bên
Mã đề 101
ĐỀ CHÍNH THỨC
(Đề có 3 trang)
Trang 2/3 - Mã đề 101
A.
( )
2; 2I
. B.
(
)
0;3I
. C.
(
)
3; 2I
. D.
( )
3; 0 .I
Câu 8:
Đường thẳng đi qua điểm
( )
2; 1A −
và nhận VTCP
( )
3;1u =
có phương trình tham số là
A.
2
3
xt
yt
= −
= +
. B.
23
1
xt
yt
= +
=−+
. C.
32
1
xt
yt
= +
= −
. D.
3
12
xt
yt
= −
= +
.
Câu 9: Cho đường thẳng
: 2 3 1 0.
dx y− +=
Một vectơ pháp tuyến của
là
A.
(1; 3) .x
= −
B.
( 3;1).
e
= −
C.
(2;1).n =
D.
(2; 3).v
= −
Câu 10: Cho bảng giá trị của hai đại lượng tương ứng
,xy
như hình bên dưới. Đại lượng
(
)
y fx=
là hàm số của đại lượng
x
.
x
0
1
2
3
( )
y fx
=
5−
2
5
2
−
Tính giá trị
( )
.
1f
A.
( )
.1 5f = −
B.
( )
.1 2f = −
C.
( )
21 .f =
D.
( )
5
1 .
f
=
Câu 11:
Khoảng cách từ điểm
( )
00
;Mx y
đến dường thẳng
22
: 0, ( 0)ax by c a b∆ + += + ≠
được tính
bởi công thức nào dưới đây?
A.
( )
00
22
00
,.
ax by c
dM
xy
++
∆=
+
. B.
( )
00
,.
ax by c
dM
ab
++
∆=
+
C.
( )
00
,.
d M ax by c∆= + +
. D.
(
)
00
22
,.
ax by c
dM
ab
++
∆=
+
Câu 12: Tìm tập xác định của hàm số
5.yx= −
A.
[
)
5; +∞
B.
(
]
;5 .−∞
C.
( )
5; .+∞
D.
{ }
\5.
Câu 13: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
2; 0 .−
B.
(
)
1; 3 .−
C.
( )
2;1 .
−
D.
( )
1;1 .−
Câu 14: Tìm tập xác định của hàm số
2
2 3.yx x=−−
A.
{ }
\ 1.−
B.
{ }
\ 3; 1 .−
C.
{ }
\ 3.
D.
.
Câu 15: Tập nghiệm của bất phương trình
2
4 30xx− +≤
là
A.
( )
( ;1) 3; .−∞ +∞
B.
.
C.
[ ]
1; 3 .
D.
.∅
Câu 16: Tập nghiệm của phương trình
2
2 49 3xx x− +=−
là
A.
.∅
B.
{0}.
C.
{ }
2; 0 .−
D.
{ }
2.−
Câu 17:
Trong mặt phẳng
Oxy
, đường thẳng đi qua hai điểm
(2; 0)A
và
(0;3)B
có phương trình là
A.
1.
32
xy
+=
B.
0.
32
xy
+=
C.
1.
23
xy
−=
D.
1.
23
xy
+=
Câu 18: Gọi
α
là góc giữa hai đường thẳng
1
:4 2 1 0dxy− +=
và
2
: 2 2 0.dx y− −=
Tính
cos .
α
Trang 3/3 - Mã đề 101
A.
2
cos .
5
α
=
B.
3
cos .
5
α
=
C.
4
cos .
5
α
=
D.
cos 1.
α
=
Câu 19: Tập giá trị của hàm số
21yx= −
là
A.
[0; ).+∞
B.
1
( ; ).
2
+∞
C.
[
)
2; .+∞
D.
1
( ; ].
2
−∞
Câu 20: Cho hàm số
2
21yx x=+−
. Hãy thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá
trị sau tại một số điểm.
x
1−
0
2
3
y
?
?
?
?
A. . B. .
C.
. D. .
PHẦN CÂU HỎI TỰ LUẬN
Câu 21: Viết phương trình đường thẳng
d
qua điểm
(1; 3)M
và cách điểm
( 1; 5)I −
một khoảng lớn
nhất.
Câu 22: Cho tam giác
ABC
có
( ) ( ) ( )
1; 3 , 1; 5 , 4; 1
AB C−−
. Viết phương trình đường cao
AH
của
tam giác
.ABC
Câu 23: Vẽ parabol
2
2 3.
yx x
=+−
Câu 24: Tính tổng tất cả các nghiệm dương của phương trình
2
4 25 19
xx−=−
.
Câu 25: Một quả bóng chuyền được phát lên từ độ cao
1
m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao
7
m sau
1
giây và đạt độ cao
9
m sau
2
giây. Trong khoảng
thời gian bao lâu thì độ cao quả bóng lớn hơn 7 m.
------ HẾT ------
Trang 1/3 - Mã đề 102
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II – NĂM HỌC 2022 - 2023
MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút; (Đề có 25 câu)
Họ và tên : ............................................................... Số báo danh : ...................
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1: Xác định hệ số a của tam thức bậc hai
( )
2
2 5 6.fx x x= ++
A.
2
2.ax=
B.
5.
a =
C.
2.a
=
D.
6.a =
Câu 2:
Đường thẳng đi qua điểm
( )
2; 1A −
và nhận VTCP
( )
3;1u =
có phương trình tham số là
A.
3
12
xt
yt
= −
= +
. B.
2
3
xt
yt
= −
= +
. C.
23
1
xt
yt
= +
=−+
. D.
32
1
xt
yt
= +
= −
.
Câu 3:
Khoảng cách từ điểm
( )
00
;Mx y
đến dường thẳng
22
: 0, ( 0)ax by c a b∆ + += + ≠
được tính
bởi công thức nào dưới đây?
A.
( )
00
22
00
,.
ax by c
dM
xy
++
∆=
+
. B.
(
)
00
22
,.
ax by c
dM
ab
++
∆=
+
C.
(
)
00
,.d M ax by c∆= + +
. D.
(
)
00
,.
ax by c
dM
ab
++
∆=
+
Câu 4: Cho hàm số bậc hai
( )
y fx=
có đồ thị như hình vẽ.
Tìm giá trị lớn nhất của hàm số
( )
.y fx=
A.
B.
2.
C.
4.
D.
3.
Câu 5:
Trong mặt phẳng
Oxy
, đường thẳng
:2 3 0d xy++=
vuông góc với đường thẳng nào dưới
đây?
A.
3
: 2 1 0.xy∆ + +=
. B.
4
: 2 3 0.xy∆ ++=
C.
1
: 2 1 0.xy∆ − +=
D.
2
: 2 1 0.xy∆ − +=
.
Câu 6: Tìm tọa độ đỉnh
I
của parabol
2
y ax bx c= ++
có đồ thị như hình vẽ bên
A.
( )
3; 0 .I
B.
( )
2; 2I
. C.
( )
3; 2I
. D.
( )
0;3I
.
Câu 7: Cho đường thẳng
: 2 3 1 0.dx y− +=
Một vectơ pháp tuyến của
là
Mã đề 102
ĐỀ CHÍNH THỨC
(Đề có 3 trang)
Trang 2/3 - Mã đề 102
A.
(2;1).
n =
B.
(1; 3) .x = −
C.
( 3;1).
e = −
D.
(2; 3).v = −
Câu 8: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
(
)
1; 3 .
−
B.
(
)
1;1 .−
C.
( )
2; 0 .−
D.
( )
2;1 .−
Câu 9:
Điểm nào dưới đây nằm trên đường thẳng
:2 1 0?xy∆ + +=
A.
( 1; 3).B
−−
B.
(1; 2).D −
C.
(1; 2).C
D.
(1; 3).A
−
Câu 10: Cho bảng giá trị của hai đại lượng tương ứng
,xy
như hình bên dưới. Đại lượng
( )
y fx=
là hàm số của đại lượng
x
.
x
0
1
2
3
( )
y fx=
5
−
2
5
2−
Tính giá trị
(
)
.1f
A.
( )
51 .f =
B.
( )
.1 2f = −
C.
(
)
.
1 5
f = −
D.
( )
21 .f =
Câu 11: Với
x
thuộc tập hợp nào sau đây thì tam thức
2
() 3 2
fx x x=++
luôn dương?
A.
( ; 2).
−∞ −
B.
( 2; 1).−−
C.
( 2; ).− +∞
D.
.
Câu 12: Tìm tập xác định của hàm số
5.yx= −
A.
[
)
5; +∞
B.
{ }
\5.
C.
(
)
5; .+∞
D.
(
]
;5 .−∞
Câu 13: Tìm tập xác định của hàm số
2
2 3.yx x=−−
A.
{ }
\ 3.
B.
.
C.
{ }
\ 1.−
D.
{ }
\ 3; 1 .−
Câu 14: Tìm trục đối xứng của parabol có đồ thị được cho như hình vẽ bên
A.
2x =
. B.
2y
=
. C.
3x =
. D.
3y =
.
Câu 15: Tập nghiệm của phương trình
2
2 49 3xx x− +=−
là
A.
{ }
2.
−
B.
{0}.
C.
.∅
D.
{ }
2; 0 .−
Câu 16: Tập nghiệm của bất phương trình
2
4 30xx
− +≤
là
A.
.∅
B.
.
C.
( )
( ;1) 3; .−∞ +∞
D.
[ ]
1; 3 .
Câu 17:
Trong mặt phẳng
Oxy
, đường thẳng đi qua hai điểm
(2; 0)A
và
(0;3)B
có phương trình là
A.
1.
23
xy
+=
B.
0.
32
xy
+=
C.
1.
32
xy
+=
D.
1.
23
xy
−=
Trang 3/3 - Mã đề 102
Câu 18: Cho hàm số
2
21yx x=+−
. Hãy thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá
trị sau tại một số điểm.
x
1−
0
2
3
y
?
?
?
?
A. . B. .
C.
. D. .
Câu 19: Tập giá trị của hàm số
21yx= −
là
A.
1
( ; ].
2
−∞
B.
1
( ; ).
2
+∞
C.
[0; ).+∞
D.
[
)
2; .+∞
Câu 20: Gọi
α
là góc giữa hai đường thẳng
1
:4 2 1 0dxy
− +=
và
2
: 2 2 0.dx y
− −=
Tính
cos .
α
A.
2
cos .
5
α
=
B.
4
cos .
5
α
=
C.
3
cos .
5
α
=
D.
cos 1.
α
=
PHẦN CÂU HỎI TỰ LUẬN
Câu 21: Vẽ parabol
2
2 3.yx x=+−
Câu 22: Cho tam giác
ABC
có
( ) ( ) ( )
1; 3 , 1; 5 , 4; 1AB C−−
. Viết phương trình đường cao
AH
của
tam giác
.ABC
Câu 23: Viết phương trình đường thẳng
d
qua điểm
(1; 3)M
và cách điểm
( 1; 5)I
−
một khoảng lớn
nhất.
Câu 24: Tính tổng tất cả các nghiệm dương của phương trình
2
4 25 19xx−=−
.
Câu 25: Một quả bóng chuyền được phát lên từ độ cao
1
m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao
7
m sau
1
giây và đạt độ cao
9
m sau
2
giây. Trong khoảng
thời gian bao lâu thì độ cao quả bóng lớn hơn 7 m?
------ HẾT ------
Trang 1/3 - Mã đề 103
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II – NĂM HỌC 2022 - 2023
MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút; (Đề có 25 câu)
Họ và tên : ............................................................... Số báo danh : ...................
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1: Tìm tập xác định của hàm số
2
2 3.yx x=−−
A.
{ }
\ 3.
B.
{ }
\ 1.
−
C.
.
D.
{ }
\ 3; 1 .−
Câu 2:
Trong mặt phẳng
Oxy
, đường thẳng
:2 3 0d xy++=
vuông góc với đường thẳng nào dưới
đây?
A.
2
: 2 1 0.
xy
∆ − +=
. B.
1
: 2 1 0.xy
∆ − +=
C.
3
: 2 1 0.xy∆ + +=
. D.
4
: 2 3 0.
xy
∆ ++=
Câu 3: Cho bảng giá trị của hai đại lượng tương ứng
,xy
như hình bên dưới. Đại lượng
( )
y fx=
là
hàm số của đại lượng
x
.
x
0
1
2
3
( )
y fx=
5−
2
5
2−
Tính giá trị
( )
.
1f
A.
( )
51 .f =
B.
( )
.1 2f = −
C.
( )
.1
5
f = −
D.
( )
21 .f =
Câu 4:
Đường thẳng đi qua điểm
( )
2; 1A −
và nhận VTCP
( )
3;1u =
có phương trình tham số là
A.
32
1
xt
yt
= +
= −
. B.
2
3
xt
yt
= −
= +
. C.
23
1
xt
yt
= +
=−+
. D.
3
12
xt
yt
= −
= +
.
Câu 5: Tìm tập xác định của hàm số
5.yx
= −
A.
[
)
5;
+∞
B.
( )
5; .+∞
C.
(
]
;5 .−∞
D.
{ }
\5.
Câu 6: Tìm tọa độ đỉnh
I
của parabol
2
y ax bx c= ++
có đồ thị như hình vẽ bên
A.
( )
3; 0 .I
B.
( )
2; 2I
. C.
( )
3; 2I
. D.
( )
0;3I
.
Câu 7:
Điểm nào dưới đây nằm trên đường thẳng
:2 1 0?xy∆ + +=
A.
( 1; 3).B −−
B.
(1; 2).C
C.
(1; 3).A −
D.
(1; 2 ).D
−
Câu 8: Cho hàm số bậc hai
( )
y fx=
có đồ thị như hình vẽ.
Mã đề 103
ĐỀ CHÍNH THỨC
(Đề có 3 trang)
Trang 2/3 - Mã đề 103
Tìm giá trị lớn nhất của hàm số
(
)
.y fx=
A.
B.
2.
C.
4.
D.
3.
Câu 9:
Khoảng cách từ điểm
(
)
00
;Mx y
đến dường thẳng
22
: 0, ( 0)ax by c a b∆ + += + ≠
được tính
bởi công thức nào dưới đây?
A.
( )
00
,.d M ax by c∆= + +
. B.
( )
00
22
00
,.
ax by c
dM
xy
++
∆=
+
.
C.
( )
00
22
,.
ax by c
dM
ab
++
∆=
+
D.
( )
00
,.
ax by c
dM
ab
++
∆=
+
Câu 10: Với
x
thuộc tập hợp nào sau đây thì tam thức
2
() 3 2fx x x=++
luôn dương?
A.
( 2; ).
− +∞
B.
( 2; 1).−−
C.
( ; 2).−∞ −
D.
.
Câu 11: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
1; 3 .−
B.
( )
2; 0 .−
C.
( )
2;1 .−
D.
( )
1;1 .−
Câu 12: Xác định hệ số a của tam thức bậc hai
( )
2
2 5 6.fx x x
= ++
A.
2
2.ax=
B.
6.
a =
C.
2.a =
D.
5.a =
Câu 13: Tìm trục đối xứng của parabol có đồ thị được cho như hình vẽ bên
A.
2x =
. B.
2y =
. C.
3y =
. D.
3x =
.
Câu 14: Cho đường thẳng
: 2 3 1 0.dx y− +=
Một vectơ pháp tuyến của
là
A.
(2;1).n
=
B.
(1; 3) .x = −
C.
(2; 3).v = −
D.
( 3;1).e = −
Câu 15: Gọi
α
là góc giữa hai đường thẳng
1
:4 2 1 0dxy− +=
và
2
: 2 2 0.dx y− −=
Tính
cos .
α
A.
2
cos .
5
α
=
B.
cos 1.
α
=
C.
4
cos .
5
α
=
D.
3
cos .
5
α
=
Câu 16:
Trong mặt phẳng
Oxy
, đường thẳng đi qua hai điểm
(2; 0)A
và
(0;3)B
có phương trình là
A.
1.
32
xy
+=
B.
1.
23
xy
−=
C.
0.
32
xy
+=
D.
1.
23
xy
+=
Câu 17: Tập nghiệm của bất phương trình
2
4 30xx− +≤
là
A.
.
B.
[ ]
1; 3 .
C.
( )
( ;1) 3; .−∞ +∞
D.
.∅
Câu 18: Tập nghiệm của phương trình
2
2 49 3xx x− +=−
là
Trang 3/3 - Mã đề 103
A.
{0}.
B.
{ }
2; 0 .−
C.
{ }
2.−
D.
.∅
Câu 19: Tập giá trị của hàm số
21
yx= −
là
A.
[
)
2; .+∞
B.
1
( ; ).
2
+∞
C.
[0; ).+∞
D.
1
( ; ].
2
−∞
Câu 20: Cho hàm số
2
21yx x
=+−
. Hãy thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá
trị sau tại một số điểm.
x
1−
0
2
3
y
?
?
?
?
A. . B. .
C.
. D. .
PHẦN CÂU HỎI TỰ LUẬN
Câu 21: Cho tam giác
ABC
có
( ) ( ) ( )
1; 3 , 1; 5 , 4; 1AB C−−
. Viết phương trình đường cao
AH
của
tam giác
.ABC
Câu 22: Viết phương trình đường thẳng
d
qua điểm
(1; 3)M
và cách điểm
( 1; 5)I
−
một khoảng lớn
nhất.
Câu 23: Vẽ parabol
2
2 3.yx x
=+−
Câu 24: Tính tổng tất cả các nghiệm dương của phương trình
2
4 25 19xx−=−
.
Câu 25: Một quả bóng chuyền được phát lên từ độ cao
1
m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao
7
m sau
1
giây và đạt độ cao
9
m sau
2
giây. Trong khoảng
thời gian bao lâu thì độ cao quả bóng không nhỏ hơn 7 m.
------ HẾT ------
Trang 1/3 - Mã đề 104
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II– NĂM HỌC 2022 - 2023
MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút; (Đề có 25 câu)
Họ và tên : ............................................................... Số báo danh : ...................
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1:
Điểm nào dưới đây nằm trên đường thẳng
:2 1 0?xy∆ + +=
A.
(1; 3).A −
B.
( 1; 3).
B −−
C.
(1; 2).C
D.
(1; 2).D −
Câu 2: Cho hàm số
( )
y fx=
có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
A.
( )
2;1 .−
B.
(
)
1; 3 .
−
C.
(
)
2; 0 .−
D.
( )
1;1 .−
Câu 3: Tìm tập xác định của hàm số
5.yx= −
A.
[
)
5; +∞
B.
{ }
\5.
C.
(
]
;5 .−∞
D.
( )
5; .+∞
Câu 4: Với
x
thuộc tập hợp nào sau đây thì tam thức
2
() 3 2
fx x x=++
luôn dương?
A.
( ; 2).
−∞ −
B.
( 2; ).− +∞
C.
( 2; 1).−−
D.
.
Câu 5:
Khoảng cách từ điểm
( )
00
;Mx y
đến dường thẳng
22
: 0, ( 0)ax by c a b
∆ + += + ≠
được tính
bởi công thức nào dưới đây?
A.
( )
00
,.
ax by c
dM
ab
++
∆=
+
B.
( )
00
22
,.
ax by c
dM
ab
++
∆=
+
C.
( )
00
22
00
,.
ax by c
dM
xy
++
∆=
+
. D.
( )
00
,.d M ax by c
∆= + +
.
Câu 6: Cho đường thẳng
: 2 3 1 0.dx y− +=
Một vectơ pháp tuyến của
là
A.
(2;1).n =
B.
(1; 3) .x = −
C.
( 3;1).e = −
D.
(2; 3).v = −
Câu 7:
Trong mặt phẳng
Oxy
, đường thẳng
:2 3 0d xy++=
vuông góc với đường thẳng nào dưới
đây?
A.
2
: 2 1 0.xy∆ − +=
. B.
1
: 2 1 0.xy∆ − +=
C.
4
: 2 3 0.xy∆ ++=
D.
3
: 2 1 0.xy∆ + +=
.
Câu 8:
Đường thẳng đi qua điểm
( )
2; 1A −
và nhận VTCP
( )
3;1u =
có phương trình tham số là
A.
2
3
xt
yt
= −
= +
. B.
32
1
xt
yt
= +
= −
. C.
3
12
xt
yt
= −
= +
. D.
23
1
xt
yt
= +
=−+
.
Câu 9: Xác định hệ số a của tam thức bậc hai
( )
2
2 5 6.fx x x= ++
A.
2
2.ax=
B.
2.a =
C.
5.a =
D.
6.a =
Câu 10: Cho bảng giá trị của hai đại lượng tương ứng
,xy
như hình bên dưới. Đại lượng
Mã đề 104
ĐỀ CHÍNH THỨC
(Đề có 3 trang)
Trang 2/3 - Mã đề 104
( )
y fx=
là hàm số của đại lượng
x
.
x
0
1
2
3
( )
y fx=
5−
2
5
2
−
Tính giá trị
( )
.1f
A.
( )
.1 5f = −
B.
( )
51 .f =
C.
( )
.
1
2
f
= −
D.
( )
21 .f =
Câu 11: Tìm tọa độ đỉnh
I
của parabol
2
y ax bx c= ++
có đồ thị như hình vẽ bên
A.
(
)
0;3I
. B.
( )
3; 0 .I
C.
( )
2; 2I
. D.
( )
3; 2I
.
Câu 12: Tìm trục đối xứng của parabol có đồ thị được cho như hình vẽ bên
A.
3x =
. B.
2x =
. C.
2y =
. D.
3
y =
.
Câu 13: Cho hàm số bậc hai
( )
y fx=
có đồ thị như hình vẽ.
Tìm giá trị lớn nhất của hàm số
( )
.y fx=
A.
3.
B.
4.
C.
D.
2.
Câu 14: Tìm tập xác định của hàm số
2
2 3.yx x=−−
A.
{ }
\ 3; 1 .−
B.
{ }
\ 3.
C.
.
D.
{ }
\ 1.−
Câu 15: Tập nghiệm của phương trình
2
2 49 3xx x− +=−
là
A.
{ }
2; 0 .−
B.
{0}.
C.
{ }
2.−
D.
.∅
Câu 16: Tập nghiệm của bất phương trình
2
4 30xx− +≤
là
A.
.∅
B.
.
C.
( )
( ;1) 3; .−∞ +∞
D.
[ ]
1; 3 .
Câu 17: : Gọi
α
là góc giữa hai đường thẳng
1
:4 2 1 0dxy− +=
và
2
: 2 2 0.dx y− −=
Tính
cos .
α
A.
4
cos .
5
α
=
B.
3
cos .
5
α
=
C.
2
cos .
5
α
=
D.
cos 1.
α
=
Câu 18:
Trong mặt phẳng
Oxy
, đường thẳng đi qua hai điểm
(2; 0)A
và
(0;3)B
có phương trình là
Trang 3/3 - Mã đề 104
A.
1.
23
xy
−=
B.
0.
32
xy
+=
C.
1.
32
xy
+=
D.
1.
23
xy
+=
Câu 19: : Cho hàm số
2
21yx x=+−
. Hãy thay dấu “?” bằng các số thích hợp để hoàn thành bảng
giá trị sau tại một số điểm.
x
1−
0
2
3
y
?
?
?
?
A. . B. .
C.
. D. .
Câu 20: Tập giá trị của hàm số
21yx
= −
là
A.
1
( ; ].
2
−∞
B.
1
( ; ).
2
+∞
C.
[0; ).+∞
D.
[
)
2; .+∞
PHẦN CÂU HỎI TỰ LUẬN
Câu 21: Vẽ parabol
2
2 3.yx x=+−
Câu 22: Viết phương trình đường thẳng
d
qua điểm
(1; 3)
M
và cách điểm
( 1; 5)I −
một khoảng lớn
nhất.
Câu 23: Cho tam giác
ABC
có
( )
( )
(
)
1; 3 , 1; 5 , 4; 1
AB C−−
. Viết phương trình đường cao
AH
của
tam giác
.ABC
Câu 24: Tính tổng tất cả các nghiệm dương của phương trình
2
4 25 19
xx−=−
.
Câu 25: Một quả bóng chuyền được phát lên từ độ cao
1
m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao
7
m sau
1
giây và đạt độ cao
9
m sau
2
giây. Trong khoảng
thời gian bao lâu thì độ cao quả bóng không nhỏ hơn 7 m.
------ HẾT ------
1
SỞ GD & ĐT QUẢNG TRỊ
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ
DE KIEM TRA GIUA KY II – NĂM HỌC 2022 - 2023
MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm:
101
102
103
104
1
C
C
C
A
2
D
C
B
D
3
C
B
D
A
4
A
D
C
A
5
B
C
A
B
6
C
A
A
D
7
D
D
C
B
8
B
B
D
D
9
D
D
C
B
10
C
D
C
D
11
D
A
D
B
12
A
A
C
B
13
D
B
A
A
14
D
A
C
C
15
C
C
C
D
16
A
D
D
D
17
D
A
B
A
18
C
B
D
D
19
A
C
C
D
20
B
B
A
C
Phần đáp án câu tự luận:
Mã đề 101:
Câu 21 : Viết phương trình đường thẳng
d
qua điểm
(1; 3)M
và cách điểm
( 1; 5)I −
một khoảng lớn
nhất.
Gợi ý làm bài:
Gọi
H
là hình chiếu của
I
trên
d
, ta có
( , ) 2 2.d I d IH IM
=≤=
Khoảng cách từ
( 1; 5)I
−
đến
d
lớn nhất khi
d
vuông góc với
IM
. Vậy
d
qua
(1; 3)
M
và có VTPT
( 2; 2) 2(1; 1)IM − =−−

nên có
phương trình
2 0.xy−+=
Câu 22 Cho tam giác
ABC
có
( ) (
) ( )
1; 3 , 1; 5 , 4; 1AB C−−
. Viết phương trình đường cao
AH
của
tam giác
.ABC
Gợi ý làm bài:
Đường thẳng
AH
đi qua
(1; 3)A
và nhận VTPT
(5; 6)BC −

nên có phương trình
5( 1) 6( 3) 0xy−− − =
hay
5 6 13 0.xy−+=
Câu 23 : Vẽ parabol
2
2 3.
yx x=+−
Gợi ý làm bài:
+ Tọa độ đỉnh của parabol là
( 1; 4).I −−
2
+ Trục đối xứng :
1.x = −
+ Parabol cắt trục tung tại điểm
(0; 3)A
−
và cắt trục hoành tại các điểm có hoành độ
1, 3.xx= = −
+ Đồ thị như hình vẽ:
Câu 24 Tính tổng tất cả các nghiệm dương của phương trình
2
4 25 19xx−=−
.
Gợi ý làm bài:
Bình phương hai vế phương trình và thu gọn ta được
2
17 38 39 0xx− −=
. Giải phương trình này ta
được hai nghiệm
12
3, 13 /17xx= = −
. Thử lại phương trình ban đầu, ta có tập nghiệm
13
3;
17
S
−

=


.
Tổng các nghiệm dương của phương trình là
3
.
Câu 25 Một quả bóng chuyền được phát lên từ độ cao
1
m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao
7
m sau
1
giây và đạt độ cao
9
m sau
2
giây. Tính khoảng thời
gian để độ cao quả bóng không nhỏ hơn 7 m.
Gợi ý làm bài:
Chọn hệ trục tọa độ
Oth
như hình vẽ
Gọi parabol
2
1, ( 0)h at bt a= ++ <
Từ giả thiết bài toán, ta có hệ
94 2 1
71
ab
ab
=++
=++
Giải hệ ta được
2
8
a
b
= −
=
.
Vậy,
2
2. 8. 1 7h tt=− + +≥
khi
1 3.t
≤≤
Mã đề 102:
Câu 21 : Vẽ parabol
2
2 3.yx x=+−
Gợi ý làm bài:
+ Tọa độ đỉnh của parabol là
( 1; 4).I −−
3
+ Trục đối xứng :
1.x = −
+ Parabol cắt trục tung tại điểm
(0; 3)A
−
và cắt trục hoành tại các điểm có hoành độ
1, 3.xx= = −
+ Đồ thị như hình vẽ:
Câu 22 Cho tam giác
ABC
có
( ) ( ) ( )
1; 3 , 1; 5 , 4; 1AB C−−
. Viết phương trình đường cao
AH
của
tam giác
.ABC
Gợi ý làm bài:
Đường thẳng
AH
đi qua
(1; 3)A
và nhận VTPT
(5; 6)BC −

nên có phương trình
5( 1) 6( 3) 0
xy−− − =
hay
5 6 13 0.xy−+=
Câu 23 : Viết phương trình đường thẳng
d
qua điểm
(1; 3)M
và cách điểm
( 1; 5)
I −
một khoảng lớn
nhất.
Gợi ý làm bài:
Gọi
H
là hình chiếu của
I
trên
d
, ta có
( , ) 2 2.d I d IH IM=≤=
Khoảng cách từ
( 1; 5)I
−
đến
d
lớn nhất khi
d
vuông góc với
IM
. Vậy
d
qua
(1; 3)M
và có VTPT
( 2; 2) 2(1; 1)
IM − =−−

nên có
phương trình
2 0.xy−+=
Câu 24 Tính tổng tất cả các nghiệm dương của phương trình
2
4 25 19xx−=−
.
Gợi ý làm bài:
Bình phương hai vế phương trình và thu gọn ta được
2
17 38 39 0xx− −=
. Giải phương trình này ta
được hai nghiệm
12
3, 13 /17xx= = −
. Thử lại phương trình ban đầu, ta có tập nghiệm
13
3;
17
S
−

=


.
Tổng các nghiệm dương của phương trình là
3
.
Câu 25 Một quả bóng chuyền được phát lên từ độ cao
1
m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao
7
m sau
1
giây và đạt độ cao
9
m sau
2
giây. Tính khoảng thời
gian để độ cao quả bóng không nhỏ hơn 7 m.
Gợi ý làm bài:
4
Chọn hệ trục tọa độ
Oth
như hình vẽ
Gọi parabol
2
1, ( 0)h at bt a= ++ <
Từ giả thiết bài toán, ta có hệ
94 2 1
71
ab
ab
=++
=++
Giải hệ ta được
2
8
a
b
= −
=
.
Vậy,
2
2. 8. 1 7
h tt=− + +≥
khi
1 3.
t≤≤
Mã đề 103:
Câu 21 Cho tam giác
ABC
có
( )
(
) (
)
1; 3 , 1; 5 , 4; 1
AB C−−
. Viết phương trình đường cao
AH
của
tam giác
.ABC
Gợi ý làm bài:
Đường thẳng
AH
đi qua
(1; 3)A
và nhận VTPT
(5; 6)BC −

nên có phương trình
5( 1) 6( 3) 0
xy−− − =
hay
5 6 13 0.xy− +=
Câu 22 : Viết phương trình đường thẳng
d
qua điểm
(1; 3)M
và cách điểm
( 1; 5)I −
một khoảng lớn
nhất.
Gợi ý làm bài:
Gọi
H
là hình chiếu của
I
trên
d
, ta có
( , ) 2 2.d I d IH IM=≤=
Khoảng cách từ
( 1; 5)
I −
đến
d
lớn nhất khi
d
vuông góc với
IM
. Vậy
d
qua
(1; 3)M
và có VTPT
( 2; 2) 2(1; 1)IM − =−−

nên có
phương trình
2 0.
xy−+=
Câu 23 : Vẽ parabol
2
2 3.yx x=+−
Gợi ý làm bài:
+ Tọa độ đỉnh của parabol là
( 1; 4).I −−
+ Trục đối xứng :
1.x
= −
+ Parabol cắt trục tung tại điểm
(0; 3)A −
và cắt trục hoành tại các điểm có hoành độ
1, 3.xx= = −
5
+ Đồ thị như hình vẽ:
Câu 24 Tính tổng tất cả các nghiệm dương của phương trình
2
4 25 19xx−=−
.
Gợi ý làm bài:
Bình phương hai vế phương trình và thu gọn ta được
2
17 38 39 0xx− −=
. Giải phương trình này ta
được hai nghiệm
12
3, 13 /17xx= = −
. Thử lại phương trình ban đầu, ta có tập nghiệm
13
3;
17
S
−

=


.
Tổng các nghiệm dương của phương trình là
3
.
Câu 25 Một quả bóng chuyền được phát lên từ độ cao
1
m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao
7
m sau
1
giây và đạt độ cao
9
m sau
2
giây. Tính khoảng thời
gian để độ cao quả bóng không nhỏ hơn 7 m.
Gợi ý làm bài:
Chọn hệ trục tọa độ
Oth
như hình vẽ
Gọi parabol
2
1, ( 0)h at bt a= ++ <
Từ giả thiết bài toán, ta có hệ
94 2 1
71
ab
ab
=++
=++
Giải hệ ta được
2
8
a
b
= −
=
.
Vậy,
2
2. 8. 1 7h tt=− + +≥
khi
1 3.t≤≤
Mã đề 104:
Câu 21 : Vẽ parabol
2
2 3.yx x=+−
Gợi ý làm bài:
+ Tọa độ đỉnh của parabol là
( 1; 4).
I −−
+ Trục đối xứng :
1.x = −
+ Parabol cắt trục tung tại điểm
(0; 3)A −
và cắt trục hoành tại các điểm có hoành độ
1, 3.
xx= = −
6
+ Đồ thị như hình vẽ:
Câu 22 : Viết phương trình đường thẳng
d
qua điểm
(1; 3)M
và cách điểm
( 1; 5)
I
−
một khoảng lớn
nhất.
Gợi ý làm bài:
Gọi
H
là hình chiếu của
I
trên
d
, ta có
( , ) 2 2.d I d IH IM=≤=
Khoảng cách từ
( 1; 5)
I
−
đến
d
lớn nhất khi
d
vuông góc với
IM
. Vậy
d
qua
(1; 3)M
và có VTPT
( 2; 2) 2(1; 1)IM − =−−

nên có
phương trình
2 0.xy−+=
Câu 23 Cho tam giác
ABC
có
( )
(
) (
)
1; 3 , 1; 5 , 4; 1AB C
−−
. Viết phương trình đường cao
AH
của
tam giác
.
ABC
Gợi ý làm bài:
Đường thẳng
AH
đi qua
(1; 3)A
và nhận VTPT
(5; 6)BC −

nên có phương trình
5( 1) 6( 3) 0xy−− − =
hay
5 6 13 0.xy− +=
Câu 24 Tính tổng tất cả các nghiệm dương của phương trình
2
4 25 19xx−=−
.
Gợi ý làm bài:
Bình phương hai vế phương trình và thu gọn ta được
2
17 38 39 0xx− −=
. Giải phương trình này ta
được hai nghiệm
12
3, 13 /17xx= = −
. Thử lại phương trình ban đầu, ta có tập nghiệm
13
3;
17
S
−

=


.
Tổng các nghiệm dương của phương trình là
3
.
Câu 25 Một quả bóng chuyền được phát lên từ độ cao
1
m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao
7
m sau
1
giây và đạt độ cao
9
m sau
2
giây. Tính khoảng thời
gian để độ cao quả bóng không nhỏ hơn 7 m.
Gợi ý làm bài:
7
Chọn hệ trục tọa độ
Oth
như hình vẽ
Gọi parabol
2
1, ( 0)h at bt a= ++ <
Từ giả thiết bài toán, ta có hệ
94 2 1
71
ab
ab
=++
=++
Giải hệ ta được
2
8
a
b
= −
=
.
Vậy,
2
2. 8. 1 7
h tt=− + +≥
khi
1 3.
t≤≤
| 1/19
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II – NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút; (Đề có 25 câu) ĐỀ CHÍNH THỨC (Đề có 3 trang)
Họ và tên : ............................................................... Số báo danh : ................... Mã đề 101
PHẦN CÂU HỎI TRẮC NGHIỆM
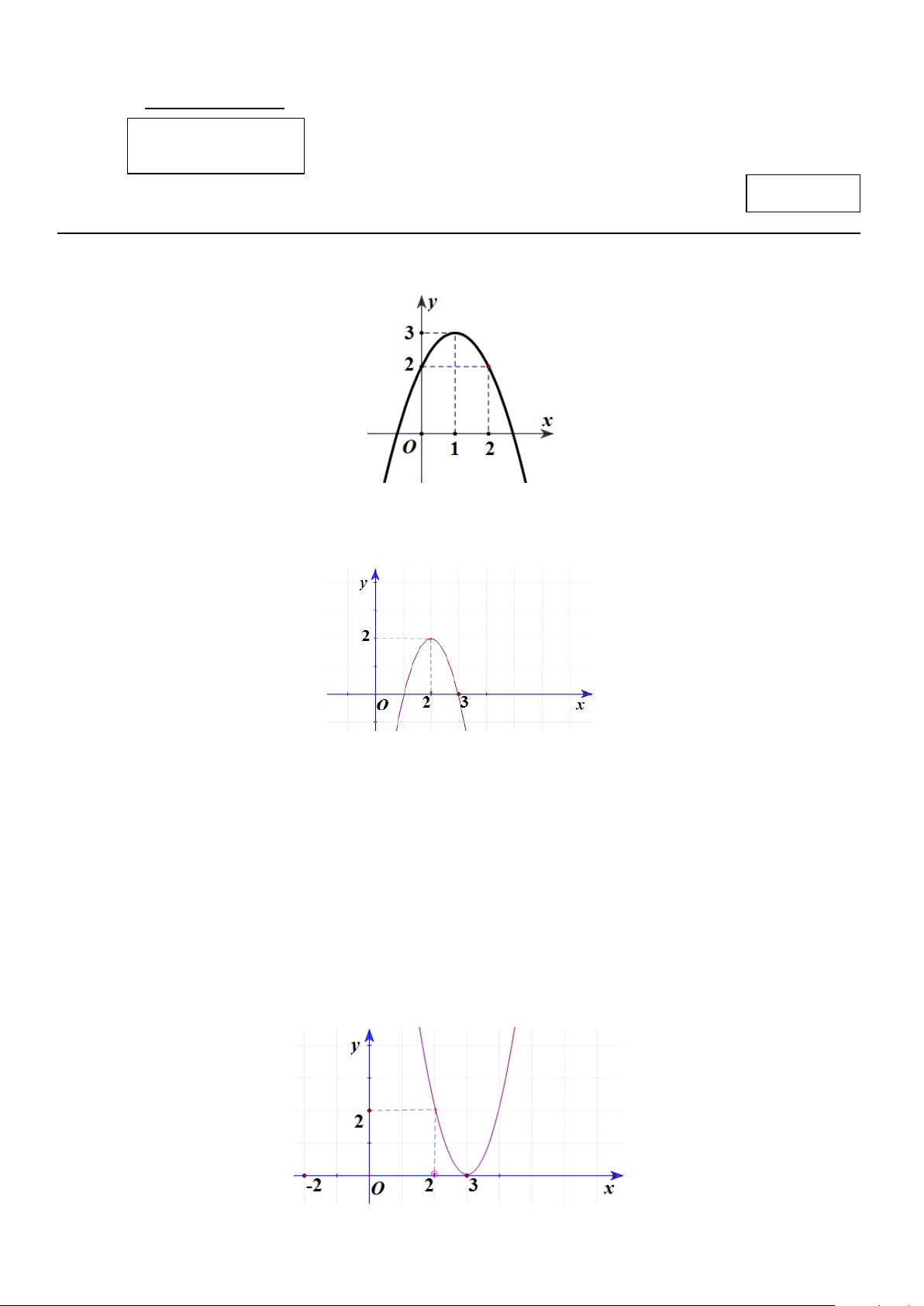
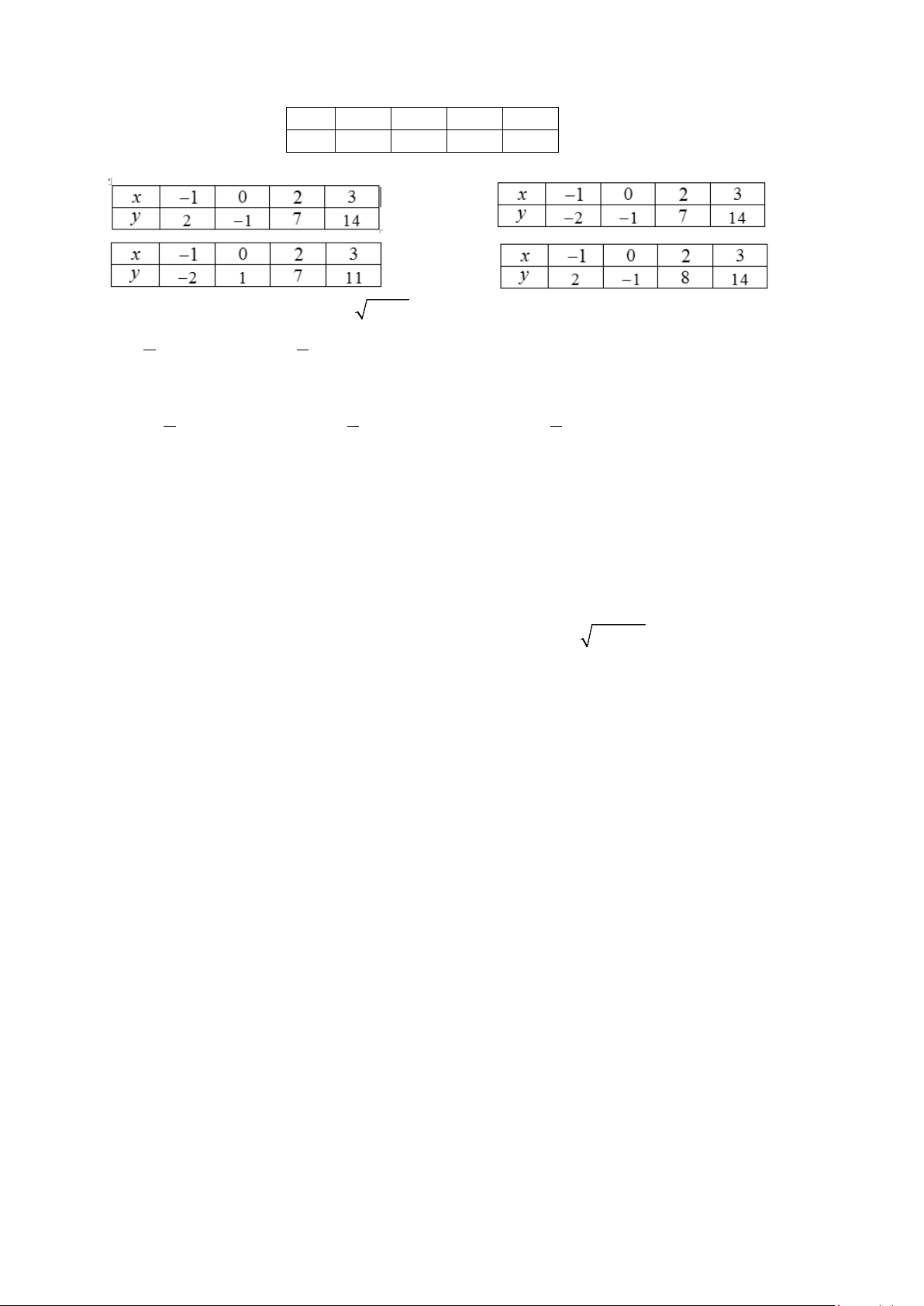
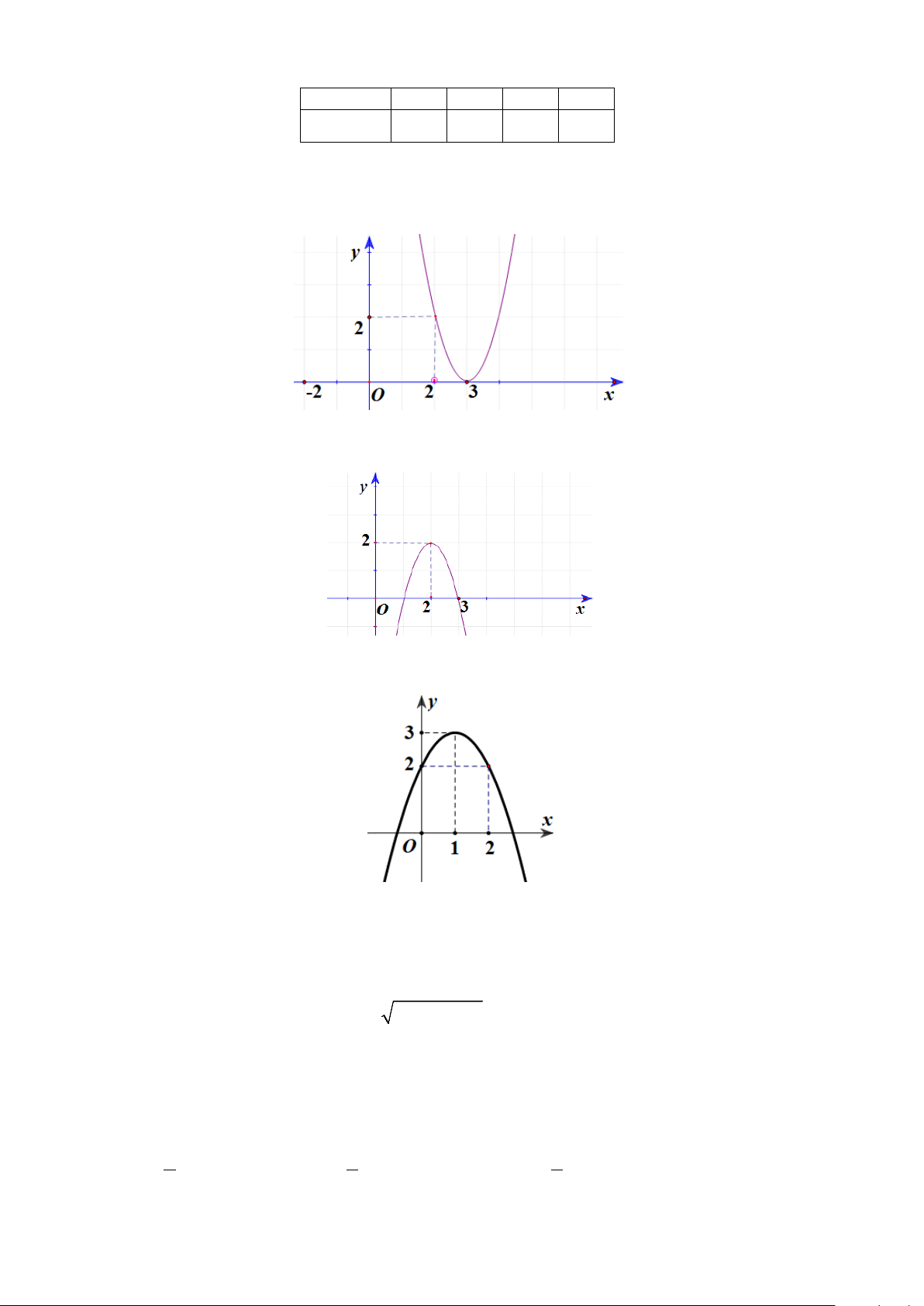
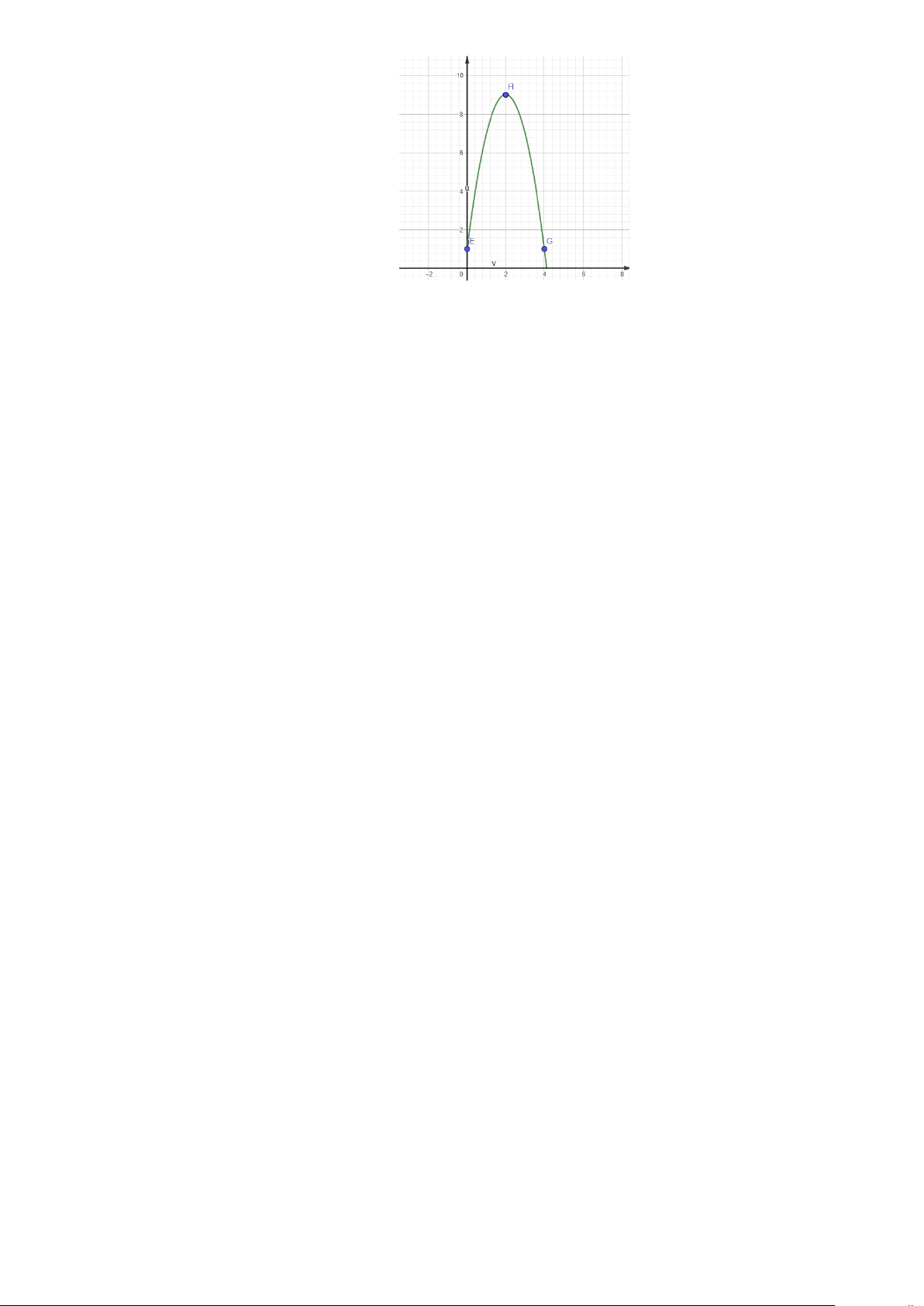
Câu 1: Cho hàm số bậc hai y = f (x) có đồ thị như hình vẽ.
Tìm giá trị lớn nhất của hàm số y = f (x). A. 4. B. 2. C. 3. D. 1.
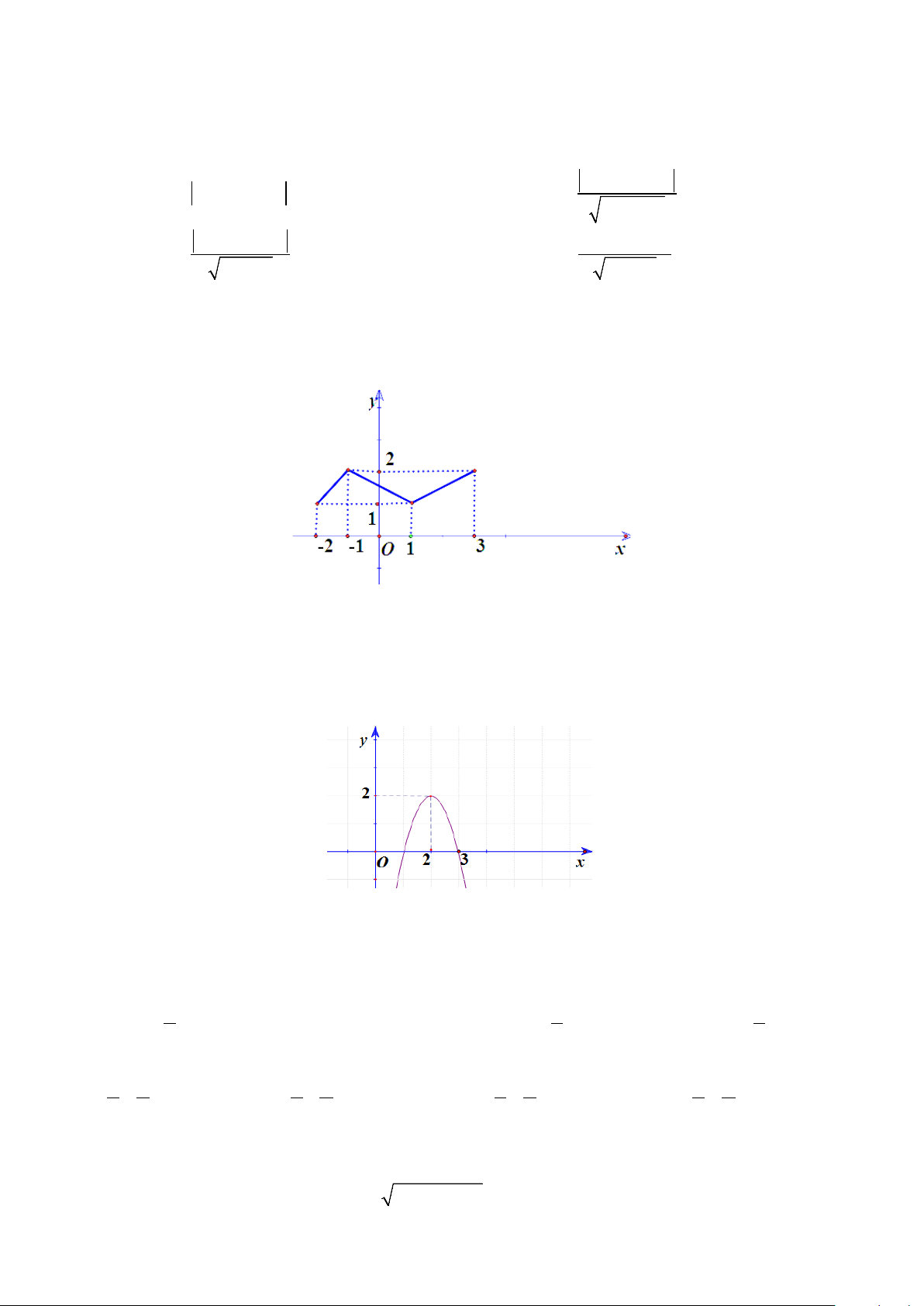
Câu 2: Tìm trục đối xứng của parabol có đồ thị được cho như hình vẽ bên A. y = 3. B. x = 3. C. y = 2 . D. x = 2 .
Câu 3: Xác định hệ số a của tam thức bậc hai f (x) 2
= 2x + 5x + 6. A. a = 6. B. 2 a = 2x . C. a = 2. D. a = 5.
Câu 4: Trong mặt phẳngOxy , đường thẳng d :2x+ y +3= 0 vuông góc với đường thẳng nào dưới đây?
A. ∆ : x − 2y +1= 0. B. ∆ : 2x + y + 3 = 0.
C. ∆ : x + 2y +1= 0.. D. ∆ : 2x − y +1= 0.. 1 4 3 2
Câu 5: Điểm nào dưới đây nằm trên đường thẳng ∆:2x+ y +1= 0? A. C(1;2). B. ( A 1; 3 − ). C. D(1; 2 − ). D. B( 1; − 3 − ).
Câu 6: Với x thuộc tập hợp nào sau đây thì tam thức 2
f (x) = x + 3x + 2 luôn dương? A. ( 2 − ; 1) − . B. .  C. ( ; −∞ 2 − ). D. ( 2; − +∞).
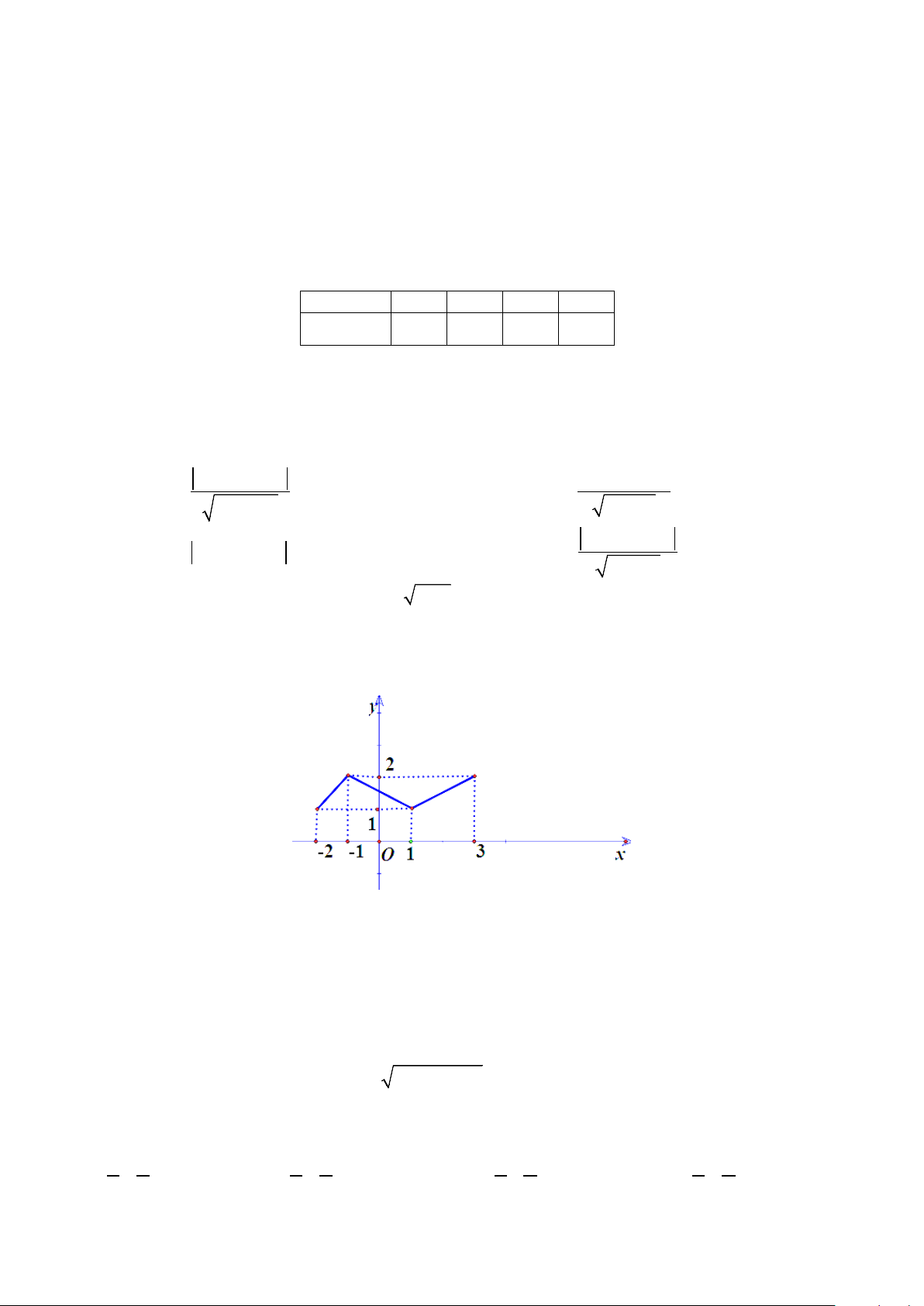
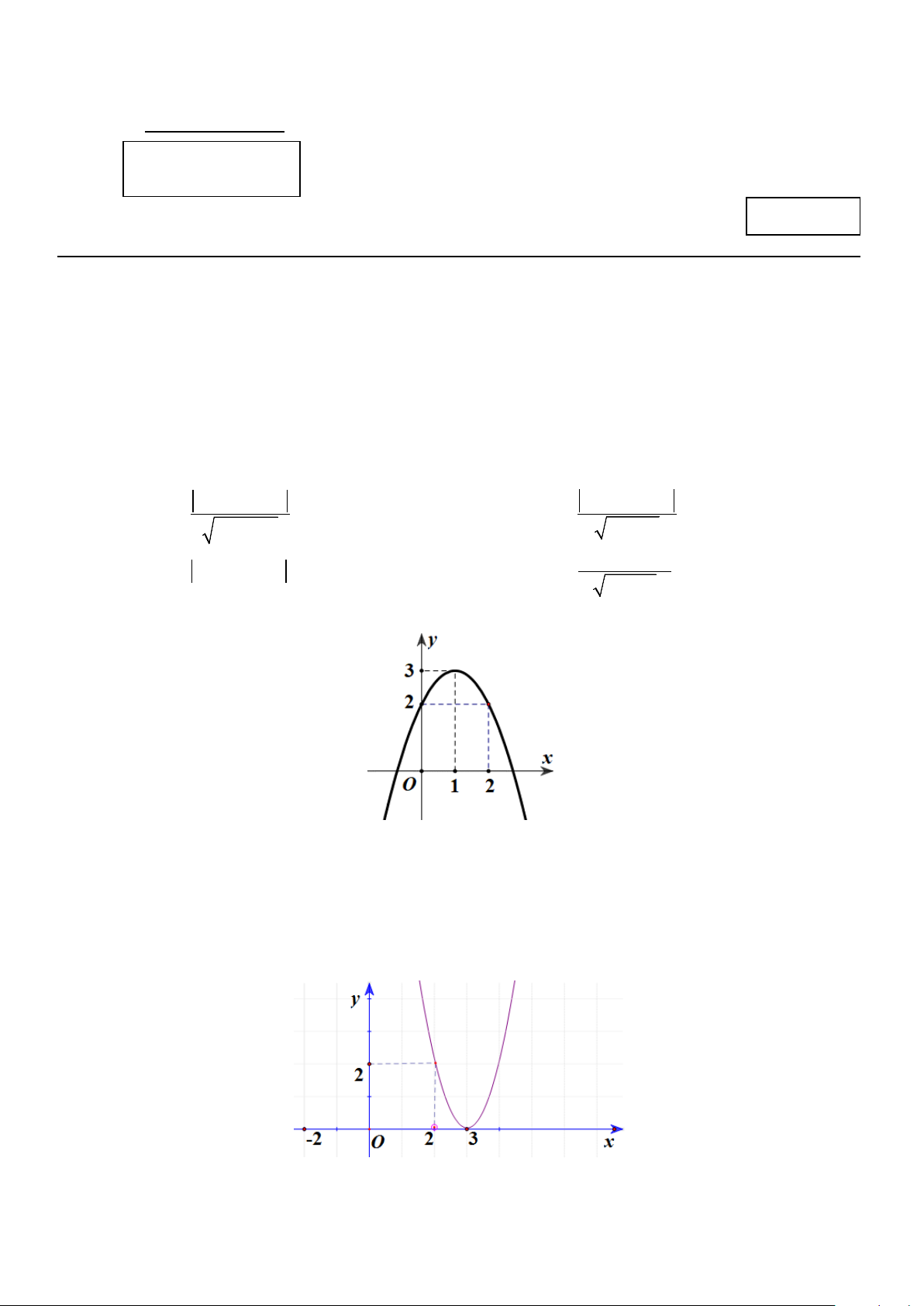
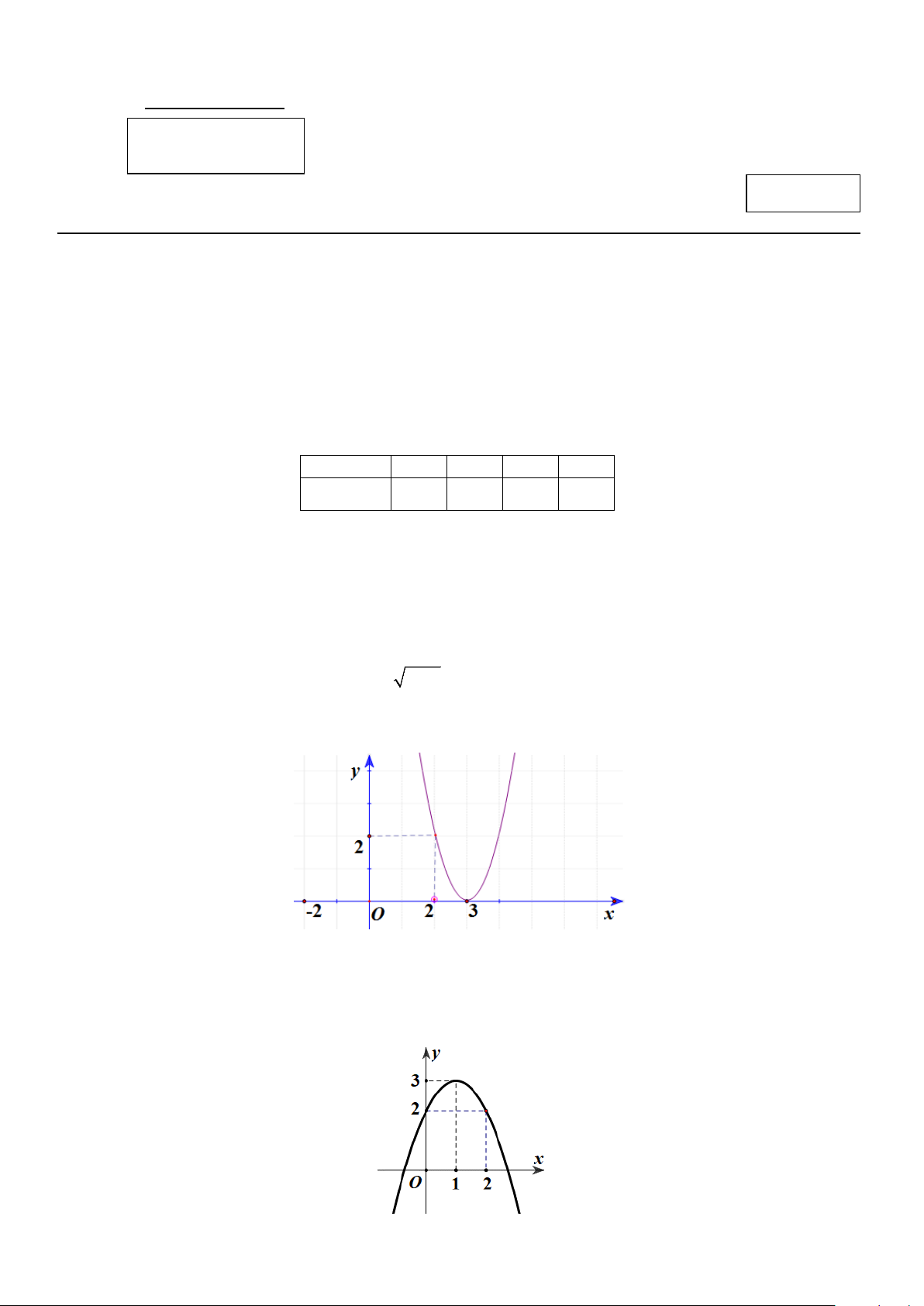
Câu 7: Tìm tọa độ đỉnh I của parabol 2
y = ax + bx + c có đồ thị như hình vẽ bên Trang 1/3 - Mã đề 101 A. I (2;2) . B. I (0;3) . C. I (3;2) . D. I (3;0). 
Câu 8: Đường thẳng đi qua điểm A(2;− )1 và nhận VTCP u = (3; )1 có phương trình tham số là x = 2 − tx = 2 + 3tx = 3+ 2tx = 3− t A.  . B.  . C.  . D.  . y = 3+ ty = 1 − + ty =1− ty =1+ 2t
Câu 9: Cho đường thẳng d : 2x −3y +1= 0. Một vectơ pháp tuyến của d là     A. x = (1; 3 − ). B. e = ( 3 − ;1). C. n = (2;1). D. v = (2; 3) − .
Câu 10: Cho bảng giá trị của hai đại lượng tương ứng x, y như hình bên dưới. Đại lượng
y = f (x) là hàm số của đại lượng x . x 0 1 2 3
y = f (x) 5 − 2 5 2 − Tính giá trị f ( ) 1 . A. f ( ) 1 = − . 5 B. f ( ) 1 = − . 2 C. f ( ) 1 = 2. D. f ( ) 1 = 5.
Câu 11: Khoảng cách từ điểm M (x ; y ∆ + + = + ≠ được tính 0 0 ) đến dường thẳng 2 2 : ax by c 0,(a b 0)
bởi công thức nào dưới đây? A. (
ax + by + c + + d M ,∆) 0 0 = ..
B. d (M ∆) ax by c 0 0 , = . 2 2 x + y a + b 0 0 + + C. ax by c
d (M ,∆) = ax + by + c ..
D. d (M ,∆) 0 0 = . 0 0 2 2 a + b
Câu 12: Tìm tập xác định của hàm số y = x −5. A. [5;+∞) B. ( ; −∞ 5]. C. (5;+∞). D.  \{ } 5 .
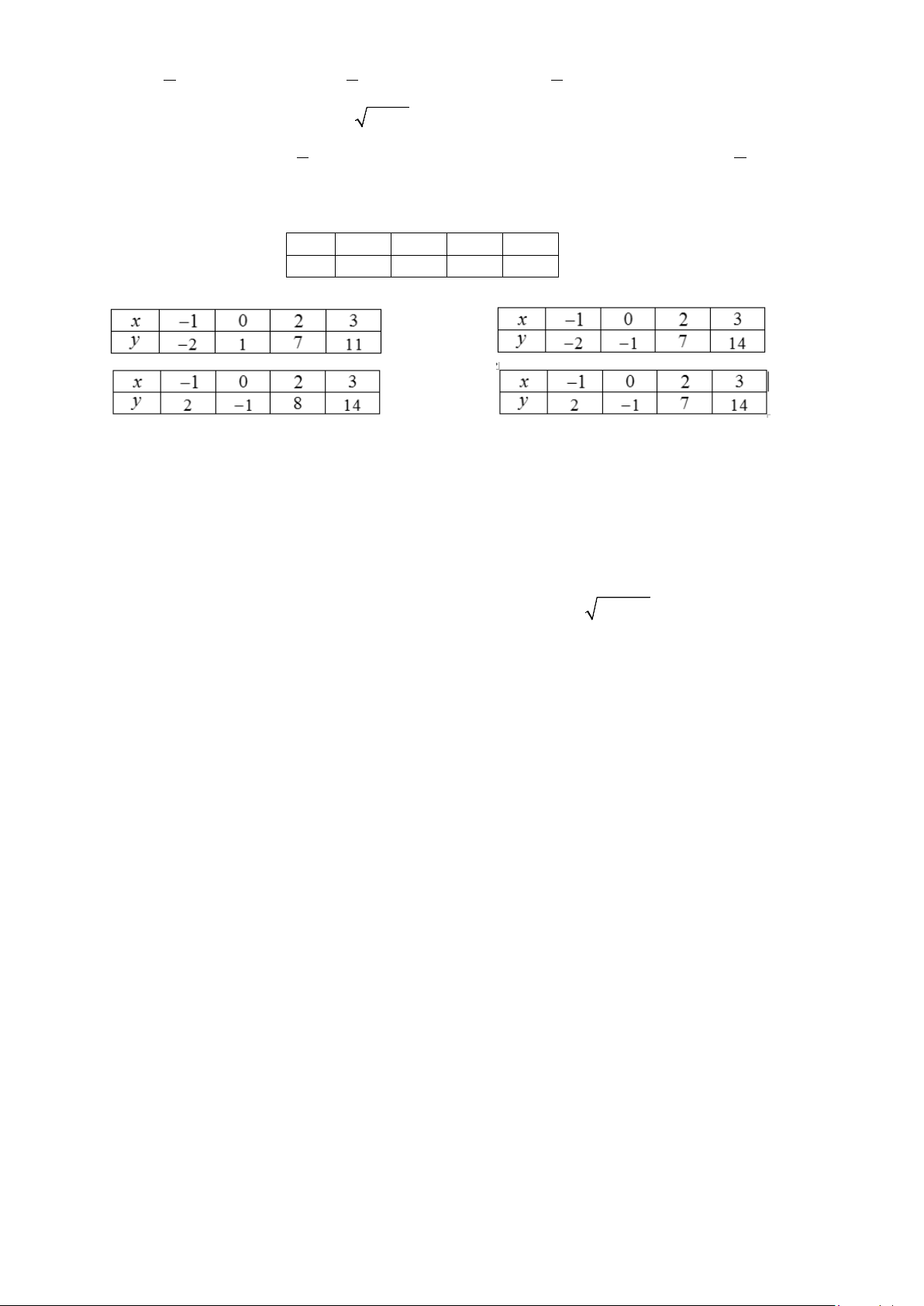
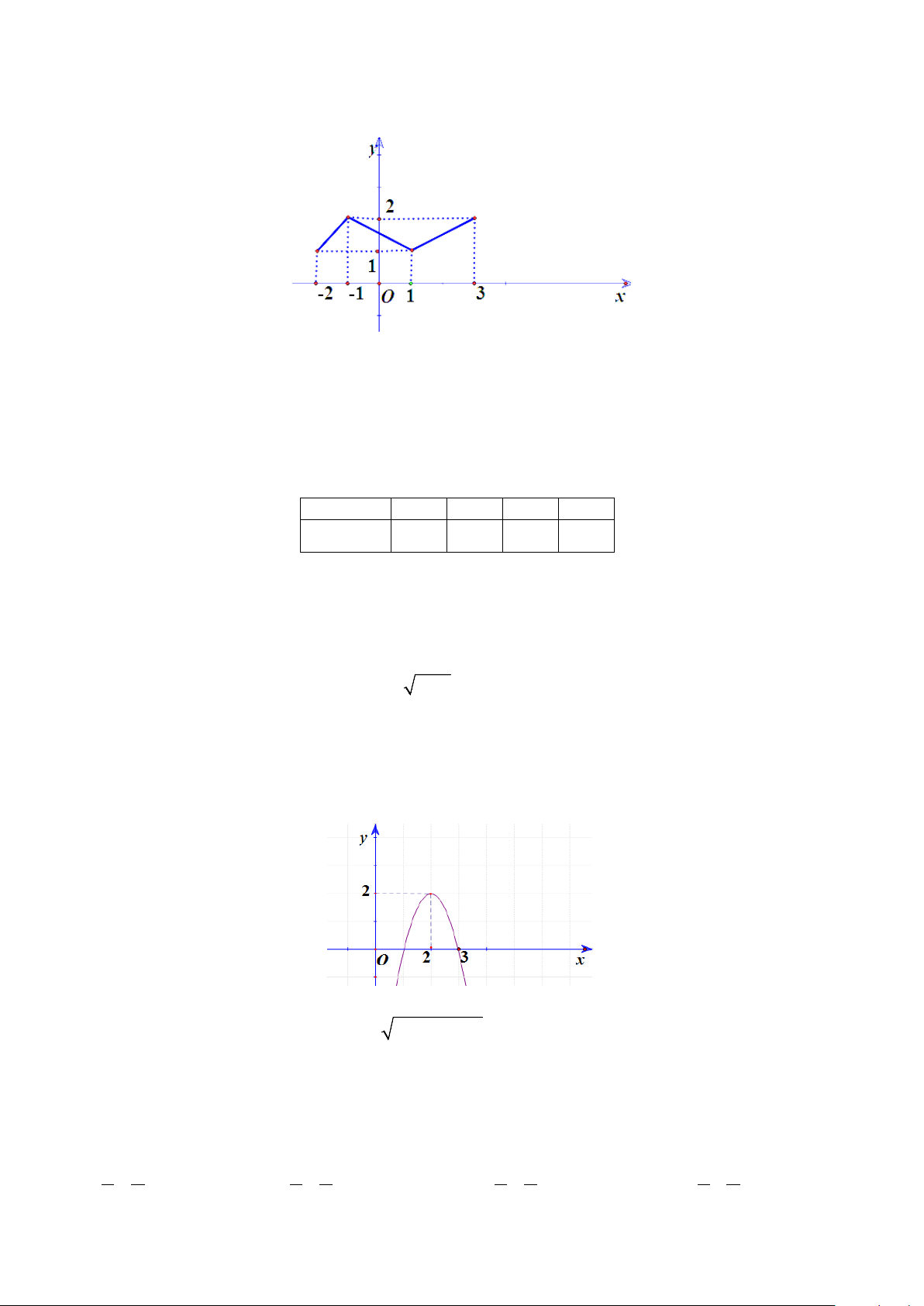
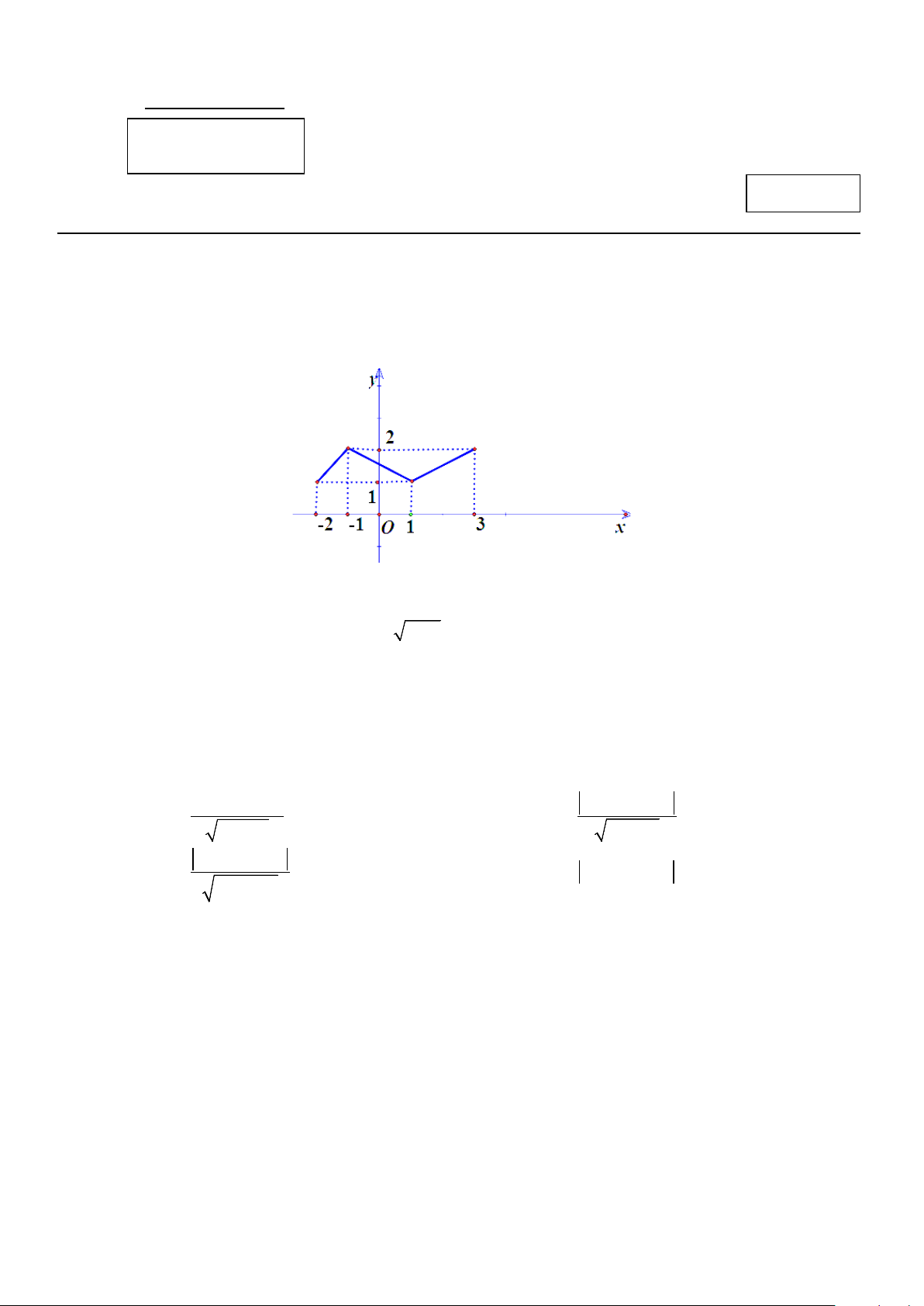
Câu 13: Cho hàm số y = f (x) có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ( 2; − 0). B. ( 1; − 3). C. ( 2; − ) 1 . D. ( 1; − ) 1 .
Câu 14: Tìm tập xác định của hàm số 2
y = x − 2x − 3. A.  \{− } 1 . B.  \{3;− } 1 . C.  \{ } 3 . D. . 
Câu 15: Tập nghiệm của bất phương trình 2
x − 4x + 3 ≤ 0 là A. ( ;
−∞ 1) (3;+∞). B. .  C. [1; ] 3 . D. . ∅
Câu 16: Tập nghiệm của phương trình 2
2x − 4x + 9 = x − 3 là A. . ∅ B. {0}. C. { 2; − } 0 . D. {− } 2 .
Câu 17: Trong mặt phẳngOxy , đường thẳng đi qua hai điểm (A2;0) và B(0;3) có phương trình là A. x y + = 1. B. x y + = 0. C. x y − =1. D. x y + = 1. 3 2 3 2 2 3 2 3
Câu 18: Gọi α là góc giữa hai đường thẳng d : 4x − 2y +1= 0 và d : x − 2y − 2 = 0.Tính cosα. 1 2 Trang 2/3 - Mã đề 101 A. 2 cosα = . B. 3 cosα = . C. 4 cosα = . D. cosα =1. 5 5 5
Câu 19: Tập giá trị của hàm số y = 2x −1 là A. [0;+∞). B. 1 ( ;+∞). C. [2;+∞). D. 1 ( ; −∞ ]. 2 2 Câu 20: Cho hàm số 2
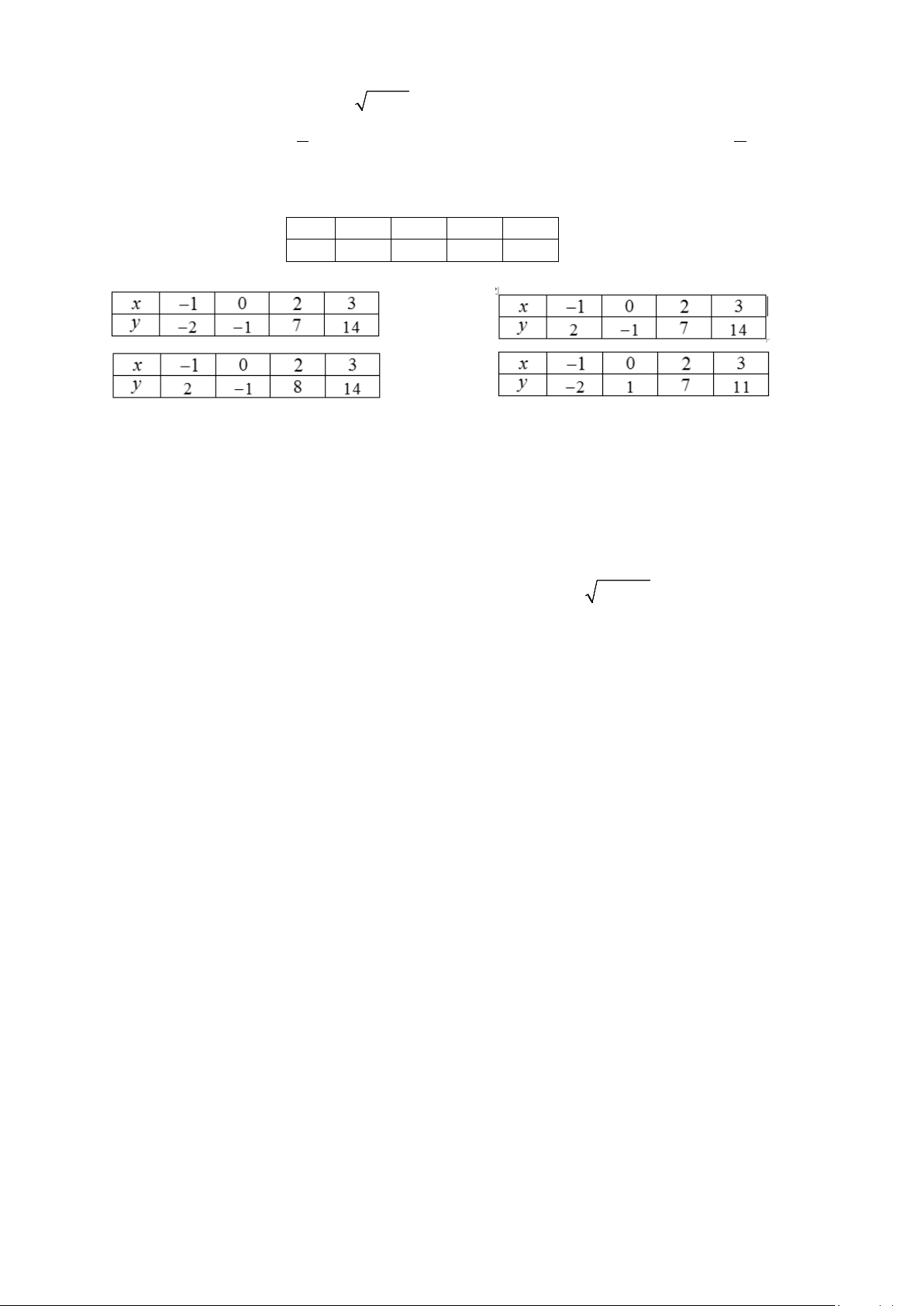
y = x + 2x −1. Hãy thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá
trị sau tại một số điểm. x 1 − 0 2 3 y ? ? ? ? A. . B. . C. . D. .
PHẦN CÂU HỎI TỰ LUẬN
Câu 21: Viết phương trình đường thẳng d qua điểm M (1;3) và cách điểm I( 1; − 5) một khoảng lớn nhất.
Câu 22: Cho tam giác ABC có A(1;3), B( 1; − 5),C (4;− )
1 . Viết phương trình đường cao AH của tam giác ABC. Câu 23: Vẽ parabol 2
y = x + 2x − 3.
Câu 24: Tính tổng tất cả các nghiệm dương của phương trình 2
4 25 − x =19 − x .
Câu 25: Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9m sau 2 giây. Trong khoảng
thời gian bao lâu thì độ cao quả bóng lớn hơn 7 m.
------ HẾT ------ Trang 3/3 - Mã đề 101
SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II – NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút; (Đề có 25 câu) ĐỀ CHÍNH THỨC (Đề có 3 trang)
Họ và tên : ............................................................... Số báo danh : ................... Mã đề 102
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1: Xác định hệ số a của tam thức bậc hai f (x) 2
= 2x + 5x + 6. A. 2 a = 2x . B. a = 5. C. a = 2. D. a = 6. 
Câu 2: Đường thẳng đi qua điểm A(2;− )1 và nhận VTCP u = (3; )1 có phương trình tham số là x = 3− tx = 2 − tx = 2 + 3tx = 3+ 2t A.  . B.  . C.  . D.  . y =1+ 2ty = 3+ ty = 1 − + ty =1− t
Câu 3: Khoảng cách từ điểm M (x ; y ∆ + + = + ≠ được tính 0 0 ) đến dường thẳng 2 2 : ax by c 0,(a b 0)
bởi công thức nào dưới đây? + + A. (
ax + by + c ax by c d M ,∆) 0 0 = ..
B. d (M ,∆) 0 0 = . 2 2 x + y 2 2 a + b 0 0
C. d (M ,∆) = ax + by + c .. D. + +
d (M ,∆) ax by c 0 0 = 0 0 . a + b
Câu 4: Cho hàm số bậc hai y = f (x) có đồ thị như hình vẽ.
Tìm giá trị lớn nhất của hàm số y = f (x). A. 1. B. 2. C. 4. D. 3.
Câu 5: Trong mặt phẳngOxy , đường thẳng d :2x+ y +3= 0 vuông góc với đường thẳng nào dưới đây?
A. ∆ : x + 2y +1= 0.. B. ∆ : 2x + y + 3 = 0.
C. ∆ : x − 2y +1= 0.
D. ∆ : 2x − y +1= 0.. 3 4 1 2
Câu 6: Tìm tọa độ đỉnh I của parabol 2
y = ax + bx + c có đồ thị như hình vẽ bên A. I (3;0). B. I (2;2) . C. I (3;2) . D. I (0;3) .
Câu 7: Cho đường thẳng d : 2x −3y +1= 0. Một vectơ pháp tuyến của d là Trang 1/3 - Mã đề 102     A. n = (2;1). B. x = (1; 3 − ). C. e = ( 3 − ;1). D. v = (2; 3) − .
Câu 8: Cho hàm số y = f (x) có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ( 1; − 3). B. ( 1; − ) 1 . C. ( 2; − 0). D. ( 2; − ) 1 .
Câu 9: Điểm nào dưới đây nằm trên đường thẳng ∆:2x+ y +1= 0? A. B( 1; − 3 − ). B. D(1; 2 − ). C. C(1;2). D. ( A 1; 3 − ).
Câu 10: Cho bảng giá trị của hai đại lượng tương ứng x, y như hình bên dưới. Đại lượng
y = f (x) là hàm số của đại lượng x . x 0 1 2 3
y = f (x) 5 − 2 5 2 − Tính giá trị f ( ) 1 . A. f ( ) 1 = 5. B. f ( ) 1 = − . 2 C. f ( ) 1 = − . 5 D. f ( ) 1 = 2.
Câu 11: Với x thuộc tập hợp nào sau đây thì tam thức 2
f (x) = x + 3x + 2 luôn dương? A. ( ; −∞ 2 − ). B. ( 2 − ; 1) − . C. ( 2; − +∞). D. . 
Câu 12: Tìm tập xác định của hàm số y = x −5. A. [5;+∞) B.  \{ } 5 . C. (5;+∞). D. ( ; −∞ 5].
Câu 13: Tìm tập xác định của hàm số 2
y = x − 2x − 3. A.  \{ } 3 . B. .  C.  \{− } 1 . D.  \{3;− } 1 .
Câu 14: Tìm trục đối xứng của parabol có đồ thị được cho như hình vẽ bên A. x = 2 . B. y = 2 . C. x = 3. D. y = 3.
Câu 15: Tập nghiệm của phương trình 2
2x − 4x + 9 = x − 3 là A. {− } 2 . B. {0}. C. . ∅ D. { 2; − } 0 .
Câu 16: Tập nghiệm của bất phương trình 2
x − 4x + 3 ≤ 0 là A. . ∅ B. .  C. ( ; −∞ 1) (3;+∞). D. [1; ] 3 .
Câu 17: Trong mặt phẳngOxy , đường thẳng đi qua hai điểm (A2;0) và B(0;3) có phương trình là A. x y + =1. B. x y + = 0. C. x y + = 1. D. x y − =1. 2 3 3 2 3 2 2 3 Trang 2/3 - Mã đề 102 Câu 18: Cho hàm số 2
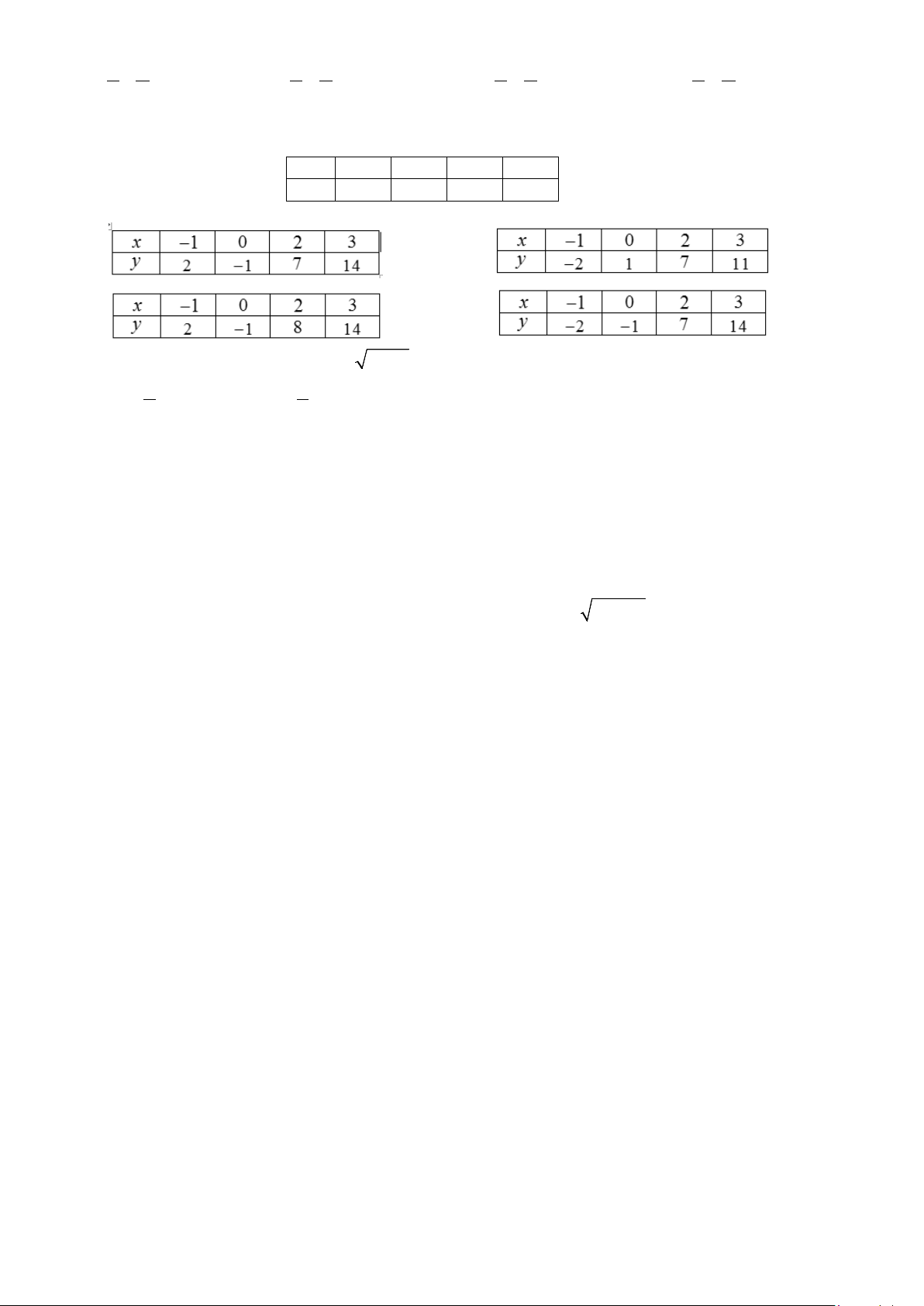
y = x + 2x −1. Hãy thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá
trị sau tại một số điểm. x 1 − 0 2 3 y ? ? ? ? A. . B. . C. . D. .
Câu 19: Tập giá trị của hàm số y = 2x −1 là A. 1 ( ; −∞ ]. B. 1 ( ;+∞). C. [0;+∞). D. [2;+∞). 2 2
Câu 20: Gọi α là góc giữa hai đường thẳng d : 4x − 2y +1= 0 và d : x − 2y − 2 = 0.Tính cosα. 1 2 A. 2 cosα = . B. 4 cosα = . C. 3 cosα = . D. cosα =1. 5 5 5
PHẦN CÂU HỎI TỰ LUẬN Câu 21: Vẽ parabol 2
y = x + 2x − 3.
Câu 22: Cho tam giác ABC có A(1;3), B( 1; − 5),C (4;− )
1 . Viết phương trình đường cao AH của tam giác ABC.
Câu 23: Viết phương trình đường thẳng d qua điểm M (1;3) và cách điểm I( 1; − 5) một khoảng lớn nhất.
Câu 24: Tính tổng tất cả các nghiệm dương của phương trình 2
4 25 − x =19 − x .
Câu 25: Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9m sau 2 giây. Trong khoảng
thời gian bao lâu thì độ cao quả bóng lớn hơn 7 m?
------ HẾT ------ Trang 3/3 - Mã đề 102
SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II – NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút; (Đề có 25 câu) ĐỀ CHÍNH THỨC (Đề có 3 trang)
Họ và tên : ............................................................... Số báo danh : ................... Mã đề 103
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1: Tìm tập xác định của hàm số 2
y = x − 2x − 3. A.  \{ } 3 . B.  \{− } 1 . C. .  D.  \{3;− } 1 .
Câu 2: Trong mặt phẳngOxy , đường thẳng d :2x+ y +3= 0 vuông góc với đường thẳng nào dưới đây?
A. ∆ : 2x − y +1= 0.. B. ∆ : x − 2y +1= 0.
C. ∆ : x + 2y +1= 0.. D. ∆ : 2x + y + 3 = 0. 2 1 3 4
Câu 3: Cho bảng giá trị của hai đại lượng tương ứng x, y như hình bên dưới. Đại lượng y = f (x) là
hàm số của đại lượng x . x 0 1 2 3
y = f (x) 5 − 2 5 2 − Tính giá trị f ( ) 1 . A. f ( ) 1 = 5. B. f ( ) 1 = − . 2 C. f ( ) 1 = − . 5 D. f ( ) 1 = 2. 
Câu 4: Đường thẳng đi qua điểm A(2;− )1 và nhận VTCP u = (3; )1 có phương trình tham số là x = 3+ 2tx = 2 − tx = 2 + 3tx = 3− t A.  . B.  . C.  . D.  . y =1− ty = 3+ ty = 1 − + ty =1+ 2t
Câu 5: Tìm tập xác định của hàm số y = x −5. A. [5;+∞) B. (5;+∞). C. ( ; −∞ 5]. D.  \{ } 5 .
Câu 6: Tìm tọa độ đỉnh I của parabol 2
y = ax + bx + c có đồ thị như hình vẽ bên A. I (3;0). B. I (2;2) . C. I (3;2) . D. I (0;3) .
Câu 7: Điểm nào dưới đây nằm trên đường thẳng ∆:2x+ y +1= 0? A. B( 1; − 3 − ). B. C(1;2). C. ( A 1; 3 − ). D. D(1; 2 − ).
Câu 8: Cho hàm số bậc hai y = f (x) có đồ thị như hình vẽ. Trang 1/3 - Mã đề 103
Tìm giá trị lớn nhất của hàm số y = f (x). A. 1. B. 2. C. 4. D. 3.
Câu 9: Khoảng cách từ điểm M (x ; y ∆ + + = + ≠ được tính 0 0 ) đến dường thẳng 2 2 : ax by c 0,(a b 0)
bởi công thức nào dưới đây? A.
ax + by + c
d (M ,∆) = ax + by + c ..
B. d (M ,∆) 0 0 = .. 0 0 2 2 x + y 0 0 + + C. ( ax by c d M , + + ∆) 0 0 = .
D. d (M ∆) ax by c 0 0 , = . 2 2 a + b a + b
Câu 10: Với x thuộc tập hợp nào sau đây thì tam thức 2
f (x) = x + 3x + 2 luôn dương? A. ( 2; − +∞). B. ( 2 − ; 1) − . C. ( ; −∞ 2 − ). D. . 
Câu 11: Cho hàm số y = f (x) có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ( 1; − 3). B. ( 2; − 0). C. ( 2; − ) 1 . D. ( 1; − ) 1 .
Câu 12: Xác định hệ số a của tam thức bậc hai f (x) 2
= 2x + 5x + 6. A. 2 a = 2x . B. a = 6. C. a = 2. D. a = 5.
Câu 13: Tìm trục đối xứng của parabol có đồ thị được cho như hình vẽ bên A. x = 2 . B. y = 2 . C. y = 3. D. x = 3.
Câu 14: Cho đường thẳng d : 2x −3y +1= 0. Một vectơ pháp tuyến của d là     A. n = (2;1). B. x = (1; 3 − ). C. v = (2; 3) − . D. e = ( 3 − ;1).
Câu 15: Gọi α là góc giữa hai đường thẳng d : 4x − 2y +1= 0 và d : x − 2y − 2 = 0.Tính cosα. 1 2 A. 2 cosα = . B. cosα =1. C. 4 cosα = . D. 3 cosα = . 5 5 5
Câu 16: Trong mặt phẳngOxy , đường thẳng đi qua hai điểm (A2;0) và B(0;3) có phương trình là A. x y + =1. B. x y − =1. C. x y + = 0. D. x y + =1. 3 2 2 3 3 2 2 3
Câu 17: Tập nghiệm của bất phương trình 2
x − 4x + 3 ≤ 0 là A. .  B. [1; ] 3 . C. ( ; −∞ 1) (3;+∞). D. . ∅
Câu 18: Tập nghiệm của phương trình 2
2x − 4x + 9 = x − 3 là Trang 2/3 - Mã đề 103 A. {0}. B. { 2; − } 0 . C. {− } 2 . D. . ∅
Câu 19: Tập giá trị của hàm số y = 2x −1 là A. [2;+∞). B. 1 ( ;+∞). C. [0;+∞). D. 1 ( ; −∞ ]. 2 2 Câu 20: Cho hàm số 2
y = x + 2x −1. Hãy thay dấu “?” bằng các số thích hợp để hoàn thành bảng giá
trị sau tại một số điểm. x 1 − 0 2 3 y ? ? ? ? A. . B. . C. . D. .
PHẦN CÂU HỎI TỰ LUẬN
Câu 21: Cho tam giác ABC có A(1;3), B( 1; − 5),C (4;− )
1 . Viết phương trình đường cao AH của tam giác ABC.
Câu 22: Viết phương trình đường thẳng d qua điểm M (1;3) và cách điểm I( 1; − 5) một khoảng lớn nhất. Câu 23: Vẽ parabol 2
y = x + 2x − 3.
Câu 24: Tính tổng tất cả các nghiệm dương của phương trình 2
4 25 − x =19 − x .
Câu 25: Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9m sau 2 giây. Trong khoảng
thời gian bao lâu thì độ cao quả bóng không nhỏ hơn 7 m.
------ HẾT ------ Trang 3/3 - Mã đề 103
SỞ GD & ĐT QUẢNG TRỊ
ĐỀ KIỂM TRA GIỮA KỲ II– NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút; (Đề có 25 câu) ĐỀ CHÍNH THỨC (Đề có 3 trang)
Họ và tên : ............................................................... Số báo danh : ................... Mã đề 104
PHẦN CÂU HỎI TRẮC NGHIỆM
Câu 1: Điểm nào dưới đây nằm trên đường thẳng ∆:2x+ y +1= 0? A. ( A 1; 3 − ). B. B( 1; − 3 − ). C. C(1;2). D. D(1; 2 − ).
Câu 2: Cho hàm số y = f (x) có đồ thị như hình vẽ.
Hàm số đã cho nghịch biến trên khoảng nào dưới đây? A. ( 2; − ) 1 . B. ( 1; − 3). C. ( 2; − 0). D. ( 1; − ) 1 .
Câu 3: Tìm tập xác định của hàm số y = x −5. A. [5;+∞) B.  \{ } 5 . C. ( ; −∞ 5]. D. (5;+∞).
Câu 4: Với x thuộc tập hợp nào sau đây thì tam thức 2
f (x) = x + 3x + 2 luôn dương? A. ( ; −∞ 2 − ). B. ( 2; − +∞). C. ( 2 − ; 1) − . D. . 
Câu 5: Khoảng cách từ điểm M (x ; y ∆ + + = + ≠ được tính 0 0 ) đến dường thẳng 2 2 : ax by c 0,(a b 0)
bởi công thức nào dưới đây? + + A. + + ax by c
d (M ∆) ax by c 0 0 , = .
B. d (M ,∆) 0 0 = . a + b 2 2 a + b C. (
ax + by + c d M ,∆) 0 0 = ..
D. d (M ,∆) = ax + by + c .. 2 2 x + y 0 0 0 0
Câu 6: Cho đường thẳng d : 2x −3y +1= 0. Một vectơ pháp tuyến của d là     A. n = (2;1). B. x = (1; 3 − ). C. e = ( 3 − ;1). D. v = (2; 3) − .
Câu 7: Trong mặt phẳngOxy , đường thẳng d :2x+ y +3= 0 vuông góc với đường thẳng nào dưới đây?
A. ∆ : 2x − y +1= 0.. B. ∆ : x − 2y +1= 0.
C. ∆ : 2x + y + 3 = 0.
D. ∆ : x + 2y +1= 0.. 2 1 4 3 
Câu 8: Đường thẳng đi qua điểm A(2;− )1 và nhận VTCP u = (3; )1 có phương trình tham số là x = 2 − tx = 3+ 2tx = 3− tx = 2 + 3t A.  . B.  . C.  . D.  . y = 3+ ty =1− ty =1+ 2ty = 1 − + t
Câu 9: Xác định hệ số a của tam thức bậc hai f (x) 2
= 2x + 5x + 6. A. 2 a = 2x . B. a = 2. C. a = 5. D. a = 6.
Câu 10: Cho bảng giá trị của hai đại lượng tương ứng x, y như hình bên dưới. Đại lượng Trang 1/3 - Mã đề 104
y = f (x) là hàm số của đại lượng x . x 0 1 2 3
y = f (x) 5 − 2 5 2 − Tính giá trị f ( ) 1 . A. f ( ) 1 = − . 5 B. f ( ) 1 = 5. C. f ( ) 1 = − . 2 D. f ( ) 1 = 2.
Câu 11: Tìm tọa độ đỉnh I của parabol 2
y = ax + bx + c có đồ thị như hình vẽ bên A. I (0;3) . B. I (3;0). C. I (2;2) . D. I (3;2) .
Câu 12: Tìm trục đối xứng của parabol có đồ thị được cho như hình vẽ bên A. x = 3. B. x = 2 . C. y = 2 . D. y = 3.
Câu 13: Cho hàm số bậc hai y = f (x) có đồ thị như hình vẽ.
Tìm giá trị lớn nhất của hàm số y = f (x). A. 3. B. 4. C. 1. D. 2.
Câu 14: Tìm tập xác định của hàm số 2
y = x − 2x − 3. A.  \{3;− } 1 . B.  \{ } 3 . C. .  D.  \{− } 1 .
Câu 15: Tập nghiệm của phương trình 2
2x − 4x + 9 = x − 3 là A. { 2; − } 0 . B. {0}. C. {− } 2 . D. . ∅
Câu 16: Tập nghiệm của bất phương trình 2
x − 4x + 3 ≤ 0 là A. . ∅ B. .  C. ( ; −∞ 1) (3;+∞). D. [1; ] 3 .
Câu 17: : Gọi α là góc giữa hai đường thẳng d : 4x − 2y +1= 0 và d : x − 2y − 2 = 0.Tính cosα. 1 2 A. 4 cosα = . B. 3 cosα = . C. 2 cosα = . D. cosα =1. 5 5 5
Câu 18: Trong mặt phẳngOxy , đường thẳng đi qua hai điểm (A2;0) và B(0;3) có phương trình là Trang 2/3 - Mã đề 104 A. x y − =1. B. x y + = 0. C. x y + =1. D. x y + =1. 2 3 3 2 3 2 2 3
Câu 19: : Cho hàm số 2
y = x + 2x −1. Hãy thay dấu “?” bằng các số thích hợp để hoàn thành bảng
giá trị sau tại một số điểm. x 1 − 0 2 3 y ? ? ? ? A. . B. . C. . D. .
Câu 20: Tập giá trị của hàm số y = 2x −1 là A. 1 ( ; −∞ ]. B. 1 ( ;+∞). C. [0;+∞). D. [2;+∞). 2 2
PHẦN CÂU HỎI TỰ LUẬN Câu 21: Vẽ parabol 2
y = x + 2x − 3.
Câu 22: Viết phương trình đường thẳng d qua điểm M (1;3) và cách điểm I( 1; − 5) một khoảng lớn nhất.
Câu 23: Cho tam giác ABC có A(1;3), B( 1; − 5),C (4;− )
1 . Viết phương trình đường cao AH của tam giác ABC.
Câu 24: Tính tổng tất cả các nghiệm dương của phương trình 2
4 25 − x =19 − x .
Câu 25: Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9m sau 2 giây. Trong khoảng
thời gian bao lâu thì độ cao quả bóng không nhỏ hơn 7 m.
------ HẾT ------ Trang 3/3 - Mã đề 104
SỞ GD & ĐT QUẢNG TRỊ
DE KIEM TRA GIUA KY II – NĂM HỌC 2022 - 2023
TRƯỜNG THPT THỊ XÃ QUẢNG TRỊ MÔN TOÁN - LỚP 10
Thời gian làm bài : 90 Phút
Phần đáp án câu trắc nghiệm: 101 102 103 104 1 C C C A 2 D C B D 3 C B D A 4 A D C A 5 B C A B 6 C A A D 7 D D C B 8 B B D D 9 D D C B 10 C D C D 11 D A D B 12 A A C B 13 D B A A 14 D A C C 15 C C C D 16 A D D D 17 D A B A 18 C B D D 19 A C C D 20 B B A C
Phần đáp án câu tự luận: Mã đề 101:
Câu 21 : Viết phương trình đường thẳng d qua điểm M (1;3) và cách điểm I( 1; − 5) một khoảng lớn nhất.
Gợi ý làm bài:
Gọi H là hình chiếu của I trên d , ta có d(I,d) = IH ≤ IM = 2 2. Khoảng cách từ I( 1; − 5) đến 
d lớn nhất khi d vuông góc với IM . Vậy d qua M (1;3) và có VTPT IM ( 2 − ;2) = 2( − 1; 1 − ) nên có phương trình
x − y + 2 = 0.
Câu 22 Cho tam giác ABC có A(1;3), B( 1; − 5),C (4;− )
1 . Viết phương trình đường cao AH của tam giác ABC.
Gợi ý làm bài: 
Đường thẳng AH đi qua (
A 1;3) và nhận VTPT BC(5; 6
− ) nên có phương trình
5(x −1) −6(y −3) = 0 hay
5x −6y +13 = 0. Câu 23 : Vẽ parabol 2
y = x + 2x − 3.
Gợi ý làm bài:
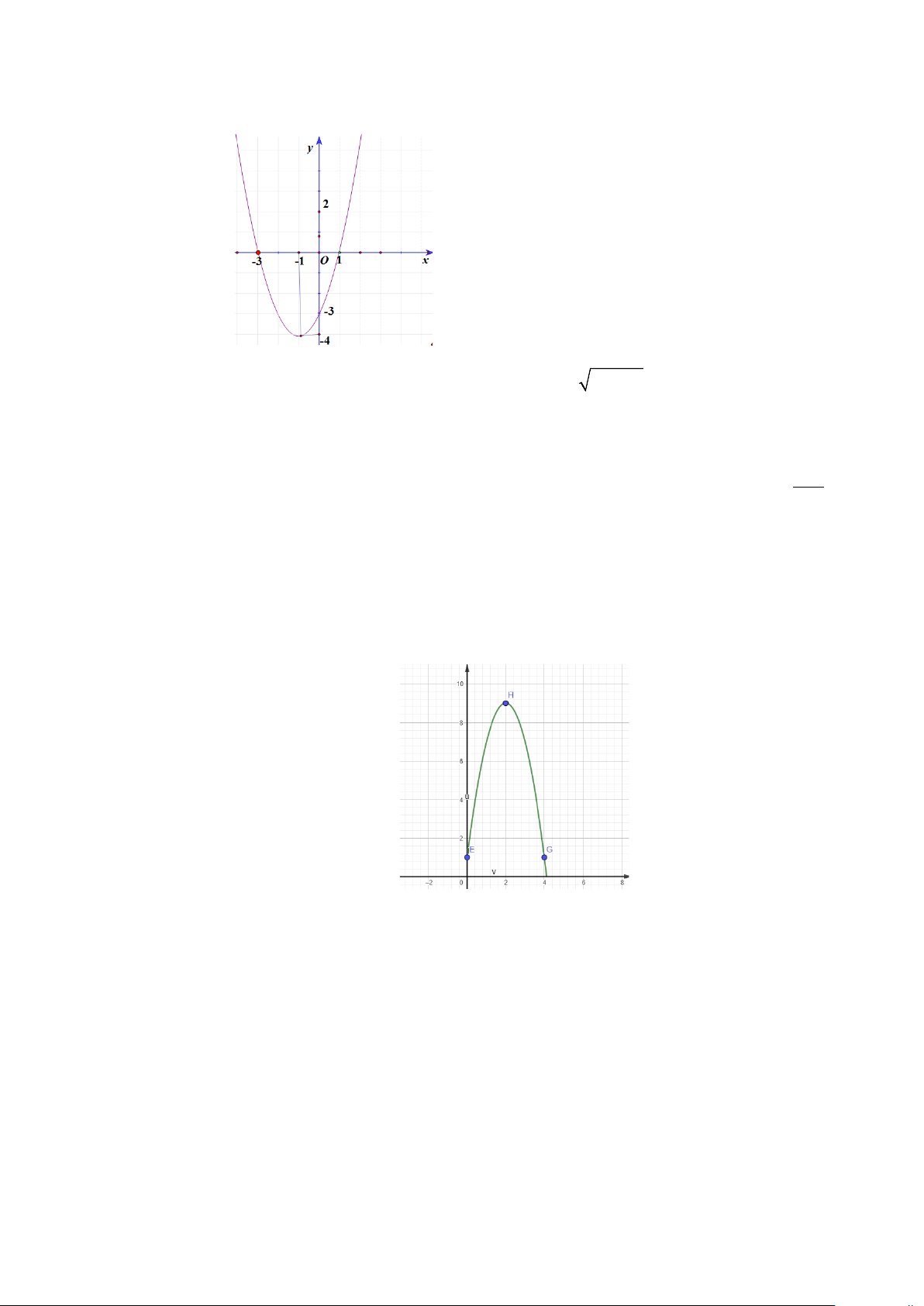
+ Tọa độ đỉnh của parabol là I( 1; − 4 − ). 1
+ Trục đối xứng : x = 1. −
+ Parabol cắt trục tung tại điểm ( A 0; 3)
− và cắt trục hoành tại các điểm có hoành độ x =1, x = 3 − .
+ Đồ thị như hình vẽ:
Câu 24 Tính tổng tất cả các nghiệm dương của phương trình 2
4 25 − x =19 − x .
Gợi ý làm bài:
Bình phương hai vế phương trình và thu gọn ta được 2
17x −38x −39 = 0. Giải phương trình này ta được hai nghiệm  − x = 3, x = 13
− /17 . Thử lại phương trình ban đầu, ta có tập nghiệm 13 S 3  ;  = . 1 2 17   
Tổng các nghiệm dương của phương trình là 3.
Câu 25 Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9m sau 2 giây. Tính khoảng thời
gian để độ cao quả bóng không nhỏ hơn 7 m.
Gợi ý làm bài:
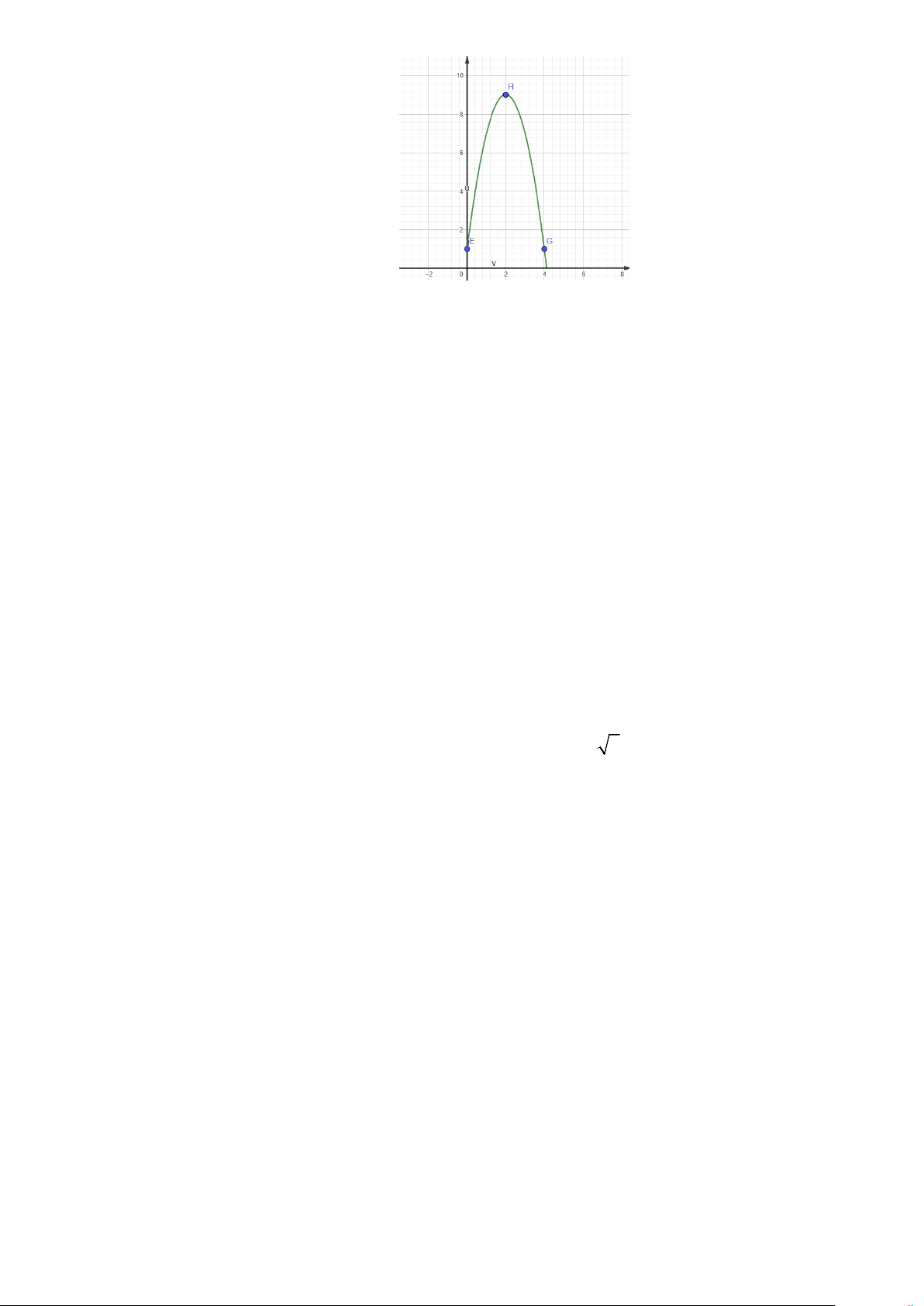
Chọn hệ trục tọa độ Oth như hình vẽ Gọi parabol 2
h = at + bt +1,(a < 0)  = + +  = −
Từ giả thiết bài toán, ta có hệ 9 4a 2b 1 a  Giải hệ ta được 2  . 7 = a + b +1 b  = 8 Vậy, 2 h = 2.
− t + 8.t +1≥ 7 khi 1≤ t ≤ 3. Mã đề 102: Câu 21 : Vẽ parabol 2
y = x + 2x − 3.
Gợi ý làm bài:
+ Tọa độ đỉnh của parabol là I( 1; − 4 − ). 2
+ Trục đối xứng : x = 1. −
+ Parabol cắt trục tung tại điểm ( A 0; 3)
− và cắt trục hoành tại các điểm có hoành độ x =1, x = 3 − .
+ Đồ thị như hình vẽ:
Câu 22 Cho tam giác ABC có A(1;3), B( 1; − 5),C (4;− )
1 . Viết phương trình đường cao AH của tam giác ABC.
Gợi ý làm bài: 
Đường thẳng AH đi qua (
A 1;3) và nhận VTPT BC(5; 6
− ) nên có phương trình
5(x −1) −6(y −3) = 0 hay
5x −6y +13 = 0.
Câu 23 : Viết phương trình đường thẳng d qua điểm M (1;3) và cách điểm I( 1; − 5) một khoảng lớn nhất.
Gợi ý làm bài:
Gọi H là hình chiếu của I trên d , ta có d(I,d) = IH ≤ IM = 2 2. Khoảng cách từ I( 1; − 5) đến 
d lớn nhất khi d vuông góc với IM . Vậy d qua M (1;3) và có VTPT IM ( 2 − ;2) = 2( − 1; 1 − ) nên có phương trình
x − y + 2 = 0.
Câu 24 Tính tổng tất cả các nghiệm dương của phương trình 2
4 25 − x =19 − x .
Gợi ý làm bài:
Bình phương hai vế phương trình và thu gọn ta được 2
17x −38x −39 = 0. Giải phương trình này ta được hai nghiệm  − x = 3, x = 13
− /17 . Thử lại phương trình ban đầu, ta có tập nghiệm 13 S 3  ;  = . 1 2 17   
Tổng các nghiệm dương của phương trình là 3.
Câu 25 Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9m sau 2 giây. Tính khoảng thời
gian để độ cao quả bóng không nhỏ hơn 7 m.
Gợi ý làm bài: 3
Chọn hệ trục tọa độ Oth như hình vẽ Gọi parabol 2
h = at + bt +1,(a < 0)  = + +  = −
Từ giả thiết bài toán, ta có hệ 9 4a 2b 1 a  Giải hệ ta được 2  . 7 = a + b +1 b  = 8 Vậy, 2 h = 2.
− t + 8.t +1≥ 7 khi 1≤ t ≤ 3. Mã đề 103:
Câu 21 Cho tam giác ABC có A(1;3), B( 1; − 5),C (4;− )
1 . Viết phương trình đường cao AH của tam giác ABC.
Gợi ý làm bài: 
Đường thẳng AH đi qua (
A 1;3) và nhận VTPT BC(5; 6
− ) nên có phương trình
5(x −1) −6(y −3) = 0 hay
5x −6y +13 = 0.
Câu 22 : Viết phương trình đường thẳng d qua điểm M (1;3) và cách điểm I( 1; − 5) một khoảng lớn nhất.
Gợi ý làm bài:
Gọi H là hình chiếu của I trên d , ta có d(I,d) = IH ≤ IM = 2 2. Khoảng cách từ I( 1; − 5) đến 
d lớn nhất khi d vuông góc với IM . Vậy d qua M (1;3) và có VTPT IM ( 2 − ;2) = 2( − 1; 1 − ) nên có phương trình
x − y + 2 = 0. Câu 23 : Vẽ parabol 2
y = x + 2x − 3.
Gợi ý làm bài:
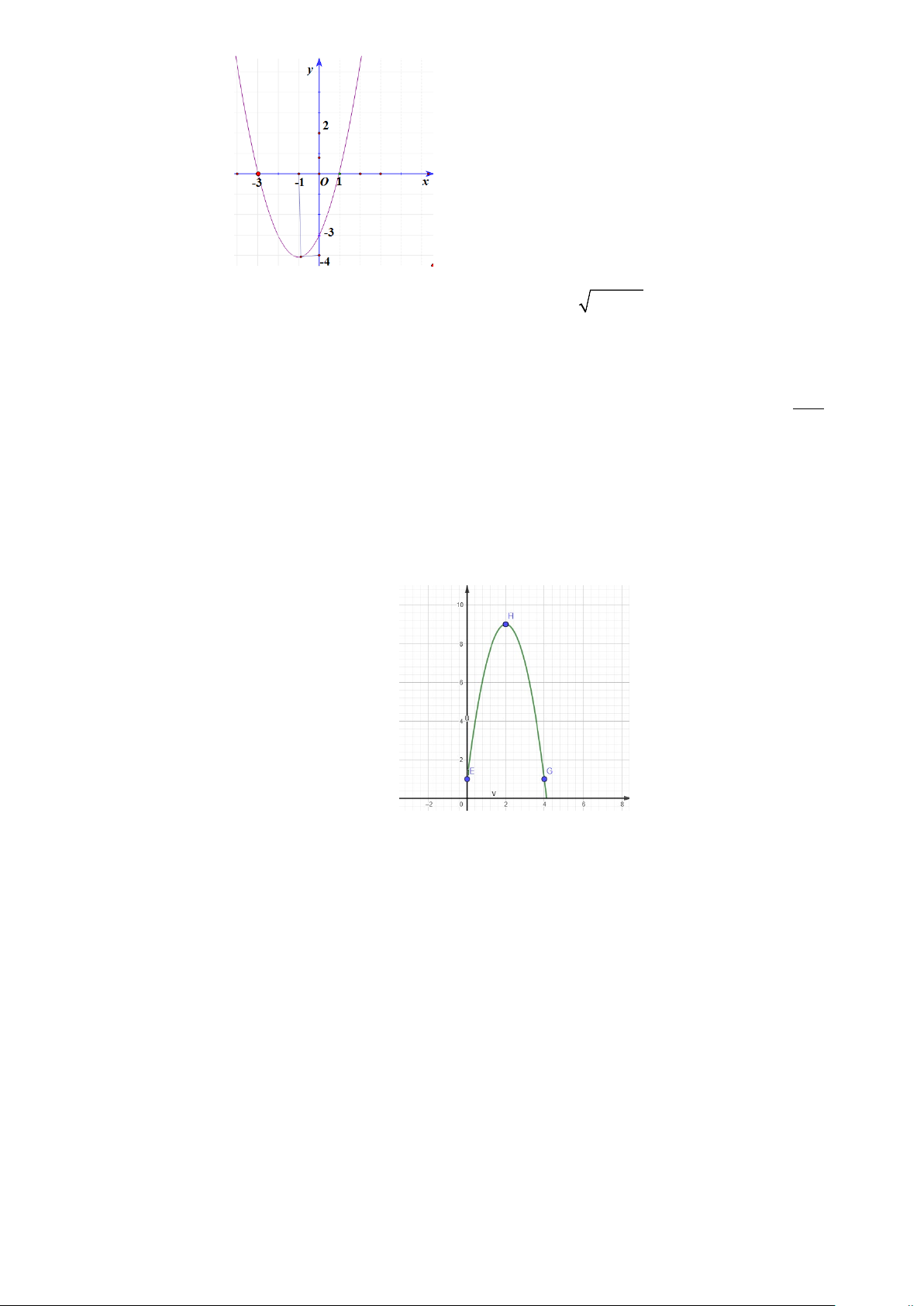
+ Tọa độ đỉnh của parabol là I( 1; − 4 − ).
+ Trục đối xứng : x = 1. −
+ Parabol cắt trục tung tại điểm ( A 0; 3)
− và cắt trục hoành tại các điểm có hoành độ x =1, x = 3 − . 4
+ Đồ thị như hình vẽ:
Câu 24 Tính tổng tất cả các nghiệm dương của phương trình 2
4 25 − x =19 − x .
Gợi ý làm bài:
Bình phương hai vế phương trình và thu gọn ta được 2
17x −38x −39 = 0. Giải phương trình này ta được hai nghiệm  − x = 3, x = 13
− /17 . Thử lại phương trình ban đầu, ta có tập nghiệm 13 S 3  ;  = . 1 2 17   
Tổng các nghiệm dương của phương trình là 3.
Câu 25 Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9m sau 2 giây. Tính khoảng thời
gian để độ cao quả bóng không nhỏ hơn 7 m.
Gợi ý làm bài:
Chọn hệ trục tọa độ Oth như hình vẽ Gọi parabol 2
h = at + bt +1,(a < 0)  = + +  = −
Từ giả thiết bài toán, ta có hệ 9 4a 2b 1 a  Giải hệ ta được 2  . 7 = a + b +1 b  = 8 Vậy, 2 h = 2.
− t + 8.t +1≥ 7 khi 1≤ t ≤ 3. Mã đề 104: Câu 21 : Vẽ parabol 2
y = x + 2x − 3.
Gợi ý làm bài:
+ Tọa độ đỉnh của parabol là I( 1; − 4 − ).
+ Trục đối xứng : x = 1. −
+ Parabol cắt trục tung tại điểm ( A 0; 3)
− và cắt trục hoành tại các điểm có hoành độ x =1, x = 3 − . 5
+ Đồ thị như hình vẽ:
Câu 22 : Viết phương trình đường thẳng d qua điểm M (1;3) và cách điểm I( 1; − 5) một khoảng lớn nhất.
Gợi ý làm bài:
Gọi H là hình chiếu của I trên d , ta có d(I,d) = IH ≤ IM = 2 2. Khoảng cách từ I( 1; − 5) đến 
d lớn nhất khi d vuông góc với IM . Vậy d qua M (1;3) và có VTPT IM ( 2 − ;2) = 2( − 1; 1 − ) nên có phương trình
x − y + 2 = 0.
Câu 23 Cho tam giác ABC có A(1;3), B( 1; − 5),C (4;− )
1 . Viết phương trình đường cao AH của tam giác ABC.
Gợi ý làm bài: 
Đường thẳng AH đi qua (
A 1;3) và nhận VTPT BC(5; 6
− ) nên có phương trình
5(x −1) −6(y −3) = 0 hay
5x −6y +13 = 0.
Câu 24 Tính tổng tất cả các nghiệm dương của phương trình 2
4 25 − x =19 − x .
Gợi ý làm bài:
Bình phương hai vế phương trình và thu gọn ta được 2
17x −38x −39 = 0. Giải phương trình này ta được hai nghiệm  − x = 3, x = 13
− /17 . Thử lại phương trình ban đầu, ta có tập nghiệm 13 S 3  ;  = . 1 2 17   
Tổng các nghiệm dương của phương trình là 3.
Câu 25 Một quả bóng chuyền được phát lên từ độ cao 1 m và chuyển động theo quỹ đạo là một
cung parabol. Quả bóng đạt độ cao 7 m sau 1 giây và đạt độ cao 9m sau 2 giây. Tính khoảng thời
gian để độ cao quả bóng không nhỏ hơn 7 m.
Gợi ý làm bài: 6
Chọn hệ trục tọa độ Oth như hình vẽ Gọi parabol 2
h = at + bt +1,(a < 0)  = + +  = −
Từ giả thiết bài toán, ta có hệ 9 4a 2b 1 a  Giải hệ ta được 2  . 7 = a + b +1 b  = 8 Vậy, 2 h = 2.
− t + 8.t +1≥ 7 khi 1≤ t ≤ 3. 7
Document Outline

  • de 101
  • de 102
  • de 103
  • de 104
  • Phieu soi dap an