Đề giữa kỳ 2 Toán 11 năm 2022 – 2023 trường THPT Gia Định – TP HCM

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra giữa học kỳ 2 môn Toán 11 năm học 2022 – 2023 trường THPT Gia Định, thành phố Hồ Chí Minh; đề thi gồm 01 trang với 03 bài toán hình thức tự luận, thời gian làm bài 60 phút, không kể thời gian phát đề; đề thi có đáp án và lời giải chi tiết. Mời bạn đọc đón xem!

42 21 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

6 trang 9 tháng trước

Tác giả:

Profile Nguyễn Trang
KIỂM TRA GIỮA HỌC KỲ 2. NK 2022-2023
Môn: TOÁN. Thời gian: 60ph
---oOo---
Khối 11
Câu 1 (2đ) Cho cấp số nhân
n
u
biết
5 3
6 8
u u 12
u u 96
.
a) Hãy tìm số hạng đầu tiên
1
u
và công bội
q
của cấp số nhân.
b) Tính
5 6 7 8 9 20
A u u u u u ........ u
Câu 2 (4đ)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh
.
SA ABCD
và
SA 2a 2
.Gọi H, K lần lượt là hình chiếu vuông góc
của A trên cạnh SB, SD. Gọi I là giao điểm của SC với mặt phẳng
AHK
và E là trung điểm OD .
a) Chứng minh:
SD ABK
và
SC AHK
b) Chứng minh:
AC EI
.
c) Tính góc giữa đường thẳng SC và mặt phẳng (SAB).
Câu 3 (4đ) Tính các giới hạn:
2 3
2
n 2n
a) lim
n 2n
n n
n 1 n
7 2.3
b) lim
7 4.5
3
2 3 2
c) lim 9n n 2 27n n
------ HẾT ------
2
ĐÁP ÁN KIỂM TRA GIỮA HỌC KỲ 2. NK 2022-2023 - MÔN TOÁN-KHỐI 11
Câu
Nội dung Điểm
1
Cho cấp số nhân
n
u
biết
5 3
6 8
u u 12
u u 96
.
2,0đ
a) Hãy tìm số hạng đầu tiên
1
u
và công bội
q
của cấp số nhân.
1,5đ
2 2
4 2
1
1 1
5 7
5 2
1 1
1
u .q q 1 12 1
u .q u .q 12
I
u .q u .q 96
u .q 1 q 96 2

0,25+ 0,25
Lấy
2
chia
1
tađược
3
q 8 q 2
.
0,5
Thếvào
1
tađược
1
u 1
.
0,5
b) Tính
5 6 7 8 9 20
A u u u u u ........ u
0,5đ
20
20 20
20 1
1 2
1 q 1 2
S u .
1 q 1 2 3

4
4 4
4 1
1 2
1 q 1 2
S u .
1 q 1 2 3
0,25
4 20
20 4
2 2
A S S 349520
3

0,25
2
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh
.
SA ABCD
và
SA 2a 2
.Gọi H, K lần lượt là hình chiếu
vuông góc của A trên cạnh SB,SD. Gọi I là giao điểm của SC
với mặt phẳng
AHK
và E là trung điểm OD .
a) Chứng minh:
SD ABK
và
SC AHK
b) Chứng minh:
AC EI
.
c)
Tính góc giữa đường thẳng SC và mặt phẳng (SAB).
4,0đ
3
H
K
O
I
E
D
C
B
A
S
a) Chứng minh:
SD ABK
và
SC AHK
2đ
SA AB
AB SAD AB SD
AD AB
0,25+0,25
SD AB
SD ABK
SD AK
0.25
0.25
BC AB
BC SAB BC AH
BC SA
0.25
BC AH
SBC AH SC 1
S A
AH
B H
0.25
CD AD
SAD CD AK
D
CD
C SA
0.25
4
CD AK
SCD AK SC 2
S A
AK
D K
AH SC
SC AHK .
AK SC
0.25
b) Chứng minh:
AC EI
.
1đ
Xác định I:
Trong
SBD : SO HK M
Trong
SAC : AM SC I
I AM, AM AHK
I SC AHK
I SC
AI AHK
AI SC
SC AHK
.
0,25
AC AB 2 2a 2
(đườngchéohìnhvuông)
Trongtamgiáccântại
A
:có
AI
làđườngcaosuyra
AI
là
đườngtrungtuyến,

I
làtrungđiểm
SC
IO
làđườngtrungbình
IO / /SA
.
0,25
IO / /SA
IO ABCD IO AC
SA ABCD
0,25
.
AC IO
AC EOI AC EI.
AC EO
0,25
c)
Tính góc giữa đường thẳng SC và mặt phẳng (SAB).
1đ
B CB SAB
CB SAB
SB
làhìnhchiếucủa
SC
trên
SAB
.
0,25
SC; SAB SC;SB BSC

0,25
Tamgiác
SAB
vuôngtạiSnên
2 2
SB SA AB 2 3a

0,25
5
Tamgiác
SBC
vuôngtại
B
BC 2a 1
tanBSC
SB
2 3a 3
.
0
BSC 30 .
Vậy
0
SC; SAB SC;SB BSC 30 .

0,25
3 Tính các giới hạn:
4,0đ
2 3
2
n 2n
a) lim
n 2n
1,5đ
3
2
1
1
n 2
2
n
n
lim lim n.
2
2
1
n 1
n
n
0,25+0,25
Vì
limn
1
2
n
lim 2 0
2
1
n

Nếu HS chưa ghi phần này mà suy ra kết quả

thì trừ 1,0đ
0,25+0,25
Nên:
1
2
n
lim n. .
2
1
n

0,5
n n
n 1 n
7 2.3
b) lim
7 4.5
1,5đ
n
n
n n
n n
n
n
3
7 1 2.
7
7 2.3
lim lim
7.7 4.5
5
7 7 4.
7
0,25+0,25
6
n
n
3
1 2.
7
lim
5
7 4.
7
0,5
1
.
7
Nếu HS chưa khử dạng vô định mà suy ra kết quả thì trừ 1,0đ
0,5
3
2 3 2
c) lim 9n n 2 27n n
1đ
3
2 3 2
lim 9n n 2 3n 3n 27n n
0,25
2
2
2
3 3
2 3 2 3 2
n 2 n
lim
9n n 2 3n
9n 3n. 27n n 27n n
2
2
2
3 3
2
2
n 1
n
n
lim
1 2
1 1
n 9 3
n 9 3. 27 27
n
n
n n
2
3 3
2
2
1
1
n
lim
1 2
1 1
9 3
9 3. 27 27
n
n
n n
0,5
1 1 7
.
3 3 9 9 9 54
Nếu HS chưa khử dạng vô định mà suy ra kết quả thì trừ
0,75đ
0,25
Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số điểm từng phần như
trong đáp án.Cho điểm từng câu ,ý ,sau đó cộng điểm toàn bài và không làm tròn ( Ví dụ:7,25__ghi bảy hai
lăm).Giám khảo ghi điểm toàn bài bằng số và bằng chữ ; giám khảo nhớ ký và ghi tên vào từng tờ bài làm
của học sinh
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

KIỂM TRA GIỮA HỌC KỲ 2. NK 2022-2023
Môn: TOÁN. Thời gian: 60ph Khối 11 ---oOo--- u   u  12 
Câu 1 (2đ) Cho cấp số nhân u biết 5 3 . n     6 u  8 u  96
a) Hãy tìm số hạng đầu tiên 1
u và công bội q của cấp số nhân. b) Tính A  5 u  6 u  7 u  8 u  9 u  ........  20 u Câu 2 (4đ)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh 2a .
SA  ABCD và SA  2a 2 .Gọi H, K lần lượt là hình chiếu vuông góc
của A trên cạnh SB, SD. Gọi I là giao điểm của SC với mặt phẳngAHK và E là trung điểm OD .
a) Chứng minh: SD  ABK và SC  AHK b) Chứng minh: AC  EI .
c) Tính góc giữa đường thẳng SC và mặt phẳng (SAB).
Câu 3 (4đ) Tính các giới hạn: 2 3 n  2n a) lim 2 n  2n n n 7  2.3 b) lim n 1  n 7  4.5  2 3 3 2 c) lim  9n n 2 27n n         ------ HẾT ------
ĐÁP ÁN KIỂM TRA GIỮA HỌC KỲ 2. NK 2022-2023 - MÔN TOÁN-KHỐI 11 Câu Nội dung Điểm 1 u   u  12  2,0đ 5 3
Cho cấp số nhân un  biết .   6 u  8 u  96
a) Hãy tìm số hạng đầu tiên 1
u và công bội q của cấp số nhân. 1,5đ 2 0,25+ 0,25  u  .q      2 4 2 1 q  1  12 1 u .q u .q 12  I 1 1     5 7 5 u  .q  u .q  96 u  .q   2 1 1 1  q  96 2 1    
Lấy 2 chia 1 ta được 3 q  8  q  2 . 0,5
Thế vào 1 ta được 1 u  1 . 0,5 b) Tính A  5 u  6 u  7 u  8 u  9 u  ........  20 u 0,5đ 1  q 1  220 20 20 1  2 S20  1 u .   1  q 1   2   3 0,25 1  q 1   2  4 4 4 1  2 S4  1 u .   1  q 1  2 3 4 20 2  2 0,25 A  S  S   3  49520 20 4 3 2
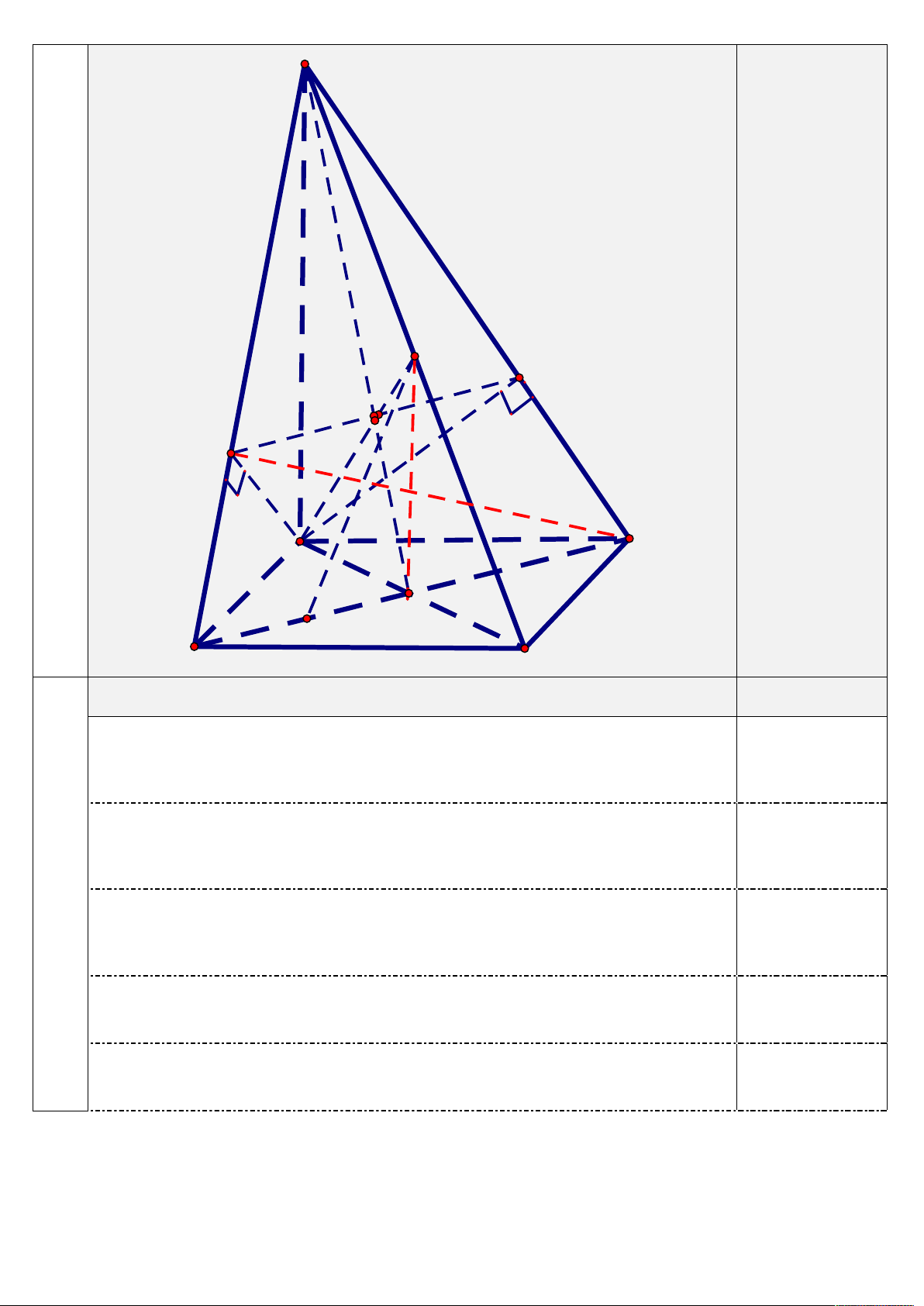
Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh
2a . SA  ABCD và SA  2a 2 .Gọi H, K lần lượt là hình chiếu
vuông góc của A trên cạnh SB,SD. Gọi I là giao điểm của SC
với mặt phẳng AHK  và E là trung điểm OD . 4,0đ
a) Chứng minh: SD  ABK  và SC  AHK 
b) Chứng minh: AC  EI .
c) Tính góc giữa đường thẳng SC và mặt phẳng (SAB). 2 S I H K A B E O D C
a) Chứng minh: SD  ABK  và SC  AHK  2đ S  A  AB 
 AB  SAD  AB  SD 0,25+0,25 AD  AB  S  D  AB 0.25   SD  ABK  SD  AK  0.25 B  C  AB 
 BC  SAB  BC  AH 0.25 BC  SA  B  C  AH 
 AH  SBC  AH  SC 1 0.25 SB  AH  CD  AD 
 CD  SAD  CD  AK 0.25 D C  SA  3 CD  AK 
 AK  SCD  AK  SC 2 SD  AK  0.25 AH  SC   SC  AHK . AK  SC 
b) Chứng minh: AC  EI . 1đ Xác định I:
Trong SBD : SO  HK  M
Trong SAC : AM  SC  I I    AM, AM   AHK  0,25   I  SC  AHK  I   SC  AI   AHK   AI  SC . SC   AHK 
AC  AB 2  2a 2 (đường chéo hình vuông)
 Trong tam giác cân tại A : có AI là đường cao suy ra AI là đường trung tuyến, 0,25  I là trung điểm SC
 IO là đường trung bình  IO / /SA . IO  / /SA  
 IO  ABCD  IO  AC 0,25 SA   ABCD  AC  IO . 
 AC  EOI  AC  EI. 0,25 AC  EO  c)
Tính góc giữa đường thẳng SC và mặt phẳng (SAB). 1đ B   CB   SAB 
 SB là hình chiếu của SC trên SAB . 0,25 CB   SAB            SC; SAB SC;SB  BSC 0,25
Tam giác SAB vuông tại S nên 2 2 SB  SA  AB  2 3a 0,25 4  BC 2a 1
Tam giác SBC vuông tại B  tanBSC    . SB 2 3a 3  0  BSC  30 . 0,25 Vậy          0 SC; SAB SC;SB  BSC  30 . 3
Tính các giới hạn: 4,0đ 2 3 n  2n a) lim 1,5đ 2 n  2n 3  1   1 n 2      2  n   n   lim  lim n.   0,25+0,25 2  2  2 n 1   1    n   n    li  m n     1   Vì  2  n   0,25+0,25 lim  2   0  2     1     n 
Nếu HS chưa ghi phần này mà suy ra kết quả  thì trừ 1,0đ  1   2   Nên : n lim n.  .   2  0,5  1    n  n n 7  2.3 b) lim 1,5đ n 1  n 7  4.5 n   n  3  7 1   2.    0,25+0,25 n n   7 7 2.3    lim lim     n n n 7.7  4.5   n  5  7 7  4.   7        5 n  3  1  2.7  0,5 lim  n  5  7  4. 7    1  . 0,5 7
Nếu HS chưa khử dạng vô định mà suy ra kết quả thì trừ 1,0đ  2 3 3 2 c) lim  9n n 2 27n n       1đ    2 3 3 2 lim  9n n 2 3n 3n 27n n          0,25      2 n 2 n     lim    2  2 9n  n  2  3n 2 3 3 2  3 3 2  9n  3n. 27n  n    27n  n          2     n 1    2    n n lim      2 1 2             2 1 1 n 9 3  3 3   2  n 9  3. 27    27  n n       n  n               2  1   1  0,5 n  lim    2  1 2 1  1 9    3   3 3  2 9  3. 27    27 n  n    n  n       1  1 7     . 3  3 9  9  9 54 0,25
Nếu HS chưa khử dạng vô định mà suy ra kết quả thì trừ 0,75đ
Nếu học sinh làm bài không theo cách nêu trong đáp án nhưng đúng thì cho đủ số điểm từng phần như
trong đáp án.Cho điểm từng câu ,ý ,sau đó cộng điểm toàn bài và không làm tròn ( Ví dụ:7,25__ghi bảy hai
lăm).Giám khảo ghi điểm toàn bài bằng số và bằng chữ ; giám khảo nhớ ký và ghi tên vào từng tờ bài làm của học sinh 6
Document Outline

  • 04-toan-11_183202312
  • 04-toan-da-11_183202312