Đề giữa kỳ 2 Toán 11 năm 2022 – 2023 trường THPT Nguyễn Thị Minh Khai – TP HCM

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề kiểm tra giữa học kỳ 2 môn Toán 11 năm học 2022 – 2023 trường THPT Nguyễn Thị Minh Khai, thành phố Hồ Chí Minh; đề thi gồm 01 trang với 02 bài toán tự luận, thời gian học sinh làm bài thi là 45 phút (không kể thời gian phát đề), đề thi có lời giải chi tiết và thang chấm điểm. Mời bạn đọc đón xem!

36 18 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề giữa HK2 Toán 11

Môn: Toán 11

Thông tin:

3 trang 7 tháng trước

Tác giả:

Profile Nguyễn Trang
Họ tên học sinh: ………………………………………………………….. SBD: …………………………………
Bài 1: (5,0 điểm) Tính các giới hạn
a)
3
2
.
2
8
lim
2
x
x
A
x x
(1,0 điểm)
b)
.
3
1 2 2
lim
12 4
x
x x
B
x
(2,0 điểm)
c)
2 2 3
3
.
lim 8 1
x
C x x x x

(2,0 điểm)
Bài 2: (5,0 điểm) Cho hình chóp
S.ABC
có đáy là
ABC
vuông tại
A
,
,
SA ABC
= 3,
SA a
= = 2
AB AC a
.
a) Chứng minh:
.
AB SAC
(2,0 điểm)
b) Gọi
I
là trung điểm
BC
,
H
là hình chiếu vuông góc của
A
lên
SI
. Chứng minh:
.
AH BC
(2,0 điểm)
c) Gọi
J
là điểm thuộc cạnh
AB
thỏa
= 3
JA JB
. Tính góc giữa đường thẳng
IJ
và mặt phẳng
HAC
.
(1,0 điểm)
HẾT
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
Năm học: 2022– 2023
Môn TOÁN – Khối: 11
Thời gian: 45 phút
(Không kể thời gian phát đề)
Đề 2
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 2 (Toán 11)
Bài 1: Tính giới hạn 5đ
Câu 1a:
3
2
2
8
lim
2
x
x
A
x x
1đ
2 2
2 2
2 4 2 4 2
lim lim 4 .
2 1 1
x x
x x x x x
A
x x x
0.25x4
Câu 1b:
.
3
1 2 2
lim
12 4
x
x x
B
x
2đ
3
1 2 2
lim
12 4 1 2 2
x
x x
B
x x x
0.5x2
.
1
3
1
lim
16
4 1 2 2
x
x x
0.5x2
Câu 1c:
2 2 3
3
lim 8 1
x
C x
x x x

2đ
2 2 3
3
lim 8 1
x
C x
x x
x x x

0.25
2 3
2 2 3 2 3
3
2
2
2 2 3 2 33 3
8 1
lim
8
. 1 1

x
x x x x x x
x x x
x x x x x x
0.25x2
2
2
3 3
3 3
1
1
8
lim
8
1 1 1 1
1 1
1 1 1
x
x
x
x x x x

0.25x2
1 13
4 .
3 3
0.25x3
Bài 2:
S.ABC
có
ABC
vuông tại
A
,
,
SA ABC
= 3,
SA a
= = 2
AB AC a
.
5đ
Câu 2a:
.
AB SAC
2đ
(do ( ))
.
SA AB SA ABC
AB SAC
AC AB
0.5x4
Câu 2b:
I
trung điểm
BC
,
H
là hình chiếu của
A
lên
SI
. Chứng minh:
.
AH BC
2đ
Δ
ABC
vuông cân tại A
AI BC
.
0.25x2
SA BC
(do
SA ABC
) nên
.
BC SIA BC AH
0.5x3
Câu 2c:
J
thuộc cạnh
AB
thỏa
= 3
JA JB
,( ) ?
IJ HAC
1đ
Trong (ABC), gọi
L IJ AC
. Trong (SBC), dựng
IK HC
tại K.
( ) .
AH BC
AH SBC AH IK
AH SI
Mà
IK HC
nên
( )
IK HAC
tại K.
LK là hcvg của LI lên (HAC).
,( ) ,
IJ HAC IL KL ILK
(do
( )
IK HAC
nên
IK KL
).
0.25
0.25
2 2
2 2 2
2 2
1 1 1
, ( ) .
2
5
AI a a a
IH BC SAI BC SI IK
SI IK IH IC
SA AI
C’ trung điểm AB IJ//CC’.
2 2
1
3 1 5
' 2
' ' ' ' .
' ' 2
2 2 2
AJ 3
IJ BI
CC BC
LI CC CC CC AC AC a
CC AC
LJ
2 2
:sin ,( ) arcsin .
5 5
IK
IKL ILK IJ HAC
IL
0.5
Hình vẽ
HẾT
L
J
A
B
C
S
I
H
C'
K
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

Đề 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO TP. HCM
ĐỀ KIỂM TRA GIỮA HỌC KỲ II
TRƯỜNG THPT NGUYỄN THỊ MINH KHAI Năm học: 2022– 2023 Môn TOÁN – Khối: 11 Thời gian: 45 phút
(Không kể thời gian phát đề)
Họ tên học sinh: ………………………………………………………….. SBD: …………………………………
Bài 1: (5,0 điểm) Tính các giới hạn 3 x  8 a) A  lim 2 . (1,0 điểm) x 2  x  x  2 1 x  2x  2 b) B  lim . (2,0 điểm) x 3  12  4x  3  c) 2 2 3
C  lim  x  8x  1 x  x . (2,0 điểm) x 
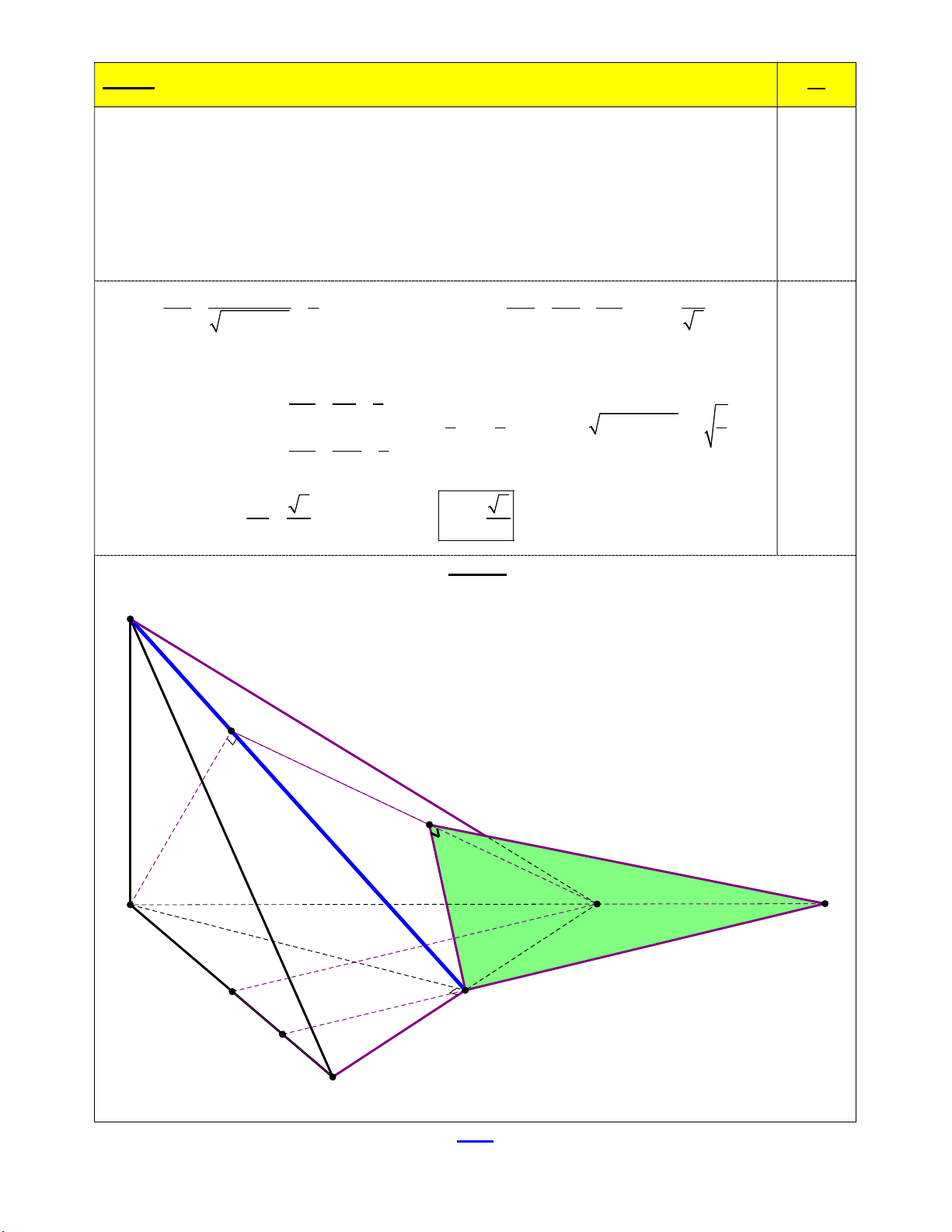
Bài 2: (5,0 điểm) Cho hình chóp S.ABC có đáy là ABC vuông tại A , SA   ABC , SA = a 3, AB = AC = a 2 .
a) Chứng minh: AB  SAC . (2,0 điểm)
b) Gọi I là trung điểm BC , H là hình chiếu vuông góc của A lên SI . Chứng minh: AH  BC. (2,0 điểm)
c) Gọi J là điểm thuộc cạnh AB thỏa JA = 3JB . Tính góc giữa đường thẳng IJ và mặt phẳng HAC  . (1,0 điểm) HẾT
ĐÁP ÁN & BIỂU ĐIỂM ĐỀ 2 (Toán 11) Bài 1: Tính giới hạn 5đ 3 x  8 Câu 1a: A  lim 1đ 2 x 2  x  x  2  x  2 2 4  2x  x  2 4  2x  x A  lim  lim  4 . 0.25x4 x 2   x  2x   x2 1 x 1 1 x  2x  2 Câu 1b: B  lim . 2đ x 3  12  4x 1 x 2x  2 B  lim x 3   0.5x2
12  4x 1 x  2x  2 1 1  lim  x 3
 4 1 x  2x  2 . 16 0.5x2 Câu 1c: C  lim     2đ   2 3 2 3 x 8x 1 x x x  C  lim       0.25   2 3 2 3 x 8x x x 1 x x x    x  8x 2  x x   3 1 x  x 3 2 2 3 2 3  lim    0.25x2 x  3 x  8x   x x  .
x 1 x  x   3 1 x  x 2 2 2 2 3 2 3    1   1  2 8   lim x   2  x 8 0.25x2  1 1  1 1 1 1     3 3 1    1      1 3 3 x  x x x x     1 13  4   . 0.25x3 3 3
Bài 2: S.ABC có ABC vuông tại A , SA   ABC , SA = a 3, AB = AC = a 2 . 5đ Câu 2a: AB  SAC . 2đ SA  AB (do SA  (ABC))   AB  SAC  . 0.5x4 AC  AB
Câu 2b: I trung điểm BC , H là hình chiếu của A lên SI . Chứng minh: AH  BC. 2đ
ΔABC vuông cân tại A  AI  BC . 0.25x2
SA  BC (do SA   ABC ) nên BC  SIA  BC  AH . 0.5x3
Câu 2c: J thuộc cạnh AB thỏa JA = 3JB  IJ HAC   ,( )  ? 1đ
 Trong (ABC), gọi L  IJ  AC . Trong (SBC), dựng IK  HC tại K. AH  BC  
 AH  (SBC) AH  IK . Mà IK  HC nên IK (HAC) tại K. 0.25 AH  SI
 LK là hcvg của LI lên (HAC).  IJ,(HAC)   IL,KL   
ILK (do IK (HAC) nên IK  KL ). 0.25 2 2 AI a a 1 1 1 a  IH  
 ,BC (SAI) BC  SI     IK  . SI SA  2 2 2 2 2 AI 2 IK IH IC 5
 C’ trung điểm AB  IJ//CC’.  IJ  BI  1 CC' BC 2 3 1 5 0.5    LI  CC  ' CC '  CC '  2 AC '  2 AC  a . CC '  AC '  2 2 2 2  LJ AJ 3  IK 2 2 I  KL : sin  ILK    IJ,(HAC)   arcsin . IL 5 5 Hình vẽ S H K C A L C' I J B HẾT