Đề giữa kỳ môn Vật lý đại cương 2 | Học viện Công Nghệ Bưu Chính Viễn Thông

ĐỀ GK MÔN VẬT LÝ ĐẠI CƯƠNG 2 - ĐỀ SỐ ...
MÃ HP: PH1120 - HỌC KỲ: 20211
Thời gian: ... phút, không kể thời gian phát đề
Chú ý: Sinh viên không được sử dụng tài liệu
Câu 1. Luỡng cực điện là một hệ gồm hai điện tích điểm +qvà −q, đặt cách nhau một khoảng d.
Chọn trục zlà trục đi qua hai điện tích điểm và đặt gốc tọa độ Oở điểm giữa của chúng. Định nghĩa
vecto moment luỡng cực điện: #» p=p #»
d(vecto dhướng từ −qđến +q) r3√1 + 2 cos2θ.B.kp r3√1 + 3 cos2θ.C.kp r3√1 + cos2θ.D.kp r3√1 + 4 cos2θ. A.kp Lời giải. Chọn đáp án B
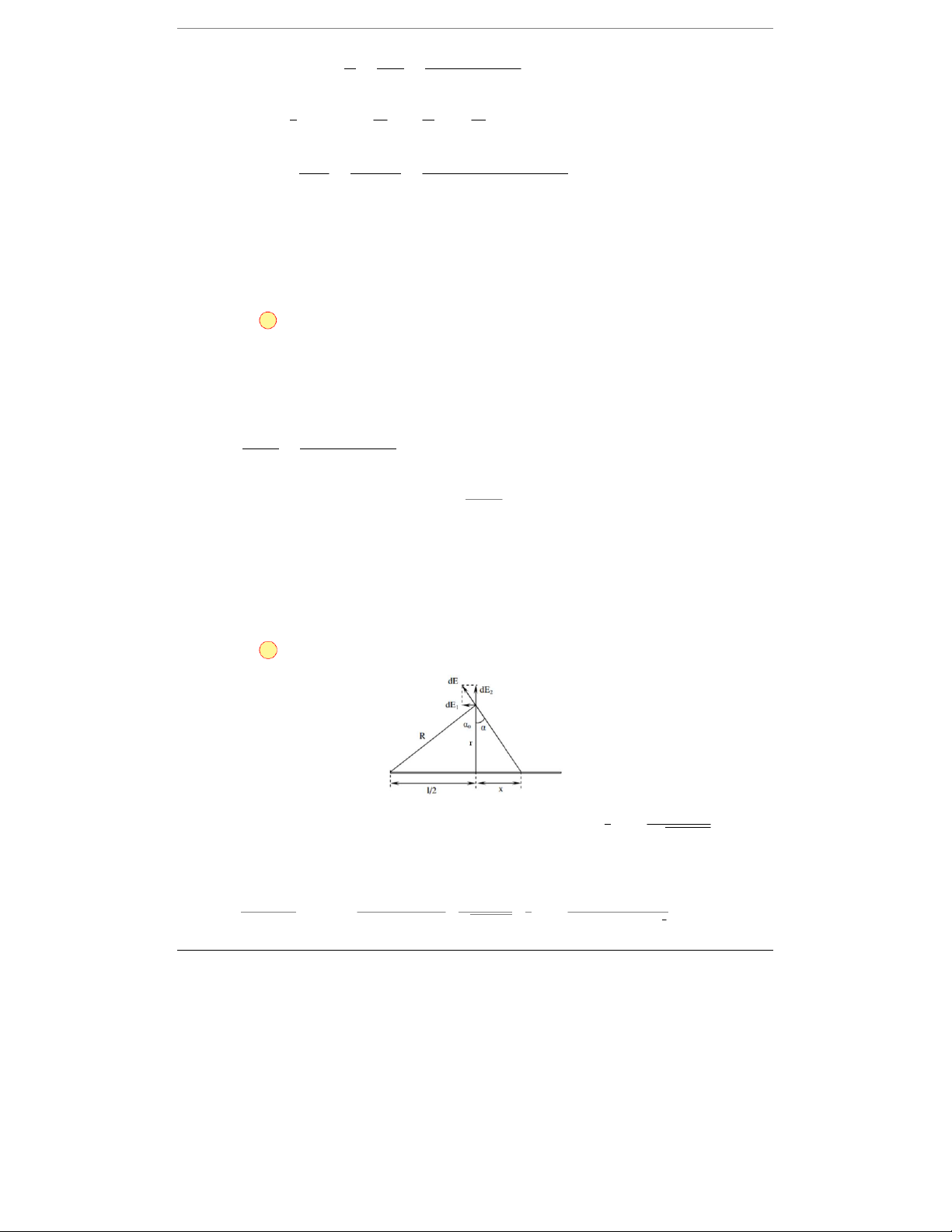
r+−1 r− =kq r−−r+r+r−
Điện thế ở điểm M(r, θ): V=kq 1
Khi r≫> d, ta có gần đúng: r−−r+≈dcos θ;r r + 2 r =−≈ kpr2 cos θ Suy ra: V=kq dcos θ r2 VIỆN VẬT LÝ KỸ THUẬT
Trở lại tọa độ Descartes: r2=x2+z2; cos θ=z r Suy ra: V=kp z r3=kp z (x2+z2)3 2 E Vậy: x=−∂V ∂x = 3kp xzr5 Ez=−∂V ∂z =kp 3z2−r2r5
Suy ra độ lớn của điện trường: z=kpr x+E2 4√r2+ 3z2 E=pE2 =kpr3√1 + 3 cos2θ
Câu 2. Một thanh dẫn điện được đặt vuông góc với một dòng điện thẳng, dài vô hạn, cường độ I.
Khoảng cách từ hai đầu thanh đến dòng điện lần lượt là a, b. Cường độ dòng điện I0đi qua thanh,
lực từ tác động lên thanh là: A.F=µµ I0I 2πln b 0 a.B.0. C.F=µµ I0I I0I 0 2πb (b−a).D.F=µµ0 2πa (b−a). Lời giải. Chọn đáp án A #» #» #»
Lực từ lên đoạn dl :d F=I0d l× B
Lực toàn phần lên thanh: #» #» F F=Rd
Mọi dF đều hướng xuống, do đó lực toàn phần cũng vậy. Nó có độ lớn: I F=ZdF =I0ZBdl với (B=µ0 2πx dl =dx Suy ra: F=µ b 0I0I dx x=µ0I0I =µ0I0I 2πln b 2πR 2πln x b a a a
Trong một từ môi đẳng hướng, từ trường tăng lên µlần, do đó: F=µ0µI0I 2πln b a
Câu 3. Một tụ điện phẳng có khoảng cách giữa hai bản tụ s= 1(mm)và diện tích mỗi bản tụ
A= 100 cm2. Một khối kim loại có bề dày d= 0,2mm và diện tích Ađược đặt ở trong tụ điện và
song song với các bản tụ như hình vẽ. Khoảng không giữa các bản tụ và khối kim loại được lấp đầy Trang 2 VIỆN VẬT LÝ KỸ THUẬT
với chất điện môi có ε= 4,5. Tìm điện dung của hệ. Nhắc lại: điện dung tương đương của môt hệ các tụ mắc nối tiếp 1 1 C= Σk . Ck
A.0,44(nF ).B.0,5(nF ).C.2,0(nF ).D.A, B, C sai. Lời giải. Chọn đáp án D
Coi tụ điện như ba tụ điện mắc nối tiếp với các điện dung: C1=εε0A s1 C2=ε0A
với s2và s3là khoảng cách giữa các mặt của tấm điện môi và các bản tụ điện. s2 C3=ε0A s3
Điện dung toàn phần của tụ điện xác định theo công thức: 1 C=1 +1 +1 =1 C ε 1 C2 C3 0A s1ε+s2+s3 =1 ε0A s1ε+s−s1 ⇒C=εε0A
εs + (1 −ε)s=4,5.8,86.10−12.100.10−4
4,5.1.10−3+ (1 −4,5) .10−3≈4.10−10 (F) = 0,4 (nF )
Câu 4. Một đĩa tròn bán kính a= 8(mm)tích điện đều với điện tích q= 0,2.10−9(C)đặt trong
chân không. Mlà một điểm nằm trên trục đối xứng của đĩa và cách tâm đĩa một đọan b= 8(cm).
Cường độ điện trường Etại Mgần nhất với giá trị nào sau đây (chú ý: b >> a, tức là Mở rất xa đĩa):
A.1,4.102(V /m).B.2,8.102(V/m).C.5,6.102(V /m).D.1,1.103(V /m). Lời giải. Chọn đáp án B
Chia đĩa thành từng dải vành khăn có bề rộng dr. Xét dải vành khăn có bán kính r(r < a). Vành
khăn có điện tích tổng cộng: dQ =σ·2πr ·dr #»
Chia vành khăn thành các điện tích điểm dq. Chúng gây ra điện trường d Etại M. Theo định lý #»
chồng chất điện trường, điện trường tại Mbằng tổng tất cả các giá trị d Eđó. Trang 3 VIỆN VẬT LÝ KỸ THUẬT #» #» #»
Điện trường d Ecó thể phân thành hai thành phần d
E1và d E2. Do tính đối xứng nên tổng các #»
thành phần d E1bằng không. Vậy: #» dE Evà OM
r=ZdE2=ZdE cos α, với αlà góc giữa d 4πεε0(r2+b2)·b √r2+b2=b
4πεε0(r2+b2)3/2·dQ =bσ ·r·dr ⇒dEr=Zdq 2εε0(r2+b2)3/2
Điện trường do cả đĩa gây ra tại Mlà: (r2 r+·d b2r)3/2=bσ =σ E=ZdE 2εε r=bσ 2εε0Za 2εε0 −1√r2+b2 a 0 1−1 p1 + a2/b2! 0 0
Vì b >> a, áp dụng công thức gần đúng: 1 p1 + a2/b2≈1−a2 2b2 Vậy: E=σ 4εε 4πεε0b2=q 2εε 0b2=σ·(πa2) 4πεε 0 1− 1−a2 2b2 =σ·a2 0b2= 2,8.102(V /m)
Câu 5. Một lưỡng cực điện gồm hai điện tích −qtại tọa độ (x;y) = (0; −d)và +qtại (0; d), với q
và ddương. Gọi E1và E2tương ứng là cường độ điện trường của lưỡng cực tại điểm Atrên trục Oy
và Btrên trục Ox, với OA =OB =a >> d. So sánh E1và E2thì:
A.E1> E2.B.E1=E2.C.E1< E2.D.E1≈E2. Lời giải. Chọn đáp án B
Câu 6. Có hai điện tích q1= 10−7(C)và q2= 9.10−7(C)dặt cách nhau 8(cm). Tại khoảng cách x
tính từ q1trên đường nối giữa q1và q2có điện tích q3và lực điện tác dụng lên nó bằng không. Tìm
x. (Chú ý: q2= 32q1có thể làm đơn giản phương trình ).
A.2(cm).B.3(cm).C.4(cm).D.A, B, C sai. Lời giải. Chọn đáp án A Vì q2= 32q1
Trên đường nối hai điện tích, điện trường do chúng gây ra luôn cùng phương ngược chiều nên ta có: E=E =q1 1−E2=q1 1−9q1 1−9 4πεε0r2 4πεε0r2 4πεε0 1r r 2 2 22
Giả sử tại điểm Mcách điện tích q1một khoảng r, điện trường triệt tiêu. Điểm Mcách điện tích
q2= 9q1một khoảng là (l−r)với 1 là khoảng cách giữa q1và 9q1. E=q1 r 4πεε 2−9 0 1 (l−r)2 = 0
⇒1 r2−9 (l−r)2= 0 ⇒(l−r)2= 9r2 ⇒l−r= 3r⇒r=l 4=8 4= 2(cm)
Vậy, điện trường giữa hai điện tích q1và q2= 9q1triệt tiêu tại điểm Mnằm trên đường nối hai
điện tích tại vị trí cách điện tích qlà 2(cm). Trang 4 VIỆN VẬT LÝ KỸ THUẬT
Câu 7. Hai tụ điện C1= 3µF và C2được tích điện sao cho U1= 10(V)và U2= 4(V). Nối song
song hai tụ điện sao cho bản tụ (+/−)của C1tương ứng được nối với bản tụ (−/+) của C2. Hiệu
điện thế của hệ hai tụ sau khi nối là U= 8(V). Điện dung C2bằng:
A.0,5µF .B.1µF .C.1,5µF .D.2µF . Lời giải. Chọn đáp án C
Hai tụ điện mắc song song có điện dung tương đương C=C1+C2
Có điện tích tương đương: q=q1+q2= (C1+C2)U
Và hiệu điện thế trên bộ tụ: U=q C⇒C2=C1(U−U1) U2−U= 1,5µF
Câu 8. Hai quả cầu kim loại bán kính R1= 5(cm)và R2= 8(cm), được nối với nhau bởi một sợi
dây dẫn mảnh có điện dung không đáng kể, và được tích một điện lượng q= 13.10−8(C). Tìm mật
độ điện mặt trên quả cầu thứ nhất. Nhắc lại: điện dung Ci= 4πε0Ri; điện tích qi=Ci·V.
A.1,6.10−6(C/m2).B.1,0.10−6(C/m2).C.1,6.10−10(C/m2).D.1,0.10−10(C/m2). Lời giải. Chọn đáp án A
Vì hai quả cầu được nối với nhâu bằng một sợi dây dẫn điện nên chúng có cùng điện thế V: Ta có: q1=C1.V = 4πεε0.R1V q2=C2.V = 4πεε0.R2V
Mặt khác: q=q1+q2= 4πεε0(R1+R2)V ⇒V=q 4πεε0(R1+R2)
⇒điện tích của quả cầu 1là q1=C1.V = 4πεε0.R1.q
4πεε0(R1+R2)=q.R1 (R1+R2)=13.10−8.0,05 0,08 + 0,05 = 5.10−8(C)
Mật độ điện mặt trên quả cầu thứ nhất: σ1=q1 =5.10−8 4πR 4π.(0,05) , .10−6(C/m2) 2 2≃1 6 1
Câu 9. Trong chân không, tại hai điểm với tọa độ (−6(cm); 0) và (6 cm; 0) tương ứng có hai điện tích Q ; công A=
1= 4.10−9(C)và Q2=−2.10−9(C). Nhắc lại công thức điện thế V=PikQi ri
q(VC−VD). Tính công của lực điện trong dịch chuyển điện tích q= 10−9Ctừ điểm C = (0; 0) điểm D = (0; 6(cm)).
A.8,6.10−8(J).B.8,6.10−10(J).C.8,8.10−5(J).D.8,8.10−10(J). Lời giải. Chọn đáp án A
Nhận xét: Đây là bài toán công dịch chuyển điện tích →phải đi xác định điện thế tại Cvà D→
áp dụng công thức: ACD =q(VC−VD).
Điện thế tại điểm Clà: VC=Q14πεε0a+Q2 4πεε0a Trang 5 VIỆN VẬT LÝ KỸ THUẬT
Điện thế tại điểm Dlà:
VD=Q14πεε0√2a+Q2 4πεε0√2a
Hiệu điện thế giữa hai điểm CD là: UCD =VC−VD=1 4πεε0a(Q1+Q2) 1−1 √2 ≈87,69(V)
Công dịch chuyển điện tích qtừ Cđến Dlà: ACD =q·UCD = 8,6·10−8(J)
Câu 10. Khoảng cách giữa hai proton (điện tích e=−1,6.10−19(C)) trong phân tử H2lấy bằng
0,074(nm). Độ lớn của lực tĩnh điện giữa chúng bằng bao nhiêu? Chú ý: k=1 4πε0≈9.109(SI)
A.2,4.10−10(N).B.2,4.10−5(N).C.4,2.10−10(N).D.4,2.10−8(N). Lời giải. Chọn đáp án D
Độ lớn lực tĩnh điện giữa hai proton: F=|qe|.| 4 q π e|
εε0r2=k|qe|.|qe|εr2=9.109. 1,6.10−19 2 0,074.10−9 2= 4,2.10−8(N)
Câu 11. Trong một điện truờng với #» E= (9/r #» #» 3) (x. #» i+y. #»j+z. k); #»i, #»
j , klà các véctơ đơn vị trên
các trục tọa độ và r2=x2+y2+z2; các đại lượng cho trong hệ SI; tìm hiệu điện thế giữa hai điểm #» # »
với tọa độ A= (1; 0; 0) và B= (0; 2; 0).Chú ý #»
r=x. #» ı+y. #» +z. k;nhắc lại: #»E=− gradV.
A.3,0(V).B.3,5(V).C.4,0(V).D.4,5(V). Lời giải. Chọn đáp án D
Nếu chiếu vectơ cường độ điện trường #»Elên ba trục Ox, Oy, Oz của hệ trục tọa độ Descartes thì
ta có: Ex=−∂V ∂x ;Ex=−∂V ∂y ;Ez=−∂V ∂z trong đó, ∂V ∂x ,∂V ∂y ,∂V
∂z là đạo hàm riêng phần của hàm điện thế V(x, y, z)đối với các biến x, y, z.
do đó, vectơ cường độ điện trường trong hệ trục tọa độ Descartes có dạng: #» #» i+∂V j+∂V #» #» E=E i+y. #» #» x·#» i+Ey.#» j+E j+z r z· k=− ∂V ∂x ·#» ∂y ·#» ∂z · k =9 r .k =9 3 x. #» r3 Hay #» # » E=− gradV Trong đó, vecto # g r a d V »= ∂V ∂x .#»i+∂V∂y .#» j+∂V #»
∂z . kgọi là gradient của điện thế V Ta có: Ex=−dV dx 1 1 0−9x(x2+y2+z2)3/2dx =9 px2+y2+z2 0= 9 (V)
⇒dV =−Exdx ⇒Vx=R−Exdx = R
Tương tự: Vy= 4,5(V); Vz= 0(V)
Vậy, vectơ cường độ điện trường tại một điểm bất kì trong điện trường bằng và ngược dấu với
gradient của điện thế tại điểm đó. Trang 6 VIỆN VẬT LÝ KỸ THUẬT
Đối với điện trường đều, nhân hai vế của E=−dV
dn với dn, rồi lấy tích phân dọc theo đường sức điện truòng, ta được: V2−V1=Z(2) dV =−EZ(2) dn = 9 −4,5 = 4,5(V) (1) (1)
Câu 12. Cho một mặt cầu bán kính R= 0,2(m)có tâm tại gốc tọa độ, với hai điện tích q1=
3.10−6(C)và q2=−3.10−6(C)tương ứng tại (x, y) = (R/2,0) và (−R/2,0). Tìm thông lượng điện gửi qua mặt cầu. A.3,4.105(Nm2/C).B.0(N m2/C).
C.6,8.105(Nm2/C).D.−3,4.105(N m2/C). Lời giải. Chọn đáp án A
Cường độ điện trường tại một điểm trên bề mặt cầu luôn vuông góc với mặt cầu tại điểm đó và có độ lớn không đổi #» E=1 q #» Ro 4πε0 R2 Do đó: #» n) = 1 #» #» Φ = ZEdS ·cos( E, #» 4πε0Iq R n dS R o 2 =1 q q 4πε R R2·4πR2 0 2IdS =1 4πε0 =q = 3,4.105(Nm2/C) ε0
⇒Khi một điện tích điểm đặt ở tâm mặt cầu, điện thông qua mặt cầu này không phụ thuộc bán kính của nó.
Câu 13. Hai bản tụ của một tụ điện cầu có bán kính R1= 1(cm)và R2= 4(cm), được tích điện
Q= 10−9(C)và −Q. Cho biết điện dung của tụ cầu: C=4πε0ε.R1.R2
, với ε= 1. Tìm hiệu điện R2−R1
thế giữa hai điểm cách tâm các bản tụ một khoảng r1= 2(cm)và r2= 3(cm).Gợi ý: nếu tại r1và
r2có đặt hai mặt cầu kim loại, chúng sẽ mang điện −Qvà Qdo điện hưởng toàn phần, và đóng vai
trò như hai bán của một tụ điện cầu.
A.6,75(V).B.675(V).C.1,50(V).D.150(V). Lời giải. Chọn đáp án B
Từ công thức tính điện dung Cta có: C=4πε0εR1R2 =q R U 2−R1
Hiệu điện thế giữa hai điểm cách tâm các bản tụ một khoảng r1= 2(cm)và r2= 3(cm) U=q C=q(R2−R1) 4πεε0.R1.R2≈675 (V)
Câu 14. Một vòng dây bán kính R= 10−2(m), tích điện đều với Q= 6,28.10−11(C). Tâm của vòng
dây tại gốc tọa độ và trục của nó dọc theo Ox. Tại điểm x=Rtrên trục, thành phần điện trường Exbằng:
A.0(V /m).B.2.103(V/m).C.4.103(V /m).D.−2.103(V /m). Lời giải. Chọn đáp án B Trang 7 VIỆN VẬT LÝ KỸ THUẬT
Ta chia nhỏ vòng dây thành những phần tử rất nhỏ sao cho điện tích dq của mỗi phần từ ấy được
coi là điện tích điểm và nó gây ra tại Mvecto’ cường độ điện trường có độ lớn: dE =k.dq εr2 #» #»
Vectơ d Eđược phân tích thành hai thành phần: thành phần pháp tuyết d Ensong song với trục #»
vòng dây và thành phần tiếp tuyến d
Etvuông góc với trục vòng dây (như hình vẽ). #»
Lấy tích phân của d Etrên toàn bộ chu vi (C) của vòng dây ta được cường độ điện trường tại M: #» #» #» #» E=I d d dE (C) E=I(C) Et+I(C) n
Vì ứng với một phân tử dq, ta luôn tìm được phân tử dq′đối xứng với dq qua tâm Ocủa vòng
dây nên luôn tồn tại # » #»
dE′đối xứng với d Equa trục của vòng dây. #» #»
Từng cặp d Evà d E′này có thành phần tiếp tuyến triệt tiêu nhau. #» Et= 0 (C) Suy ra, Hd Do đó: #» #» k·d εrq E=I dEn=#» 2·x r=#» n0·k·x dq =#»n0·k·x (C) n0·I(C) dE ·cos α=#» n0·I(C) εr3·I(C) εr3·Q #» E=#» n0·k.Q.x ⇒ 3 ε(R2+x2) 2
Trong đó #»n0là pháp vectơ đơn vị của mặt phẳng vòng dây - quy ước #» n0luôn hướng ra xa tâm
O. Chứng tỏ vecto cường độ điện trường #» E:
+ Có phương: là trục vòng dây;
+ Có chiều: hướng xa tâm Onếu Q > 0, hướng gần Onếu Q < 0; + Có độ lớn: E=k.Q.x 3 (∗) ε(R2+x2) 2
+ Có điểm đặt: tại điểm khảo sát M. Từ (⋆)suy ra: + Khi x=Rthì E=k|Q| 2√2εR2= 2.103(V /m)
Câu 15. Một electron (điện tích −1,6.10−19(C); khối lượng 9,11.10−31(kg)) chuyển động ngang
với vận tốc v0= 6,0.105(m/s), đi vào vùng có điện trường đều hướng thẳng đứng lên trên với
E= 0,2(V /cm). Bỏ qua tác dụng của trọng trường. Sau một quãng đường x= 100(mm)theo
phương ngang, vị trí của electron theo phương thẳng đứng bị lệch đi so với ban đầu một khoảng y.
Tìm y.Gợi ý: tìm gia tốc aytheo phương y; thời gian chuyển động của electron .
A.4(cm).B.5(cm).C.4(mm).D.5(mm). Lời giải. Chọn đáp án A
Gia tốc aycủa electron theo phương Oy: Trang 8 VIỆN VẬT LÝ KỸ THUẬT
ay=F m=|e|Em= −1,6.190,−1.1910−3 .11=01,76.1012(m/s2) Mặt khác: y=1 2a =2y yt2⇒t2=2y ay⇒ x v0 2 ay ⇒y=x2.ay =x2.|e|.E
0.m = 100.10−3 2.1,6.10−19.10 2v2 2v 0 2
2. 6.105 2.9,1.10−31 ≈0,04 (m) = 4 (cm)
Câu 16. Một electron (điện tích −1,6.10−19(C); khối lượng 9,11.10−31(kg)) được gia tốc trong một
điện trường đều E= 10(V /m). Vận tốc ban đầu của nó bằng không. Bỏ qua tác dụng của trọng
trường. Tính vận tốc của electron sau quãng đường s= 10(cm).Gợi ý: định lý công - động năng.
A.5,0.106(m/s).B.6,0.106(m/s).C.0,5.106(m/s).D.0,6.106(m/s). Lời giải. Chọn đáp án B
Chọn trục Ox, có gốc Olà vị trí mà elctron bắt đầu bay vào điện trường, chiều dương trùng với chiều chuyển động.
Khi bay trong điện trường, electron chịu tác dụng của lực điện #» F
Định luật II Niu-tơn: #»F= ma (1) #» #» Vì q=e < 0⇒
F↑↓ E, mà #»v0cùng hướng với #»Enên #»Engược chiều dương
Chiếu (1) lên Ox ta có: −F=ma ⇔ −|q|E = ma
⇒a=−|q|E m=− |1,6.10−19|.10
9,1.10−31 =−1,76.1012 (m/s2)
Vậy electron chuyền động chậm dần với gia tốc a = −1,76.1012 (m/s2)
Vận tốc của electron sau quãng đường s= 10(cm):
v2−v2 0= 2 |a|s⇒v2−0 = 2 |a|.s ⇒v=p2|a|.s ≈6.106(m/s)
Câu 17. Một thanh mảnh mang điện tích q= 2.10−11(C)phân bố đều trên thanh đặt trong chân
không. Mlà một điểm nằm cách trung điểm của thanh một đoạn r= 1(cm)và cách hai đầu thanh
một đoạn R= 10(cm). Cuờng độ điện trường Etại Mgần nhất với giá trị nào sau đây? (Gợi ý:
R >> r và định lý O.G có thể giúp ích ):
A.9(V /m).B.90(V/m).C.18(V /m).D.180(V /m). Lời giải. Chọn đáp án D
Chia thanh thành những đoạn nhỏ dx. Chúng có điện tích là: dq =q ldx =q 2√R2−r2dx Xét điện trường # d»
E gây ra do đoạn dx gây ra tại điểm đang xét. Ta có thể tách # » dE thành hai thành phần # d E » xvà # d »
Ey. Điện trường tổng cộng #»Elà tổng tất cả các điện trường # »dE đó. Do tính đối
xứng nên tổng tất cả các thành phần # »dEybằng 0 . Ta có: dEx=dq4πεε0·r2·cos α=1 4πεε0(r2+x2)·r √r2+x2·q ldx =qr dx 4πεε0l(r2+x2)3 2 Trang 9 VIỆN VẬT LÝ KỸ THUẬT l/2 qr qr α0 r 4πεε0l(r2+x2)3/2dx = cos2α(r2+r2.tan2α)3/2dα ⇒E=RdEx= − R l/2 x=r.tanα 4πεε0l −R α0 ⇔E=q −α0cos αdα =q 4πεε =2q4πεε0lr =q 0lr (sin α)|α0 2πεε0lr ·l 2R=q 4πεε0lr Rα0 −α 4πεε0Rr 0 Thay số: E=2·10−11
4π·1.8,86 ·10−12 ·0,1·0,01 ≈180(V /m) Trang 10