Đề HK1 Toán 10 (chuyên) năm 2021 – 2022 trường chuyên Nguyễn Tất Thành – Kon Tum

Đề HK1 Toán 10 (chuyên) năm 2021 – 2022 trường chuyên Nguyễn Tất Thành – Kon Tum dành cho học sinh các lớp 10 theo học chương trình chuyên Toán, đề thi 100% tự luận mời bạn đọc đón xem

17 9 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề HK1 Toán 10

Môn: Toán 10

Thông tin:

6 trang 8 tháng trước

Tác giả:

Profile Thanh Tâm
SỞ GD&ĐT KON TUM
TRƯỜNG THPT CHUYÊN
NGUYỄN TẤT THÀNH
KIỂM TRA CUỐI HỌC KỲ I NĂM HỌC 2021-2022
Ngày kiểm tra: ......./12/2021
Môn: Toán Lớp: 10 Toán
Thời gian làm bài: 90 phút
(Không kể thời gian giao đề)
ĐỀ
Bài 1. (2.0 điểm)
a. Tìm tham số
m
để hệ bất phương trình
3 1 0
2 3 0
x m
x m
có nghiệm.
b. Xét tính chẵn lẻ của hàm số ( ) 2021 2021
f x x x
.
Bài 2. (2.0 điểm) Cho tam giác
ABC
có trọng tâm
G
. Gọi
và
E
lần lượt là các điểm thỏa mãn
đẳng thức
2 ;
AD AB AE xAC
.
a. Phân tích vectơ
AG
theo hai vectơ
AB
và
AC
.
b.Tìm
x
để ba điểm
, ,
D G E
thẳng hàng. Với giá trị tìm được của
x
, hãy tính tỉ số
DG
DE
.
Bài 3. (2.5 điểm) Trong hệ trục tọa độ
Oxy
cho
(1; 1), ( 2;2), (0;1)
A B C
.
a. Chứng minh rằng
, ,
A B C
là ba đỉnh của một tam giác cân.
b. Tìm tọa độ trực tâm
H
của tam giác
ABC
.
c. Tìm điểm
M
trên trục hoành sao cho
MA MB MC
đạt giá trị nhỏ nhất.
Bài 4. (2.5 điểm) Một hộp có
15
bi đỏ được đánh số từ
1
đến
15
;
20
bi vàng được đánh số từ
1
đến
20
và
25
bi xanh được đánh số từ
1
đến
25
. Lấy ngẫu nhiên từ hộp ra ba viên bi.
a. Hỏi có tất cả bao nhiêu cách lấy được ba viên bi cùng màu.
b. Hỏi có tất cả bao nhiêu cách lấy được ba bi khác màu và khác số (từng đôi một).
c. Hỏi có tất cả bao nhiêu cách lấy để tổng các số ghi trên ba viên bi được lấy ra là một số chia hết
cho 3.
Bài 5. (1.0 điểm) Xác định hàm số :f
biết rằng:
3 1 1
2 1
x x
f
x x
với
1, 2
x x
.
...............................................................................Hết...................................................................
SỞ GD&ĐT KON TUM
TRƯỜNG THPT CHUYÊN
NGUYỄN TẤT THÀNH
KIỂM TRA CUỐI HỌC KỲ I NĂM HỌC 2021-2022
Ngày kiểm tra: ......./12/2021
Môn: Toán Lớp: 10 Toán
Thời gian làm bài: 90 phút
(Không kể thời gian giao đề)
HƯỚNG DẪN CHẤM
Bài Đáp án Điểm
Bài 1.
(2.0 điểm)
a. Tìm tham số
m
để hệ bất phương trình
3 1 0
2 3 0
x m
x m
có
nghiệm.
1.0 điểm
Ta có
1
3 1 0
3
2 3 0
3
2
m
x
x m
x m
m
x
.
0.25
Hệ phương trình đã cho có nghiệm
1 3
; ;
3 2
m m
 
0.5
3 1 2
2 3 7
m m
m
0.25
b. Xét tính chẵn lẻ của hàm số ( ) 2021 2021
f x x x
.
1.0 điểm
Ta có
D
là tập đối xứng.
0.25
Với mọi x
ta có:
( ) 2021 2021 2021 2021 ( )
f x x x x x f x
.
0.5
Suy ra
( )
f x
là hàm chẵn. 0.25
Cho tam giác
ABC
có trọng tâm
G
. Gọi
D
và
E
lần lượt là
các điểm thỏa mãn đẳng thức
2 ;
AD AB AE xAC
.
a. Phân tích vectơ
AG
theo hai vectơ
AB
và
AC
.
1.0 điểm
Bài 2.
(2.0 điểm)
Gọi M là trung điểm của BC .
Ta có
2
3
AG AM

0.25
2 1
.
3 2
AB AC
 
0.5
1
3
AB AC
0.25
b. Tìm x để ba điểm , ,D G E thẳng hàng. Với giá trị tìm
được của x , hãy tính tỉ số
DG
DE
.
1.0 điểm
Ta có
5 1
3 3
DG AG AD AB AC

0.25
2DE AB xAC
0.25
Ba điểm , ,D G E thẳng hàng
5 1
2
3 3
2 5
x
x
0.25
Khi đó
5
6
DG DE
nên
5
6
DG
DE
.
0.25
Bài 3.
(2.5 điểm)
Trong hệ trục tọa độ Oxy cho (1; 1), ( 2;2), (0;1)A B C
.
a. Chứng minh rằng , ,A B C là đỉnh của một tam giác cân.
1.0 điểm
Ta có
3;3 , 1;2 , 2; 1AB AC BC
.
0.5
Vì
,
AB AC

không cùng phương nên
, ,
A B C
là 3 đỉnh của tam
giác.
0.25
Vì
5
AC BC
nên tam giác
ABC
cân tại C.
0.25
b. Tìm tọa độ trực tâm
H
của tam giác
ABC
.
0.75 điểm
Gọi
;
H x y
là trực tâm của tam giác
ABC
.
Ta có
1; 1
AH x y
;
2; 2
BH x y
.
0.25
H
là trực tâm của tam giác
ABC
. 0 2 3
2 6
. 0
AH BC x y
x y
BH AC
.
0.25
4
5
x
y
. Vậy
(4;5)
H .
0.25
c. Tìm điểm
M
trên trục hoành sao cho
MA MB MC
đạt
giá trị nhỏ nhất.
0.75 điểm
Gọi
G
là trọng tâm tam giác
ABC
. Ta có
1 2
;
3 3
G
.
0.25
Khi đó
3
MA MB MC MG
.
MA MB MC
nhỏ nhất khi
MG
nhỏ nhất
M
là hình
chiếu của
G
xuống trục
Ox
.
0.25
Do đó
1
;0
3
M
là điểm cần tìm.
0.25
Bài 4.
(2.5 điểm)
Một hộp có
15
bi đỏ được đánh số từ
1
đến
15
,
20
bi vàng
được đánh số từ
1
đến
20
và
25
bi xanh được đánh số từ
1
đến
25
. Lấy ngẫu nhiên từ hộp ra ba viên bi.
a. Hỏi có tất cả bao nhiêu cách lấy được ba viên bi cùng màu.
0.75 điểm
Số cách lấy được ba bi cùng màu là
3 3 3
15 20 25
3895
C C C .
0.75
b. Hỏi có tất cả bao nhiêu cách lấy được ba bi khác màu và
khác số (từng đôi một).
1.0 điểm
Chọn 1 bi đỏ: 15 cách.
0.25
Chọn 1 bi vàng (khác số với bi đỏ đã chọn): 19 cách.
0.25
Chọn 1 bi xanh (khác số với 2 bi đã chọn): 23 cách.
0.25
Vậy có tất cả 15.19.23=6555 cách lấy được 3 bi khác màu và
khác số.
0.25
c. Hỏi có tất cả bao nhiêu cách lấy để tổng các số trên ba viên
bi được lấy ra là một số chia hết cho 3.
0.75 điểm
Đặt
{1;2;...15}
A
;
1;2;...;20
B ;
C=
1;2;...;25
.
0.25
Kể cả số lần lặp lại, ta thấy rằng trong tập
, ,
A B C
có tất cả 19 số
chia hết cho 3, có 21 số chia 3 dư 1 và có 20 số chia 3 dư 2.
Ta nhận xét rằng
0(mod3)
1(mod3)
3
2(mod3)
0(mod3), 1(mod3), 2(mod3)
a b c
a b c
a b c
a b c
a b c
.
0.25
Suy ra số cách lấy để tổng các số trên ba viên bi được lấy ra là
một số chia hết cho 3 là
3 3 3
19 20 21
19.20.21 11419
C C C .
0.25
Bài 5.
(1.0 điểm)
Xác định hàm số :f
biết rằng:
3 1 1
2 1
x x
f
x x
với
1, 2
x x
(*).
1.0 điểm
Đặt
3 1 2 1
2 3
x t
t x
x t
.
Do đó tập giá trị của t khi
1, 2
x x
là
2
\ 3;
3
.
0.25
Thay vào (*) ta được:
2 1
1
4
3
( ) ;( 3)
2 1
3 2
1
3
t
t
t
f t t
t
t
t
.
0.25
Suy ra
4 2
, 3;
3 2 3
( ) , 3
2
, .
3
x
x
x
f x a x
b x
.
0.25
Thử lại: Hàm số f thỏa mãn đề bài.
Vậy:
4 2
, 3;
3 2 3
( ) , 3
2
, .
3
x
x
x
f x a x
b x
.
0.25
Lưu ý: Các cách giải khác nếu đúng đều được tính điểm.
| 1/6
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT KON TUM
KIỂM TRA CUỐI HỌC KỲ I NĂM HỌC 2021-2022 TRƯỜNG THPT CHUYÊN
Ngày kiểm tra: ......./12/2021 NGUYỄN TẤT THÀNH Môn: Toán Lớp: 10 Toán
Thời gian làm bài: 90 phút
(Không kể thời gian giao đề) ĐỀ Bài 1. (2.0 điểm) 3  x  m 1  0
a. Tìm tham số m để hệ bất phương trình  có nghiệm. 2x  3m  0
b. Xét tính chẵn lẻ của hàm số f (x)  2021 x  2021 x .
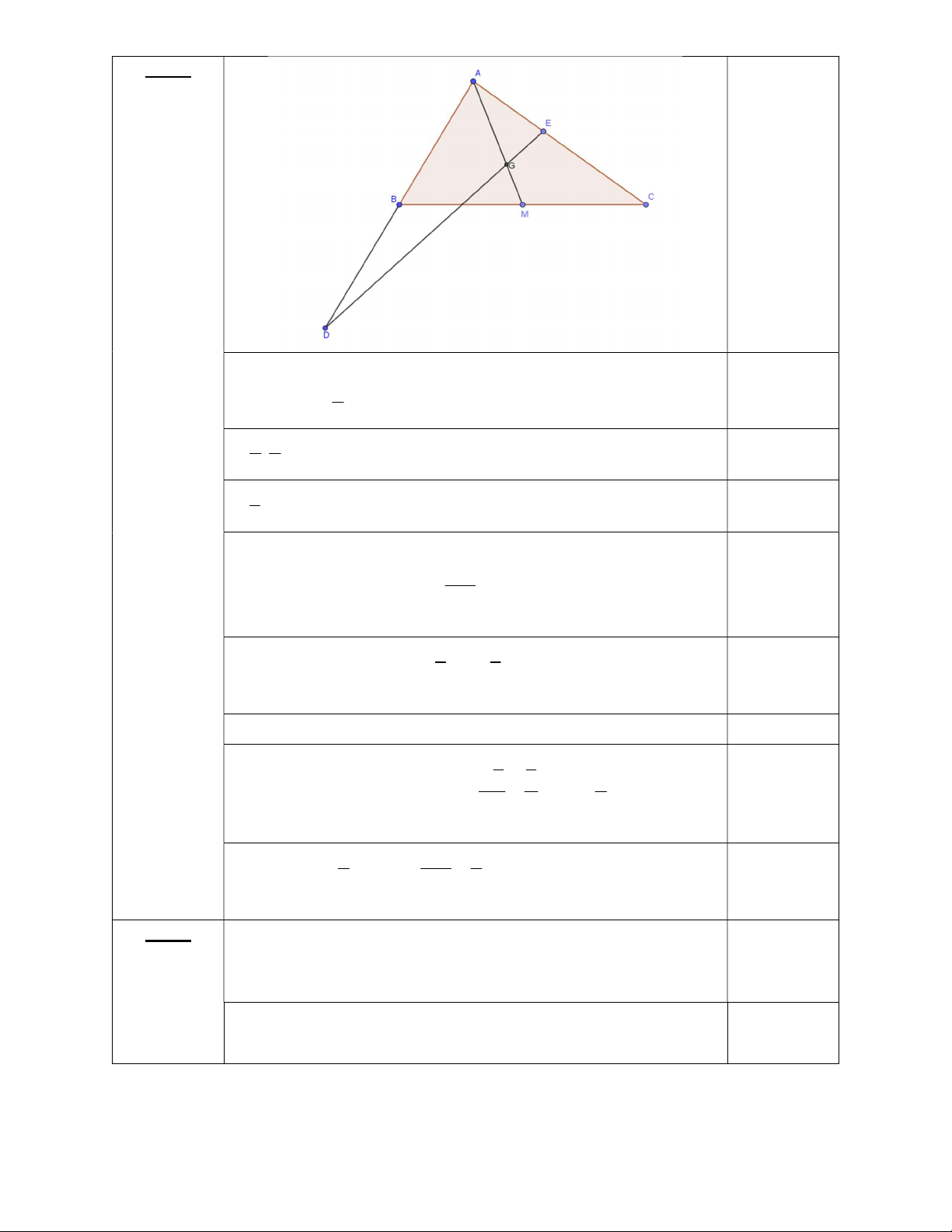
Bài 2. (2.0 điểm) Cho tam giác ABC có trọng tâm G . Gọi D và E lần lượt là các điểm thỏa mãn    
đẳng thức AD  2AB; AE  x AC .   
a. Phân tích vectơ AG theo hai vectơ AB và AC . DG
b.Tìm x để ba điểm D,G, E thẳng hàng. Với giá trị tìm được của x , hãy tính tỉ số . DE
Bài 3. (2.5 điểm) Trong hệ trục tọa độ Oxy cho ( A 1; 1  ), B( 2  ;2), C(0;1) . a. Chứng minh rằng ,
A B,C là ba đỉnh của một tam giác cân.
b. Tìm tọa độ trực tâm H của tam giác ABC .
  
c. Tìm điểm M trên trục hoành sao cho MA  MB  MC đạt giá trị nhỏ nhất.
Bài 4. (2.5 điểm) Một hộp có 15 bi đỏ được đánh số từ 1 đến 15 ; 20 bi vàng được đánh số từ 1
đến 20 và 25 bi xanh được đánh số từ 1đến 25 . Lấy ngẫu nhiên từ hộp ra ba viên bi.
a. Hỏi có tất cả bao nhiêu cách lấy được ba viên bi cùng màu.
b. Hỏi có tất cả bao nhiêu cách lấy được ba bi khác màu và khác số (từng đôi một).
c. Hỏi có tất cả bao nhiêu cách lấy để tổng các số ghi trên ba viên bi được lấy ra là một số chia hết cho 3.  3x 1 x 1
Bài 5. (1.0 điểm) Xác định hàm số f :    biết rằng: f    với x  1, x  2  .  x  2  x 1
...............................................................................Hết................................................................... SỞ GD&ĐT KON TUM
KIỂM TRA CUỐI HỌC KỲ I NĂM HỌC 2021-2022 TRƯỜNG THPT CHUYÊN
Ngày kiểm tra: ......./12/2021 NGUYỄN TẤT THÀNH Môn: Toán Lớp: 10 Toán
Thời gian làm bài: 90 phút
(Không kể thời gian giao đề) HƯỚNG DẪN CHẤM Bài Đáp án Điểm 3  x  m 1  0 1.0 điểm
a. Tìm tham số m để hệ bất phương trình  có 2x  3m  0 nghiệm.  m 1  3   1  0 x x m  Bài 1. Ta có 3    .    0.25 (2.0 điểm) 2x 3m 0 3m x   2
Hệ phương trình đã cho có nghiệm  m 1   3m  0.5  ;    ;       3 2      3m m 1 2    0.25 m  2 3 7
b. Xét tính chẵn lẻ của hàm số f (x)  2021 x  2021 x . 1.0 điểm
Ta có D   là tập đối xứng. 0.25 Với mọi x   ta có:
f (x)  x  2021  x  2021  x  2021  x  2021  f (x) . 0.5 Suy ra f (x) là hàm chẵn. 0.25
Cho tam giác ABC có trọng tâm G . Gọi D và E lần lượt là    
các điểm thỏa mãn đẳng thức AD  2AB; AE  x AC . 1.0 điểm   
a. Phân tích vectơ AG theo hai vectơ AB và AC . Bài 2. (2.0 điểm)
Gọi M là trung điểm của BC .  2  0.25 Ta có AG  AM 3 2 1    0.5 .  AB  AC 3 2 1     AB  AC 3 0.25
b. Tìm x để ba điểm D,G, E thẳng hàng. Với giá trị tìm DG 1.0 điểm
được của x , hãy tính tỉ số . DE
   5  1 
Ta có DG  AG  AD   AB  AC 3 3 0.25    DE  2  AB  x AC 0.25 5 1  2
Ba điểm D,G, E thẳng hàng 3 3    x  0.25 2 x 5  5  DG 5 Khi đó DG  DE nên  . 6 DE 6 0.25 Bài 3.
Trong hệ trục tọa độ Oxy cho ( A 1; 1  ), B( 2  ;2), C(0;1) .
(2.5 điểm) a. Chứng minh rằng ,
A B,C là đỉnh của một tam giác cân. 1.0 điểm    Ta có AB   3  ;3, AC   1  ;2, BC  2;  1 . 0.5  
Vì AB, AC không cùng phương nên , A B,C là 3 đỉnh của tam giác. 0.25
Vì AC  BC  5 nên tam giác ABC cân tại C. 0.25
b. Tìm tọa độ trực tâm H của tam giác ABC . 0.75 điểm Gọi H  ;
x y là trực tâm của tam giác ABC .   0.25
Ta có AH   x 1; y  
1 ; BH   x  2; y  2 .
H là trực tâm của tam giác ABC   AH.BC  0 2x  y  3 0.25
     . BH.AC  0 x  2y  6 x  4   . Vậy H (4;5) . y  5 0.25
  
c. Tìm điểm M trên trục hoành sao cho MA  MB  MC đạt 0.75 điểm giá trị nhỏ nhất.  1 2  0.25
Gọi G là trọng tâm tam giác ABC . Ta có G  ;   .  3 3  Khi đó
   MA  MB  MC  3MG .
   0.25
MA  MB  MC nhỏ nhất khi MG nhỏ nhất  M là hình
chiếu của G xuống trục Ox .  1  Do đó M  ;0   là điểm cần tìm.  3  0.25 Bài 4.
Một hộp có 15 bi đỏ được đánh số từ 1 đến 15 , 20 bi vàng
(2.5 điểm) được đánh số từ 1đến 20 và 25 bi xanh được đánh số từ 1
đến 25 . Lấy ngẫu nhiên từ hộp ra ba viên bi. 0.75 điểm
a. Hỏi có tất cả bao nhiêu cách lấy được ba viên bi cùng màu.
Số cách lấy được ba bi cùng màu là 3 3 3 C  C  C  3895 . 0.75 15 20 25
b. Hỏi có tất cả bao nhiêu cách lấy được ba bi khác màu và
khác số (từng đôi một). 1.0 điểm Chọn 1 bi đỏ: 15 cách. 0.25
Chọn 1 bi vàng (khác số với bi đỏ đã chọn): 19 cách. 0.25
Chọn 1 bi xanh (khác số với 2 bi đã chọn): 23 cách. 0.25
Vậy có tất cả 15.19.23=6555 cách lấy được 3 bi khác màu và 0.25 khác số.
c. Hỏi có tất cả bao nhiêu cách lấy để tổng các số trên ba viên
bi được lấy ra là một số chia hết cho 3. 0.75 điểm Đặt A  {1; 2;...15}; B  1;2;...;2  0 ; 0.25 C= 1;2;...;2  5 .
Kể cả số lần lặp lại, ta thấy rằng trong tập , A B,C có tất cả 19 số
chia hết cho 3, có 21 số chia 3 dư 1 và có 20 số chia 3 dư 2. Ta nhận xét rằng a  b  c  0(mod 3) a  b  c 1(mod3) 0.25 a  b  c3   . a  b  c  2(mod3) 
a  0(mod3), b 1(mod 3), c  2(mod 3)
Suy ra số cách lấy để tổng các số trên ba viên bi được lấy ra là
một số chia hết cho 3 là 3 3 3
C  C  C 19.20.21  11419 . 0.25 19 20 21 Bài 5.  3x 1 x 1
Xác định hàm số f :    biết rằng: f  với (1.0 điểm)    x  2  x 1 x  1, x  2  (*). 1.0 điểm 3x 1 2  t 1 Đặt t   x  . x  2 t  3  2 0.25
Do đó tập giá trị của t khi x  1, x  2  là  \ 3; .  3 2t 1 1  t  4 Thay vào (*) ta được: t 3 f (t)   ;(t  3)  . 2t 1 3t  2 1 0.25 t  3 Suy ra  x  4  2 , x  3   ;  3x  2  3  f (x)   a, x  3 . 0.25  2  b, x  .  3 
Thử lại: Hàm số f thỏa mãn đề bài.  x  4  2 , x  3   ;  3x  2  3  Vậy: f (x)   a, x  3 .  0.25 2  b, x  .  3 
Lưu ý: Các cách giải khác nếu đúng đều được tính điểm.