Đề học kì 1 Toán 10 năm 2022 – 2023 trường THPT Dương Văn Thì – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2022 – 2023 THÀNH PHỐ HỒ CHÍ MINH MÔN TOÁN - LỚP 10
TRƯỜNG THPT DƯƠNG VĂN THÌ
(Thời gian làm bài 60 phút, không kể thời gian phát đề) ĐỀ CHÍNH THỨC
Họ và tên thí sinh:……………………………………Số báo danh…………..
Câu 1: (1 điểm). Cho A = ( 3
− ;4);B = [1;+∞) . Tìm A∩ B, A∪ B, A \ B,C A. R
Câu 2: (1 điểm). Tìm tập xác định của hàm số: 3x − 4 y = ( x − ) 1 (2x − 4)
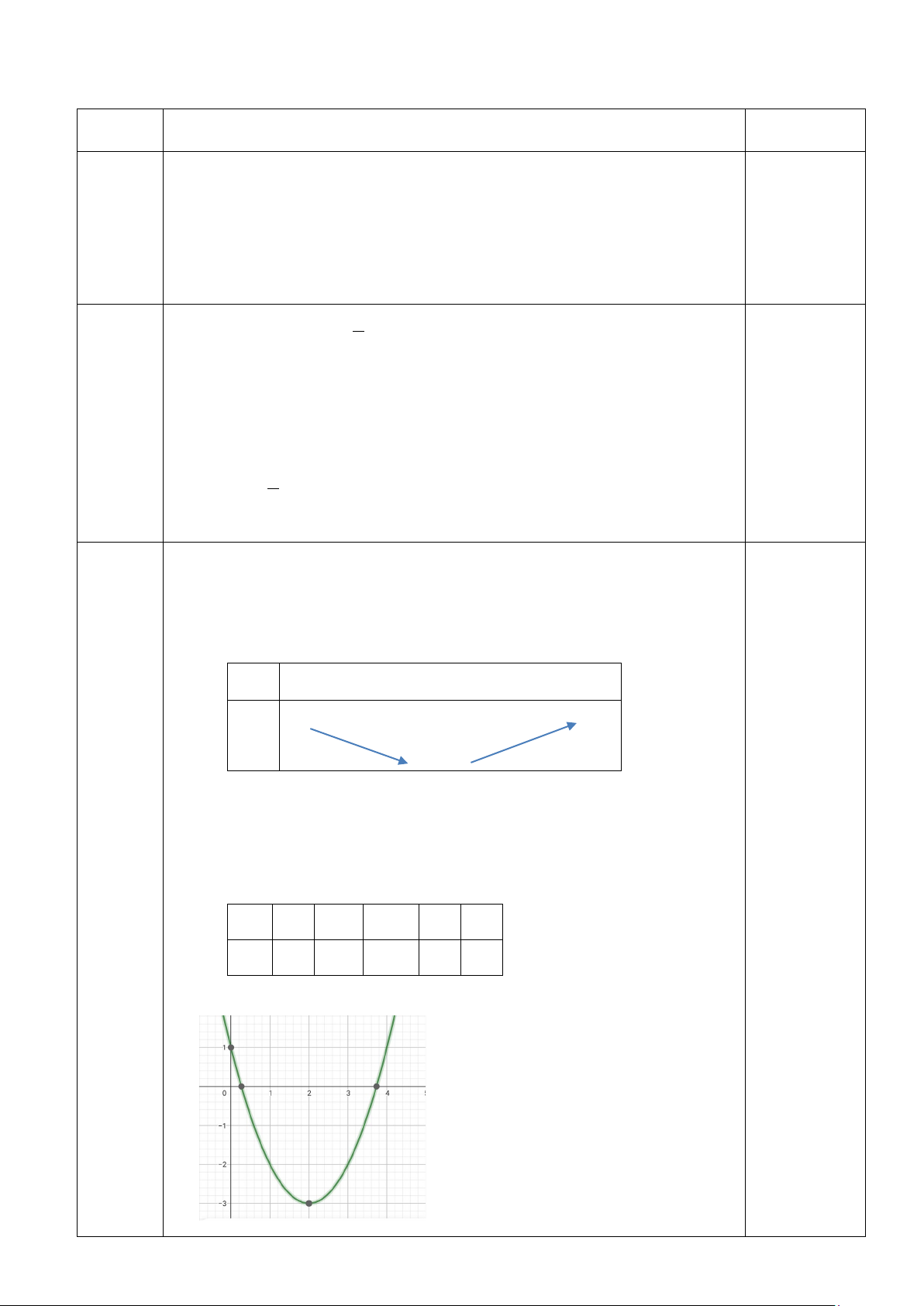
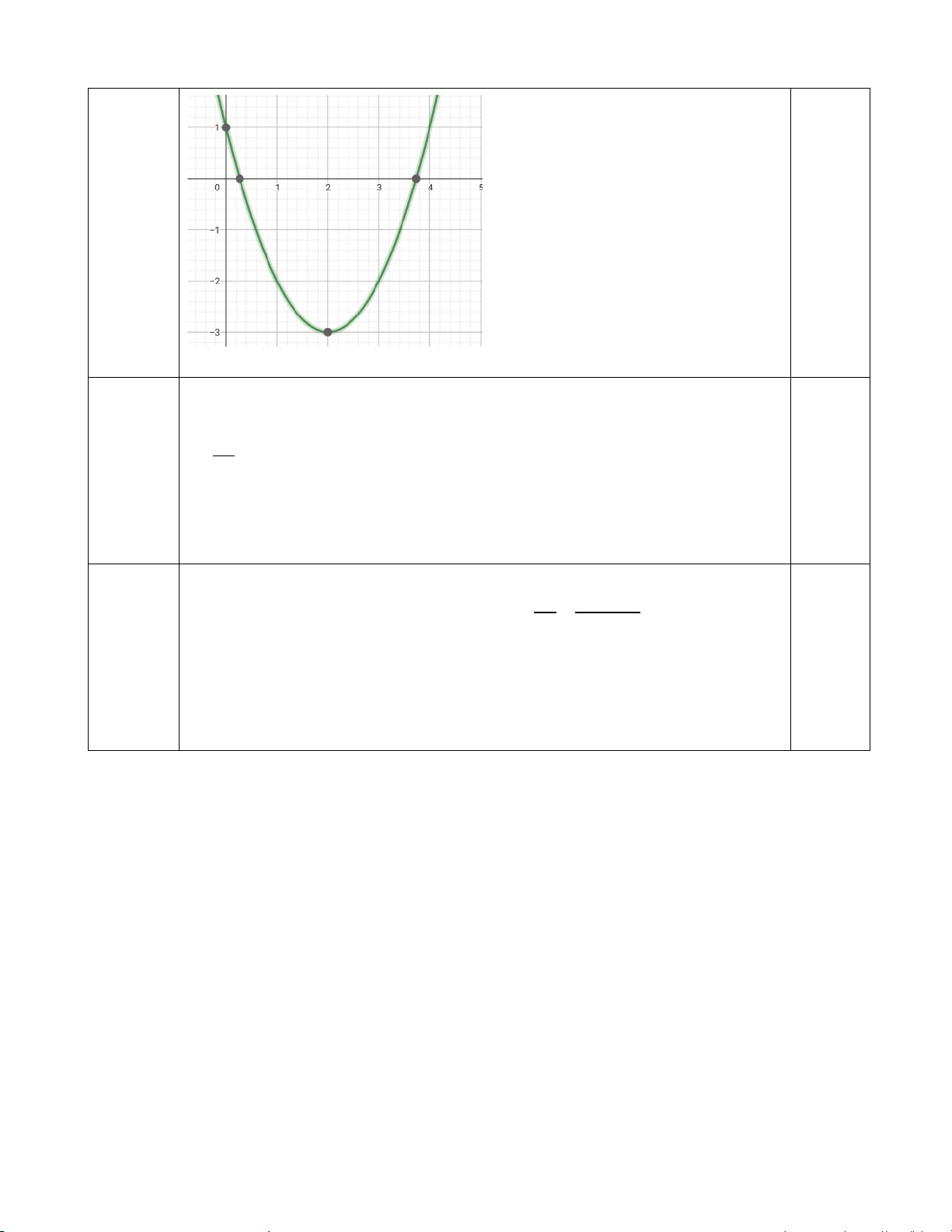
Câu 3: (1 điểm). Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: 2
y = x − 4x +1
Câu 4: (1 điểm). Cho hàm số 2
y = ax + bx + c có đồ thị (P) . Xác định (P) biết (P) có đỉnh I ( 2;
− 3) và đi qua điểm A(1; ) 1 . x ≥ 0 
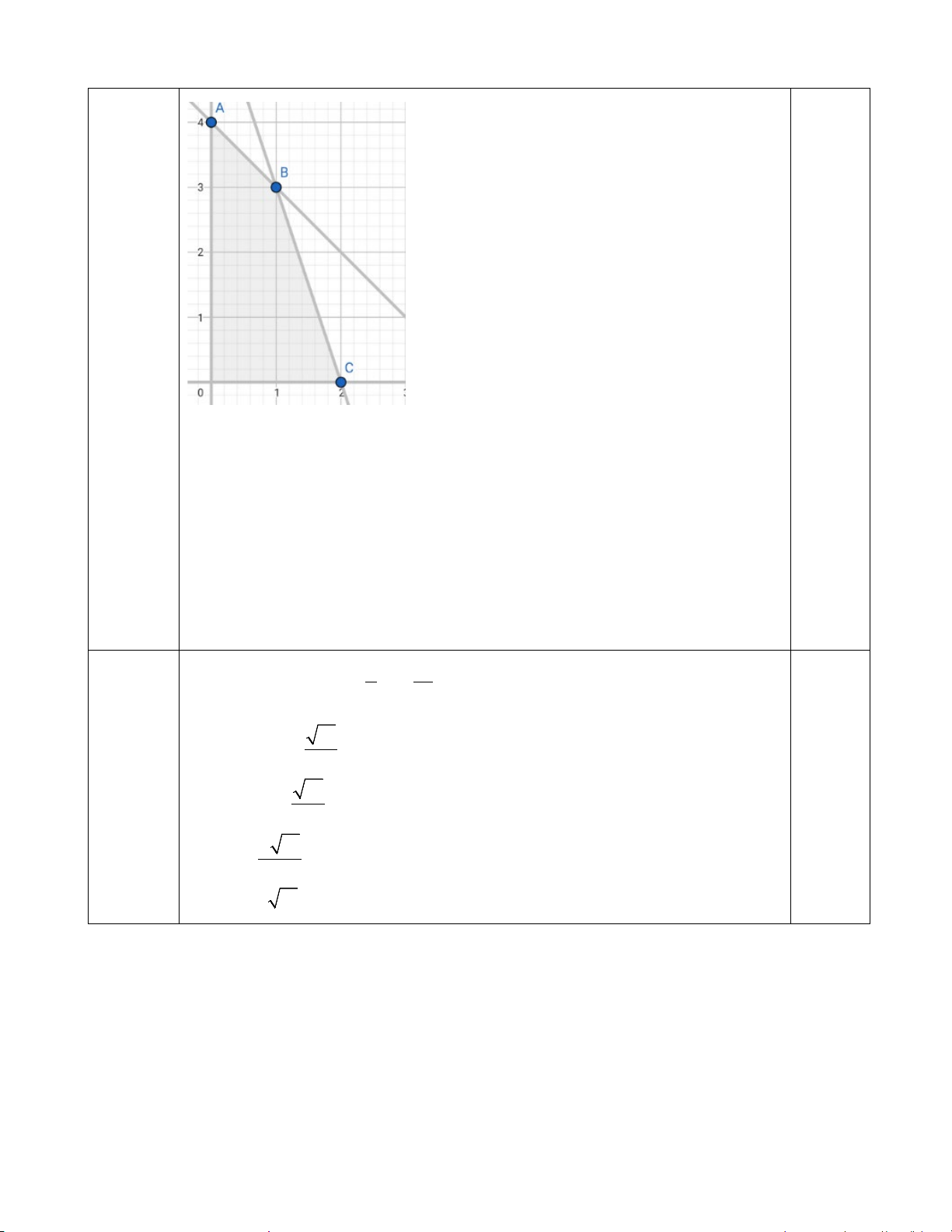
Câu 5: (1 điểm). Tìm cặp số ( y ≥ 0 ;
x y) thỏa mãn hệ bất phương trình  sao cho x + y ≤ 5 
4x + y ≤ 8
F = 2x +10y đạt giá trị lớn nhất.
Câu 6:(1 điểm). Sức mạnh của động cơ ( tính bằng đơn vị mã lực) sinh ra từ máy của một ca nô
có tốc độ quay là r vòng/phút được xác định bởi hàm số sau: p(r) 2 = 0
− ,0000147r + 0,2352r − 251
. Vậy sức mạnh lớn nhất của động cơ này đạt được là bao nhiêu mã lực? Khi đó, động cơ phải quay bao nhiêu vòng/phút?
Câu 7: (1 điểm). Cho 2
sin x = , với 90° < x <180°. Tính các giá trị lượng giác còn lại của góc x . 3
  
  
Câu 8: (1 điểm): Cho 6 điểm ,
A B,C, D, E, F . Chứng minh rằng: AD + BE + CF = AE + BF + CD .  
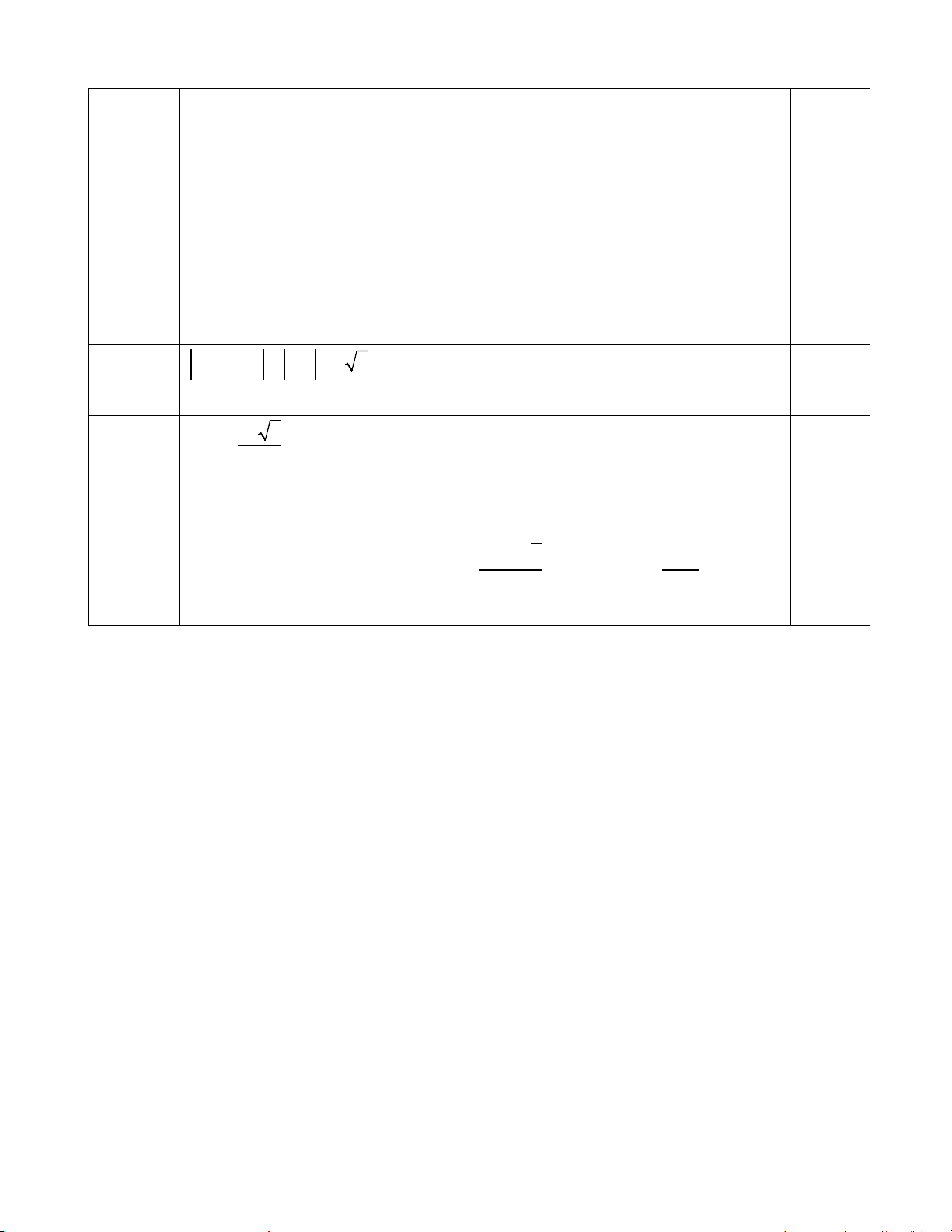
Câu 9: (1 điểm): Cho hình vuông ABCD cạnh 3a . Tính AB + AD
Câu 10: (1 điểm): Cho tam giác ABC đều cạnh bằng 2a, H là trung điểm của BC. Tính tích vô   hướng . HA AB
------------ Hết -----------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm. ĐÁP ÁN Câu Lời giải Điểm
Câu 1: A∩ B = [1;4) 0.25 điểm 0,25 điểm A∪ B = ( 3 − ;+∞) 0.25 điểm A \ B = ( 3 − ; ) 1 0,25 điểm
C A = −∞ − ∪ +∞ R ( ; ] 3 [4; ) Câu 2  4 3  − 4 ≥ 0 x x ≥  3   dk : 0.75 điểm
x −1 ≠ 0 ⇔ x ≠ 1 2x 4 0  − ≠ x ≠  2   TXĐ: 4 D  ;  = +∞   \{ } 2 0.25 điểm 3  Câu 3 • TXĐ: D=R I 2; 3 − • Đỉnh ( ) 0.25điểm
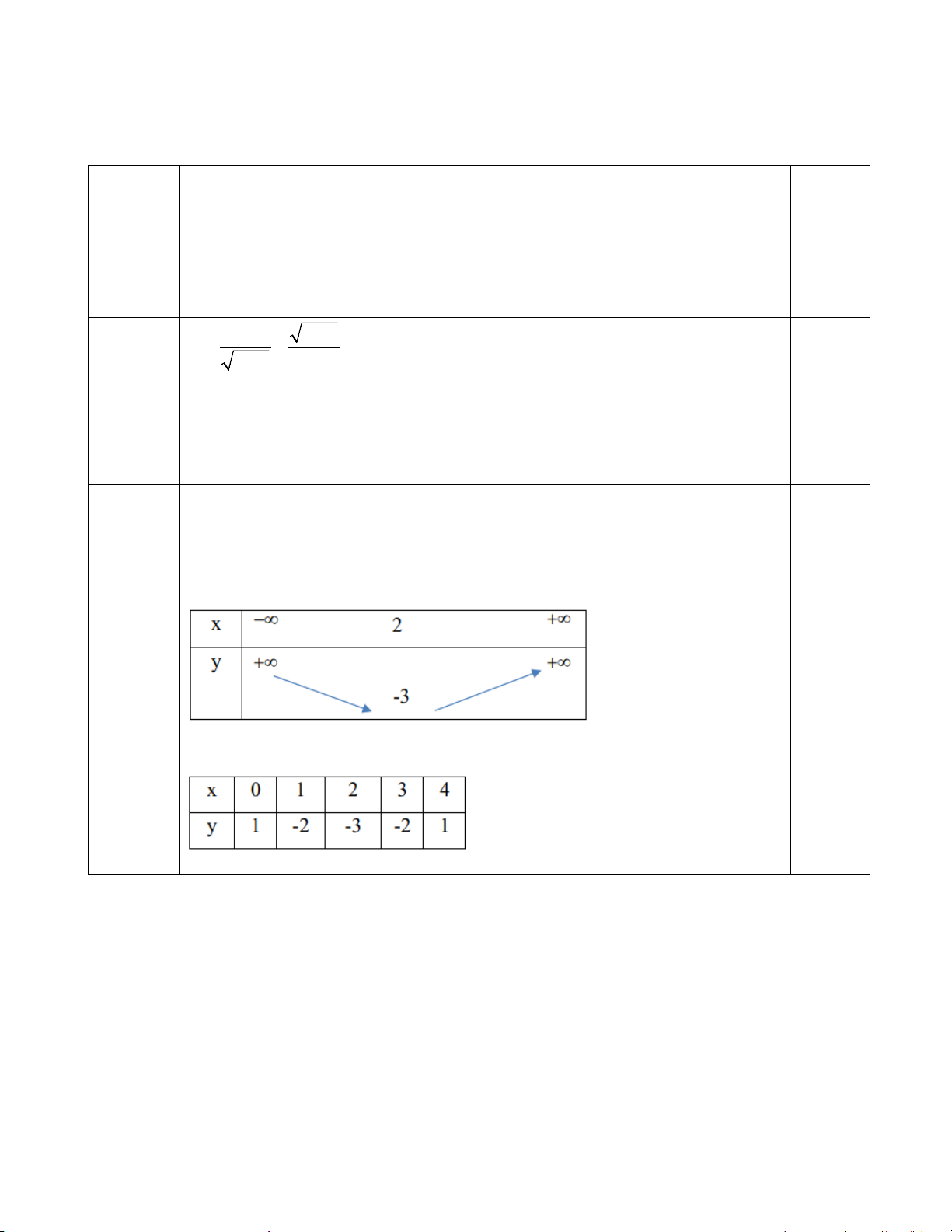
• Trục đối xứng: x = 2 • BBT: x −∞ 2 +∞ y +∞ +∞ -3 0.25điểm
Hàm số đồng biến trên (2;+∞)
Hàm số đồng biến trên ( ;2 −∞ ) • BGT: x 0 1 2 3 4 y 1 -2 -3 -2 1 • Vẽ đồ thị 0.5điểm
Câu 4 Theo yêu cầu đề bài ta có:  1  b − 2 a = = −   9 2a 4a − b = 0   0.75 điểm 
a (− )2 + b(− )   4 . 2
2 + c = 3 ⇔ 4a − 2b + c = 3 ⇔ b  = 9  2 .1 a + .1 b + c = 4  a b c 4  + + =   31 c =   9 1 4 31 Vậy (P) 2
: y = x + x + 9 9 9 0.25 điểm Câu 5 0.25 điểm 0.25 điểm
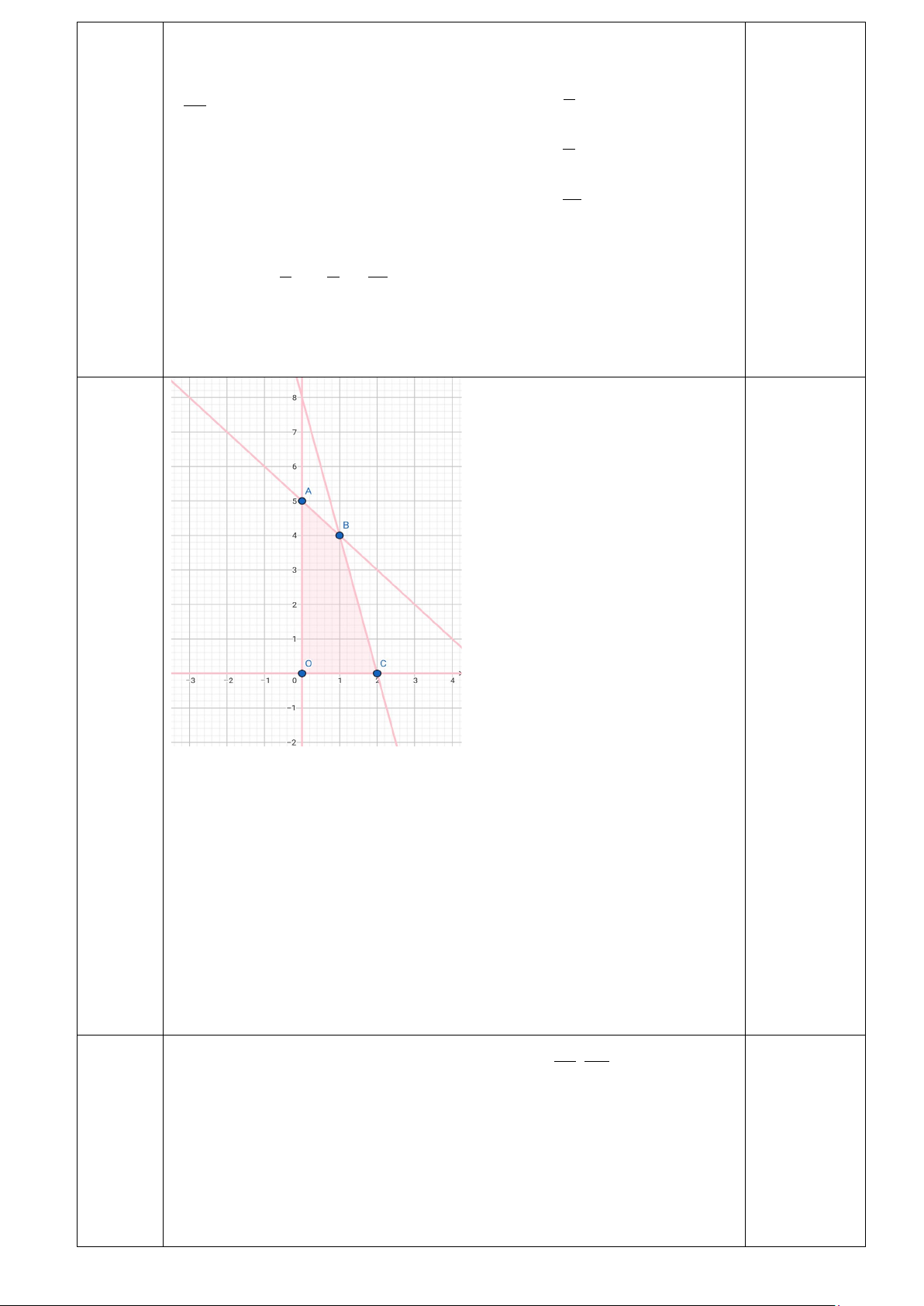
Dựa vào hình vẽ ta có: O(0;0); A(0;5);B(1;4);C(2;0)
Khi O(0;0) => F = 2.0 +10.0 = 0
Khi A(0;5) => F = 2.0 +10.5 = 50 0.25 điểm
Khi B(1;4) => F = 2.1+10.4 = 42
Khi C (2;0) => F = 2.2 +10.0 = 4 0.25 điểm
Vậy F đạt giá trị lớn nhất khi x=0 và y=5 Câu 6 0.25 điểm p(r) 2 = 0
− ,0000147r + 0,2352r − 251 có đỉnh  b I − ; −∆   2a 4a    Suy ra I (8000;689,8) 0.25 điểm
Vậy sức mạnh lớn nhất của động cơ ca nô là 689,8 mã lực. 0.25 điểm
Khi đó động cơ quay với tốc độ là 8000 vòng/phút. 0.25 điểm Câu 7 2 2 2  2  5
cos x =1− sin x =1− =  3   9  5 cos x = (l) 3 0.5 điểm =>  5 cos x = − (n)  3 2 sin x 3 2 5 tan x = = = − 0.25 điểm cos x − 5 5 3 1 5 cot x = = − 0.25 điểm tan x 2
Câu 8      
AD + BE + CF = AE + BF + CD 0.25 điểm
      
⇔ AD − AE + BE − BF + CF − CD = 0 0.25 điểm
   
⇔ ED + FE + DF = 0    0.25 điểm ⇔ ED + DE = 0   ⇔ EE = 0(ld ) 0.25 điểm Câu 9   
Ta có: AB + AD = AC = AC = 3a 2 (vì AC là đường chéo hình vuông 1 điểm ABCD) Câu 10 0,25 điểm Ta có: 2a 3 AH = = a 3 2         H .
A AB = −AH.AB = − AH . AB .cos( AH, AB) 0,25 điểm = −AH.A . B cosBAH 0,25 điểm 0 2 = −a 3.2 . a cos30 = 3 − a 0,25 điểm
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2022 – 2023 THÀNH PHỐ HỒ CHÍ MINH MÔN TOÁN - LỚP 10
TRƯỜNG THPT DƯƠNG VĂN THÌ
(Thời gian làm bài: 60 phút, không kể thời gian phát đề) ĐỀ CHÍNH THỨC
Họ và tên thí sinh:……………………………………Số báo danh…………..
Câu 1: (1 điểm) Cho A = (2;+∞);B = [ 2;
− 3) . Tìm A∩ B, A∪ B, A\ B, C B R .
Câu 2: (1 điểm) Tìm tập xác định của hàm số: 2022 x + 3 y = + . 3− x x − 2
Câu 3: (1 điểm) Khảo sát sự biến thiên và vẽ đồ thị hàm số sau: 2
y = x − 4x +1.
Câu 4: (1 điểm) Cho hàm số 2
y = ax + bx + c có đồ thị (P) . Xác định (P) biết (P) có đỉnh I( 1;
− 2) và đi qua điểm A(1;6).
Câu 5: (1 điểm) Một quả bóng được ném lên trên theo phương thẳng đứng từ mặt đất. Khi bỏ
qua sức cản của không khí, độ cao của quả bóng so với mặt đất có thể mô tả bởi phương trình 2 h(t) = 4,
− 9t +14,7t (tính bằng mét), t là thời gian (tính bằng giây). Vậy sau khi ném bao nhiêu
lâu thì quả bóng đạt độ cao lớn nhất? Tìm độ cao lớn nhất của quả bóng. 3  x + y ≤ 6  x + y ≤ 4
Câu 6: (1 điểm) Tìm cặp số ( ;x y) thỏa mãn hệ bất phương trình  sao cho x ≥ 0  y ≥ 0
F =10x + 8y đạt giá trị lớn nhất.
Câu 7: (1 điểm) Cho 1
sinα = với 90° < α <180°. Tính các giá trị lượng giác còn lại của gócα. 4
     
Câu 8: (1 điểm) Cho 6 điểm A, B, C, D, E, F. Chứng minh AE + BF + CD = AF + BD + CE .  
Câu 9: (1 điểm) Cho hình vuông ABCD có cạnh 2a . Tính AB + AD .
Câu 10: (1 điểm) Cho tam giác ABC đều cạnh 3a , đường cao AH . Tính tích vô hướng   . HA AC
------------ Hết -----------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm. ĐÁP ÁN Câu Lời giải Điểm
Câu 1 Cho tập A = (2;+∞);B = −  2; ) 3
𝐴𝐴 ∪ 𝐵𝐵 = [−2; +∞); 𝐴𝐴 ∩ 𝐵𝐵 = (2; 3) 0.25 0.25
𝐴𝐴\𝐵𝐵 = [3; +∞); 𝐶𝐶𝑅𝑅𝐵𝐵 = (−∞; −2) ∪ [3; +∞) 0.25 0.25 Câu 2 2022 x + 3 y = + 3− x x − 2 x + 3 ≥ 0 x ≥ 3 −  0.25 3 x 0 
− > ⇔  x < 3 ĐK: 0.25 x 2 0  − ≠ x ≠   2 0.25
TXĐ: 𝐷𝐷 = [−3; 3)\{2} 0.25
Câu 3 Ta có: y = 2 x − 4x +1 + TXD: D=R 0.25 + Đỉnh : I(2;-3) 0.25 + Trục đối xứng: x=2 +BBT
HS nghịch biến: (-∞;2) ; HS đồng biến: (2;+∞) +BGT 0.25 0.25 +Vẽ đồ thị: Câu 4 = 2
y ax + bx + c
Theo yêu cầu đề bài ta có:  b − = 1 −  2a 2a − b = 0 a = 1 0.25  0.25 2 a( 1) b( 1) c 2  a b c 2 b  − + − + = ⇔
− + = ⇔  = 2 => P y = 2 ( ) : x + 2x + 3  0.25 2 .1 a + .1 b + c = 6  a b c 6  + + = c = 3  0.25 
Câu 5 Quả bóng đạt độ cao lớn nhất là tung độ của đỉnh parabol tại thời gian
ứng với hoành độ đỉnh của parabol là: b − 1 − 4,7 t = = = (giây) o 1,5 2a 2.( 4 − ,9) 0.5
Vậy sau khi ném 1,5 giây thì quả bóng đạt độ cao lớn nhất. ta có: 2 h(1,5) = 4
− ,9.(1,5) +14,7.1,5 =11,025
Độ cao lớn nhất của quả bóng là 11,025 m. 0.5 Câu 6 0.25
Dựa vào hình vẽ ta có: O(0;0), (
A 0;4), B(1;3),C(2;0) . 0.25
Ta có: F =10x +8y
Tính giá trị của F tại các đỉnh của tứ giác:
Tại O(0;0) :F =10.0 +8.0 = 0 Tại (
A 0;4) : F =10.0 + 8.4 = 32 0.25
Tại B(1;3) : F =10.1+8.3 = 34
Tại C(2;0) : F =10.2 +8.0 = 20 0.25
F đạt giá trị lớn nhất bằng 34 tại B(1;3) . Câu 7 2 0.25 2 2  1  15
cos x =1− sin x =1− =  4   16  15 cosα = − (n) 4 =>  15 0.25 cosα = (l)  4 − 15 tanα = 0.25 15 cotα = − 15 0.25
Câu 8      
AE + BF + CD = AF + BD + CE 0.25
      
⇔ AE + BF + CD − AF − BD − CE = 0       
⇔ (AE − AF) + (BF − BD) + (CD − CE) = 0
   
⇔ FE + DF + ED = 0     0.25
⇔ (FE + ED) + DF = 0      ⇔ FD + DF = 0    
⇔ FF = 0 ⇔ 0 = 0(ld) 0.25 0.25 Câu 9   
AB + AD = AC = 2 2a 0.5x2 Câu 10 3a 3 0.25 AH = 2 𝐻𝐻 ��𝐴𝐴
��⃗. 𝐴𝐴��𝐶𝐶�⃗ = −𝐴𝐴��𝐻𝐻
��⃗. 𝐴𝐴��𝐶𝐶�⃗ = −�𝐴𝐴��𝐻𝐻
��⃗��𝐴𝐴��𝐶𝐶�⃗�cos�𝐴𝐴��𝐻𝐻
��⃗, 𝐴𝐴��𝐶𝐶�⃗� 0.25
= −𝐴𝐴𝐻𝐻. 𝐴𝐴𝐶𝐶. cos 300 0.25 −27
= −3𝑎𝑎√3 . 3𝑎𝑎.cos300 = 𝑎𝑎2 2 4 0.25
TP. Hồ Chí Minh, ngày 10 tháng 12 năm 2022 GIÁO VIÊN RA ĐỀ Trần Thị Ly Ly
SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KIỂM TRA HỌC KÌ I NĂM HỌC 2022 – 2023 THÀNH PHỐ HỒ CHÍ MINH MÔN TOÁN - LỚP 10
TRƯỜNG THPT DƯƠNG VĂN THÌ
(Thời gian làm bài: 60 phút, không kể thời gian phát đề) ĐỀ CHÍNH THỨC
Họ và tên thí sinh:……………………………………Số báo danh…………..
Câu 1: (1điểm) Cho A = (−∞;2);B = −1;   
4 . Tìm A∩ B , A∪ B , C , A C B .  
Câu 2: (1điểm) Tìm tập xác định của hàm số:
3x −1 + 5 − x y = 2 x + 2x − 3
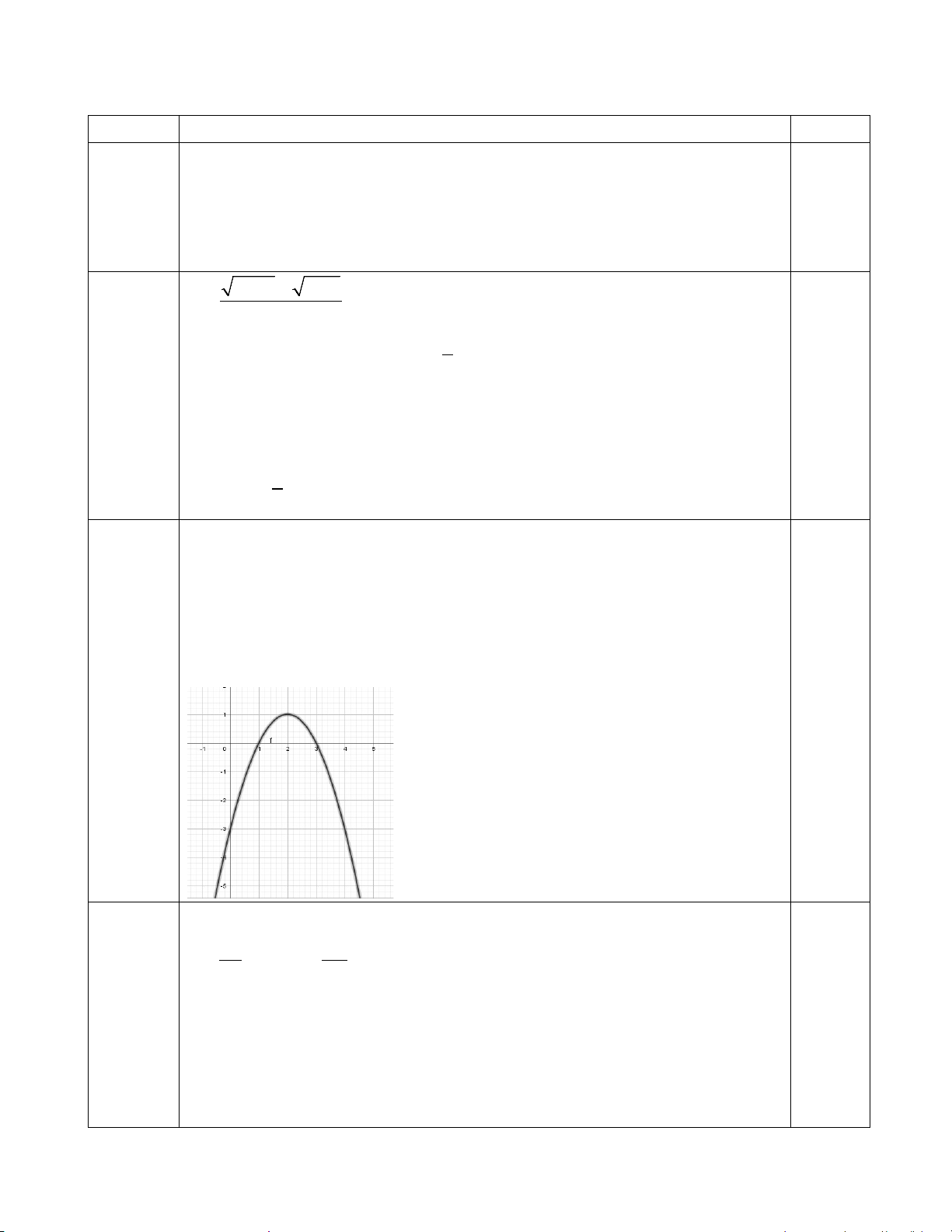
Câu 3: (1điểm) Khảo sát sự biến thiên và vẽ đồ thị các hàm số sau: y = − 2 x + 4x − 3
Câu 4: (1điểm) Cho hàm số y = 2
2x + bx + c có đồ thị (P) . Xác định (P) biết (P) Đi qua
N (1;−2) và có trục đối xứng x = −2.
Câu 5: (1điểm) Một quả bóng được ném vào không trung có chiều cao tính từ lúc bắt đầu ném
ra được cho bởi công thức 2 h(t) = t
− + 2t + 3 (tính bằng mét), t là thời gian tính bằng giây ( t ≥0).
Hỏi sau bao lâu quả bóng sẽ rơi xuống mặt đất ? 3x + y ≤ 6 
Câu 6: (1 điểm) Tìm cặp số ( x + y ≤ 4 ;
x y) thỏa mãn hệ bất phương trình  sao cho x ≥  0 y ≥ 0
F =10x + 8y đạt giá trị lớn nhất. Câu 7: (1điểm) Cho 1
sinα = , với 0° < α < 90°. Tính các giá trị lượng giác còn lại của góc α . 4
Câu 8: (1điểm) Cho hình bình hành ABCD tâm 0, M là một điểm tùy ý trong mặt phẳng. Chứng minh:    
MA+ MC = MB + MD  
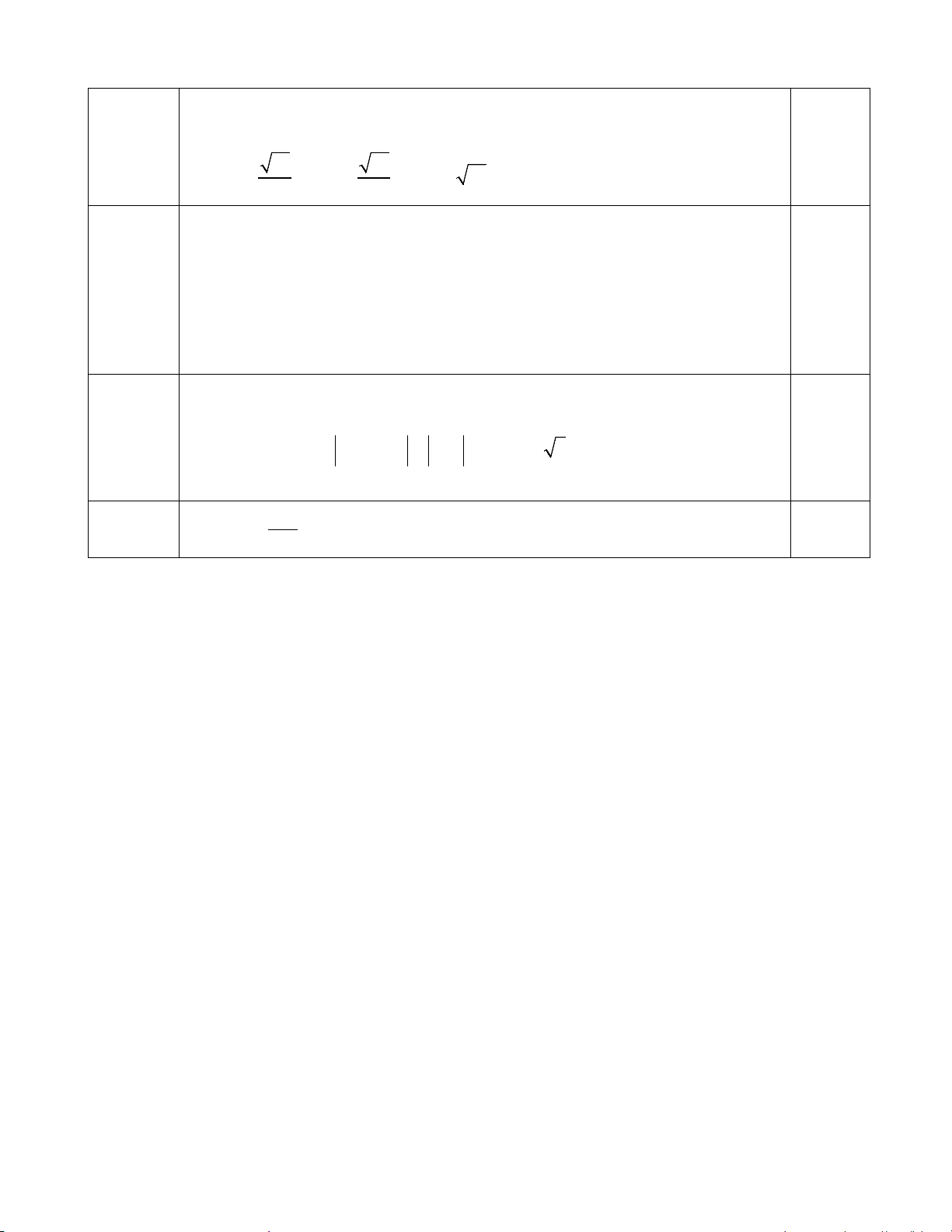
Câu 9: (1điểm) Cho hình vuông ABCD có cạnh a. Tính độ dài vectơ sau: AB + AC .  
Câu 10: (1điểm) Cho tam giác ABC đều cạnh a , đường cao AH . Tính tích vô hướng AH.AC
------------ Hết -----------
Thí sinh không được sử dụng tài liệu. Giám thị coi thi không giải thích gì thêm. ĐÁP ÁN Câu Lời giải Điểm
Câu 1 Cho tập A= ( ;2 −∞ ) ; B= [ 1; − 4]. + A∪ B = [ 1
− ;2); A∩ B = (− ;4 ∞ ] 0.25x2 0.25x2
+ A = [2;+∞); A C C = ( ; −∞ − ) 1 ∪(4;+∞   ) Câu 2
3x −1 + 5 − x y = 2 x + 2x − 3  1  3 −1 ≥ 0 x x ≥  3 0.25x2    5 − x ≥ 0 ⇔  x ≤ 5 ĐK:  2 x 2x 3 0  + − ≠
x ≠ 1∧ x ≠ 3 −    1 KL : D  ;5 = \{ } 1 3    0.25x2
Câu 3 Ta có: y = − 2 x + 4x − 3 + Đỉnh : I(2;1) 0.25x2 + Trục đối xứng: x=2
+ HS đồng biến: (-∞;2) ; nghịch biến: (2;+∞) + Qua A(1,0); B(3;0) 0.25x2 Câu 4 2 y 2x bx c = + + b b + − = 2 − ⇔ − = 2 − ⇔ b = 8 2a 2.2 0.25x2 + Qua N(1;-2): 2
− = 2.1+ 8.1+ c ⇒ c = 12 − 0.25x2 Vậy: y = 2 2x + 8x −12 Câu 5 0.25 0.25 0.25 0.25 Câu 6 0.25x2
Miền không gạch chéo (miền tứ giác
OABC , bao gồm cả các cạnh) trong
hình trên là phần giao của các miền nghiệm và cũng là phần biểu diễn
nghiệm của hệ bất phương trình đã cho.
Với các đỉnh O(0;0), (
A 0;4), B(1;3),C(2;0) .
Ta có: F =10x +8y
Tính giá trị của F tại các đỉnh của tứ giác:
Tại O(0;0), F =10.0 +8.0 = 0 Tại (
A 0;4) : F =10.0 + 8.4 = 32
Tại B(1;3), F =10.1+8.3 = 34
Tại C(2;0)⋅ F =10.2 +8.0 = 20
F đạt giá trị lớn nhất bằng 34 tại B(1;3) . 0.25x2 Câu 7 Ta có: 0.25x4 15 15 cosα = ;tanα = ;cotα = 15 4 15 Câu 8    
MA+ MC = MB + MD 0.25x4        
⇔ (MO +OA)+(MO +OC) = (MO +OB)+(MO +OD) b)      
⇔ 2MO + (OA+OC) = 2MO +(OB +OD)   ⇔ 2MO = 2MO
Câu 9   AB + AC 0.25x4
+ Gọi I là trung điểm của BC      
AB + AC = 2AI ⇒ AB + AC = 2AI = 2AI = a 5 Câu 10 2   3 0.25x4 . a AH AC = 4
TP. Hồ Chí Minh, ngày 12 tháng 12 năm 2022 GIÁO VIÊN RA ĐỀ Vũ Thị Lệ Thủy
MA TRẬN ĐỀ KIỂM TRA HỌC KÌ I
MÔN: TOÁN, LỚP 10 – THỜI GIAN LÀM BÀI: 60 PHÚT
Mức độ nhận thức Tổng % TT Nội dung kiến Nhận biết Thông hiểu Vận dụng Vận dụng thức
Đơn vị kiến thức cao Số CH tổng Thời Thời Thời Thời Thời điểm Số Số Số Số gian CH gian CH gian CH
gian CH gian TN TL (phút) (phút) (phút) (phút) (phút)
1 1. Mệnh đề. Tập Các phép toán trên tập hợp hợp 1 4 1 4 10 2. Bất phương
Bất phương trình, hệ bất phương
2 trình và hệ bất trình bậc nhất hai ẩn và ứng dụng phương trình 1 8 1 8 10
bậc nhất hai ẩn 3.1 Hàm số và đồ thị 1 4 1 4 10 3 3. Hàm số bậc
nhất và bậc hai 3.2 Hàm số bậc hai 1 4 1 6 1 10 3 20 30 4. Hệ thức
Giá trị lượng giác của một góc từ 4 lượng trong 0 0 đến 0 180 1 6 1 6 10 tam giác
5.1 Vectơ và các phép toán cộng, 5 5. Vectơ trừ, nhân với một số 1 6 1 8 2 14 20
5.2 Tích vô hướng của hai vectơ 1 4 1 4 10 Tổng 4 16 3 18 2 16 1 10 10 60 100 Tỉ lệ (%) 40 30 20 10 100 Tỉ lệ chung (%) 70 30 100
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA HỌC KỲ I
MÔN: TOÁN 10 – THỜI GIAN LÀM BÀI: 60 phút
Số câu hỏi theo mức độ nhận Đơn vị thức TT Nội dung
kiến thức kiến
Mức độ kiến thức, kĩ năng cần kiểm tra, đánh giá Vận thức Nhận Thông Vận biết hiểu dụng dụng cao Nhận biết
– Biết được phép toán trên các tập hợp (hợp, giao, hiệu của hai tập hợp, phần bù của một tập con). 1. Mệnh
Các phép Thông hiểu 1 đề. Tập
toán trên – Thực hiện được phép toán trên các tập hợp (hợp, giao, hiệu của hai tập hợp, phần bù 1 hợp tập hợp
của một tập con) và biết dùng biểu đồ Ven để biểu diễn chúng trong những trường hợp cụ thể. Vận dụng
– Mô tả được một số vấn đề thực tiễn gắn với phép toán trên tập hợp ( ví dụ: những bài
toán liên quan đến đếm số phần tử của hợp các tập hợp,...) 2. Bất Bất Nhận biết: phương phương
– Nhận biết được bất phương trình và hệ bất phương trình bậc nhất hai ẩn. trình và
trình, hệ Thông hiểu: bất
– Mô tả được miền nghiệm của bất phương trình và hệ bất phương trình bậc nhất hai ẩn 2 hệ bất phương phương
trên mặt phẳng toạ độ. 1 trình bậc trình Vận dụng: nhất hai
bậc nhất – Vận dụng được kiến thức về bất phương trình, hệ bất phương trình bậc nhất hai ẩn vào ẩn
hai ẩn và giải quyết bài toán thực tiễn (ví dụ: bài toán tìm cực trị của biểu thức F = ax + by trên
ứng dụng một miền đa giác,...). Nhận biết: 3. Hàm số
– Nhận biết được những mô hình thực tế (dạng bảng, biểu đồ, công thức) dẫn đến khái 3
bậc hai và 3.1 Hàm niệm hàm số. 1 đồ thị
số và đồ Thông hiểu: thị
– Mô tả được các khái niệm cơ bản về hàm số: định nghĩa hàm số, tập xác định, tập giá
trị, hàm số đồng biến, hàm số nghịch biến, đồ thị của hàm số.
– Mô tả được các đặc trưng hình học của đồ thị hàm số đồng biến, hàm số nghịch biến. Vận dụng:
– Vận dụng được kiến thức của hàm số vào giải quyết bài toán thực tiễn (ví dụ: xây dựng
hàm số bậc nhất trên những khoảng khác nhau để tính số tiền y (phải trả) theo số phút
gọi x đối với một gói cước điện thoại,...). Nhận biết:
– Nhận biết được các tính chất cơ bản của Parabola như đỉnh, trục đối xứng. Thông hiểu:
3.2 Hàm – Tính được bảng giá trị của hàm số bậc hai. số bậc
– Vẽ được Parabola (parabol) là đồ thị hàm số bậc hai. 1 1 1 hai
– Nhận biết và giải thích được các tính chất của hàm số bậc hai thông qua đồ thị. Vận dụng:
– Vận dụng được kiến thức về hàm số bậc hai và đồ thị vào giải quyết bài toán thực tiễn
(ví dụ: xác định độ cao của cầu, cổng có hình dạng Parabola,...). Giá trị Nhận biết: 4. Hệ lượng
- Biết khái niệm giá trị lượng giác của một góc bất kì từ 0° đến 180 . ° thức
giác của - Biết giá trị lượng giác của các góc đặc biệt. 4 lượng
một góc - Biết khái niệm góc giữa hai vectơ. 1 trong tam Thông hiểu: giác từ 0
0 đến - Xác định được góc giữa hai vectơ. 0 180
- Tính được các giá trị lượng giác của góc bất kì từ 0° đến 180 . ° 5.1 Nhận biết:
Vectơ và – Nhận biết được khái niệm vectơ, vectơ bằng nhau, vectơ-không.
các phép Thông hiểu: toán
– Mô tả được một số đại lượng trong thực tiễn bằng vectơ. 1 1
cộng, trừ, – Thực hiện được các phép toán trên vectơ (tổng và hiệu hai vectơ, tích của một số với 5 5. Vectơ
nhân với vectơ, tích vô hướng của hai vectơ) và mô tả được những tính chất hình học (ba điểm một số
thẳng hàng, trung điểm của đoạn thẳng, trọng tâm của tam giác,...) bằng vectơ. Vận dụng:
5.2 Tích – Sử dụng được vectơ và các phép toán trên vectơ để giải thích một số hiện tượng có liên
vô hướng quan đến Vật lí và Hoá học (ví dụ: những vấn đề liên quan đến lực, đến chuyển động,...). của 2 1
– Vận dụng được kiến thức về vectơ để giải một số bài toán hình học và một số bài toán vectơ
liên quan đến thực tiễn (ví dụ: xác định lực tác dụng lên vật,...) Tổng 4 3 2 1
BẢNG ĐẶC TẢ KĨ THUẬT ĐỀ KIỂM TRA HỌC KÌ I
MÔN: TOÁN LỚP 11 – THỜI GIAN LÀM BÀI: 60 phút
Mức độ kiến thức, kĩ năng
Số câu hỏi theo mức độ nhận thức Tổng TT Nội dung kiến thức
Đơn vị kiến thức
cần kiểm tra, đánh giá
Nhận biết Thông hiểu Vận Vận dụng dụng cao Hàm số Hàm số lượng giác Nhận biết: lượng giác
Tìm tập xác định của hàm số 1 1 1 và phương Thông hiểu: trình lượng Một số phương trình
Giải phương trình lượng giác đặt ẩn 1 1 giác
lượng giác thường gặp phụ. Vận dụng:
Khai triển nhị thức Niu-tơn trong Nhị thức Niu tơn
trường hợp cụ thể, tìm ra được số hạng 1 1 2 Tổ hợp –
thứ k trong khai triển, tìm ra hệ số của Xác suất xk trong khai triển. Thông hiểu: Xác suất của biến cố
Biết cách tính xác suất của biến cố trong 1 1
các bài toán cụ thể. Phương pháp quy nạp Vận dụng: toán học
Áp dụng PP quy nạp toán học để giải
quyết các bài toán chứng minh chia hết, 1 1 Dãy số - cấp
chứng minh tổng, hiệu, tích… 3
số cộng – cấp Cấp số cộng Nhận biết: số nhân
Nắm được công thức số hạng tổng quát. 1 1 Cấp số nhân Thông hiểu:
Áp dụng được công thức số hạng
tổng quát và công thức tính tổng n số 1 1
hạng đầu tiên vào giải bài toán Đại cương về đường Nhận biết: 4
Đường thẳng thẳng và mặt phẳng
Tìm giao tuyến hai mặt phẳng có yếu tố 1 1 1 và mặt trong không gian song song phẳng trong Vận dụng cao: không gian.
Nắm vững cách tìm giao tuyến, giao Quan hệ
Đường thẳng song song điểm. Vận dụng được các cách chứng 1 1 song song mặt phẳng
minh đt song song song mặt phẳng để giải quyết bài toán Thông hiểu: Hai mặt phẳng song song
Biết cách chứng minh 2 mp song song. 1 1 Tổng 4 3 2 1 10
Document Outline

• DE 1
• DE 2 (đã thi)
• DE 3
• MA TRAN - HK1.2022-2023
• BẢN ĐẶC TẢ-HK1.2022.2023