PHÒNG GD – ĐT QUẬN HOÀN KIẾM
ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THCS THANH QUAN MÔN: TOÁN 8
Năm học : 2023 – 2024 ĐỀ 1
Ngày: 27/12/2023 – Thời gian : 90 phút
(Không kể thời gian phát đề)
Bài 1. (1,5 điểm): Tìm x : a) 2 4x − 6x = 0 b) (x + )2
2 − x(x + 2) = 3 c) 2
x − 7x − 18 = 0
Bài 2. (2,0 điểm) Thực hiện phép tính: 2 4 2 2 a) 2x y + 3 3 −
b) x − 4 x + 4x + 4 : 5 5 2xy 2xy x + 3 2x + 6 Bài 3. (2,0 điểm) Cho hai biểu thức: x − 2 6x − 4 A + = + ; x 1 B = với x ≠ 1; − x ≠ ±2 2 x + 2 x − 4 x − 2
a) Tính giá trị biểu thức B biết x = 3 b) x Chứng minh: A = x − 2
c) Tìm x nguyên để biểu thức P = A + B đạt giá trị nguyên ? Bài 4. (1,0 điểm)
Hiện tại bạn An để dành được 500 000 đồng. Bạn An đang có ý định mua
một chiếc xe đạp trị giá 1 750 000 đồng. Để thực hiện được điều trên, bạn An đã
lên kế hoạch hằng ngày đều tiết kiệm 10 000 đồng. Gọi y (đồng) là số tiền bạn
An tiết kiệm được sau x ngày.
a) Viết công thức biểu thị y theo x ?
b) Hỏi sau bao nhiêu ngày kể từ ngày bắt đầu tiết kiệm thì bạn An mua được chiếc xe đạp đó? Bài 5. (3,0 điểm) Cho A
∆ BC vuông tại B (BC > BA), với M là trung điểm của AC. Từ M kẻ
ME vuông góc với BC (E ∈ BC), MD vuông góc với AB (D∈ AB)
a) Chứng minh tứ giác BDME là hình chữ nhật.
b) Lấy điểm F thuộc tia đối tia ME sao cho MF = ME.
Chứng minh: BE = EC và tứ giác AFCE là hình bình hành.
c) Gọi I, K lần lượt là giao điểm của BM, BF với AE. Tính IK ? FC Bài 6. (0,5 điểm) Cho + 0 a b
< a < b và ( 2 2 3 a + b ) =10 .
ab Tính giá trị của biểu thức M = . a − b
----------------Hết----------------
PHÒNG GD – ĐT QUẬN HOÀN KIẾM
ĐỀ KIỂM TRA HỌC KỲ I
TRƯỜNG THCS THANH QUAN MÔN: TOÁN 8
Năm học : 2023 – 2024 ĐỀ 2
Ngày: 27/12/2023 – Thời gian : 90 phút
(Không kể thời gian phát đề)
Bài 1. (1,5 điểm): Tìm x : a) 2 6x − 10x = 0 b) (x + )2
3 − x(x + 3) = 8 c) 2
x − 5x − 14 = 0
Bài 2. (2,0 điểm) Thực hiện phép tính: 2 3 2 2 a) 3x y + 2 2 −
b) x − 9 x + 6x + 9 : 4 4 3xy 3xy x + 2 3x + 6 Bài 3. (2,0 điểm) Cho hai biểu thức: x − 3 9x − 9 M + = + ; x 1 N = với x ≠ 2; − x ≠ ±3 2 x + 3 x − 9 x − 3
a) Tính giá trị biểu thức N biết x =1 b) x Chứng minh: M = x − 3
c) Tìm x nguyên để biểu thức P = M + N đạt giá trị nguyên. Bài 4. (1,0 điểm)
Hiện tại bạn An để dành được 400 000 đồng. Bạn An đang có ý định mua
một chiếc xe đạp trị giá 1 850 000 đồng. Để thực hiện được điều trên, bạn An đã
lên kế hoạch hằng ngày đều tiết kiệm 10 000 đồng. Gọi y (đồng) là số tiền bạn
An tiết kiệm được sau x ngày.
a) Viết công thức biểu thị y theo x ?
b) Hỏi sau bao nhiêu ngày kể từ ngày bắt đầu tiết kiệm thì bạn An mua được chiếc xe đạp đó? Bài 5. (3,0 điểm) Cho A
∆ BC vuông tại C (CB > CA), với E là trung điểm của AB. Từ E kẻ
ED vuông góc với BC (D∈ BC), EH vuông góc với AC (H ∈ AC)
a) Chứng minh tứ giác DCHE là hình chữ nhật.
b) Lấy điểm M thuộc tia đối tia ED sao cho EM = ED.
Chứng minh: DC = DB và tứ giác AMBD là hình bình hành.
c) Gọi I, N lần lượt là giao điểm của CM, CE với AD. Tính IN ? MB Bài 6. (0,5 điểm) Cho + 0 m n
< m < n và ( 2 2 3 m + n ) =10 .
mn Tính giá trị của biểu thức A = . m − n
----------------Hết---------------- HƯỚNG DẪN CHẤM ĐỀ 1 Bài Nội dung Biểu điểm Bài 1. a) 2 4x − 6x = 0 (1,5đ)
a) 0,5đ 2x(2x − 3) = 0 0,25đ b) 0,5đ
c) 0,5đ Tìm được x = 0 hoặc 3 x = 0,25đ 2
Học sinh thiếu 1 trong 2 trường hợp: – 0,25đ b) (x + )2
2 − x(x + 2) = 3 2x = 1 − 0,25đ Tìm được 1 x = − 0,25đ 2 c) 2
x − 7x − 18 = 0
(x − 9)(x + 2) = 0 0.25đ
Tìm được x = 9 hoặc x = 2 − 0,25đ
Học sinh thiếu 1 trong 2 trường hợp: – 0,25đ Bài 2. 2 4 2x y + 3 3 (2,0đ) a) − 5 5 2xy 2xy a) 1,0đ b) 1,0đ 2 4 2x y + 3 − 3 = 5 2xy 0,25đ 2 4 2x y = 5 2xy 0,5đ x = y 0,25đ 2 2
b) x − 4 x + 4x + 4 : x + 3 2x + 6
(x − )(x + ) (x + )2 2 2 2 = : 0,5đ x + 3 2(x + 3)
(x − 2)(x + 2) 2(x + 3) = . x + 3 ( 0,25đ x + 2)2 2(x − 2) = 0,25đ x + 2
Bài 3. a) Với x = 3 (t/m) thì giá trị B là: (2,0đ) 3 1 a) 0,5đ B + = = 4 0,25đ 3 − 2
b) 1,0đ Vậy B = 4 khi x = 3 0,25đ c) 0,5đ x − 2 6x − 4 b) A = + 2 x + 2 x − 4 x − 2 6x − 4 = +
x + 2 (x − 2)(x + 2)
(x − 2)(x − 2) 6x 0,25đ − 4 = ( +
x − 2)(x + 2) (x − 2)(x + 2) 2
x − 4x + 4 + 6x − 4 = ( x − 2)(x + 2) 0,25đ 2 x + 2x x(x+ 2) = ( =
x − 2)(x + 2) (x − 2)(x + 2) 0,25đ x = 0,25 đ x − 2 c) 2x +1 5
P = A + B = = 2 + x − 2 x − 2
P nguyên khi 5 x − 2 0,25đ x − 2∈Ư(5) = { 1; ± 5 ± } Tìm được x∈{ 3 − ;1;3; } 7 0,25đ
Bài 4. a) Công thức biểu diễn y theo x: y = 500 000 +10000x 0,5đ
(1,0đ) b) Để An mua được chiếc xe đạp đó thì cần số ngày là:
a) 0,5đ (1750 000−500 000) :10 000 =125 b) 0,5đ (ngày) 0,5đ Bài 5. A (3,0đ) a) M 1,25đ D 0,25đ b) 1,25đ B E C c) 0,5đ
Học sinh vẽ hình đúng đến câu a.
a) ME ⊥ AC(gt) ⇒ 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 90° 0,25đ
MD ⊥ AB(gt) ⇒ 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 90° 0,25đ A
∆ BC vuông tại B (gt) ⇒𝑀𝑀𝑀𝑀𝑀𝑀 � = 90° 0,25đ
Xét tứ giác BDME có: 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 90° (cmt) 0,25đ
⇒ BDME là hình chữ nhật (cmt) A F D M B E C b) Xét A
∆ BC vuông tại B có BM là đường trung tuyến
(M là trung điểm AC) BC 0,25đ
⇒ AM = BM = CM =
(đường tt ứng với ch) 2 C1: C2: Xét B ∆ MC có: Xét ME ∆ B và ME ∆ C có: BM = MC (cmt) ME chung ⇒ B
∆ MC cân (dhnb) có BM = MC (cmt) 0,5đ
đường cao ME đồng thời 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 90° là đường trung tuyến M ∆ EB = M
∆ EC (ch − cgv) ⇒ BE = BC
Xét tứ giác AFCE có:
M là trung điểm EF (ME = MF)
M là trung điểm AC (gt) 0,5đ
AC cắt EF tại M
⇒ AFCE là hình bình hành (dhnb)
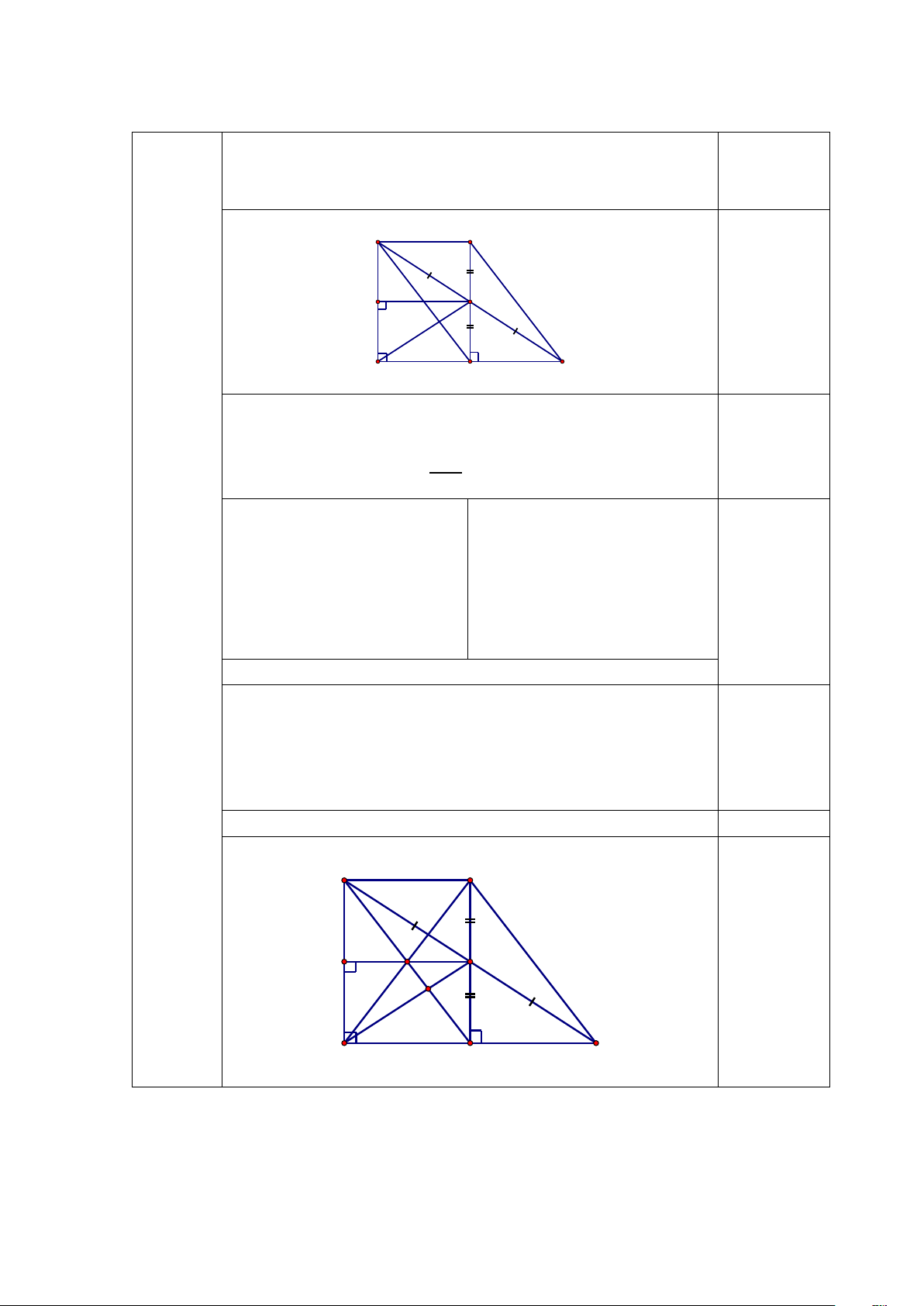
HS thiếu một yếu tố: - 0,25đ A F K D M I B E C
c) AFCE là hình bình hành (cmt) FA / /CE ⇒ 
FA = CE, AE = CF
FA / /CE(cmt) ∈
( )  ⇒ FA / /BE E BC gt 
FA = CE(cmt) =
( )  ⇒ FA = BE = EC BE EC gt 
Xét tứ giác AFEB có:
FA / /BE(cmt)⇒ AFEB là hình bình hành (dhnb)
FA = BE(cmt)
Xét hình bình hành AFEB có 𝑀𝑀𝑀𝑀𝑀𝑀 � = 90°
⇒ AFEB là hình chữ nhật (dhnb) AE = BF 
⇒ KA = KE (t/c) KB =  KF ⇒ 1 1
KE = KA = KF = KB = AE = FC 2 2 0,25đ Xét E ∆ BF có:
EK là đường trung tuyến (KB = KF)
BM là đường trung tuyến (ME = MF)
EK cắt BM tại I 0,25đ
⇒ I là trọng tâm E ∆ BF 1 1
⇒ KI = KE = FC 3 6 Bài 6. 3( 2 2
a + b ) =10ab (0,5đ) 2 2
3a + 3b −10ab = 0 2 2
3a − 9ab − ab + 3b = 0
(a − 3b)(3a − b) = 0 0,25đ
Tính được 2 trường hợp
TH1: a − 3b = 0 hay a = 3b . Loại vì a < b 0,25đ
TH2: 3a − b = 0 hay b = 3a . Tính được M = 2 −
*Lưu ý: HS làm cách khác chính xác, GV vẫn cho điểm tối đa HƯỚNG DẪN CHẤM ĐỀ 2 Bài Nội dung Biểu điểm Bài 1. a) 2 6x − 10x = 0 (1,5đ)
a) 0,5đ 2x(3x − 5) = 0 0,25đ b) 0,5đ
c) 0,5đ Tìm được x = 0 hoặc 5 x = 0,25đ 3
Học sinh thiếu 1 trong 2 trường hợp: – 0,25đ b) (x + )2
3 − x(x + 3) = 8 3x = 1 − 0,25đ Tìm được 1 x = − 0,25đ 3 c) 2
x − 5x − 14 = 0
(x − 7)(x + 2) = 0 0.25đ
Tìm được x = 7 hoặc x = 2 − 0,25đ
Học sinh thiếu 1 trong 2 trường hợp: – 0,25đ Bài 2. 2 3 3x y + 2 2 (2,0đ) a) − 4 4 3xy 3xy a) 1,0đ b) 1,0đ 2 3 3x y + 2 − 2 = 4 3xy 0,25đ 2 3 3x y = 4 3xy 0,5đ x = y 0,25đ 2 2
b) x − 9 x + 6x + 9 : x + 2 3x + 6
(x − )(x + ) (x + )2 3 3 3 = : 0,5đ x + 2 3(x + 2)
(x − 3)(x + 3) 3(x + 2) = . x + 2 ( 0,25đ x + 3)2 3(x − 3) = 0,25đ x + 3 Bài 3.
(2,0đ) a) Với x =1 (t/m) thì giá trị N là: 1 1 N + = = 1 − 0,25đ 1− 3
a) 0,5đ Vậy N = -1 khi x =1 0,25đ b) 1,0đ x − 3 9x − 9 c) 0,5đ b) M = + 2 x + 3 x − 9 x − 3 9x − 9 = +
x + 3 (x − 3)(x + 3)
(x − 3)(x − 3) 0,25đ 9x − 9 = ( +
x − 3)(x + 3) (x − 3)(x + 3) 2
x − 6x + 9 + 9x − 9 = ( x − 2)(x + 2) 0,25 đ 2 x + 3x x(x+3) = ( =
x − 3)(x + 3) (x − 3)(x + 3) 0,25đ x = 0,25 đ x − 3 c) 2x +1 7
P = M + N = = 2 + x − 3 x − 3
P nguyên khi 7  x − 3 0,25đ x − 3∈Ư(7) = { 1; ± 7 ± } Tìm được x∈{ 4; − 2;4;1 } 0 0,25đ
Bài 4. a) Công thức biểu diễn y theo x: y = 400 000 +10000x 0,5đ
(1,0đ) b) Để An mua được chiếc xe đạp đó thì cần số ngày là:
a) 0,5đ (1850 000− 400 000):10 000 =145 b) 0,5đ (ngày) 0,5đ Bài 5. A (3,0đ) a) 1,25đ b) H E 1,25đ 0,25đ c) 0,5đ C D B
Học sinh vẽ hình đúng đến câu a
a) DE ⊥ BC(gt) ⇒ 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 90° 0,25đ
EH ⊥ AC (gt) ⇒ 𝑀𝑀𝐸𝐸𝑀𝑀 � = 𝑀𝑀𝐸𝐸𝑀𝑀 � = 90° 0,25đ A
∆ BC vuông tại C (gt) ⇒𝑀𝑀𝑀𝑀𝑀𝑀 � = 90° 0,25đ
Xét tứ giác CHED có: 𝑀𝑀𝐸𝐸𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀 � 𝑀𝑀 = 90° (cmt) 0,25đ
⇒ CHED là hình chữ nhật (cmt) A M H E C D B b) Xét A
∆ BC vuông tại C có CE là đường trung tuyến
(E là trung điểm AB) 0,25đ BA
⇒ AE = BE = CE =
(đường tt ứng với ch) 2 C1: C2: Xét B ∆ EC có: Xét E ∆ DC và E ∆ DB có: BE = EC (cmt) ED chung ⇒ B
∆ EC cân (dhnb) có BE = EC (cmt) 0,5đ
đường cao ED đồng thời 𝑀𝑀𝑀𝑀𝑀𝑀 � = 𝑀𝑀𝑀𝑀𝑀𝑀 � = 90° là đường trung tuyến E ∆ DC = E
∆ DB(ch − cgv) ⇒ CD = BD
Xét tứ giác AMBD có:
E là trung điểm MD (ME = ED)
E là trung điểm AB (gt) 0,5đ
AB cắt MD tại E
⇒ AMBD là hình bình hành (dhnb)
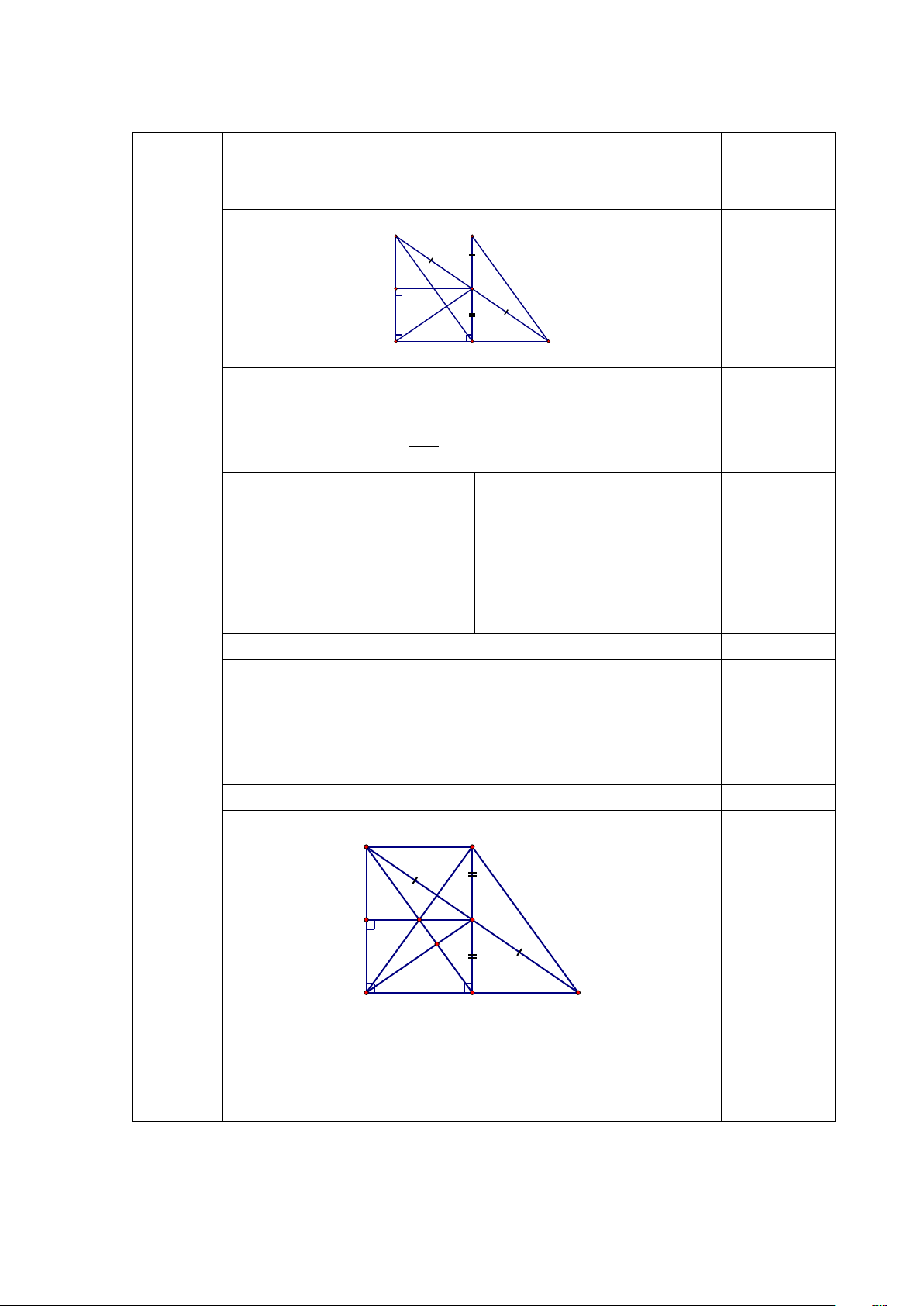
HS thiếu một yếu tố: - 0,25đ A M H E IN C D B
c) AMBD là hình bình hành (cmt) AM / /BD ⇒ 0,25đ 
AM = BD, AD = MB
AM / /BD(cmt) ∈ ( )  ⇒ MA / /CD D BC gt 
MA = BD(cmt) =
( )  ⇒ MA = BD = CD CD BD gt 
Xét tứ giác AMDC có:
AM / /CD(cmt)⇒ AMDC là hình bình hành (dhnb)
AM = CD(cmt)
Xét hình bình hành AMDC có 𝑀𝑀𝑀𝑀𝑀𝑀 � = 90°
⇒ AMDC là hình chữ nhật (dhnb) AD = MC 
⇒ IA = ID (t/c) IC =  IM ⇒ 1 1
IM = IA = IC = ID = AD = MB 2 2 Xét MD ∆ C có:
DI là đường trung tuyến (IM = IC)
CE là đường trung tuyến (ME = ED)
DI cắt CE tại I 0,25đ
⇒ I là trọng tâm MD ∆ C 1 1
⇒ IN = ID = MB 3 6 Bài 6. 3( 2 2
m + n ) =10mn (0,5đ) 2 2
3m + 3n −10mn = 0 2 2
3m − 9mn − mn + 3n = 0 (
m − 3n)(3m − n) = 0 0,25đ
Tính được 2 trường hợp 0,25đ
TH1: m − 3n = 0 hay m = 3n . Loại vì m < n
TH2: 3m − n = 0 hay n = 3m. Tính được A = 2 −
*Lưu ý: HS làm cách khác chính xác, GV vẫn cho điểm tối đa