PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I NĂM HỌC 2023-2024 KIẾN XƯƠNG MÔN TOÁN 8
(Thời gian làm bài: 120 phút )
I. TRẮC NGHIỆM. (2,0 điểm)
Chọn chữ cái in hoa đứng trước câu trả lời em cho là đúng trong mỗi câu sau:
Câu 1: Kết quả phép chia đa thức 2 2
3x y + 3xy cho đơn thức 3xy có kết quả là: A. x + y
B. 3x + 3y C. 3x + y
D. x + 3y
Câu 2: Giá trị của biểu thức 2 9x − − 6x + 5 tại 1 x = − là: 3 A. 1 B. 1 − C. 6 D. – 6 3 3
Câu 3: Trong các điểm sau, điểm nào thuộc đồ thị hàm số: y = 2x +3 ? A. (– 2; 0) B. ( 4 ; 6 ) C. (1; – 5) D. (1; 5)
Câu 4: Hình bình hành có một đường chéo là phân giác của một góc là:
A. Hình thang cân B. Hình thoi C. Hình vuông D. Hình chữ nhật
II. TỰ LUẬN. (8,0 điểm)
Bài 1: (1,5 điểm)
1) Phân tích các đa thức sau thành nhân tử: a) x2 – xy + 5x – 5y b) 2 2
x − 2xy − 25 + y
2) Chứng minh rằng giá trị biểu thức sau không phụ thuộc vào giá trị của biến x:
A = (x – 5)(x + 5) – x(x + 1) + x + 12  x 2 1  3
Bài 2: (2,0 điểm) Cho biểu thức: A = − +   : với x ≠ 2 ± 2
 x − 4 x − 2 x + 2  x − 2
a) Rút gọn biểu thức A b) Tính giá trị của A khi x thoả mãn: 2 x − 2x = 0
c) Tìm x nguyên lớn nhất để biểu thức A nhận giá trị nguyên.
Bài 3: (1,5 điểm) Cho hàm số: y = (m – 1)x − 1 có đồ thị là đường thẳng d.
1) Tìm điều kiện của m để hàm số trên là hàm số bậc nhất.
2) Khi m = 3, hãy vẽ đồ thị hàm số rồi tính khoảng cách từ gốc toạ độ O(0; 0) đến đường thẳng d.
Bài 4: (2,5 điểm) 1) Cho AB ∆
C vuông tại A có đường cao AH. Từ H kẻ HN ⊥ AC , HM ⊥ AB .
a) Chứng minh tứ giác AMHN là hình chữ nhật.
b) Lấy D sao cho M là trung điểm của DH, lấy E sao cho N là trung điểm của EH.
Chứng minh tứ giác AMNE là hình bình hành. c) Chứng minh: 2 2 2 BC = BD + CE + 2BH.HC .
2) Một khối Rubik có dạng hình chóp tam giác đều. Biết
chiều cao bằng 5,2 cm, thể tích của khối Rubic là 45,24 cm3.
Tính diện tích đáy của khối Rubik.
Bài 5: (0,5 điểm) Cho 3 số a, b, c thỏa mãn đồng thời: a + b + c = 6 và 2 2 2 a + b + c =12.
Tính giá trị của biểu thức: = ( − )2023 + ( − )2023 + ( − )2023 P a 3 b 3 c 3 .
Họ và tên học sinh:...................................................Số báo danh:..........
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KHẢO SÁT CHẤT LƯỢNG KIẾN XƯƠNG
HỌC KỲ I NĂM HỌC 2023 – 2024 MÔN TOÁN 8
I/ TRẮC NGHIỆM. (2,0 điểm) Mỗi câu đúng được 0,5 điểm Câu 1 2 3 4 Đáp án A C D B
II/ TỰ LUẬN. (8,0 điểm)
Bài 1: (1,5 điểm)
1. Phân tích các đa thức sau thành nhân tử. a) x2 – xy + 5x – 5y b) 2 2 x − 2xy − 25 + y
2. Chứng minh giá trị biểu thức sau không phụ thuộc vào giá trị của biến x.
A = ( x – 5)( x + 5) – x( x+ 1) + x + 12 Bài Nội dung Điểm
1.a) x2 – xy + 5x – 5y
= (x2 – xy) + (5x – 5y) = x(x – y) + 5(x - y) 0,25 = (x – y)(x + 5) 0,25 1.b) 2 2
x − 2xy − 25 + y 2 2 2 2
= (x − 2xy + y ) − 25 = (x − y) − 5 0,25
= (x − y − 5)(x − y + 5) 0,25 Bài 1
(1,5 đ) 2. Ta có: A = (x + 5 )(x – 5) – x(x + 1) + x + 12 2 2 2 2
= x − 25 − x − x + x +12 = (x − x ) + (x − x) + ( 25 − +12) 0,25 = 0 + 0 + ( 13 − ) = 13 −
Vậy giá trị của biểu thức A không phụ thuộc vào giá trị của biến x. 0,25  x 2 1  3
Bài 2: (2,0 điểm) Cho biểu thức: A = − +   : với x ≠ 2 ± 2
 x − 4 x − 2 x + 2  x − 2
b) Rút gọn biểu thức A b) Tính giá trị của A khi x thoả mãn: 2 x − 2x = 0
c) Tìm x nguyên lớn nhất để biểu thức A nhận giá trị nguyên. Bài Đáp án Điểm  x 2 1  3 ≠ ± A = − +   : ĐKXĐ: x 2 2  x − 4 x − 2 x + 2  x − 2 Bài 2:  x 2 1  3 (2,0 đ) A = − +   : 0,25đ
 (x − 2)(x + 2) x − 2 x + 2  x − 2  x 2(x + 2) 1(x − 2)  x − 2 A = − +  .
(x − 2)(x + 2) (x − 2)(x + 2) (x − 2)(x + 2)  3
x − 2x − 4 + x − 2 x − 2 A = . 0,25đ (x − 2)(x + 2) 3 6 − x − 2 A = . (x − 2)(x + 2) 3 2 A − = x 0,25đ + 2 . 2 − Vậy A = ≠ ± x với x 2 + 2 0,25đ
b) Tính giá trị của A khi x thoản mãn: 2 x − 2x = 0 Ta có: 2 x − 2x = 0
⇔ x(x − 2) = 0 x = 0
x = 0 (Tm x ≠ 2) ± ⇔ ⇔  x 2 0  − =
x = 2 (Ktm x ≠ 2) ± 0,25 2
Với x = 0 thay vào biểu thức A ta được: A − = = 1 − 0 + 2
Vậy A = - 1 khi x thỏa mãn: 2 x − 2x = 0 0,25
( Không đối chiếu với ĐKX Đ trừ 0,25 điểm )
c) Tìm x nguyên lớn nhất để biểu thức A nhận giá trị nguyên. 2 − Ta có: A = với x ≠ 2 ± x + 2
Do x nguyên nên x + 2 nguyên.
Khi đó biểu thức A nhận giá trị nguyên khi 2 − nhận giá trị nguyên x + 2 0,25
⇔ 2 (x + 2) ⇔ x + 2 là ước của 2 ⇔ x + 2∈{ 1; ± ± } 2
Vì x là số nguyên lớn nhất nên x + 2 nhận ước nguyên lớn nhất
⇒ x + 2 = 2 ⇒ x = 2 − 2 = 0 (T / m)
Vậy x = 0 là giá trị cần tìm. 0,25
(Không đối chiếu với ĐKX Đ trừ 0,25 điểm )
Bài 3: (1,5 điểm) Cho hàm số: y = (m – 1)x − 1 có đồ thị là đường thẳng d.
1) Tìm điều kiện của m để hàm số trên là hàm số bậc nhất.
2) Khi m = 3, hãy vẽ đồ thị hàm số rồi tính khoảng cách từ gốc toạ độ O(0; 0) đến đường thẳng d. Bài Nội dung Điểm
1/a) Để hàm số y = (m – 1)x − 1 là hàm số bậc nhất thì m −1 ≠ 0 ⇔ m ≠ 1 0,25
Vậy với m ≠ 1 thì hàm số trên là hàm số bậc nhất.
c) Vẽ đồ thị hàm số:
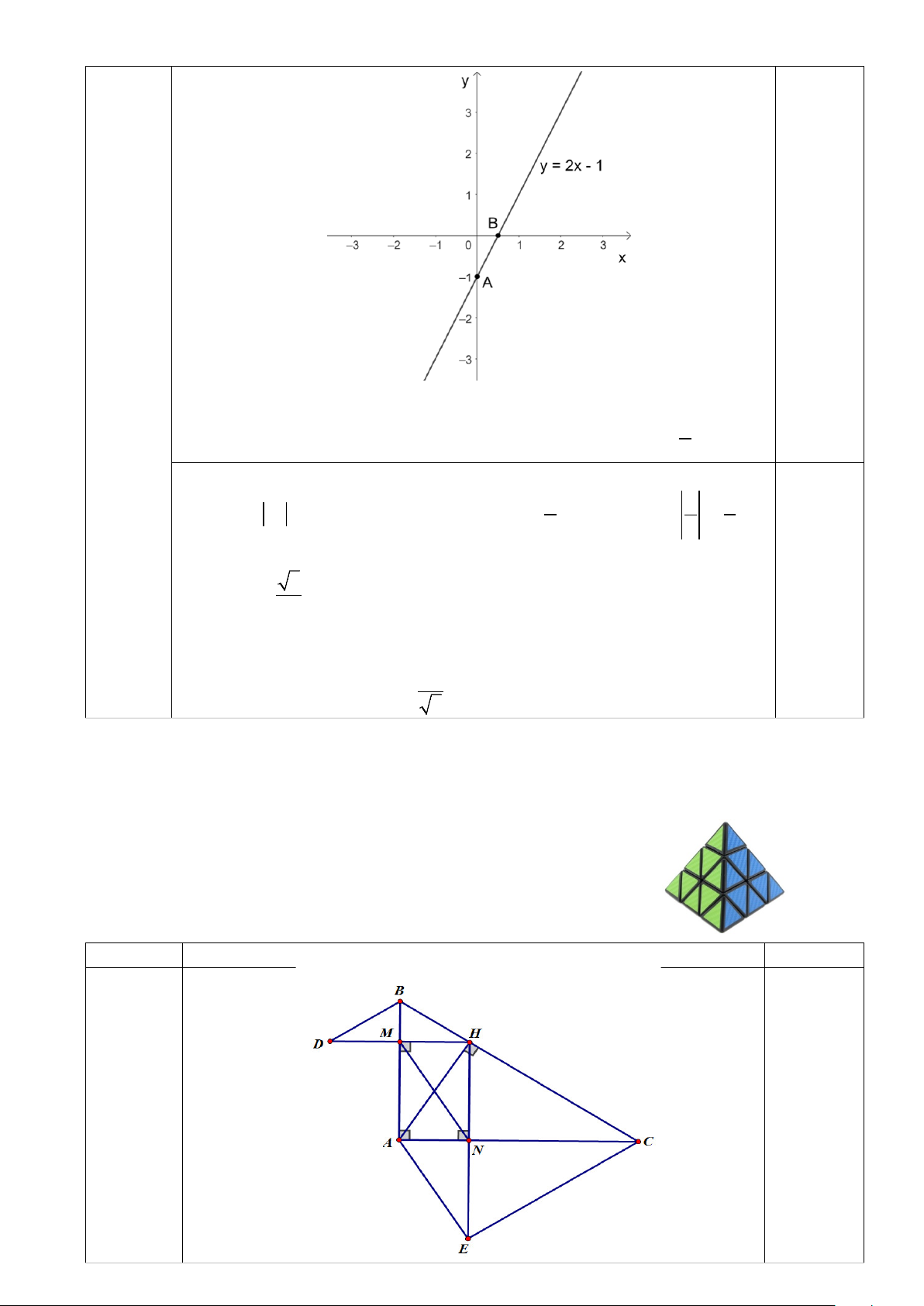
Bài 3 +Với m = 3 hàm số trở thành: y = 2x − 1 0,25
(1,5 đ) + Chox = 0 => y = 1 − => A(0;− ) 1 ∈Oy 0,25 Cho 1  1 y 0 x B ;0 = => = ⇒ ∈   Ox 2  2  +Vẽ đồ thị hàm số. 0,25 Vậy với m = 3:
Đồ thị hs là đường thẳng đi qua 2 điểm A (0; −1) và B( 1 ; 0) 2
b) Khi m = 3, đồ thị hàm số y = 2x − 1 cắt trục Oy tại điểm A(0; -1) => OA = 1
− = 1 và cắt trục Ox tại điểm B( 1 ; 0) => OB 1 = = 1 2 2 2
+ Do tam giác OAB vuông tại O nên áp dụng định lý pytago tính được AB = 5 0,25 2
+Vẽ OH ⊥(d) (H thuộc d) => khoảng cách từ O(0;0) đến d bằng OH, Ta có: OA. OB = OH.AB (= 2S OAB) (1)
Từ đó tính được OH = 1 5 0,25
Bài 4: (2,5 điểm) 1) Cho AB ∆
C vuông tại A có đường cao AH. Từ H kẻ HN ⊥ AC , HM ⊥ AB .
a) Chứng minh tứ giác AMHN là hình chữ nhật.
b) Lấy D sao cho M là trung điểm của DH, lấy E sao cho N là trung điểm của EH.
Chứng minh tứ giác AMNE là hình bình hành. c) Chứng minh: 2 2 2 BC = BD + CE + 2BH.HC .
2) Một khối Rubik có dạng hình chóp tam giác đều. Biết
chiều cao bằng 5,2 cm, thể tích của khối Rubic là 45,24 cm3.
Tính diện tích đáy của khối Rubik. Bài 4 Nội dung Điểm 1) (2,0 đ) Xét tứ giác AMNH có:  MAN = 90° ( A
∆ BC vuông tại A ) 
AMH = 90° (HM ⊥ AB) 0,5 
ANH = 90° (HN ⊥ AC)
Vậy tứ giác AMHN là hình chữ nhật (vì có 3 góc vuông) 0,5
b) Tứ giác: AMNE có: AM =
HN (cạnh đối hình chữ nhật AMHN) EN =
HN (N là trung điểm của EH) ⇒ AM = NE Lại có 0,25
AM //NE ( AM // HN và H, N, E thẳng hàng)
Vậy tứ giác AMNE là hình bình hành (Tứ giác có 2 cạnh đối
song song và bằng nhau là hình bình hành) 0,25
c) Ta có AB ⊥ DH tại M (gt)
M là trung điểm của DH (gt)
⇒ AB là đường trung trực của DH
⇒ BD = BH ( 1 )
Tương tự có CE = HC ( 2 ) + Do 0,25
BC = BH + HC 2 2 2
⇒ BC = BH + HC + 2 BH. HC ( 3 ) Từ (1), (2) và (3) 2 2 2
⇒ BC = BD + EC + 2 BH. HC (đpcm) 0,25
2) 0,5đ 2) Diện tích đáy của khối Rubik đó là : Ta có: 1 2
V = S.h ⇒ S = 3V : h = 3.45,24 : 5,2 = 26,1cm 0,25 3
Vậy diện tích đáy của khối Rubik là 2 26,1cm 0,25
Bài 5: (0,5 điểm) Cho a, b, c thỏa mãn đồng thời a + b + c = 6 và 2 2 2 a + b + c =12.
Tính giá trị của biểu thức : = ( − )2023 + ( − )2023 + ( − )2023 P a 3 b 3 c 3 . Bài Nội dung Điểm Ta có : 2 2 2 2 2 2
a + b + c = 12 ⇒ a + b + c −12 = 0 2 2 2 2 2 2
⇔ a + b + c − 24 +12 = 0 ⇔ a + b + c − 4(a + b + c) +12 = 0 2 2 2
⇔ a − 4a + 4 + b − 4b + 4 + c − 4c + 4 = 0 Bài 5
⇔ (a − )2 + (b − )2 + (c − )2 2 2 2 = 0 (0,5 đ) a − 2 = 0 
⇔ b − 2 = 0 ⇔ a = b = c = 2 0,25  c − 2 =  0
Thay a = b = c = 2 vào P, ta được
⇒ P = (2 − 3)2023 + (2 − 3)2023 + (2 − 3)2023 = (− )2023 1 + (− )2023 1 + (− )2023 1 = 3 − 0,25
Vậy P = - 3 khi a, b, c thỏa mãn đề bài.
Chú ý: Học sinh làm cách khác đúng vẫn được điểm tối đa.
Điểm bài khảo sát là tổng điểm các bài thành phần, làm tròn đến 0,5.