UBND THÀNH PHỐ THÁI BÌNH
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I NĂM HỌC 2023 - 2024
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN 8
Thời gian làm bài: 90 phút (không kể thời gian giao đề) (Đề gồm 02 trang)
I. TRẮC NGHIỆM (3,0 điểm). Hãy chọn đáp án phù hợp nhất trong các câu hỏi sau:
Câu 1. Bậc của đơn thức 2023xy3z4 là: A. 7 B. 12 C. 8 D. 9
Câu 2. Đồ thị hàm số y  2
 x  3 song song với đồ thị hàm số: A. y  2  x 1 B. y  2x  3 C. y  2  x  3 D. y  4x  7
Câu 3. Điều kiện xác định của biểu thức 2023x Q  x  là: 2 A. x  0 B. x  0 ; x  2 C. x  2  D. x  2
Câu 4. Kết quả phép nhân x  2y2x  y là: A. 2 2 2x  2y B. 2 2 2x  3xy  2y C. 2 2 2x  3xy  2y D. 2 2 2x  5xy  2y
Câu 5. Trong các hàm số sau, hàm số bậc nhất là: 2 A. y  4  x  3 B. y   3 C. 2 y  2x  1 D. y  x  2 x
Câu 6. Cho đa thức P thỏa mãn    3
x 1 P  x 1. Khi đó đa thức P là: A. 2 x x 1 B. 2 x  2x 1 C. 2 x  x 1 D. 2 x  2x 1
Câu 7. Hình nào sau đây là hình vuông ?
A. Tứ giác có ba góc vuông.
B. Hình bình hành có một góc vuông.
C. Hình thang cân có một góc vuông.
D. Hình chữ nhật có hai cạnh kề bằng nhau.
Câu 8. Cho một hình chóp tam giác đều có diện tích đáy là 15cm2 và chiều cao là 8cm. Khi đó
thể tích của hình chóp tam giác đều đó là: A. 48cm3 B. 30cm3 C. 60cm3 D. 40cm3
Câu 9. Cho hình chữ nhật MNPQ. Đoạn thẳng MP bằng đoạn thẳng nào sau đây ? A. MN B. NQ C. MQ D. NP
Câu 10. Tứ giác ABCD có µ o µ o o
A  60 ; B  70 ; C  80 . Khi đó µ D bằng: A. 130o B. 160o C. 150o D. 140o
Câu 11. Cho hình thoi ABCD có AC = 6cm; BD = 8cm. Khi đó cạnh của hình thoi bằng: A. 5cm B. 6cm C. 8cm D. 10cm   2 3 b a
Câu 12. Rút gọn phân thức 9a  ta được kết quả là: b b  a a  b a  b A. B. C. 3a  b D. 3 6 3
II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)  Cho biểu thức x 3 6x 4 P       . 2 x 1 x 1 x  với x 1 ; x 1 1 1. Rút gọn P.
2. Tính giá trị của P khi x  2 .
Bài 2. (2,0 điểm)
1. Phân tích mỗi đa thức sau thành nhân tử: a) 2 2 3x y  9xy b) 2 2 x  2x  y  2y  
2. Biết rằng đồ thị hàm số y  ax  2 đi qua điểm 1 K ; 1  
 . Tìm a và vẽ đồ thị của hàm số  2 
với giá trị a vừa tìm được.
Bài 3. (3,0 điểm)
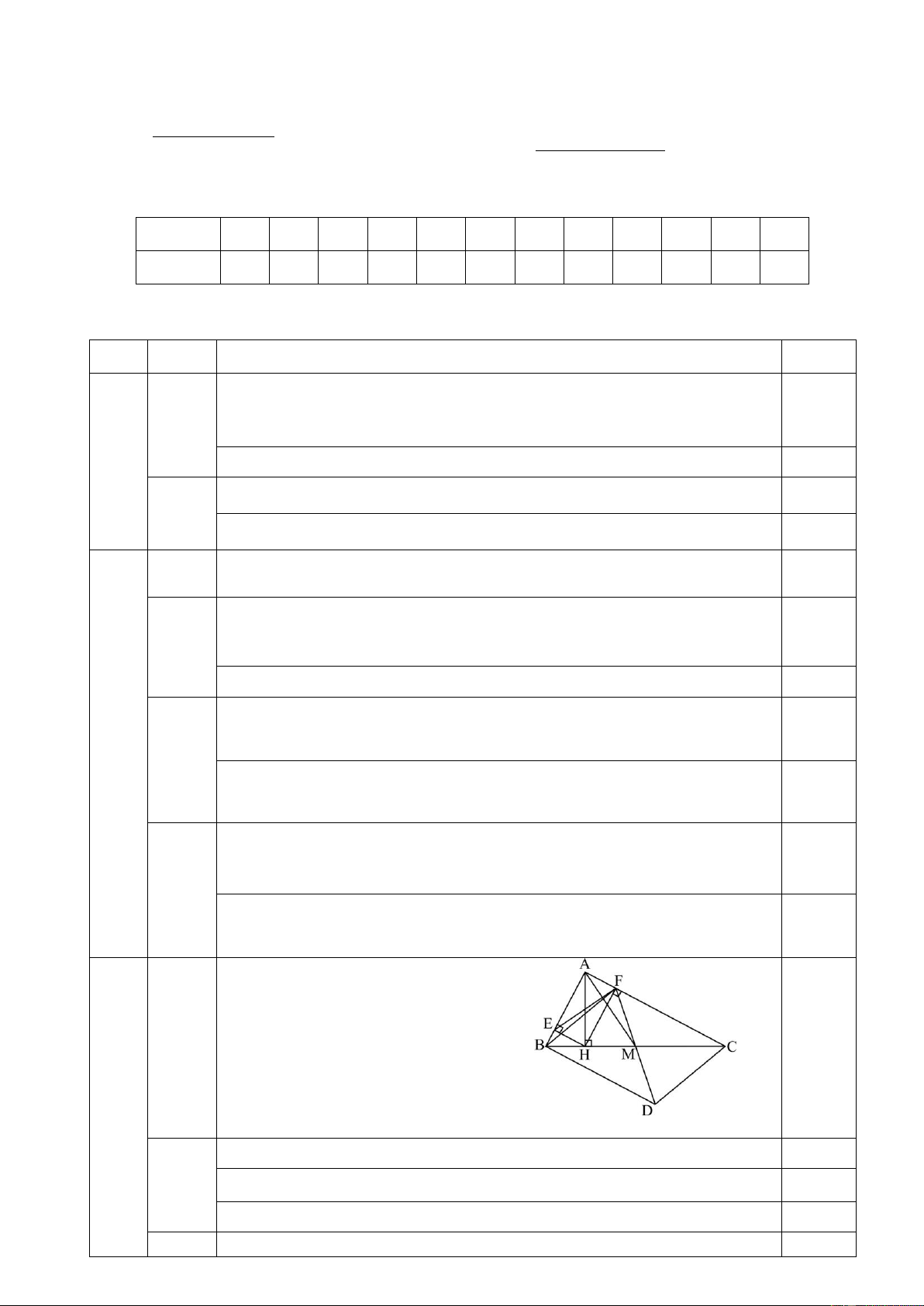
Cho tam giác ABC vuông ở A (AB < AC) đường cao AH, trung tuyến AM. Gọi E, F lần lượt
là hình chiếu vuông góc của H trên AB, AC.
1. Chứng minh tứ giác AEHF là hình chữ nhật.
2. Đường thẳng qua B vuông góc với AB cắt đường thẳng FM ở D. Chứng minh tứ giác BDCF là hình bình hành.
3. Chứng minh AM vuông góc với EF.
Bài 4. (0,5 điểm) Tìm a, b thỏa mãn 4 4    2 2      2 2 a b a b
6 2ab 3  3a b  9  0 . ----- Hết -----
Họ và tên học sinh:…………………………………….. Số báo danh: …………….. UBND THÀNH PHỐ THÁI BÌNH
HƯỚNG DẪN CHẤM KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2023 – 2024 MÔN: TOÁN 8
(Hướng dẫn chấm gồm 02 trang)
I. PHẦN TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C A D B A C D D B C A D II. PHẦN TỰ LUẬN Bài Câu Nội dung Điểm x 3 6x  4 x x   1  3x   1  6x  4 P    0,25 2 x 1 x 1 x  = 1 x   1 x   1 2 2
x  x  3x  3  6x  4 x  2x 1   0,25 1 x   1 x   1 x   1 x   1 (1,0)   2 x 1 x 1    x   1 x   1 1 x  0,25 1 (1,5)  Vậy với x 1 x  1 ; x  1  ta có P  x  0,25 1
Xét x  2 thấy thỏa mãn x  1 ; x  1   0,25 2
Thay x  2 vào biểu thức P ta có 2 1 P  2  1 (0,5) 1  1 P 
. Vậy với x  2 thì P  0,25 3 3 1.a 2 2
3x y  9xy  3xyx  3y 0,5 (0,5) 2 2      2 2 x 2x y 2y
x  y   2x  2y 1.b 0,25
 x  yx  y  2x  y (0,5)
 x  yx  y  2 0,25  
Do đồ thị hàm số y  ax  2 đi qua điểm 1 K ; 1    nên thay  2  0,25 1 a x  ; y  1
 vào y  ax  2 ta có:  2  1  2 2 2 (2,0) a
  1  a  2. Vậy a  2 là giá trị cần tìm. 0,25 2 2
* Với a  2 ta có y  2x  2 (1,0) + Cho x  0  y  2
 . Đồ thị hàm số đi qua điểm A0; 2   0,25
+ Cho y  0  x  1. Đồ thị hàm số đi qua điểm B1;0 * Vẽ đồ thị hàm số
Đồ thị hàm số là đường thẳng đi 0,25 qua hai điểm A và B.
Vẽ hình chính xác và ghi đầy 0,5
đủ giả thiết, kết luận. 0,5 Do A  BC vuông ở A µ o  A  90 0,25 1 Ta có · · o
HE  AB, HF  AC  AEH  AFH  90 0,5 (1,0) Xét tứ giác AEHF có µ µ o A  E  F
$  90  AEHFlà hình chữ nhật 0,25 Do A
 BC vuông ở A  AB  AC. Theo giả thiết BD  AB 3 · · 0,25 2
 BD / /AC  CBD  BCF (So le trong) (3,0) (1,0) Chứng minh được B  MD  C  MF (g.c.g)  MF  MD 0,5
Tứ giác BDCF có BM = MC, MF = MD  BDCFlà hình bình hành. 0,25 · ·
AEF  EAH (Do AEHF là hình chữ nhật) (1) A
 BC vuông tại A, AM là trung tuyến nên 1 AM  MC  BC 2 · · 0,25 3  A
 MC cân tại M  CAM  ACM (2) (0,5) · ·
Mà ACM  EAH (Cùng phụ với · HAC ) (3) Từ (1), (2), (3)  · · CAM  AEF Do A  BC vuông ở A · · o  CAM  EAM  90 . 0,25 Khi đó · · o
AEF  EAM  90 . Vậy AM  EF.
Biến đổi phương trình trở thành     2    2 2 2 a ab b 3 3 a b  0 0,25 4 2 2  (0,5) a  ab  b  3    a  b  1
 . Vậy a;b  1;  1 ; 1  ;  1 0,25 a  b ----- Hết -----
Chú ý: - Trên đây chỉ là hướng dẫn chấm điểm theo bước cho một cách giải. Các cách giải
chính xác khác, giám khảo cho điểm tương ứng.
- Điểm toàn bài bằng tổng điểm từng bài, làm tròn đến chữ số phần thập phân thứ nhất. UBND THÀNH PHỐ THÁI BÌNH
ĐỀ KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I NĂM HỌC 2023 - 2024
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO MÔN: TOÁN 8
Thời gian làm bài: 90 phút (không kể thời gian giao đề) (Đề gồm 02 trang)
I. TRẮC NGHIỆM (3,0 điểm). Hãy chọn đáp án phù hợp nhất trong các câu hỏi sau:
Câu 1. Bậc của đơn thức 2023xy3z4 là: A. 7 B. 12 C. 8 D. 9
Câu 2. Trong các đơn thức sau, đơn thức đồng dạng với đơn thức 4x3y2 là: 3 A. 3 2 5x y B. 2 3 4x y C. 4 2xy D. 3 2 x y z 4
Câu 3. Kết quả khai triển   2 2x 1 là: A. 2 4x  4x 1 B. 2 2x  4x 1 C. 2 4x  4x 1 D. 2 4x  4x 1
Câu 4. Kết quả phép nhân x  2y2x  y là: A. 2 2 2x  2y B. 2 2 2x  3xy  2y C. 2 2 2x  3xy  2y D. 2 2 2x  5xy  2y 2 2
Câu 5: Kết quả rút gọn biểu thức 2x  y  x  y là: A. 2 2 x  6xy  y B. 2 2 x  y C. 2 2 2x  2xy  y D. 2 x  6xy
Câu 6. Cho đa thức P thỏa mãn    3
x 1 P  x 1. Khi đó đa thức P là: A. 2 x x 1 B. 2 x  2x 1 C. 2 x  x 1 D. 2 x  2x 1
Câu 7. Hình nào sau đây là hình vuông ?
A. Tứ giác có ba góc vuông.
B. Hình bình hành có một góc vuông.
C. Hình thang cân có một góc vuông.
D. Hình chữ nhật có hai cạnh kề bằng nhau.
Câu 8. Cho tam giác ABC phân giác AD DBC . Biết AB = 2cm, AC = 3cm, BD = 1,6cm.
Khi đó độ dài CD bằng: A. 2,8cm B. 1,8cm C. 2,2cm D. 2,4cm
Câu 9. Cho tam giác ABC, trên hai cạnh AB, AC lấy hai điểm E, F sao cho EF//BC. Biết
AE = 6cm, BE = 4cm, CF = 6cm. Khi đó độ dài AF bằng: A. 4cm B. 9cm C. 12cm D. 8cm
Câu 10. Cho tam giác ABC có chu vi là 22cm. Gọi M, N, P lần lượt là trung điểm của các
cạnh AB, AC, BC. Khi đó chu vi tam giác MNP là: A. 18cm B. 44cm C. 11cm D. 12cm
Câu 11. Cho biểu đồ biểu diễn kết quả học
tập của học sinh khối 8 năm học 2022 - 2023.
Số học sinh học lực trung bình ít hơn số học sinh học lực khá là: A. 64 B. 60 C. 74 D. 40
Câu 12. Muốn biểu diễn số ngày trời không mưa, mưa nhỏ, mưa vừa, mưa to trong một tháng ta nên dùng biểu đồ:
A. Biểu đồ đoạn thẳng. B. Biểu đồ cột kép.
C. Biểu đồ hình quạt tròn. D. Biểu đồ cột.
II. TỰ LUẬN (7,0 điểm)
Bài 1. (1,5 điểm)
1. Rút gọn biểu thức  
       2 P 3x y x 3y 3 x y 2. Cho x  y  2
 . Tính giá trị biểu thức       2 2 Q x 2x y 1 y 1  2023 .
Bài 2. (2,0 điểm)
1. Phân tích mỗi đa thức sau thành nhân tử: a) 2 2 3x y  9xy b) 2 2 x  2x  y  2y 2. Tìm x biết: a) 2 x  2x  0 b) 2 x x   1  4x  4  0
Bài 3. (3,0 điểm)
Cho tam giác ABC vuông ở A (AB < AC) đường cao AH. Gọi E, F lần lượt là hình chiếu
vuông góc của H trên AB, AC.
1. Chứng minh tứ giác AEHF là hình chữ nhật.
2. Gọi M là trung điểm của BC. Đường thẳng qua B vuông góc với AB cắt đường thẳng FM ở
D. Chứng minh tứ giác BDCF là hình bình hành.
3. Chứng minh BE.AC  CF.AB  AB.AC.
Bài 4. (0,5 điểm) Tìm a, b thỏa mãn 4 4    2 2      2 2 a b a b
6 2ab 3  3a b  9  0 . ----- Hết -----
Họ và tên học sinh:…………………………………….. Số báo danh: …………….. UBND THÀNH PHỐ THÁI BÌNH
HƯỚNG DẪN CHẤM KHẢO SÁT CHẤT LƯỢNG HỌC KỲ I
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
NĂM HỌC 2023 – 2024 MÔN: TOÁN 8
(Hướng dẫn chấm gồm 02 trang) I. TRẮC NGHIỆM Câu 1 2 3 4 5 6 7 8 9 10 11 12 Đáp án C A D B A C D D B C A D II. TỰ LUẬN Bài Câu Nội dung Điểm
         2 P 3x y x 3y 3 x y 0,5 0,75 2 2      2 2 3x 10xy 3y 3 x  2xy  y  1 2 2 2 2
 3x 10xy  3y  3x  6xy  3y  4xy 0,25 (1,5)       2      2 2 Q x 2x y 1 y 1 2023 x y 1  2023 0,5 0,75 Thay x  y  2
 vào biểu thức Q ta có   2 Q 1  2023  2024 0,25 1.a 2 2
3x y  9xy  3xyx  3y 0,5 (0,5) 2 2      2 2 x 2x y 2y
x  y   2x  2y 1.b 0,25
 x  yx  y  2x  y (0,5)
 x  yx  y  2 0,25 x  0 2
x  2x  0  x x  2  0   0,25 2    2.a x 2 0 (2,0) (0,5) x  0   Vậy x 0;  2 0,25 x  2 2    2 x
x 1  4x  4  0  x x   1  4x   1  0 0,25 2     2.b x  1 x 4 0 (0,5) x 1  0 x  1     Vậy x 1,  2 0,25 2 x  4  0 x  2 
Vẽ hình chính xác và ghi đầy 0,5
đủ giả thiết, kết luận. 0,5 3 (3,0) Do A  BC vuông ở A µ o  A  90 0,25 1 Ta có · · o
HE  AB, HF  AC  AEH  AFH  90 0,5 (1,0) Xét tứ giác AEHF có µ µ o A  E  F
$  90  AEHFlà hình chữ nhật 0,25 2 Do A
 BC vuông ở A  AB  AC. Theo giả thiết BD  AB 0,25 (1,0) · ·
 BD / /AC  CBD  BCF (So le trong) Chứng minh được B  MD  C
 MFg.c.g  MF  MD 0,5
Tứ giác BDCF có BM = MC, MF = MD  BDCFlà hình bình hành. 0,25
Do HE//AC, HF//AB. Áp dụng định lý ta lét ta có: 3 BE BH CF CH BE CF  0,25 ;     1 (0,5) AB BC AC BC AB AC  BE.AC CF.AB  AB.AC 0,25
Biến đổi phương trình trở thành     2    2 2 2 a ab b 3 3 a b  0 0,25 4 2 2  (0,5) a  ab  b  3    a  b  1
 . Vậy a;b  1;  1 ; 1  ;  1 0,25 a  b ----- Hết -----
Chú ý: - Trên đây chỉ là hướng dẫn chấm điểm theo bước cho một cách giải. Các cách giải
chính xác khác, giám khảo cho điểm tương ứng.
- Điểm toàn bài bằng tổng điểm từng bài, làm tròn đến chữ số phần thập phân thứ nhất.
Document Outline

• Toán 8 HKI 23_24 _Cánh Diều_
• Toán 8 HKI 23_24 _Kết nối TT_