Đề học sinh giỏi cấp tỉnh Toán 11 chuyên năm 2020 – 2021 sở GD&ĐT Lạng Sơn

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN
LỚP 11 NĂM HỌC 2020 - 2021
Môn thi: TOÁN lớp 11 CHUYÊN ĐỀ THI HÍNH THỨ
Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi: 18/3/2021
(Đề thi gồm 01 trang, 05 câu)
Câu 1 (5 điểm). Giải hệ phương trình sau trên tập số thực . 2 3 2
x  x y  xy  xy  y 1  4 2
x  y  xy  2x   1  1 u   m 
Câu 2 (6 điểm). ho số u c nh i 1  n  2 * u 
 u  2u  2, n    n 1 n n 3 a) Khi m 
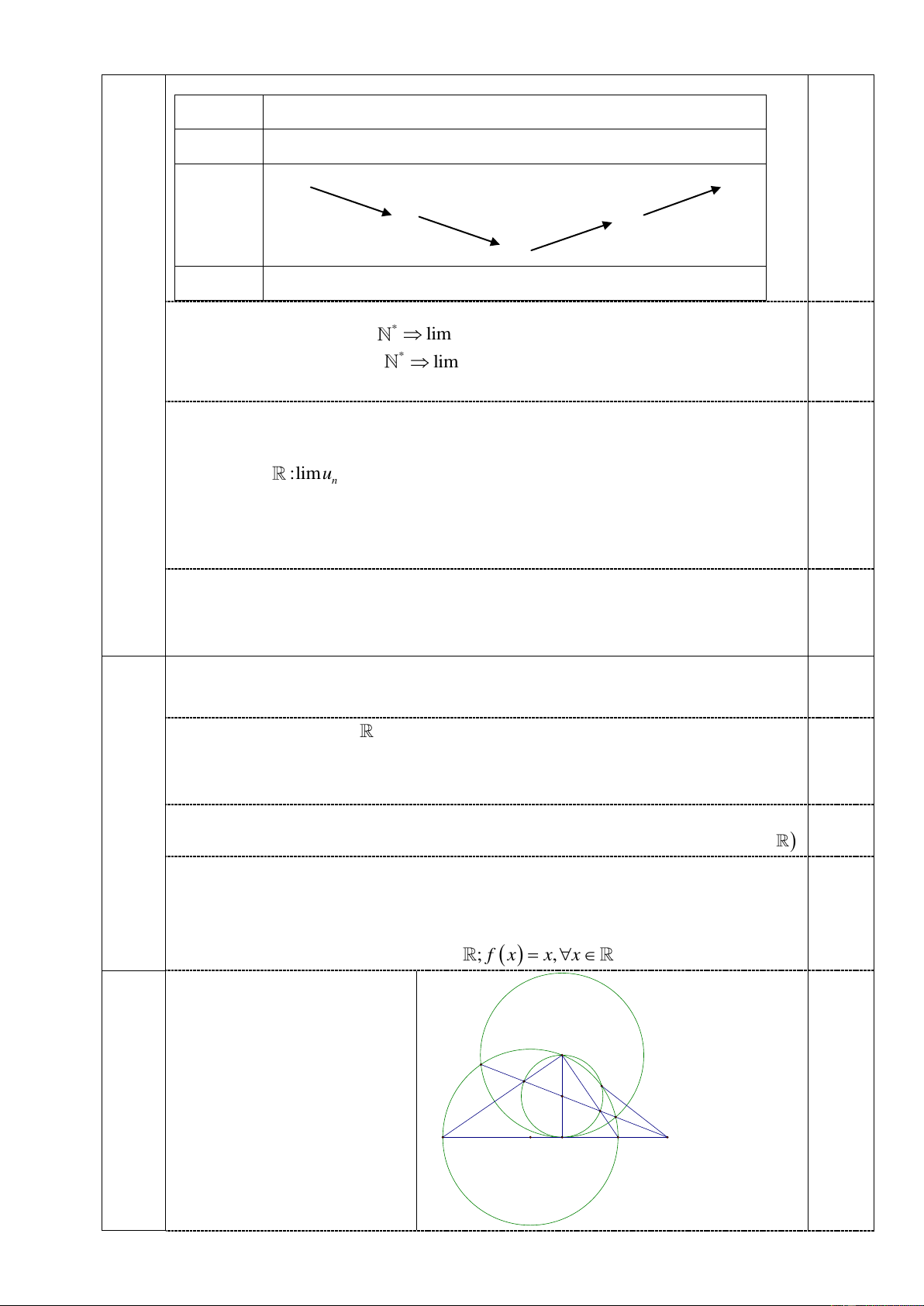
, ch ng minh số c gi i h n h u h n v tìm gi i h n 2
c nh t t cả c c gi tr c a m số u c gi i h n h u h n. n 
Câu 3 (2 điểm). Tìm t t cả các h m số f :  thỏa m n iều kiện: f   x  
1 f  y  yf  f  x 1 ,  , x y      .
Câu 4 (5 điểm). ho ường tròn tâm O ường kính AB . L i m H trên o n thẳng
AB ( H không trùng , A ,
O B ) Đường thẳng qua H vuông g c v i AB cắt ường tròn
O t i C Đường tròn ường kính CH cắt AC, BC và O lần lượt t i , D E và F .
a) h ng minh rằng các ường thẳng A ,
B DE và CF ồng qu
b) Đường tròn tâm C bán kính CH cắt O t i P và Q h ng minh rằng bốn i m , P ,
D E, Q thẳng h ng
Câu 5 (2 điểm). ho 167 tập hợp A , A , ,  A có tính ch t: 1 2 167
i) A  A  A  2004; 1 2 6 1 7
ii) A  A . A  A v i i, j  1, 2, ,
 167 và i  j . i j i j Hãy:
a h ng minh rằng | A |12 v i i 1,2,...,167. i 167 b) Tính  A . i i 1 
--------------------Hết---------------------
Họ v tên thí sinh: …………………………………… Số o anh: ……………………
h kí gi m th số 1:……………………… h kí gi m th số 2:…………………………
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH LẠNG SƠN
LỚP 11 NĂM HỌC 2020 - 2021
HƯỚNG DẪN CHẤM THI MÔN TOÁN LỚP 11 CHUYÊN
(Hướng dẫn chấm gồm 03 trang)
Chú ý: Nh ng c ch giải kh c HD m úng thì cho i m theo thang i m nh Câu Nội dung Điểm 1  2  x  y 
 xy 2x  y xy 1 (5đ)   1   1.0  x  y  2 2  xy  1 2
a  x  y
a  ab  b  1 Đặt  . Hệ tr th nh:    * b   xy 2 a  b  1 3 2
a  a  2a  0 a 2 a  a  2    0 1.0 *     2 2 b   1 a b   1 a Từ ta c :  ; a b    0; 1;1;0; 2  ; 3   2 x  y  0 V i  ; a b  0;  1 ta c hệ: 
 x  y  1 1.0 xy  1 2 x  y  1 V i  ;
a b  1;0 ta c hệ:    ; x y    0; 1;1;0; 1  ;0 1.0 xy  0 2 x  y  2  V i  ; a b   2  ; 3   ta c hệ:  xy  3   3  3 y   y      x  x   x  1  ; y  3 1.0  3 
x  2x  3  0 x   1 
 2x  x 3  0
Kết luận: Hệ phương trình c c c nghiệm:
 ;x y 1; 1;0; 1;1;0; 1  ;0; 1  ;3 2
a) Bằng quy n p, ch ng minh ược u  1;2   1 1.0 n 
(6 đ) Xét f x 2
 x  2x  2, x  1;2 0.5
f ' x  2x  2  0, x  1;2 5 Có 2
u  u  2u  2 
 u . Suy ra u là dãy giảm 2 1.0 n  2 1 1 1 4 Từ   1 ,2 suy ra L
  :limu  L 0  L  2 . n 
L  1 (t / ) m 1.0 Chuy n qua gi i h n, ược: 2
L  L  2L  2   L  2 (l) Vậy limu  1. 0.5 n
b) Xét f  x 2
 x  2x  2
f ' x  2x  2  0  x  1   f  x x 1  x   0.5 x  2 Bảng biến thiên x  0 1 2  f ' x   0     f  x 2 2 1
f  x  x   0  0 
Từ ảng iến thiên, ta có: TH1: *
m  1  u  1, n    limu  1 n n 0.5 TH2: *
m  2  u  2, n    limu  2 n n
TH3: m  0  u  2  u  2, n
  2  limu  2 2 n n
TH4: m  1;2 , tương tự ý a) suy ra limu  1 n
TH5: m  2; . u là dãy tăng Giả sử u b chặn trên. n  n  Khi ó L
  :limu  L L  2 n  0.5 L  1 (l) Chuy n qua gi i h n, ược: 2
L  L  2L  2   L  2 (l)
Vậy limu   . n TH6: m  0; 
1  u  1; 2 . Theo TH4, suy ra limu  1. 2   n TH7: m   ;
 0  u  2; . Theo TH5, suy ra limu  . 0.5 2   n
Vậ m 0;2 thì dãy số có gi i h n h u h n 3 f   x  
1 f  y  yf  f  x 1       * (2 đ) 0.5 Chọn x  1
 ; y  0  f 0  0
Cố nh x ; L y , y 
sao cho f  y  f y . Thay vào * , ược 1   2  1 2
y f  f x 1  f  x 1 f y   f  x 1 f y   y f  f x 1  y  y 0.5 1        1 
  2  2     1 2
Suy ra f là ơn ánh.
Cho y  1, kết hợp f là ơn ánh. Ta có: 0.5 f   x    1 f  
1   f  f   x 1   x   1 f  
1  f x 1  f x  ax  , b a,b  b   0 
Thử l i th a  0 thỏa mãn.  0.5 a  1
Vậ hàm số cần tìm là f  x  0, x
  ; f x  , x x   . 4 (5 đ) C a) Ta có P F D 2 C .
ACD  CH  C . B CE , suy 1.0
ra t giác ABED nội tiếp E Q A O H B M
AB là trục ẳng phương c a O v ường tròn  ABED 0.5
DE là trục ẳng phương c a  ABED v ường tròn ường kính CH 0.5
CF là trục ẳng phương c a O v ường tròn ường kính CH 0.5
Suy ra DE, AB và CF ồng qu 0.5
b) Gọi M l giao i m c a DE, AB và CF . 0.5
Ta có PQ l trục ẳng phương c a C  và O nên OC  PQ .
Ta cũng ễ th OC  DE . 0.5
Hơn n a M chính l tâm ẳng phương c a a ường tròn C , O v ường tròn ường 0.5
kính CH . Suy ra PQ i qua M .
Vậ DE, PQ cùng i qua M v cùng vuông g c v i OC nên trùng nhau. Suy ra 0.5 , P ,
D E,Q thẳng hàng. 5
a) Giả | A  A | k  1. Suy ra A  k. A , i
 , j  1,167,i  j (mâu thuẫn) 0.5 (2 đ) i j i j
Do ó | A  A |  1
và A  12 v i i, j  1, 2, ,1
 67 và i khác j . 0.5 i j i 167 Ta sẽ ch ng minh A  1 (*). i i 1 
Thật vậ , ét tập A . Từ | A  A | 1 v i i  2, ,  167 su ra mỗi tập 1 1 i A , A , ,
 A ch a úng một phần tử c a A . Do A  12 nên theo nguyên lí 2 3 167 1 1
Đirichlet thì tồn t i v c th giả sử l 0.5 A , ,
 A cùng ch a phần tử a thuộc A . 2 15 1
Nếu có i  15 sao cho a  A thì | A  A |  1 |  A  A a  . j  \{ i  } | 1 i i j
Vậ : A   A \{a  }  b v i j  2,3, ,
 15 (1 Dễ th c c b là phân iệt nên j i  j j
từ (1) suy ra A ch a qu 12 phần tử Tr i v i kết luận A  12 . i i
Từ (* v | A  A | 1, i, j  1, 2, ,
 167 và i khác j suy ra: i j 167 167 167 0.5 A  ( ( A \ {a}) {a}  (
( A \ {a})  | {a}|=167.11+1=1838. i i i i 1  i 1  i 1 