SỞ GD&ĐT PHÚ THỌ
ĐỀ THI HỌC SINH LỚP 8 NĂM HỌC 2022-2023 Môn: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
(Không kể thời gian giao đề) Đề có 03 trang
PHẦN I: TRẮC NGHIỆM KHÁCH QUAN (8 điểm).
Chọn phương án trả lời đúng Câu 1: Cho 2
x  x  1.Giá trị biểu thức Q  6 x  5 x  4 x  3 x  2 2 2 2
2x  2x  1 bằng A. 1. B. 2. C. 3. D. 4.
Câu 2: Số dư trong phép chia x  3x  5x  7x  9 2038 cho 2
x  12x  30 bằng A. 1. B. 2038. C. 0. D. 2023. 2 2 2 2 2
Câu 3: Giá trị của phân thức
x  ax  a  a  a x  1 A  tại x  2022 2023 và a  5 bằng 2 x  2 ax a  2 a  2 2 a x  1 A. 5  . B . 31 . C. 2019 . D. 5 . 4 21 5 2022 2023 Câu 4: Phân thức 12 A 
có giá trị nhỏ nhất khi giá trị của x bằng: 2 x  4x  6 A. 2 . B . 4 . C. 2. D. 2 và 1.
Câu 5: Giá trị biểu thức  a  b  c C
với abc  1 bằng 1 a ab 1 b bc 1 c ca A. 1. B . 2. C. 2. D. 1.
Câu 6: Tổng các nghiệm của phương trình x    x 2 2 3 4
x  4x  4  0 là A. 1 11  . B. 1 . C.  . D. 11 . 3 3 3 3
Câu 7: Cho phương trình x m x  5 
 2 (ẩn x , tham số m ). Điều kiện của m để phương x  5 x  m
trình có một nghiệm duy nhất là A. m  5. B. m  5. C. m  5 . D. m  5. 3 3
Câu 8: Số nghiệm của phương trình: x  3 x   1  36 là: A. 1. B. 4 . C. 2. D. 3 . Câu 9: Ch o
hình ch ữ nhật ABC D , dự ng AH vuông
góc với BD(H ∈ BD) biết HD  9cm và
HB  16cm . Diện tích hình chữ nhật ABCD bằng A. 2 300cm . B. 2 280cm . C. 2 302cm . D. 2 310cm .
Câu 10: Cho hình bình hành ABCD , dựng AE vuông góc với CD và AF vuông góc với CB (
E;F thứ tự thuộc các cạnh CD và BC), Biết AC  25cm và EF  24cm . Khoảng cách từ A
đến trực tâm H của tam giác AEF bằng Trang 1 / 15 A. 5cm . B. 7cm . C. 8cm . D. 1cm .
Câu 11: Cho hình thangABDC(AB / /CD) có đường trung bình bằng 7cm ; độ dài đáy
AB  4cm khi đó đáy CD bằng A. 4cm .
B. 10cm . C. 7cm . D. 18cm .
Câu 12: Cho tam giác ABC có AB  6 , cm AC
 8cm . Các đường trung tuyến BD và CE
vuông góc với nhau. Độ dài BC là
A. 3 . B.2 5 . C. 5 . D. 5 . 2 2 3
Câu 13: Cho tam giác ABC vuông tại A ; đường cao AH vuông góc với BC, H  BC . Biết HB  9 ,
cm HC  16cm . Độ dài cạnh ,
AB AC lần lượt là
A. 15cm và 20cm. B. 12 cm và 23cm. C. 14cm và 21cm. D. 18cm và 17cm.
Câu 14: Trong tam giác ABC , đường trung tuyến AM M  BC ,K là một điểm nằm trên đoạn thẳng AK AM sao cho 1
 , BK cắt AC ở N . Biết diện tích tam giác ABC bằng KM 2 2
60cm , khi đó diện tích tam giác AKN là A. 2 20cm . B. 2 30cm . C. 2 3cm . D. 2 2cm .
Câu 15. Số bàn thắng ghi được trong mỗi trận đấu (không tính loạt sút luân lưu) của một giải
bóng đá được ghi lại trong bảng sau: Số bàn thắng 0 1 2 3 4 5 Số trận 4 7 8 9 2 2
Hỏi trong giải đấu đó có thể có nhiều nhất bao nhiêu trận đấu kết thúc với tỉ số hòa (trong 90
phút thi đấu chính thức)? A.32. B.4. C. 7. D. 14.
Câu 16: Trong một kì thi Hội khỏe Phù Đổng trường A có 12 học sinh giành được các giải
thưởng, trong đó: 7 học sinh giành được ít nhất 2 giải, 4 học sinh giành được ít nhất 3 giải, 2 học
sinh giành được số giải nhiều nhất, mỗi em 4 giải. Số giải trường A giành được là: A. 26. B. 25. C. 24 . D. 23.
II. PHẦN TỰ LUẬN (12,0 điểm) Câu 1. (3,0 điểm)
a) Tìm tất cả các số tự nhiên n để 4 2
B  n  27n  121 là số nguyên tố
b) Giải phương trình nghiệm nguyên sau: 2
x  x   4 4 1 y . c) Biết ;
a b là các số nguyên dương thỏa mãn 2 2
a − ab + b chia hết cho 9, chứng minh rằng
cả a và b đều chia hết cho 3. Trang 2 / 15 Câu 2. (4,0 điểm)
a) Cho hai số thực khác nhau 1 1 2
a,b thóa mãn:   , 2 2 a  1 b  1 1  ab
Tính giá trị của biểu thức: 1 1 M   . 2023 2023 a  1 b  1  2   x  2 2  3 x   3 7x   9
b) Giải phương trình      6    0. x  2    x  2 2 x  4
c) Tìm a,b để f x 3 2
 ax  bx  10x  4 chia hết cho đa thức g x 2
 x  x  2 .
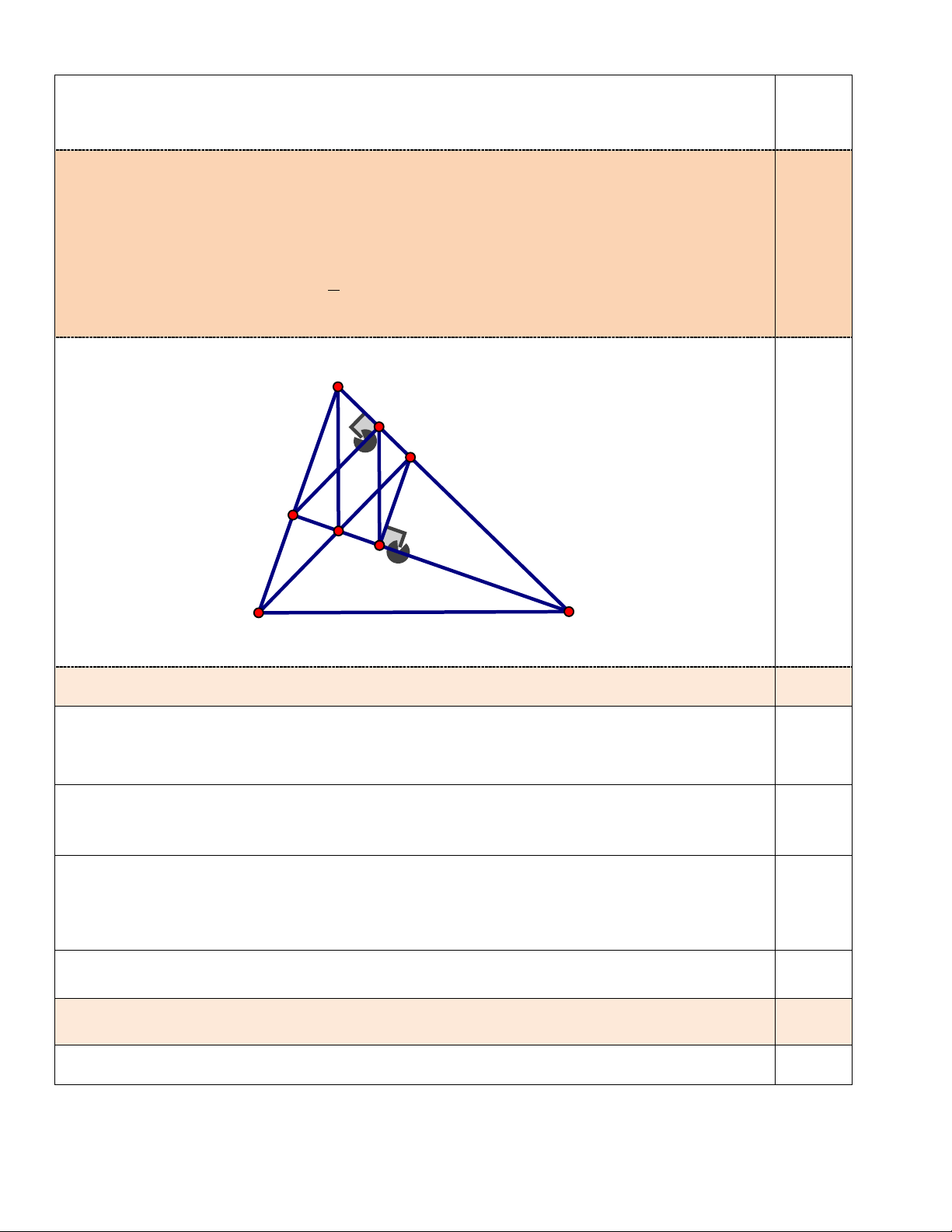
Câu 3. (4 điểm) Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau ở H.
a) Chứng minh: AB  D  AC  E
b) Chứng minh: CH.CE  CD.CA
c) Kẻ EK  AC tại K; DI  EC tại I. Chứng minhAH / /IK d) Chứng minh 1 S  S EI  K 4 A  BC
Câu 4 (1 điểm). Cho x, y là các số dương thỏa mãn điều kiện x  y  6.Tìm giá trị nhỏ nhất của biểu thức 6 8
M  3x  2y    x y
Thí sinh không được sử dụng tài liệu
Cán bộ coi thi không giải thích gì thêm!!! ----- Hết-----
Họ và tên: ……………………………………………………. SBD:…………………… Trang 3 / 15
ĐỀ THI CHỌN HỌC SINH GIỎI
SỞ GD&ĐT PHÚ THỌ NĂM HỌC 2022-2023 Môn: Toán 8
Thời gian làm bài: 150 phút Đề chính thức
( không kể thời gian giao đề) HƯỚNG DẪN CHẤM
(Mỗi câu trả lời đúng được 0,5 điểm) Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
Đ.A D D B C D A C C A B C B A D D C
Hướng dẫn chi tiết Câu 1: Cho 2
x  x  1.Giá trị biểu thức 6 5 4 3 2
Q  x  2x  2x  2x  2x  2x  1 là A. 1 B. 2 C. 3 D. 4 Lời giải Ta có 2 2
x  x  1  x  x  1  0. Ta có 6 5 4 3 2
Q  x  2x  2x  2x  2x  2x  1 4 Q  x  2 x  x   3 1  x  2 x  x   2 1  2x  2 x  x   1  x  2 x  x   1  3 2 x  x   1  4  4 Chọn D.
Câu 2: Số dư trong phép chia x  3x  5x  7x  9 2038 cho 2
x  12x  30 là A. 1 B. 2038 C. 0 D. 2023 Lời giải
Ta có: x  x  x  x     2 x  x   2 3 5 7 9 2035 12 27 x  12x   35  2035 Đặt 2
x  12x  30  a ta có  2 x  x 
 2x  x   2 12 27 12
35  2035  a  2a  2023 Chọn D. 2 2 2 2 2
Câu 3: Giá trị của phân thức
x  ax  a  a  a x  1 A  tại 2022 x  2023 và a  5 là: 2 2 2 2 2
x ax a  a  a x  1 A. 5  B . 31 C. 2019 D. 5 4 21 5 2022 2023 Lời giải 1  2x  1 2 2 2 2 2 2 a  a x ax a a a x        2 1 Ta có: a  a  1 A    . 2 2 2 2 2
x ax a  a  a x  1
 2x  1 2a a   2 1 a a  1 Trang 4 / 15 Chọn B. Câu 4: Phân thức 12 A 
có giá trị nhỏ nhất khi giá trị của x bằng: 2 x  4x  6 A. 2 B . 4 C. 2 D. 2 và 1 Lời giải Ta có: 12 12 A   . Chọn C. 2 x  4x  6 x 22  2
Câu 5: Giá trị biểu thức a b c C   
(với abc  1) là : 1 a ab 1 b bc 1 c ca A. 1 B . 2 C. 2 D. 1 Lời giải Ta có: a b c a b bc C       1 a ab 1 b bc 1 c ca
abc a ab 1 b bc
b bc bca 1 b bc     1. Chọn D. bc  b  1 1  b  bc 1  b  bc
Câu 6: Tổng các nghiệm của phương trình x    x 2 2 3 4
x  4x  4  0 là A. 1  B. 1 C. 11  D. 11 3 3 3 3 Lời giải
Ta có: x    x 2 x  x   2 2 3 4 4
4  0  3x  x  10  0 . Chọn A.
Câu 7: Cho phương trình x m x  5 
 2 (ẩn x , tham số m ). Điều kiện của m để phương x  5 x  m
trình có một nghiệm duy nhất là A. m  5 B. m  5 C. m  5 D. m  5 Lời giải    Điều kiện x 5  . x   m   x  m x  5 
 2  2x m  5 2
 m  10m  25  0 . x  5 x  m m   5 
Để phương trình có nghiệm duy nhất thì  m   5   5 
 m  5 . Chọn C.  2  m   5  m    2
Câu 8: Số nghiệm của phương trình: x  3 x  3 3 1  36 là: A. 1 B. 4 C. 2 D. 3
Lời g iả i Trang 5 / 15
x  3 x  3 2 3
1  36  6x  24x  10  0 . Chọn C.
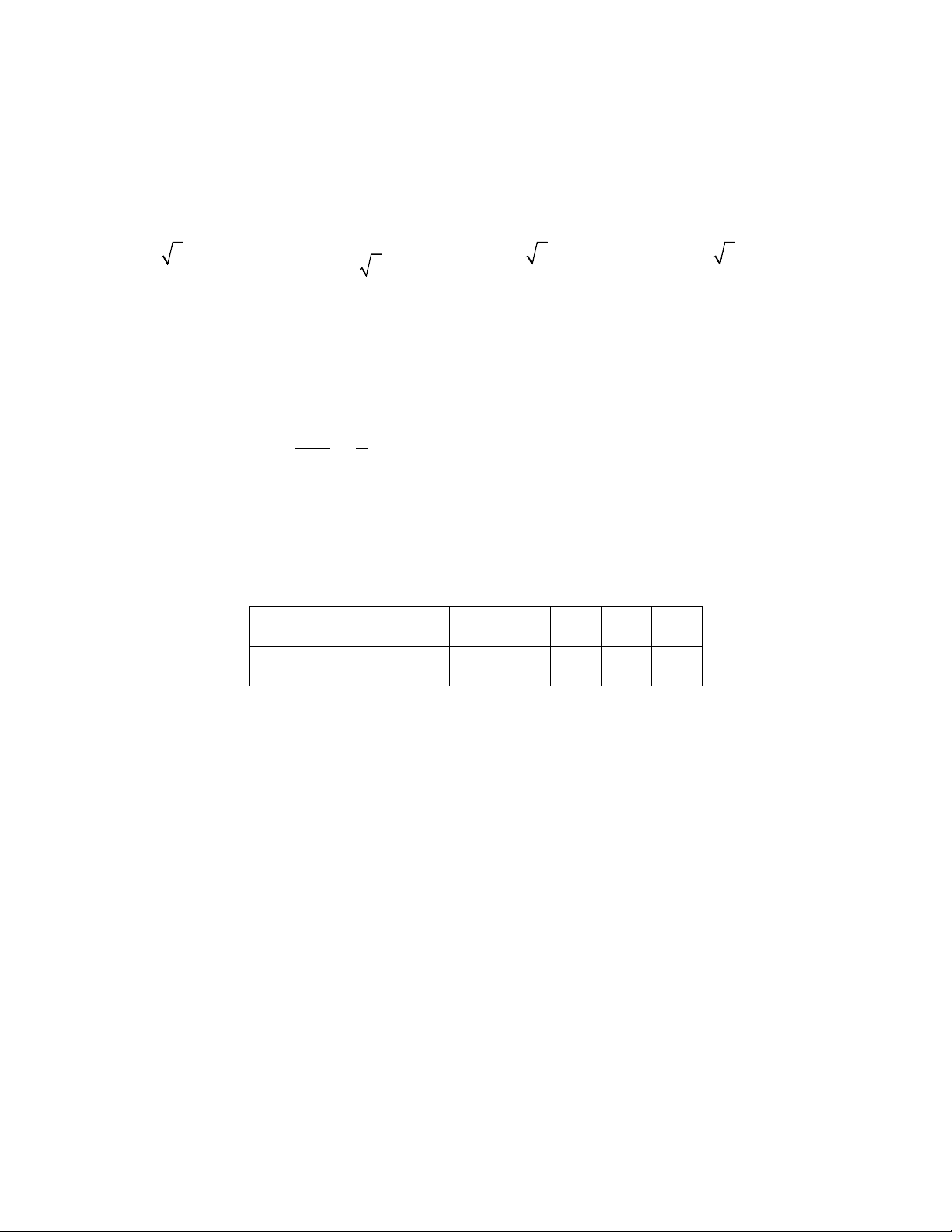
Câu 9: Cho hình chữ nhật ABCD , dựng AH vuông góc với BD(H ∈ BD) biết HD  9cm và
HB  16cm . Diện tích hình chữ nhật ABCD là A. 2 300cm B. 2 280cm C. 2 302cm D. 2 310cm Lời giải A B H D C Ta có 2
AH  HD.HB  AH  12  S  2S  300 . Chọn A. ABCD AD  B
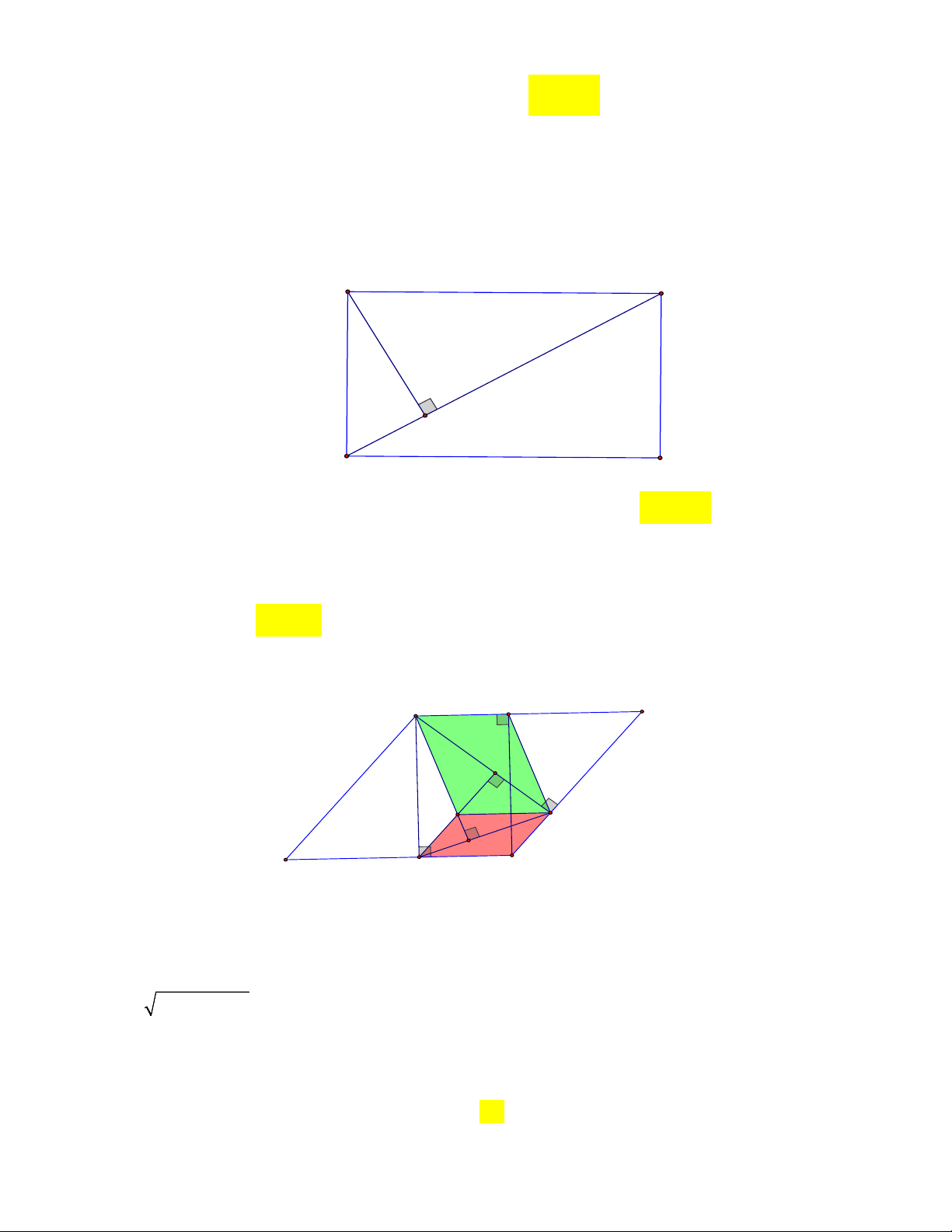
Câu 10: Cho hình bình hành ABCD , dựng AE vuông góc với CD và AF vuông góc với CB (
E;F thứ tự thuộc các cạnh CD và BC), Biết AC  25cm và EF  24cm . Khoảng cách từ A
đến trực tâm H của tam giác AEF là A. 5cm B. 7cm C. 8cm D. 1cm Lời giải A K B H F D E C
Dựng CK  AB , ta có AKCE là hình chữ nhật nên AC  EK , CEHF và AHFK
là hình bình hành và, nên AH  KF , Mặt khác 
KFE  90 , theo Pytago ta có: 2 2
KF  EK  EF  7 . Chọn B.
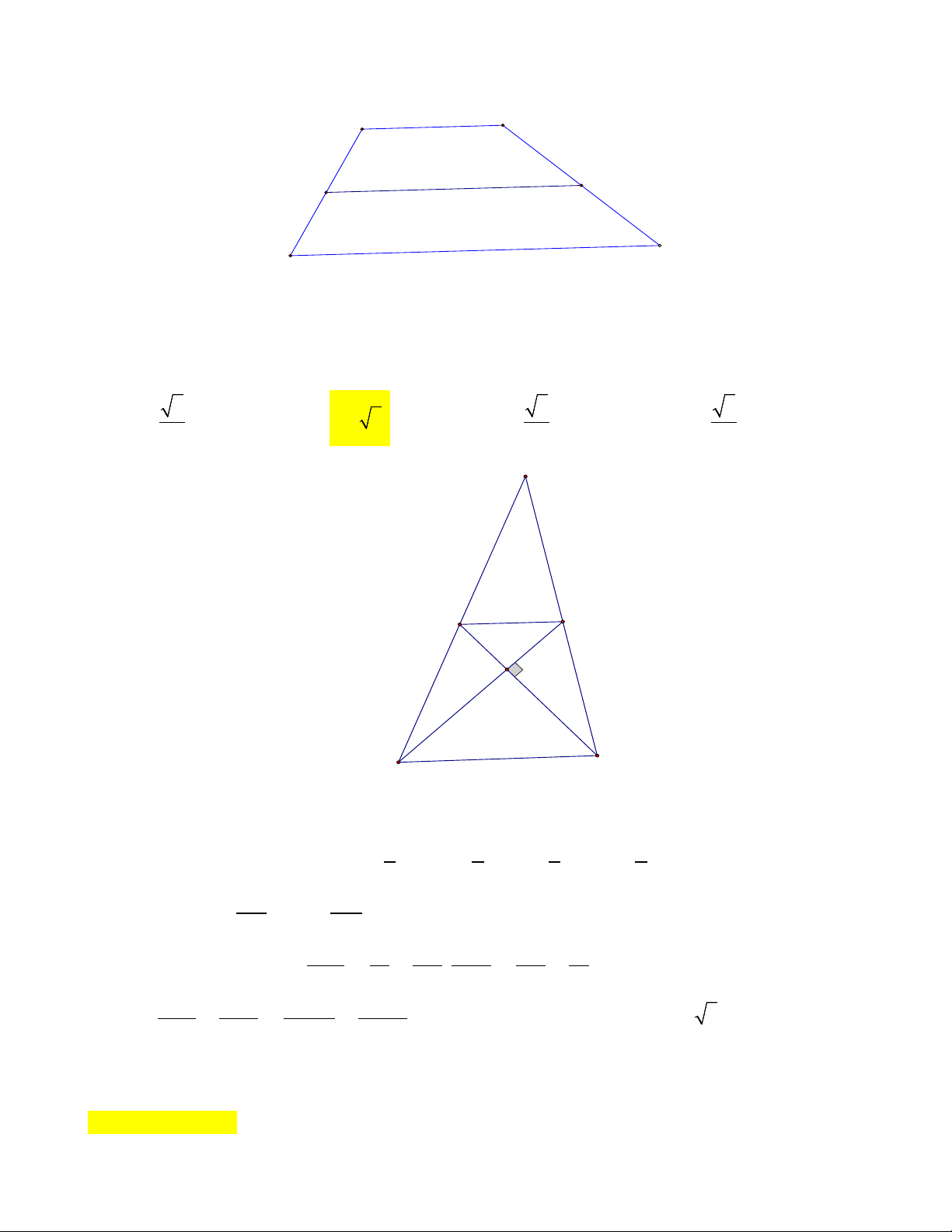
Câu 11: Cho hình thangABDC(AB / /CD) có đường trung bình bằng 7cm ; độ dài đáy
AB  4cm khi đó đáyCD bằng A. 4cm
B. 10cm C. 7cm D. 18cm Trang 6 / 15 Lời giải A B N M C D
Ta có: DC  2MN  AB  10cm . Chọn B.
Câu 12: Cho tam giác ABC có AB  6 ,
cm AC  8cm . Các đường trung tuyến BD và CE
vuông góc với nhau. Độ dài BC là
A. 3 . B.2 5 . C. 5 . D. 5 . 2 2 3 A E D M B C Lời giải Đặt 2 x 2 y
BD  x,CE  y  BM  x,MD  ,CM  , y ME  3 3 3 3 Ta có AB AC EB  ,DC  . 2 2 2 2 2 2 2 2
Theo Py ta go ta có: AB y 4x AC 4y x   ,   . 4 9 9 4 9 9 2 2 2 2 AB AC 5BM 5CM 2 2 2    
 AB  AC  5BC  BC  2 5 . Chọn B 4 4 4 4
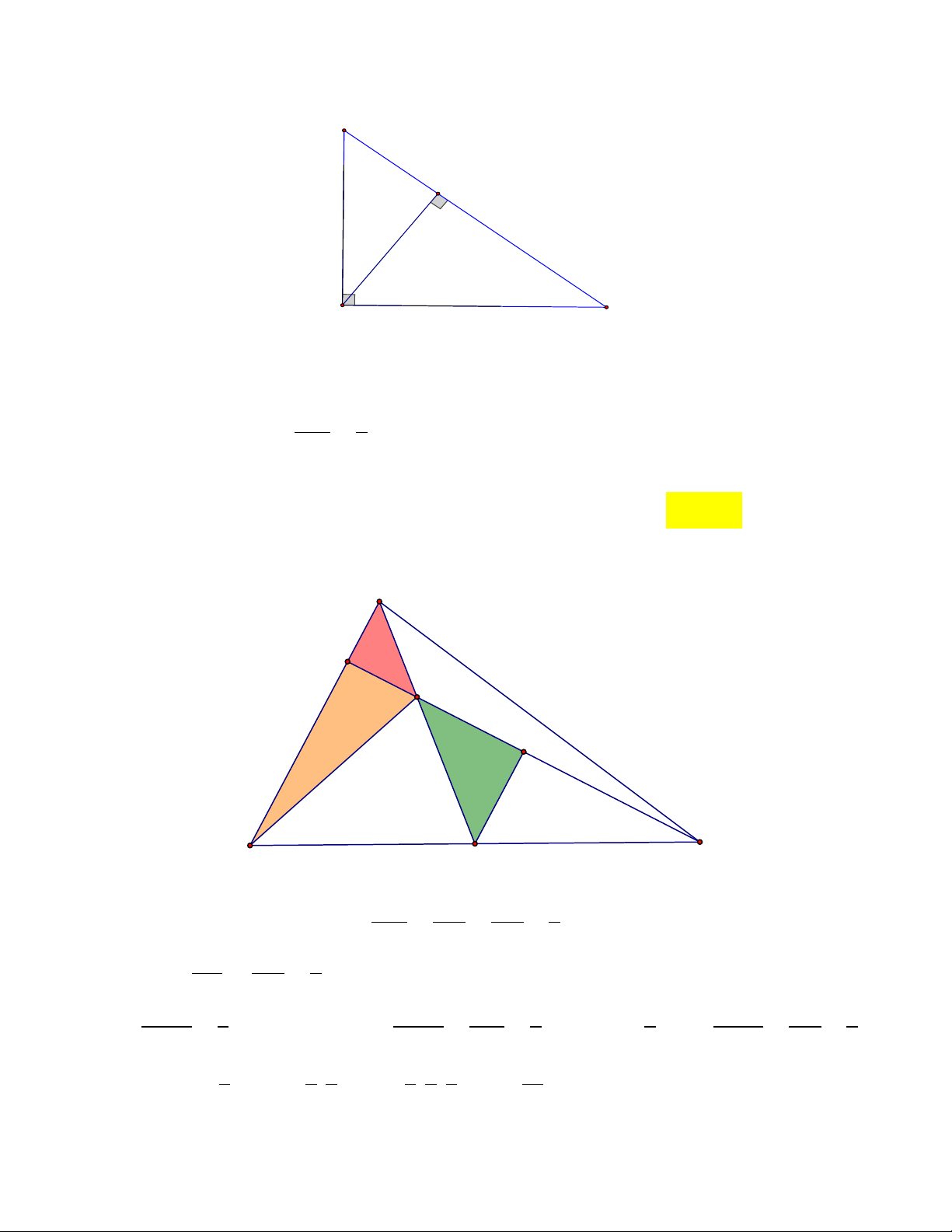
Câu 13: Cho tam giác ABC vuông tại A ; đường cao AH vuông góc với BC, H  BC . Biết HB  9 ,
cm HC  16cm . Độ dài cạnh ,
AB AC lần lượt là
A. 15cm và 20cm. B. 12 cm và 23cm. C. 14cm và 21cm. D. 18cm và 17cm. Trang 7 / 15 Lời giải B H A C Ta có 2
AH  HB.HC  AH  12 . Theo Pytago ta có AB  15,AC  20 . Chọn A.
Câu 14: Trong tam giác ABC , đường trung tuyến AM M  BC ,K là một điểm nằm trên đoạn thẳng AK AM sao cho 1
 , BK cắt AC ở N . Biết diện tích tam giác ABC bằng KM 2 2
60cm , khi đó diện tích tam giác AKN là A. 2 20cm . B. 2 30cm . C. 2 3cm . D. 2 2cm . Lời giải A N K I C M B Ta có  AK NK AN
AKN # MKI (g-g) nên 1    . KM KI MI 2 Ta có CN AN 1 MI    . 2 AC 5 Ta có S 1 S AK 1 1 S AN 1 AC  M   S  2S ; AK  C    S  S ; AK  N   S 2 AC  B AC  M S AM 3 AK  C 3 AC  M S AC 5 AC  B AM  C AK  C Ta có: 1 1 1 1 1 1 60 S  S  . S  . . S 
 2 cm . Chọn D. ANK  AK  C AMC ABC  2 5 5 3 5 3 2 30 Trang 8 / 15
Câu 15. Số bàn thắng ghi được trong mỗi trận đấu (không tính loạt sút luân lưu) của một giải
bóng đá được ghi lại trong bảng sau: Số bàn thắng 0 1 2 3 4 5 Số trận 4 7 8 9 2 2
Hỏi trong giải đấu đó có thể có nhiều nhất bao nhiêu trận đấu kết thúc với tỉ số hòa (trong 90
phút thi đấu chính thức)? A.32. B.4. C. 7. D. 14. Lời giải
Số trận đấu kết thúc với tỉ số hòa thì số bàn thắng có thể là 0,2,4 vậy có thể có tối đa 14 trận hòa Chọn D.
Câu 16: Trong một kì thi Hội khỏe Phù Đổng trường A có 12 học sinh giành được các giải
thưởng, trong đó: 7 học sinh giành được ít nhất 2 giải, 4 học sinh giành được ít nhất 3 giải, 2 học
sinh giành được số giải nhiều nhất, mỗi em 4 giải. Số giải trường A giành được là: A. 26. B. 25. C. 24 . D. 23. Lời giải
Số học sinh được 4 giải là 2 em.
Số học sinh được dành được 3 giải là 2 em
Số học sinh được 2 giải là 3 em
Số học sinh được 1 giải là 4 em
Vậy tổng số giải của trường A là: 24 giải . Chọn C Trang 9 / 15
Phần II: TỰ LUẬN (12 điểm) Nội dung Điểm
Câu 1 (3,0 điểm).
a) Tìm tất cả các số tự nhiên n để 4 2
B  n  27n  121 là số nguyên tố
b) Giải phương trình nghiệm nguyên sau: 2 4
x  4x  1  y 3,0 c) Biết ;
a b là các số nguyên dương thỏa mãn 2 2
a − ab + b chia hết cho 9, chứng
minh rằng cả a và b đều chia hết cho 3.
a) Tìm tất cả các số tự nhiên n để 4 2
B  n  27n  121 là số nguyên tố 1,0 Ta có 4 2
B = n − n + = ( 4 2 n + n + ) 2 − n = ( 2 n + + n)( 2 27 121 22 121 49 11 7 n +11− 7n) 0,25
Với n = 0 , không thỏa mãn 0,25 Với * n∈ N thì 2 2
n +11+ 7n > n +11− 7n
Do đó để B là số nguyên tố thì điều kiện cần để B là số nguyên tố là 2
n − 7n +11 =1 ⇔ n = 5;n = 2 0,25
Thử lại ta có n = 5,n = 2 thỏa mãn 4 2
B  n  27n  121 là số nguyên tố. 0,25
b) Giải phương trình nghiệm nguyên sau: 2 4
x  4x  1  y 1,0
Ta có: x  x   y  x  2 2 4 4  y    2
x   y  2 4 1 2 3 2
x  2  y   3 0,25 Do 2 2
x  2  y  x  2  y nên ta có: 2 0,5 x
  2 y  3   2  x   2  y  1   (I ) hoặc  (II ) 2 x
  2  y  1 2   
x  2  y  3 
Từ (I) và (II) ta tìm được: (x;y)  4; 1,4; 1,0; 1,0; 1 0,25 c) Biết ;
a b là các số nguyên dương thỏa mãn 2 2
a − ab + b chia hết cho 9, chứng 1,0
minh rằng cả a và b đều chia hết cho 3. Ta có: ( 2 2
a + ab + b )9 ⇒ ( 2 2
4 a + ab + b )9 ⇒ ( a −b)2 2 2 + 3  b 9 (1)   0,25 Trang 10 / 15 Mà 2
3b 3nên ( a −b)2 2
3 mà 3 là số nguyên tố nên (2a − b)3 nên ( a −b)2 2 9 .(2) 0,25 Từ ( ) 1 và (2) 2 ⇒ 3b 9 2
⇒ b 3 mà 3 là số nguyên tố ⇒ b3 .
(2a −b)3 và b3 ⇒ 2a3 mà (2;3) =1 nên a3. 0,25
Vậy cả a vàb đều chia hết cho 3. Câu 2.
a) Cho hai số thực khác nhau 1 1 2
a,b thóa mãn:   , 2 2 a  1 b  1 1  ab
Tính giá trị của biểu thức: 1 1 M   4,0 2023 2023 a  1 b  1 2 2     7  3    3    2x x x   9
b) Giải phương trình    6       0.      2 x 2  x  2 x  4
c) Tìm a,b để f x 3 2
 ax  bx  10x  4 chia hết cho đa thức g x 2
 x  x  2
a) Cho hai số thực khác nhau 1 1 2
a,b thóa mãn:   , 2 2 a  1 b  1 1  ab 1,5
Tính giá trị của biểu thức: 1 1 M   2023 2023 a  1 b  1 Xét: 1 1 2 1 1 1 1        0 2 2 2 2 a  1 b  1 1  ab a  1 1  ab b  1 1  ab 0,25 1  ab   2 a   1 1  ab   2 b   2 2 1 ab a ab b     0    0 2 a   1 1  ab
 2b  11ab
 2a  11ab  2b  11ab
a b a
b a b
a b  b a        0      0 2   a   1 1  ab  2 b   1 1  ab 2 2 1  ab b
  1 a  1  0,5 2 ba    b   2 ab    a b  a 2 2          a b ba b ab a             1  ab   0 0    2 b   1  2 a   1  1  ab      2 b   1  2 a   1  
 ab a b  a b     a b a b 2 ab  1       0,5 1  ab   0 . 0  2 b   1  2 a   1  1  ab 
 2b  1 2a  1 Trang 11 / 15
TH1: a b  0  a  b (Loại) vì a  b TH2: 1 1 1
ab  1  a  thay vào biểu thức: M   b 2023 2023 a  1 b  1 2023 2023 1 1 b 1 b  1 0,25 M       1. 2023 2023 2023 2023 2023 1 b  1 b  1 b  1 b  1      1 b     2 2     7  3    3    2x x x   9
a) Giải phương trình    6       0. 1,5      2 x 2  x  2 x  4 ĐKXĐ: x  2 2 Đặt x  3 x  3 x  3 x  3 x  9  a;  b  ab    , ta có x  2 x  2 2 x  2 x  2 x  4 0,25 2 2
a  6b  7ab  0  (a b)(a  6b)  0  a  b hoặc a  6b Với x  x 
a  b ta có: 3 3 
 (x  3)(x  2)  (x  2)(x  3) x  2 x  2 2 2
 x  5x  6  x  5x  6 0,5
 10x  0  x  0 (thỏa mãn ĐKXĐ). Với x  x 
a  6b , ta có: 3 3  6 
 (x  3)(x  2)  6(x  2)(x  3) x  2 x  2 2 2
 x  5x  6  6x  30x  36 2
 5x  35x  30  0 2
 x  7x  6  0 0,5
 (x  1)(x  6)  0
 x  1 (thỏa mãn ĐKXĐ) hoặc x  6 (thỏa mãn ĐKXĐ).
Vậy tập nghiệm của phương trình là S  {0;1;6} 0,25
b) Tìm a,b để f x 3 2
 ax  bx  10x  4 chia hết cho đa thức g x 2
 x  x  2 1,0
Ta có: g x 2
 x  x  2  x   1 x  2 . 0,25 f x 3 2
 ax  bx  10x  4 chia hết cho g x nên 0,25  f x 3 2
 ax  bx  10x  4  x  
1 x  2.Q x
Với x  1 và x  2 ta có a b  6 và 8a  4b  24  0  a  4;b  2 0,25 Trang 12 / 15
Vậy để f x 3 2
 ax  bx  10x  4 chia hết cho đa thức g x 2
 x  x  2 thì 0,25
a  4;b  2.
Câu 3. Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE cắt nhau ở H.
a) Chứng minh AB  D á AC  E
b) Chứng minh CH.CE  CD.CA
c) Kẻ EK  AC tại K; DI  EC tại I. Chứng minhAH / /IK 4,0 d) Chứng minh 1 S  S EI  K 4 A  BC A K D E H I B C
a) Chứng minh AB  D á AC  E 1,0
Có BD là đường cao của tam giác ABC   0
 BD  AC  BDA  BDC  90 0,25
Có CE là đường cao của tam giác ABC   0,25 0
 CE  AB  CEB  CEA  90 Xét tam giác AB  D & AC  E có   0,25 0
BDA  CEA  90 .  BAC chung  AB  D á AC  E(g.g) 0,25
b) Chứng minh CH.CE  CD.CA 1,0
Xét tam giác CHD và tam giác CHE có 0,5 Trang 13 / 15  ECA chung      CH  Dá CA  E(g.g) 0 CDH CEA 90     CH CD  
 CH.CE  CD.CA 0,5 CA CE
c) Kẻ EK  AC tại K; DI  EC tại I. Chứng minhAH / /IK 1,0 Xét CI  D và C  KE có:   0
CID  CKE  90  ICD chung CI  Dá CK  E (g-g) 0,25 CI CD  
(1) mà CH.CE  CD.CA (cm b) CD CH   (2) 0,25 CK CE CE CA Từ (1), (2) CI CH CI CK     CK CA CH CA 0,25 Xét CA  H có: CI CK  (cmt) CH CA
 IK / /AH ( ĐL Ta-lét đảo) 0,25 d) Chứng minh 1 S  S 1,0 EI  K 4 A  BC
Có IK / /AH (cm c)  
 KIE  AHE (đồng vị) 0,25 Mà  
ABC  AHE (cùng phụ với  EAH )  
 ABC  KIE Xét EI  K và A  BC có:  
KIE  ABC (cmt)  
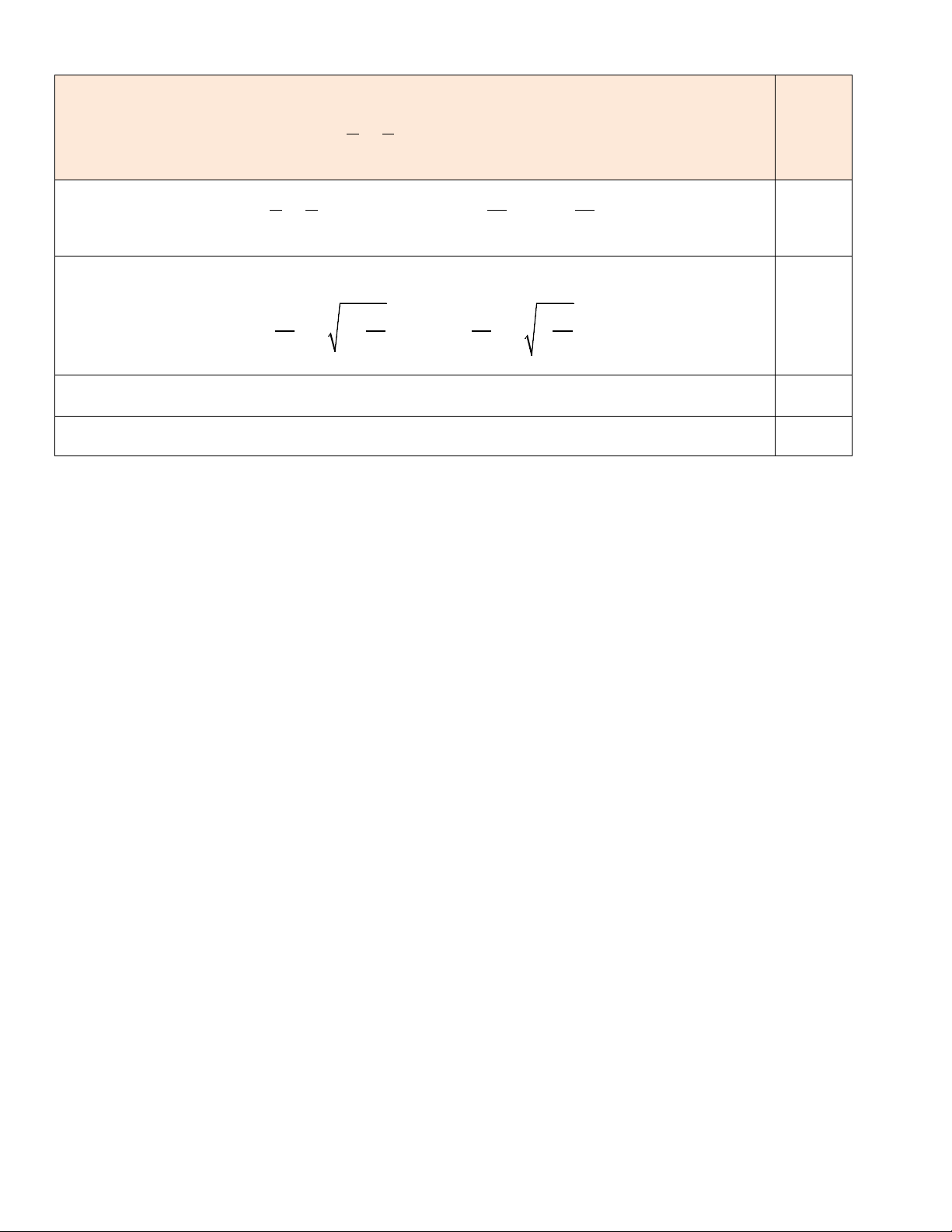
IEK  BAC (cùng phụ với  AEK ) 0,25  EI  Ká A  BC (g-g) 2 2 S EK    EK EIK        2 S AC  AC ABC Chứng minh: A  EK á EC  K (g-g) 0,25 AK EK 2  
 EK  AK.CK EK CK S AK.CK 4AK.CK AK CK2 2 AC 1 EIK       0,25 2 2 2 2 S AC 4AC 4AC 4AC 4 ABC
Dấu “=” xảy ra  AK  CK . Trang 14 / 15
Câu 4. (1 điểm) Cho x, y là các số dương thỏa mãn điều kiện x  y  6.Tìm giá trị nhỏ nhất của biểu thức 6 8
M  3x  2y    1,0 x y       Ta có 6 8 M    x  y        x y 12   16 2 2 3 2 3  3x    y    0,25        x y   x     y 
Từ giả thiết và theo BĐT Cô – si, ta có: 0,25 x y 12 12 16 16 3  3.6  18; 3x   2 3x.  12; y   2 y.  8 x x y y
Do đó, 2M  18  12  8  38  M  19 0,25
Vậy minM = 19. Dấu “=” xảy ra khi x = 2; y = 4. 0,25
Chú ý: Nếu thí sinh làm cách khác mà đúng vẫn cho điểm tối đa Trang 15 / 15