Đề học sinh giỏi cấp tỉnh Toán THPT năm 2022 – 2023 sở GD&ĐT Quảng Ninh

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH THPT NĂM 2022 TỈNH QUẢNG NINH
Môn thi: TOÁN - Bảng: B TOANMATH.com Ngày thi: 02/12/2022
ĐỀ THI CHÍNH THỨC
Thời gian làm bài: 180 phút (không kể thời gian giao đề)
Câu 1. (4,5 điểm) Cho hàm số 3 2
y  x  mx   2 m   3 3 3
1 x  m  m có đồ thị C  và điểm I  1  ;3.
a) Tìm các giá trị của tham số m để hàm số nghịch biến trên khoảng 2022; .
b) Tìm các giá trị của tham số m sao cho C  có hai điểm cực trị, đồng thời hai điểm cực trị của C  cùng
với điểm I tạo thành một tam giác vuông tại I.
Câu 2. (4,0 điểm)
a) Cho tam giác đều ABC. Trên mỗi cạnh AB, BC, CA lần lượt lấy 4 điểm phân biệt và không điểm nào trùng
với các đỉnh A, B, C. Hỏi lập được bao nhiêu tam giác mà các đỉnh của nó thuộc tập hợp 15 điểm đã cho (tính
cả các điểm A, B, C)?
b) Một người chọn ngẫu nhiên một số điện thoại, trong đó mỗi số có mười chữ số và ba chữ số đầu cố định là
099. Số điện thoại này được gọi là may mắn nếu bốn chữ số tiếp theo là các chữ số chẵn đôi một khác nhau,
ba chữ số cuối là các số lẻ và tổng ba chữ số này bằng 9. Tính xác suất để người đó nhận được số điện thoại may mắn.
Câu 3. (5,5 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB  3 , BC  6 , đường thẳng SA vuông góc với mặt 1
phẳng  ABCD . Điểm M thuộc đoạn BC sao cho BM  BC . Góc giữa đường thẳng SC và mặt phẳng 3 SAB bằng 45°.
a) Tính thể tích khối chóp S.ABCD.
b) Tính khoảng cách giữa hai đường thẳng SM và AC.
c) Gọi H và K lần lượt là hình chiếu vuông góc của A trên SM và SC. Chứng minh hình chóp A.CMHK nội
tiếp một mặt cầu. Tính bán kính mặt cầu đó.
Câu 4. (1,5 điểm)
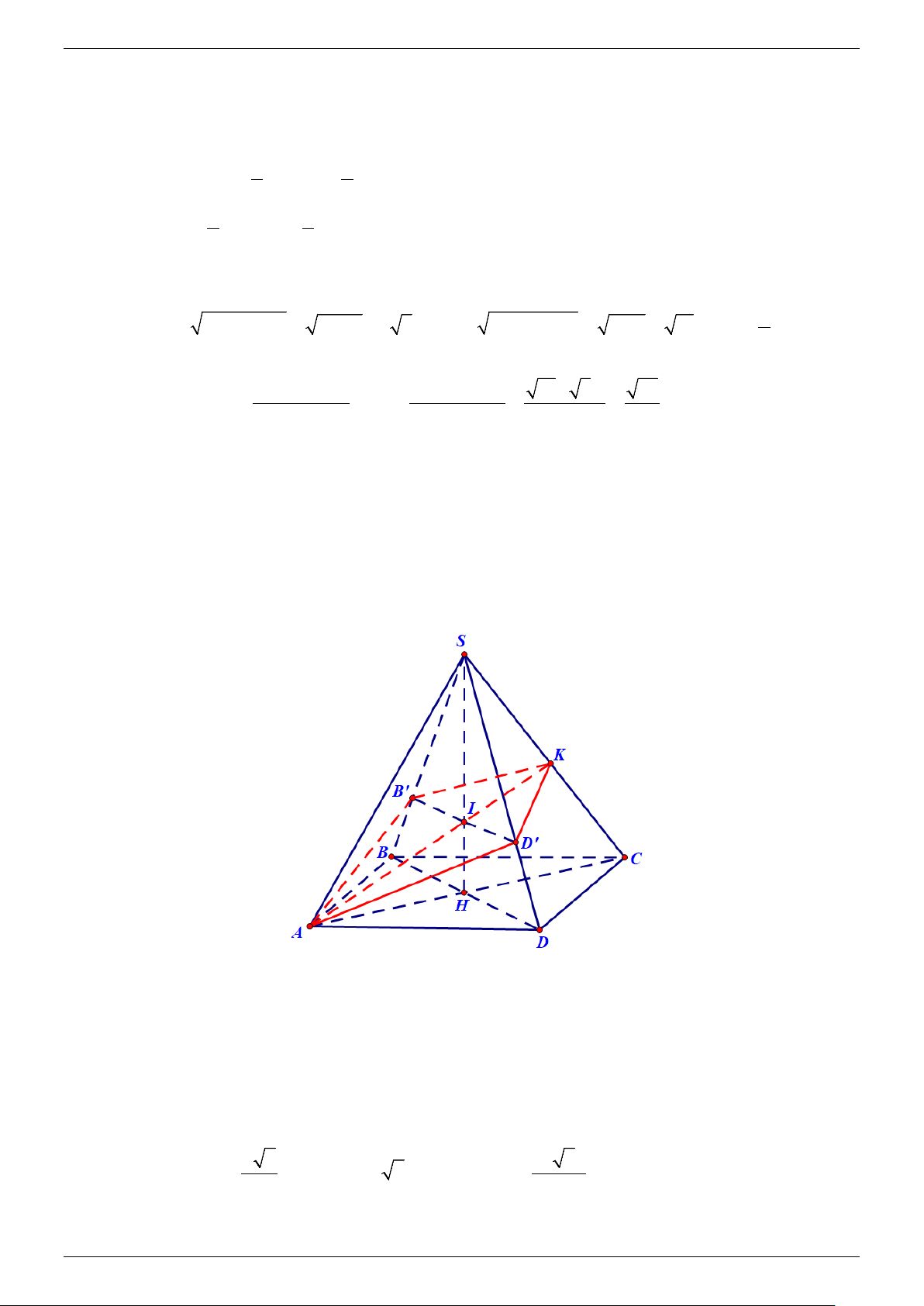
Cho hình chóp tứ giác đều S.ABCD có góc  SAC    45 .
 Mặt phẳng P qua A và vuông góc với đường
thẳng SC cắt hình chóp theo một thiết diện. Tính tỉ số diện tích của thiết diện và diện tích đáy ABCD theo .
Câu 5. (3,0 điểm) 4   3 3 2
x 1  y  x  2
1  y  2x
Giải hệ phương trình: 
 x, y   . 2
 3y 5  4x 3  2x 1 
Câu 6. (1,5 điểm) 1
Cho các số thực a, b, c thỏa mãn  a, ,
b c  1. Chứng minh: 3  3 1   3 1   3 1  log b   log c   log a   9 . a        4 4 b   4 4 c   4 4 
--------------- HẾT ---------------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay. Giám thị coi thi không giải thích gì thêm./.
Họ và tên thí sinh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Số báo danh: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 HƯỚNG DẪN GIẢI Câu 1: (4.5 điểm) Cho hàm số 3 2
y = −x + mx − ( 2 m − ) 3 3 3
1 x + m − m có đồ thị (C) và điểm I ( 1; − 3)
a) Tìm các giá trị của tham số m để hàm số nghịch biến trên khoảng (2022;+∞) .
b) Tìm các giá trị của tham số m sao cho (C) có hai điểm cực trị, đồng thời hai điểm cực trị
của (C) cùng với điểm I tạo thành một tam giác vuông tại I . Lời giải
a) Tập xác định D =  2
y′ = − x + mx − ( 2 3 6 3 m − ) 1 2
y′ = ⇔ − x + mx − ( 2 m − ) 2
= ⇔ −x + mx − ( 2 0 3 6 3 1 0 2 m − ) 1 = 0 (*) Ta có 2 2 2
∆′ = b′ − ac = m − m +1 =1 > 0 m ∀ ∈  .
⇒ pt (*) có hai nghiệm phân biệt ⇒ (C) luôn có hai điểm cực trị. x = m +1 1 y′ = 0 ⇔  x = m −  1 2
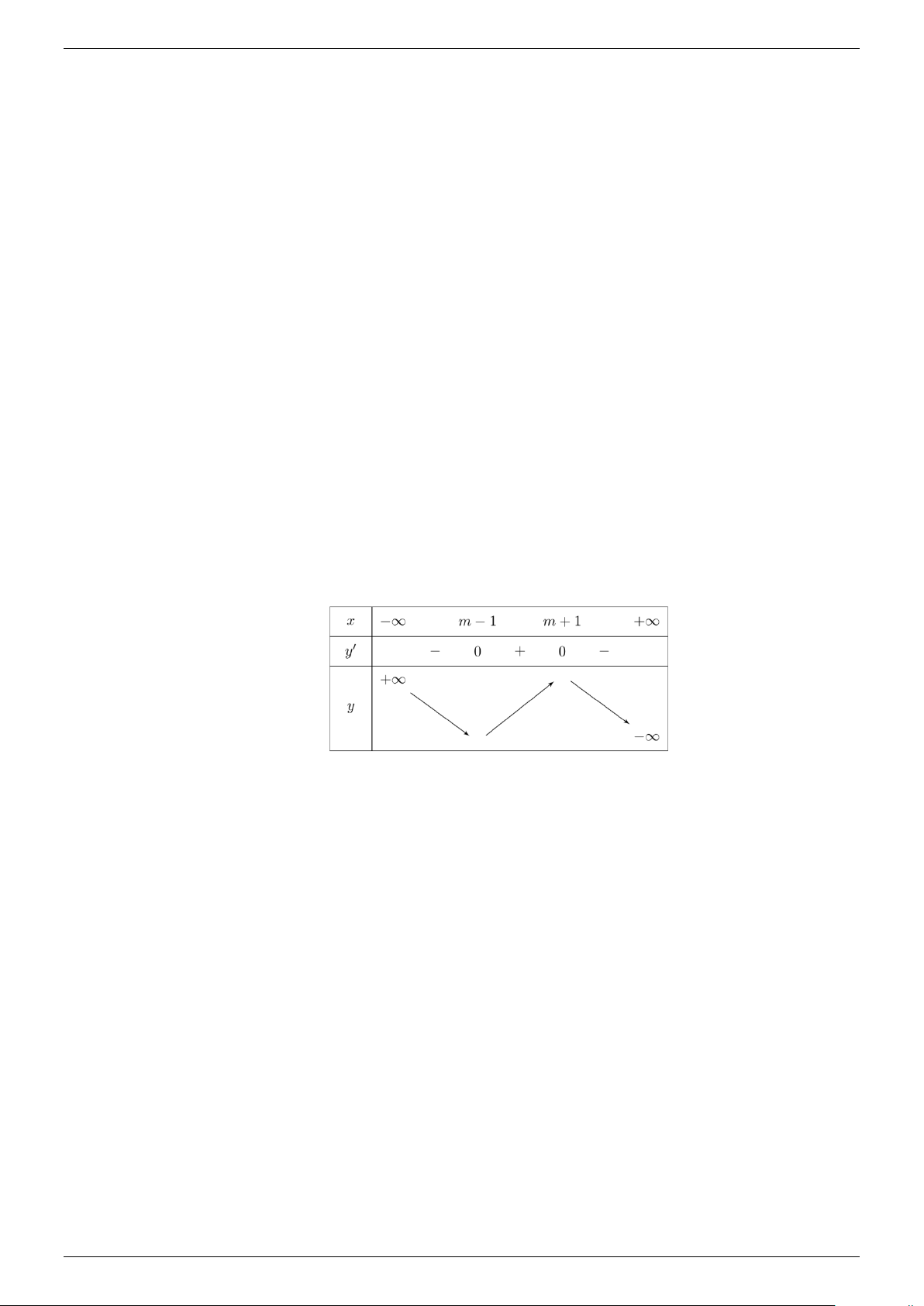
Dễ thấy x > x 1 2 Bảng biến thiên
Dựa vào bảng biến thiên, hàm số nghịch biến trên (2022;+∞) khi và chỉ khi
m +1≤ 2022 ⇔ m ≤ 2021
Vậy m ≤ 2021 thỏa yêu cầu.
b) Hai điểm cực trị của (C) là A(m +1;2m + 2), B(m −1;2m − 2) .  
IA(m + 2;2m − ) 1 , IB ( ; m 2m − 5)
Theo giả thiết tam giác ABI vuông tại I   ⇔ .
IA IB = 0 ⇔ m(m + ) + ( m − )( m − ) 2 2 2 1 2
5 = 0 ⇔ 5m −10m + 5 = 0 ⇔ m =1 Vậy m =1. Câu 2: (4.0 điểm)
a) Cho tam giác đều ABC . Trên mỗi cạnh AB, BC,CA lần lượt lấy 4 điểm phân biệt và không
điểm nào trùng với các đỉnh ,
A B,C . Hỏi lập được bao nhiêu tam giác mà các đỉnh của nó
thuộc tập hợp 15 điểm đã cho (tính cả các điểm , A B,C ). Lời giải
Số cách lấy 3 điểm tùy ý từ tập hợp 15 điểm là 3 C . 15
Số cách lấy 3 điểm thuộc cùng một cạnh của tam giác là 3 3C . 6
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 3
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
Vậy số tam giác có các đỉnh thuộc tập hợp 15 điểm đã cho là 3 3 C −3C = 395. 15 6
b) Một người chọn ngẫu nhiên một số điện t hoại, trong đó mỗi số có mười chữ số và ba chữ số
đầu cố định là 099 . Số điện thoại này được gọi là may mắn nếu bốn chữ số tiếp theo là các
chữ số chẵn đôi một khác nhau, ba chữ số cuối là các số lẻ và tổng ba chữ số này bằng 9. Tính
xác suất để người đó nhận được số điện thoại may mắn. Lời giải
Giả sử số điện thoại là: 099a a a a a a a
1 2 3 4 5 6 7 (trong đó a a a a a a a ∈ ) 1, 2 , 3 , 4 , 5 , 6 , 7 {0;1;..,; } 9 Ta có: n(Ω) 7 = 10
Gọi A = “Số điện thoại may mắn” Khi đó: Có 4 A
a ,a ,a ,a 5 cách chọn 1 2 3 4 TH1: a a a
5 , 6 , 7 là bộ số (1;3;5) ⇒ 3! cánh chọn TH2: a a a
5 , 6 , 7 là bộ số (1;1; 7) ⇒ 3 cánh chọn TH3: a a a
5 , 6 , 7 là bộ số (3; 3; 3) ⇒ 1 cánh chọn ⇒ n( A) 4 = A 3!+ 3+1 =1200 5 ( ) n A 1200
Xác suất để người đó nhận được số điện thoại may mẵn là P ( A) ( ) = = = . n(Ω) 0,00012 7 10 Câu 3: (5.5 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = 3 , BC = 6 , đường thẳng SA
vuông góc với mặt phẳng ( ABCD). Điểm M thuộc đoạn BC sao cho 1
BM = BC . Góc giữa 3
đường thẳng SC và mặt phẳng (SAB) bằng 45°.
a) Tính thể tích khối chóp S.ABCD .
b) Tính khoảng cách giữa hai đường thẳng SM và AC .
c) Gọi H và K lần lượt là hình chiếu vuông góc của A trên SM và SC . Chứng minh hình chóp .
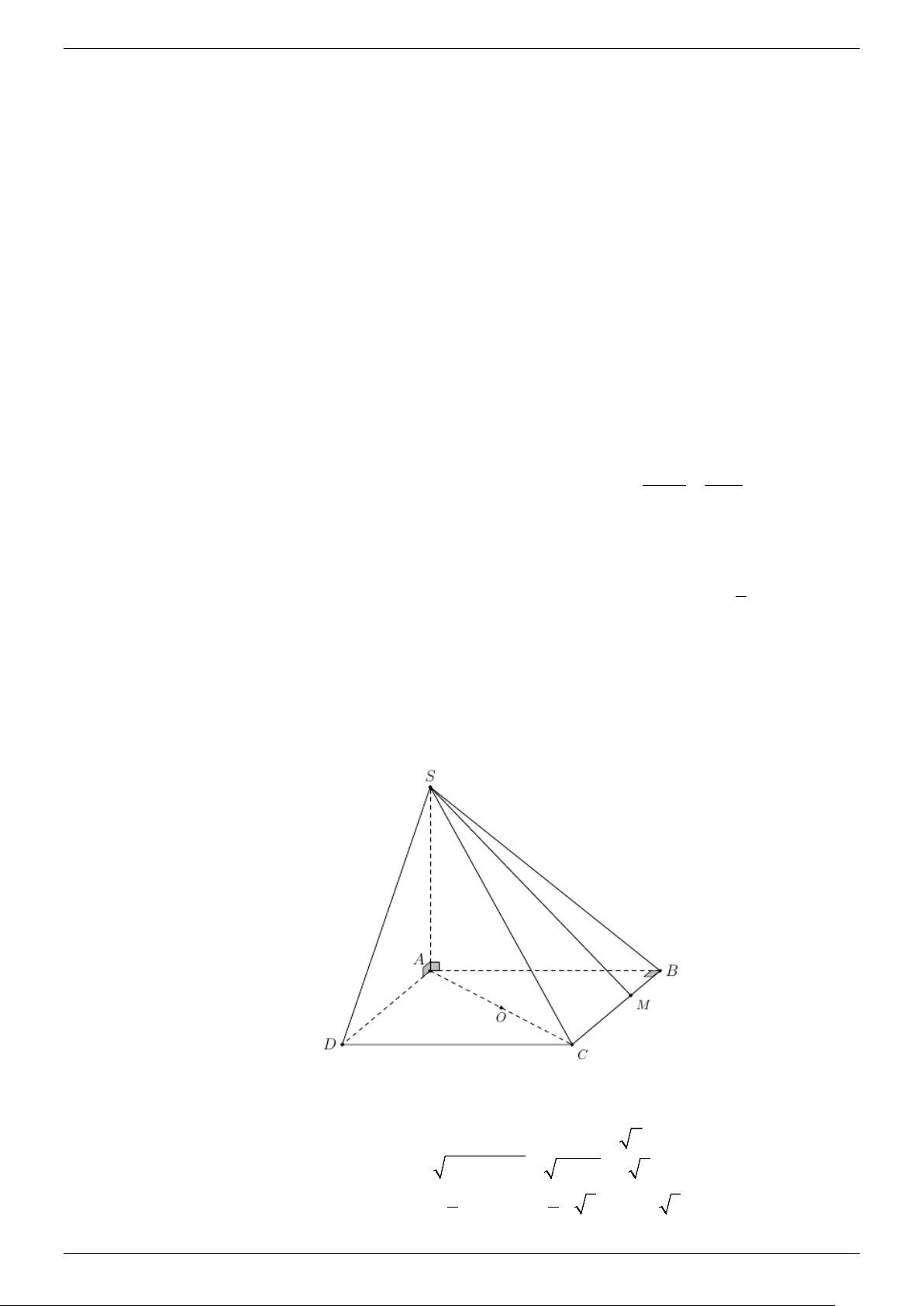
ACMHK nội tiếp một mặt cầu. Tính bán kính mặt cầu đó. Lời giải BC ⊥ AB a) Do 
⇒ BC ⊥ (SAB) . Ta có (SC (SAB)) = (SC SB)  , , = CSB = 45° . BC ⊥ SA Suy ra S
∆ BC vuông cân tại B . Khi đó SB = BC = 6 và SC = 6 2 . Trong S
∆ AB vuông tại A , ta có 2 2
SA = SB − AB = 36 − 9 = 3 3 .
Vậy thể tích khối chóp S.ABCD là 1 1 V = . . SA S = = (đvtt). ABCD .3 3.3.6 18 3 3 3 Trang 4
TÀI LIỆU ÔN THI HỌC SINH GIỎI
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 b) Cách 1:
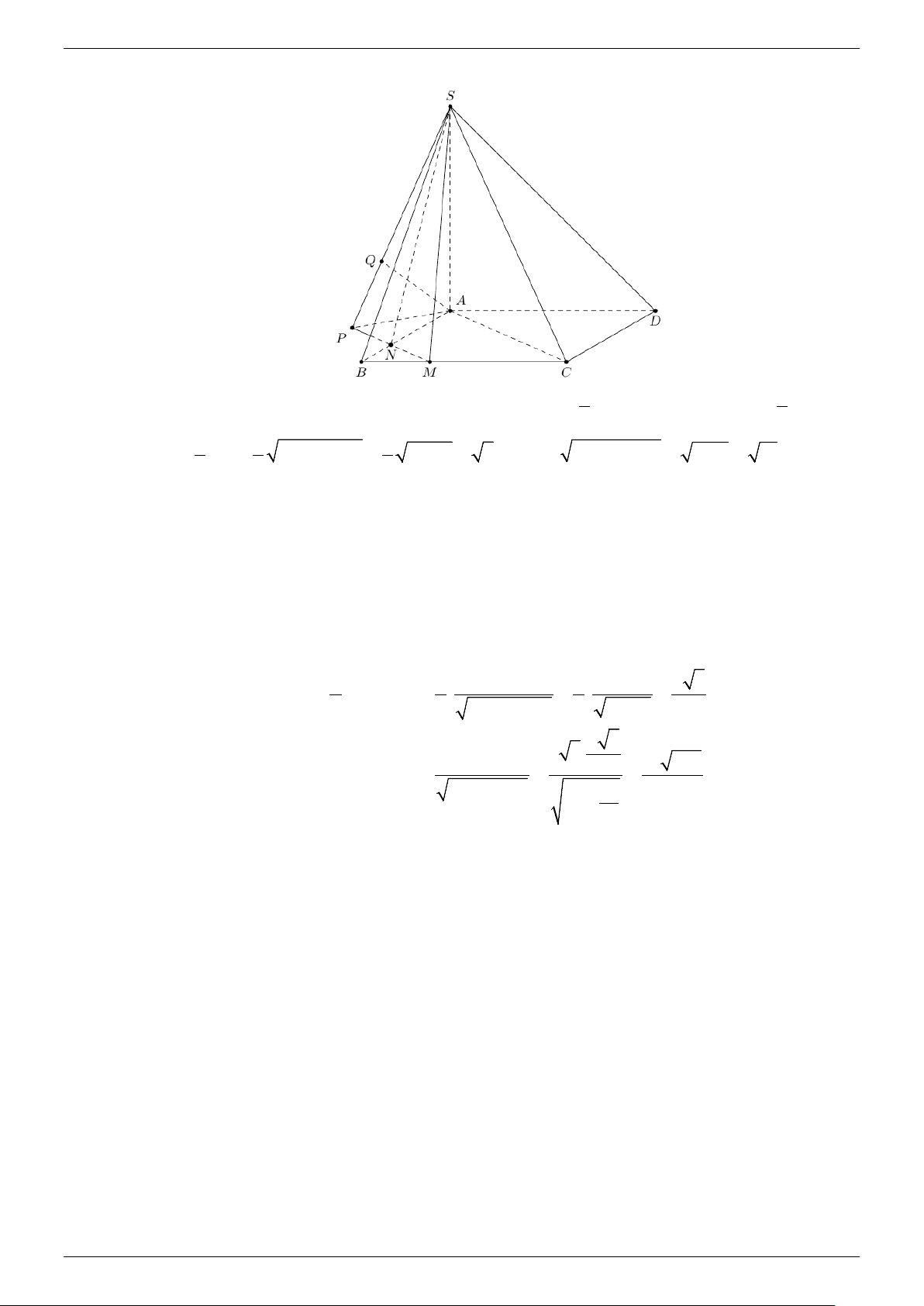
Trong ( ABCD) kẻ MN / / AC với N ∈ AB . Suy ra 1
BN = AB =1; AN = 2; 1 BM = BC = 2 ; 3 3 1 1 2 2 1 MN = AC = AB + BC = 9 + 36 = 5 ; 2 2
AM = AB + BM = 9 + 4 = 13 . 3 3 3
Khi đó AC / / (SMN ) ⇒ d( AC, SM ) = d( AC,(SMN )) = d( , A (SMN )).
Trong ( ABCD) kẻ AP ⊥ MN với P ∈ MN .
Trong (SAP) kẻ AQ ⊥ SP ( )
1 với Q ∈ SP . MN ⊥ AP Do 
⇒ MN ⊥ (SAP) ⇒ AQ ⊥ MN (2) . MN ⊥ SA
Từ (1) và (2) suy ra AQ ⊥ (SMN ) . Vậy d( AC,SM ) == d( ,
A (SMN )) = AQ .
Ta có AP = ( A MN ) 2 = (B AC) 2 A . B BC 2 3.6 4 5 d , d , = . = . = . 2 2 3 3 AB + BC 3 9 + 36 5 4 5 3 3. S . A AP 5 12 453 Trong S
∆ AP vuông tại A ta có AQ = = = . 2 2 SA + AP 16 151 27 + 5 Cách 2:
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 5
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
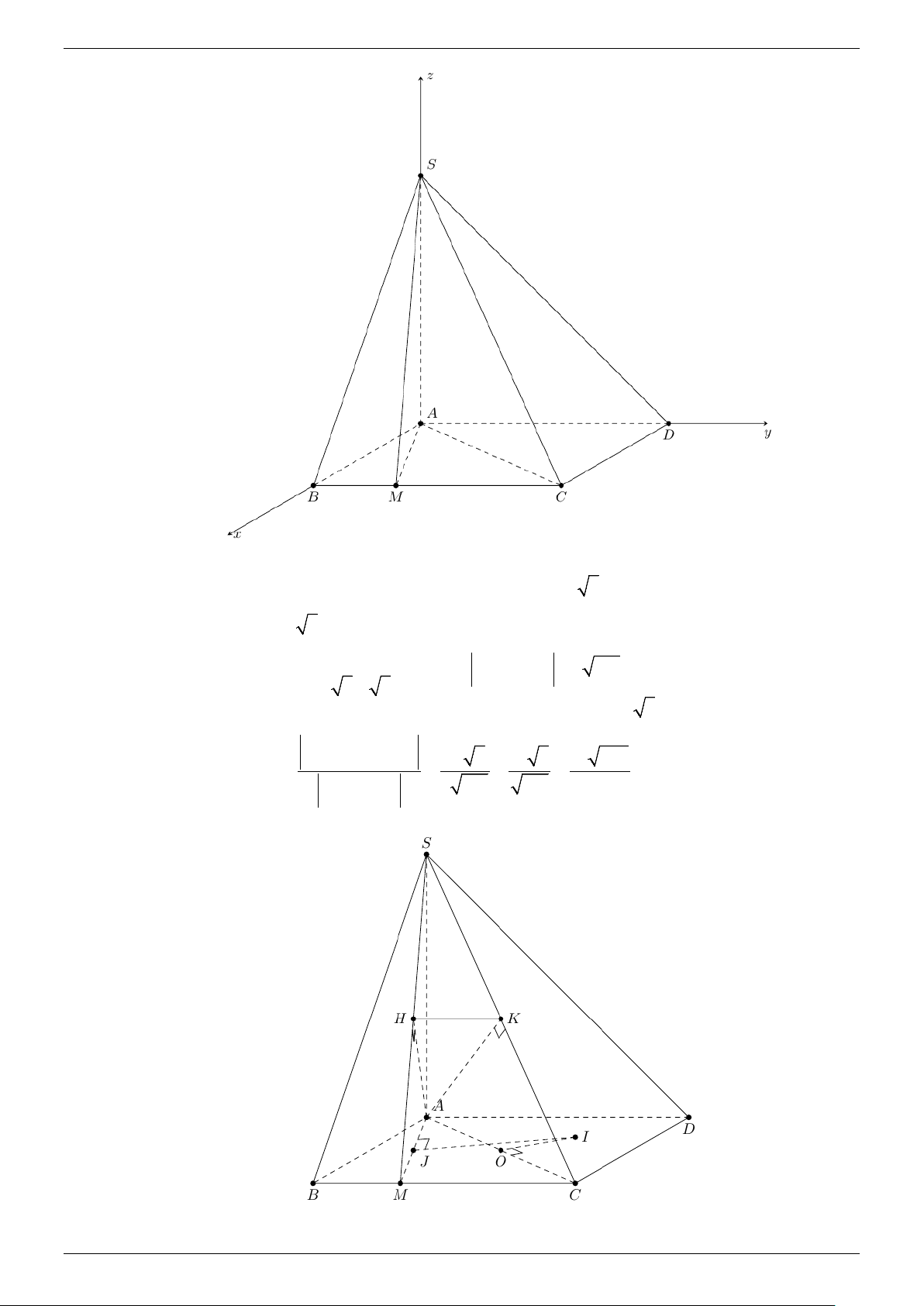
Chọn hệ trục tọa độ Oxyz như hình vẽ với
A ≡ O(0;0;0) ; B(3;0;0) ; D(0;6;0) ; C (3;6;0); S (0;0;3 3) ; M (3;2;0).    Ta có SM = (3;2; 3
− 3) và AC = (3;6;0), AM = (3;2;0) .       AC SM  = Suy ra AC SM  = (− − ) , 3 151     , 18 3;9 3; 12 ⇒   
   .
AM.AC, SM  = 36 − 3   
  
AM.AC, SM    36 3 12 3 12 453
Ta có d( AC, SM ) =   = = = . AC,SM  3 151 151 151   c)
Gọi O , J lần lượt là trung điểm của AC , AM . Trang 6
TÀI LIỆU ÔN THI HỌC SINH GIỎI
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023
Dựng trục của các A ∆ HM và A
∆ KC . Hai trục này là trung trực của các đoạn thẳng AC , AM
nên giao điểm I là tâm đường tròn ngoại tiếp A ∆ CM .
Vậy bán kính mặt cầu ngoại tiếp hình chóp .
ACMHK chính là bán kính đường tròn ngoại tiếp A ∆ CM . Ta có 1 1 S = = = ∆ AB BC ABC . . .3.6 9 (đvdt). 2 2 1 1 S = = = ∆ AB BM ABM . . .3.2 3 (đvdt). 2 2 Suy ra S = − = − = ∆ S∆ S AMC ABC ABM ∆ 9 3 6 (đvdt). Mặt khác 2 2
AC = AB + BC = 9 + 36 = 3 5 ; 2 2
AM = AB + BM = 9 + 4 = 13 ; 2 MC = BC = 4 . 3
Gọi R là bán kính đường tròn ngoại tiếp A ∆ CM . Ta có AM.AC.MC AM.AC.MC 13.3 5.4 65 S = ⇔ = = = ∆ R AMC (đvtt). 4R 4S A∆MC 4.6 2 Vậy:  0   0
C =180 − A − B = 75 . Câu 4: (1.5 điểm)
Cho hình chóp tứ giác đều S.ABCD có góc  0
SAC = α > 45 . Mặt phẳng (P) qua A và vuông
góc với đường thẳng SC cắt hình chóp theo một thiết diện. Tính tỉ số diện tích của thiết diện
và diện tích đáy ABCD theo α . Lời giải
Gọi H = AC ∩ BD ⇒ SH ⊥ ( ABCD) .
Gọi K là giao điểm của (P) và SC ⇒ AK ⊥ SC và AK ∩ SH = I .
Ta có SC ⊥ BD ⇒ (P) //BD ⇒ (P) ∩(SBD) = B D
′ ′//BD và B D ′ ′ đi qua I .
Vậy thiết diện của (P) với hình chóp S.ABCD là tứ giác AB K
′ D′ có AK ⊥ B D ′ ′ .
Theo giả thiết tam giác SAC là tam giác cân tại S và   0
SAC = SCA = α > 45 .
Đặt cạnh đáy của hình vuông ABCD là a . Ta có: a 2 a 2 SH =
tanα, AK = a 2 sinα, SA = SC = . 2 2cosα
Trong tam giác vuông SAK ta có
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 7
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 2 2 2 2 2a 2a 1− 4sin α cos α  a 2 cos 2α 2 2 2 2
SK = SA − AK = − 2a sin α =   = . 2 2 4cos α 4  cos α  2cosα SK.SC cos 2α
Vì tứ giác CHIK nội tiếp nên: SI.SH = SK.SC ⇒ SI = = a 2 = a 2 cot 2α SH sin 2α SI cot 2α Vậy ta có B D ′ ′ = .BD = 2a 2 . SH tanα 1
Diện tích tứ giác AB K ′ D′ là 2 S = ′ ′ = ′ ′ AK B D a α α AB KD . 2 cos . cot 2 . 2
Diện tích tứ giác ABCD là 2 S = a . 2
S ′ ′ 2a cosα. cot 2α
Vậy tỉ số diện tích là: AB KD = = 2cosα. cot 2α . 2 S a ABCD Câu 5: (3.0 điểm) 4  ( 3 3 2
x +1 − y − x ) 2 +1 = y − 2x
Giải hệ phương trình: 
(x, y ∈) . 2
 3y −5 + 4x −3 = 2x +  1 Lời giải 2 2 3  y − 5 ≥ 0 3  y − 5 ≥ 0
Điều kiện của hệ phương trình:   ⇔  3 . 4x − 3 ≥ 0 x ≥  4 4(3 3 2
x +1 − y − x ) 2 +1 = y − 2x   ( 2 x y ) 4 2 1 1 ⇔ + − + = 0   3  (x + )2 + 3 1
(x + )1( 2y − x) 3 + ( 2 y − x)2    2 2x +1 = y (3)  ⇔  4 +1 = 0 (4)  3  ( x + )2 + 3 1
(x + )1( 2y − x) 3 2 + 4 y − x  3  +  3 x +1 2 x 1 3 3 2 + + 3 3 2 3 2 ( )2 2 3 (x )1
(x + )1( y − x) 2
+ y − x =  y − x +  + > 0, x ∀ ≥ ,3y − 5 ≥ 0 2 4 4   Do đó (4) vô nghiệm. Thay 2
y = 2x +1(3) vào phương trình 2
3y − 5 + 4x − 3 = 2x +1 ta được phương trình
6x − 2 + 4x −3 = 2x +1 Cách 1:  3 x ≥ 
6x − 2 + 4x −3 = 2x +1  4 ⇔  ( x ) 1 2 1 1  + − = 0    6x 2 4x 3   − − −  Trang 8
TÀI LIỆU ÔN THI HỌC SINH GIỎI
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023  3 x ≥  3  4 x ≥ ⇔  ⇔  4 1  3
−1 = 0 Do 2x +1> 0 x   ∀ ≥  
 6x − 2 − 4x − 3 =1
 6x − 2 − 4x −3  4   3  3  3 x ≥ x ≥ x ≥ ⇔  4 ⇔  4 ⇔  4
 6x 2 4x 3 1 6x 2 4x 3 1 2 4x 3  − = − + − = − + + − x = 4x − 3  3  3 x ≥ x  ≥  4 x =1 ⇔  4 ⇔  . x 1 ⇔  =  2  x = 3
x − 4x + 3 = 0  x = 3
Thay x =1 vào (3) ta được 2
y = 3 ⇔ y = ± 3 (nhận).
Thay x = 3 vào (3) ta được 2
y = 7 ⇔ y = ± 7 (nhận).
Vậy hệ đã cho có tập nghiệm S = ({1; 3),(1;− 3),(3;− 7),(3; 7)}. Cách 2:
6x − 2 + 4x −3 = 2x +1 ⇔ 6x − 2 −(x + )
1 + 4x − 3 − x = 0 2
−x + 4x − 3 = 0 2 2 −x + 4x − 3 −x + 4x − 3 ⇔ + = 0  ⇔ 6  1 1  3 x − 2 + x +1 4x − 3 + x + = 0 VN voi x  ≥  6x 2 x 1 4x 3 x 4   − + + − +   x =1 ⇔  . x = 3
Thay x =1 vào (3) ta được 2
y = 3 ⇔ y = ± 3 (nhận).
Thay x = 3 vào (3) ta được 2
y = 7 ⇔ y = ± 7 (nhận).
Vậy hệ đã cho có tập nghiệm S = ({1; 3),(1;− 3),(3;− 7),(3; 7)}. Câu 6. (1.5 điểm) 1
Cho các số thực a , b , c thỏa mãn < a,b,c < 1. Chứng minh 3  3 1   3 1   3 1 log  b   c   a  − + − + − ≥ . a logb logc  9  4 4   4 4   4 4  Lời giải
Áp dụng bất đẳng thức AM − GM cho các số thực dương ta có  3 1  1  b − = ( b − ) 1 1 3 1 = . .(3b − ) 3 1 ≤   b  4 4  4 2 2   3 1  1 1  c − =  ( c − ) 1 1 3 1 = . .(3c − ) 3
1 ≤ c , kết hợp với < a,b,c <1 ta được:  4 4   4 2 2 3  3 1  1  a − =  ( a − ) 1 1 3 1 = . .(3a − ) 3 1 ≤ a   4 4  4 2 2  3 1   3 1   3 1 log  b   c   a  − + − + − 3 3 3 ≥ log b + c + a a logb log a logb log 4 4 4 4 c 4 4        c
TÀI LIỆU ÔN THI HỌC SINH GIỎI Trang 9
NHÓM TOÁN VDC&HSG THPT NĂM HỌC 2022 - 2023 ( − = b + c + a ≥ b c a = a b c ) AM GM 3 3 log log log
9 loga .logb .logc 9 V       ậy 3 1 3 1 3 1 log  b − +   c − +   a − ≥ . a logb logc  9  4 4   4 4   4 4  D 1
ấu " = " xảy ra khi: a = b = c = . 2
----------- Hết ---------- Trang 10
TÀI LIỆU ÔN THI HỌC SINH GIỎI
Document Outline

• de-hoc-sinh-gioi-cap-tinh-toan-thpt-nam-2022-2023-so-gddt-quang-ninh
• Đợt-14-ĐỀ-HSG-LỚP-12-TỈNH-QUẢNG-NINH-BẢNG-B-2022-2023.