Đề học sinh giỏi cấp tỉnh Toán THPT năm 2022 – 2023 sở GD&ĐT Sóc Trăng

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH SÓC TRĂNG Năm học: 2022-2023 ¯¯¯¯¯¯¯¯¯¯¯¯
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ĐỀ CHÍNH THỨC Môn: TOÁN
(Thời gian làm bài 180 phút, không kể thời gian phát đề) ¯¯¯¯¯¯¯¯¯¯¯¯ Đề thi này có 02 trang Bài 1: (6,0 điểm)   
1) Giải phương trình cos3x  3 sin 3x  2sin 3x   2 2 sin . x    3  2) Cho các số thực ,
x y thỏa mãn: y  2 10 và 3 2 2 2 x  3x  y
40  y  43 40  y . Tìm
giá trị lớn nhất của biểu thức 2 2 P  x  y  x  3 . y
3) Vào lúc 5 giờ chiều, ở một công ty tại khu công nghiệp An Nghiệp - Sóc Trăng có 12
xe đưa công nhân về một bến. Mỗi tài xế có hai lựa chọn để đi là:
+ Đi theo đường quốc lộ, không bị kẹt xe nhưng phải đi vòng, thời gian để đi là 60 phút.
+ Đi theo đường nội thành, đường ngắn hơn nhưng nhỏ và vào giờ cao điểm nên nếu xe
đầu tiên đi thì mất 25 phút, khi có thêm một xe nữa cùng đi (chỉ xét xe của công ty này) thì
thời gian của các xe đi sau sẽ tăng thêm 5 phút so với xe đi ngay trước đó.
Hỏi các tài xế của công ty phải tính toán cho bao nhiêu xe đi theo đường nội thành và bao
nhiêu xe đi theo đường quốc lộ để tổng thời gian các xe di chuyển là nhỏ nhất?
Bài 2: (2,0 điểm) Cho dãy số u được xác định bởi n  u  1, u  3 và u
 n  3 u  n  2 u , n     . n2   n 1   1 2 n
1) Tìm công thức tổng quát của dãy số u . n
2) Chứng minh rằng với mọi số nguyên dương n lớn hơn 9 thì u luôn chia hết cho 11. n Bài 3: (4,0 điểm) _______
1) Có bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau có dạng abcd mà a  b và c  d ?
2) Xếp ngẫu nhiên 6 học sinh gồm 2 học sinh lớp 10, 2 học sinh lớp 11 và 2 học sinh lớp
12 thành một hàng ngang. Tính xác suất để trong 6 học sinh trên không có 2 học sinh cùng lớp đứng cạnh nhau. Trang 1
Bài 4: (4,0 điểm) Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : x  y  4  0 và đường tròn C 2 2
: x  y  2x  6y  6  0.
1) Từ điểm S nằm trên đường thẳng d kẻ hai tiếp tuyến S ,
A SB của đường tròn C với ,
A B là các tiếp điểm và A có hoành độ dương. Đường thẳng AB đi qua K  2  ; 7. Tìm tọa độ điểm S.
2) Đường thẳng qua B song song SA cắt đường tròn C tại D D  B. Gọi C là giao
điểm thứ hai của SD với đường tròn C. Tìm tọa độ giao điểm M của BC và S . A
Bài 5: (4,0 điểm) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và BC  4a,
cạnh SA vuông góc với mặt phẳng đáy và SA  2a 2.
1) Tính góc giữa đường thẳng SC và mặt phẳng SAB.  
2) Gọi M , N lần lượt là trung điểm A ,
B SA và R là điểm thỏa mãn AC  2CR. Xác định
và tính diện tích thiết diện tạo bởi mặt phẳng MNR với hình chóp S.ABC. ------ Hết ------
Họ tên thí sinh: ......................................................... Số báo danh: ...........................................
Chữ ký của Cán bộ coi thi 1: ........................Chữ ký của Cán bộ coi thi 2: ............................... Trang 2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI THPT CẤP TỈNH SÓC TRĂNG Năm học: 2022-2023 ¯¯¯¯¯¯¯¯¯¯¯¯
¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯¯ ĐÁP ÁN CHÍNH THỨC Môn: TOÁN
(Thời gian làm bài 180 phút, không kể thời gian phát đề) ¯¯¯¯¯¯¯¯¯¯¯¯ HƯỚNG DẪN CHẤM
(Hướng dẫn chấm có 07 trang) Bài Đáp án Điểm    1
1) Giải phương trình cos3x  3 sin 3x  2sin 3x   2 2 sin . x   2,0  3  điểm   
Ta có cos3x  3 sin 3x  2sin 3x   2 2 sin x    3  1 3     cos3x  sin 3x  sin 3x   2 sin x   2 2  3  1,0       cos3 . x cos  sin 3 . x sin  sin 3x   2 sin x   3 3  3         cos 3x   sin 3x   2 sin x      3   3  2    2     cos 3x   sin 3x   sin x     2  3  2  3           sin 3x  .cos  cos 3x  .sin  sin x     0,5  3  4  3  4  7   sin 3x   sin x    12   7  7 3x   x  k2  x    k 12    24   , k  .  7  5  3x     x  k2     x k 0,5  12  48 2 7 5 
Vậy nghiệm của phương trình đã cho là: x    k , x   k , k  .  24 48 2 2) Cho các số thực , x y thỏa mãn: y  2 10 và 2,0 1 3 2 2 2 x  3x  y
40  y  43 40  y . Tìm giá trị lớn nhất của biểu thức điểm 2 2 P  x  y  x  3y. Ta có 3 2 2 2 x  3x  y 40  y  43 40  y 3  x  x   2  y  2 2 3 40 40  y  3 40  y  0  x    y 3 3 2   2 40 3 x  40  y   0 0,5     x   y  x  x  y     y 2 2 2 2 2    2 40 40 40 3 x  40  y   0       x   y  x  x  y     y 2 2 2 2 2 40 40 40  3  0    1 Bài Đáp án Điểm 2 2  1  3 Mà 2 2 x  x 40  y   2 40  y  2  3  x  40  y     2 40  y   3  0,  2  4 0,25 với y  2 10. x  0 Nên 2 x  40  y  0 2  x  40  y   (1). 0,25 2 2 x  y  40
Khi đó P  40  x  3y
Áp dụng bất đẳng thức Bunhiacopski, ta có
x  y2     2 2  2 2 3 1 3 x  y   400 0,5   Suy ra x  3y  20 Do đó P  60 0,25  x  0  x  2
Dấu “=” xảy ra khi và chỉ khi 2 2 x  y  40     y  6 x y   0,25 1 3 x  2
Vậy giá trị lớn nhất của P là 60 khi  .  y  6
3) Vào lúc 5 giờ chiều, ở một công ty tại khu công nghiệp An Nghiệp - Sóc Trăng
có 12 xe đưa công nhân về một bến. Mỗi tài xế có hai lựa chọn để đi là:
+ Đi theo đường quốc lộ, không bị kẹt xe nhưng phải đi vòng, thời gian để đi là 60 phút.
+ Đi theo đường nội thành, đường ngắn hơn nhưng nhỏ và vào giờ cao điểm 2,0 1
nên nếu xe đầu tiên đi thì mất 25 phút, khi có thêm một xe nữa cùng đi (chỉ xét xe điểm
của công ty này) thì thời gian của các xe đi sau sẽ tăng thêm 5 phút so với xe đi ngay trước đó.
Hỏi các tài xế của công ty phải tính toán cho bao nhiêu xe đi theo đường nội
thành và bao nhiêu xe đi theo đường quốc lộ để tổng thời gian các xe di chuyển là nhỏ nhất?
Gọi x (xe) là số xe đi theo đường nội thành  x  , x 12. 0,25
Khi đó có 12  x (xe) đi theo đường quốc lộ.
Tổng thời gian của các xe đi theo đường quốc lộ là 6012  x  720  60x (phút) 0,25
 Trường hợp 1: x  0 0,25
Tổng thời gian các xe di chuyển là 12.60  720 (phút).
 Trường hợp 2: 1 x 12
Thời gian các xe đi trong nội thành là một cấp số cộng với số hạng đầu u  25 1 0,25
(phút) và công sai d  5 (phút).
Tổng thời gian của các xe đi theo dương nội thành là 50   x  15 x  5 0,25 2 45 S   x  x (phút). x 2 2 2 5 75
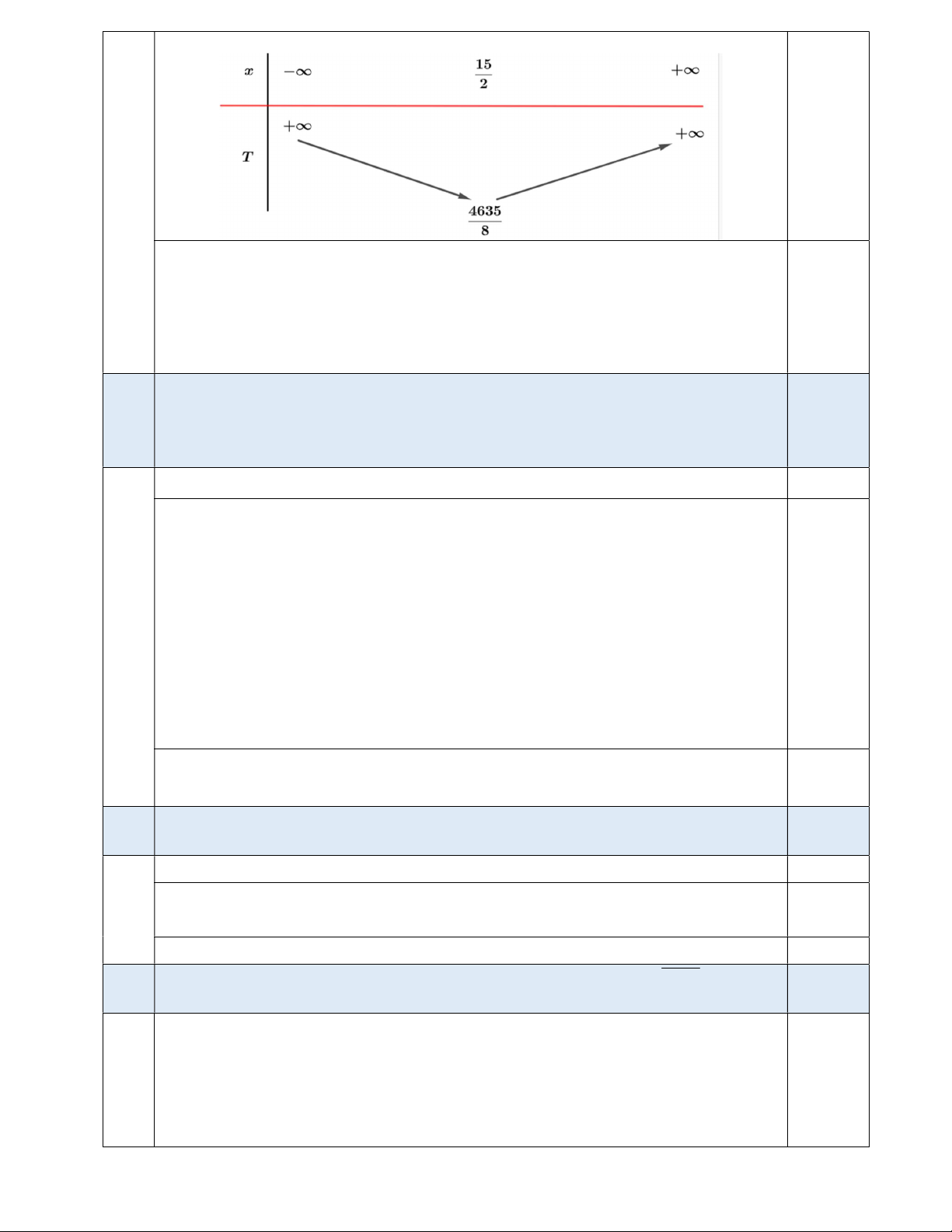
Tổng thời gian các xe di chuyển là 2 T  x  x  720 (phút). 0,25 2 2 2 Bảng biến thiên 0,25
Mà x  nên T đạt giá trị nhỏ nhất khi x  8 hoặc x  7. + Khi x  8 thì T  580. + Khi x  7 thì T  580. 0,25
Vậy tổng thời gian các xe di chuyển nhỏ nhất là 580 phút, khi 8 xe đi theo đường
nội thành, 4 xe đi theo đường quốc lộ hoặc khi 7 xe đi theo đường nội thành, 5 xe
đi theo đường quốc lộ.
Cho dãy số u được xác định bởi n  1,0 2 u  1, u  3 và u
 n  3 u  n  2 u , n     . n2   n 1   1 2 n điểm
1) Tìm công thức tổng quát của dãy số u . n Ta có u
 n  3 u  n  2 u  u  u  n  2 u  u 0,25 n2   n 1   n n2 n 1    n 1 n 
Ta chứng minh u  1! 2! ....  n!, n   * (*). n + Ta có u  1. 1
Do đó (*) đúng với n 1.
+ Giả sử (*) đúng với n  k k    * , tức là
u  1! 2! ....  k   1 ! k!. k 0,5
+ Ta cần chứng minh (*) đúng với n  k 1, tức là chứng minh u
1! 2! .... k! k 1 !. k 1    Thật vậy, ta có u  u  k 1 u  u  k 1 .k!  k 1 ! k 1  k   k k 1     Suy ra u
 u  k 1 ! 1! 2! .... k 1 !. k 1  k    
Theo nguyên lý quy nạp, ta được công thức tổng quát của dãy số u là n  0,25
u  1! 2! ....  n!, n    *. n
2) Chứng minh rằng với mọi số nguyên dương n lớn hơn 9 thì u luôn chia hết 1,0 2 n cho 11. điểm Chứng minh được u 1  1 10 0,5
Mà u  u 11!12!13! ....  n!, n  10 nên với mọi số nguyên dương n lớn n 10 0,25
hơn 10 thì u luôn chia hết cho 11. n
Vậy với mọi số nguyên dương n lớn hơn 9 thì u luôn chia hết cho 11. n 0,25 2,0 3
1) Có bao nhiêu số tự nhiên chẵn có 4 chữ số khác nhau có dạng abcd mà a  b và c  d ? điểm
 Trường hợp 1: d  0. Khi đó có 9 cách chọn . c
Chọn một tập con gồm hai phần tử của tập 0; 1; 2; 3; 4; 5; 6; 7; 8;  9 \  ; c d có 2
C cách chọn. Với tập con vừa chọn, ta có b là chữ số lớn hơn và a là chữ số 0,5 8 nhỏ hơn.
Trường hợp này có tất cả 2 9.C  252 (số) 8 3
 Trường hợp 2: d  2. Khi đó có 7 cách chọn . c
Chọn một tập con gồm hai phần tử của tập 1; 2; 3; 4; 5; 6; 7; 8;  9 \  ; c d có 2 C 7
cách chọn. Với tập con vừa chọn, ta có b là chữ số lớn hơn và a là chữ số nhỏ 0,5 hơn.
Trường hợp này có tất cả 2 7.C  147 (số). 7
 Trường hợp 3: d  4. Khi đó có 5 cách chọn . c
Chọn một tập con gồm hai phần tử của tập 1; 2; 3; 4; 5; 6; 7; 8;  9 \  ; c d có 2 C 7
cách chọn. Với tập con vừa chọn, ta có b là chữ số lớn hơn và a là chữ số nhỏ 0,25 hơn.
Trường hợp này có tất cả 2 5.C  105 (số). 7
 Trường hợp 4: d  6. Khi đó có 3 cách chọn . c
Chọn một tập con gồm hai phần tử của tập 1; 2; 3; 4; 5; 6; 7; 8;  9 \  ; c d có 2 C 7
cách chọn. Với tập con vừa chọn, ta có b là chữ số lớn hơn và a là chữ số nhỏ 0,25 hơn.
Trường hợp này có tất cả 2 3.C  63 (số). 7
 Trường hợp 5: d  8. Khi đó có 1 cách chọn . c
Chọn một tập con gồm hai phần tử của tập 1; 2; 3; 4; 5; 6; 7; 8;  9 \  ; c d có 2 C 7
cách chọn. Với tập con vừa chọn, ta có b là chữ số lớn hơn và a là chữ số nhỏ 0,25 hơn.
Trường hợp này có tất cả 2 C  21 (số) 7
Vậy có 252 147 105  63  21  588 số tự nhiên thỏa yêu cầu bài toán. 0,25
2) Xếp ngẫu nhiên 6 học sinh gồm 2 học sinh lớp 10, 2 học sinh lớp 11 và 2 học 2,0 3
sinh lớp 12 thành một hàng ngang. Tính xác suất để trong 6 học sinh trên không điểm
có 2 học sinh cùng lớp đứng cạnh nhau?
Số phần tử của không gian mẫu n  6!  720. 0,5
Gọi A là biến cố trong 6 học sinh thì 2 học sinh cùng lớp không đứng cạnh nhau;
M là tập hợp cách xếp mà 2 học sinh lớp 10 đứng cạnh nhau;
N là tập hợp cách xếp mà 2 học sinh lớp 11 đứng cạnh nhau; 0,25
P là tập hợp cách xếp mà 2 học sinh lớp 12 đứng cạnh nhau.
Khi đó M  N  P  2!.5!  240.
M  N  N  P  P  M  2!.2!.4!  96. 0,5
M  N  P  2!.2!.2!3!  48.
Số cách xếp có ít nhất 2 học sinh cùng lớp đứng cạnh nhau là
M  N  P  M  N  P  M  N  N  P  P  M  M  N  P  480. 0,25
Số phần tử của biến cố A là n A  720  480  240. 0,25 n A 240 1
Xác suất cần tính là P  A      0,25 n . 720 3
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d : x  y  4  0 và đường tròn C 2 2
: x  y  2x  6y  6  0. 2,0 4
1) Từ điểm S nằm trên đường thẳng d kẻ hai tiếp tuyến S , A SB của đường tròn  điểm C  với ,
A B là các tiếp điểm và A có hoành độ dương. Đường thẳng AB đi qua K  2
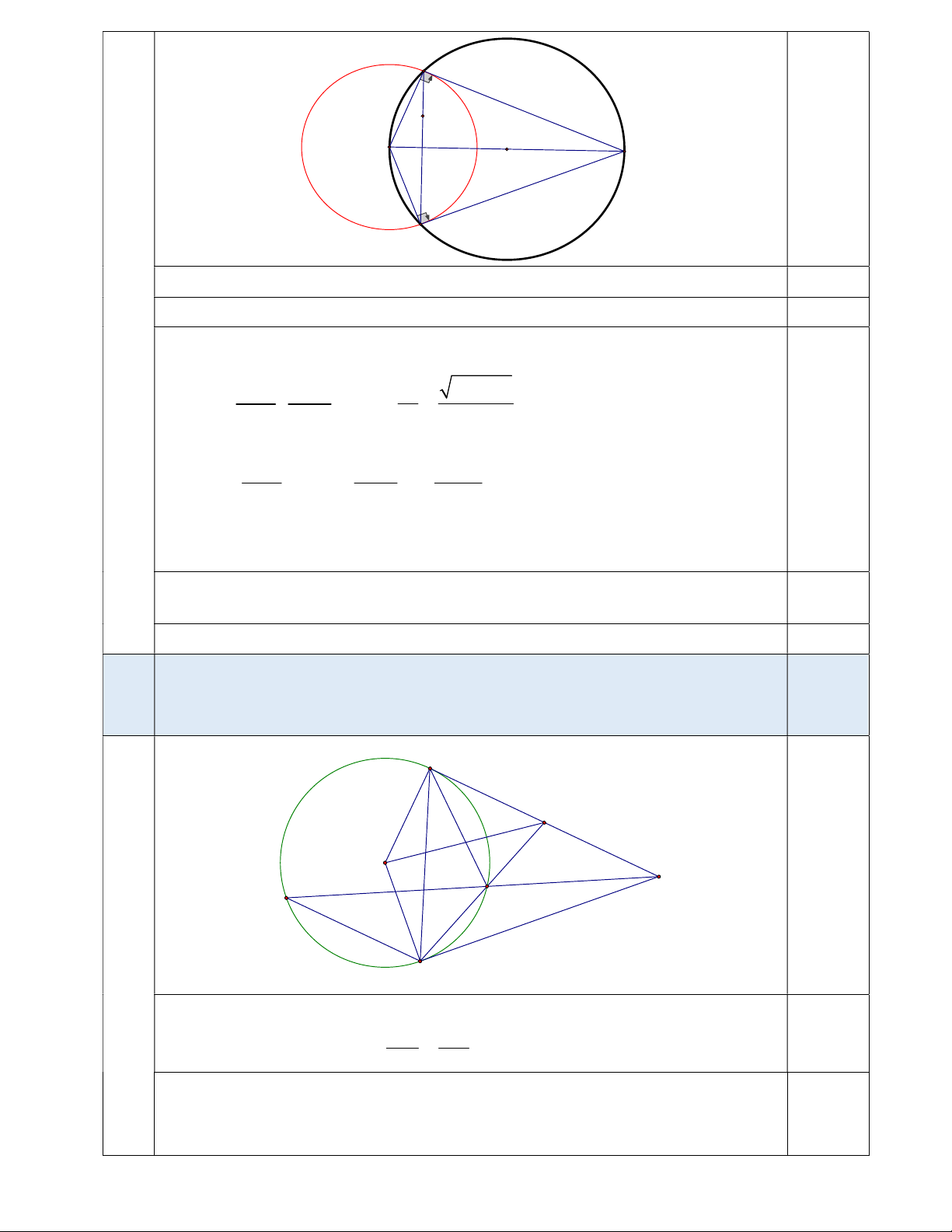
 ; 7. Tìm tọa độ điểm S. 4 A K I T S B
Đường tròn C có tâm I 1; 3, bán kính R  2. 0,25 Gọi S  ; m m  4  d. 0,25 Gọi T là trung điểm SI.
Tứ giác SAIB nội tiếp đường tròn đường kính SI.  m 1 m  7  2 IS 2m  2 Ta có T ; ,   TS   .  2 2  2 2
Phương trình đường tròn ngoại tiếp tứ giác SAIB là 0,5 2 2 2         T  m 1 m 7 m 1 : x   y   .      2   2  2 Hay T  2 2 : x  y  m  
1 x  m  7 y  4m 12  0 (1) Mà C 2 2
: x  y  2x  6y  6  0 (2)
Lấy (2) trừ (1), ta được phương trình đường thẳng AB là AB : m   1 x  m   1 y  4m  6  0. 0,5 Mà AB qua K  2  ; 7 nên m  3  . Khi đó S  3  ;  1 . 0,5
2) Đường thẳng qua B song song SA cắt đường tròn C tại D D  B. Gọi C 2,0 4
là giao điểm thứ hai của SD với đường tròn C. Tìm tọa độ giao điểm M của điểm BC và S . A A M I S C D B Xét M  AC và MBA có  M chung và  MAC   MBA (cùng chắn  AC ). MA MB 0,5 Khi đó M  AC  M  BA nên 2   MA  M . B MC (1). MC MA Ta có  SBC   SDB (cùng chắn  BC ) và  ASD   SDB (so le trong). Suy ra  SBC   ASD hay  SBM   MSC. 0,5 Xét M  SC và M  BS có  M chung và  MSC   SBM (chứng minh trên). 5 MS MB Khi đó M  SC  M  BS nên 2   MS  M . B MC (2). MC MS
Từ (1) và (2), ta được MA  MS hay M là trung điểm AS. 0,25
Phương trình đường thẳng AB là 2x  y  3  0. 0,25  3 2x  y  3  0 x   x  1  Xét hệ phương trình  5   v  . 2 2
x  y  2x  6y  6  0  y  1 21  y  0,25  5 Suy ra A1;  1 .
Ta có M là trung điểm SA nên M  1  ;  1 . 0,25
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và BC  4a, 1,5 5
cạnh SA vuông góc với mặt phẳng đáy và SA  2a 2. điểm
1) Tính góc giữa đường thẳng SC và mặt phẳng SAB. S N P C A R Q M B
Ta có AC  AB (giả thiết) và AC  SA SA   ABC. 0,5 Suy ra AC  SAB.
Khi đó SA là hình chiếu của SC trên SAB. 0,5 Suy ra SC,SAB     SC,SA  ASC (do S  AC vuông tại A). BC Xét A
 BC vuông cân tại A nên AB  AC   2a 2. 2 AC a Xét S  AC vuông tại , A có  2 tan ASC    1. 0,5 SA a 2 Vậy SC,SAB     ASC  45 .   
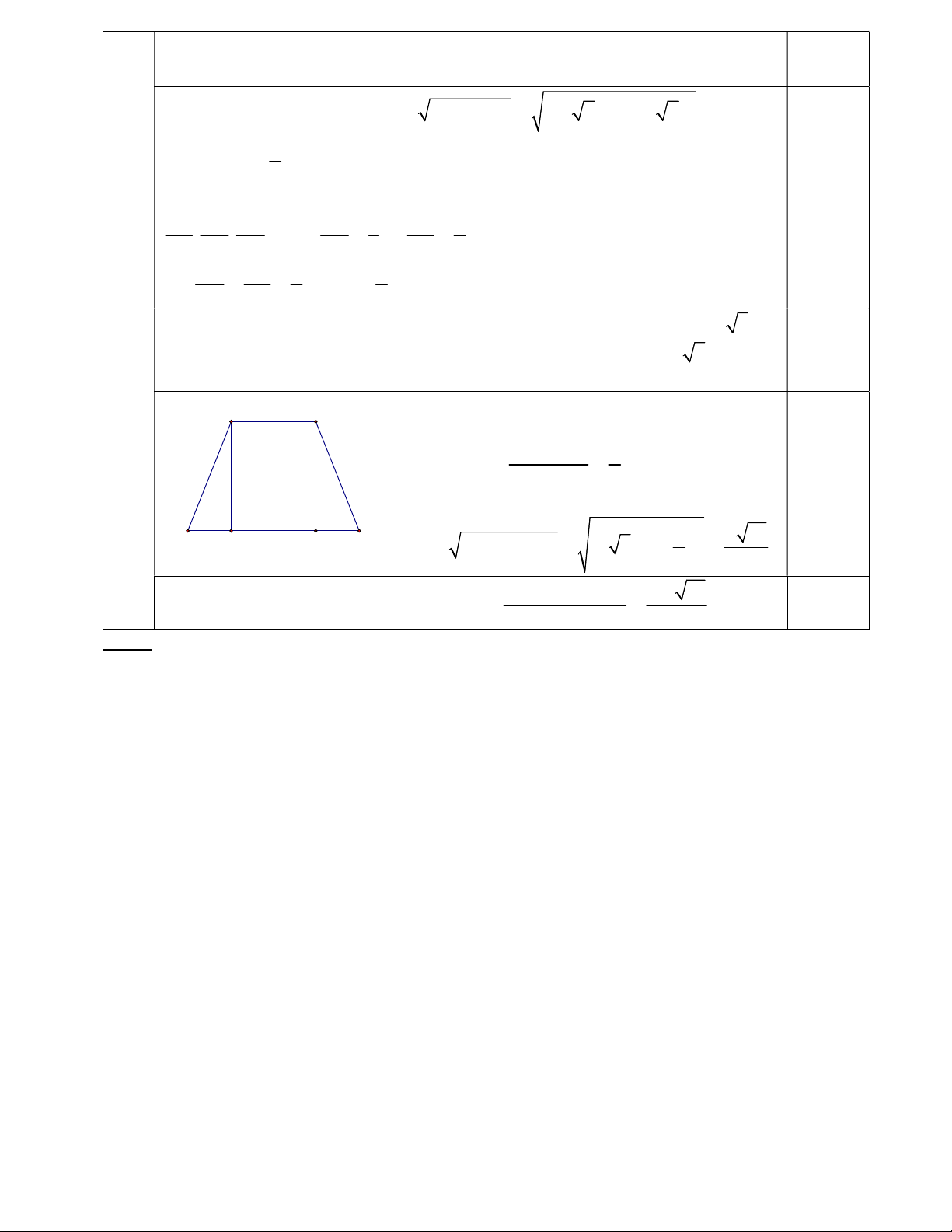
2) Gọi M, lần lượt là trung điểm AB, SA và R là điểm thỏa mãn AC  2C . R 2,5 5
Xác định và tính diện tích thiết diện tạo bởi mặt phẳng MNR và hình chóp điểm S.ABC.
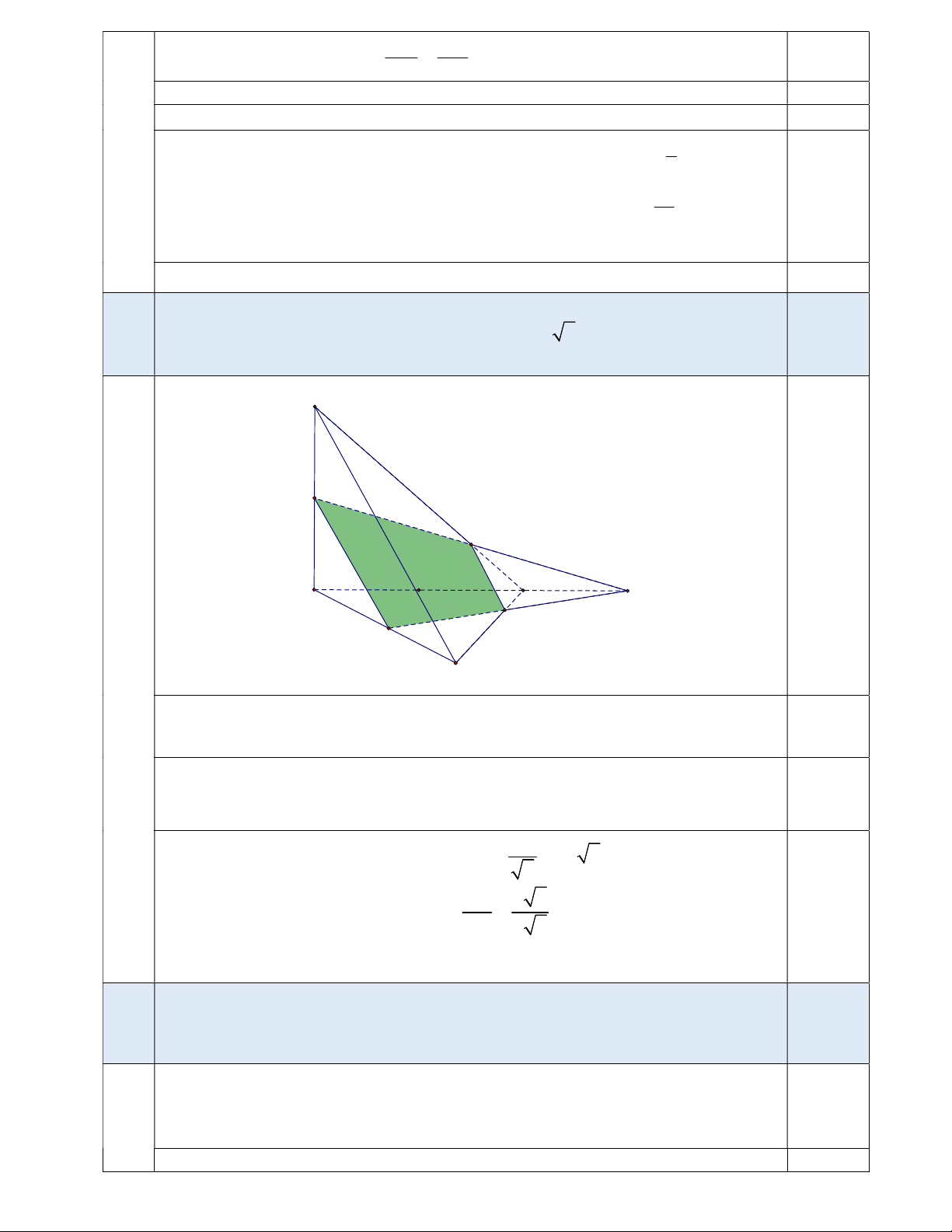
Trong mặt phẳng SAC, gọi P là giao điểm của SC và N . R
Trong mặt phẳng  ABC, gọi Q là giao điểm của BC và M . R 0,5
Khi đó thiết diện là tứ giác MNP . Q
Ta có MN là đường trung bình của S  AB nên MN / /S . B 0,5 6
MNRSBC  PQ  PQ / /MN
Suy ra tứ giác MNPQ là hình thang. 2 2 Xét S  AB vuông tại , A có 2 2
SB  SA  AB  2a 2   2a 2  4 . a 1 Suy ra MN  SB  2 . a 2
Áp dụng định lí Menelaus cho SAC, với N , P, R thẳng hàng. Ta có 0,5 NS RA PC PC CP . .  1 1   1   . NA RC PS PS 3 CS 4 PQ CP 1 1 Mà    PQ  SB  . a SB CS 4 4 Xét BMQ có 2 2 2 2 MQ  BM  BQ  2BM.B .
Q cos MBQ  5a  MQ  a 5. Xét S  NP có 2 2 2 2 NP  SN  SP  2SN.S .
P cos NSP  5a  NP  a 5. 0,5
Khi đó tứ giác MNPQ là hình thang cân
Gọi H , K lần lượt là hình chiếu của Q, P trên Q P MN. MN  HK a Khi đó MH   . 2 2 0,25
Xét tam giác MHQ vuông tại H có M H K N   QH  MQ  MH  a  2 2 2 2 a a 19 5   .    2  2 MN  PQ 2 QH 3a 19
Diện tích hình thang cân MNPQ là S   . 0,25 MNPQ 2 4
Chú ý: Nếu thí sinh có cách giải khác và đúng vẫn cho đủ số điểm. 7
Document Outline

• ToanCT_2023_De
• ToanCT_2023_HDC