Đề học sinh giỏi cấp tỉnh Toán THPT năm 2022 – 2023 sở GD&ĐT Tiền Giang

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH TỈNH TIỀN GIANG
TRUNG HỌC PHỔ THÔNG Năm học 2022-2023
ĐỀ THI CHÍNH THỨC Môn: TOÁN
Thời gian: 180 phút (không kể thời gian giao đề) Ngày thi: 03/3/2023
(Đề thi có 2 trang, gồm 6 bài)
_________________________________________________
Bài 1: (5,0 điểm) a) Cho hàm số 1 3 1
y = x − (2m + 3) 2 x + ( 2
m + 3m + 2)x +1, trong đó m là tham 3 2
số thực. Tìm tất cả các giá trị nguyên của tham số m∈( 2023 − ;2023) sao cho hàm số
đã cho đồng biến trên khoảng (0;2) . b) Cho hàm số x + 2 y =
có đồ thị (C). Tìm trên (C) hai điểm A(x y , A; A ) x −1
B(x y sao cho x < < x và khoảng cách giữa hai điểm ,
A B là ngắn nhất. B 1 B ; B ) A
Bài 2: (4,0 điểm) 4cos π   π x 2sin 2x − + − −     1 a) Giải phương trình  6   6  = 0. cos x 3
2y + y = (3− 2x) 1− x
b) Giải hệ phương trình 
, trong đó x, y ∈ . 2
y − x + 4 = x + 9x +19
Bài 3: (2,0 điểm)
Cho tập X = {1; 2; 3; 4; 5; 6; 7; 8; }
9 . Có bao nhiêu số tự nhiên có năm chữ số đôi
một khác nhau, các chữ số thuộc tập X và không có hai chữ số liên tiếp nào cùng lẻ?
Bài 4: (4,0 điểm)
a) Cho hai số thực x, y ≥1 thay đổi thỏa mãn 2 2
x + y = 4. Tìm giá trị lớn nhất và
giá trị nhỏ nhất của biểu thức M = ( 3 3
2 x + y ) − (x + y). u  = 2
b) Cho dãy số (u xác định bởi 1 . Tính giới hạn n )  * u  = + + ∀ ∈ + u n n n n 2 1, 1  lim un . 2n Môn Toán - trang 1/2
Bài 5: (3,0 điểm)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1, cạnh bên SA
vuông góc với mặt phẳng ( ABCD) và khoảng cách giữa hai đường thẳng BD và SC
bằng 6 . Gọi M là điểm di động trên đoạn CB và N là điểm di động trên đoạn CD 6 sao cho 
MAN = 60° . Tính độ dài cạnh SA và tìm giá trị nhỏ nhất của thể tích khối chóp S.AMN .
Bài 6: (2,0 điểm)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC nội tiếp đường tròn tâm I . Biết rằng điểm 1 1 E ;   
là trung điểm cạnh AB , 4 22 H  −  ;
là hình chiếu vuông góc của 2 2      5 5 
điểm A trên đường thẳng CI và đường thẳng BC có phương trình là x + y − 4 = 0.
Tìm tọa độ các đỉnh của tam giác ABC .
------------------------------------------------- HẾT -----------------------------------------------
Thí sinh không được sử dụng tài liệu và máy tính cầm tay.
Cán bộ coi thi không giải thích gì thêm.
Họ và tên thí sinh: ........................................ Số báo danh:……………………………. Môn Toán - trang 2/2
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ T HI CHỌN HỌC SINH GIỎI CẤP TỈNH TỈNH TIỀN GIANG
TRUNG HỌC PHỔ THÔNG Năm học 2022-2023 ĐÁP ÁN
ĐỀ THI CHÍNH THỨC Môn: TOÁN Ngày thi: 03/3/2023
(Đáp án gồm có 06 trang) Bài Nội dung Điểm 1 1 3 1 2 2
(5đ) a) Cho hàm số y = x − (2m + 3) x + (m + 3m + 2) x +1, trong đó m là tham số thực. Tìm tất 3 2
cả các giá trị nguyên của tham số m∈( 2023 −
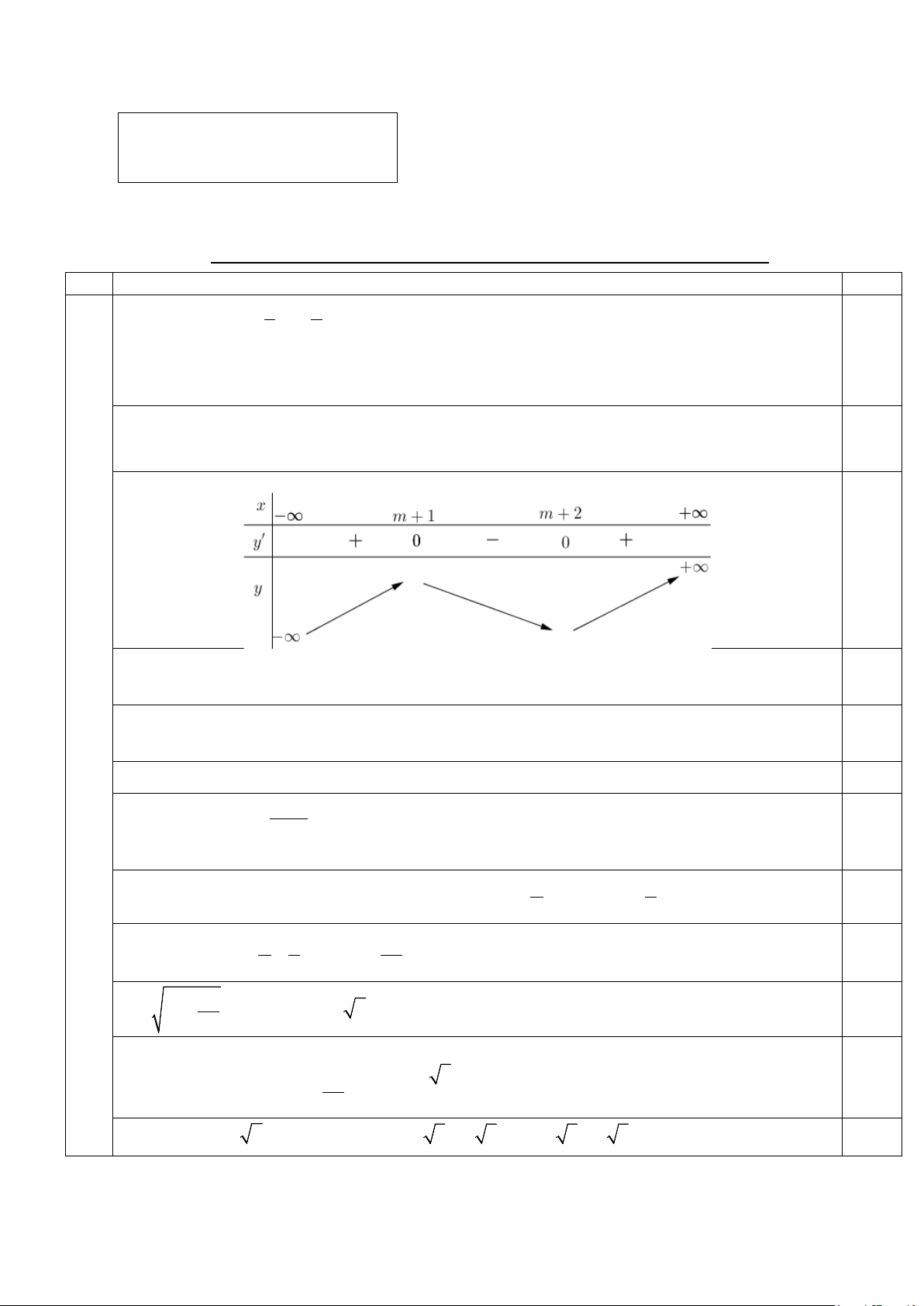
;2023) sao cho hàm số đã cho đồng biến trên 2,5 khoảng (0;2).  x = m +1 Ta có 2
y′ = x − ( m + ) 2 2
3 x + m + 3m + 2 ; y′ = 0 ⇔  . x = m + 2 0,5 Bảng biến thiên: 0,5  ≤ m +
Dựa vào bảng biến thiên suy ra hàm số đồng biến trên khoảng ( ) 2 1 0;2 ⇔  0,5 m + 2 ≤ 0  m ≥1 ⇔  . 0,5 m ≤ 2 − Vậy m∈{ 2022 − ; 2021 − ; ; … − } 2 ∪{1;2; ; … } 2022 0,5 b) Cho hàm số x + 2 y =
có đồ thị (C). Tìm trên (C) hai điểm A(x y B x y sao cho A; A ) , ( B; B ) x −1 2,5
x < < x và khoảng cách giữa hai điểm ,
A B là ngắn nhất. B 1 A
Đặt a = x − b = − x . Ta có a,b > 0 và  3   3 Aa 1;1 , B 1 ;1 b  + + − − . A 1, 1 B 0,5 a b      2
AB = (a + b)2 2  3 3  36 + + ≥  4ab +  0,5  a b  ab 36 ≥ 2. 4 . ab = 24 ⇒ AB ≥ 2 6. 0,5 ab  a = b > 0 Dấu “=” xảy ra  ⇔ 
36 ⇔ a = b = 3 . 0,5 4ab =  ab
Vậy minAB = 2 6 khi và chỉ khi A(1+ 3;1+ 3), B(1− 3;1− 3). 0,5 Trang 1/6 2  π   π  (4đ) 4.cos − x + 2.sin − 2x −     1 a) Giải phương trình  6   6  = 0. 2 cos x
Điều kiện cos x > 0     Phương trình 3 1 1 3 ⇔ 4
cos x + sin x + 2 cos 2x − sin 2x =1  . 0,5 2 2   2 2     
⇔ 2( 3 cos x +sin x)+(cos2x − 3sin 2x) =1 ⇔ 3(2cos x −sin 2x)+ 2sin x + cos2x −1= 0 0,5 2
⇔ 2 3 cos x(1− sin x) + 2sin x − 2sin x = 0 ⇔ (1− sin x)(2 3 cos x + 2sin x) = 0 .  π x = + k2  sin x =1 π  2 ⇔  ⇔  (k ∈) . 0,5 tan x = − 3 π x = − + kπ  3 π
So sánh với điều kiện ta được nghiệm của phương trình là x = − + k2π ,k ∈ . 0,5 3 3
2y + y = (3− 2x) 1− x
b) Giải hệ phương trình 
, trong đó x, y ∈ . 2 2
y − x + 4 = x + 9x +19 Điều kiện 4 − ≤ x ≤1.
Phương trình thứ nhất tương đương với: 3
2y + y = 2(1− x) 1− x + 1− x .(*) 0,5
Xét hàm số f (t) 3
= 2t + t, với t ∈  . Khi đó (*) thành f ( y) = f ( 1− x ). Ta có f ′(t) 2
= 6t +1 > 0, t ∀ ∈  . 0,5
Do đó f đồng biến trên  nên suy ra y = 1− x .
Thế y = 1− x vào phương trình thứ hai ta được: 2
1− x − x + 4 = x + 9x +19 ⇔ ( − x − )−( x + − ) 2 1 2
4 1 = x + 9x +18 0,5 3 − − x x + 3 − ⇔ − = (x + 3)(x + 6) 1 1 ⇔ x = 3 − hoặc − = x + 6.( **) 1− x + 2 x + 4 +1 1− x + 2 x + 4 +1 Vì 4
− ≤ x ≤1 nên VT(**) < 0 < x + 6 . Do đó (**) vô nghiệm. 0,5
Vậy tập nghiệm của hệ phương trình là S = ( { 3 − ;2)}.
3 Cho tập X = {1;2;3;4;5;6;7;8; }
9 . Có bao nhiêu số tự nhiên có năm chữ số đôi một khác nhau, (2đ) 2
các chữ số thuộc tập X và không có hai chữ số liên tiếp nào cùng lẻ?
Xét các số tự nhiên có năm chữ số đôi một khác nhau, các chữ số thuộc tập X .
Vì một số tự nhiên có 5 chữ số lẻ hoặc 4 chữ số lẻ và 1 chữ số chẵn luôn luôn có hai chữ số lẻ
đứng cạnh nhau nên ta chỉ xét các trường hợp sau:
TH1: Số tự nhiên có 1 chữ số lẻ và 4 chữ số chẵn khác nhau. 0,5
Trong trường hợp này số được tạo thành luôn luôn không có hai chữ số liên tiếp nào cùng lẻ. Có 1
C cách chọn chữ số lẻ và 1 cách chọn 4 chữ số chẵn khác nhau. Sau đó hoán vị các chữ số 5
này tạo được 5! số. Do đó trường hợp này có 1 C .5!= 600 số. 5
TH2: Số tự nhiên có 3 chữ số lẻ khác nhau và 2 chữ số chẵn khác nhau.
Trong trường hợp này để số được tạo thành không có hai chữ số liên tiếp nào cùng lẻ thì vị trí 0,5
các chữ số phải là: lẻ - chẵn - lẻ - chẵn - lẻ. Trang 2/6
Có 2A cách chọn 2 chữ số chẵn khác nhau, có 3A cách chọn 3 chữ số lẻ khác nhau sắp xếp 4 5
vào vị trí như trên. Do đó trường hợp này có 3 2
A .A = 720 số. 5 4
TH3: Số tự nhiên có 2 chữ số lẻ khác nhau và 3 chữ số chẵn khác nhau.
Cách 1: Trong trường hợp này để số được tạo thành không có hai chữ số liên tiếp nào cùng lẻ
thì vị trí các chữ số như sau:
+ Chẵn - lẻ - chẵn - lẻ - chẵn;
+ Chẵn - lẻ - chẵn - chẵn - lẻ;
+ Chẵn - chẵn - lẻ - chẵn - lẻ;
+ Lẻ - chẵn - lẻ - chẵn - chẵn;
+ Lẻ - chẵn - chẵn - lẻ - chẵn; 0,5
+ Lẻ - chẵn - chẵn - chẵn - lẻ. Có 3
A cách chọn 3 chữ số chẵn khác nhau, có 2
A cách chọn 2 chữ số lẻ khác nhau sắp xếp 4 5
vào mỗi vị trí như trên. Do đó trường hợp này có 3 2
6.A .A = 2880 số. 4 5
Cách 2: Xếp 3 số chẵn thành hàng ngang, giữa và hai đầu các số chẵn này có 4 chỗ trống. Ta
xếp 2 số lẻ vào 4 chỗ trống này tạo được số tự nhiên thỏa yêu cầu bài toán. Do đó có 2 3 2
C .A .A = 2880 số. 4 4 5
Vậy số tất cả các số tự nhiên cần tìm là: 600 + 720 + 2880 = 4200 số. 0,5
4 a) Cho hai số thực x, y ≥1 thay đổi thỏa mãn 2 2
x + y = 4. Tìm giá trị lớn nhất và giá trị nhỏ
(4đ) nhất của biểu thức M = ( 3 3
2 x + y ) −(x + y). 2 2
Đặt S = x + y, P = x .
y Ta có: S = x + y ≥ 2 ; 2 S 4 S 2P 4 P − − = ⇒ = . 2 2
(x − )( y − ) S − 4 1
1 ≥ 0 ⇒ P − S +1≥ 0 ⇒
− S +1≥ 0 ⇒ S ≥1+ 3. 0,5 2 Vì 2 S ≥ 4P nên 2 2
S ≥ 2S −8 ⇒ 2
S ≤ 8 ⇒ S ≤ 2 2.
Vậy 1+ 3 ≤ S ≤ 2 2. Ta có: 3 3
M = S − PS − S = S − S ( 2 S − ) 3 2( 3 ) 2 3
4 − S = −S +11S. Đặt f (S ) 3
= −S +11S , với 1+ 3 ≤ S ≤ 2 2. 0,5
Ta có: f ′(S ) 2 = 3
− S +11< 0, S ∀ ∈ 1  + 3;2 2.  
Do đó f nghịch biến trên đoạn 1  + 3;2 2.  
Suy ra f (2 2) ≤ f (S) ≤ f (1+ 3), S ∀ ∈ 1  + 3;2 2.   0,5
Hay 6 2 ≤ f (S ) ≤1+ 5 3, S ∀ ∈ 1  + 3;2 2.    Vậy minM  = = 6 2 S ⇔ 2 2  ⇔ x = y = 2.  P = 2 0,5 S =1+ 3  x =1  maxM =1+ 5 3 x = ⇔  ⇔  hoặc 3  .  P = 3 y = 3  y =1
Ghi chú: Nếu HS có cách giải khác, chỉ tìm được GTLN hoặc GTNN của M thì được 1,0 điểm. u  =  2
b) Cho dãy số (u xác định bởi: 1
. Tìm giới hạn lim un . n )  2 * u  = + + ∀ ∈  2n + u n n n n 2 1, 1  Trang 3/6  u − u = − + − n n n 2 1 1 1 ( ) u   − = − + − u − n n n 2 2 1 1 2 ( ) Ta có:  .   0,5  u − u = 2.1+  1 2 1
Cộng tất cả các đẳng thức trên vế theo vế ta được: u − u = + +…+ n − + n − n 2 1 2 1 1 . 1 ( ( )) ( ) n − n Vì + +…+ (n − ) ( )1 1 2 1 =
nên u = n − n + n + = n + n ∀ ∈ 0,5 n ( ) 2 * 1 1 1,  . 2 n n n − n − n n ! 1 2 0 1 2 3 ( )( )
Ta có: 2 = C + C + C +…+ C > C = = n ∀ ≥ n n n n n (n − ) , 3. 3! 3 ! 6 0,5 2 Suy ra: u n + n 6( 1) 0 < < , n ∀ ≥ 3. n 3 2 2
n − 3n + 2n  1 1 6  + 2  3  Vì 6(n +1) lim lim  n n  = = 0 nên lim un = 0. 0,5 3 2
n − 3n + 2n 3 2 n 1− + 2 2 n n
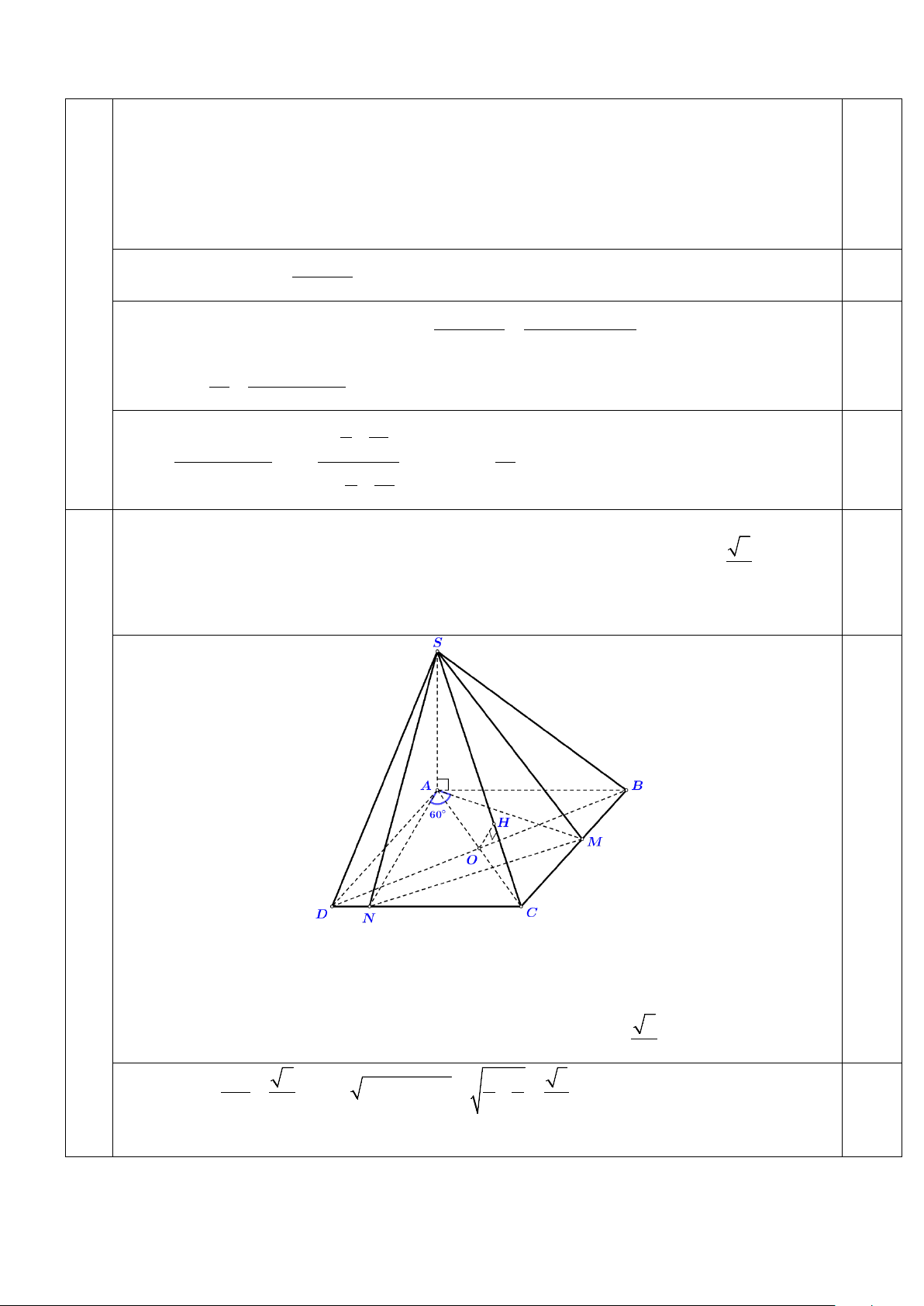
5 Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng 1, cạnh bên SA vuông góc
(3đ) với mặt phẳng (ABCD) và khoảng cách giữa hai đường thẳng BD và SC bằng 6. Gọi M 6 3
là điểm di động trên đoạn CB và N là điểm di động trên đoạn CD sao cho  0 MAN = 60 . Tính
độ dài cạnh SA và tìm giá trị nhỏ nhất của thể tích khối chóp S.AMN . 0,5
Gọi O là tâm hình vuông ABC .
D Vẽ OH ⊥ SC.
Ta có BD ⊥ AC,
BD ⊥ SA (do SA ⊥ ( ABCD) ⊃ BD ). Mà AC, SC là hai đường thẳng cắt nhau
nằm trong mặt phẳng (SAC) nên BD ⊥ (SAC) ⊃ OH ⇒ BD ⊥ OH.
Do đó OH là đoạn vuông góc chung của BD và SC. Suy ra 6 OH = . 6 Ta có: AC 2 2 2 1 1 3 OC = =
; HC = OC − OH = − = . 2 2 2 6 3 0,5 Trang 4/6 6 . 2 Ta có S ∆ AC ~ OHC ∆
( g.g) nên SA AC OH.AC 6 = ⇒ SA = = = 1. OH HC HC 3 3
Đặt BM = x, DN = .
y Ta có 0 ≤ x, y ≤1. Đặt  = α  BAM , DAN = β . Ta có 0 α + β = 30 và tan BM α = = , tan DN x β = = . y AB AD 0,5 (α + + β ) tanα + tan β Vì tan = nên 1 x y =
⇒1− xy = 3 (x + y). 1− tanα.tan β 3 1− xy
Ta có x + y ≥ 2 xy nên 1− xy ≥ 2 3 xy ⇒ xy + 2 3. xy −1≤ 0 0,5
⇒ xy ≤ 2 − 3 ⇒ xy ≤ 7 − 4 3. 1 1 1 S = S − S − S − S
= − x − y − − x − y = − xy . AMN ABCD ABM ADN MNC ( )( ) 1 1 1 1 (1 ) 2 2 2 2 0,5 Suy ra 1 1 2 3 3 V SA S xy − = = − ≥ S AMN . . AMN 1 . . ( ) 3 6 3
Dấu “=” xảy ra ⇔ x = y = 2 − 3. 0,5
Vậy giá trị nhỏ nhất của thể tích khối chóp S.AMN là 2 3 − 3. 3
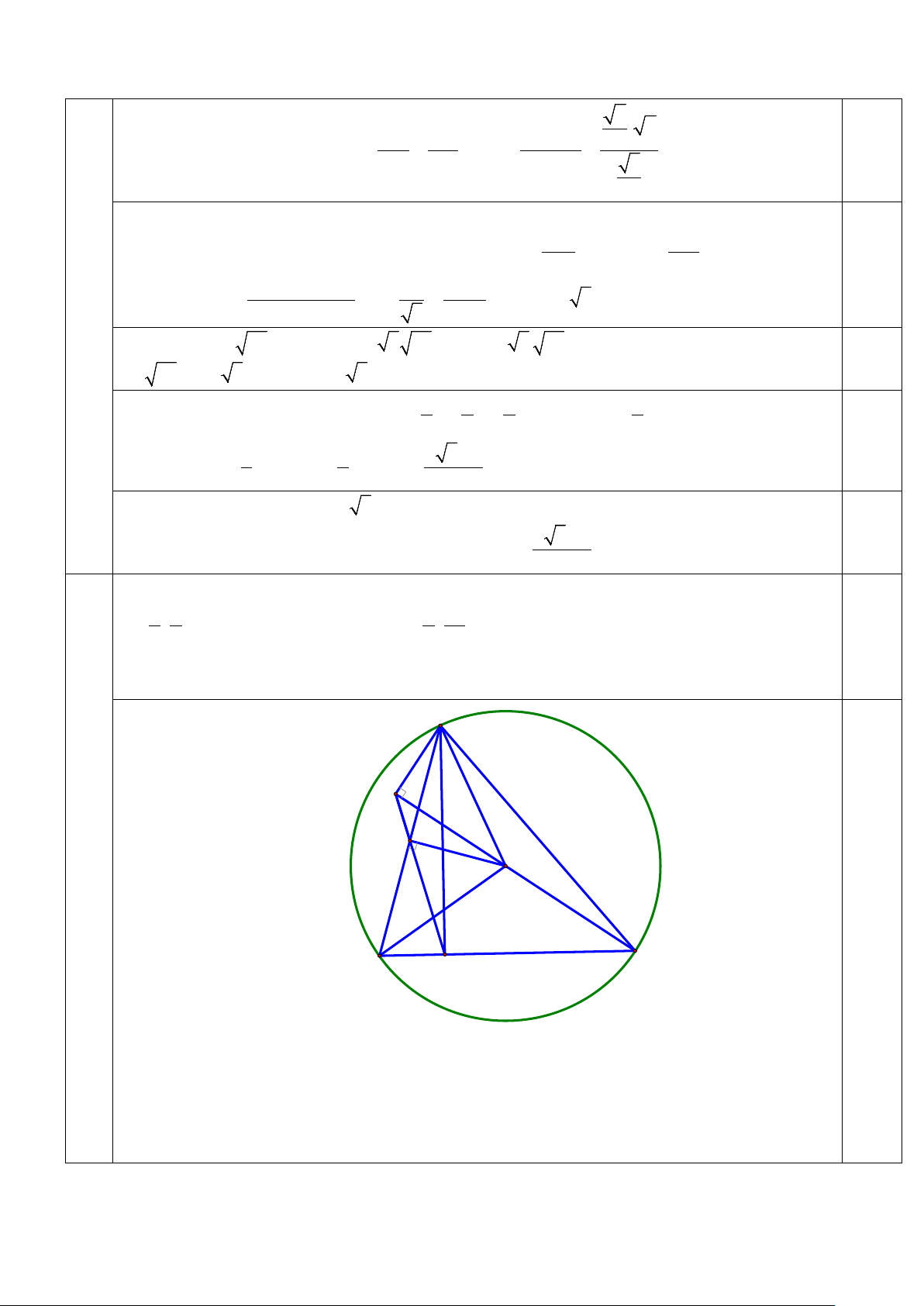
6 Trong mặt phẳng tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I . Biết rằng điểm (2đ) 1 1 E  ;   
là trung điểm cạnh AB , 4 22 H  −  ;
là hình chiếu vuông góc của điểm A trên đường 2 2      5 5  2
thẳng CI và đường thẳng BC có phương trình là x + y − 4 = 0 . Tìm tọa độ các đỉnh của tam giác ABC. A H E I 0,5 F C B
Gọi F là giao điểm của hai đường thẳng HE và BC .
Ta có đường thẳng HE có phương trình là: 3x + y − 2 = 0 . 3
 x + y − 2 = 0 x = 1 −
Tọa độ điểm F là nghiệm của hệ phương trình  ⇔  .
 x + y − 4 = 0  y = 5 Suy ra: F ( 1 − ; 5). Trang 5/6
Ta có tứ giác AHEI nội tiếp.
Suy ra  =  +  =  +  =  +  = 
EFB EHC HCB EAI ICB IBE IBC EBF. 0,5
⇒ ∆ EBF cân tại E ⇒ EB = EF = EA ⇒ ∆ ABF vuông tại F ⇒ AF ⊥ BC.
Đường thẳng AF đi qua F vuông góc với BC có phương trình là: x − y + 6 = 0.
Phương trình đường tròn tâm E bán kính EF có phương trình là: 2 2  1   1  45 x − + y − =     ⇔ 2 2
x + y − x − y − 22 = 0.  2   2  2
Tọa độ điểm A , là giao điểm thứ hai khác F của đường thẳng AF với đường tròn (E; EF ) , 0,5
x − y + 6 = 0 là một nghiệm khác ( 1;
− 5) của hệ phương trình  . 2 2
 x + y − x − y − 22 = 0 Do đó A( 4; − 2).
x = x − x = + = B 2 E A 1 4 5
E là trung điểm AB nên  ⇒ B(5;− ) 1 .
y = y − y = − = −  B 2 E A 1 2 1
Đường thẳng IC đi qua H và vuông góc với AH có phương trình là 4x + 3y −10 = 0 . 0,5
Tọa độ điểm C là giao điểm của hai đường thẳng IC và BC là nghiệm của hệ phương trình:
 4x + 3y −10 = 0  ⇒ C ( 2; − 6).
x + y − 4 = 0 Ghi chú:
+ Ở ý 2, tùy hình vẽ HS (tam giác tù, vị trí điểm H khác với hình vẽ trên,…) có thể chứng minh
AF ⊥ BC bằng cách khác. Nếu HS chứng minh đúng với hình vẽ của mình thì được trọn điểm ý 2.
+ Nếu HS không chứng minh được AF ⊥ BC mà làm các ý sau thì các ý sau không cho điểm.
Ghi chú: Các cách giải khác, nếu thí sinh làm đúng vẫn cho trọn số điểm. Mỗi ý làm đúng HS được
0,5 điểm, nếu HS chỉ làm đúng được nửa ý của mỗi ý nhỏ này thì được 0,25 điểm. Trang 6/6
Document Outline

• TIEN GIANG DE THI 2022-2023
• TIEN GIANG DAP AN 2022-2023