PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN HUYỆN KIM THÀNH Môn : Toán Lớp 7
Thời gian làm bài 120 phút
(Đề khảo sát gồm 01 trang) ĐỀ CHÍNH THỨC Câu 1 (4,0 điểm): 3 3 3 1 1 1     a) Tính A = 4 11 13 2 3 4  5 5 5 5 5 5     4 11 13 4 6 8
b) Chứng minh rằng với n nguyên dương thì 3n+2 - 2n+2 + 3n - 2n chia hết cho 10. Câu 2 (4,0 điểm):
a) Tìm các cặp số nguyên (x,y) thỏa mãn: x + 2y = 3xy + 3 b) Cho A= 1 1 1 1    ...  ; B = 1 2 3 2015 2016    ...  . Tính A 2 3 4 2017 2016 2015 2014 2 1 B Câu 3 (3,0 điểm): a) Cho 2016
x  2  y 1  (x  y  z  2)
 0 . Tính giá trị của : A = 5 x2y2016z2017  2016 a  b 2017 2016  2017 a  b 2016 2017
b) Cho các số dương a,b,c,d; c  d và a c  . CMR  b d  2016 c  d 2017 2016  2017 c  d 2016 2017 Câu 4 (3,0 điểm):
a) Cho a + b + c + d = 2000 và 1 1 1 1 1     a  b  c b  c  d c  d  a d  a  b 40 Tính giá trị của : S = a b c d    b  c  d c  d  a d  a  b a  b  c
b) Xác định tổng các hệ số của đa thức f(x) =   x  x 2016   x  x 2017 2 2 5 6 . 5 6 Câu 5 (6,0 điểm):
Cho tam giác ABC có ba góc nhọn (AB < AC). Vẽ về phía ngoài tam giác ABC
các tam giác đều ABD và ACE. Gọi I là giao của CD và BE, K là giao của AB và DC.
a) Chứng minh rằng: ADC = ABE.
b) Gọi M và N lần lượt là trung điểm của CD và BE. Chứng minh rằng AMN đều.
c) Chứng minh rằng IA là phân giác của góc DIE.
-------------Hết------------
Họ và tên thí sinh::........................................................... SBD........................................
Chữ ký giám thị 1: ……………………..………… Giám thị 2: ………………………………
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN KIM THÀNH
KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI NĂM HỌC 2016 - 2017 Môn : Toán lớp 7 Câu Ý Nội dung Điểm 3 3 3 1 1 1  1 1 1  3 .    1 1 1       0,75 A = 4 11 13 2 3 4  =  4 11 13  2 3 4 5 5 5 5 5 5      1 1 1  5  1 1 1  5 .    .    a 4 11 13 4 6 8  4 11 13  2  2 3 4  0,75 (2,0) 3 1 1 A =  = 3 2  . 5 5 5 5 (4,0) 2 A= 5  0,5 1. Vậy A = 1 5 Ta có 3n+2 - 2n+2 + 3n - 2n
= ( 3n+2 + 3n ) – (2n+2 +2n ) 0,5 b
= 3n .( 32 + 1 ) – 2n-1 . ( 23 + 2 ) 0,5 (2,0) = 3n .10 - 2n-1.10 0,5
= ( 3n - 2n-1 ).10 10. Vậy 3n+2 - 2n+2 + 3n - 2n  10 0,5 Ta có x + 2y = 3xy + 3
 3x + 6y = 9xy + 9  ( 3x – 9xy ) + ( 6y -2 ) = 7 0,25
 3x.( 1 - 3y ) -2.( 1-3y ) = 7  ( 3x – 2 ). ( 1 – 3y ) = 7 0,25
Vì x, y  Z nên 3x – 2 ; 1-3y là các số nguyên.
Mà ( 3x - 2 ).( 1 – 3y ) = 7  3x – 2 ; 1-3y là ước của 7. 0,5 a Ta lại có Ư(7) =  ; 1  
7  3x – 2 ; 1-3y   ; 1   7 0,25 (2,0) Bảng giá trị 3x-2 -7 -1 1 7 2 1-3y -1 -7 7 1 (4,0) x -5/3 1/3 1 3 y 2/3 8/3 -2 0 KTM KTM TM TM 0,5 Vậy (x,y)    ;1 2  ; 0 ; 3  0,25 B = 1 2 3 2015 2016    ...  2016 2015 2014 2 1  1   2   3   2015  b B= 1   1   1  ...   1  1  2016   2015   2014   2  0,75 (2,0) B = 2017 2017 2017 2017 2017    ...   2016 2015 2014 2 2017 B = 2017.  1 1 1 1  0,75     ...    2 3 4 2017  Do đó A = 1 0,5 B 2017
Vì x  2  0 với x; y 1  0 với x ;( x+y-z-2)2016 0 với x,y,z 0,25 Do đó 2016
x  2  y 1  (x  y  z  2)  0 khi  x  2  0 x  2  x  a  0  2    (1,5)  y 1  0  y 1  0  y  1 0,5     x  y   22016 z  0 x  y  z  2  0 z  1
Do đó A = 5. 22 .12016 .12017 = 5.4.1.1 = 20 0,5 3 Vậy A = 20 0,25 (3,0)
Vì a,b,c,d là các số dương và c  d, mà a c  nên a b  b d c d 0,25 2017 2017 2016 2016 2016 2016 2016 2016 2016 a b a  b  a   a  b       2016 2016 2016 2016  2016   2016 2016  c d c  d  c   c  d  2016 2 . 017 a  2016 a  b 2017 2016 hay  (1) 0,25 2016.2017 c  2016 c  d 2017 2016 2016 2016 2017 2017 2017 2017 2017 2017 2017 a b a  b  a   a  b  b      2017 2017 2017 2017  2017   2017 2017  c d c  d  c  c  (1,5)  d  2017 2 . 016 a  2017 a  b 2016 2017 hay  (2) 0,25 2017.2016 c  2017 c  d 2016 2017  2016 a  b 2017 2016  2017 a  b 2016 2017 Từ (1) và (2)    2016 c  d 2017 2016  2017 c  d 2016 2017 0,5  2016 a  b 2017 2016  2017 a  b 2016 2017 Vậy   0,25 2016 c  d 2017 2016  2017 c  d 2016 2017 Ta có S = a b c d    b  c  d c  d  a d  a  b a  b  c
S + 4 = a  b  c  d a  b  c  d a  b  c  d a  b  c  d    0,25 b  c  d c  d  a d  a  b a  b  c 4 a S + 4 = (a + b + c+ d ).  1 1 1 1       0,25 (3,0) (1,5)  b  c  d c  d  a d  a  b a  b  c  Do đó S = - 4 + 2000. 1 40 0,5 = -4 + 50 = 46 . Vậy S = 46 0,5
Vì tổng các hệ số của đa thức f(x) bằng f(1). Mà đa thức 0,5
f(x) =   x  x 2016   x  x 2017 2 2 5 6 . 5 6 b 0,5
(1,5) có f(1) = ( 5-6.1+12 )2016. ( 5+6.1+12 )2016 0,25 = 0.(5+6.1+12 )2016 = 0 0,25
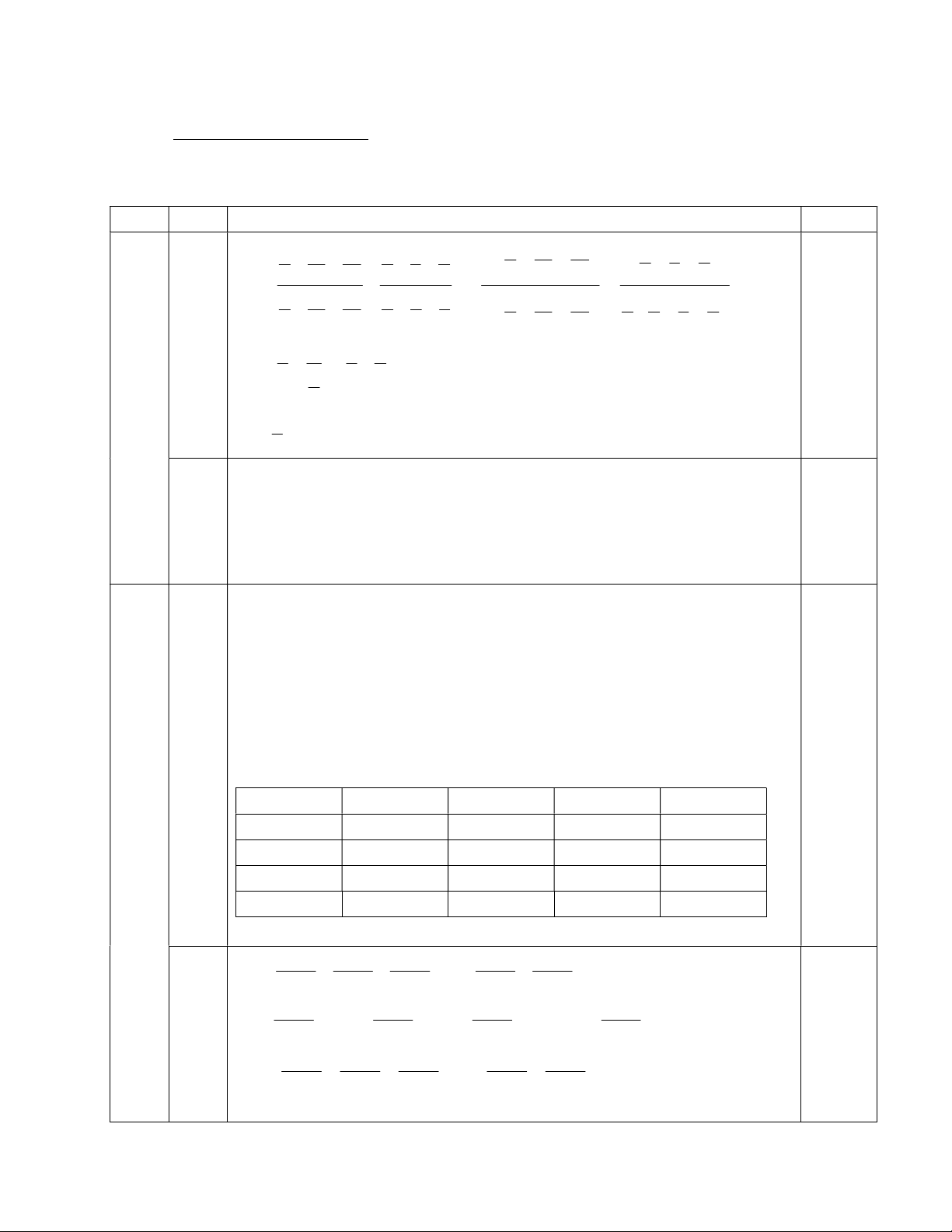
Vậy đa thức đã cho có tổng các hệ số bằng 0 E A D a 0,5 (2,0) K I C B Ta có: AD = AB;  DAC =  BDE và AC = AE 0,75
Suy ra ADC = ABE (c.g.c). Vậy ADC = ABE 0,75
Từ ADC = ABE (câu a) =>  ABE =  ADC 0,25 mà  BKC =  AKD (đối đỉnh).
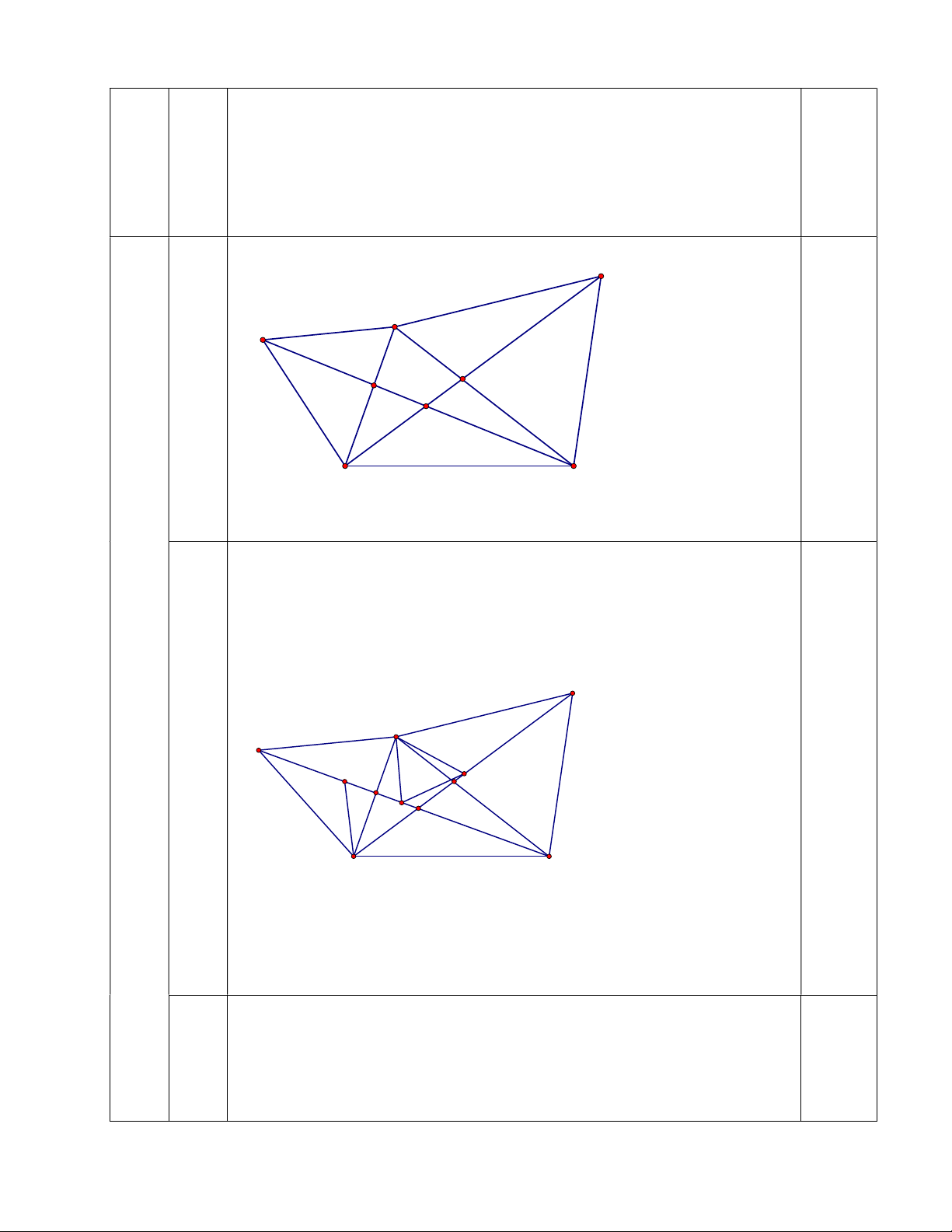
Khi đó xét BIK và DAK suy ra  BIK =  DAK = 600 (đpcm) 0,5 5 E (6,0) A D b N J (2,0) K M I C B
Từ ADC = ABE (câu a)  CM = EN và 0,25  ACM =  AEN
ACM = AEN (c.g.c)  AM = AN và  CAM =  EAN 0,5  MAN = 
CAE = 600 Do đó AMN đều. 0,5 Vậy AMN đều. 0,5 c
Trên tia ID lấy điểm J sao cho IJ = IB  BIJ đều 0,5 (2,0)  BJ = BI và  JBI =  DBA = 60 0 suy ra  IBA =  JBD , kết hợp BA = BD 0,5
IBA = JBD (c.g.c) =>  AIB =  DJB = 1200 mà  BID = 600 =>  DIA = 600
Từ đó suy ra IA là phân giác của góc :  0,5 DIE
Chú ý: Nếu học sinh làm theo cách khác đúng vẫn cho điểm tối đa.