

Preview text:
UBND HUYỆN KỲ ANH
ĐỀ THI HỌC SINH GIỎI CẤP HUYỆN
PHÒNG GIÁO DỤ C VÀ ĐÀO TẠO NĂM HỌC 2022 - 2023 Môn: Toán 7 ĐỀ CHÍNH THỨC
Thời gian: 120 phút (không kể thời gian giao đề) Bài 1: Tìm x biết a) 15 − 22x 14 − x 4 : = :13 23 7 11 5 b) 1 1 1 1 x − ≤ − − 2 2 4 2 Bài 2:
a) Tìm x, y, z biết: 10x − −
= 6y = 5z và 2x 3y 3 2z = 2z + 3 4x
b) Tìm các hệ số a, b biết rằng đa thức 3 2
ax + bx − 3x + 3 chia cho (x − ) 1 (x + ) 1 được dư là 7.
Bài 3: Ba anh An, Bình, Dũng cùng góp vốn để thành lập công ty với tổng số tiền góp là
294 triệu đồng. Biết rằng 1 số tiền anh An góp bằng 1 số tiền anh Bình góp; 1 số tiền 9 8 10
anh Dũng góp bằng 1 số tiền anh An góp. 12
a) Tính số tiền góp của mỗi người.
b) Theo thỏa thuận, lợi nhuận được chia theo tỷ lệ góp vốn. Năm 2022 lợi nhuận thu
về của công ty là 120 triệu đồng. Em hãy tính số tiền lợi nhuận mà mỗi người nhận được trong năm 2022.
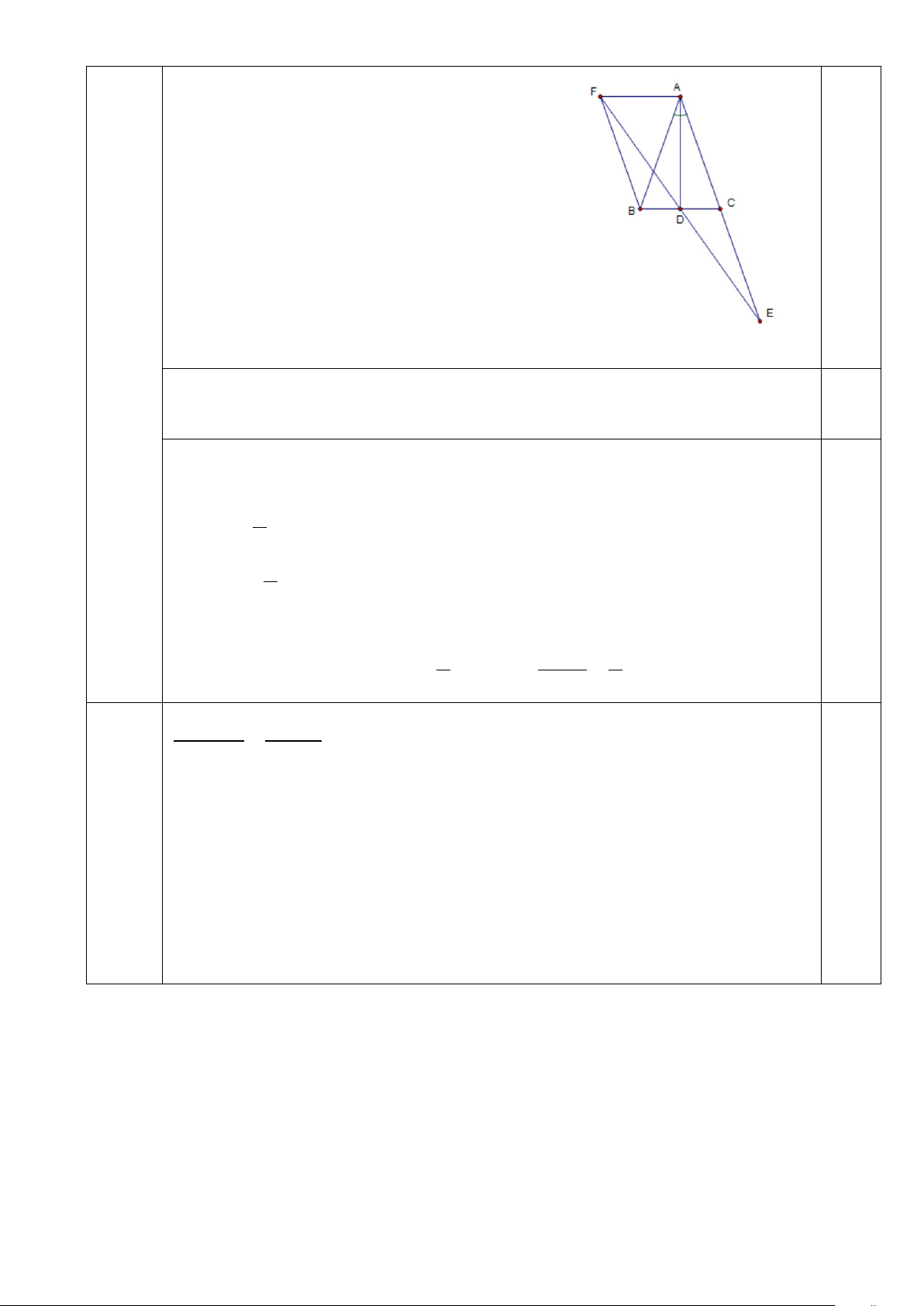
Bài 4: Cho tam giác ABC cân tại A. Vẽ đường phân giác AD. Lấy điểm E trên tia đối của
tia CA sao cho CE=CA. Qua điểm B, kẻ đường thẳng song song với AC cắt đường thẳng DE tại F.
a) Chứng minh rằng tam giác ABF cân. b) Tính số đo góc DAF?
c) Tính tỷ số diện tích tam giác CDE và tam giác ADF? (x − )2 2 5
Bài 5: Tìm số nguyên x, y thõa mãn: 7 − y = 3 2 ---Hết---
Họ và tên: ………………………………………….; SBD: …………..
HƯỚNG DẪN CHẤM HSG TOÁN 7 Bài Gợi ý đáp án Điểm a) 15 − 22x 14 − x 4 22x 14 − x 15 − 69 : = :13 ⇒ ⋅ = ⋅ 23 7 11 5 7 11 23 5 3 2 2 9 ⇒ 4 − ⋅ x = 9 − ⇒ x = ⇒ 3 x = hoặc 3 x − = Bài 1 4 2 2 4 đ b) 1 1 1 1 1 1 1 − 1 1 1 1 1
x − ≤ − − ⇒ x − ≤ −
⇒ x − ≤ − ⇒ x − ≤ 2 2 4 2 2 2 4 2 2 4 2 4 1 1 − 1 1 ⇒ ≤ x − ≤ 1 3 ⇒ ≤ x ≤ 4 2 4 4 4
a) 2x − 3y 3 − 2z =
⇒ 4x(2x − 3y) = (2z + 3)(3 − 2z) 2z + 3 4x 2 2 2 2 9
⇒ 8x −12xy = 9 − 4z ⇒ 2x − 3xy + z = 2 10 = 6 = 5 x y z x y z ⇒ = = 3 5 6 2 2 2 2 2 2 x xy z 2x 3xy z
2x − 3xy + z 9 1 ⇒ = = = = = = = :9 = 2 9 15 36 18 45 36 18 − 45 + 36 4 4 2 9 ⇒ x = ⇒ 3 x = hoặc 3 x − = Bài 2 4 2 2 4 đ TH1: 3 5
x = ⇒ 6y = 5z =15 ⇒ y = ;z = 3 2 2 TH2: 3 − 5 x 6y 5z 15 y − = ⇒ = = − ⇒ = ;z = 3 − 2 2
b) Gọi q(x) là thương của phép chia đa thức 3 2
ax + bx − 3x + 3 cho
(x − )1(x + )1 . Ta có: 3 2
ax + bx − 3x + 3 = (x − )
1 (x +1)q(x) + 7 2
Thay x =1 vào ta được: a + b = 7 Thay x = 1
− vào ta được: b − a =1
Suy ra: a = 3;b = 4
a) Gọi số tiền ba anh An, Bình, Dũng góp lần lượt lá a (triệu đồng), b
(triệu đồng), c (triệu đồng). Ta có: a b c a a b c
a + b + c 294 = ; = ⇒ = = = = = 3 9 8 10 12 36 32 30 98 98 2
⇒ a =108;b = 96;c = 90 Bài 3
4 đ b) Tỷ lệ góp vốn của anh An, Bình và Dũng lần lượt là:
108 ≈36,7% ; 96 ≈32,7% 90 ≈30,6% 294 294 294
Số tiền lợi nhuận mà anh An, Bình và Dũng:người nhận được lần lượt là: 2
36,7% ⋅120 = 44,04(triệu đồng); 32,7% ⋅120 = 39,24(triệu đồng);
30,6% ⋅120 = 36,72 (triệu đồng); a) A ∆ DB = A
∆ DC(c − g − c) ⇒ DB = DC Xét 2 tam giác DC ∆ E và DB ∆ F có : =
CDE BDF (đối đỉnh) 2
DB = DC (Chứng minh trên) =
DCE DBF (CE BF ) DC ∆ E = DB ∆
F ⇒ CE = BF(1) +CE = (
CA gt) ⇒ CE = B ( A 2)
Từ (1) và (2) suy ra: BF = BA ⇒ tam giác ABF cân tại B Bài 4 6đ b) =
CAB ABF(AC BF) ⇒ A ∆ BC = B
∆ AF(c − g − c) 2 ⇒ =
ABC BAF ⇒ BC AF . Mà ⊥ ⇒ ⊥ ⇒ 0 AD BC AD AF DAF = 90 c) Ta có: (3)
SCDE = SACD ( Hai tam giác có chung đường cao kẻ từ đỉnh
D và có 2 cạnh đáy CE=CA) + 1 (4) SACD = ⋅ S
( Hai tam giác có chung đường cao AD và có cạnh 2 ABC đáy 1 DC = ⋅ BC ) 2 2 Chứng minh được (5)
SADF = SABF = SABC Từ (3), (4), (5) suy ra: 1 SCDE 1 SCDE = ⋅ S ⇒ = 2 ADF SADF 2 (x −5)2 2 7 − y = ⇒ 2(x − 5)2 = 3( 2
7 − y ) ⇒ 2(x −5)2 2 + 3y = 21 3 2 Vì: 2
3y 3;213 ⇒ 2(x − 5)23; mà ( ) = ⇒ (x − )2 2,3 1
5 3 ⇒ (x − 5)3
Bài 5 Đặt(x − 5) = 3k;(k ∈Z)ta có: ( k)2 2 2 2 2 3
+ 3y = 21⇒ 6k + y = 7 : 2đ 2
k = 0 không thõa mãn.
Vậy k ≠ 0 , k ∈Z 2 2 2
⇒ 6 ≤ 6k < 7 ⇒ k =1; y =1
+ k =1⇒ x − 5 = 3 ⇒ x = 8 +k = 1 − ⇒ x − 5 = 3 − ⇒ x = 2
Vây có 4 cặp số x,y gồm (2; 1); (2; -1); (8; 1); (8; -1)
Lưu ý: Mọi cách giải đúng đều cho điểm tối đa.




