Đề học sinh giỏi thành phố Toán THPT năm 2022 – 2023 sở GD&ĐT Hải Phòng

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH HẢI PHÒNG MÔN TOÁN THPT NĂM HỌC 2022 - 2023
Thời gian làm bài: 180 phút (không kể thời gian phát đề) Câu 1: (2,0 điểm) 3
a) Tìm các giá trị của tham số m để hàm số x 2 y =
− 2x + mx −1 có hai điểm cực trị x , x thỏa 3 1 2
mãn x − x = 2 . 1 2 b) Cho hàm số 3 2
y = x + 3x + (m + 4) x + m + 2 có đồ thị là (C và điểm 3 M 2;  − . Tìm các m ) 2   
giá trị thực của tham số m để đường thẳng d có phương trình y = 2x + 2 cắt (C tại ba điểm m ) phân biệt A( 1;
− 0), B , C sao cho MB ∆
C là tam giác đều. Lời giải
a) Ta có f ′(x) 2
= x − 4x + m = 0 ( ) 1 .
Hàm số có hai điểm cực trị ⇔ 4 − m > 0 ⇔ m < 4 . x + x = 4 1 2 
Hàm số có 2 điểm cực trị x , x thỏa mãn x x 2  − = ⇔ x x = m 1 2 1 2 1 2 (   x − x  )2 = 4 1 2 x + x = 4 1 2  ⇔ x x = m
⇒ 16 − 4m = 4 ⇒ m = 3 (Thỏa mãn). 1 2 (   x + x  )2 − 4x x = 4 1 2 1 2
b) PTHĐGĐ của (C và 3 2
x + 3x + m + 4 x + m + 2 = 2x + 2 m ) d : ( ) x = 1 − 3 2
⇔ x + 3x + (m + 2) x + m = 0 ⇔  2
x + 2x + m = 0  (*) 1  − m > 0
d cắt (C tại 3 điểm phân biệt ⇔ (*) có 2 nghiệm phân biệt khác 1 − ⇔  ⇔ m <1 m )  1 − + m ≠ 0
Giả sử B(x ;2x + 2 , C x ;2x + 2 , với x , x là nghiệm phương trình (*) 1 1 ) ( 2 2 ) 1 2 3 4 + + 2 BC 3 2 3 MB ∆
C đều ⇔ d (M ;d ) = ⇔
= 5. (x − x )2 . 2 1 2 5 2
⇔ (x − x )2 = ⇔ (x + x )2 1 3
− 4x x = 3 ⇔ 1− 4m = 3 ⇔ m = − (thỏa mãn). 2 1 1 2 1 2 2 Câu 2: (1,0 điểm)
Cho hai số thực a , b thỏa mãn a > b > 1 và 1 1 + = 2022 . log a b b loga
Tính giá trị biểu thức 1 1 P = − . log b a ab logab Ta có 1 1 +
= 2022 ⇔ log b + log a = a b 2022 log a b b loga 2   Ta có 2 1 1 P =  −
 = (log ab − log ab)2 = (log a − log a)2
 log b log a  b a b b ab ab 2 2 2
⇔ P = log a − 2log a log a + log b = (log a + log a)2 − 4 = 2018 ⇒ P = . b b b a b b 2018 Câu 3: (1,0 điểm) 2
Giải phương trình 2 3 sin x − 3 cos x − 2sin x ( x . − x) = cos 1 2cos tan x  1 sin x ≠  2 
Điều kiện: sin x ≠ 0 . cos x ≠ 0   Phương trình 2
⇔ 2 3 sin x − 3 cos x − 2sin x = sin x − 2cos xsin x 2
⇔ 2 3 sin x + 2cos xsin x − 3 cos x − 3sin x = 0
⇔ 2sin x( 3sin x + cos x) − 3( 3sin x + cos x) = 0
⇔ (2sin x − 3)( 3sin x + cos x) = 0  π
x = + k2π (n)  3  3 2sin x 3 0 sin   − = x =  2π ⇔  ⇔ 2 ⇔ x =
+ k2π (n),(k ∈ ).
 3 sin x cos x 0   + = 3 cot = − 3  π −  x = + kπ (n)  6
Vậy tập nghiệm phương trình  π 2π π S k  | k2π; k2π; − kπ  = ∈ + + + . 3 3 6    Câu 4: (1,0 điểm)
Tìm các giá trị thực của tham số m để hệ phương trình sau có bốn nghiệm thực phân biệt 2 2
x + y − mx −1= 0  (*) 2 2
x − y + x + y − 2m(x − y + ) 1 = 0. Lời giải 2 2
x + y − mx −1 = 0 +) Hệ (*) ⇔ 
(x − y +1)(x + y − 2m) = 0 2 2
x + y − mx −1= 0 (1) 
x − y +1 = 0 (2) ⇔  2 2
x + y − mx −1 = 0 (1) 
x + y − 2m = 0 (3) 2
(1) là phương trình của đường tròn (C) có tâm I m ;0 m + 4  và bán kính R = . 2    2
(2), (3) lần lượt là phương trình các đường thẳng (∆2), (∆3).
Do đó, hệ (*) có bốn nghiệm phân biệt khi và chỉ khi hai đường thẳng (∆2), (∆3) cắt đường tròn
(C) tại bốn điểm đôi một phân biệt. m +1 2 ( + ∆ 2 m 4
2) cắt (C) tại hai điểm phân biệt ⇔ 2 <
⇔ m − 4m + 4 > 0 ⇔ m ≠ 2. 2 2 m −2m 2 ( + 8 8 ∆ 2 m 4
3) cắt (C) tại hai điểm phân biệt ⇔ < ⇔ − < m < . 2 2 7 7
Bốn giao điểm đôi một phân biệt khi giao điểm của (∆2) và (∆3) không thuộc (C) m ≠ 1 −  +  ⇔ 2m 1 2m 1 M − ;   ∉(C) ⇔  2 2  1   m ≠  .  2   Kết luận: 8 8  1 m  ;  \  1;  ∈ − − .  7 7     2 Câu 5: (1,0 điểm)
Gọi A là tập hợp tất cả các số tự nhiên có 5 chữ số. Chọn ngẫu nhiên một số từ tập hợp A . Tính
xác suất để chọn được một số chia hết cho 7 và chữ số hàng đơn vị bằng 1 . Lời giải
Số các số tự nhiên có 5 chữ số là 99999 −10000 +1 = 90000 .
Giả sử số tự nhiên có 5 chữ số chia hết cho 7 và chữ số hàng đơn vị bằng 1 là: abcd1
Ta có abcd1 =10.abcd +1 = 3.abcd + 7.abcd +1 chia hết cho 7 khi và chỉ khi 3.abcd +1 chia hết cho 7 . Đặt h −1
3.abcd +1 = 7h ⇔ abcd = 2h + ( *
h∈ ) là số nguyên khi và chỉ khi h = 3t +1 3
Khi đó ta được: abcd = t + ⇒ ≤ t + ≤ ( *
7 2 1000 7 2 9999 t ∈ ) 998 9997 ⇔ ≤ t ≤ ⇔ t ∈{143, 144,..., }
1428 suy ra số cách chọn ra t sao cho số abcd1 chia hết 7 7
cho 7 và chữ số hàng đơn vị bằng 1 là 1286.
Vậy xác suất cần tìm là: 1286 643 = . 90000 45000
Câu 6: (2,0 điểm)
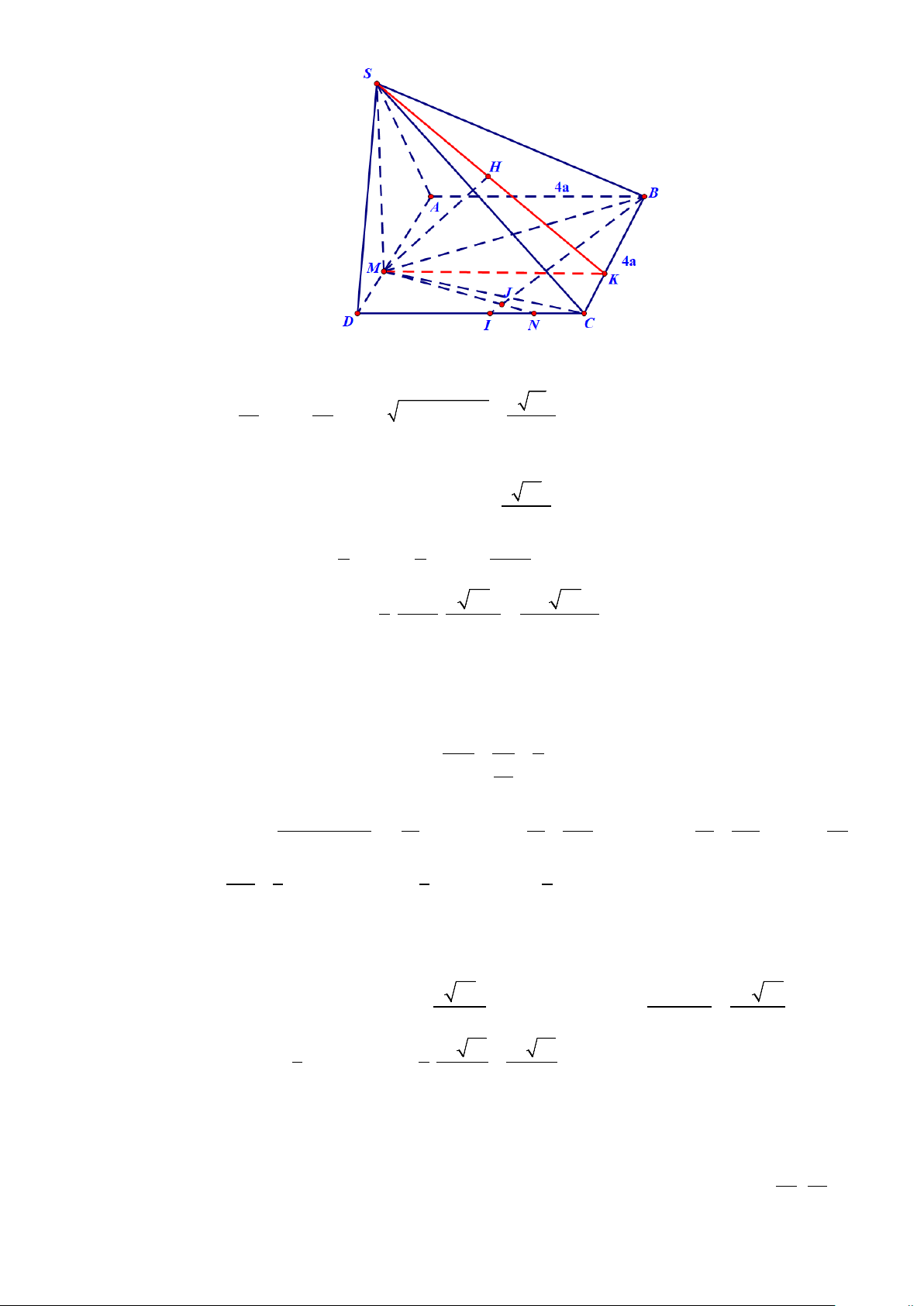
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 4a . Biết hình chiếu vuông góc của đỉnh  
S trên mặt phẳng ( ABCD) là điểm M thoả mãn AD = 3MD . Trên cạnh CD lấy các điểm I, N sao cho  = 
ABM MBI và MN ⊥ BI . Biết góc giữa đường thẳng SC và mặt phẳng ( ABCD) bằng 0 60 .
a) Tính thể tích khối chóp S.AMCB theo a .
b) Tính khoảng cách từ điểm N đến mặt phẳng (SBC) theo a . Lời giải
a) Tính thể tích khối chóp S.AMCB theo a . Ta có 8a 4a 2 2 4 10 = , = , a AM MD
MC = MD + DM = . 3 3 3
Góc giữa SC và mặt phẳng ( ABCD) bằng góc  0 SCM = 60 . Xét tam giác vuông 0 4 30 ⇒ = .tan 60 a SMC SM MC = . 3 2 Diện tích tứ giác 5 5 2 40a S = S = a = . AMCB ABCD .16 6 6 3 2 3 Thể tích khối chóp
1 40a 4 30a 160 30 . . . a S AMCB = = . 3 3 3 27
b) Tính khoảng cách từ điểm N đến mặt phẳng (SBC) theo a .
Gọi J = MN ∩ BI . Theo giả thiết  = 
ABM MBI và MN ⊥ BI nên ⇒ ∆ = ∆ ⇒  =  MAB MJB AMB JMB . Xét tam giác vuông ⇒  AB 4a 3 MAB tan AMB = = = AM 8a 2 3 Suy ra   2 tan AMB 12 = = − ⇒  12 DN 12 16a 4 tan tan = = ⇒ = . a NMA NMD DN MD = ⇒ NC = 2 −  1 tan AMB 5 5 MD 5 5 5 Vậy ta có: NC 1
= ⇒ d (N (SBC)) 1
= d (D (SBC)) 1 , ,
= d (M ,(SBC)) . DC 5 5 5
Kẻ MK ⊥ BC ⇒ MK / / CD ⇒ (SMK ) ⊥ (SBC) .
Gọi H là hình chiếu vuông góc của M trên SK ta có MH ⊥ (SBC) ⇒ d (M,(SBC)) = MH . Trong tam giác vuông a SM MK a SMK có 4 30 SM = , MK = 4a . 4 30 ⇒ MH = = . 3 SK 13
Vậy d (N (SBC)) 1
= d (M (SBC)) 1 4a 30 4a 30 , , = . = . 5 5 13 65 Câu 7: (1,0 điểm)
Trong mặt phẳng Oxy , cho hình thang ABCD có góc  =  0
BAD ADC = 90 , D(2;2) và CD 
= 2AB . Gọi H là hình chiếu vuông góc của D lên đường thẳng AC . Điểm 22 14 M  ; là 5 5   
trung điểm đoạn HC . Tìm toạ độ các điểm ,
A B và C , biết rằng đỉnh B thuộc đường thẳng d
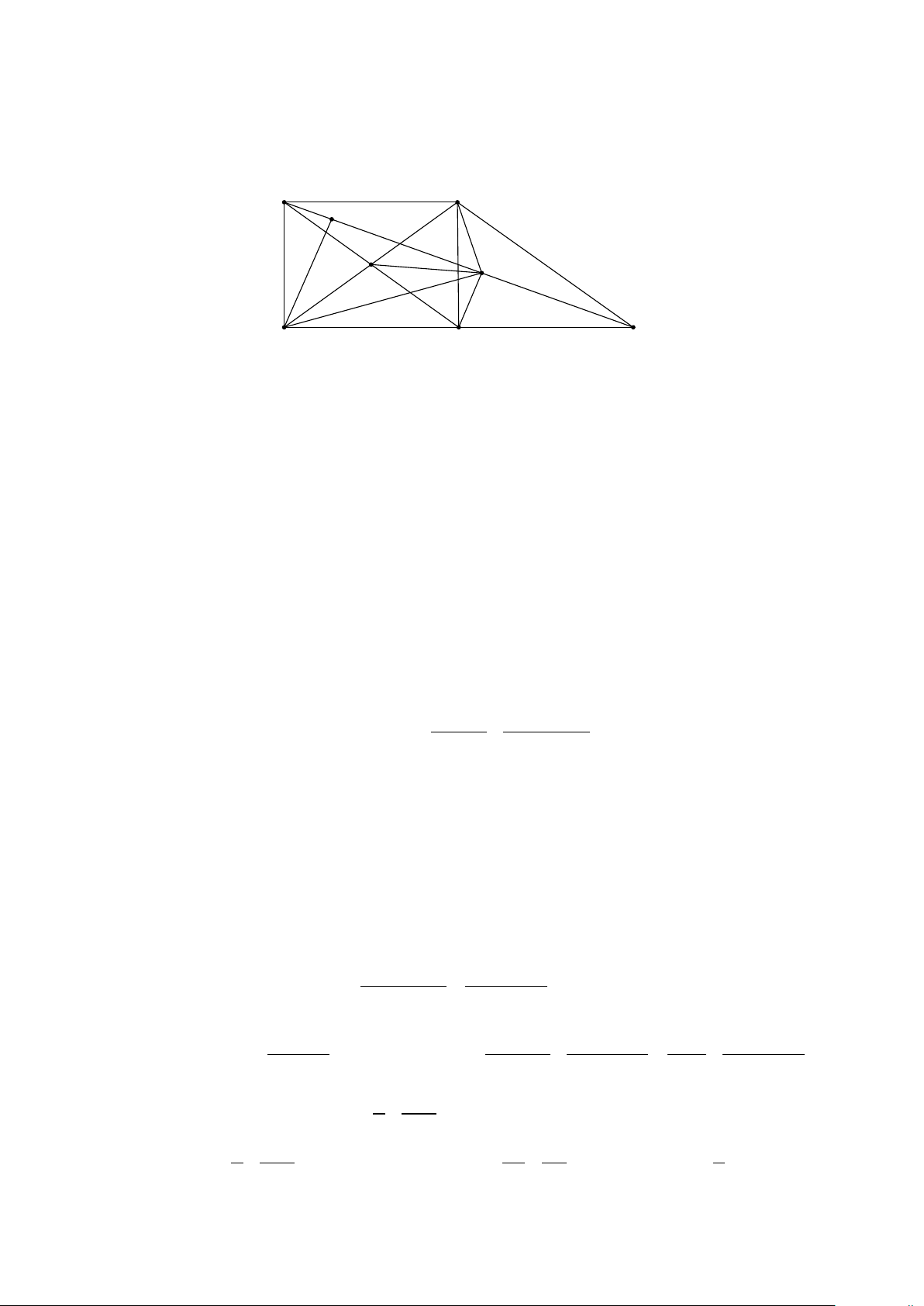
có phương trình x − 2y + 4 = 0 Lời giải. A B(4;4) H I M D(2;2) E C
Gọi E là trung điểm DC ⇒ ABDE là hình chữ nhật ⇒ ABDE là tứ giác nội tiếp (1)
Mà EM ⊥ AC ⇒ ADEM là tứ giác nội tiếp (2) (1), (2) suy ra ,
A B, M , E, D cùng thuộc một đường tròn
⇒ ABDM là tứ giác nội tiếp ⇒  =  0
DAB DMB = 90 ⇒ DM ⊥ BM
⇒ (DM ) : x − 3y + 4 = 0 ; (BM ) :3x + y −16 = 0
x − 2y + 4 = 0
Do B ∈d : x − 2y + 4 = 0 . Suy ra toạ độ điểm B là nghiệm của hệ:  ⇒ B(4;4) . 3
 x + y −16 − 0
Câu 8: (1,5 điểm)
Cho các số thực dương x, y, z thoả mãn ( 2 2 2
5 x + y + z ) = 9(xy + 2yz + zx)
Tìm giá trị lớn nhất của biểu thức x 1 P = − 2 2 y + z
(x + y + z)3 Lời giải Giả thiết suy ra 2
5x − 9( y + z) x + 5( y + z)2 = 28zy 2
⇒ 5x − 9( y + z) x + 5( y + z)2 ≤ 7( y + z)2 2
⇔ 5x − 9( y + z) x − 2( y + z)2 ≤ 0
−( y + z) ≤ x ≤ 2( y + z)
Suy ra 0 < x ≤ 2( y + z) − −
Ta có x + y + z ≤ ( y + z) 1 1 3 ⇒ ≤
(x + y + z)3 27( y + z)3 y + z 4( y + z) 2 2 ( )2 1 4 1
Lại có y + z ≥
Từ đó ta được P ≤ − = − 2
( y + z)2 27( y + z)3 y + z 27( y + z)3
Đặt t = y + z > 0 khi đó 4 1 P ≤ − . 3 t 27t Xét f (t) 4 1 − = −
,t ∈ 0;+∞ , Ta có f ′(t) 4 1 1 = +
⇒ f ′ t = 0 ⇔ t = . 2 4 ( ) 3 ( ) t 27t t 9t 6
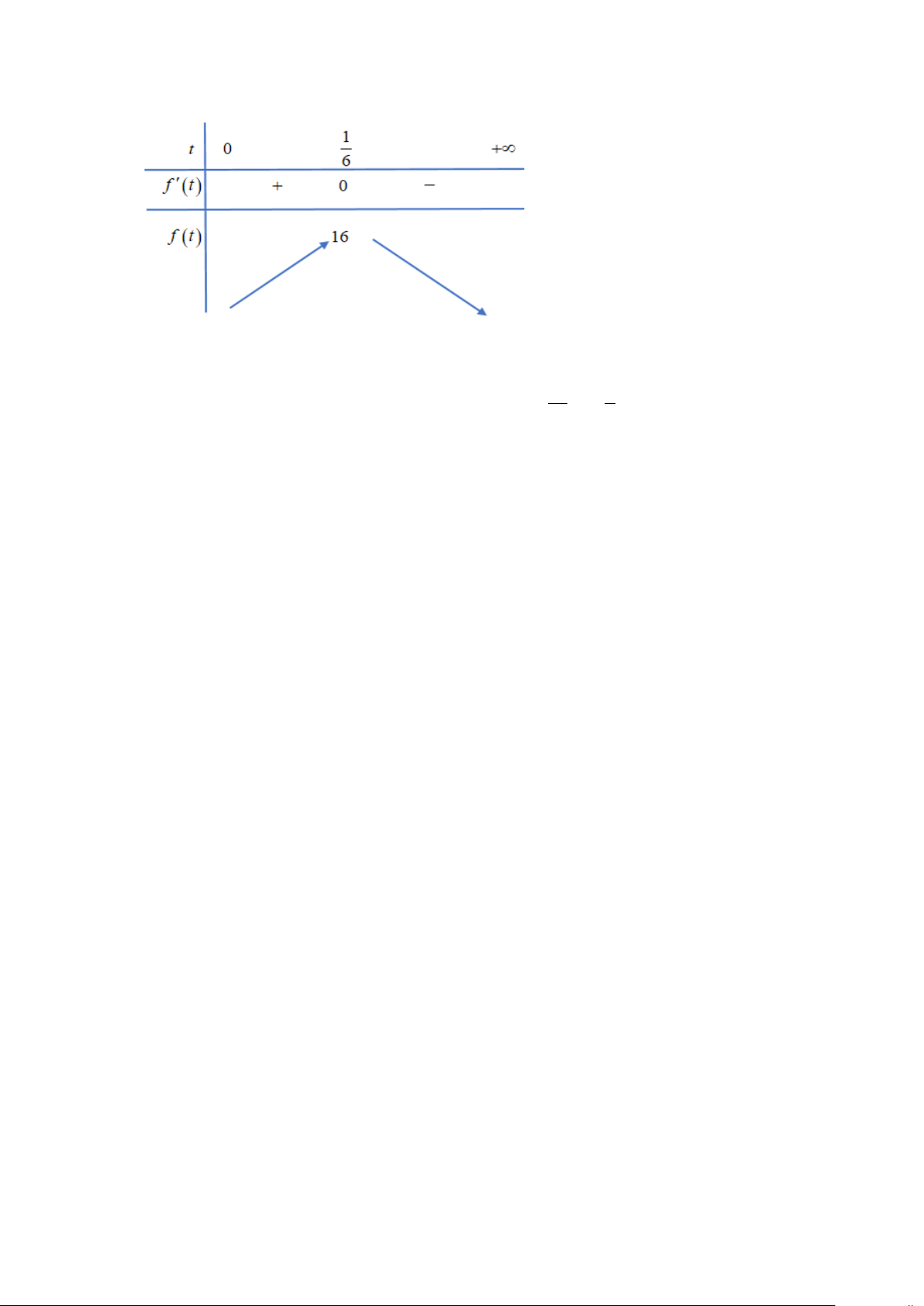
Bảng biến thiên của f (t)
ta suy ra f (t) ≤16.
Vậy giá trị lớn nhất của P bằng 16 đạt được khi 1 1 y = z = ; x = . 12 3
--------------- TOANMATH.com ---------------
Document Outline

• de-hoc-sinh-gioi-thanh-pho-toan-thpt-nam-2022-2023-so-gddt-hai-phong
• DE-HDG-HSG12-HAI-PHONG-2022-2023