

Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG TRƯỜNG THPT LƯU HOÀNG NĂM HỌC 2018 – 2019 Môn thi: Toán - Lớp: 11 ĐỀ CHÍNH THỨC
(Thời gian làm bài: 150 phút, không kể thời gian giao đề)
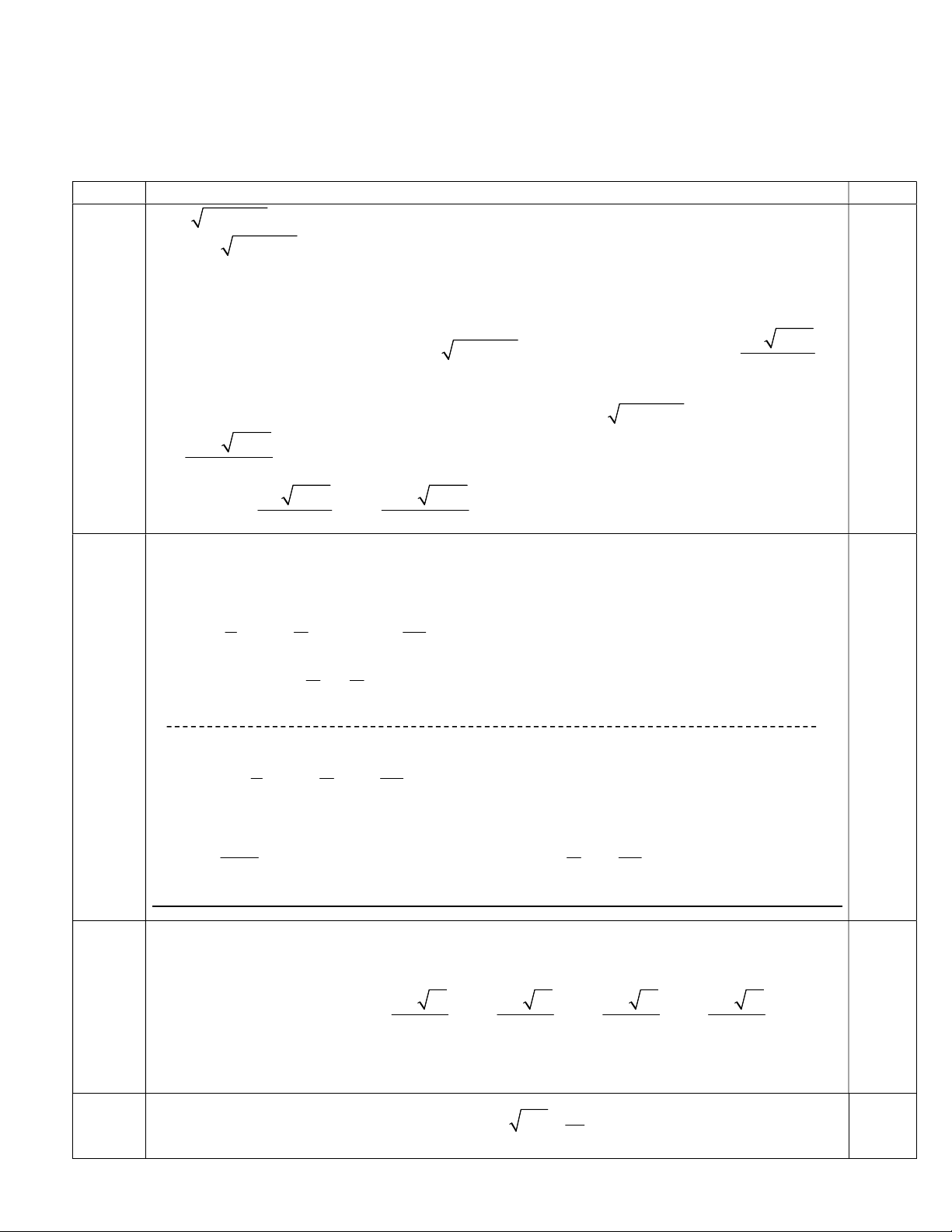
Câu 1 (2,0 điểm). Giải phương trình sau: 2 x x 2013 2013
Câu 2 (3,0 điểm). Cho phương trình (2sin x 1)(2cos 2x 2sin x m) 1 2cos2x (Với m là tham số)
a) Giải phương trình với m = 1.
b) Tìm m để phương trình có đúng 2 nghiệm thuộc 0; . Câu 3 (5,0 điểm). 2 2
x y 3x 4y 1
a) Giải hệ phương trình: 2 2 3
x 2y 9x 8y 3
b) Một người bỏ ngẫu nhiên 4 lá thư và 4 chiếc phong bì thư đã để sẵn địa chỉ. Tính
xác suất để có ít nhất một lá thư bỏ đúng địa chỉ.
Câu 4 (4,0 điểm). Cho A, B, C là ba góc của tam giác ABC.
a) Chứng minh rằng tam giác ABC vuông nếu: cos B cosC sin A sin B sin C 2 2 2
b) Tìm giá trị lớn nhất của biểu thức: sin A sin B sin C M 2 2 2 cos A cos B cos C
Câu 5 (3,0 điểm). Trong mặt phẳng Oxy, cho đường tròn (C1): 2 2
x y 13 , đường tròn (C2): 2 2 (x 6) y 25 .
a) Tìm giao điểm của hai đường tròn (C1) và (C2).
b) Gọi giao điểm có tung độ dương của (C1) và (C2) là A viết phương trình đường
thẳng đi qua A cắt (C1) và (C2) theo hai dây cung có độ dài bằng nhau.
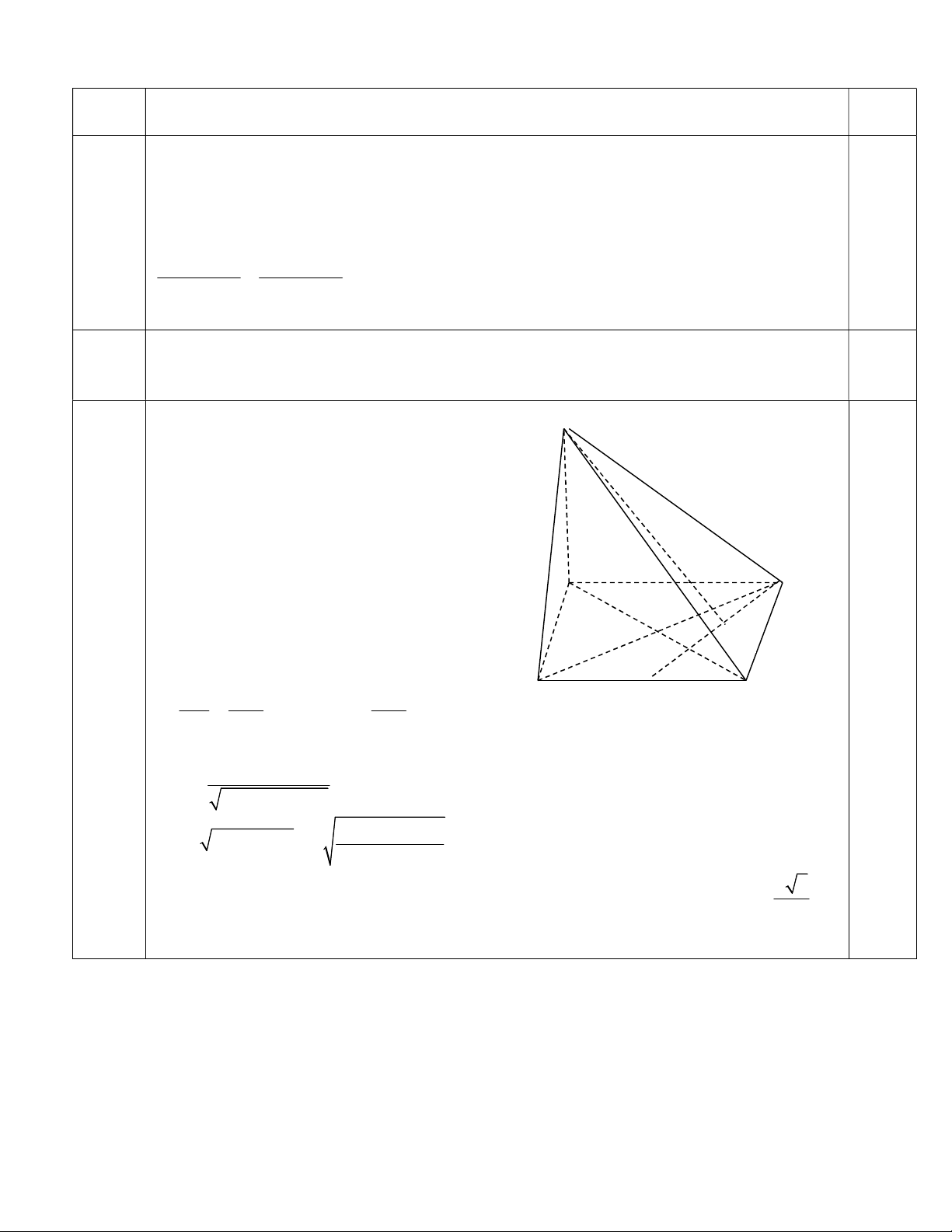
Câu 6 (3,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, cạnh SA = a
và vuông góc với mặt phẳng (ABCD).
a) Chứng minh rằng các mặt bên của hình chóp là những tam giác vuông.
b) M là điểm di động trên đoạn BC và BM = x, K là hình chiếu của S trên DM. Tính
độ dài đoạn SK theo a và x. Tính giá trị nhỏ nhất của đoạn SK.
----------------HẾT----------------
Cán bộ coi thi không giải thích gì thêm!
Họ và tên thí sinh: ...................................... Số báo danh: ................
Chữ ký giám thị coi thi số 1:
Chữ ký giám thị coi thi số 2:
ĐÁP ÁN THI CHỌN HỌC SINH GIỎI LỚP 11 CẤP TRƯỜNG Môn : TOÁN Câu Đáp án Điểm Câu 1 2
x x 2013 2013 . ĐK x 2013 0,25 Đặt t x 2013 ( với t 2 2
t 0) t x 2013 t x 2013 . Ta có hệ PT: 0,5 2 x t 2013
(x t)(x t 1) 0 2 t x 2013 0,5 1 8053
+ Với x +t =0 ta được t = -x x 2013 x . Giải ra ta được x là 2 0,25 nghiệm.
+ Với x – t +1 = 0 ta được : x +1 = t x 1 x 2013 . Giải ra ta được 0,25 1 8049 x là nghiệm 2 0,25 1 8053 1 8049 Đáp số : x , x 2 2
Câu 2 (2sin x 1)(2co s 2x 2sin x m) 1 2cos2x a , Với m =1 ta được phương trình :
(2sin x 1)(2co s 2x 2sin x 1) 1 2cos2x (2sin x 1).cos2x 0 0,5 1 5 + sin x x k2 x k2 1,5 2 6 6
+ cos 2x 0 x k 0,5 4 2
b, Phương trình đã cho tương đương với : (2sin x 1)(2cos 2x m 1) 0 0,25 1 5
Với sin x x x 0; 2 6 6 0,25
Để phương trình đã cho có đúng 2 nghiệm thuộc 0; thì phương trình : 0,25 1 m 5 cos2x
vô nghiệm hoặc có hai nghiệm x ; x
.Từ đó ta được m <-1v 2 6 6 m >3 v m =0 . 0,25 2 2
x y 3x 4y 1 2 2
x 3x y 4y 1 2 x 3x 1 0 0,5 Câu 3 0,5 2 2 2 2 2 3
x 2y 9x 8y 3 3
(x 3x) 2(y 4y) 3 y 4y 0 0,5
3 13 3 13 3 13 0,5
Ta được nghiệm của hệ là : 3 13 ;0; ; 4; ;0; ; 4; 2 2 2 2 0,5 Câu 4 , Tìm hệ số của 4 1 n x trong khai triển sau: 3 5 nx
biết n là số nguyên thoả mãn 3 x hệ thức 1 2 2 2C C n 20 . n n Từ hệ thức 1 2 2 2C C n 20 . Đk 2
n 2, n Z n 3n 40 0 n 8 n 5 n n 0,5
Ta được n= 8 thoả mãn . 0,5 8 8 k 8 40 1 4k Ta có : 3 1 1 5 3 5 k 8k 3 8x 2 x C .2 .x . Khai triển chứa x4m 3 3 8 0,5 x x k 0 40 14k 4 k 2 . 0,5 3 0,5
Vậy hệ số của x4 là 2 6 C .2 1792 8 Câu 5 cos B cosC
a, Chứng minh rằng tam giác ABC vuông nếu : sin A sin B sin C A 0,5 sin cos B cosC A A A 0,5 Từ 2 2 sin A 2sin .cos 2cos
1 cos A 0 Â là góc 0,5 sin B sin C 2 2 A 2 cos 2 0,5
vuông.Vậy tam giác ABC vuông tại A. 2 2 2 sin A sin B sin C 2 2 2 sin A sin B sin C b, M M 1 1 2 2 2 cos A cos B cos C 2 2 2 cos A cos B cos C 0,5 3 3 2 2 2 M 1
cos A cos B cos C . Biến đổi về 2 2 2 cos A cos B cos C M 1 0,25 3 2
cos C cosC.cos(A B) 1 0 0,25 M 1 3 3 2 2
cos (A B) 4 1 0 4 1 cos (A B) 1 0,25 M 1 M 1 3 1 0,25 1 M 3 M 1 4 0,25 2 cos (A B) 1 0,25 0 M 3 A B C 60 1 cos C cos( A B) 2
Vậy MaxM = 3 khi tam giác ABC đều. 0,25 (C 0,25
1) có tâm O(0;0),bán kính R 13 1
(C2) có tâm I(6;0),bán kính R 5 0,25 2 . Giao điểm của (C
1) và (C2) là A (2;3) và B(2;-3).Với A có tung độ dương nên A(2;3) 1,0
Với A có tung độ dương nên A(2;3) 0,25
Đường thẳng d qua A có pt:a(x-2)+b(y-3)=0 hay ax+by-2a-3b=0
Gọi d d(O, d); d d(I, d) 1 2 0,25
Yêu cầu bài toán trở thành: 2 2 2 2 2 2
R d R d d d 12 2 2 1 1 2 1 2 2 (4a 3b) (2a 3b) b 0 0,25 2 12 b 3ab 0 2 2 2 2 a b a b b 3a
*b=0 ,chọ a=1,suy ra pt d là:x-2=0 0,25
*b=-3a ,chọ a=1,b=-3,suy ra pt d là:x-3y+7=0
a, SA vuông góc với mp(ABCD) nên S 0,25
SA vuông góc với AB và AD. Vậy các tam
giác SAB và SAD vuông tại A 0,25
Lại có SA vuông góc với (ABCD) và AB
Vuông góc với BC nến SB vuông góc với BC 0,25
Vởy tam giác SBC vuông tại C. A 0,25
Tương tự tam giác SDC vuông tại D.
b, Ta có BM =x nên CM = a- x D 0,25 AKD DCM K 0,25 (vì có 0 ˆ ˆ ˆ ˆ
AKD DCM 90 , DAK CDM ) AK AD AD 0,25 AK DC. B M C DC DM DM 0,25 2 a = . Tam giác SAK vuông tại A nên 0,25 2 2 x 2ax 2a 0,25 2 2 x 2ax 3a 2 2 SK SA AK a . 2 2 x 2ax 2a 0,25 a 6
SK nhỏ nhất khi và chỉ khi AK nhỏ nhất K O x 0 SK nhỏ nhất 2 0,25
-----------------------------------------------Hết---------------------------------------------------------
Ghi chú: - Nêú học sinh làm theo cách khác mà đúng vẫn cho điểm tối đa
- Chỉ chấm bài hình khi học sinh vẽ hình đầy đủ và chính xác




