Đề học sinh giỏi Toán 12 cấp tỉnh năm 2022 – 2023 sở GD&ĐT Đồng Tháp

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi chọn học sinh giỏi môn Toán 12 cấp tỉnh năm học 2022 – 2023 sở Giáo dục và Đào tạo tỉnh Đồng Tháp; kỳ thi được diễn ra vào ngày 02 tháng 04 năm 2023; đề thi có đáp án và hướng dẫn chấm điểm.

 

12 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

17 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG THÁP
________________
ĐỀ CHÍNH THỨC
(Đề gồm có 14 trang)
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
NĂM HỌC 2022 - 2023
Môn: TOÁN
Ngày thi: 02/4/2023
Thời gian làm bài: 90 phút, không kể thời gian phát đề
Câu 1: Hệ phương trình
2 1 2
2 1 2
x y x
y x y
có tất cả bao nhiêu nghiệm?
A. 1. B. 0. C. 2. D. 3.
Câu 2: Gọi
S
là tập hợp các giá trị nguyên của tham số
m
sao cho phương trình
2
3 2( 2) 3 3 0
x x x x m
có 2 nghiệm phân biệt. Số phần tử của
S
là
A. 25. B. 24. C. 23. D. 26.
Câu 3: Cho
0
và
3
sin
5
. Giá trị
sin
4
bằng
A.
7 2
10
. B.
2
10
. C.
2
10
. D.
3 2
5 2
.
Câu 4: Một mảng tường hình vuông được minh họa bằng hình vẽ (hình vuông
,
ABCD E
là trung
điểm
AB
,
CF DE
). Biết rằng phần tô đậm (tam giác
CEF
) đã được sơn với chi phí
300.000 đồng. Nếu muốn sơn thêm phần còn lại của mảng tường hình vuông đó với chất lượng
như phần đã sơn thì số tiền phải trả thêm là
F
E
B
A
D
C
A. 700.000 đồng. B. 1.000.000 đồng. C. 900.000 đồng. D. 800.000 đồng.
Câu 5: Trong mặt phẳng tọa độ
Oxy
cho hai điểm
(0;2), ( 1; 5)
B C
. Điểm
A
thuộc đường tròn
2 2
: ( 3) ( 2) 25
C x y
. Gọi
H
là trực tâm của tam giác
ABC
. Độ dài đoạn thẳng
OH
có giá trị nhỏ nhất bằng
A.
5 17
. B.
5 17
. C.
5 2
2
. D.
50 5
.
Câu 6: Cho
x
thỏa mãn
2 2
4
2cos sin .
3
x x
Giá trị của biểu thức
2 2
cos 2sin
P x x
là
A.
5
3
P
.
B.
1
P
. C.
4
3
P
. D.
2
3
P
.
Câu 7: Có tất cả bao nhiêu số nguyên
m
để phương trình
12sin 5cos 1
x x m
có nghiệm?
A.
27
. B.
26
. C.
169
. D.
339
.
Câu 8: Có tất cả bao nhiêu số tự nhiên có 3 chữ số sao cho tích các chữ số bằng 6?
2
A.
9
. B.
6
. C.
7
. D.
8
.
Câu 9: Một câu lạc bộ Toán học có
n
học sinh tham gia. Qua một cuộc khảo sát biết được: cứ mỗi học
sinh nam thì quen với đúng 10 bạn nữ và mỗi học sinh nữ thì quen với đúng 8 bạn nam. Biết
rằng số học sinh nam và số học nữ chênh lệch nhau 6 em. Chọn ngẫu nhiên 2 học sinh thuộc
câu lạc bộ. Xác suất của biến cố chọn được 2 học sinh khác giới bằng
A.
80
159
. B.
40
159
. C.
80
153
. D.
40
153
.
Câu 10: Cho cấp số cộng
n
u
với
2 8
20
u u
. Giá trị của
5
u
bằng
A.
10
. B.
15
. C.
1
5
. D.
5
.
Câu 11: Cho tam giác
ABC
vuông tại
C
có các cạnh
; ;
BC x AC y AB z
thoả mãn
2
; ;4
3
x y z
theo thứ tự lập thành một cấp số nhân. Giá trị
cos
B
là
A.
1
cos
3
B
. B.
3
cos
2
B
. C.
1
cos
B
. D.
cos
B
.
Câu 12: Cho lăng trụ đứng
.
ABC A B C
có đáy
ABC
là tam giác đều cạnh
2 3
a
và
4
AA a
. Gọi
M
là trung điểm của
CC
(tham khảo hình bên). Khoảng cách từ điểm
M
đến mặt phẳng
A BC
bằng
A.
6
5
a
. B.
12
5
a
. C.
5
a
. D.
5
12
.
Câu 13: Cho hình chóp
.
S ABC
có đáy
ABC
là tam giác vuông cân tại
A
. Biết
2
AB
,
SA
vuông góc
với mặt phẳng đáy và
3
SA
. Gọi
M
là trung điểm của
BC
. Khoảng cách giữa hai đường
thẳng
AC
và
SM
bằng
A.
3 10
10
. B.
6 13
13
. C.
1
. D.
3
.
Câu 14: Số đường tiệm cận đứng của đồ thị hàm số
3
2
3
x
y
x x
là
A.
1
. B.
3
. C.
0
. D.
2
Câu 15: Bảng biến thiên trong hình vẽ là của hàm số nào sau đây?
3
A.
1
12
x
x
y
. B.
1
2
1
x
x
y
. C.
1
12
x
x
y
. D.
2
1
x
y
x
.
Câu 16: Hàm số nào sau đây đồng biến trên R?
A.
3
y x x
. B.
1
x
y
x
. C.
2
1
y x
. D.
3 2
y x x
.
Câu 17: Cho hàm số
( )
y f x
có đạo hàm
2 2
( ) ( 1) (2 )
f x x x x x
. Số điểm cực trị của hàm số
( )
y f x
là
A. 1. B. 4. C. 2. D. 3.
Câu 18: Đồ thị hàm số
2
2 2
2
x x
y
x
có tất cả bao nhiêu đường tiệm cận ngang?
A.
2
. B.
3
. C.
1
. D.
0
.
Câu 19: Cho hàm số bậc ba
y f x
có đồ thị như hình vẽ. Phương trình
2 1 0
f x
có bao nhiêu
nghiệm?
A. 3. B. 1. C. 0. D. 2.
Câu 20: Với các giá trị nào của tham số
m
thì hàm số
1 2 2
m x m
y
x m
nghịch biến trên
1;

?
A.
1 2
m
. B.
1 2
m
. C.
1
2
m
m
. D.
1 2
m
.
Câu 21: Trong mặt phẳng toạ độ
Oxy
gọi
,
M N
tương ứng là điểm cực đại và điểm cực tiểu của đồ thị
hàm số
3 2
3 5
y x x
. Điểm
F
thuộc trục hoành
Ox
, giá trị nhỏ nhất
FM FN
bằng
A.
2 10
. B.
5 5
. C.
2 5
. D.
26 2
.
Câu 22: Cho hàm số
y f x
có đồ thị như hình vẽ. Trong khoảng
0;2
, phương trình
1 cos 1 cos
f x x
có tất cả bao nhiêu nghiệm?
A. 2. B. 3. C. 5. D. 4.
4
Câu 23: Cho hàm đa thức bậc bốn
y f x
có
1 2
f
;
2
1
3
f
; đồ thị của hàm số
y f x
được cho như hình vẽ. Xét hàm số
2
6
g x f x f x
, mệnh đề nào sau đây đúng?
A.
R
min 8.
g x
B.
R
max 8.
g x
C.
R
32
min .
9
g x
D.
R
32
max .
9
g x
Câu 24: Cho hàm số
( )
y f x
liên tục trên R và có đồ thị như hình vẽ. Hàm số
2
2
y f x x
đồng
biến trên khoảng nào sau đây?
A.
(1;2)
. B.
( 1;1)
. C.
( ;2)
. D.
(2; )

.
Câu 25:
Cho
f x
là hàm đa thức bậc bốn thỏa mãn
0 0
f
. Hàm số
y f x
có đồ thị như hình vẽ. Hàm số
2 4 3 2
2 2 2
g x f x x x x x x
có tất cả bao nhiêu điểm cực trị?
A.
7
. B.
5
. C.
6
. D.
4
.
Câu 26: Cho hàm số
2
log
y x
có đồ thị như hình vẽ,
B
là trung điểm của đoạn thẳng
AC
. Khẳng
định nào sau đây là đúng về giá trị của các số
, ,
a b c
?
5
A.
2
ac b
. B.
2
a c b
. C.
2
2
ac b
. D.
ac b
.
Câu 27:
Có bao nhiêu giá trị nguyên của
m
để hàm số
2
1
15
x
m
y
nghịch biến trên R.
A.
4
. B.
7
. C.
8
. D.
9
.
Câu 28: Gọi
1 2
,
x x
là các nghiệm của phương trình
2
1
2 3
x x x
. Giá trị của biểu thức
1 2
3 3
x x
M
là
A.
5
M
. B.
12
M
. C.
4
M
. D.
6
M
.
Câu 29: Cho
,
x y
là các số thực dương thỏa mãn
2 2 4 2
2 2
2
1
log log log
4
x x y y
, giá trị của biểu thức
2 2
F x y
bằng
A.
6
. B.
5
. C.
14
. D.
10
.
Câu 30: Cho
,
x y
là các số thực dương sao cho
2 3 2
ln 1 3 7 3 ln 2
x
x x y y xy
y
. Giá trị nhỏ
nhất của biểu thức
2
1
3
T x
x y
bằng
A.
3
4
. B.
1
4
. C.
1
12
. D.
1.
Câu 31: Bất phương trình
4 5 2 4 1 0
x x
x x
có tập nghiệm
; ;S a b c

. Tính tổng
a b c
.
A.
3
. B.
2
3
. C.
5
. D.
12
.
Câu 32: Cho hàm số
y f x
có đồ thị như hình vẽ. Giá trị của tích phân
2
2
I f x dx
là
A.
3
I
. B.
3
I
. C.
4
I
. D.
4
I
.
6
Câu 33: Cho hàm số
f x
liên tục trên R và thỏa mãn
1
0
( )
x
xf
d
e f xx
x
. Giá trị của
0
f
bằng
A. 3. B. 0. C. 1. D. 2.
Câu 34: Cho hàm số
2
1 khi 2
2 1 khi 2
x x
f x
x x
. Tích phân
1
3
1ln
e
f
I d
x
x
x
bằng
A.
74
3
I
. B.
52
3
I
. C.
56
3
I
. D.
20
I
.
Câu 35:
Cho
f x
là hàm số liên tục trên
0;

thỏa mãn
2 . 2
x f x f x x x
và
1 1.
f
Giá
trị
4
f
bằng
A.
17
4
. B.
5
4
. C.
17
2
. D.
7
2
.
Câu 36: Cho
( )
f x
là hàm số có đạo hàm trên
0;2
đồng thời
( )
f x
liên tục trên
0;2
và thỏa mãn
điều kiện
3
( ) ( ) , 0;2
f x f x x x
. Giá trị của tích phân
2
0
f x dx
bằng
A.
5
4
. B.
5
2
. C.
4
3
. D.
5
2
.
Câu 37: Cho
y f x
là hàm đa thức bậc ba và
y g x
là hàm bậc hai, có đồ thị như hình vẽ. Hai
đồ thị cắt nhau tại các giao điểm có hoành độ lần lượt là
1; 1; 2.
Biết
1 2
9
S S
(với
1 2
,
S S
tương ứng là diện tích của các miền gạch sọc tại đó). Giá trị của
2
0
f x dx
bằng
A.
16
3
. B.
8
3
. C.
4
3
. D.
2
.
Câu 38: Hình chóp ngũ giác có số đỉnh của hình đa diện đã cho là
A.
6
. B.
5
. C.
7
. D.
10
.
Câu 39: Hình lập phương có tổng diện tích tất cả các mặt là
2
54 .
a
Thể tích của khối lập phương là
A.
3
27
a
. B.
3
64
a
. C.
3
9
a
.
7
D.
3
64
3
a
.
Câu 40: Cho khối chóp đều
.
S ABCD
có
2 2
AC a
, hai mặt phẳng
SAB
và
SCD
vuông góc với
nhau. Thể tích khối chóp đã cho bằng
A.
3
4
3
a
. B.
3
4
a
. C.
3
32
3
a
. D.
3
2 2
3
a
.
Câu 41: Cho hình nón đỉnh
S
. Một mặt phẳng
P
đi qua
S
hợp với trục của nón một góc
o
30
, cắt
hình nón theo thiết diện là một tam giác vuông có diện tích bằng
2
50( )
cm
. Bán kính đáy của
hình nón bằng
A.
5 10
( )
2
cm
. B.
5 13
( )
2
cm
. C.
5 14
( )
2
cm
. D.
5 22
( )
2
cm
.
Câu 42: Đặt thăng bằng một chiếc bình hình trụ có chứa nước trên một bề mặt nằm ngang, biết mực
nước trong bình cao bằng
h
. Người ta bỏ một quả cầu bằng thép đặc có bán kính
r
lọt vừa khít
vào bình nước và thấy lượng nước dâng lên vừa ngập hết quả cầu (xem hình minh họa bên). Tỉ
số
h
r
bằng
A.
2
3
. B.
3
4
. C.
4
3
. D.
3
2
.
Câu 43: Một hợp tác xã xoài ở Đồng Tháp sản xuất mặt hàng xoài sấy. Thành phẩm xoài sấy được chứa
trong những hộp hình trụ với thể tích
3
270
V cm
. Để chi phí nguyên liệu làm vỏ hộp thấp
nhất, người ta thiết kế hình trụ có diện tích toàn phần nhỏ nhất. Khi đó bán kính đáy của hộp
xoài sấy gần nhất với giá trị nào sau đây?
A.
7
( )
2
cm
. B.
13
( )
2
cm
. C.
11
( )
3
cm
. D.
8
( )
3
cm
.
Câu 44: Trong không gian với hệ trục toạ độ
Oxyz
, tọa độ điểm
M
thuộc trục
Ox
và cách đều hai
điểm
5; 3;4
A
và
3; 5; 8
B
là
A.
3;0;0
M
. B.
3;0;0
M
. C.
5;0;0
M
. D.
5;0;0
M
.
Câu 45: Trong không gian
Oxyz
, cho hai điểm
3;1; 2 , ( 1;5;6)
A B
. Biết
C
là điểm đối xứng của
A
qua
B
. Tọa độ điểm
C
là
A.
5;9;14
. B.
1;3;2
. C.
1;11;10
. D.
7; 3; 10
.
8
Câu 46: Trong không gian
Oxyz
, cho mặt cầu
2 22
8 12 4 25:
0
S x y x y zz
. Thể tích khối
cầu
S
là
A.
972
V
B.
2916
V
. C.
729
V
. D.
81
V
.
Câu 47: Trong không gian với hệ trục toạ độ
Oxyz
, cho hai điểm
5;1; 3
A
và
7; 3;9
B
. Phương
trình mặt cầu nhận
AB
làm đường kính là
A.
2 2 2
( 1) ( 1) ( 3) 76
x y z
. B.
2 2 2
( 5) ( 1) ( 3) 19
x y z
.
C.
2 2 2
( 7) ( 3) ( 9) 44
x y z
. D.
2 2 2
( 1) ( 1) ( 3) 304
x y z
.
Câu 48: Trong không gian
Oxyz
cho các điểm
2;1;3
A
,
1;1;4
B
,
1;2; 1
C
và
; ;0
I a b
. Biết
rằng biểu thức
. 2 .
S IAIB IB IC
đạt giá trị nhỏ nhất. Khi đó
S a b
có giá trị là
A.
3
2
S
. B.
3
2
S
. C.
13
2
S
. D.
9
2
S
.
Câu 49: Trong không gian với hệ trục toạ độ
Oxyz
, cho hai điểm
0;0;6
A
và
3;4;3 .
I
Điểm
M
di
động trên mặt phẳng
Oxy
sao cho
10.
MI
Trong trường hợp
AM
đạt giá trị nhỏ nhất thì
diện tích tam giác
OAM
bằng
A.
12
. B.
10
. C.
18
. D.
24
.
Câu 50: Trong không gian với hệ trục toạ độ
Oxyz
, cho ba điểm
;0;0 ,
A a
0; ;0 ,
B b
0;0;
C c
với
0
abc
và thỏa mãn
2 3 28.
a b c
Xét mặt cầu
S
ngoại tiếp tứ diện
OABC
. Trong
trường hợp
S
có diện tích nhỏ nhất, thể tích tứ diện
OABC
bằng
A.
8
. B.
5488
243
. C.
16
. D.
1372
81
.
1
SỞ GIÁO DỤC VÀ ĐÀO TẠO
TỈNH ĐỒNG THÁP
________________
HƯỚNG DẪN CHẤM
ĐỀ CHÍNH THỨC
(HDC
g
ồm có
9
trang)
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
NĂM HỌC 2022 - 2023
Môn: TOÁN
Ngày thi: 02/4/2023
Họ và tên người ra đề: Nguyễn Xuân Thu-Bùi Phú Hữu-Nguyễn Trần Mỹ
Phương Trang
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
1
A
2 1 2
2( ) 1 1 0
2 1 2
x y x
x y y x x y
y x y
(1)
2( )
2( ) 0
1 1 1 (2)
1 1
x y
x y
x y
y x x yy x x y
*
1
(1)
2
x y
thỏa mãn.
*
(2) 2 2 1 1 1
y x x y
vô lý.
Phương trình có nghiệm duy nhất.
2
A
2
2
3 2( 2) 3 3 0 3 4 3 0
x x x x m x x x x m
Đặt
3
t x x
đồng biến trên
3;

và
( 3) 3
t
Ta được
2 2
4 0 4 (*)
t t m m t t
t
3
2 +
f t
4
21
-
Phương trình đã cho có hai nghiệm phân biệt khi (*) có hai nghiệm phân
biệt, khi
21 4
m
có 25 giá trị m.
3
A
0
,
3 4
sin cos
5 5
;
3 2 4 2 7 2
sin sin cos sin cos . .
4 4 4 5 2 5 2 10
4
A
F
E
B
A
D
C
2
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
Đặt
2
2
2
ABCD EDC
x
AB x S x S
2
2
5 2 3 3
;
2 10
5 2 5
EDC
CEF
Sx x
DE CE CF EF x S x
DE
3
10
CEF ABCD
S S
Chi phí sơn toàn bộ hình vuông là 1.000.000 đồng
Trả thêm 700.000 đồng.
5
A
, ,
A B C
cùng thuộc đường tròn tâm
(3; 2)
I
bán kính
5
r
H
là trực tâm tam giác
ABC
nên
H
thuộc đương tròn tâm
,
I
bán kính
5
r
với
I
đối xứng với I qua
.
BC
Có
( 4; 1)
I
min 5 17
OH OI R
6
A
Ta có
2 2
4 5
3 cos sin 3 .
3 3
P x x P
7
A
Phương trình đã cho có nghiệm khi
12 14.
m
Có 27 giá trị m thỏa.
8
A
TH1: có 3 số gồm 2 chữ số 1 và 1 chữ số 6.
TH2: có 3! số gồm có 1 chữ số 2, 1 chữ số 3 và 1 chữ số 1.
Vậy tổng số là
3 6 9
số.
9
A
Gọi
x
là số học sinh nam và
y
là số học sinh nữ.
Do cứ mỗi học sinh nam thì quen với đúng 10 bạn nữ và mỗi học sinh nữ thì
quen với đúng 8 bạn nam, nên ta có số cặp nam nữ quen nhau được tính theo
hai cách lần lượt là
10
x
và
8 .
y
Ta có hệ phương trình
10 8
24
6
30
x y
x
x y
y
Vậy tổng số học sinh là 54.
Xác suất cần tìm là
2
54
30.24 80
.
159
C
10
A
2 8
5
10
2
u u
u
11
A
Do tam giác
ABC
vuông tại
C
nên
2 2 2
z x y
và
2 2
2 8
.4
3 3
y x z y xz
.
Từ đó ta có
2
2 2
1
( )
8
3
3 8 3 0
3
3 ( )
x
n
x x
z
z x xz
xz z
l
z
.
12
Gọi
,
H K
lần lượt là hình chiếu của
A
lên
BC
và
A H
.
3
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
K
H
Ta có
1 1 1
, , ,
2 2 2
d M A BC d C A BC d A A BC AK
.
Mà
2 3. 3
3
2
a
AH a
;
4
AA a
nên
2 2
. 12 1 12 6
, .
5 2 5 5
AH AA a a a
AK d M A BC
AH AA
.
13
Gọi
N
là trung điểm
.
AB
Ta có
//
MN AC
suy ra
, ,
d AC SM d AC SMN AH
Với
H
là hình chiếu của
A
lên cạnh
.
SN
Ta có
1, 3
AN SA
suy ra
. 3 10
10
AN SA
AH
SN
.
14
A
Tiệm cận đứng
3
x
15
A
' 0
y
16
A
2
' 3 1
y x
17
A
'( ) 0
f x
có ba nghiệm 0, 1, 2 trong đó 0, 1 là các nghiệm kép.
18
A
Tiệm cận ngang
3, 1
y y
19
A
1
2 1 0
2
f x f x
có 3 nghiệm.
20
A
1 2 2
m x m
y
x m
xác định khi
x m
nên
1; 1 1
m m m

.
2
2
1 2 2
' 0 2 0 1 2
m m m
y m m m
x m
.
Do đó
1 2
m
.
21
A
Điểm cực trị
(0;5), (2;1)
M N
Gọi
M
đối xứng với
M
qua
(0; 5)
, MOx
.
FM FN
nhỏ nhất khi
F
là
giao điểm của
Ox
và
.
M N
Khi đó
2 2
min( ) ' 2 6 2 10
FM FN M N
22
A
Đặt
0;2 cos 1;1
x x
4
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
1 cos 1;0
(1 cos ) 1 cos 1 cos 0;1
1 cos 2
cos 1 2; 1
cos 1 1;0
cos 1
x a
f x x x b
x
x a L
x b
x L
Vậy phương trình có 2 nghiệm.
23
A
2
6 ' 2 ' 6 ' 2 3 '
g x f x f x g x f x f x f x f x f x
x
-
∞
-1 1 +
∞
f’(x) + 0 + 0 -
f(x) 2
2
3
( ) 3 ( ) 3 0
f x x R f x x R
'( ) 0 '( ) 0
g x f x
x
-
∞
-1 1 +
∞
f’(x) + 0 + 0 -
g’(x) - 0
- 0 +
g(x)
32
9
-8
24
A
2
2
y f x x
2
2 2 . 2
y x f x x
2
2
f x x
đồng biến khi
2
2 2 . 2 0
x f x x
2
2 2
2
2 2
2 2 0
1
2 0
1 2 0; 2 1
2 2 0
11
2 0
2 1;0 2 1
x
x
f x x
x x x x
x
x
f x x
x x x x
Các khoảng đồng biến là
1 2;0 , 1;2 , 1 2;

.
25
A
2 4 3 2
2 2 2
g x f x x x x x x
Xét hàm số
2 4 3 2
2 2 2
h x f x x x x x x
có
5
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
2 3 2
2 2
' 2 2 1 ' 4 6 2 2
2 2 1 ' 1
h x x f x x x x x
x f x x x x
2
2 2
2
2
1
2
2 1 0
1
2
' 0 2; 1; ;0;1
' 1
2
0
2
x
x
x x
h x x
f x x x x
x x
x x
x
1
2 1 0 1
2

h’(x) - 0 + 0 - 0 + 0 - 0 +
h(x) 0 0
2 4 3 2
2 2 2
y h x f x x x x x x
có 5 điểm cực trị và đồ thị của nó
cắt Ox tại 2 điểm nên hàm số
( )
g x
h x
có tất cả 7 điểm cực trị.
26
A
B
là trung điểm của
AC
nên ta có
2
2 2 2
log log 2log . .
a c b a c b
27
A
Hàm số nghịch biến trên R khi và chỉ khi
2
2
2
1 0
1
0 1 1 4 2; 3;2;3
15
1 15
m
m
m m
m
28
A
2
1
2 3
x x x
2
1
3 3
log 2 log 3
x x x
2
3
1 log 2
x x x
3
1 1 log 2
x x x
3
3
1
1 log 2 0
log 2
x
x x
x
.
3
1 2
log 2
1
3 3 3 3 3 2 5.
x x
M
29
A
Điều kiện:
0, 0.
x y
2 2 4 2
2 2
2
1
log log log
4
x x y y
2 2
2 2
2
2
log 1 2log 1 0
log 1
2log 1
2
2
x y
x
y
x
y
2 2
6
x y
.
6
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
30
A
2 3 2
ln 1 3 7 3 ln 2 1
x
x x y y xy
y
3
3
ln 1 8 ln 2
x
x y y
y
3 3
ln ln 2 2 2
x y x y y y
Xét hàm đặc trưng
3
ln 0
f t t t t
Ta có
2
1
3 0, 0.
f t t t
t
1 2 .
x y y y x
2 2 2
1 1 1 1 3
3 4 8 8 4
T x x x
x y x x x
Suy ra
3
4
MinT
khi
2
1 1
.
8 2
x x y
x
31
A
Đặt
2
x
t
,
0
t
.
Bất phương trình đã cho trở thành:
2
5 4 1 0
t x t x
4 1 0
t t x
TH1:
4 0 4 2 4
1 0 1 0
2 1
x
x
t t
t x t x
x
TH2:
4 0 4 2 4
1 0 1 0
2 1
x
x
t t
t x t x
x

Dựa vào đồ thị ta thấy tập ngiệm là
0;1 2;

S
.
Suy ra
0, 1, 2.
a b c
32
A
2
2
2 2 3.
I f x dx f f
33
A
Đặt
1
0
( ) .
x
x f x dx a f x e a
Theo đề ta có
1
0
x x x
e a e x e a dx
7
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
1 1
0 0
x
a xe dx a xdx
1 2
2
a
a a
2 0 3.
x
f x e f
34
A
Ta có
2 2
lim lim 2 5
x x
f x f x f
nên hàm số liên tục tại
2
x
.
Vậy hàm số
f x
liên tục trên
.
Đặt
ln 1
dx
t x dt
x
.
Đổi cận:
3
1 1; 4
x t x e t
.
Khi đó
3
4 2 4
1 1 1 2
1ln
e
f
tI f
x
x t t
d f t d f t d t d
x
.
2 4
2
1 2
74
2 1 1 .
3
t d t dt t
35
A
. . .
2
f x
f x x x f x x x f x x
x
.
f x x x
Lấy nguyên hàm hai vế
2
.
2
x
f x x C
Mà
1 1
f
suy ra
2
1 1 17
4 .
2 4
2
x
C f x f
x
36
A
Ta có
3
(0) (0) 0 (0) 0
f f f
3
(2) (2) 2 (2) 1
f f f
2 2
2
0
0 0
( ) ( ) . ( )
I f x dx xf x x f x dx
2
4 2
2
3
0
0
( ) ( ) 1 1 5
2 ( ) ( ) . ( ) 2 2 .
4 2 4 2 4
f x f x
f x f x f x dx
37
A
Đồ thị hàm số
y g x
đi qua ba điểm
1;1 , 1;1 , 2;4
A B C
nên ta có
2
.
y g x x
Đồ thị hàm số
y f x
và
y g x
cắt nhau tại ba điểm như hình vẽ nên ta
có
2
1 2
f x g x a x x
với
0
a
.
Khi đó:
1 2
1 2
2 2
1 1
9
1 2 1 2 9
S S
a x x dx a x x dx
8 5 9
9 9 4
3 12 4
a a a
a
.
8
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
Suy ra
2 2 2
4 1 2 4 1 2
f x x x g x x x x
.
Vậy
2 2
2 2
0 0
16
4 1 2 .
3
f x dx x x x dx
38
A
Số đỉnh là 6
39
A
Diện tích mỗi mặt bằng
2
9
a
Suy ra cạnh bằng
3
a
.
Thể tích
3
27
a
.
40
A
3
2
1 1 4
. . . .4
3 3 3
hv
a
V SO S a a
41
A
2
2.50 100 10
l l
Đường cao thiết diện
5 2
0
5 6
5 2.sin 60
2
h
2 2
75 5 10
100
2 2
r l h
42
A
Ta có
2 3 2
4 2
.2 .
3 3
h
r h r r r
r
43
A
Gọi
0
r r
là bán kính đáy của lon nước ép. Khi đó
2
2
V
V
r h h
r
.
Diện tích toàn phần:
2 2 2
2
2
2 2 2 2 2
V V
S r rh r r r r
r r
.
Ta có
3
2 2
2 3 2
V V
r V
r r
.
Đẳng thức xảy ra khi
2
3
270
2 3,5
2
V
r r
r
.
44
A
MA MB
suy ra
3;0;0
M
.
45
A
B
là trung điểm
AC
nên
5;9;14 .
C
46
A
3
4
972
3
kc
V R
.
47
A
Tâm
1; 1;3 , 76
I R
.
48
A
2 ;1 ;3
IA a b
,
1 ;1 ;4
IB a b
,
1 ;2 ; 1
IC a b
.
2 2
11
2
I aA IB a b b
,
2 2
3 3
IB IC a b b
.
2 2
2 2
4
6
1
1 5
6
3 3 8 5 3 3
12
3
a
T a a b b a b
b
Vậy
3
2
S a b
9
CÂU
HỎI
PHƯƠNG
ÁN
ĐÚNG
TÓM TẮT LỜI GIẢI
49
A
Do
10
MI
nên
M
nằm trên mặt cầu
S
tâm
I
bán kính
10.
R
Mặt khác
M
thuộc
Oxy
suy ra
M
sẽ di động trên đường tròn
C
là giao
tuyến của
S
và
Oxy
.
C
có bán kính
10 10 9 1.
r IH
(với
H
là hình chiếu của
I
lên
Oxy
)
AM
nhỏ nhất khi
OM
nhỏ nhất.
min
4
OM OH r
.
Suy ra
1
.6.4 12.
2
OAM
S
50
A
Bán kính mặt cầu
2 2 2
1
2
R a b c
.
(S) có diện tích nhỏ nhất khi R nhỏ nhất, tức là
2 2 2
a b c
nhỏ nhất.
Ta có
2 2 2
28 2 3 1 4 9 2 . 14
a b c a b c R
suy ra
14.
R
Đẳng thức xảy ra khi
2
4
2 3
2 3 28
6
a
b c
a
b
a b c
c
.
Suy ra thể tích tứ diện
OABC
là
8
.
--- HẾT---
| 1/17
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH TỈNH ĐỒNG THÁP NĂM HỌC 2022 - 2023 ________________ Môn: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 02/4/2023
(Đề gồm có 14 trang)
Thời gian làm bài: 90 phút, không kể thời gian phát đề
2x y x 1  2
Câu 1: Hệ phương trình 
có tất cả bao nhiêu nghiệm?
2y x y 1  2  A. 1. B. 0. C. 2. D. 3.
Câu 2: Gọi S là tập hợp các giá trị nguyên của tham số m sao cho phương trình 2
x  3x  2(x  2) x  3  m  3  0 có 2 nghiệm phân biệt. Số phần tử của S là A. 25. B. 24. C. 23. D. 26.  3   
Câu 3: Cho 0   
và sin  . Giá trị sin     bằng 2 5  4  7 2 2 2 3 2 A. . B. . C.  . D.  . 10 10 10 5 2
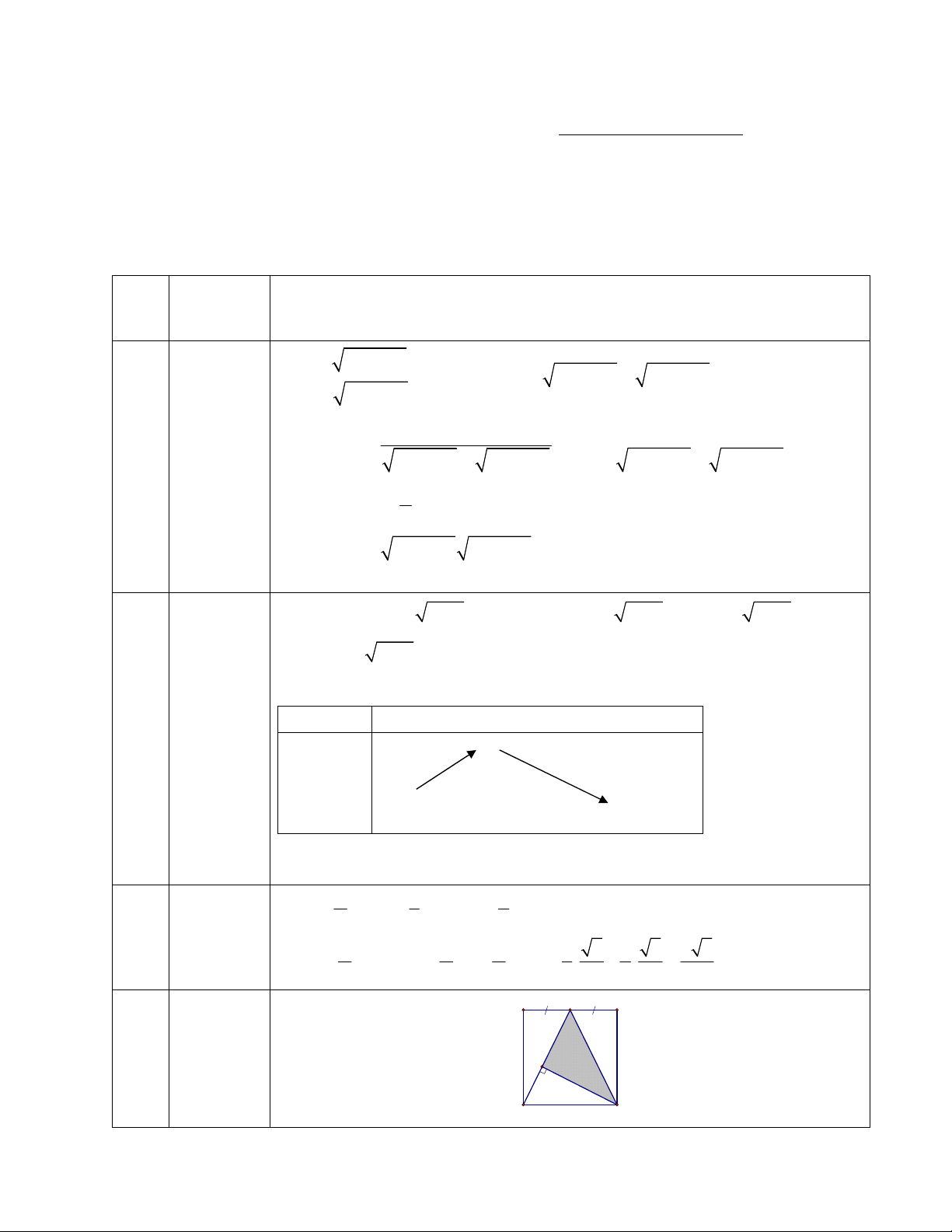
Câu 4: Một mảng tường hình vuông được minh họa bằng hình vẽ (hình vuông ABCD, E là trung
điểm AB , CF DE ). Biết rằng phần tô đậm (tam giác CEF ) đã được sơn với chi phí
300.000 đồng. Nếu muốn sơn thêm phần còn lại của mảng tường hình vuông đó với chất lượng
như phần đã sơn thì số tiền phải trả thêm là A E B F D C A. 700.000 đồng. B. 1.000.000 đồng. C. 900.000 đồng. D. 800.000 đồng.
Câu 5: Trong mặt phẳng tọa độ Oxy cho hai điểm B(0; 2),C(1;5) . Điểm A thuộc đường tròn C 2 2
: (x  3)  ( y  2)  25 . Gọi H là trực tâm của tam giác ABC . Độ dài đoạn thẳng OH
có giá trị nhỏ nhất bằng 5 2 A. 5  17 . B. 5  17 . C. . D. 50  5 . 2
Câu 6: Cho x thỏa mãn 2 2 4
2cos x  sin x  . Giá trị của biểu thức 2 2
P  cos x  2sin x là 3 5 4 2 A. P  . B. P  1 . C. P  . D. P  . 3 3 3
Câu 7: Có tất cả bao nhiêu số nguyên m để phương trình 12sin x  5cos x 1  m có nghiệm? A. 27 . B. 26 . C. 169 . D. 339 .
Câu 8: Có tất cả bao nhiêu số tự nhiên có 3 chữ số sao cho tích các chữ số bằng 6? 1 A. 9. B. 6 . C. 7 . D. 8.
Câu 9: Một câu lạc bộ Toán học có n học sinh tham gia. Qua một cuộc khảo sát biết được: cứ mỗi học
sinh nam thì quen với đúng 10 bạn nữ và mỗi học sinh nữ thì quen với đúng 8 bạn nam. Biết
rằng số học sinh nam và số học nữ chênh lệch nhau 6 em. Chọn ngẫu nhiên 2 học sinh thuộc
câu lạc bộ. Xác suất của biến cố chọn được 2 học sinh khác giới bằng 80 40 80 40 A. . B. . C. . D. . 159 159 153 153
Câu 10: Cho cấp số cộng u với u u  20 . Giá trị của u bằng n  2 8 5 1 A. 10 . B. 15. C. . D. 5. 5 2
Câu 11: Cho tam giác ABC vuông tại C có các cạnh BC x; AC y ; AB z thoả mãn x; y; 4z 3
theo thứ tự lập thành một cấp số nhân. Giá trị cos B là 1 3 1 2 A. cos B  . B. cos B  . C. cos B  . D. cos B  . 3 2 2 3
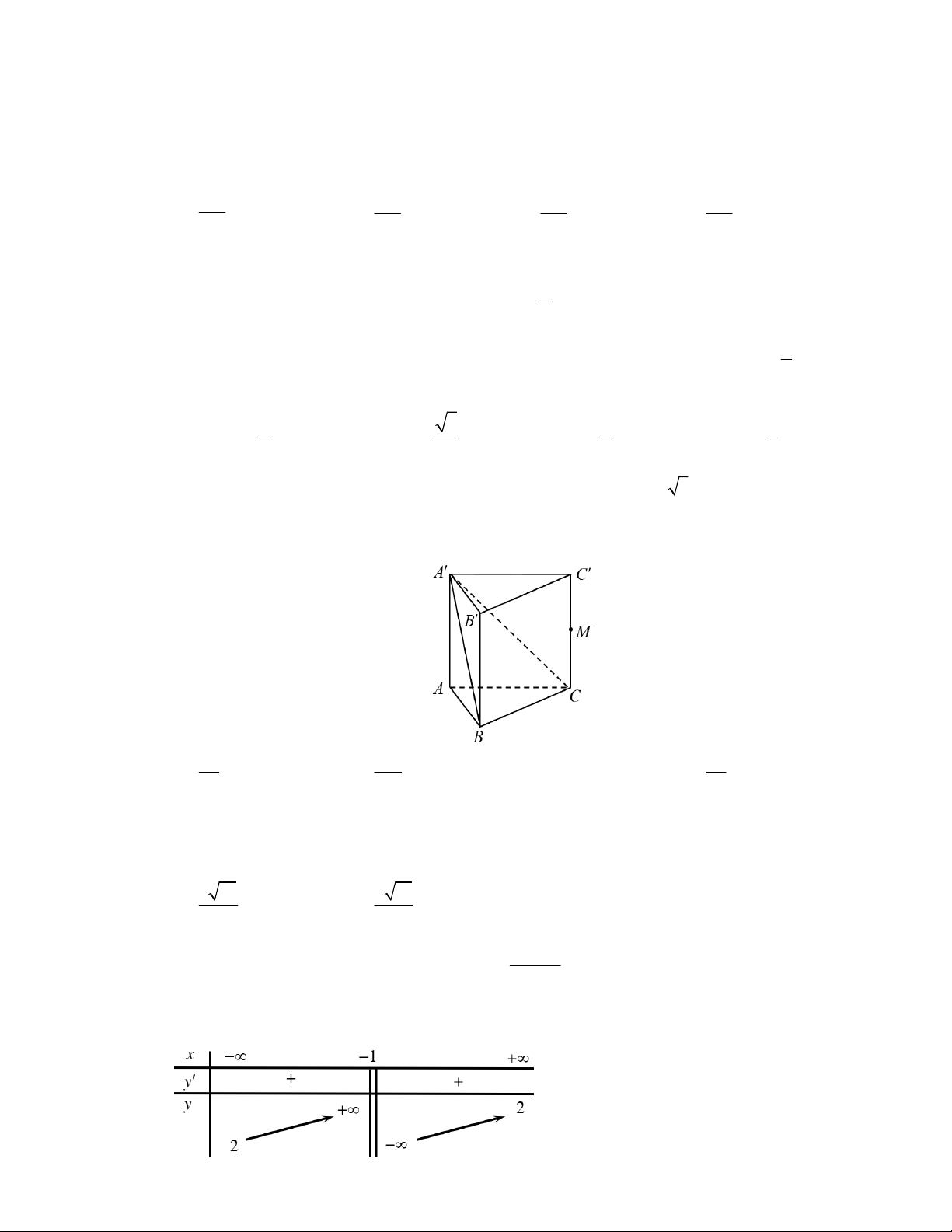
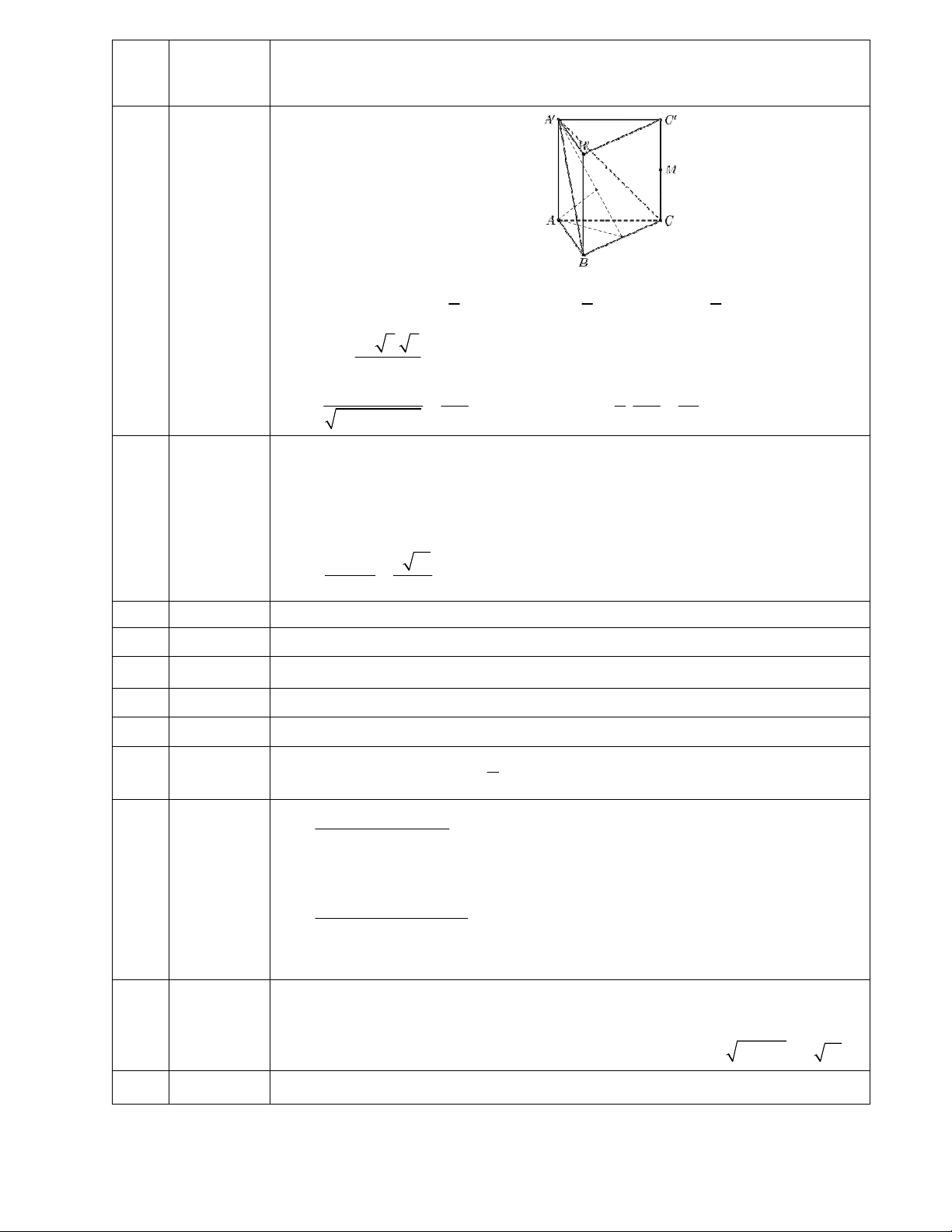
Câu 12: Cho lăng trụ đứng ABC.AB C
  có đáy ABC là tam giác đều cạnh 2a 3 và AA  4a . Gọi M
là trung điểm của CC (tham khảo hình bên). Khoảng cách từ điểm M đến mặt phẳng  ABC  bằng 6a 12a 5a A. . B. . C. 5a . D. . 5 5 12
Câu 13: Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A . Biết AB  2 , SA vuông góc
với mặt phẳng đáy và SA  3. Gọi M là trung điểm của BC . Khoảng cách giữa hai đường
thẳng AC và SM bằng 3 10 6 13 A. . B. . C. 1. D. 3 . 10 13 3 x
Câu 14: Số đường tiệm cận đứng của đồ thị hàm số y  là 2 x  3x A. 1. B. 3 . C. 0 . D. 2
Câu 15: Bảng biến thiên trong hình vẽ là của hàm số nào sau đây? 2 x x x x  2 A. 2 1 1 2 1 y  . B. y  . C. y  . D. y  . x  1 2x  1 x 1 x  1
Câu 16: Hàm số nào sau đây đồng biến trên R? x A. 3
y x x . B. y  . C. 2 y x 1. D. 3 2
y x x . x 1
Câu 17: Cho hàm số y f (x) có đạo hàm 2 2 f (
x)  x(x 1) (2x x ) . Số điểm cực trị của hàm số
y f (x) là A. 1. B. 4. C. 2. D. 3. 2 2x x  2
Câu 18: Đồ thị hàm số y
có tất cả bao nhiêu đường tiệm cận ngang? x  2 A. 2 . B. 3 . C. 1. D. 0 .
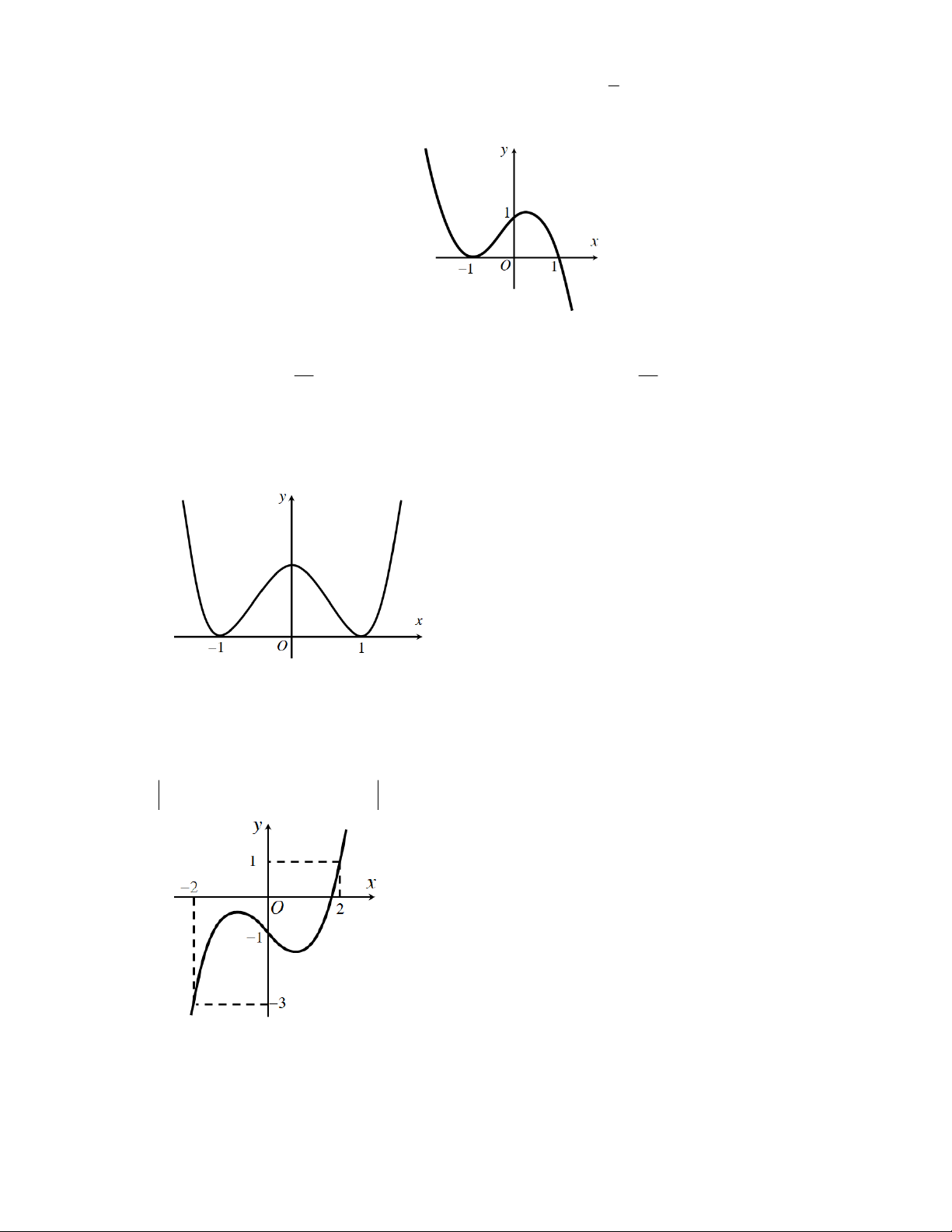
Câu 19: Cho hàm số bậc ba y f x có đồ thị như hình vẽ. Phương trình 2 f x 1  0 có bao nhiêu nghiệm? A. 3. B. 1. C. 0. D. 2.
m 1 x  2m 2
Câu 20: Với các giá trị nào của tham số m thì hàm số y  nghịch biến trên x m  1  ; ? m  1 
A. 1  m  2 .
B. 1  m  2 . C.  .
D. 1  m  2 . m  2
Câu 21: Trong mặt phẳng toạ độ Oxy gọi M , N tương ứng là điểm cực đại và điểm cực tiểu của đồ thị hàm số 3 2
y x  3x  5 . Điểm F thuộc trục hoành Ox , giá trị nhỏ nhất FM FN bằng A. 2 10 . B. 5  5 . C. 2 5 . D. 26  2 .
Câu 22: Cho hàm số y f x có đồ thị như hình vẽ. Trong khoảng 0;2  , phương trình
f 1 cos x 1 cos x có tất cả bao nhiêu nghiệm? A. 2. B. 3. C. 5. D. 4. 3
Câu 23: Cho hàm đa thức bậc bốn y f x có f  
1  2 ; f   2
1  ; đồ thị của hàm số y f  x 3
được cho như hình vẽ. Xét hàm số g x 2
f x  6 f x, mệnh đề nào sau đây đúng?
A. min g x  8.
B. max g x  8. R R 32 32
C. min g x   .
D. max g x   . R 9 R 9
Câu 24: Cho hàm số y f (x) liên tục trên R và có đồ thị như hình vẽ. Hàm số y f  2
x  2x đồng
biến trên khoảng nào sau đây? A. (1; 2) . B. (1;1) . C. (; 2) . D. (2; ) . Câu 25:
Cho f x là hàm đa thức bậc bốn thỏa mãn f 0  0. Hàm số y f  x có đồ thị như hình vẽ. Hàm số
g x  f  2 x x 4 3 2 2
x  2x x  2x có tất cả bao nhiêu điểm cực trị? A. 7 . B. 5 . C. 6 . D. 4 .
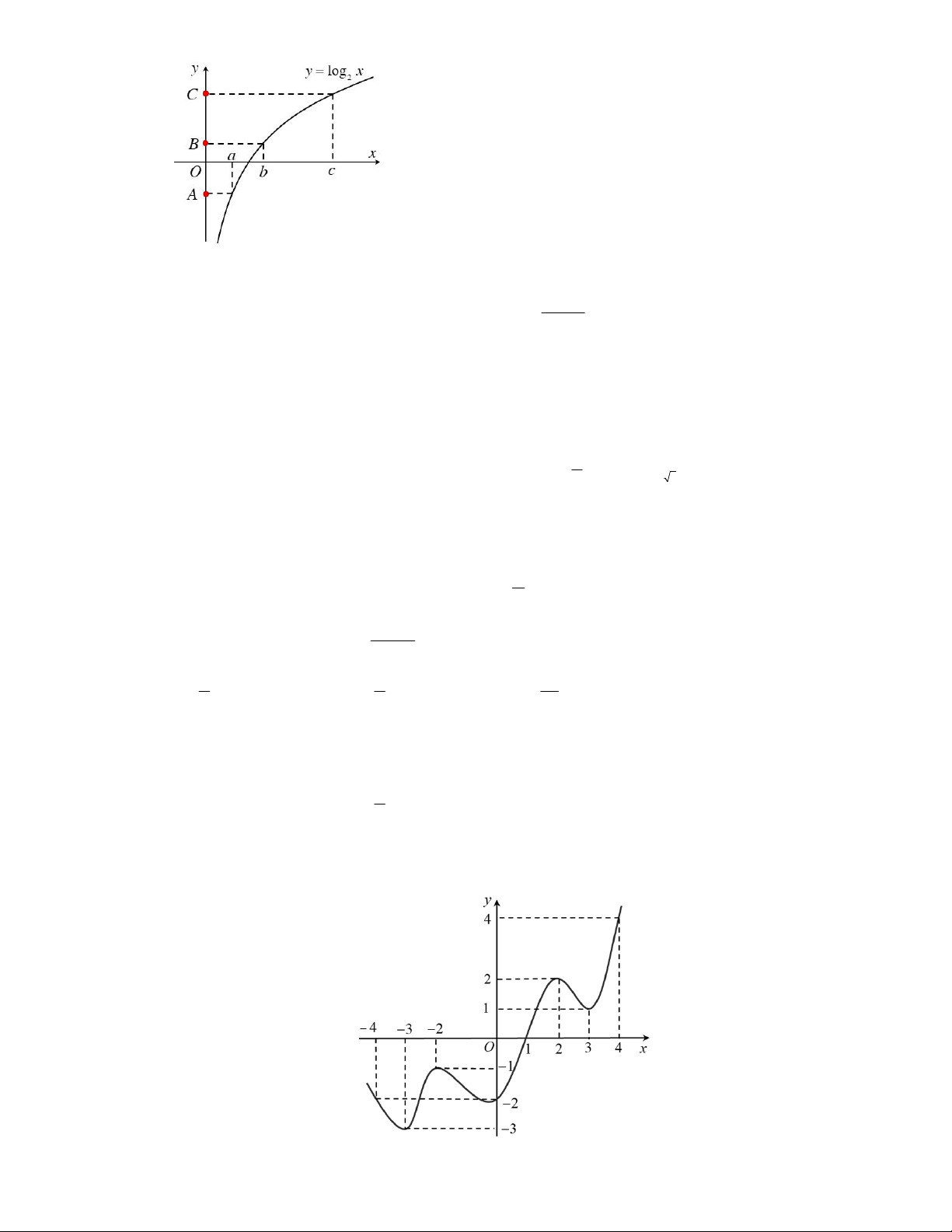
Câu 26: Cho hàm số y  log x có đồ thị như hình vẽ, B là trung điểm của đoạn thẳng AC . Khẳng 2
định nào sau đây là đúng về giá trị của các số a, , b c ? 4 A. 2 ac b .
B. a c  2b . C. 2 ac  2b .
D. ac b . x 2  m   Câu 27: 1
Có bao nhiêu giá trị nguyên của m để hàm số y    nghịch biến trên R.  15  A. 4 . B. 7 . C. 8 . D. 9 . 2
Câu 28: Gọi x , x là các nghiệm của phương trình x 1
2   3x x . Giá trị của biểu thức 1 x 2 3 3x M   là 1 2 A. M  5. B. M  12 . C. M  4 . D. M  6 .  1  Câu 29: Cho ,
x y là các số thực dương thỏa mãn 2 2 4 2 log x  log
x y  log y , giá trị của biểu thức 2 2   2  4  2 2
F x y bằng A. 6 . B. 5 . C. 14. D. 10.  x
Câu 30: Cho x, y là các số thực dương sao cho 2   x   x y 3 2 ln 1 3
 7y  3xy  ln 2 . Giá trị nhỏ  y  1 nhất của biểu thức 2 T x  bằng x  3y 3 1 1 A. . B. . C. . D. 1. 4 4 12
Câu 31: Bất phương trình 4x    5 2x x  4 x  
1  0 có tập nghiệm S   ;
a bc;. Tính tổng
a b c . 2 A. 3 . B. . C. 5  . D. 12 . 3 2
Câu 32: Cho hàm số y f x có đồ thị như hình vẽ. Giá trị của tích phân I f
 xdx là 2  A. I  3. B. I  3  . C. I  4 . D. I  4  . 5 1
Câu 33: Cho hàm số f x liên tục trên R và thỏa mãn f (x) xe xf
 xdx. Giá trị của f 0 bằng 0 A. 3. B. 0. C. 1. D. 2. 2
x 1 khi x  2 3
e f ln x   1
Câu 34: Cho hàm số f x   . Tích phân I dx  bằng
2x 1 khi x  2  x 1 74 52 56 A. I  . B. I  . C. I  . D. I  20 . 3 3 3
Cho f x là hàm số liên tục trên 0; thỏa mãn 2 .
x f  x  f x  2x x và f   1  1. Giá Câu 35: trị f 4 bằng 17 5 17 7 A. . B. . C.  . D.  . 4 4 2 2
Câu 36: Cho f ( )
x là hàm số có đạo hàm trên 0;2 đồng thời f (x) liên tục trên 0;2 và thỏa mãn 2 điều kiện 3
f (x)  f (x)  , x x  0; 
2 . Giá trị của tích phân f xdx  bằng 0 5 5 4 5 A. . B. . C. . D.  . 4 2 3 2
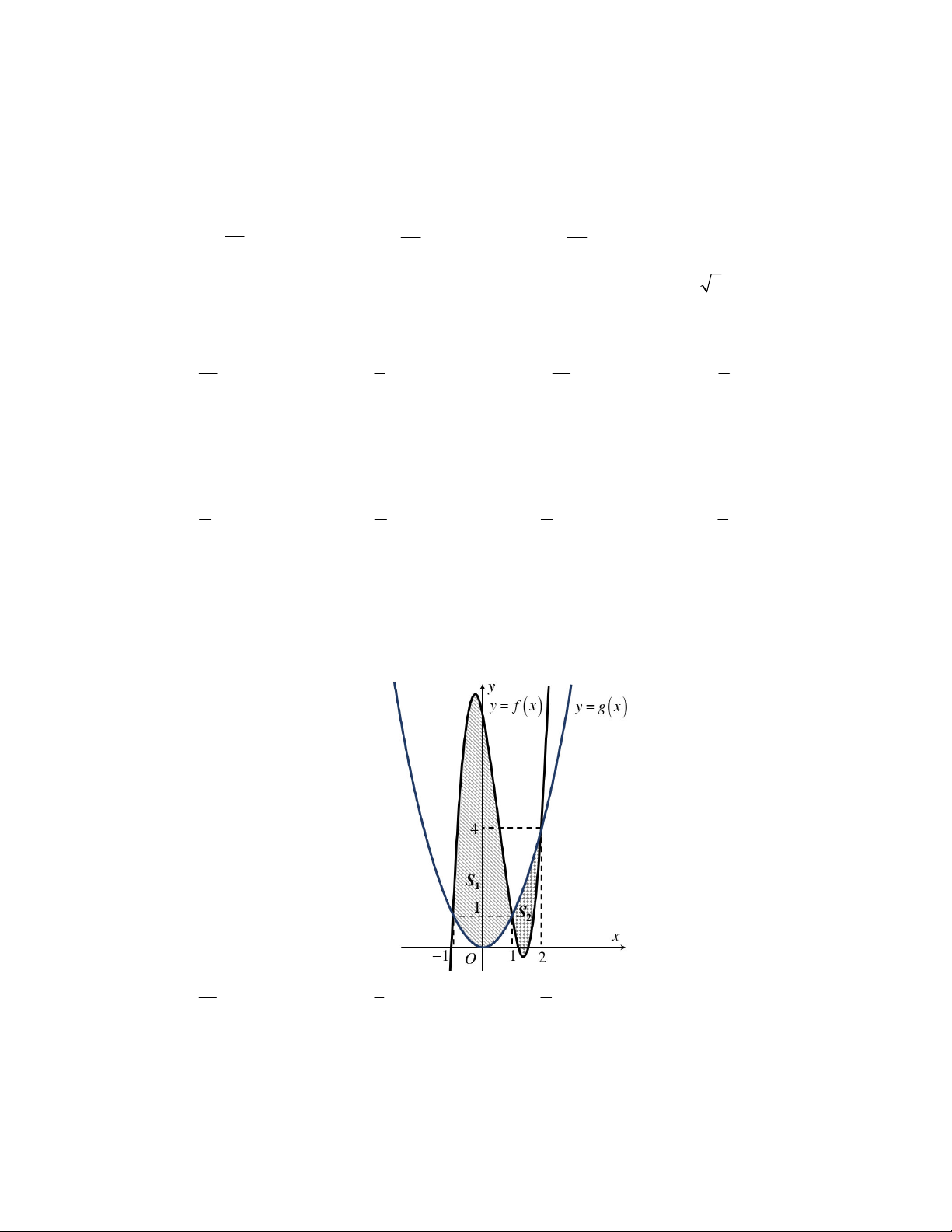
Câu 37: Cho y f x là hàm đa thức bậc ba và y g x là hàm bậc hai, có đồ thị như hình vẽ. Hai
đồ thị cắt nhau tại các giao điểm có hoành độ lần lượt là 1; 1; 2. Biết S S  9 (với S , S 1 2 1 2 2
tương ứng là diện tích của các miền gạch sọc tại đó). Giá trị của f xdx  bằng 0 16 8 4 A. . B. . C. . D. 2 . 3 3 3
Câu 38: Hình chóp ngũ giác có số đỉnh của hình đa diện đã cho là A. 6 . B. 5 . C. 7 . D. 10.
Câu 39: Hình lập phương có tổng diện tích tất cả các mặt là 2
54a . Thể tích của khối lập phương là A. 3 27a . B. 3 64a . C. 3 9a . 6 3 64a D. . 3
Câu 40: Cho khối chóp đều S.ABCD có AC  2a 2 , hai mặt phẳng SAB và SCD vuông góc với
nhau. Thể tích khối chóp đã cho bằng 3 4a 3 32a 3 2a 2 A. . B. 3 4a . C. . D. . 3 3 3
Câu 41: Cho hình nón đỉnh S . Một mặt phẳng P đi qua S hợp với trục của nón một góc o 30 , cắt
hình nón theo thiết diện là một tam giác vuông có diện tích bằng 2
50(cm ) . Bán kính đáy của hình nón bằng 5 10 5 13 5 14 5 22 A. (cm) . B. (cm) . C. (cm) . D. (cm) . 2 2 2 2
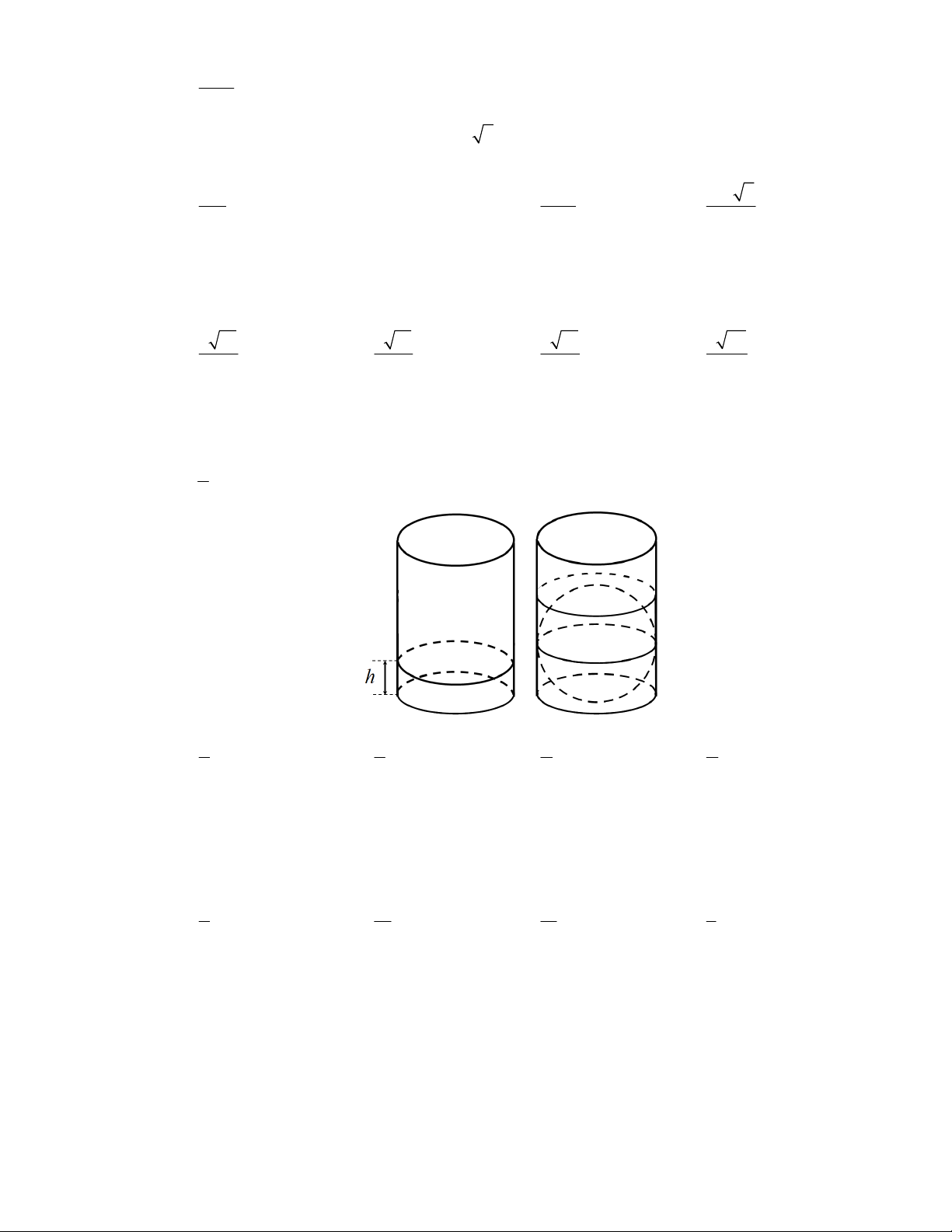
Câu 42: Đặt thăng bằng một chiếc bình hình trụ có chứa nước trên một bề mặt nằm ngang, biết mực
nước trong bình cao bằng h . Người ta bỏ một quả cầu bằng thép đặc có bán kính r lọt vừa khít
vào bình nước và thấy lượng nước dâng lên vừa ngập hết quả cầu (xem hình minh họa bên). Tỉ h số bằng r 2 3 4 3 A. . B. . C. . D. . 3 4 3 2
Câu 43: Một hợp tác xã xoài ở Đồng Tháp sản xuất mặt hàng xoài sấy. Thành phẩm xoài sấy được chứa
trong những hộp hình trụ với thể tích V   3
270 cm  . Để chi phí nguyên liệu làm vỏ hộp thấp
nhất, người ta thiết kế hình trụ có diện tích toàn phần nhỏ nhất. Khi đó bán kính đáy của hộp
xoài sấy gần nhất với giá trị nào sau đây? 7 13 11 8 A. (cm) . B. (cm) . C. (cm) . D. (cm). 2 2 3 3
Câu 44: Trong không gian với hệ trục toạ độ Oxyz , tọa độ điểm M thuộc trục Ox và cách đều hai điểm A 5  ; 3  ;4 và B3; 5  ; 8   là
A. M 3;0;0 . B. M  3  ;0;0 .
C. M 5;0;0 . D. M  5  ;0;0 .
Câu 45: Trong không gian Oxyz , cho hai điểm A3;1; 2  , B( 1
 ;5;6) . Biết C là điểm đối xứng của A
qua B . Tọa độ điểm C là A.  5  ;9;14 . B. 1;3;2. C. 1;11;10 . D. 7; 3  ; 1  0. 7
Câu 46: Trong không gian Oxyz , cho mặt cầu S  2 2 2
: x y z  8x 12y  4z  25  0 . Thể tích khối cầu S  là A. V  972
B. V  2916 .
C. V  729 .
D. V  81 .
Câu 47: Trong không gian với hệ trục toạ độ Oxyz , cho hai điểm A 5  ;1; 3   và B7; 3  ;9 . Phương
trình mặt cầu nhận AB làm đường kính là A. 2 2 2
(x 1)  ( y 1)  (z  3)  76 . B. 2 2 2
(x  5)  ( y 1)  (z  3)  19 . C. 2 2 2
(x  7)  ( y  3)  (z  9)  44 . D. 2 2 2
(x 1)  ( y 1)  (z  3)  304 .
Câu 48: Trong không gian Oxyz cho các điểm A2;1;  3 , B 1
 ;1;4, C1;2;  1 và I  ; a ; b 0 . Biết    
rằng biểu thức S I . A IB  2I .
B IC đạt giá trị nhỏ nhất. Khi đó S a b có giá trị là 3 3  13 9 A. S  . B. S  . C. S  . D. S  . 2 2 2 2
Câu 49: Trong không gian với hệ trục toạ độ Oxyz , cho hai điểm A0;0;6 và I 3;4;3. Điểm M di
động trên mặt phẳng Oxy sao cho MI  10. Trong trường hợp AM đạt giá trị nhỏ nhất thì
diện tích tam giác OAM bằng A. 12. B. 10 . C. 18 . D. 24 .
Câu 50: Trong không gian với hệ trục toạ độ Oxyz , cho ba điểm A ;
a 0;0, B0; ;
b 0, C 0;0;c với
abc  0 và thỏa mãn a  2b  3c  28. Xét mặt cầu S  ngoại tiếp tứ diện OABC . Trong
trường hợp S  có diện tích nhỏ nhất, thể tích tứ diện OABC bằng 5488 1372 A. 8 . B. . C. 16 . D. . 243 81 8
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH TỈNH ĐỒNG THÁP NĂM HỌC 2022 - 2023 ________________ Môn: TOÁN HƯỚNG DẪN CHẤM Ngày thi: 02/4/2023 ĐỀ CHÍNH THỨC
(HDC gồm có 9 trang)
Họ và tên người ra đề: Nguyễn Xuân Thu-Bùi Phú Hữu-Nguyễn Trần Mỹ Phương Trang PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG
2x y x 1  2 
 2(x y)  y x 1  x y 1  0
2y x y 1  2   x y (1) 2(x y)
 2(x y)   0   A
y x 1  x y 1
y x 1  x y 1  1 (2)  1
* (1)  x y  thỏa mãn. 2
* (2)  2  2 y x 1 x y 1  1 vô lý. 1
Phương trình có nghiệm duy nhất. 2 2
x  3x  2(x  2) x  3  m  3  0  x x  3  4x x  3  m  0
Đặt t x x  3 đồng biến trên  3  ; và t( 3  )  3  Ta được 2 2
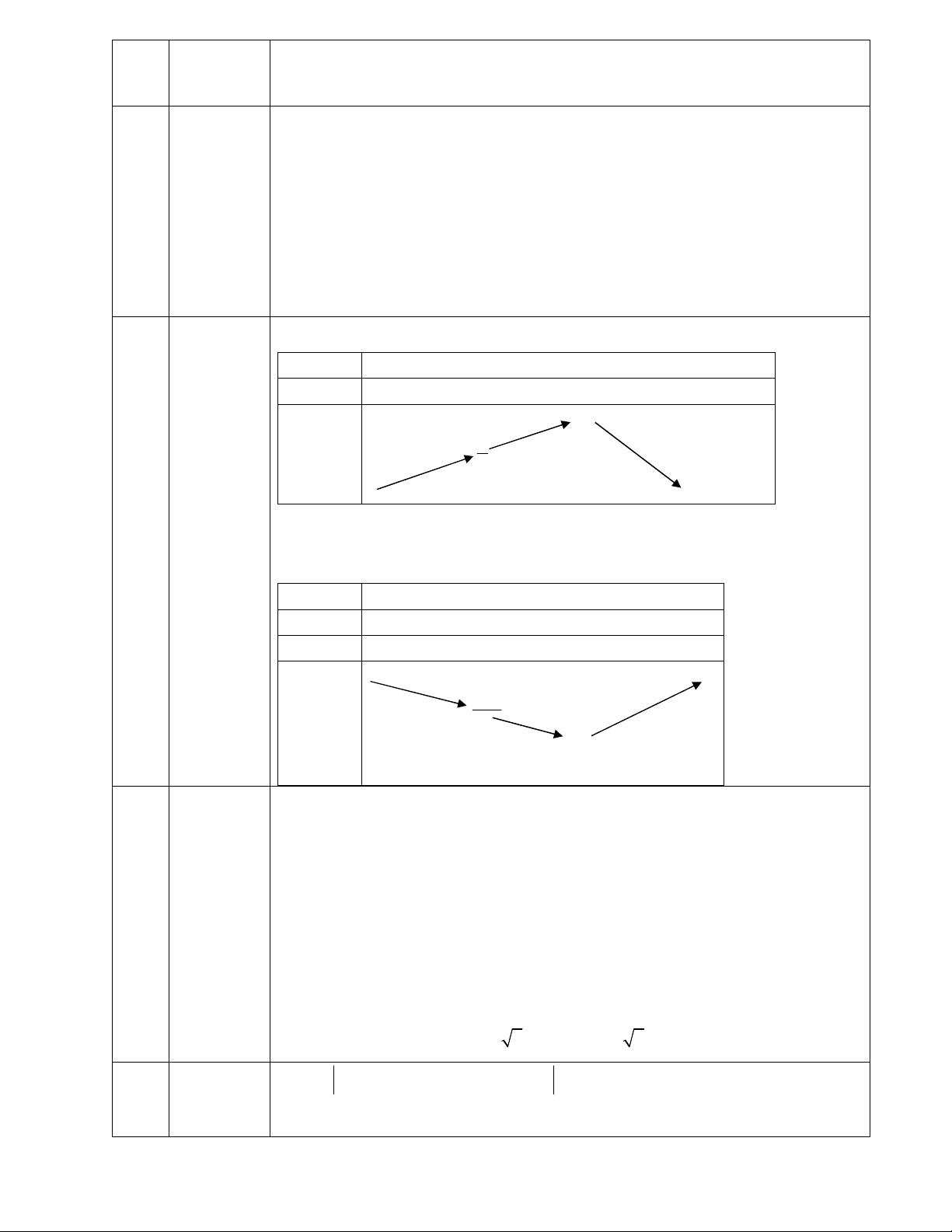
t  4t m  0  m t   4t (*) t 3 2 +  A
f t 4 21 - 
Phương trình đã cho có hai nghiệm phân biệt khi (*) có hai nghiệm phân 2
biệt, khi 21  m  4  có 25 giá trị m.  3 4 0    , sin   cos  ; 2 5 5 A      3 2 4 2 7 2 sin  
 sin cos  sin cos  .  .    3  4  4 4 5 2 5 2 10 A E B A F 4 D C 1 PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG 2 x Đặt 2
AB x Sx SABCD EDC 2 x 5 2S 2x 3 3 EDC 2 DE CE  ;CF    EF x Sx 2 DE 5 2 5 CEF 10 3  SS CEF 10 ABCD
 Chi phí sơn toàn bộ hình vuông là 1.000.000 đồng
 Trả thêm 700.000 đồng. ,
A B, C cùng thuộc đường tròn tâm I (3;2) bán kính r  5
H là trực tâm tam giác ABC nên H thuộc đương tròn tâm I , bán kính A
r  5 với I đối xứng với I qua BC.     5 Có I ( 4  ; 1  ) min OH
OI R  5  17 4 5 Ta có  P  3 2 2
cos x  sin x  3 P  . 6 A 3 3 7 A
Phương trình đã cho có nghiệm khi 1
 2  m 14. Có 27 giá trị m thỏa.
TH1: có 3 số gồm 2 chữ số 1 và 1 chữ số 6.
TH2: có 3! số gồm có 1 chữ số 2, 1 chữ số 3 và 1 chữ số 1. 8 A
Vậy tổng số là 3  6  9 số.
Gọi x là số học sinh nam và y là số học sinh nữ.
Do cứ mỗi học sinh nam thì quen với đúng 10 bạn nữ và mỗi học sinh nữ thì
quen với đúng 8 bạn nam, nên ta có số cặp nam nữ quen nhau được tính theo
hai cách lần lượt là 10x và 8 . y Ta có hệ phương trình 1  0x  8y  x  24   
x y  6  y  30
Vậy tổng số học sinh là 54.
Xác suất cần tìm là 30.24 80  . 2 9 A C 159 54 u u 2 8 u   10 10 A 5 2 A
Do tam giác ABC vuông tại C nên 2 2 2
z x y và 2 2 2 8 y  .
x 4z y xz . 3 3  x 1 2  (n) 8 x x    Từ đó ta có 2 2 z 3
z x xz  3  8  3  0     . 3  z z x   3  (l) 11  z 12
Gọi H, K lần lượt là hình chiếu của A lên BC và A H  . 2 PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG K H 1 1 1
Ta có d M, A B
C  d C , ABC  d  , A A B
C  AK . 2 2 2 2a 3. 3 Mà AH   3a ; A A  4a nên 2 AH.AA 12a    
ABC 1 12a 6a AK d M ,  .  . 2 2 AH AA 5 2 5 5
Gọi N là trung điểm . AB
Ta có MN // AC suy ra d AC, SM   d AC,SMN   AH
Với H là hình chiếu của A lên cạnh SN.
Ta có AN  1, SA  3suy ra AN.SA 3 10 AH   . 13 SN 10 14 A
Tiệm cận đứng x  3 15 A y '  0 16 A 2 y '  3x 1 17 A
f '(x)  0 có ba nghiệm 0, 1, 2 trong đó 0, 1 là các nghiệm kép. 18 A
Tiệm cận ngang y  3, y  1 A
f x    f x 1 2 1 0   có 3 nghiệm. 19 2
m  1 x  2m  2 y
xác định khi x  m nên x mm 1
 ;  m  1   m 1. A
m  1m 2m  2 2 y ' 
 0  m m  2  0  1  m  2 . x m2 20
Do đó 1  m  2 .
Điểm cực trị M (0;5), N (2;1) A
Gọi M  đối xứng với M qua Ox, M (0;5) . FM FN nhỏ nhất khi F là 21
giao điểm của Ox và M N  . Khi đó 2 2
min(FM FN)  M ' N  2  6  2 10 22 A
Đặt x 0;2   cos x 1   ;1 3 PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG 1
  cos x a  1  ;0 
f (1 cos x)  1 cos x  1
  cos x b 0;  1 1   cos x  2 
cos x a 12;  1 L   cos x   b 1 1  ;0 cos x 1  L
Vậy phương trình có 2 nghiệm. g x 2
f x  6 f x  g 'x  2 f xf 'x  6 f ' x  2  f
  x  3 f '  xx -∞ -1 1 +∞ f’(x) + 0 + 0 - f(x) 2 2 3
f (x)  3 x
  R f (x)  3  0x R A
g '(x)  0  f '(x)  0 x -∞ -1 1 +∞ f’(x) + 0 + 0 - g’(x) - 0 - 0 + g(x) 32  9 -8 23 y f  2 x  2x
y   x   f  2 2 2 . x  2xf  2
x  2x đồng biến khi  x   f  2 2 2 .
x  2x  0 2x  2  0  x 1 A    f    2 x  2x 2 2  0  1
  x  2x  0; x  2x 1 2x  2  0  x 11    f    2 x  2x 2 2  0
x  2x  1
 ;0  x  2x  1
Các khoảng đồng biến là 1 2;0,1;2,1 2;. 24
g x  f  2 x x 4 3 2 2
x  2x x  2x A
Xét hàm số hx  2 f  2 x x 4 3 2     có 25 x 2x x 2x 4 PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG
h ' x  22x   1 f ' 2 x x 3 2
 4x  6x  2x  2  22x   1  f ' 2
x x   2 x x   1  1 x   2 2x 1  0     h ' x 2 1  0  
 x x    x     f '   2 2; 1; ;0;1 2 x x 2  x x 1  2  2  x x  0  2
x x  2 x 1    2 1 0 1   2 h’(x) - 0 + 0 - 0 + 0 - 0 + h(x) 0 0
y hx  f  2 x x 4 3 2 2
x  2x x  2x có 5 điểm cực trị và đồ thị của nó
cắt Ox tại 2 điểm nên hàm số g x  h(x) có tất cả 7 điểm cực trị. 26 A
B là trung điểm của AC nên ta có 2
log a  log c  2log b  . a c b . 2 2 2
Hàm số nghịch biến trên R khi và chỉ khi 2 2 m 1 m 1 0 0   1  
 1 m  4  m 2; 3  ;2;  3 2 27 A 15 m 115 2 x 1
2   3x x 2 x 1
 log 2   log 3x x 3 3  x   2
1 log 2  x x 3
xx   1   x   1 log 2 3     x   x 1 1 x  log 2  0  . 3  x  log 2  3 28 A 1 x 2 x 1 l 3 og 2
M  3  3  3  3  3 2  5.
Điều kiện: x 0, y 0.  1 2 2 4  2 log x  log x y  log y 2 2   2  4   log x  2
1  2log y  2 1  0 2 2 log x 1 2   2log y  1  2 x  2   y  2 2 2 29 A
x y  6 . 5 PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG x  2   x   x y 3 2 ln 1 3
 7y  3xy  ln 2   1  y   x     
  x y3 3 ln 1  8y  ln 2  y  
x y x y3   y  y3 ln ln 2 2 2 Xét hàm đặc trưng 3
f t   ln t t t  0
Ta có f t 1 2
  3t  0, t  0. t  
1  x y  2 y y  . x 1 1 1 1 3 2 2 2 T x   x   x    x  3y 4x 8x 8x 4 3 Suy ra MinT  khi 2 1 1 x
x y  . 30 A 4 8x 2 Đặt 2x t  , t  0 .
Bất phương trình đã cho trở thành: 2
t   x  5t  4 x  
1  0  t  4t x   1  0 t   4  0 t   4 2x  4 TH1:      t   x 1  0 t   x 1  0 2x x 1  t   4  0 t   4 2x  4 TH2:      t   x 1 0 t   x 1  0
2x x 1
Dựa vào đồ thị ta thấy tập ngiệm là S  0  ;1 2; . 31 A
Suy ra a  0,b  1,c  2. 2 I f
 xdx f 2 f  2    3. 32 A 2  Đặt 1 ( )      x x f x dx a f x e  . a 0 Theo đề ta có 1 x x x
e a e x e adx 33 A    0 6 PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG 1 1 x
a xe dx a xdx   0 0 a
a 1  a  2 2     x f x
e  2  f 0  3.
Ta có lim f x  lim f x  f 2  5 nên hàm số liên tục tại x  2 . x 2 x 2  
Vậy hàm số f x liên tục trên  . Đặt dx
t  ln x 1  dt  . x Đổi cận: 3
x 1 t  1; x e t  4. 3 e
f ln x   4 2 4 1 Khi đó I dx f
 ttd f
 ttd f
 ttd . x 1 1 1 2 2 4
 2t  1dt   74 2 t   1 dt  . 34 A 3 1 2 f x   f  x   . x
x f x. x  x .f x  x   f x. x  x 2 x   2
Lấy nguyên hàm hai vế   x f x . x   C 2 2 1 x 1 17 Mà f  
1 1 suy ra C   f x   f 4  . 35 A 2 2 x 4 Ta có 3
f (0)  f (0)  0  f (0)  0 3
f (2)  f (2)  2  f (2) 1 2 2 2 I
f (x)dx xf (x)  . x f (  x)dx   0 0 0 2 4 2 2   3 f (x) f (x)  1 1  5
 2   f (x)  f (x) .
f (x)dx  2         2    .   0 36 A 4 2    4 2  4 0
Đồ thị hàm số y g x đi qua ba điểm A 1   ;1 , B 1; 
1 ,C 2;4 nên ta có
y g x 2  x .
Đồ thị hàm số y f x và y g x cắt nhau tại ba điểm như hình vẽ nên ta có
f x  g x  a  2 x  
1  x  2 với a  0 . Khi đó: S S  9 1 2 1
a  x   2 2
1  x  2 dx a  2x  
1  x  2 dx  9 1 1 8a 5a 9    a 9   9  a  4 . 37 A 3 12 4 7 PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG
Suy ra f x   2
x  x    g x   2
x  x   2 4 1 2 4 1 2  x . 2 2 Vậy f
 xdx  4    16 2 x   1  x  2 2  x dx  .  3 0 0 38 A Số đỉnh là 6 A
Diện tích mỗi mặt bằng 2 9a
Suy ra cạnh bằng 3a . 39 Thể tích 3 27a . A 3 1 1 4a 2 V  . . SO S  . .4 a a  40 3 hv 3 3 2
l  2.50  100  l  10 Đường cao thiết diện 5 6 5 2 0
h  5 2.sin 60  2 75 5 10 2 2
r l h  100   41 A 2 2 Ta có 4 h 2 2 3 2
r h   r   r .2r   . 42 A 3 r 3 A Gọi V
r r  0 là bán kính đáy của lon nước ép. Khi đó 2
V   r h h  . 2  r
Diện tích toàn phần: S rV 2V 2 2 2
 2 rh  2 r  2 r  2 r   2 r . 2  r r Ta có V V 2 3 2
  2 r  3 2V . r r
Đẳng thức xảy ra khi V 270 2 3
 2 r r   3,5. 43 r 2 A 44
MA MB suy ra M 3;0;0 . A 45
B là trung điểm AC nên C  5  ;9;14. A 4 3
V   R  972 . 46 kc 3 Tâm I 1; 1  ;3, R  76 . 47 A    A IA  2 ; a 1 ; b  3 , IB   1   ; a 1 ;
b 4 , IC  1 ; a 2  ; b   1 .     2 2
IAIB a b a  2b 11, 2 2
IBIC a b 3b 3.  1 2 2 a   1   4  5  2 2 6
T  3a a  3b 8b  5 3 a  3 b          6   3  12 4 b   3 3
Vậy S a b  48 2 8 PHƯƠNG CÂU ÁN
TÓM TẮT LỜI GIẢI HỎI ĐÚNG A
Do MI  10 nên M nằm trên mặt cầu S  tâm I bán kính R  10.
Mặt khác M thuộc Oxy suy ra M sẽ di động trên đường tròn C là giao
tuyến của S  và Oxy .
C có bán kính r  10 IH  109 1. (với H là hình chiếu của I lên Oxy)
AM nhỏ nhất khi OM nhỏ nhất. OM
OH r  4 . min 1 Suy ra S  .6.4  12. 49 OAM 2 A 1 Bán kính mặt cầu 2 2 2 R
a b c . 2
(S) có diện tích nhỏ nhất khi R nhỏ nhất, tức là 2 2 2
a b c nhỏ nhất. Ta có
a b c      2 2 2 28 2 3
1 4 9 a b c   2 .
R 14 suy ra R  14.  b ca  2 a   
Đẳng thức xảy ra khi  2 3  b   4 .
a  2b 3c  28 c  6  50
Suy ra thể tích tứ diện OABC là 8 . --- HẾT--- 9
Document Outline

  • HSG_L12_20222023_ DT DE_toan CT_
  • HSG_L12_20222023 DT _HDC_toan CT_