Đề học sinh giỏi Toán 12 cấp tỉnh năm 2023 – 2024 sở GD&ĐT Bà Rịa – Vũng Tàu

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
TỈNH BÀ RỊA – VŨNG TÀU
NĂM HỌC 2023 – 2024
ĐỀ THI CHÍNH THỨC MÔN : TOÁN
Thời gian làm bài : 180 phút Ngày thi : 19/12/2023
(Đề thi gồm có 01 trang) Bài 1 (3,0 điểm). 1. Giải phương trình 2
sin x + sin x + 3sin 2x = (sin x + cos x)2 − cos x(cos x + 3).
2. Gọi S là tập hợp tất cả ước nguyên dương của số a = 648000. Chọn ngẫu nhiên hai phần tử
khác nhau của S. Tính xác suất để hai số được chọn đều không chia hết cho 3.
Bài 2 (3,5 điểm). Giải các phương trình sau: 2 1. 3 2 x + x − 3 3
3x −10x +11x − 3 = 3 . 3 2. 2
4log x + xlog (x + 2) = 2log .x x + log (x + 2) . 2 2 2 [ 2 ] Bài 3 (5,5 điểm).
1. Tìm tất cả giá trị thực của tham số m để hàm số cot x − 3  π π y =
nghịch biến trên khoảng ;   . cot x + m  4 2  2. Cho hàm số 2x +1 y =
có đồ thị (C) và đường thẳng (d ) : y = 3 − x + .
m Tìm tất cả giá trị thực x −1
của tham số m để (d ) cắt (C) tại hai điểm ,
A B và (d ) lần lượt cắt trục hoành, trục tung tại
hai điểm C, D mà diện tích tam giác OCD gấp đôi diện tích tam giác OAB (trong đó O là gốc tọa độ).
3. Với hai số thực a,b thay đổi trên đoạn [1; ]
3 , tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu 2 2 thức a b = + + 96. ab P . 2 2 2 2 b a
a + ab + b
Bài 4 (5,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và AB = 2a, AD = . a
Hình chiếu vuông góc của S trên mặt phẳng ( ABCD) là trung điểm H của .
OA Gọi M , N lần lượt
là trung điểm của SB, .
AD Biết rằng góc giữa hai mặt phẳng (SBC) và ( ABCD) là 0 45 .
1. Tính thể tích khối chóp S.ABC . D
2. Cho điểm Q trên đoạn thẳng SA mà QS = 2 .
QA Tính thể tích khối đa diện ABCNQM.
3. Tính khoảng cách giữa hai đường thẳng SN,CM. Bài 5 (3,0 điểm).
1. Tìm tất cả bộ hai số thực (x, y) thỏa mãn đẳng thức log2 x y x (x ) y 1 4 5 2 + + + − + 57 =18 . x
2. Cho ba số thực x, y, z không âm sao cho không có hai số nào cùng bằng 0. Chứng minh rằng (  
x + y + z)2 1 1 36 63 + + ≥   . 2 2 2
 2 x y + y z + z x  x + y + z +1 4
------------HẾT------------
Lưu ý : Thí sinh được sử dụng máy tính cầm tay.
Họ và tên thí sinh : ………………………………………………… ; Số báo danh : ………………..
Chữ ký của CBCTh số 01 : …………………………
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
TỈNH BÀ RỊA – VŨNG TÀU
NĂM HỌC 2023 – 2024
HƯỚNG DẪN CHẤM ĐỀ THI CHÍNH THỨC MÔN : TOÁN
(Hướng dẫn chấm gồm có 07 trang) Bài 1 (3,0 điểm). 1. Giải phương trình 2
sin x + sin x + 3sin 2x = (sin x + cos x)2 − cos x(cos x + 3).
2. Gọi S là tập hợp tất cả ước nguyên dương của số a = 648000. Chọn ngẫu nhiên hai phần tử khác
nhau của S. Tính xác suất để hai số được chọn đều không chia hết cho 3. Câu Nội dung Điểm 2
sin x + sin x + 3sin 2x = (sin x + cos x)2 − cos x(cos x + 3) 2 2
⇔ sin x + sin x + 6sin xcos x =1+ 2sin xcos x − cos x − 3 cos x 0,25
⇔ 3 cos x + sin x = 4 − sin xcos x 0,25 3 1 0,25 ⇔
cos x + sin x = −sin 2x 2 2  π  0,25
1. (1,5đ) ⇔ sin x + = sin( 2 −   x)  3   π x + = 2 − x + k2π  3 0,25 ⇔  π
x + = π + 2x + k2π  3  π k2π x = − +  9 3 0,25 ⇔  , k ∈ .   2π x = − − k2π  3 Ta có 3 6 4 a = 648000 = 5 .2 .3 0,25
Mỗi ước nguyên dương của a đều có dạng 5i.2j.3k 0,25
i ∈ 0,1,2,3 ; j ∈ 0,1,2,3,4,5,6 ; k ∈ 0,1,2,3,4 với { } { } { }.
Số ước nguyên dương của a bằng số bộ (i, j,k) với i, j,k thuộc các tập trên. 0,25
Do đó số phần tử của S là: 4.5.7 =140 số.
2. (1,5đ) Khi đó: n(Ω) 2 = C . 0,25 140
Gọi A là biến cố “lấy được hai số từ S mà chúng đều không chia hết cho 3”. 0,25
Ước của a mà không chia hết cho 3 có dạng i j 0
5 .2 .3 . Số ước của a không chia
hết cho 3 là: 4.7 = 28 số. Khi đó: n( A) 2 = C . 0,25 28 2 n A Vậy P( A) ( ) C 27 28 = = = n(Ω) . 2 C 695 140 1
Bài 2 (3,5 điểm). Giải các phương trình sau: 2 1. 3 2 x + x − 3 3
3x −10x +11x − 3 = 3 . 3 2. 2
4log x + xlog (x + 2) = 2log .x x + log (x + 2) . 2 2 2 [ 2 ] Câu Nội dung Điểm 2 x + x − 3 3 2 3
3x −10x +11x − 3 = 3 . 3 2 3 2 2 x + x − 3 0,25 3
⇔ 3(x − 3x + 3x −1) + 3(x −1) = x + x − 3 + 3 3 2 2 3 x + x − 3 x + x − 3 3
⇔ (x −1) + (x −1) = + (*) 0,25 1. (1,5đ) 3 3 Xét hàm số 3 2
f (t) = t + t, f '(t) = 3t +1 > 0 t
∀ ∈  ⇒ f (t) đồng biến trên .  0,25  2  2 Khi đó x + x − 3 x + x − 3 3 3
(*) ⇔ f (x −1) = f   ⇔ x −1 =  3  3 0,25   2
⇔ (x − )3 x + x − 3 3 2 1 =
⇔ 3x −10x + 8x = 0 3 0,25  x = 0 0,25  ⇔ x( 2
3x −10x + 8) = 0 ⇔ x =  2 .  4 x =  3
Điều kiện: x > 0. 0,25 2
4log x + xlog (x + 2) = 2log .x x + log (x + 2) . 2 2 2 [ 2 ] 2
⇔ 4log x + xlog (x + 2) − 2xlog x − 2log (x + 2)log x = 0 2 2 2 2 2
⇔ 2log x 2log x − x + log (x + 2) x − 2log x = 0 0,25 2 ( 2 ) 2 ( 2 )
⇔ (2log x − x 2log x − log (x + 2) = 0 2 )[ 2 2 ]
2log x − log (x + 2) = 0 (1) 0,25 2 2 ⇔
2log x − x =  0 (2) 2 2. (2,0đ) x = 1 − 0,25 Giải (1): 2
(1) ⇔ x = x + 2 ⇔ 
. Kiểm tra điều kiện chọn x = 2. x = 2 Giải (2): 2 x ln x ln 2 (2) ⇔ x = 2 ⇔ = 0,25 x 2 Xét hàm ln ( ) x f x − = trên (0;+∞), có 1 ln '( ) x f x =
; f '(x) = 0 ⇔ x = e 0,25 x 2 x 2 Bảng biến thiên x 0 e +∞ f '(x) + 0 - 1 ≈ 0.368 e f (x) 0 −∞ 0,5 Ta thấy ln 2 f (2) = f (4) =
. Do đó phương trình (2) có 2 nghiệm x = 2; x = 4. 2
Vậy tập nghiệm phương trình đã cho là S = {2; } 4 . Bài 3 (5,5 điểm).
1. Tìm tất cả giá trị thực của tham số m để hàm số cot x − 3  π π y =
nghịch biến trên khoảng ;   . cot x + m  4 2  2. Cho hàm số 2x +1 y =
có đồ thị (C) và đường thẳng (d ) : y = 3 − x + .
m Tìm tất cả giá trị thực của x −1
tham số m để (d ) cắt (C) tại hai điểm ,
A B và (d ) lần lượt cắt trục hoành, trục tung tại hai điểm
C, D mà diện tích tam giác OCD gấp đôi diện tích tam giác OAB (trong đó O là gốc tọa độ).
3. Với hai số thực a,b thay đổi trên đoạn [1; ]
3 , tìm giá trị nhỏ nhất và giá trị lớn nhất của biểu thức 2 2 a b = + + 96. ab P . 2 2 2 2 b a
a + ab + b Câu Nội dung Điểm m + 3  1  0,5 Ta có y ' = . −  . (cot x + m)2 2  sin x   π π  0,25
Hàm số nghịch biến trên khoảng  ; 4 2    m + 3  1   π π  1. (2,0đ) ⇔ . − < 0 x ∀ ∈    ; (cot  x + m)2 2  sin x   4 2  m + 3  π π 0,25 0 x ;  ⇔ > ∀ ∈  * 2 ( ) (cot x + m)  4 2  0,25
Đặt t = cot x ⇒ t ∈(0; ) 1 khi  π π x ;  ∈ .  4 2  m > 3 − 0,25 ( ) m + 3 > 0 *  ⇔  ⇔ − ≤ −m ∉  ( ) m 0 0;1  −m ≥ 1 3 m > 3 − 0,5   3 − < m ≤ 1 − ⇔ m ≥ 0 ⇔  .  m ≥ 0 m ≤ 1 −
Phương trình hoành độ giao điểm của (d) và (C) là: 2x +1 0,25 2 3 − x + m =
⇔ 3x − (m + )
1 x + m +1 = 0 (*) , (x ≠ ) 1 − x 1
(d) cắt (C) tại hai điểm phân biệt ⇔(*) có 2 nghiệm phân biệt x , x khác 1 0,25 1 2 ∆ >  0 ⇔ 3   −  (m + ) 1 + m +1 ≠ 0 0,25 ⇔ (  < −
m + )2 − (m + ) > ⇔ (m + )(m − ) m 1 1 12 1 0 1 11 > 0 ⇔  m > 11 2. (2,0đ)  m +1 x + x =  1 2
Khi đó: A(x ; 3
− x + m , B x ; 3
− x + m và  3 1 1 ) ( 2 2 )  m +1 0,25 x x = 1 2  3 0,25
(d) cắt Ox , Oy lần lượt tại hai điểm phân biệt ,  m C D C ;0 ⇒  , D(0;m)  3 
Tam giác OCD và tam giác OAB có cùng đường cao hạ từ O 0,25 nên 2 2 S = ⇔ = ⇔ = ∆ S∆ CD AB CD AB OCD 2 OAB 2 4 2 2 m 0,25 2 ⇔ + = 4( − + 9 m m x x x − x  ⇔ = 4 x − x 1 2 )2 ( 1 2)2 ( 1 2)2 9   9 2 2 2 m ⇔ = (  +   +  x + x )2 m m 1 m 1 4 − 4x x ⇔ = 4 −   4    1 2 1 2   9   9  3   3     20 + 2 133 0,25 m = 2 3
⇔ 3m − 40m − 44 = 0 ⇔  .  20 − 2 133 m =  3
Kiểm tra điều kiện ta chọn 20 + 2 133 20 − 2 133 m = ;m = . 3 3 2  a b  1 Ta có P = + − 2 +   96 .  b a  a b + +1 0,25 b a Đặt a b
t = + ta được P = f (t) 2 96 = t + − 2. b a t +1 a    0,25 Do a b∈[ ] 1 ,
1;3 ⇒ x = ∈ ;3 . Khi đó = ( ) 1
t g x = x + với 1 x  ∈ ;3 . b 3  x 3    2 g (x) 1 x −1 ' = 1− =
. Phương trình g '(x) = 0 ⇔ x =1. 2 2 x x 0,25 4   Ta có : g ( ) g ( ) 1 10 1 2; 3 g   = = = ⇒ 
miền giá trị của t là 10 2; . 3    3  3    3. (1,5đ) f (t) 48 2 ' = 2t − =
(t (t+ )31 −24 3 3 ) (t + ) 1 (t + )1
Phương trình f (t) = ⇔ t (t + )3 ' 0 . 1 = 24 0,5
Dễ thấy t < ⇒ t (t + )3 3
1 < 24 và t > ⇒ t (t + )3 3
1 > 24 nên phương trình có
nghiệm duy nhất t = 3. f ( ) f ( ) 10 82 3 2 2 32 3; 3 55; f   = + = = +  96 ⇒ 
giá trị nhỏ nhất của biểu  3  9 13 0,25
thức là 55 và giá trị lớn nhất là 2 + 32 3.
Bài 4 (5,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật tâm O và AB = 2a, AD = . a
Hình chiếu vuông góc của S trên mặt phẳng ( ABCD) là trung điểm H của .
OA Gọi M , N lần lượt là trung điểm của SB, .
AD Biết rằng góc giữa hai mặt phẳng (SBC) và ( ABCD) là 0 45 .
1. Tính thể tích khối chóp S.ABC . D
2. Cho điểm Q trên đoạn thẳng SA mà QS = 2 .
QA Tính thể tích khối đa diện ABCNQM.
3. Tính khoảng cách giữa hai đường thẳng SN,CM. Câu Nội dung Điểm
Kẻ HE ⊥ BC tại ⇒  E
SEH = ((SBC) ( ABCD)) 0 , = 45 . 0,5 5 HE CH 3 3 = = ⇒ HE = . a 0,5 AB CA 4 2
1. (2,0 đ) Tam giác SHE vuông cân nên 3 SH = HE = . a 0,5 2 2 S = AB AD = a ABCD . 2 . 0,5
Vậy thể tích khối chóp S.ABCD là 1 1 3 2 3 V = SH.S = a a = a ABCD . .2 . 3 3 2
Gọi T là giao điểm của CN, AB ⇒ A là trung điểm của TB ⇒ Q là trọng tâm
tam giác SBT ⇒ T,Q,M thẳng hàng. 0,5
2. (1,5 đ) Ta có S = S
và M là trung điểm 1 SB ⇒ V = V MCBT S ABCD. CBT ABCD . 2 V 0,5
Theo công thức tỉ lệ thể tích thì TAQN TA TN TQ 1 1 2 1 = . . = . . = . V TB TC TM TBMC 2 2 3 6 5 5 5 3 ⇒ V = V = V = a 0,5 ABCNQM MCBT S ABCD . . 6 12 12
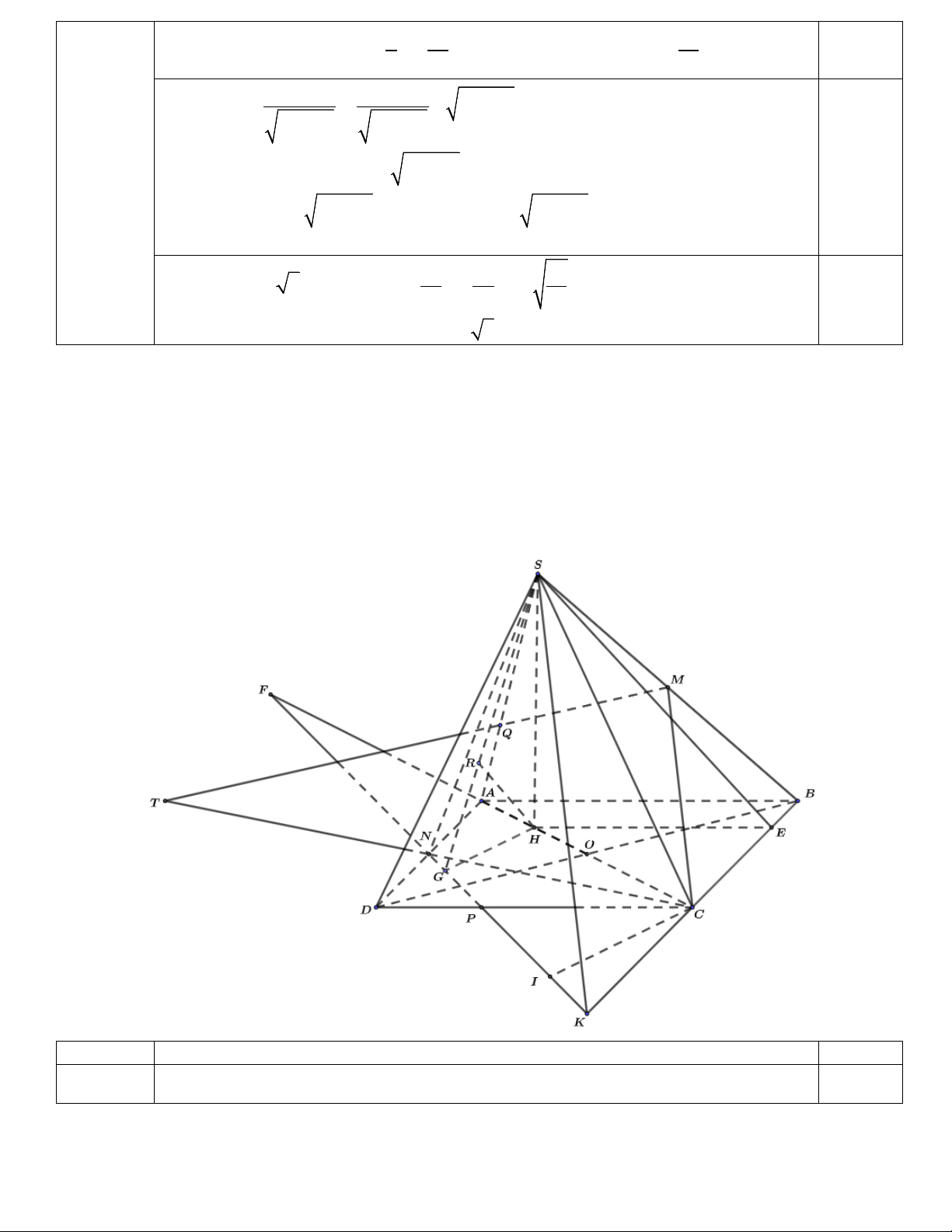
Lấy K đối xứng với B qua C ⇒ CM || SK ⇒ CM || (SNK ).
d CM ;SN = d (C; SNK ) Khi đó ( ) ( ) . 0,5 Cho ,
CA KN cắt nhau tại F ⇒ A là trung điểm FC và
d (C;(SNK )) FC 8 8 =
= ⇒ d (C; SNK ) = d (H;(SNK )).
d (H;(SNK )) ( ) FH 5 5
Kẻ HG,CI vuông góc với FK tại G, I. Kẻ HR ⊥ SG tại R ⇒ HR ⊥ (SNK ).
FK cắt CD tại 2 4
P ⇒ CP = CD = . a 3. (1,5 đ) 3 3 0,5 Ta có 1 1 1 25 4 = + = ⇒ CI = . a 2 2 2 2 CI CP CK 16a 5 Dễ thấy GH 5 1 = ⇒ GH = . a CI 8 2 Ta có 1 1 1 40 3 = + = ⇒ HR = . a 2 2 2 2 HR HS HG 9a 2 10 0,5
Vậy d (CM SN ) 8 6 10 ; = HR = . a 5 25 Bài 5 (3,0 điểm).
1. Tìm tất cả bộ hai số thực (x, y) thỏa mãn đẳng thức : log2 x y x (x ) y 1 4 5 2 + + + − + 57 =18 . x
2. Cho ba số thực x, y, z không âm sao cho không có hai số nào cùng bằng 0. Chứng minh rằng : (  
x + y + z)2 1 1 36 63 + + ≥   . 2 2 2
 2 x y + y z + z x  x + y + z +1 4 6 Câu Nội dung Điểm
Điều kiện : x > 0. 0,25 Đặt t log = log ⇒ = 2 ⇒ = 2 t x t = 2t t x x x 2 ( ) 2 2 2 t +4 2 2 Ta có : t t 2 2t 2 log2 x 2 2 +16 ≥ 2 2 .16 = 2.2
≥ 2.2 = 2x ⇒ x ≥ 2x −16. 0,5 Từ giả thiết được 2
18 ≥ 2 + 4y + 2 .2y −10.2y x x x + 41 1. (1,5 đ) ⇒ ≥ ( y + )2 2 18 2 + −10.2y x x x + 41 ⇒ ( y + )2 − ( y x x + ) 2 2 10
2 + 25 + x −8x +16 ≤ 0 0,5 ⇒ ( y x + − )2 + (x − )2 2 5 4 ≤ 0
x + 2y − 5 = 0 x = 4 Do đó  ⇔ 
. Vậy có duy nhất cặp số ( ; x y) = (4;0) thỏa 0,25 x − 4 = 0 y = 0
mãn yêu cầu của bài toán.
Không giảm tổng quát giả sử y nhận giá trị ở giữa x, z ⇒ ( y − x)( y − z) ≤ 0 2 2 2 2 0,5
⇒ y + xz ≤ xy + yz ⇒ y z + z z ≤ xyz + yz Do đó 2 2 2 2 2
x y + y z + z x ≤ x y + xyz + yz = y( 2 2
x + xz + z ) ≤ y(x + z)2 . 3
Ta có y (x + z)(x + z)  2y + x + z + x + z  8 2 . ≤ = (x + y +   z)3 0,25  3  27 2 2 2 4
2. (1,5 đ) ⇒ x y + y z + z x ≤
(x + y + z)3 27
Đặt t = x + y + z (t > 0) và ký hiệu P là vế trái của bài toán thì 0,25 2  1 27  36 1 2 27 36 P ≥ t + + =  t + +  3
 2 4t  t +1 2 4t t +1 3 0,25
Áp dụng bất đẳng thức Cô si thì 1 2 27 1 2 1 2 27 27t 9 3 t + = t + t + ≥ 3 = t 2 4t 4 4 4t 64 4 0,25 Do đó 9 36 9 P ≥ t + = (t + ) 36 9 9 + − ≥ (t + ) 36 9 63 1 2 1 . − = . 4 t +1 4 t +1 4 4 t +1 4 4
------------HẾT------------ 7
Document Outline

• toanchinhthuc
• hdc.toanchinhthuc