Đề học sinh giỏi Toán 12 cấp tỉnh năm 2023 – 2024 sở GD&ĐT Hà Nam

UBND TỈNH HÀ NAM
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO Năm học 2023 - 2024 Môn: Toán ĐỀ CHÍNH THỨC
Thời gian làm bài: 180 phút
(Đề thi gồm 01 trang)
Câu I (5,0 điểm). 1. Cho hàm số x − 3 y =
có đồ thị (C) . Tìm trên (C) các điểm M sao cho tiếp tuyến tại M x +1
của (C) tạo với hai đường tiệm cận của (C) một tam giác có bán kính đường tròn nội tiếp lớn nhất.
2. Cho hàm số y = f (x) có đạo hàm ( ) = ( − )2024 ( 2x x f x x − + )( 2 ' 3 5
5 1 x − 2x) . Tìm tất cả các
giá trị thực của tham số m để hàm số g (x) = f ( 2
x − 8x + m) có đúng ba điểm cực trị x , x , x thỏa 1 2 3 mãn 2 2 2
x + x + x = 50. 1 2 3
Câu II (4,0 điểm).
1. Có tất cả bao nhiêu cặp số nguyên ( ;
x y) thoả mãn log (x + 2y) 2 2
+ x + 2y + 3xy − x − y = 0 2
và x + y > 0; x ∈[ 2024 − ;2024]?  2 2y + 1+ 4y 1 log = 2log ⋅log 2y 1 3 9 ( )
2. Giải hệ phương trình sau trên tập số thực:  2 x + x 1+  x 9 3  2x(1−y) 2024 +1 = 2x  ( 2
1+ 2y − 2y +1). π
4 1+ xcos x(4 + 2sin 2x + xcos2x)
Câu III (2,0 điểm). Tính tích phân I = d .x ∫ + 0 cos x 2 sin 2x
Câu IV (5,0 điểm).
1. Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình thang vuông tại A và B, AD =15, 5
BC = AB = . Góc giữa mặt phẳng (SBC) và mặt phẳng ( ABCD) bằng 0 60 . Gọi M là  
trung điểm của cạnh SD và I là điểm thỏa mãn ID = 2AI . Gọi E, F lần lượt là hình chiếu vuông
góc của điểm A trên các cạnh SB, SC . Gọi H là giao điểm của hai đường thẳng SI và AM .
a) Tính thể tích khối tứ diện CDMI và khoảng cách giữa hai đường thẳng AM và SC .
b) Tính thể tích khối nón có đáy là hình tròn ngoại tiếp E
∆ FH và đỉnh thuộc mặt phẳng ( ABCD).
2. Cho hình lăng trụ đứng ABC.A'B'C ' , ABC ∆
vuông tại A, AB = 2AC . Gọi E là điểm thỏa   mãn EC ' = 2
− EC . Khoảng cách từ điểm C ' đến mặt phẳng ( A'BE) bằng 12. Gọi α là góc giữa mặt
phẳng ( A'BE) và mặt phẳng ( ABC) . Tìm cosα để thể tích khối lăng trụ ABC.A'B'C ' đạt giá trị nhỏ nhất.
Câu V (2,0 điểm). Trong không gian với hệ tọa độ Oxyz, cho các điểm B( 9 − ;1; 4 − ) , C ( 9; − 7;4) . Trong các ABC ∆
thỏa mãn điểm A thuộc mặt phẳng (Oxy), các đường trung tuyến kẻ từ đỉnh B và
C vuông góc với nhau sao cho góc A lớn nhất. Viết phương trình mặt cầu đường kính OA với O là gốc tọa độ.
Câu VI (2,0 điểm). Cho các số thực dương x, y, z thỏa mãn 2 2 2
x + y + z +1≤ 2x + 3 . y 3 2 3 2 3 2
Tìm giá trị nhỏ nhất của biểu thức
x + x + 36 y + y + 36 2z + z + 9 P = ( + + x + ) ( y + ) . 2 1 4 1 2z +1 -----HẾT-----
Họ và tên thí sinh:.................................................................................Số báo danh:...............................................................................................
Người coi thi số 1:................................................................................Người coi thi số 2:................................................................................ UBND TỈNH HÀ NAM
KỲ THI CHỌN HỌC SINH GIỎI LỚP 12 CẤP TỈNH
SỞ GIÁO DỤC VÀ ĐÀO TẠO Năm học 2023 - 2024
(Hướng dẫn chấm thi có 08 trang) Môn: Toán
HƯỚNG DẪN CHẤM – CHÍNH THỨC
I. HƯỚNG DẪN CHUNG
o Hướng dẫn chấm chỉ trình bày sơ lược các bước giải, lời giải của học sinh cần lập luận chặt
chẽ, hợp logic. Nếu học sinh trình bày cách làm khác mà đúng thì vẫn được điểm theo thang điểm tương ứng.
o Đối với bài toán hình học nếu học sinh chứng minh có sử dụng đến hình vẽ thì yêu cầu phải
vẽ hình, nếu học sinh vẽ hình sai hoặc không vẽ hình thì không cho điểm phần tương ứng.
o Điểm toàn bài không làm tròn.
II. ĐÁP ÁN VÀ THANG ĐIỂM Câu
Sơ lược lời giải Điểm 1. Cho hàm số x − 3 y =
có đồ thị (C). Tìm trên (C) các điểm M sao cho tiếp x +1
tuyến tại M của (C) tạo với hai đường tiệm cận của (C) một tam giác có bán 2,5
kính đường tròn nội tiếp lớn nhất. Ta có 4 4 y =1− ⇒ y ' = , 1. x ≠ − Gọi  4 M  ;1 a  − , a ≠ 1 − . x +1 (x + )2 1  a +1 0,25
Phương trình tiếp tuyến của (C) tại M là 4 4 d : y = x − a +1− . 2 ( ) (a + ) 1 a +1
Gọi A và B lần lượt là giao điểm của tiếp tuyến d với đường tiệm cận đứng
và tiệm cận ngang; I là giao điểm của hai tiệm cận. 0,25
Tiệm cận đứng x = 1,
− tiệm cận ngang y =1⇒ I ( 1; − ) 1 .
Giao điểm của d và tiệm cận đứng là  8 A 1;1  − −  . 0,25  a +1
Giao điểm của d và tiệm cận ngang là B(2a +1; ) 1 . 0,25 Suy ra 8 IA =
, IB = 2 a +1 , AB = (a + )2 64 4 1 + . a +1 ( 0,25 a + )2 1 I
(5,0 điểm) Vì IA
∆ B vuông tại I nên 1 S = ⋅ = ∆ IA IB IAB 8. 0,25 2 Nửa chu vi của IA + + ∆ B là IA IB AB 4 p = = + a + + (a + )2 16 1 1 + 2 a +1 (a + )2 1 0,25
Bán kính đường tròn nội tiếp IA ∆ B là S IA ∆ B r =
nên r lớn nhất khi p nhỏ nhất. p
Áp dụng bất đẳng AM-GM ta có
4 + a+ + (a+ )2 16 4 16 1 1 + ≥ 2
⋅ a +1 + 2⋅ a +1 ⋅ = 4 + 2 2 2 ( )2 a +1 (a + )1 a +1 (a + )2 1 0,25 Suy ra p ≥ 4 + 2 2. a =
p đạt giá trị nhỏ nhất bằng 4 + 2 2 khi 4 = a +1 ⇔ (a + )2 1 1 = 4 ⇔ a +1  0,25 a = 3. −
Vậy có hai điểm thỏa mãn yêu cầu bài toán là M (1;− ) 1 , M ( 3 − ;3). 0,25
2. Cho hàm số y = f (x) có đạo hàm ( ) = ( − )2024 ( 2x x f x x − + )( 2 ' 3 5 5 1 x − 2x).
Tìm tất cả các giá trị thực của m để hàm số g (x) = f ( 2x −8x + m) có đúng ba 2,5
điểm cực trị x , x , x thỏa mãn 2 2 2
x + x + x = 50. 1 2 3 1 2 3 2 Câu
Sơ lược lời giải Điểm Ta có
g '(x) = (2x −8) f '( 2
x −8x + m) ( 0,25
2x 8)(x 8x m 3)2024 ( 2 2
5 x − x+ m 5x − x+m )1(x 8x m)2 2 2 16 2 8 2 2( 2 x 8x m) = − − + − − + − + − − +   Vì ( 2 )2024 2 2 2x 16x 2m x 8 8 3 0; 5 5 x m x x m − + − + − + − ≥ −
+1 > 0 nên dấu của g '(x) cùng 0,25
dấu với ( x )(x x m)2 2 ( 2 2 8 8 2 x 8x m) − − + − − +  .   Ta có x = 4 x = 4
(2x −8) (x −8x + m)2 2 − 2( 2
x −8x + m)  2    2
= 0 ⇔ x −8x + m = 0 ⇔ x −8x = −m  0,25       2  2
x −8x + m = 2 x −8x = 2 −   . m
Xét hàm số h(x) 2
= x −8x trên  , có h'(x) = 2x −8;h'(x) = 0 ⇔ x = 4. Bảng biến thiên 0,25
Hàm số g (x) có ba điểm cực trị ⇔ g '(x) = 0 có đúng 3 nghiệm bội lẻ. 0,5
Dựa vào bảng biến thiên suy ra −m ≤ 16
− < 2 − m ⇔ 16 ≤ m <18. Giả sử x = 4
x , x là hai nghiệm của 2
x −8x = 2 − m thỏa mãn 2 2 x + x = 34. 3 thì 1 2 1 2 0,25  + = Ta có x x 8 2 2
x −8x = 2 − m ⇔ x −8x + m − 2 = 0. Định lí Vi-ét, ta có 1 2  0,25 x x = m −  2. 1 2 Khi đó 2 2
x + x = 34 ⇔ x + x
− 2x x = 34 ⇔ 64 − 2(m − 2) = 34 ⇔ m =17. 0,25 1 2 ( 1 2)2 1 2
Đối chiếu điều kiện suy ra m =17 thỏa mãn bài. 0,25
1. Có tất cả bao nhiêu cặp số nguyên ( ; x y) thoả mãn 2,0 log (x + 2y) 2 2
+ x + 2y + 3xy − x − y = 0 và x + y > 0; x ∈[ 2024 − ;2024]? 2
Điều kiện: x + 2y > 0. Ta có: x+ y > 0 nên log (x+2y) 2 2
+ x + 2y + 3xy − x − y = 0 2
(x + y)(x + 2y) 0,25 2 2 ⇔ log
+ x + 2y + 3xy − x − y = 0 2 x + y ⇔ log ( 2 2
x + 2y + 3xy) − log (x + y) 2 2
+ x + 2y + 3xy − x − y = 0 2 2 II 0,25 2 2 2 2
(5,0 điểm) ⇔ log x + 2y + 3xy + x + 2y + 3xy = log x + y + x + .y 1 2 ( ) 2 ( ) ( )
Xét hàm số f (t) 1
= log t + t; t > 0 , ta có: f '(t) =
+1 > 0,t ∈(0;+∞) nên hàm 2 t ln 2 0,25
số f (t) đồng biến trên (0;+∞). Do đó ( ) ⇔ f ( 2 2
x + y + xy) = f (x + y) 2 2 1 2 3
⇔ x + 2y + 3xy = x + y 0,25
⇔ (x + y)(x + 2y − ) 1 = 0 ⇔ x =1− 2 . y 0,25
Vì x + y > 0 nên x + y =1− y > 0 ⇒ y <1 Do 2024 −
≤ x ≤ 2024 suy ra 2024 −
≤1− 2y ≤ 2024 ⇔ 1011 − ,5 ≤ y ≤1012,5 . 0,25 3 Câu
Sơ lược lời giải Điểm Suy ra 1011 − ,5 ≤ y <1.
Mặt khác y ∈ nên suy ra y∈{ 1011 − ; 1010 − ;; 1 − ; } 0 . 0,25
Với mỗi giá trị của y cho ta 1 giá trị của x thoả mãn bài.
Vậy có 1012 cặp số nguyên ( ;x y)thoả mãn yêu cầu bài toán. 0,25
2. Giải hệ phương trình sau trên tập số thực: 2  2y + 1+ 4y 1 log = 2log ⋅log 2y 1 1 3 9 ( ) ( )  2 x + x 1+  x 9 3 2,0  2x(1− y) 2024 +1 = 2x  ( 2
1+ 2y − 2y +1) (2)
Điều kiện: x > 0, y > 0. Ta có 2 ( ) 2y + 1+ 4 1 ⇔ log y = 2log 2y 3 3 ( ) 2
x + x 1+ x 0,25 2 2y + 1+ 4 + + ⇔ log y = log (4y ) 2 2 2y 1 4y 2 ⇔ = 4y 3 3 2 2
x + x 1+ x
x + x 1+ x 2 2y + 1+ 4y 2 1 1 1 2 ⇔
= x + x 1+ x ⇔ +
+1 = x + x 1+ x 3 0,25 2 2 ( ) 4y 2y 2y 4y 2
Xét hàm số f (t) 2
= t + t 1+ t , t > 0. Ta có '( ) 2 =1+ 1 t f t + t + > 0, t ∀ > 0. 2 1+ t 0,25
⇒ f (t) liên tục và đồng biến trên (0;+∞), do đó ( ) 1 1 3 ⇔ x = ⇔ y = . 2y 2x ( )   2x 1 − 1 1 2 ⇔ 2024 +1 = 2x1+ − +1 2 2x x   2x 1 − 2 ⇔ 2024
+1 = 2x + 2 − 4x + 4x 0,25
⇔ 2024 x− = 2x −1+ (2x − )2 2 1 1 +1 (4)
Đặt a = 2x −1, phương trình (4) trở thành a 2 = + + ⇔ ( a a a ) = ( 2 a + a + ) ⇔ ( 2 2024 1 ln 2024 ln 1
ln a + a +1)−aln2024 = 0 0,25
Xét hàm số g (a) = ( 2
ln a + a +1)−aln2024, a∈. Ta có g (a) 1 ' = − ln 2024 < 0,∀∈ 1  vì ≤ 1; ln 2024 >1. 0,25 2 a +1 2 a +1
Suy ra hàm số g (a) nghịch biến trên  .
Mà g (0) = 0 , do đó phương trình g (a) = 0 có nghiệm duy nhất a = 0. 0,25 Với a = 0 thì 1
2x −1 = 0 ⇔ x = ⇒ y =1 (thỏa mãn). 2
Hệ đã cho có nghiệm duy nhất là (x y)  1 ; ;1 =  . 0,25  2  π III
4 1+ x cos x 4 + 2sin 2x + x cos 2x (2,0 điểm) Tính ( ) I = d . x ∫ 2,0 + 0 cos x 2 sin 2x 4 Câu
Sơ lược lời giải Điểm π π 4 4 1
x cos x(4 + 2sin 2x) 2
+ x cos x cos 2x I = dx + dx ∫ ∫ + + 0 cos x 2 sin 2x 0 cos x 2 sin 2x π π π 4 4 4 2 1 x cos 2 = d + 2 2 + sin 2 d x I x x x x +
dx = A + B + C. ∫ ∫ ∫ + + 0,25 0 cos x 2 sin 2x 0 0 2 sin 2x π  cos 2x 4 u  = 2 + sin 2x du = dx
B = 2x 2 + sin 2xd . x ∫ Đặt  ⇒  2 + sin 2x 0 dv = 2 d x x  2 v = x 0,25 π π π 4 2 2 4 2 2 cos 2 π 3 x cos 2x 4 = ⋅ 2 + sin 2 | x x B x x − dx = − C ∫ với C = d . x ∫ 0 2 + sin 2x 16 + 0 0 2 sin 2x π π 4 4 1 d = d x A x = ∫ ∫ 2 2 + 0 cos x 2 sin 2x
0 cos x 2 tan x + 2(1+ tan x) π 0,25 4 d x = ∫ 2 0 2  1  3 2 cos x tan x + +  2    4 3 2 Đặt 1 1 1 dt
t = tan x + ⇒ dt =
dx . Suy ra A = . 2 2 cos ∫ x 2 0,25 1 2 3 t + 2 4 Đặt 3 3 2  π π t = tan u ⇒ dt =
(1+ tan t)dt , u ;  ∈ −  . 2 2  2 2  π π 0,25 3 3 1 1 1 cos = d u A u = du ∫ ∫ 2 2 π cosu 2 π cos u 6 6 π π 3 3 1 1 1  1 1 A d sin u  = = + ∫ ∫ d sin u 2 ( ) ( ) 2 −  − + 0,25 π 1 sin u
2 2 π 1 sin u 1 sin u  6 6 π 3 1 1+ sin u 2 7 + 4 3 A = ln = ln . 0,25 2 2 1− sin u π 4 3 6 2 Vậy 2 7 + 4 3 π 3
I = A + B + C = ln + . 0,25 4 3 16
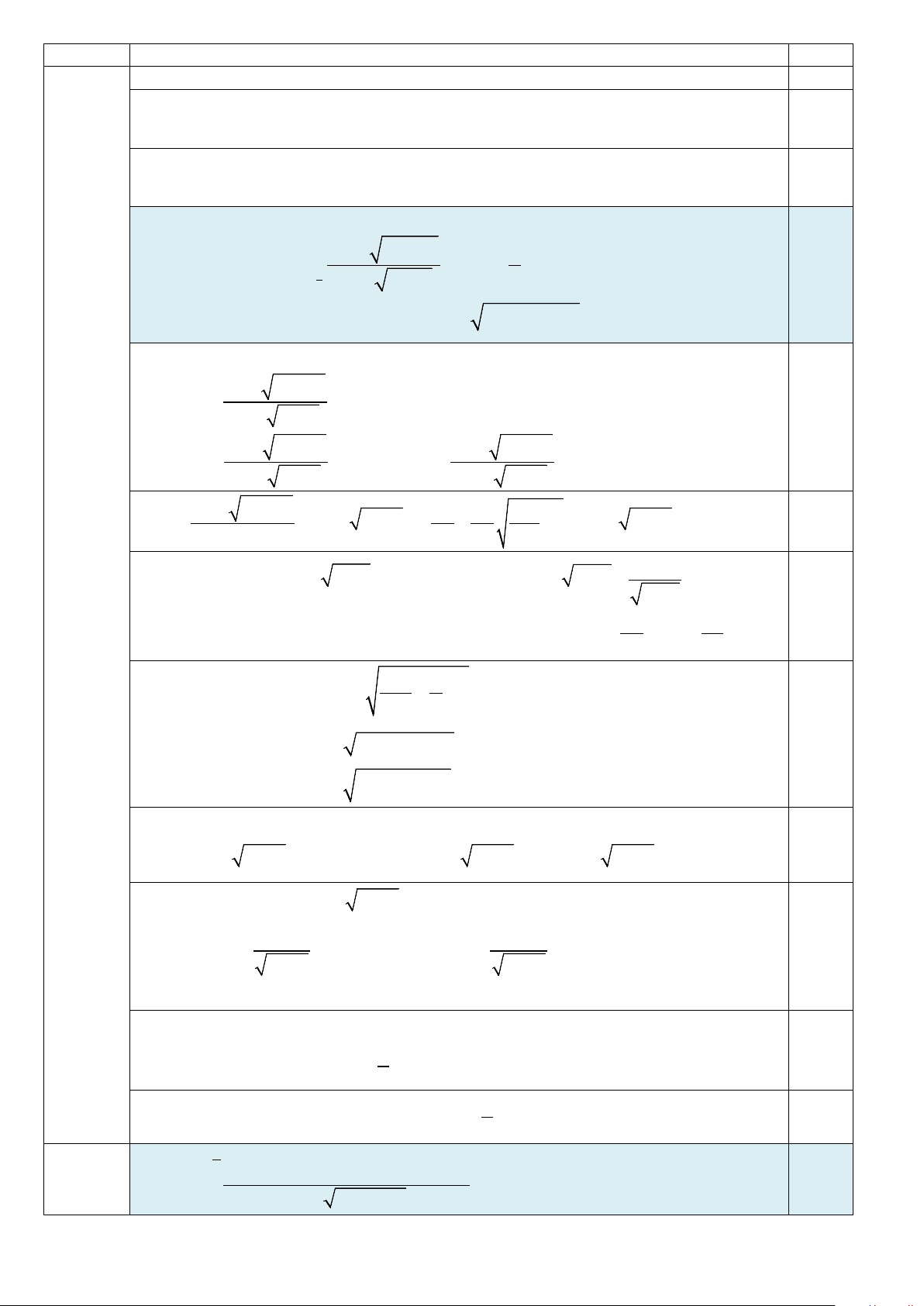
1. Cho hình chóp S.ABCD có SA ⊥ ( ABCD) , đáy ABCD là hình thang vuông
tại A và B, AD =15, 5
BC = AB = . Góc giữa mặt phẳng (SBC) và mặt
phẳng ( ABCD) bằng 0
60 . Gọi M là trung điểm của cạnh SD và I là điểm  
thỏa mãn ID = 2AI . Gọi E, F lần lượt là hình chiếu vuông góc của điểm A IV
(5,0 điểm) trên các cạnh SB, SC . Gọi H là giao điểm của hai đường thẳng SI và AM . 2,5
a) Tính thể tích khối tứ diện CDMI và khoảng cách giữa hai đường thẳng
AM và SC .
b) Tính thể tích khối nón có đáy là hình tròn ngoại tiếp E ∆ FH và đỉnh
thuộc mặt phẳng ( ABCD). 5 Câu
Sơ lược lời giải Điểm 0,25
Góc giữa hai mặt phẳng (SBC) và ( ABCD) là  ⇒  0 SBA SBA = 60 .
Xét tam giác SAB vuông tại A 0
⇒ SA = AB ⋅ tan 60 = 5 3.
Gọi M ′ là hình chiếu vuông góc của điểm M trên mặt phẳng ( ABCD) . SA//MM ′ 0,25
Trong tam giác SAD , có 1 5 3  ⇒ MM ' = SA = . MS = MD 2 2 C
∆ DI vuông tại I 1 1 ⇒ S = ⋅ = ⋅ ⋅ = ∆ CI DI CDI 5 10 25. 0,25 2 2
Vậy thể tích khối tứ diện CDMI là 1 1 5 3 125 3 V = ⋅ S ⋅ = ⋅ ⋅ = . 0,25 ∆ MM CDMI CDI ' 25 3 3 2 6
Ta có: CI ⊥ (SAD) ⇒ CI ⊥ AM ( ) 1 .
Trong tam giác vuông SAD , có: 2 2
SD = SA + AD = 75 + 225 =10 3. Suy ra AI 3 o 0,25 = = = ⇒  0 SM AM SA 5 3 SAM = 60 ;  = = ⇒  tan ASI ASI = 30 . SA 3 ⇒  0
SHA = 90 ( H là giao điểm của SI và AM ). Do đó SI ⊥ AM (2) . Từ ( )
1 và (2) suy ra AM ⊥ (SIC) ⇒ AM ⊥ HF.
Ta có AE ⊥ (SBC) ⇒ AE ⊥ SC AE ⊥ EF ( ; 3)
AM ⊥ (SIC) ⇒ AH ⊥ (SIC) ⇒ AH ⊥ SC; AH ⊥ HF (4) .
Mặt khác AF ⊥ SC (5) . 0,25
Từ (3),(4),(5) suy ra bốn điểm A, E , F , H đồng phẳng và SC ⊥ ( AEFH )
Suy ra SC ⊥ HF mà AM ⊥ HF ⇒ d( AM;SC) = HF. Tam giác 2 2 SAC vuông tại 2 2
A ⇒ SC = SA + AC = (5 3) +(5 2) = 5 5. 5 3 2 SA ( )2 2
Ta có SF ⋅SC = SA ⇔ SF = = = 3 5. SC 5 5
Tam giác SAI vuông tại A ⇒ SI = SA + AI = ( )2 2 2 2 5 3 + 5 =10. 0,25 Vì ⋅ ⋅ S
∆ HF đồng dạng SC
∆ I nên HF SF SF CI 3 5 5 3 5 = ⇔ HF = = = . CI SI SI 10 2 Vậy ( AM SC) 3 5 d ; = . 2 6 Câu
Sơ lược lời giải Điểm b) Từ (3),(4) ⇒  =  0
AEF AHF = 90 hay tứ giác AEFH nội tiếp đường tròn
đường kính AF . Do đó tâm đường tròn ngoại tiếp tam giác EFH là trung 0,25
điểm K của đoạn AF . Gọi K′ là trung điểm của đoạn AC .
Vì KK′// FC và SC ⊥ (AEFH ) nên KK′ ⊥ (EFH ) hay K′ là đỉnh hình nón. Trong S ∆ AC , có
SA⋅ AC 5 3 ⋅5 2
AF ⋅ SC = SA⋅ AC ⇔ AF = = = 30. SC 5 5 0,25 Suy ra 1 30 KF 1 = AF =
; FC = SC − SF = 5 5 −3 5 = 2 5 ⇒ KK ' = FC = 5. 2 2 2 2  
Thể tích khối nón cần tìm là 1 2 1 30 5π 5
V ' = π ⋅ KF ⋅ KK ' = π ⋅  ⋅ 5 = . 0,25 3 3  2  2  
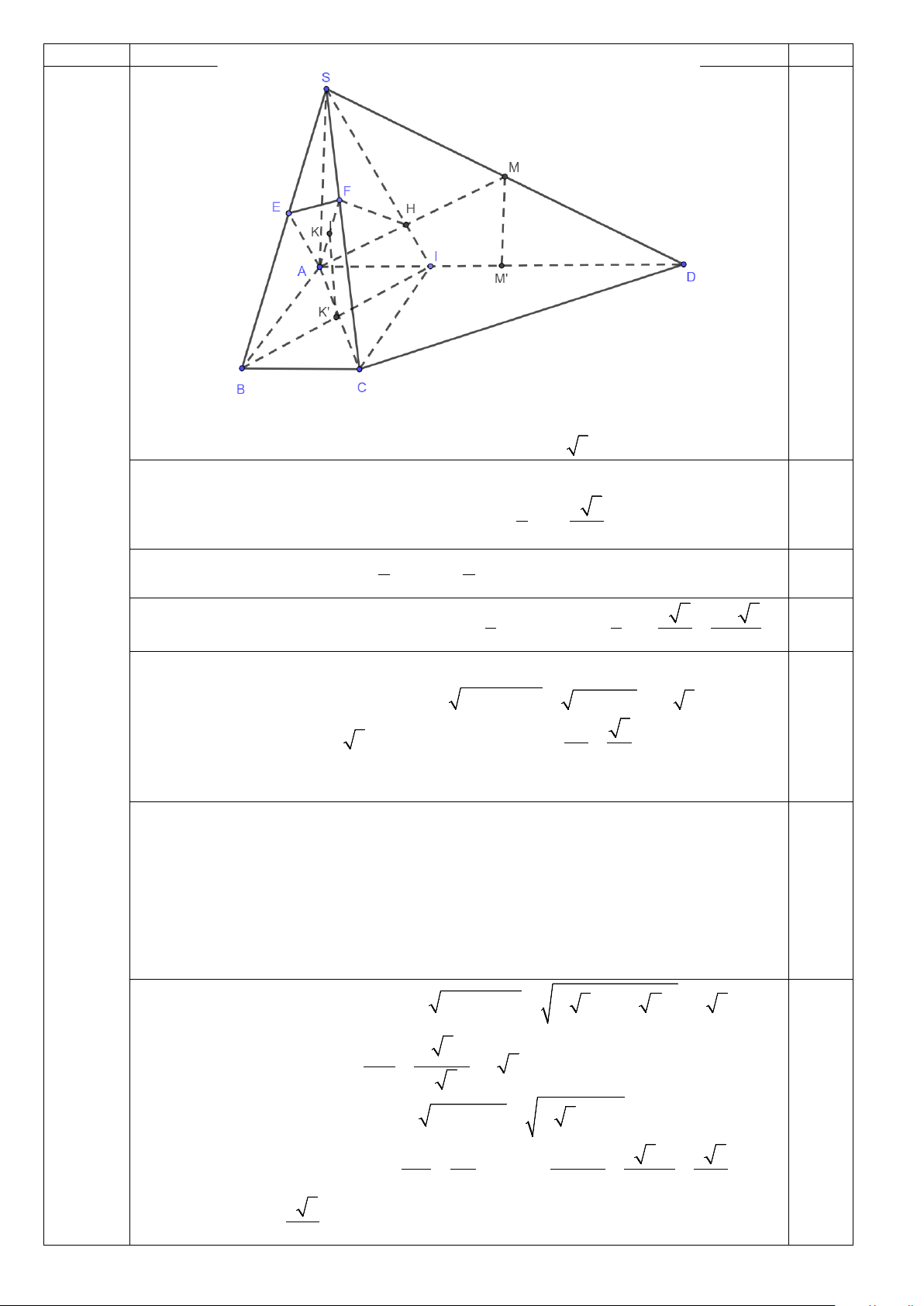
2. Cho hình lăng trụ đứng ABC.A'B'C ' , ABC ∆
vuông tại A, AB = 2AC . Gọi  
E là điểm thỏa mãn EC ' = 2
− EC . Khoảng cách từ điểm C ' đến mặt phẳng
( A'BE) bằng 12. Gọi α là góc giữa mặt phẳng ( A'BE) và mặt phẳng ( ABC). 2,5
Tìm cosα để thể tích khối lăng trụ ABC.A'B'C ' đạt giá trị nhỏ nhất.
Gọi I, F lần lượt là giao điểm của A'E với AC 'và AC.
d (C ',(A'BE)) Ta có
IC ' C 'E 2 3 = = = ⇒ = = d ( A A BE ) d ( , A (A'BE))
d (C ',(A'BE)) 18. ,( ' ) IA AA' 3 2 0,25
Kẻ AK ⊥ BF tại K và AH ⊥ A'K tại H.
Vì BF ⊥ ( A' AK ) nên góc giữa ( A'BE) và ( ABC) là  ⇒  A'KA A'KA = α. 0,25
Ta có AH ⊥ A'K và AH ⊥ BF nên AH ⊥ ( A'BF ) ⇒ d ( ;
A ( A'BE)) = AH =18. 0,25 Đặt AC EC CF x
= x > 0 ⇒ AB = 2 . x Vì 1 3 3 CE  AA' ⇒ = = ⇒ AF = AC = . AA' AF 3 2 2 2
Xét tam giác ABF vuông tại 2 2 ( )2 3x 5 2 x A BF AB AF x   ⇒ = + = + =   . 0,25  2  2 Mặt khác
AB ⋅ AF 6x
AK ⋅ BF = AB ⋅ AF ⇔ AK = = . BF 5 Xét A ∆ HK vuông tại 6x 15
H ⇒ AH = AK ⋅sinα ⇔ ⋅sinα =18 ⇔ x = . 5 sinα 0,25 Xét A
∆ A' K vuông tại 6x 18
A ⇒ A' A = AK ⋅ tanα = ⋅ tanα = . 5 cosα Ta có 1 2 225 S = ⋅ = =
Thể tích khối lăng trụ ABC.A'B'C ' là ∆ AB AC x ABC . 2 2 sin α 225 18 4050 0,25 V = S ⋅ = ⋅ = ∆ A A ABC ' . 2 2 sin α cosα sin α ⋅cosα 7 Câu
Sơ lược lời giải Điểm
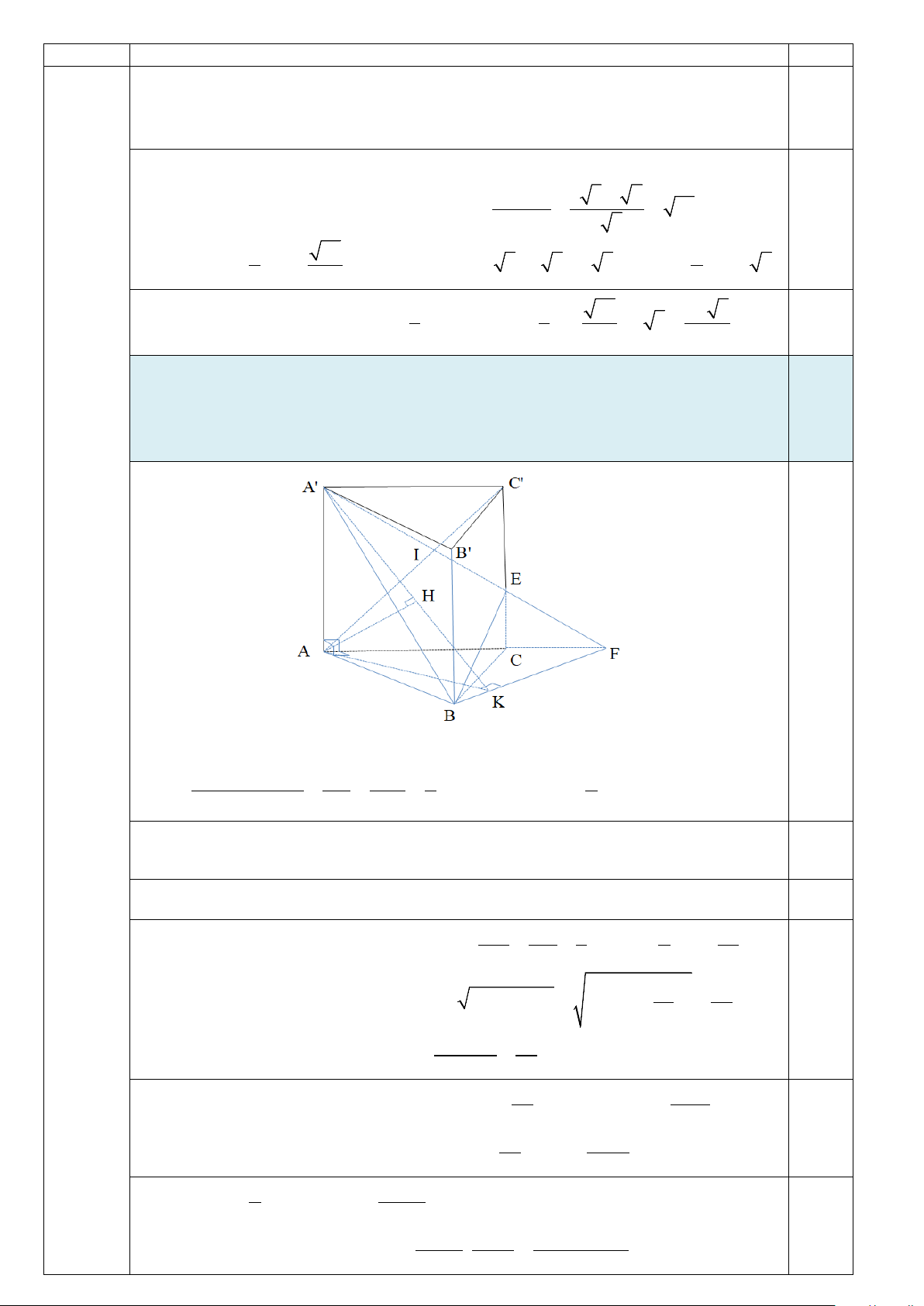
Đặt t = cosα ∈(0; )
1 . Xét hàm số f (t) = t ( 2 − t ) 3 1 = t
− + t;t ∈(0; ) 1 . 0,25 Suy ra f (t) 2
= − t + f (t) 1 ' 3 1; ' = 0 ⇔ t = vì t ∈(0; ) 1 . 3 Bảng biến thiên: 0,5 Suy ra f (t) 2 3 18225 3 ≤ ⇒ V ≥ . 9 3
Thể tích khối lăng trụ đạt giá trị nhỏ nhất là 18225 3 khi 1 3 t = ⇒ cosα = . 0,25 3 3 3
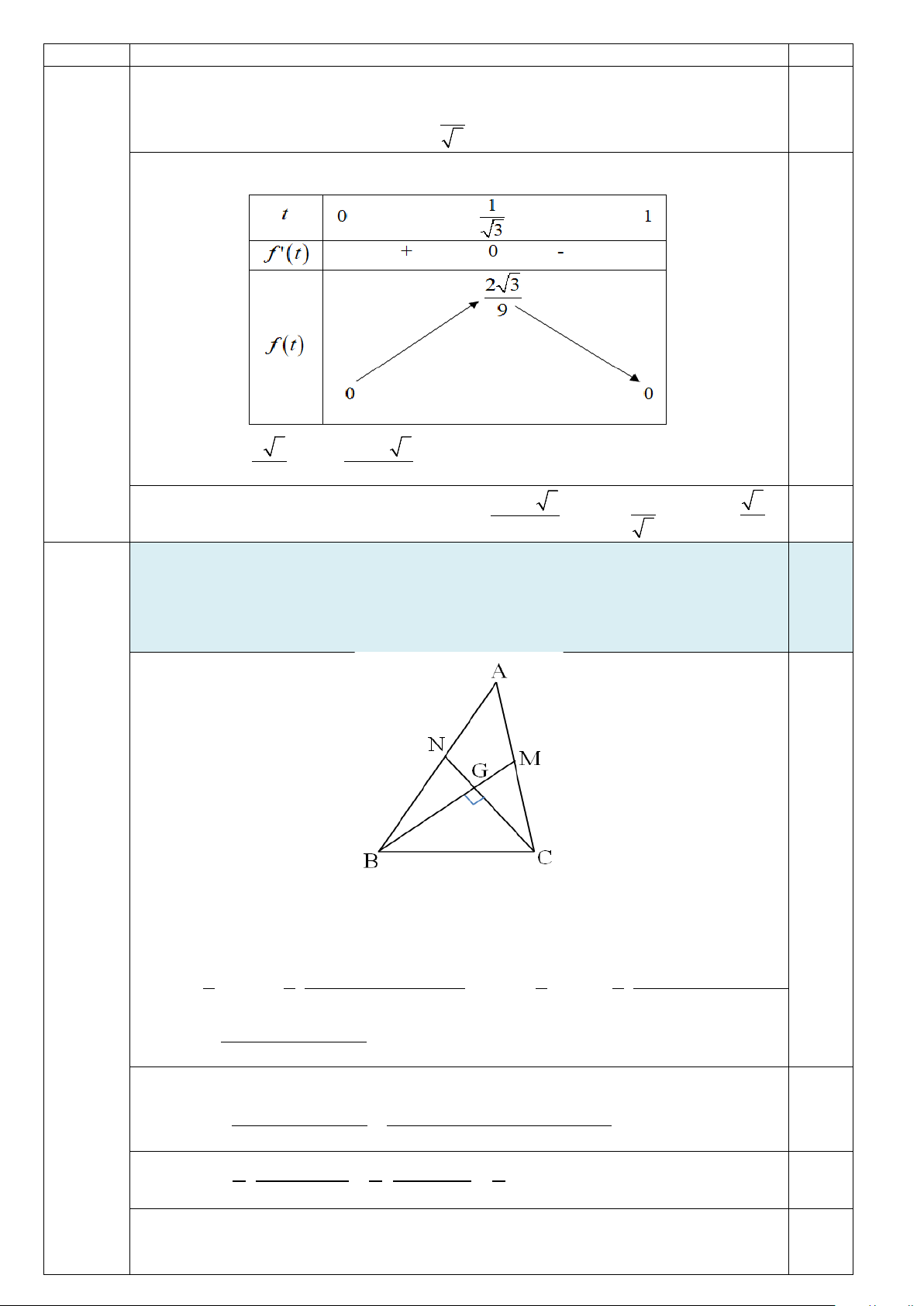
Trong không gian với hệ tọa độ Oxyz, cho các điểm B( 9 − ;1; 4 − ) , C ( 9; − 7;4) . Trong các A
∆ BC thỏa mãn điểm A thuộc mặt phẳng (Oxy), các đường trung 2,0
tuyến kẻ từ đỉnh B và C vuông góc với nhau sao cho góc A lớn nhất. Viết
phương trình mặt cầu đường kính OA với O là gốc tọa độ. 0,25 V
Gọi M , N lần lượt là trung điểm của AC , AB và G = BM ∩CN.
(2,0 điểm) Ta có BM ⊥ CN nên 2 2 2
BC = BG + GC .
Theo công thức tính đường trung tuyến, ta có 2 2 4 2( 2 2 BA + BC ) 2 2 − AC 2 4 2 CA + CB −     AB 2 2 ( 2 2 ) 2 BG = BM = ⋅ 
;CG =  CN = ⋅  3 9 4 3      9 4 2 2 2 2
AB + AC + 4BC 2 2 2 ⇒ BC =
⇒ AB + AC = 5BC . 9
Góc A lớn nhất ⇔ cos A nhỏ nhất.
AB + AC − BC ( 2 2 AB + AC ) −( 2 2 2 2 2 5 AB + AC ) 0,25 Mà cos A = = 2A . B AC 10A . B AC 2 2 2 AB + AC 2 2AB ⋅ AC 4 = ⋅ ≥ ⋅
= . Dấu " = " xảy ra ⇔ AB = AC . 0,25 5 AB ⋅ AC 5 AB ⋅ AC 5  
Vì A∈(Oxy) nên A( ; a ;0
b ) . Ta có AB = ( 9 − − a;1− ; b 4 − ) , AC = ( 9 − − ;7 a − ; b 4)  0,25 Ta có BC = ( ) 2 2 2 2
0;6;8 ⇒ BC = 0 + 6 + 8 =100 . 8 Câu
Sơ lược lời giải Điểm
Do AB = AC nên (− − a)2 + ( −b)2 + (− )2 = (− − a)2 + ( −b)2 2 9 1 4 9 7 + 4 ⇔ b = 4. 0,25 Do 2 2 2
AB + AC = 5BC và AB = AC nên 2 2 2AB = 5BC
⇔ (− − a)2 + ( − b)2 + (− )2 2 9 1 4  = 500   0,25 ⇔ (  = − − a)2 + + = ⇔ (a + )2 a 6 9 9 16 250 9 = 225 ⇔  a = 24. −
* Với a = 6 ⇒ A(6;4;0), I là trung điểm OA ⇒ I (3;2;0) ⇒ OI = 13. 0,25
Mặt cầu đường kính OA có phương trình là (x − )2 + ( y − )2 2 3 2 + z =13. * Với a = 2 − 4 ⇒ A( 2
− 4;4;0), K là trung điểm OA ⇒ K ( 12
− ;2;0) ⇒ OK = 148. 0,25
Mặt cầu đường kính OA có phương trình là (x + )2 + ( y − )2 2 12 2 + z =148.
Cho các số thực dương x, y, z thỏa mãn 2 2 2
x + y + z +1≤ 2x + 3 .
y Tìm giá trị nhỏ 3 2 3 2 3 2 nhất của biểu thức
x + x + 36 y + y + 36 2z + z + 9 P = ( + + 2,0 x + ) ( y + ) . 2 1 4 1 2z +1 Ta có 2 2 18 9 9 x y 2  2 1 1  1 P = + + + + + z = 9 + + + ( 2 2 2 2x + y +   4z ) 0,25
x +1 y +1 2z +1 2 4
 x +1 y +1 2z +1 4 Ta có 2 2 2
x + y ≥ x + y + z + = ( 2 x + ) + ( 2 y + ) + ( 2 2 3 1 4 4 z + )
1 −8 ≥ 4x + 4y + 2z −8.
Suy ra 0 < 2x + y + 2z ≤ 8. 0,25
Áp dụng bất đẳng thức 1 1 4 + ≥
với a,b > 0 , ta có a b a + b 2 1 1 4  1 1  4 4 16 0,25 + + = + + ≥ + ≥
x 1 y 1 2z 1 2x 2  y 1 2z 1 + + + + +
+  2x + 2 y + 2z + 2 2x + y + 2z + 4 2 2 2 2 2 2 VI
Áp dụng bất đẳng thức (a +b + c )(m + n + p ) ≥ (am +bn + cp)2 .
(2,0 điểm) Ta có ( + + )( 2 2 2
2 1 1 2x + y + 4z ) ≥ (2x + y + 2z)2 . 0,25 Suy ra 2 2 2 1
2x + y + 4z ≥ (2x + y + 2z)2 . 4 Do đó 9⋅16 1 P ≥ +
(2x + y + 2z)2 .
2x + y + 2z + 4 4⋅4 0,25 Đặt t 144 1
= 2x + y + 2z, t ∈( 0;8] và 2 P ≥ + t . t + 4 16
Xét hàm số f (t) 144 1 2 = +
t ,t ∈(0;8]. Ta có f (t) 144 1 ' = − + t. t + 4 16 (t + 4)2 8 0,25
Suy ra f (t) = ⇔ t (t + )2 = ⋅ ⇔ (t − )( 2 ' 0 4 8 144
8 t +16t +144) = 0 ⇔ t = 8.
Vì f '(t) < 0, t
∀ ∈(0;8) nên min f (t) = f (8) =16. ( 0,25 0;8]
Do đó P ≥16. Dấu bằng xảy ra khi t = 8 hay x = y = 2; z =1.
Vậy giá trị nhỏ nhất của P là 16 khi x = y = 2; z =1. 0,25 -----HẾT-----
Document Outline