







Preview text:
SỞ GD&ĐT THANH HÓA
KỲ THI CHỌN ĐỘI TUYỂN HSG CẤP TỈNH
TRƯỜNG THPT TĨNH GIA 1 NĂM HỌC 2022 - 2023 -------------------- MÔN: TOÁN
Thời gian làm bài: 90 phút
(Đề thi có 50 câu, gồm 06 trang)
(không kể thời gian phát đề)
Họ và tên: ............................................................................
Số báo danh: ............ Mã đề 111
Câu 1: Tập xác định của hàm số y = sin 2x +1 là
A. D = \{kπ | k ∈ Z}. B. D = . π π π C. D \ kπ; kπ | k Z = + + ∈ .
D. D = \ + k2π | k ∈ Z . 4 2 2
Câu 2: Có bao nhiêu cách chọn ra 6 học sinh từ 40 học sinh lớp 11A để làm một ban bầu cử gồm một trưởng
ban, một phó ban và bốn ủy viên? A. 6 A . B. 2 4 A .C . C. 2 4 C .A . D. 4 2!C . 40 40 38 40 38 38
Câu 3: Cho dãy số có các số hạng đầu là:5;10;15;20;25;... Số hạng tổng quát của dãy số này là:
A. u = n − u = n u = + n u = n + n 5( 1) . B. n 5 . C. n 5 . D. n 5. 1.
Câu 4: Bảng biến thiên dưới đây là của hàm số nào? A. x − 3 y − + + = . B. x 1 y = . C. x 1 y = . D. x 3 y = . x − 2 2x + 2 x − 2 2 + x
Câu 5: Cho a >1. Mệnh đề nào sau đây là đúng? 3 2 1 A. 1 1 − 1 <
. B. a >1. C. 3
a > a . D. 3 a > . 2016 2017 a a a 5 a
Câu 6: Biết (H ) là đa diện đều loại {5; }
3 với số đỉnh và số cạnh lần lượt là a và b . Tổng a + b là:
A. a + b = 40 .
B. a + b = 50 .
C. a + b = 32 .
D. a + b = 42 .
Câu 7: Cho khối trụ có bán kính hình tròn đáy bằng r và chiều cao bằng h . Hỏi nếu tăng chiều cao lên 2 lần và
tăng bán kính đáy lên 3 lần thì thể tích của khối trụ mới sẽ tăng lên bao nhiêu lần? A. 18 lần. B. 6 lần. C. 36 lần. D. 12 lần
Câu 8: Cho tam giác ABC vuông tại A . Khi quay tam giác đó quanh cạnh góc vuông AB , đường gấp khúc
BCA tạo thành hình tròn xoay nào trong bốn hình sau đây. A. Hình nón. B. Hình trụ. C. Hình cầu. D. Mặt nón.
Câu 9: Biết F (x) x 2
= e + x là một nguyên hàm của hàm số f (x) trên . Khi đó f
∫ (2x)dx bằng A. x 2
2e + 2x + C. B. 1 2x 2 e 1 + x + C. C. 2x 2
e + 2x + C. D. 2x 2
e + 4x + C. 2 2 π π 2 2 Câu 10: Cho f
∫ (x)dx = 5. Tính I = f
∫ (x)+ 2sin xdx = 5 . 0 0 A. π I = 7
B. I = 5 +
C. I = 3 D. I = 5 +π 2
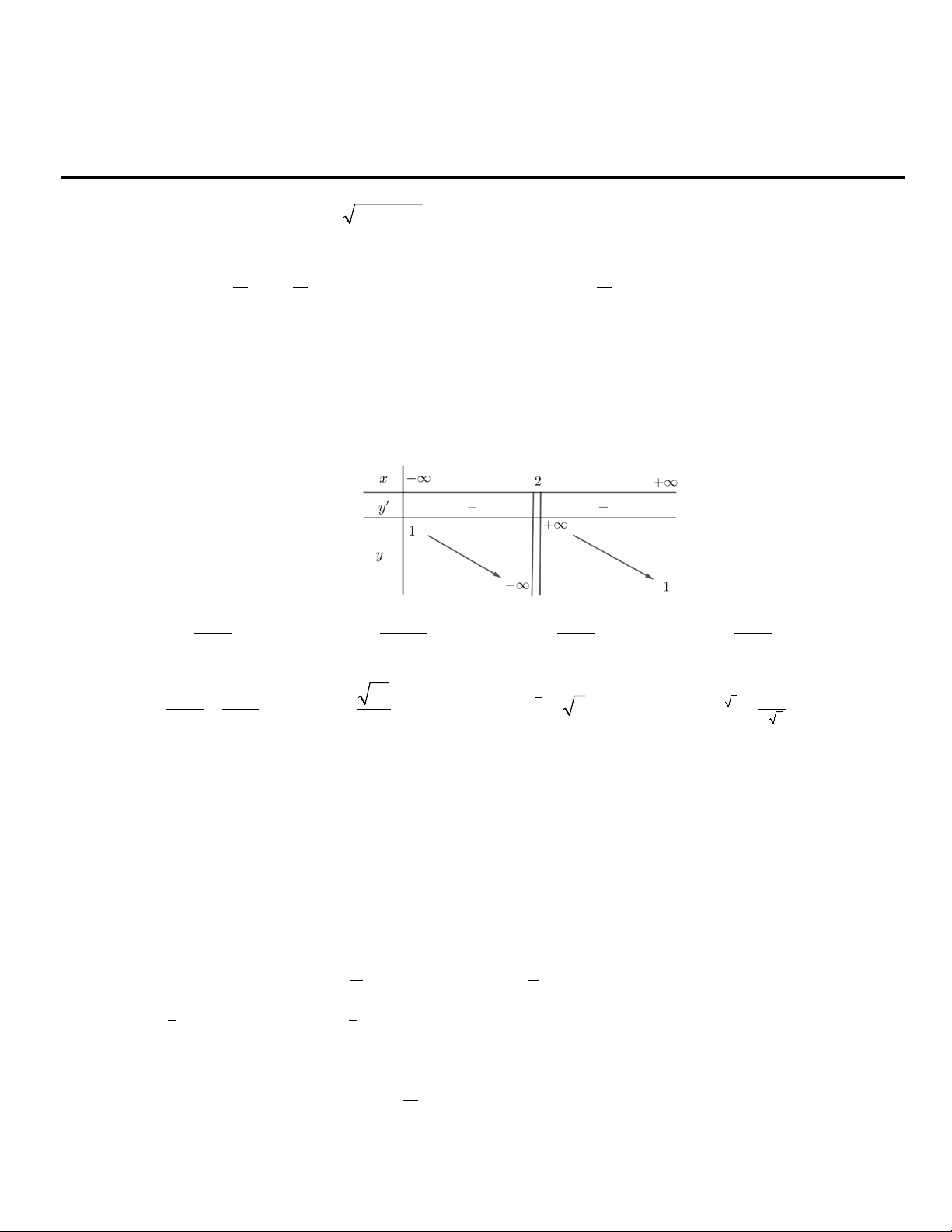
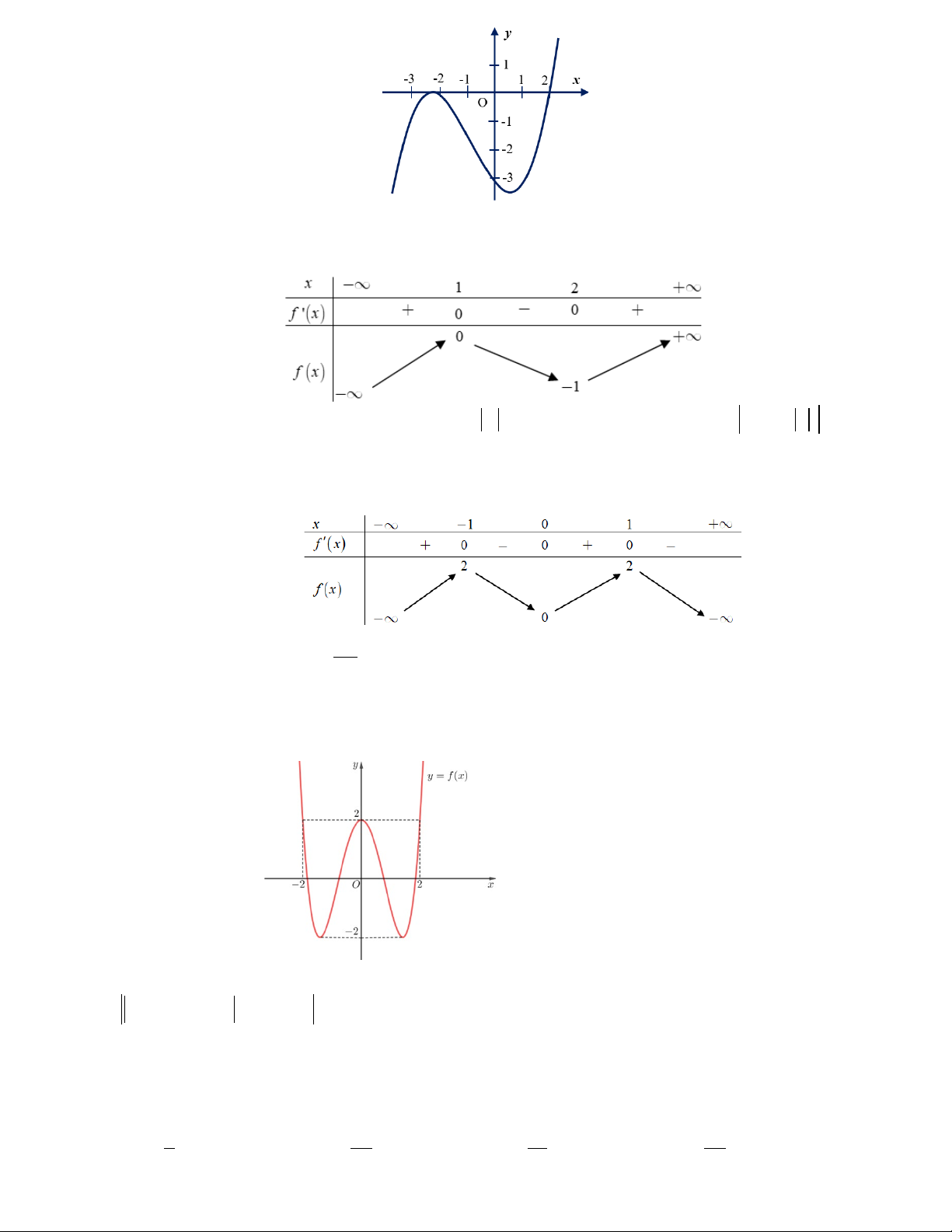
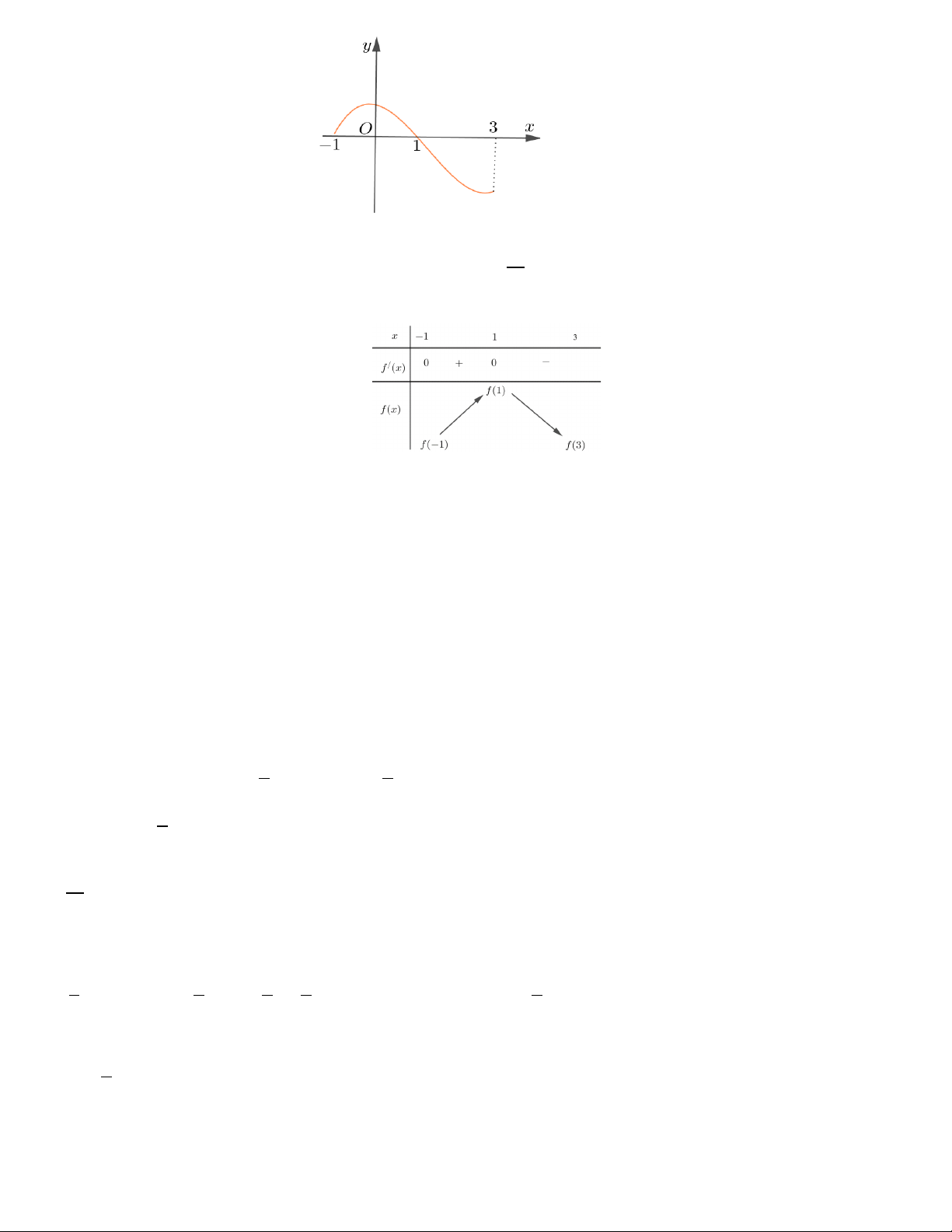
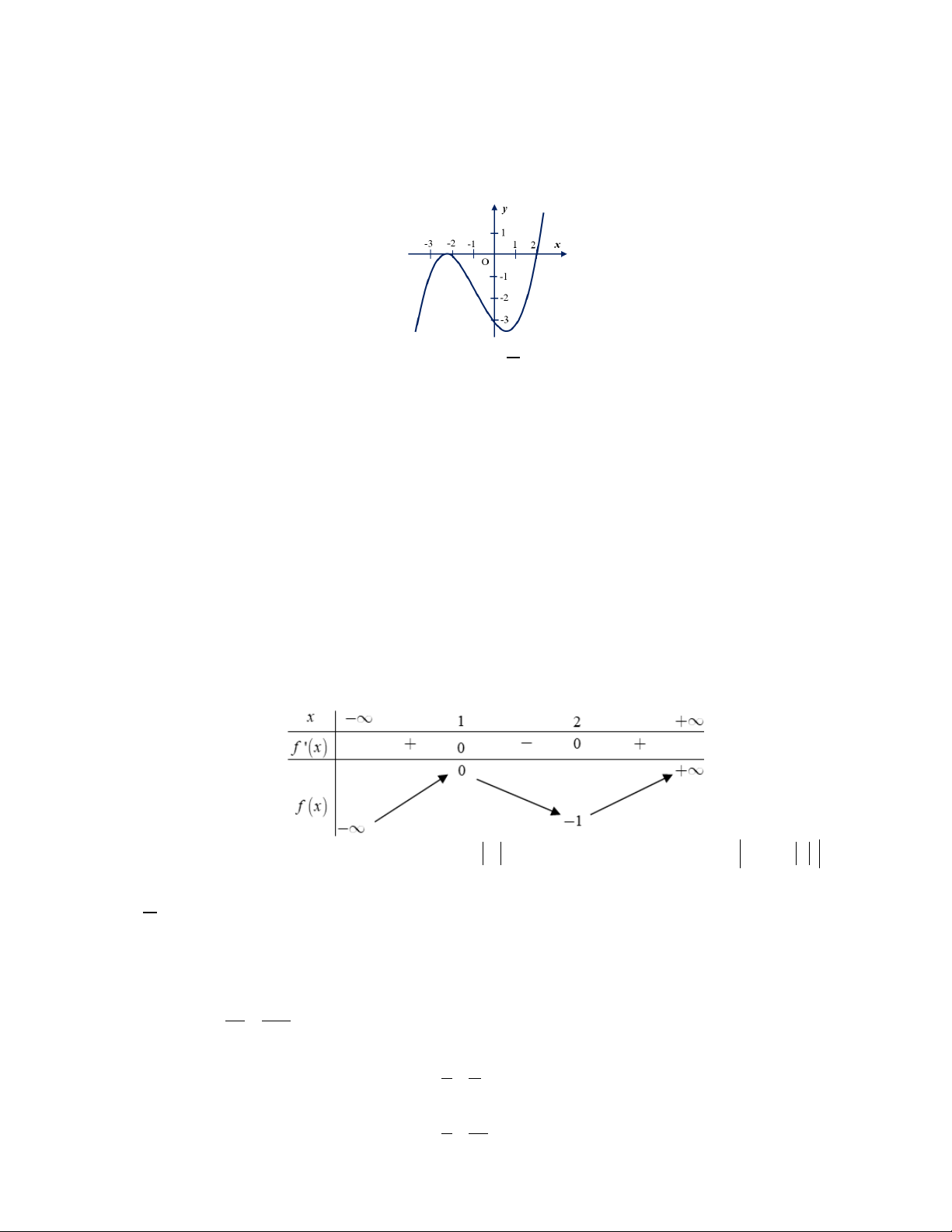
Câu 11: Cho hàm số y = f (x) . Hàm số y = f '(x) có đồ thị như hình bên. Hàm số y = f (2 − x) đồng biến trên khoảng A. (1;3). B. (2;+∞) . C. ( 2; − ) 1 . D. ( ; −∞ 2 − ).
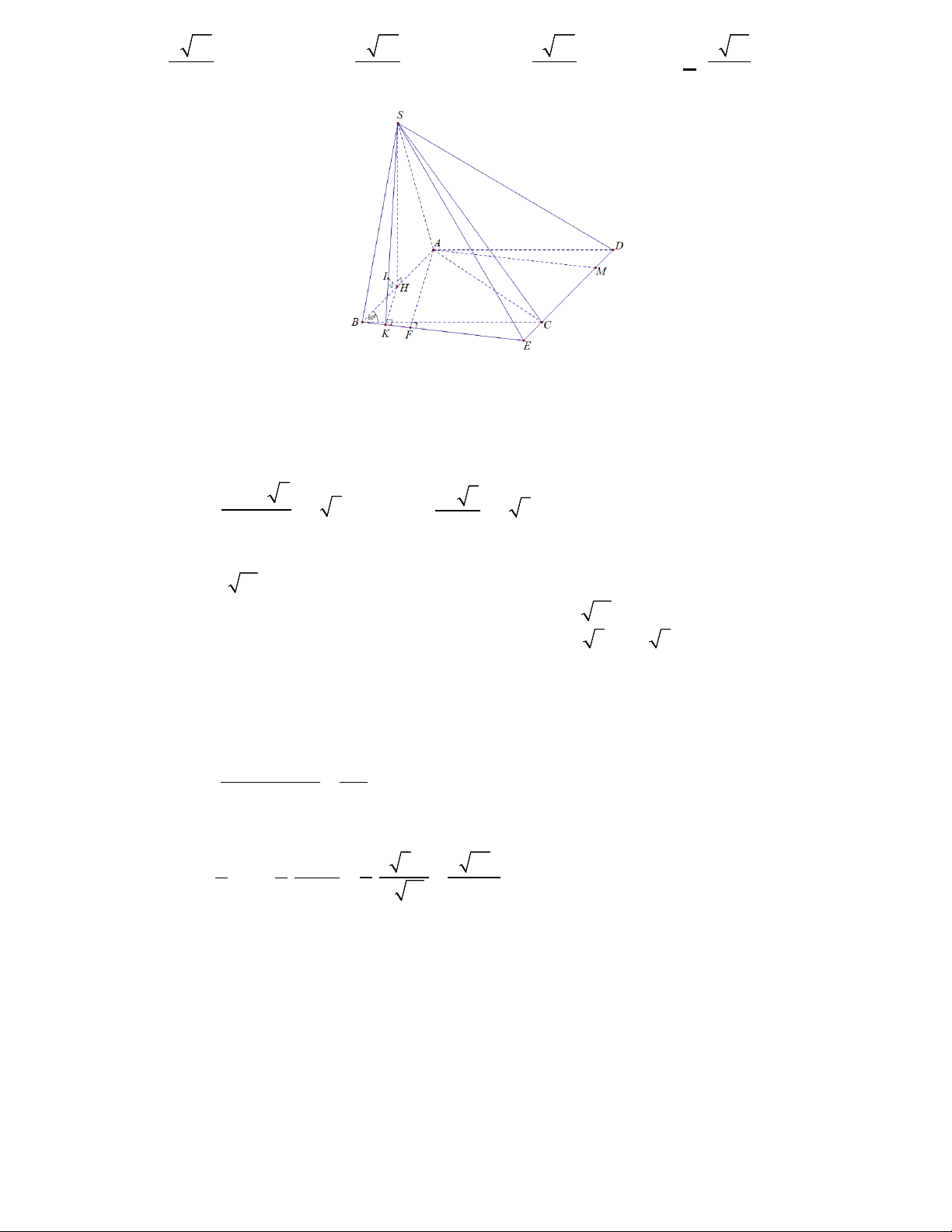
Câu 12: Cho khối chóp S.ABC có SA ABC, tam giác ABC vuông tại B , AC 2a , BC a ,
SB 2a 3 . Tính góc giữa SA và mặt phẳng SBC. A. 45. B. 30 . C. 60. D. 90 .
Câu 13: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng A. 2 . B. 1. C. 0 . D. 3.
Câu 14 : Trong các mệnh đề nào sau
I. f (x)dx = ∫
( f∫ (x)dx)2 2
với mọi hàm số f (x) liên tục trên . II. f ′
∫ (x)dx = f (x)+C với mọi hàm số f (x) có đạo hàm trên . II. (∫ ( ) )'
f x dx = f (x) với mọi hàm số f (x)liên tục trên . IV. kf
∫ (x)dx = k f
∫ (x)dx với mọi hằng số k và với mọi hàm số f (x) liên tục trên . Số mệnh đề đúng là A. 2 B. 1 C. 3 D. 4
Câu 15: Tìm các giá trị thực của tham số m để hàm số 1 3 2
y = x − mx + ( 2
m − 4) x + 3 đạt cực đại tại x = 3. 3
A. m =1,m = 5 . B. m = 5. C. m =1. D. m = 1 − .
Câu 16: Với n là số nguyên dương thỏa mãn 3 2 3C − =
− . Trong khai triển biểu thức ( 3 2 + 2 )n x y , + A n n 3 n 52 1 1 ( )
gọi T là số hạng mà tổng số mũ của x và T là k
y của số hạng đó bằng 34 . Hệ số của k A. 54912 . B. 1287 . C. 2574 . D. 41184 .
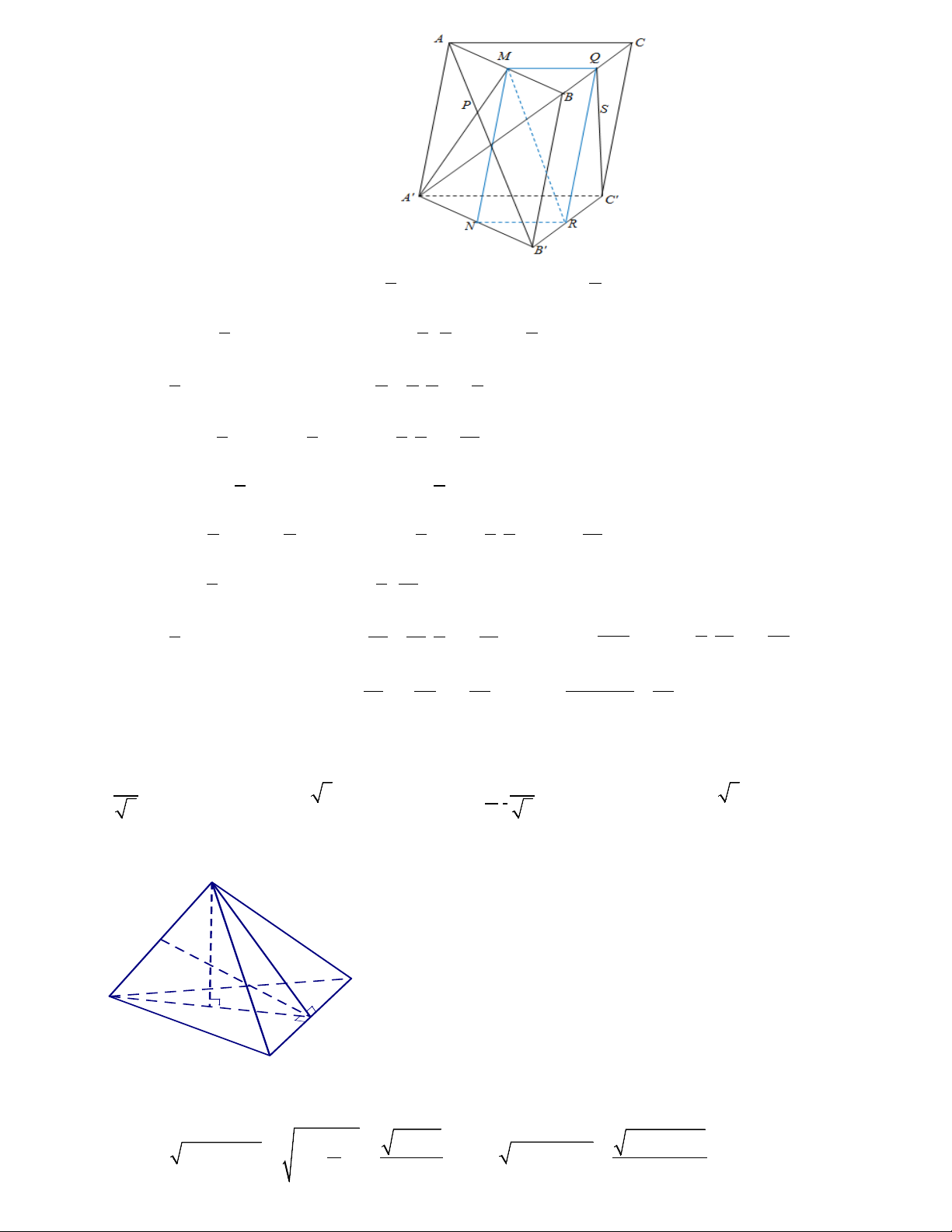
Câu 17: Cắt khối lăng trụ MN . P M N ′ P
′ ′ bởi các mặt phẳng (MN P
′ ′) và (MNP′) ta được những khối đa diện nào?
A. Ba khối tứ diện. B. Hai khối tứ diện và một khối chóp tứ giác.
C. Hai khối tứ diện và hai khối chóp tứ giác. D. Một khối tứ diện và một khối chóp tứ giác.
Câu18: Cho a,b > 0 , nếu 2
log a + log b = 5 và 2
log a + log b = 7 thì giá trị của ab bằng 8 4 4 8 A. 9 2 . B. 8 . C. 18 2 . D. 2 . 2
Câu 19: Cho số thực a thỏa mãn
a 2x + 3 + 2017 1 lim
= . Khi đó giá trị của a là x→+∞ 2x + 2018 2 A. 2 a = . B. 2 a − = . C. 1 a = . D. 1 a = − . 2 2 2 2
Câu 20: Một khối cầu ngoại tiếp khối lập phương. Tỉ số thể tích giữa khối cầu và khối lập phương là A. 3 . B. 3 3 . C. π 3 . D. 3π 3 . 2 8 2 8 4
Câu 21: Biết I = xln
∫ ( 2x +9)dx = aln5+bln3+c trong đó a , b , c là các số thực. Tính giá trị của biểu thức 0
T = a + b + c . A. T = 9 . B. T =11. C. T = 8. D. T =10 .
Câu 22: Cho tứ diện SABC có các cạnh ,
SA SB, SC đôi một vuông góc với nhau. Biết
SA = 3a, SB = 4a, SC = 5a Tính theo a thể tích V của khối tứ diện SABC 3 A. 3 V =10a B. 3 V = 20a C. 5a V = D. 3 V = 5a 2
Câu 23: Tập nghiệm của bất phương trình x + 2 log ≥ 0 là: 1 3− 2x 2 A. 1 T 2; = − B. 1 T = 2; − C. 3 T = ;+∞ D. 1 T = ; −∞ 3 3 2 3
Câu 24: Tìm tập xác định của hàm số: x
y = 2 + log(3− x) A. 0;+∞ ) . B. (0;3) . C. ( ;3 −∞ ) . D. 0;3 ).
Câu 25: Cho khối lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác cân với AB = AC = a , BAC =120° . Mặt phẳng (AB C
′ )′ tạo với đáy một góc 60°. Tính thể tích V của khối lăng trụ đã cho. 3 3 3 3 A. 3a V = B. 9a V = C. a V = D. 3a V = 8 8 8 4
Câu 26: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình π
3 sin x + cos x + 2 + 2 sin x + + m −1 =
0 có nghiệm. Số phần tử của S là 4 A. 18 . B. 19 . C. 6 . D. 7 .
Câu 27: Cho hình lăng trụ đều ABC.A′B C
′ ′ có tất cả các cạnh bằng nhau. Gọi α là góc giữa hai mặt phẳng ( AB C
′ ′) và ( A′BC) , thì cosα bằng A. 1 . B. 21 . C. 7 . D. 4 . 7 7 7 7 Câu 28: Cho hàm số 4 2
y = x − 2mx +1 ( )
1 . Tổng lập phương các giá trị của tham số m để đồ thị hàm số ( ) 1 có
ba điểm cực trị và đường tròn đi qua 3 điểm này có bán kính R =1 bằng A. 5 − 5 + . B. 1 5 . C. 2 + 5 . D. 1 − + 5 . 2 2
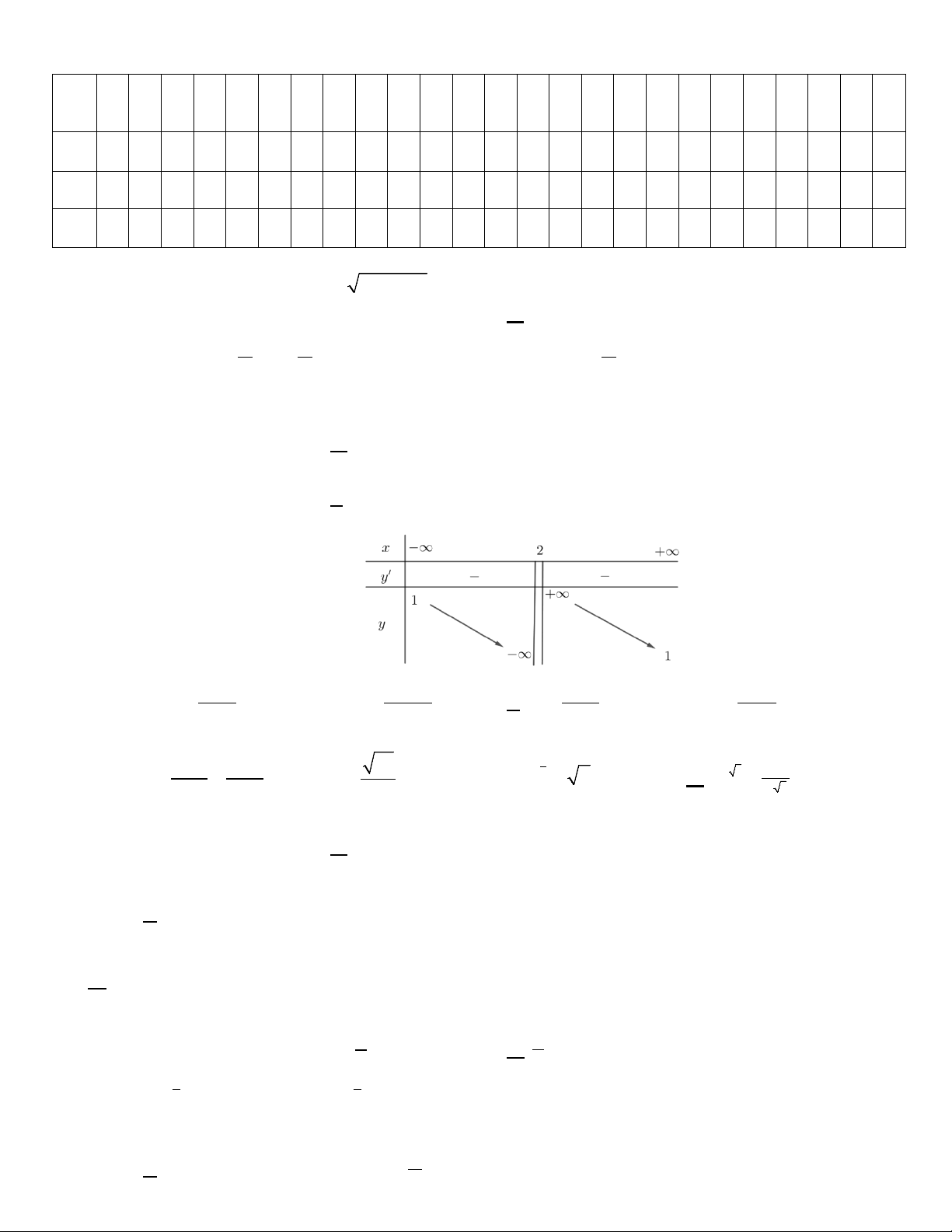
Câu 29: Cho hàm số y = f ( x) . Đồ thị y = f ′(x) như hình vẽ sau Biết f (− )
1 + f (0) − 2 f ( )
1 = f (3) − f (2) . Tìm giá trị nhỏ nhất của hàm số g (x) = f (x − 2) trên đoạn [1;5]. A. f (2) . B. f (1) . C. f (3) . D. f ( 1) − . Câu 30: Cho hàm số 1 3 2 1
y = x − 2x + 3x − có đồ thị là (C). Biết có duy nhất một giá trị m để đường thẳng 3 3 0 1
d : y = mx − cắt đồ thị (C) tại ba điểm phân biệt A, B, C với A cố định và S = S Chọn khẳng định OBC 2 OAB. 3 đúng? A. m ∈ 0;1 . m ∈ 1;2 . C. m ∈ 2;3 . D. m ∈ 3;4 . 0 ( ) 0 ( ) 0 ( ) B. 0 ( )
Câu 31: Cho hình trụ có O, O ' là tâm của hai đáy. Xét hình chữ nhật ABCD có ,
A B cùng thuộc đường tròn
đáy (O) và C, D cùng thuộc đường tròn đáy (O ') sao cho AB = a 3, BC = 2a đồng thời (ABCD) tạo với
mặt phẳng đáy hình trụ góc 0
60 . Thể tích của khối trụ bằng 3 π a 3 3 π a 3 A. . B. 3 2π a 3 . C. 3 π a 3 . D. . 9 3
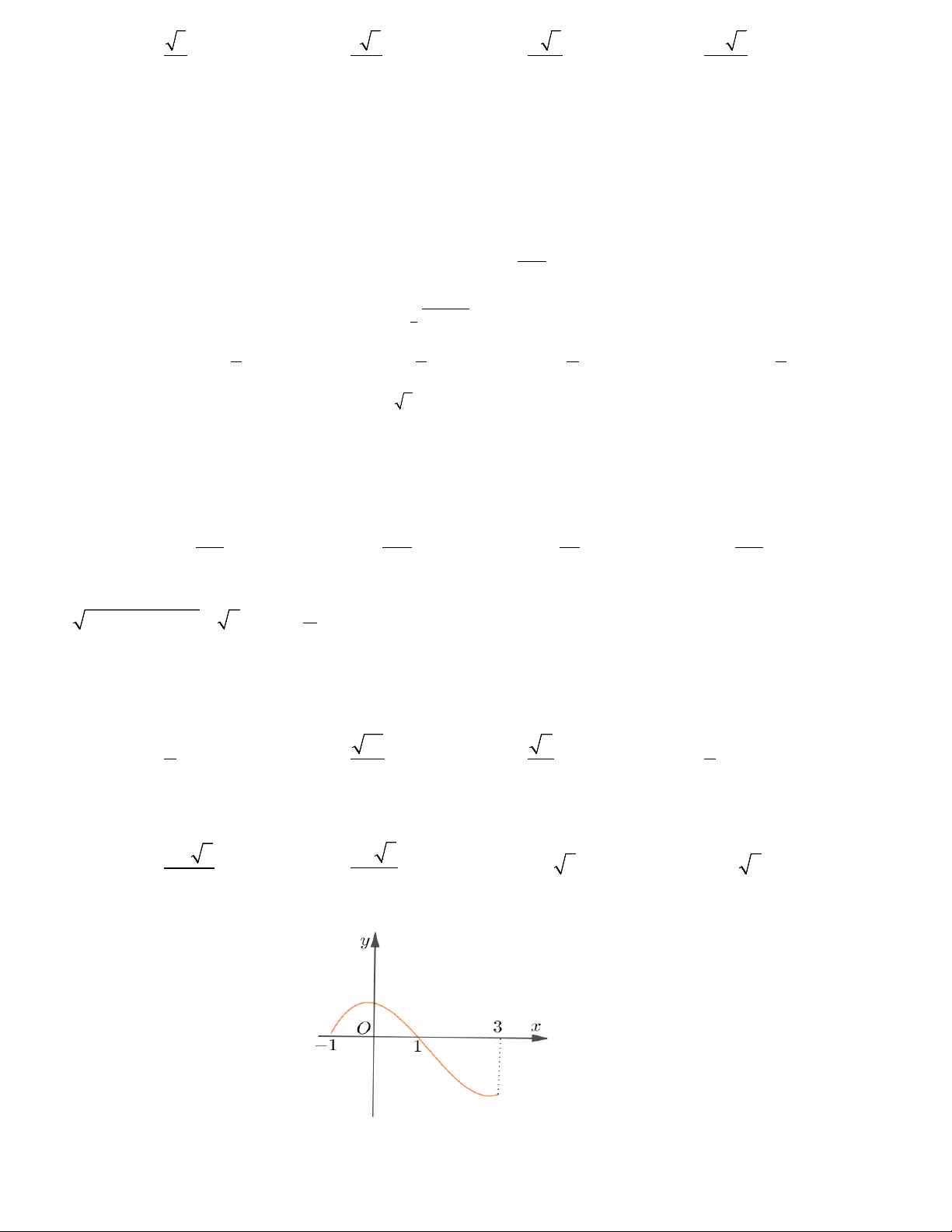
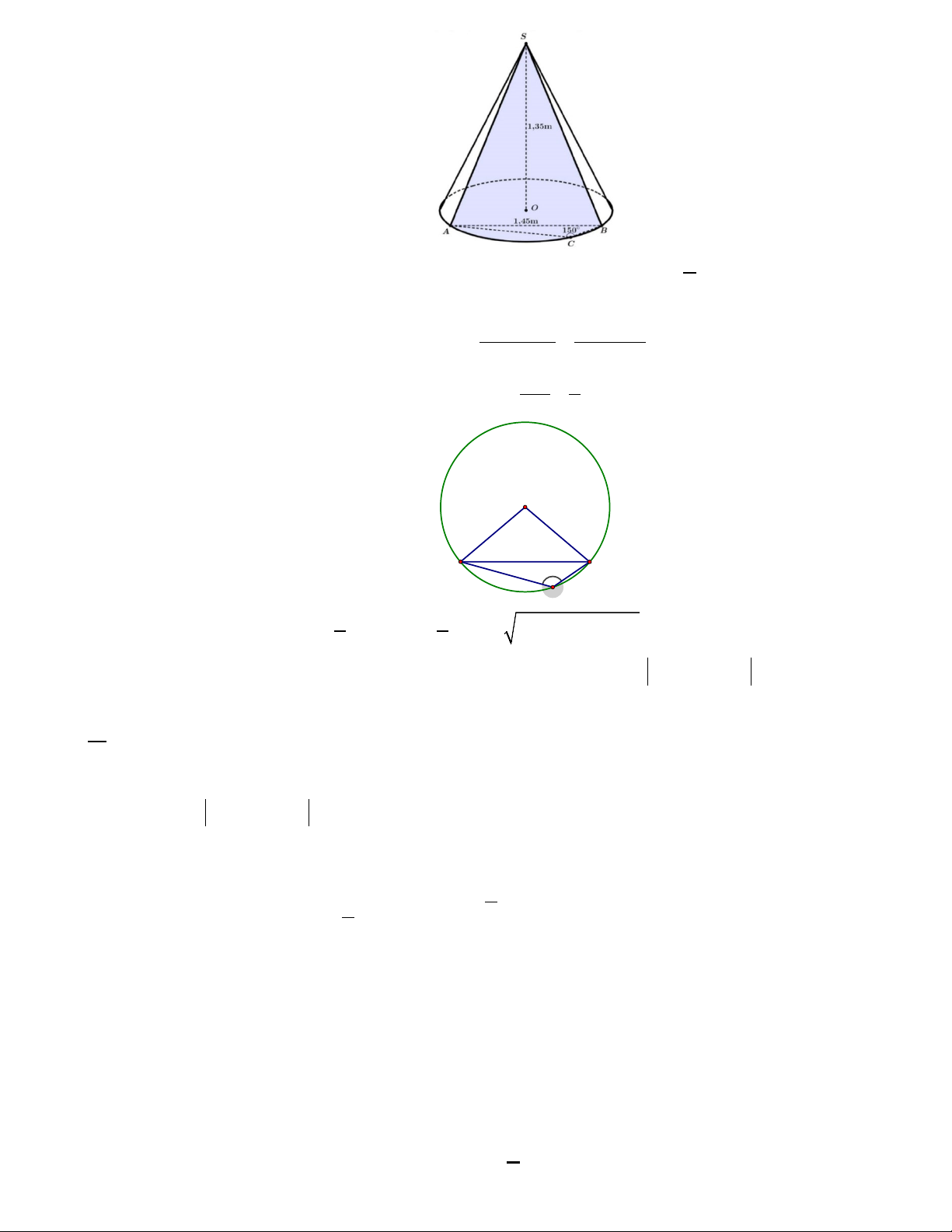
Câu 32: Cửa hàng A có đặt trước sảnh một cái nón lớn với chiều cao 1,35 m và sơn cách điệu hoa văn
trang trí một phần mặt ngoài của hình nón ứng với cung nhỏ
AB như hình vẽ. Biết AB =1,45 m,
ACB =150° và giá tiền trang trí là 2.000.000 đồng mỗi mét vuông. Hỏi số tiền (làm tròn đến
hàng nghìn) mà cửa hàng A cần dùng để trang trí là bao nhiêu? A. 4.215.000 đồng. B. 4.510.000 đồng. C. 3.021.000 đồng. D. 3.008.000 đồng.
Câu 33: Có bảo nhiêu số nguyên m thuộc khoảng ( 10 − ;10) để hàm số 3
y = 2x − 2mx + 3 đồng biến trên (1;+ ∞) ? A. 12. B. 8 . C. 11. D. 7 .
Câu 34:Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A
lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương anh A đều
cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh A
mua được ô tô giá 500 triệu biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe? A. 11. B. 12. C. 13. D. 10.
Câu 35: Cho hình chóp S.ABC có ABC là tam giác đều cạnh 3a , 0
SAB = SCB = 90 , góc giữa (SAB) và (SCB) bằng 0
60 . Thể tích khối chóp S.ABC bằng 3 3 3 3
A. 3 2a . B. 2a . C. 2a . D. 9 2a . 8 3 24 8
Câu 36: Ta có bao nhiêu giá trị nguyên của m thuộc khoảng ( 2022 − ;2022) để hàm số 2
y = x + m + x + 2(m + ) 2
1 x + m + 2m + 4 + log ( 2
x − m + 2x +1 Ta có tập xác định là 2 ) D = ?
A. 2020. B. 2023. C. 2022 . D. 2021.
Câu 37: Có bao nhiêu số nguyên x thỏa mãn ( x x 1 9 10.3 + − + )
81 4 − log 2x ≥ 0 ? 2 ( ) A. 7 . B. 6 . C. 8 . D. 5.
Câu 38: Cho hàm số y = f (x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương
trình f ( f (x) + 2m) +1 = f (x) + 2m có đúng 3 nghiệm phân biệt trên[ 1; − ] 1 là A. 0 . B. 1. C. 2 . D. 3.
Câu 39: Cho hàm số f (x) có đạo hàm trên thỏa mãn( + 2) ( ) + ( + ) 1 ′( ) = ex x f x x f x và f ( ) 1 0 = .Tính 2 f (2) 2 2 A. e e f ( ) e 2 = . B. f ( ) e 2 = . C. f (2) = . D. f (2) = . 3 6 3 6
Câu 40: Cho hàm số y = f (x) liên tục và là hàm số chẵn trên . Biết 2 2
f (2x −1) + 2 f (2x − 3) = 24x − 28x + 20, x
∀ ∈ , tính f (x)dx ∫ ? 0 A. 24 . B. 36. C. 12. D. 36 − .
Câu 41: Mỗi lượt, ta gieo một con súc sắc (loại 6 mặt, cân đối) và một đồng xu (cân đối). Tính xác suất để
trong 3 lượt gieo như vậy, có ít nhất một lượt gieo được kết quả con xúc sắc xuất hiện mặt 1 chấm, đồng thời
đồng xu xuất hiện mặt sấp. A. 397 . B. 1385 . C. 1331 . D. 1603 . 1728 1728 1728 1728
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 4a , S
∆ AB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy,
ABC = 60 . Gọi M là điểm trên cạnh CD sao cho CM= 3a . Khoảng cách giữa hai
đường thẳng SB và AM bằng A. 4 51 a . B. 4 39 a . C. 8 39 a . D. 8 51 a . 17 13 13 17 x Câu 43: Cho hàm số 2 + 2 f (x) = log
. Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 2x 4 +
f ( 2x + x −( 2 2 2
3− x )3 + 3)+ f ( x + m)3 + 2m−6) ≥ 1
− nghiệm đúng với mọi x ∈[ 1; − ] 3 . A. 13 m ; ∈ +∞ B. 15 m ∈ ;+∞ C. m∈[ 9; − +∞) D. m∈[3;+∞) 4 4
Câu 44: Có bao nhiêu số nguyên của x sao cho tồn tại số thực y thỏa m 2log (x + y + ) 1 = log ( 2 2
x + 2x + 2y +1 ? 3 2 ) A.2. B. 1. C. 3. D. 4.
Câu 45: Cho hàm số y = f (x) có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của tham số m để bất phương trình f (sin x) x (m − 2 ) f (sin x) 2 f (x) + 2.2 + m − 3. (2 − )
1 ≥ 0 nghiệm đúng với mọi x ∈ . Số tập con của tập hợp S là A. 4 . B. 1. C. 2 . D. 3.
Câu 46: Cho hàm số bậc ba y = f (x) có bảng biến thiên như hình vẽ:
Hỏi có bao nhiêu giá trị của tham số m (với m∈ ; m ≤ 2021) để đồ thị hàm số y = m + f ( x ) có đúng 7 điểm cực trị? A. 2026 . B. 2025 . C. 4 . D. 2022 .
Câu 47: Cho hàm số y = f (x) có bảng biến thiên như sau: π Số nghiệm thuộc đoạn 9 0;
của phương trình f ( f (cos x)) = 2 là 2 A.3 . B.5 . C. 7 . D.9 .
Câu 48: Cho hàm số bậc bốn y = f (x) có đồ thị như hình vẽ bên.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;20] sao cho giá trị nhỏ nhất của hàm số
g (x) = 2 f (x) + m + 4 − f (x) −3 trên đoạn [ 2;
− 2] không bé hơn 1? A. 18. B. 19. C. 20 . D. 21.
Câu 49: Cho lăng trụ ABC.A′B C
′ ′. Gọi M , N , Q , R lần lượt là trung điểm của các cạnh AB , A′B′ , BC , B C
′ ′ và P , S lần lượt là trọng tâm của các tam giác AA′B , CC B
′ . Tỉ số thể tích khối đa diện MNRQPS và
khối lăng trụ ABC.A′B C ′ ′ là A. 1 . B. 5 . C. 1 . D. 2 . 9 54 10 27
Câu 50: Cho hình chóp S.ABC có SA = x, BC = y, AB = AC = SB = SC =1. Thể tích khối chóp S.ABC đạt giá
trị lớn nhất khi tổng (x + y) bằng A. 2 . B. 3 . C. 4 . D. 4 3 . 3 3
----------- HẾT ---------- ĐÁP ÁN CHI TIẾT
Câu 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
ĐA B B B C D B A A C A C B D A B D A A A C C B A D A
Câu 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
ĐA C A D C A C D A C D C A A D C A D A A C A D B B C
Câu 1: Tập xác định của hàm số y = sin 2x +1 là
A. D = \{kπ | k ∈ Z}. B. D = . π π π C. D \ kπ; kπ | k Z = + + ∈ .
D. D = \ + k2π | k ∈ Z . 4 2 2
Câu 2: Có bao nhiêu cách chọn ra 6 học sinh từ 40 học sinh lớp 11A để làm một ban bầu cử gồm một trưởng
ban, một phó ban và bốn ủy viên? A. 6 A . B. 2 4 A .C . C. 2 4 C .A . D. 4 2!C . 40 40 38 40 38 38
Câu 3: Cho dãy số có các số hạng đầu là:5;10;15;20;25;... Số hạng tổng quát của dãy số này là:
A. u = n − . u = n . u = + n . u = n + . n 5( 1) B. n 5 C. n 5 D. n 5. 1
Câu 4: Bảng biến thiên dưới đây là của hàm số nào? A. x − 3 y − + + = . B. x 1 y = . C. x 1 y = . D. x 3 y = . x − 2 2x + 2 x − 2 2 + x
Câu 5: Cho a >1. Mệnh đề nào sau đây là đúng? 3 2 1 A. 1 1 − 1 <
. B. a >1. C. 3
a > a . D. 3 a > . 2016 2017 a a a 5 a
Câu 6: Biết (H ) là đa diện đều loại {5; }
3 với số đỉnh và số cạnh lần lượt là a và b . Tổng a + b là:
A. a + b = 40 .
B. a + b = 50 .
C. a + b = 32 .
D. a + b = 42 .
Câu 7: Cho khối trụ có bán kính hình tròn đáy bằng r và chiều cao bằng h . Hỏi nếu tăng chiều cao lên 2 lần và
tăng bán kính đáy lên 3 lần thì thể tích của khối trụ mới sẽ tăng lên bao nhiêu lần? A. 18 lần. B. 6 lần. C. 36 lần. D. 12 lần
Câu 8: Cho tam giác ABC vuông tại A . Khi quay tam giác đó quanh cạnh góc vuông AB , đường gấp khúc
BCA tạo thành hình tròn xoay nào trong bốn hình sau đây. A. Hình nón. B. Hình trụ. C. Hình cầu. D. Mặt nón.
Câu 9: Biết F (x) x 2
= e + x là một nguyên hàm của hàm số f (x) trên . Khi đó f
∫ (2x)dx bằng A. x 2
2e + 2x + C. B. 1 2x 2 e 1 + x + C. C. 2x 2
e + 2x + C. D. 2x 2
e + 4x + C. 2 2 π π 2 2 Câu 10: Cho f
∫ (x)dx = 5. Tính I = f
∫ (x)+ 2sin xdx = 5 . 0 0 A. π I = 7
B. I = 5 +
C. I = 3 D. I = 5 +π 2
Câu 11: Cho hàm số y = f (x) . Hàm số y = f '(x) có đồ thị như hình bên. Hàm số y = f (2 − x) đồng biến trên khoảng A. (1;3). B. (2;+∞) . C. ( 2; − ) 1 . D. ( ; −∞ 2 − ).
Câu 12: Cho khối chóp S.ABC có SA ABC, tam giác ABC vuông tại B , AC 2a , BC a ,
SB 2a 3 . Tính góc giữa SA và mặt phẳng SBC. A. 45. B. 30 . C. 60. D. 90 .
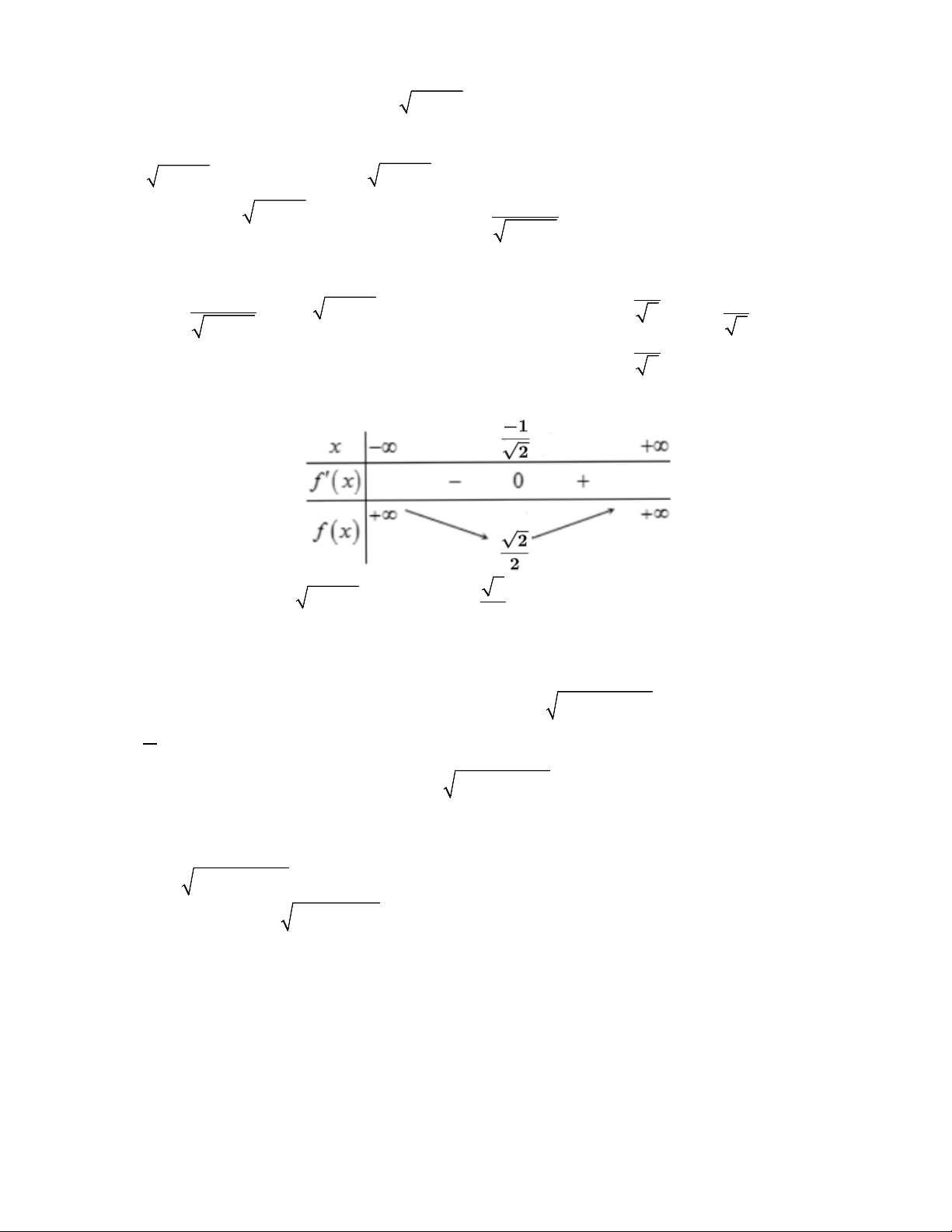
Câu 13: Cho hàm số y = f (x) có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng A. 2 . B. 1. C. 0 . D. 3.
Câu 14 : Trong các mệnh đề nào sau
I. f (x)dx = ∫
( f∫ (x)dx)2 2
với mọi hàm số f (x) liên tục trên . II. f ′
∫ (x)dx = f (x)+C với mọi hàm số f (x) có đạo hàm trên . II. (∫ ( ) )'
f x dx = f (x) với mọi hàm số f (x)liên tục trên . IV. kf
∫ (x)dx = k f
∫ (x)dx với mọi hằng số k và với mọi hàm số f (x) liên tục trên . Số mệnh đề đúng là A. 2 B. 1 C. 3 D. 4
Câu 15: Tìm các giá trị thực của tham số m để hàm số 1 3 2
y = x − mx + ( 2
m − 4) x + 3 đạt cực đại tại x = 3. 3
A. m =1,m = 5 . B. m = 5 . C. m =1. D. m = 1 − .
Câu 16: Với n là số nguyên dương thỏa mãn 3 2 3C − =
− . Trong khai triển biểu thức ( 3 2 + 2 )n x y , + A n n 3 n 52 1 1 ( )
gọi T là số hạng mà tổng số mũ của x và T là k
y của số hạng đó bằng 34 . Hệ số của k A. 54912 . B. 1287 . C. 2574 . D. 41184 .
Câu 17: Cắt khối lăng trụ MN . P M N ′ P
′ ′ bởi các mặt phẳng (MN P
′ ′) và (MNP′) ta được những khối đa diện nào?
A. Ba khối tứ diện. B. Hai khối tứ diện và một khối chóp tứ giác.
C. Hai khối tứ diện và hai khối chóp tứ giác. D. Một khối tứ diện và một khối chóp tứ giác.
Câu18. Cho a,b > 0 , nếu 2
log a + log b = 5 và 2
log a + log b = 7 thì giá trị của ab bằng 8 4 4 8 A. 9 2 . B. 8 . C. 18 2 . D. 2 . 2
Câu 19: Cho số thực a thỏa mãn
a 2x + 3 + 2017 1 lim
= . Khi đó giá trị của a là x→+∞ 2x + 2018 2 A. 2 a = . B. 2 a − = . C. 1 a = . D. 1 a = − . 2 2 2 2
Câu 20: Một khối cầu ngoại tiếp khối lập phương. Tỉ số thể tích giữa khối cầu và khối lập phương là A. 3 . B. 3 3 . C. π 3 . D. 3π 3 . 2 8 2 8 4
Câu 21: Biết I = xln
∫ ( 2x +9)dx = aln5+bln3+c trong đó a , b , c là các số thực. Tính giá trị của biểu thức 0
T = a + b + c . A. T = 9 . B. T =11. C. T = 8. D. T =10 .
Câu 22: Cho tứ diện SABC có các cạnh ,
SA SB, SC đôi một vuông góc với nhau. Biết
SA = 3a, SB = 4a, SC = 5a Tính theo a thể tích V của khối tứ diện SABC 3 A. 3 V =10a B. 3 V = 20a C. 5a V = D. 3 V = 5a 2
Câu 23: Tập nghiệm của bất phương trình x + 2 log ≥ 0 là: 1 3− 2x 2 A. 1 T 2; = − B. 1 T = 2; − C. 3 T = ;+∞ D. 1 T = ; −∞ 3 3 2 3
Câu 24: Tìm tập xác định của hàm số: x
y = 2 + log(3− x) A. 0;+∞ ) . B. (0;3) . C. ( ;3 −∞ ) . D. 0;3 ).
Câu 25: Cho khối lăng trụ đứng ABC.A′B C
′ ′ có đáy ABC là tam giác cân với AB = AC = a , BAC =120° . Mặt phẳng (AB C
′ )′ tạo với đáy một góc 60°. Tính thể tích V của khối lăng trụ đã cho. 3 3 3 3 A. 3a V = B. 9a V = C. a V = D. 3a V = 8 8 8 4
Câu 26: Gọi S là tập hợp tất cả các giá trị nguyên của tham số m để phương trình π 3 sin x cos x 2 2 sin x + + + + + m −1 =
0 có nghiệm. Số phần tử của S là 4 A. 18 . B. 19 . C. 6 . D. 7 . Lời giải π π Phương trình đã cho 3 2 sin x 2 2 sin x ⇔ + + + + + m −1 = 0 . 4 4 Đặt π π 2 t = 2 sin x + + 2 ⇒ 2 sin x + = t −
2 , điều kiện: t ∈ 2 − 2; 2 + 2 . 4 4
Khi đó ta có phương trình 2t + 3t − 3 = −m (2)
Ta đi lập bảng biến thiên của hàm số 2
y = t + 3t − 3 trên đoạn 2 2; 2 2 − + .
Từ bảng biến thiên ta thấy, để phương trình đã cho có nghiệm ⇔ (2) có nghiệm
t ∈ − 2 + 2; 2 + 2
⇔ 3 2 − 2 −1− 2 ≤ −m ≤ 3 2 + 2 −1+ 2 ⇔ 3 −
2 + 2 +1− 2 ≤ m ≤ 3 − 2 − 2 +1+ 2 .
Vì m∈ Z ⇒ m = 5 − ; 4 − ; 3 − ; 2 − ; 1 − ;0 .
Câu 27: Cho hình lăng trụ đều ABC.A′B C
′ ′ có tất cả các cạnh bằng nhau. Gọi α là góc giữa hai mặt phẳng ( AB C
′ ′) và ( A′BC) , thì cosα bằng A. 1 . B. 21 . C. 7 . D. 4 . 7 7 7 7 Lời giải
Giả sử cạnh của hình lăng trụ đều ABC.A′B C
′ ′ có độ dài bằng a .
Gọi M = A′B ∩ AB′ và N = A′C ∩ AC′ . a 3 1 a 7
Gọi J là trung điểm BC . AJ = , 2 2 7
A′J = AA′ + AJ =
a ⇒ A′I = A′J = . 2 2 2 4
AI + A′I − AA′ − Xét tam giác A ∆ ′IA có: 2 2 2 1 cos A′IA = = ⇒ α = ( AI A′I ) = − ( A′IA) 1 cos cos , cos 180 = .
2.AI.A′I 7 7 Câu 28: Cho hàm số 4 2
y = x − 2mx +1 ( )
1 . Tổng lập phương các giá trị của tham số m để đồ thị hàm số ( ) 1 có
ba điểm cực trị và đường tròn đi qua 3 điểm này có bán kính R =1 bằng A. 5 − 5 + . B. 1 5 . C. 2 + 5 . D. 1 − + 5 . 2 2 Lời giải 3 2
y ' = 4x − 4mx = 4x(x − m). Để đồ thị hs (1) có 3 điểm cực trị ⇔ m > 0. Gọi 2 2 (
A 0;1), B( m;−m +1),C(− m;−m +1) là các điểm cực trị của đồ thị hs (1), 2
I(0;−m +1) là trung điểm BC. Ta có 2 4
AI = m , AB = AC = m + m .Suy ra 1 A . B AC.BC A . . B AC AI BC = ⇔ R = 2 4R 2AI m = 0 (l) m =1 (n) 2 2m 4 2 1 − − 5 ⇔
=1 ⇔ m − 2m + m = 0 ⇔ 4 m = (l) m + m 2 1 − + 5 m = (n) 2
Câu 29: Cho hàm số y = f ( x) . Đồ thị y = f ′(x) như hình vẽ sau Biết f (− )
1 + f (0) − 2 f ( )
1 = f (3) − f (2) . Tìm giá trị nhỏ nhất của hàm số g (x) = f (x − 2) trên đoạn [1;5]. A. f (2) . B. f (1). C. f (3) . D. f ( 1) − . Lời giải
Bảng biến thiên của hàm số y = f (x)
Đặt t = x − 2 , x
∀ ∈[1;5]ta có: 1≤ x ≤ 5 ⇔ 1
− ≤ x − 2 ≤ 3 ⇒ t ∈[ 1; − ] 3
Khi đó hàm số g (x) = f (x − 2) trở thành y = f (t) với t ∈[ 1; − ] 3 .
Do đó, giá trị lớn nhất của hàm số g = f (x −3) trên đoạn [1;5] bằnggiá trị lớn nhất của hàm số y = f (t) trên đoạn [ 1; − ]3.
Từ bảng biến thiên ta có f (0) < f ( )
1 , f (2) < f ( )
1 vậy f (0) + f (2) < 2 f ( ) 1 Khi đó f (− )
1 + f (0) − 2 f ( )
1 = f (3) − f (2) ⇔ f (0) + f (2) − 2 f ( )
1 = f (3) − f (− ) 1
⇒ f (3) − f (− )
1 < 0 ⇒ f (3) < f (− ) 1
Ta có: min f (x − 2) = min f (t) = f (3) khi t = 3 . [1;5] [ 1 − ; ] 3
Suy ra giá trị nhỏ nhất của hàm số g (x) = f (x − 2) bằng f (3) khi x = 5. Câu 30: Cho hàm số 1 3 2 1
y = x − 2x + 3x − có đồ thị là (C). Biết có duy nhất một giá trị m để đường thẳng 3 3 0 1
d : y = mx − cắt đồ thị (C) tại ba điểm phân biệt A, B, C với A cố định và S = S Chọn khẳng định OBC 2 OAB. 3 đúng? A. m ∈ 0;1 . m ∈ 1;2 . C. m ∈ 2;3 . D. m ∈ 3;4 . 0 ( ) 0 ( ) 0 ( ) B. 0 ( ) Lời giải Chọn A
Xét phương trình hoành độ giao điểm của (C) và d : 1 3 2 1 1 1 3 2 x 2x 3x mx
x 2x (3 m) 1 2 x 0 x x 2x (3 m) − + − = − ⇔ − + − = ⇔ − + − = 0 3 3 3 3 3 x = 0 ⇔ 1 2
x − 2x + 3− m = 0 (2) 3
(C) cắt d tại ba điểm phân biệt khi phương trình (2) có hai nghiệm phân biệt khác 0 ∆ > 0 m > 0 ⇔ 1 ⇔ (*) 2
.0 − 2.0 + 3 − m ≠ 0 m ≠ 3 3
Khi đó x x là nghiệm của phương trình (2) và theo định lí Vi-et ta có x + x = x x = − m . Suy ra B C 6; B C 9 3 B ; C 1 1 1 A 0; ; B x x − − − B ; mx B ;C C;mxC . 3 3 3 Ta có: S = S ⇔ BC = AB ⇔ x − x + y − y = x − x + y − y OBC OAB
( C B )2 ( C B )2 ( B A)2 ( B A)2 2 2 2 ⇔ (x − x + m x − x = x + m x ⇔ x − x + m = x + m C B )2 ( C B )2 ( B )2 2 ( B )2 ( C B )2 ( 2 ) 2B ( 2 2 1 4 1 ) ⇔ (x − x
= x ⇔ x + x − x x = x ⇔
= x x + x ⇔ = x ⇔ x = C B )2 2B ( C B )2 2 B C B B ( B C ) 3 4 4 4 36 4 3 2 B B . 2 Nên 9 x = .Thay 3 x = , 9 x = vào (2) ta có: 3 m = . C 2 B 2 C 2 4
Câu 31: Cho hình trụ có O, O ' là tâm của hai đáy. Xét hình chữ nhật ABCD có ,
A B cùng thuộc đường tròn
đáy (O) và C, D cùng thuộc đường tròn đáy (O ') sao cho AB = a 3, BC = 2a đồng thời (ABCD) tạo với mặt
phẳng đáy hình trụ góc 0
60 . Thể tích của khối trụ bằng 3 π a 3 3 π a 3 A. . B. 3 2π a 3 . C. 3 π a 3 . D. . 9 3 Lời giải
Gọi H là giao điểm của OB với đường tròn đáy nên AH ⊥ AB
Ta có: ABCD là hình chữ nhật nên DA ⊥ AB
Khi đó: góc giữa (ABCD) với mặt phẳng đáy bằng 0 DAH = 60
Tam giác DAH vuông tại H có 0 h = DH = .
DA sin 60 = a 3 và 0 AH = . DA cos60 = a Tam giác BH
BAH vuông tại A có 2 2 2 2
BH = AB + AH = 3a + a = 2a ⇒ r = = a 2 Thể tích hình trụ là: 2 2 3
V = hπ r = a 3.π.a = π a 3
Câu 32: Cửa hàng A có đặt trước sảnh một cái nón lớn với chiều cao 1,35 m và sơn cách điệu hoa văn
trang trí một phần mặt ngoài của hình nón ứng với cung nhỏ
AB như hình vẽ. Biết AB =1,45 m,
ACB =150° và giá tiền trang trí là 2.000.000 đồng mỗi mét vuông. Hỏi số tiền (làm tròn đến
hàng nghìn) mà cửa hàng A cần dùng để trang trí là bao nhiêu? A. 4.215.000 đồng. B. 4.510.000 đồng. C. 3.021.000 đồng. D. 3.008.000 đồng. Lời giải
Bán kính đáy của hình nón là bán kính đường tròn ngoại tiếp tam giác ABC .
Áp dụng định lí sin trong tam giác ta có: AB 1,45 r = = =1,45 ⇒ OA ∆ B đều, tức là 2sin ACB 2sin150°
AOB = 60° . Do đó diện tích mặt được sơn chiếm 60 1
= diện tích mặt xung quanh của nón. 360 6 O A 150° B C
Vì vậy số tiền cần sơn là 1 6 1
π rl.2.10 = π.1,45. (1,45)2 + (1,35)2 6 .2.10 ≈ 3008000 đồng. 6 6
Câu 33: Có bảo nhiêu số nguyên m thuộc khoảng ( 10 − ;10) để hàm số 3
y = 2x − 2mx + 3 đồng biến trên (1;+ ∞) ? A. 12. B. 8 . C. 11. D. 7 . Lời giải Xét g (x) 3
= 2x − 2mx + 3. Ta có g′(x) 2
= 6x − 2m và g ( ) 1 = 5 − 2m . Để hàm số 3
y = 2x − 2mx + 3 đồng biến trên (1;+ ∞) thì có hai trường hợp sau
Trường hợp 1: Hàm số g (x) đồng biến trên (1;+ ∞) và g ( ) 1 ≥ 0. 2 2
m ≤ 3x , x ∀ > 1
6x − 2m ≥ 0, x ∀ > 1 ⇔ 5 ⇔ 5 ⇔ m ≤ . 5 − 2m ≥ 0 m ≤ 2 2
Kết hợp giả thiết suy ra có 12 giá trị nguyên của m thỏa mãn.
Trường hợp 2: Hàm số g (x) nghịch biến trên (1;+ ∞) và g ( ) 1 ≤ 0.
Điều này không xảy ra vì ( 2
lim 6x − 2m) = +∞ > 0. x→+∞
Vậy có 12 giá trị nguyên của m thỏa mãn.
Câu 34:Trong năm đầu tiên đi làm, anh A được nhận lương là 10 triệu đồng mỗi tháng. Cứ hết một năm, anh A
lại được tăng lương, mỗi tháng năm sau tăng 12% so với mỗi tháng năm trước. Mỗi khi lĩnh lương anh A đều
cất đi phần lương tăng so với năm ngay trước để tiết kiệm mua ô tô. Hỏi sau ít nhất bao nhiêu năm thì anh A
mua được ô tô giá 500 triệu biết rằng anh A được gia đình hỗ trợ 32% giá trị chiếc xe? A. 11. B. 12. C. 13. D. 10. Lời giải
Số tiền anh A cần tiết kiệm là 500 − 500.0,32 = 340 (triệu).
Gọi số tiền mà anh A nhận được ở mỗi tháng trong năm đầu tiên là u =10 (triệu). 1
Thì số tiền mà anh A nhận được ở mỗi tháng trong năm thứ hai là
u = u . 1+ 0,12 = u .1,12 (triệu). 2 1 ( ) 1
Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ ba là
u = u .(1+ 0,12)2 = u .(1,12)2 (triệu). 3 1 1 …
Số tiền mà anh A nhận được ở mỗi tháng trong năm thứ n là u u − = + . 1,12 n u − = (triệu). 1 ( ) 1 n .(1 0,12)n 1 1
Vậy số tiền mà anh A tiết kiệm được sau n năm là 12.(u −u + u −u +⋅⋅⋅+ u − + − − u − u u 2 1 3 2 n 1 n 2 n n 1 − )
= 12.(u − u =12. . 1,12 n u − − u 1 ( ) 1 n 1 ) 1 .
Cho 12. u .(1,12)n 1− − u = 340 n− ⇔ = 23 ⇔ = + ⇒ n =13. 1 1 ( ) 1 23 1,12 n log 1 6 1,12 6
Vậy sau ít nhất 13 năm thì anh A sẽ tiết kiệm đủ tiền để mua ô tô.
Câu 35: Cho hình chóp S.ABC có ABC là tam giác đều cạnh 3a , 0
SAB = SCB = 90 , góc giữa (SAB) và (SCB) bằng 0
60 . Thể tích khối chóp S.ABC bằng 3 3 3 3
A. 3 2a . B. 2a . C. 2a . D. 9 2a . 8 3 24 8 Lời giải
Trong mặt phẳng (ABC) lấy D nằm trên đường trung trực của AC sao cho SD ⊥ (ABC) và 0 BCD = BAD = 90 0
⇒ SAB = SCB = 90 2 Gọi BC
O = AC ∩ BD ⇒ BD =
= 2a 3 ⇒ CD = a 3 OB
Dựng AM ⊥ SB , do S ∆ AB = S
∆ CB ⇒ CM ⊥ SB ⇒ ((SAB),(SCB)) = (AM,CM) + Nếu 0 OC
AMC = 60 ⇒ MC =
= 3a = BC vô lí vì tam giác MBC vuông tại M 0 sin30 + Nếu 0 OC 3a 2 3a 6
AMC = 120 ⇒ MC = = 3 ⇒ SC = ⇒ SB = 0 sin60 2 2 2 3 2 2 a 6 1 1 9a 3 a 6 9a 3
SD = SB − BD = ⇒V = .S .SD = . . = S . 2 ABC 3 ABC 3 4 2 8
Câu 36: Ta có bao nhiêu giá trị nguyên của m thuộc khoảng ( 2022 − ;2022) để hàm số 2
y = x + m + x + 2(m + ) 2
1 x + m + 2m + 4 + log ( 2
x − m + 2x +1 Ta có tập xác định là 2 ) D = ?
A. 2020. B. 2023. C. 2022 . D. 2021. Lời giải 2 x + 2(m + ) 2
1 x + m + 2m + 4 ≥ 0
Hàm số xác định với mọi x∈ ⇔
luôn đúng với mọi x∈ . 2
x − m + 2x +1 > 0
+) Ta có: x + (m + ) x + m + m + = x + (m + ) 2 2 2 2 1 2 4 1 + 3 > 0 , x ∀ ∈ . +) 2
x − m + 2x +1 > 0 , x ∀ ∈ 2
⇔ x + 2x +1 > , m x ∀ ∈
Xét hàm số f (x) 2 = x + 2x +1 2x
với x∈ ; f ′(x) =1+ . 2 2x +1 x ≤ 0 − ≥ 1 = f ′(x) 2x 2x 0 2 x = 0 ⇔ 1+ = 0 ⇔ 2x +1 = 2 − x ⇔ ⇔ 2 1 x − ⇔ = . 2 2 2 2x +1 2x +1 = 4x 2 1 x − = 2
Bảng biến thiên của hàm số f (x)
Từ bảng biến thiên suy ra: 2 2 x + 2x +1 > , m x ∀ ∈ ⇔ > m . 2 m∈ Kết hợp điều kiện
⇒ có 2022 giá trị của m thỏa mãn bài toán. m∈ ( 2022 − ;2022)
Câu 37: Có bao nhiêu số nguyên x thỏa mãn ( x x 1 9 10.3 + − + )
81 4 − log 2x ≥ 0 ? 2 ( ) A. 7 . B. 6 . C. 8 . D. 5. Lời giải
Xét bất phương trình: ( x x 1 9 10.3 + − + )
81 4 − log 2x ≥ 0 1 2 ( ) ( ) x > 0 x > 0 x > 0 ĐKXĐ: ⇔ ⇔ ⇔ < x ≤ 4 − log (2x) 0 8(*) ≥ 0 2x ≤ 16 x ≤ 8 2
Nếu 4 − log 2x = 0 ⇔ x = 8 thì ( ) 1 được thỏa mãn. 2 ( )
Nếu 0 < x < 8 thì 2 − log(4x) > 0 , bất phương trình tương đương ≥ ≥ + 3x 27 x 3 x x 1 2
9 −10.3 + 81≥ 0 ⇔ 3 x − 30.3x + 81≥ 0 ⇔ ⇔ 3x ≤ 3 x ≤ 1
Kết hợp điều kiện 0 < x < 8 ta có x∈(0; ] 1 ∪[3;8) .
Vậy tập nghiệm BPT là S = (0; ]
1 ∪[3;8]Mà x∈ nên có tất cả 7 giá trị nguyên x thỏa mãn
Câu 38: Cho hàm số y = f (x) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số m để phương trình
f ( f (x) + 2m) +1= f (x) + 2m có đúng 3 nghiệm phân biệt trên[ 1; − ] 1 là A. 0 . B. 1. C. 2 . D. 3. Lời giải
Ta có f ( f (x) + 2m) +1= f (x) + 2m ⇔ f (t) = t −1
Với t f x2m t 2
f x2m 2
Dựa vào đồ thị ta có f t t 1 t
0 f x 2m t 2
f x 2m 2
Dựa vào đồ thị trên ; 1
1 , phương trình f ( f (x)+ 2m)+1= f (x)+ 2m ⇔ f (t) = t −1có đúng 3
3 2m 2 1 3 2m 1 nghiệm phân biệt khi 1 3 2m 1
12m 3 m . 2 3 2m 2 1 12m 5
Vậy không có giá trị nguyên nào của tham số m thỏa mãn bài toán.
Câu 39: Cho hàm số f (x) có đạo hàm trên thỏa mãn ( + 2) ( ) + ( + ) 1 ′( ) = ex x f x x f x và f ( ) 1 0 = . Tính 2 f (2) . 2 2 A. e e f ( ) e 2 = . B. f ( ) e 2 = . C. f (2) = . D. f (2) = . 3 6 3 6 Lời giải Ta có
( + 2) ( )+( + )1 ′( ) = ex x f x x f x ⇔ ( + ) 1 ( ) + ( ) + ( + ) 1 ′( ) = ex x f x f x x f x ( ) 1 ( ) ( ) 1 ( ) ex x f x x f x ′ ⇔ + + + = x ( ) ( ) x ( ) ( ) 2 e 1 e 1 e x x f x x f x ′ ⇔ + + + = x ⇔ ( + ) ( ) 2 e 1 = e x x f x ′ x ′ x x 1 x ⇒
∫ (x+ ) f (x) 2 e 1 dx = e dx ∫ ⇔ e (x + ) 1 f (x) 2 = e + C 2 x Mà f ( ) 1
0 = ⇒ C = 0 . Vậy f (x) 1 e = . 2 2 x +1
Câu 40: Cho hàm số y = f (x) liên tục và là hàm số chẵn trên . Biết 2 2
f (2x −1) + 2 f (2x − 3) = 24x − 28x + 20, x
∀ ∈ , tính f (x)dx ∫ ? 0 A. 24 . B. 36. C. 12. D. 36 − . Lời giải Ta có 2
f (2x −1) + 2 f (2x − 3) = 24x − 28x + 20, x ∀ ∈ 3 3 3 2 2 2 2
⇒ f (2x −1)dx + 2 f (2x − 3)dx = (24x − 28x + 20)dx =18 ∫ ∫ ∫ 1 1 1 2 2 2 3 2 Tính M t
= f (2x −1)dx ∫ : Đặt d t = 2x −1⇒ = dx . Đổi cận: 1 3
x = → t = 0 ; x = → t = 2 1 2 2 2 2 3 2 2 1 1 2 ⇒ M = f (t)dt = f (x)dx.
N = 2 f (2x − 3)dx
t = x − ⇒ t = x . 2 ∫ 2 ∫ Tính ∫ : Đặt 2 3 d 2d 0 0 1 2 0 0 2 Đổi cận 1 3 x = → t = 2
− ; x = → t = 0 ⇒ N = f (t)dt = f (x)dx = f (x)dx. 2 2 ∫ ∫ ∫ 2 − 2 − 0 0 2 2 (Vì 1
f (x) là hàm số chẵn nên f (x)dx =
f (x)dx = f (x)dx ∫ ∫ ∫ ) − 2 2 2 − 0 2 2 2 Suy ra 1 M + N =
f (x)dx + f (x)dx =18 ⇒ f (x)dx =12 2 ∫ ∫ ∫ . 0 0 0
Câu 41: Mỗi lượt, ta gieo một con súc sắc (loại 6 mặt, cân đối) và một đồng xu (cân đối). Tính xác suất để
trong 3 lượt gieo như vậy, có ít nhất một lượt gieo được kết quả con xúc sắc xuất hiện mặt 1 chấm, đồng thời đồng xu xuất hiện mặt sấp. A. 397 . B. 1385 . C. 1331 . D. 1603 . 1728 1728 1728 1728 Lời giải Gọi Ω = (
{ x ;y ):x =1,. ,6, y ∈{S;N},i =
là biến cố xuất hiện trong 3 lần gieo, với (x y lượt gieo i ; i ) i i i i 1,2, } 3
thứ i con súc sắc xuất hiện mặt x chấm, đồng xu suất hiện mặt y với x ∈
và y ∈ S N . i { ; } i {1;2;3;4;5; } 6 i i
Khi gieo 3 lần, con súc sắc và đồng xu xuất hiện mặt bất kì ta có: gieo lần 1 (lần 2 hoặc lần 3) có 6.2 số
phần tử của không gian mẫu là n(Ω) = ( )3
6.2 =1728 . Gọi A là biến cố trong 3 lượt gieo ít nhất một lượt
gieo được kết quả con xúc sắc xuất hiện mặt 1 chấm, đồng thời đồng xu xuất hiện mặt sấp. Khi đó biến cố A
xảy ra các khả năng như sau:
TH1: Gọi biến cố A chỉ có một lần gieo kết quả con xúc sắc xuất hiện mặt 1
1 chấm, đồng thời đồng xu xuất
hiện mặt sấp thì A có số phần tử là n( A =11 .3 = 363 (do biến cố (1;S ) xuất hiện ở một trong 3 lần gieo 1 ) 2 1 có 1
C = 3 khả năng xảy ra, hai lần gieo còn lại không xuất hiện biến cố đó mỗi lần còn 11 khả năng xảy ra). 3
TH2: Gọi biến cố A có 2
2 lần gieo kết quả con xúc sắc xuất hiện mặt 1 chấm, đồng thời đồng xu xuất hiện
mặt sấp thì A có số phần tử là n( A = 3.11= 33 (do 2 trong 3 lần gieo xuất hiện biến cố (1;S ) có 2 C = 3 2 ) 2 3
khả năng, lần gieo còn lại không xuất hiện biến cố đó có 11 khả năng xảy ra).
TH3: Gọi biến cố A cả 3 lần gieo kết quả con xúc sắc xuất hiện mặt 3
1 chấm, đồng thời đồng xu xuất hiện
mặt sấp thì A có số phần tử là n( A =1. 3 ) 3
Do đó n( A) = n( A + n A + n A = 363+ 33+1 = 397 . 1 ) ( 2) ( 3) n A
Vậy xác suất cần tìm là P( A) ( ) 397 = . n( ) = Ω 1728
Câu 42: Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh 4a , S
∆ AB là tam giác đều và nằm trong mặt
phẳng vuông góc với đáy,
ABC = 60 . Gọi M là điểm trên cạnh CD sao cho CM= 3a . Khoảng cách giữa hai
đường thẳng SB và AM bằng A. 4 51 a . B. 4 39 a . C. 8 39 a . D. 8 51 a . 17 13 13 17 Lời giải (
SAB) ⊥ ( ABCD) Ta có: (
SAB) ∩ ( ABCD) = AB ⇒ SH ⊥ ( ABCD) . Tr (SAB) ong , SH ⊥ AB
Theo giả thiết ta có: AB = BC = 4a và 0 ABC = 60 nên A
∆ BC là tam giác đều, cạnh 4a . (4a)2 3 2 ⇒ S = = a a = = ABC 4 3 và 4 3 SH 2 3a . 4 2 Ta có: 2 2 2 = + − AM AD DM 2A .
D DM.cos ADM = ( a)2 2 2 4 + a − 2.4 . a .
a cos60° =13a .
⇒ AM = a 13 . Trên tia đối của tia CD lấy điểm E sao cho CE = a .
Khi đó, tứ giác AMEB là hình bình hành⇒ BE = AM = a 13 . Mặt khác, A ∆ DM = B ∆ CE 2 2 ⇒ S = S = S = a = a . AMEB ABCD 2 ABC 2.4 3 8 3 AM ⊄ (SBE)
Ta có: AM // BE
⇒ AM // (SBE) . Do đó d( AM ,SB) = d( AM ,(SBE)) = d( , A (SBE)). BE ⊂ (SBE) d( , A (SBE)) Ta lại có: AB ( = = ⇒ d( ,
A (SBE)) = 2d(H,(SBE)) . H (SBE)) 2 d , HB
Trong ( ABCD) , gọi K và F lần lượt là hình chiếu của H và A lên BE . 1 1 2 1 8 3a 4 39a
⇒ HK = AF = . SAMEB = . =
(do HK là đường trung bình của A ∆ BF ). 2 2 EB 2 a 13 13 BE ⊥ HK
BE ⊥ SH ( Do SH ⊥(ABCD) ⊃ BE) Ta có:
⇒ BE ⊥ (SHK ). Mà BE ⊂ (SBE) ⇒(SBE) ⊥ (SHK ) .
HK, SH ⊂ (SHK )
HK ∩ SH = H
Ta lại có: (SBE) ∩(SHK ) = SK. ⇒ HI ⊥ (SBE)
Trong (SHK ) , kẻ HI ⊥ SK (I ∈ SK )
⇒ d(H,(SBE)) = HI . Tam giác 1 1 1 1 1 17
SHK vuông tại H , đường cao HI nên = + = + = 2 2 2 HI SH HK (2 3a)2 2 2 48 4 39 a a 13 . Do đó: 4 51 HI =
a .Vậy d ( AM SB) 8 51 , = a . 17 17 x Câu 43: Cho hàm số 2 + 2 f (x) = log
. Tìm tất cả các giá trị thực của tham số m để bất phương trình 2 2x 4 +
f ( 2x + x −( 2 2 2
3− x )3 + 3)+ f ( x + m)3 + 2m−6) ≥ 1
− nghiệm đúng với mọi x ∈[ 1; − ] 3 . A. 13 m ; ∈ +∞ B. 15 m ∈ ;+∞ C. m∈[ 9; − +∞) D. m∈[3;+∞) 4 4 Lời giải
f (x) là hàm đồng biến, f (u) + f (3− u) = 1 − . Bpt ⇔ − f ( 2 − x − x + ( 2 2 2
3− x )3)+ f ( x + m)3 + 2m−6) ≥ 0 2
⇔ − x − x + ( 2 2 2
3− x )3 ≤ (x + m)3 + 2m − 6 ⇔ ( 2 − x ) + ( 2 2 3
3− x )3 ≤ (x + m)3 + 2(x + m) (1)
Xét hàm số g (t) 3
= t + 2t trên R Ta có: g (t) 2
' = 3t + 2 > 0 t
∀ nên hàm số g (t) đồng biến trên R 2 2
(1) ⇔ 3− x ≤ x + m ⇔ m ≥ −x − x + 3 x ∀ ∈[ 1; − ]3 Ta có ⇔ m ≥ ( 2 −x − x + ) 13 max 3 ⇔ m ≥ x [ ∈ 1 − ; ] 3 4
Câu 44: Có bao nhiêu số nguyên của x sao cho tồn tại số thực y thỏa mãn 2log (x + y + ) 1 = log ( 2 2
x + 2x + 2y +1 ? 3 2 ) A.2. B. 1. C. 3. D. 4. Lời giải
Đặt 2log (x + y + ) 1 = log ( 2 2
x + 2x + 2y +1 = 2t 3 2 )
x + y +1= 3t
x + y +1= 3t ⇒ ⇔ . 2 2
x + 2x + 2y +1 = 4t ( x + )2 2 1 + 2y = 4t 2 Ta có: t = ( + ) 2 + = ( + ) 1 1 + ≤ + ( + )2 2 3 9 1 1. 1 . 2 1 1 + 2 = .4t x y x y x y 2 2 2 9 t 3 1 1 ⇒ ≤ ⇒ t ≤ 2 2 t 2
. Lại có (x + ) + y = ⇒ (x + ) t 2 1 2 4
1 ≤ 4 ≤ 4 = 2 ⇒ x∈{ 2 − ; 1; − } 0 (do x∈). 4 2 2
Nếu x = 0 ta có phương trình 2log ( y + ) 1 = log ( 2
2y +1 . Ta thấy phương trình này có nghiệm 3 2 ) y = 0 Nếu x = 1 − ta có phương trình t log 4 2 y = 3 2 t t 9
2log y = log 2y = 2t ⇒
⇒ 2.9 = 4 ⇒ t = log 2 ⇒ y = 3 3 2 4 . 2 2y = 4t 9 log 2
Ta thấy phương trình này có nghiệm 4 9 y = 3 . Nếu x = 2
− ta có phương trình 2log ( y − ) 1 = log ( 2 2y +1 = 2t 3 2 ) t y −1= 3 ⇒
⇒ 2.9t + 4.3t + 3 = 4t (*) . 2 t 2y +1= 4 Ta có t 2
4 = 2 +1≥1⇒ ≥ 0 ⇒ 2.9t > 4t y t . Suy ra (*) 4t VT
> nên phương trình (*) vô nghiệm.
Vậy có 2 giá trị nguyên của x thỏa mãn yêu cầu bài toán.
Câu 45: Cho hàm số y = f (x) có đồ thị như hình vẽ. Gọi S là tập hợp các giá trị của tham số m để bất phương trình f (sin x) x (m − 2 ) f (sin x) 2 f (x) + 2.2 + m − 3. (2 − )
1 ≥ 0 nghiệm đúng với mọi x ∈ . Số tập con của tập hợp S là A. 4 . B. 1. C. 2 . D. 3. Lời giải
Nhận xét phương trình f (x) 2
−1 = 0 có một nghiệm bội lẻ x = 2 nên biểu thức f (x) 2
−1 sẽ đổi dấu khi đi qua
điểm x = 2 . Do đó để bất phương trình đã cho nghiệm đúng với mọi x∈ thì phương trình m =1 f (sin x) x(m − ) f (sin x) 2 2 + 2.2
+ m − 3 = 0 phải có một nghiệm x = 2 2
⇒ m + 2m − 3 = 0 ⇔ . m = 3 −
Thử lại với m =1 ta có: f (sin x) x f sin x f x (1− 2 ) f (sin x) f (x) + 2.2
− 2(2 − )1 ≥ 0 ⇔ (x −2) ( ) (1−2 ) ( ) (2 − )1≥0 f (sin x) ⇔ 2
≤1 ⇔ f (sin x) ≤ 0 ⇔ sin x ≤ 2 luôn đúng với mọi x∈ R ⇒ m =1 thỏa mãn ycbt. Thử lại với m = 3 − ta có: f (sin x) x f sin x f x ( 3 − − 2 ) f (sin x) f (x) + 2.2
+ 6(2 − )1 ≥ 0 ⇔ −(x −2) ( ) (3+2 ) ( ) (2 − )1≥0 f (sin x) ⇔ 3+ 2
≤ 0 (vô lý) ⇒ m = 3
− không thỏa mãn ycbt. Vậy S = { }
1 . S có 2 tập con đó là { } 1 và ∅ .
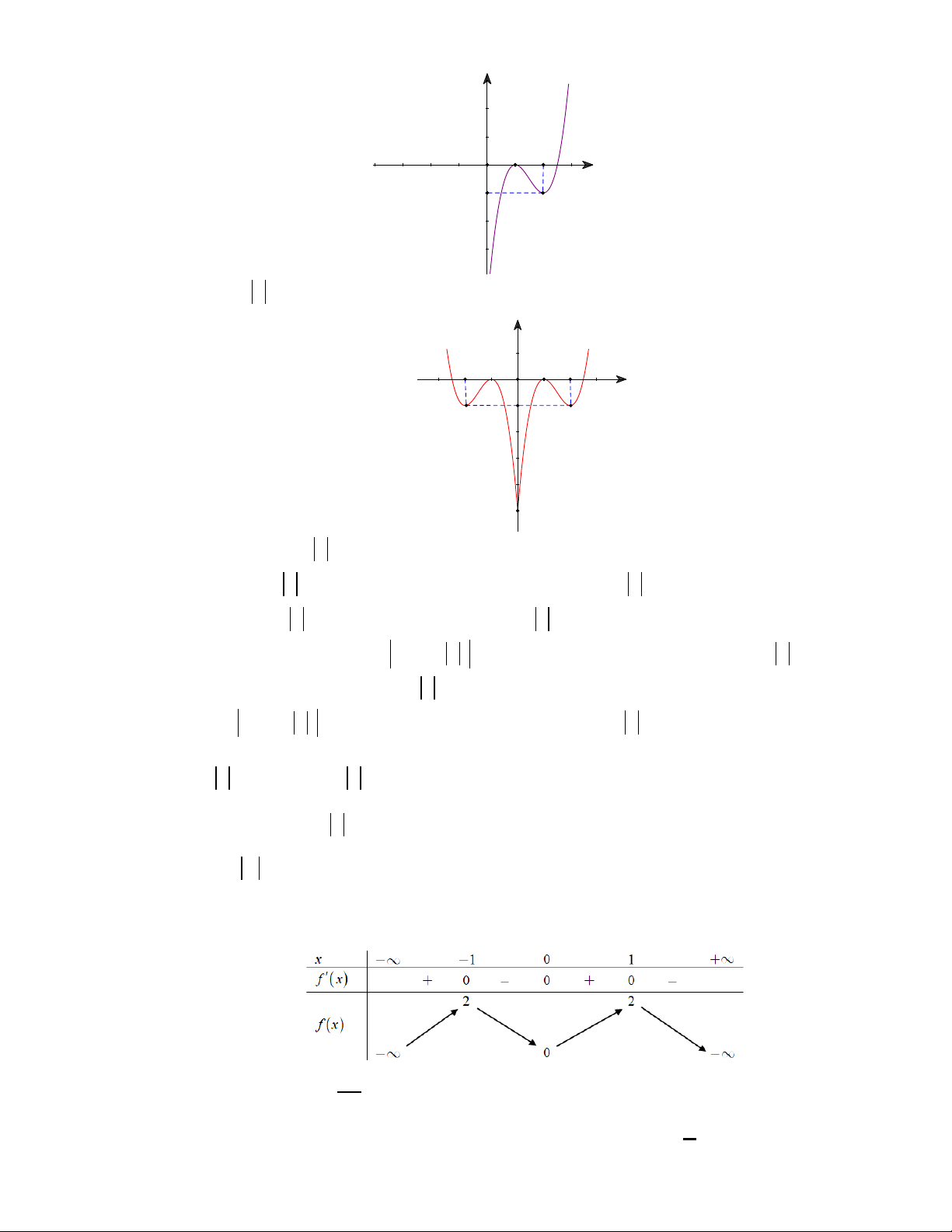
Câu 46: Cho hàm số bậc ba y = f (x) có bảng biến thiên như hình vẽ:
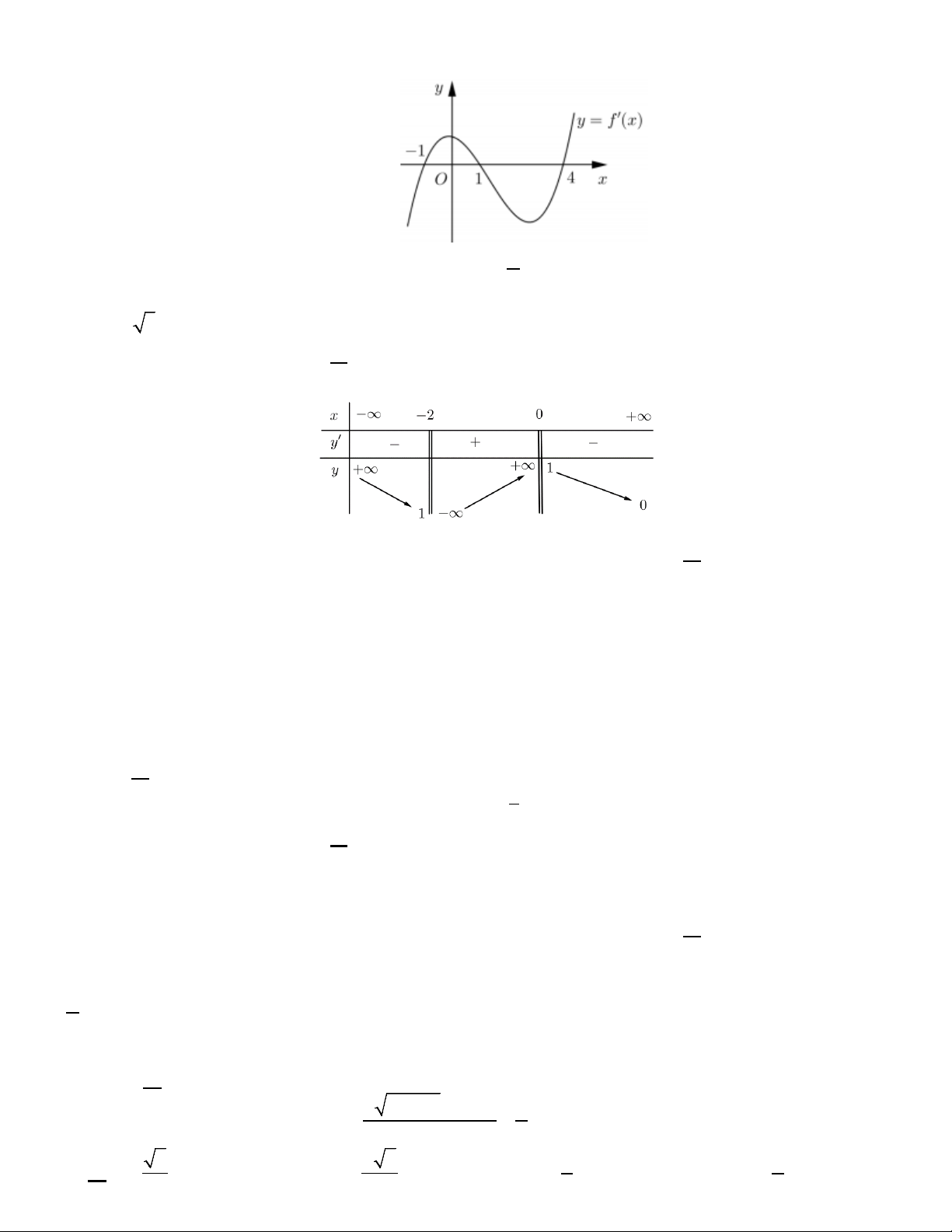
Hỏi có bao nhiêu giá trị của tham số m (với m∈ ; m ≤ 2021) để đồ thị hàm số y = m + f ( x ) có đúng 7 điểm cực trị? A. 2026 . B. 2025 . C. 4 . D. 2022 . Lời giải
Từ bảng biến thiên của hàm số bậc ba y = f (x) , ta có f ′(x) = a( 2
x − 3x + 2) . Suy ra 3 2 ( ) x 3x f x = a − + 2x + d . 3 2 1 3 a 2 − + + d = 0 3 2 Mặt khác, f ( ) 1 = 0, f (2) = 1 − nên . 8 12 a − + 4 + d = 1 − 3 2
Do đó, a = 6 và d = 5 − hay f (x) 3 2
= 2x − 9x +12x − 5.
Đồ thị y f x y
y = f(x) -1 1 2 O x -1
Đồ thị y f x y -2 2 O -1 1 x -1 -5
Từ đồ thị ta có y f x có 5 điểm cực trị.
Vì hàm số y f x có 5 điểm cực trị nên hàm số y m f x cũng có 5 điểm cực trị (Vì đồ thị
hàm số y m f x được suy ra từ đồ thị y f x bằng cách tịnh tiến theo phương trục Oy ).
Số điểm cực trị của hàm số y = m + f ( x ) bằng số cực trị của hàm số y = m + f ( x ) và số nghiệm
đơn hoặc bội lẻ của phương trình f ( x ) + m = 0.
Vậy để y = m + f ( x ) có 7 điểm cực trị thì phương trình f x m 0 có hai nghiệm đơn hoặc bội lẻ.
Ta có f ( x ) + m = 0 ⇔ f ( x ) = −m. 5 − < −m ≤ 1 − 1 ≤ m < 5
Từ đồ thị hàm số y = f ( x ) ta có: ⇔ ( )1 0 m ≤ − m ≤ 0
Từ giả thiết m ≤ 2021 ⇔ 2021 − ≤ m ≤ 2021 (2) Vậy từ ( )
1 , (2) và kết hợp điều kiện m , ta có 2026 giá trị nguyên của m
Câu 47: Cho hàm số y = f (x) có bảng biến thiên như sau: π Số nghiệm thuộc đoạn 9 0;
của phương trình f ( f (cos x)) = 2 là 2 A.3 . B.5 . C.7 . D.9 . Lời giải
cos x = a ∈( ; −∞ − ) 1 ( )1
cos x = b ∈( 1; − 0) (2) f (cos x) 1 =
cos x = c∈(0; ) 1 (3)
f ( f (cos x)) = 2 ⇔ ⇔ f (cos x) 1 = −
cos x = d ∈(1;+∞) (4)
x = e∈(−∞ − ) e < a (5 cos ; 1 , ) cos x = f ∈ (1;+∞) (6) f < d π Xét trên đoạn 9 0; ta có: Phương trình ( )
1 , (4) , (5), (6) vô nghiệm. 2
Phương trình (2) có 4 nghiệm, phương trình (3) có 5 nghiệm. Vậy phương trình đã cho có 9 nghiệm.
Câu 48: Cho hàm số bậc bốn y = f (x) có đồ thị như hình vẽ bên.
Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [0;20] sao cho giá trị nhỏ nhất của hàm số
g (x) = 2 f (x) + m + 4 − f (x) −3 trên đoạn [ 2;
− 2] không bé hơn 1? A. 18. B. 19. C. 20 . D. 21. Lời giải
Dựa vào hình vẽ ta có: 2
− ≤ f (x) ≤ 2, x ∀ ∈[ 2;
− 2] (*) .⇒ 2 f (x) + 4 ≥ 0, x ∀ ∈[ 2; − 2] .
Vì m∈[0;20] nên 2 f (x) + m + 4 ≥ 0
suy ra 2 f (x) + m + 4 = 2 f (x) + m + 4, x ∀ ∈[ 2 − ;2].
Ta có: g (x) = 2 f (x) + m + 4 − f (x) − 3 = 2 f (x) + m + 4 − f (x) −3 = f (x) + m +1 , x ∀ ∈[ 2; − 2].
+) Với m = 0 ⇒ g (x) = f (x) +1 , x ∀ ∈[ 2; − 2]. (*) ⇔ 1
− ≤ f (x) +1≤ 3, x ∀ ∈[ 2
− ;2].⇒ 0 ≤ f (x) +1 ≤ 3, x ∀ ∈[ 2
− ;2] ⇔ 0 ≤ g (x) ≤ 3, x ∀ ∈[ 2 − ;2].
⇒ min g (x) = 0 ⇒ m = 0 không thỏa yêu cầu bài toán. [ 2; − 2]
+) Với m∈[1;20] ⇒ f (x) + m +1≥ 0 ⇒ g (x) = f (x) + m +1.
Từ (*) ta có: f (x) + m +1≥ m −1 ⇒ min g (x) = m −1. [ 2; − 2]
Yêu cầu bài toán: min g (x) ≥1 ⇔ m −1≥1 ⇔ m ≥ 2 ⇒ m∈[2;20]. Vậy có 19 giá trị nguyên [ 2; − 2]
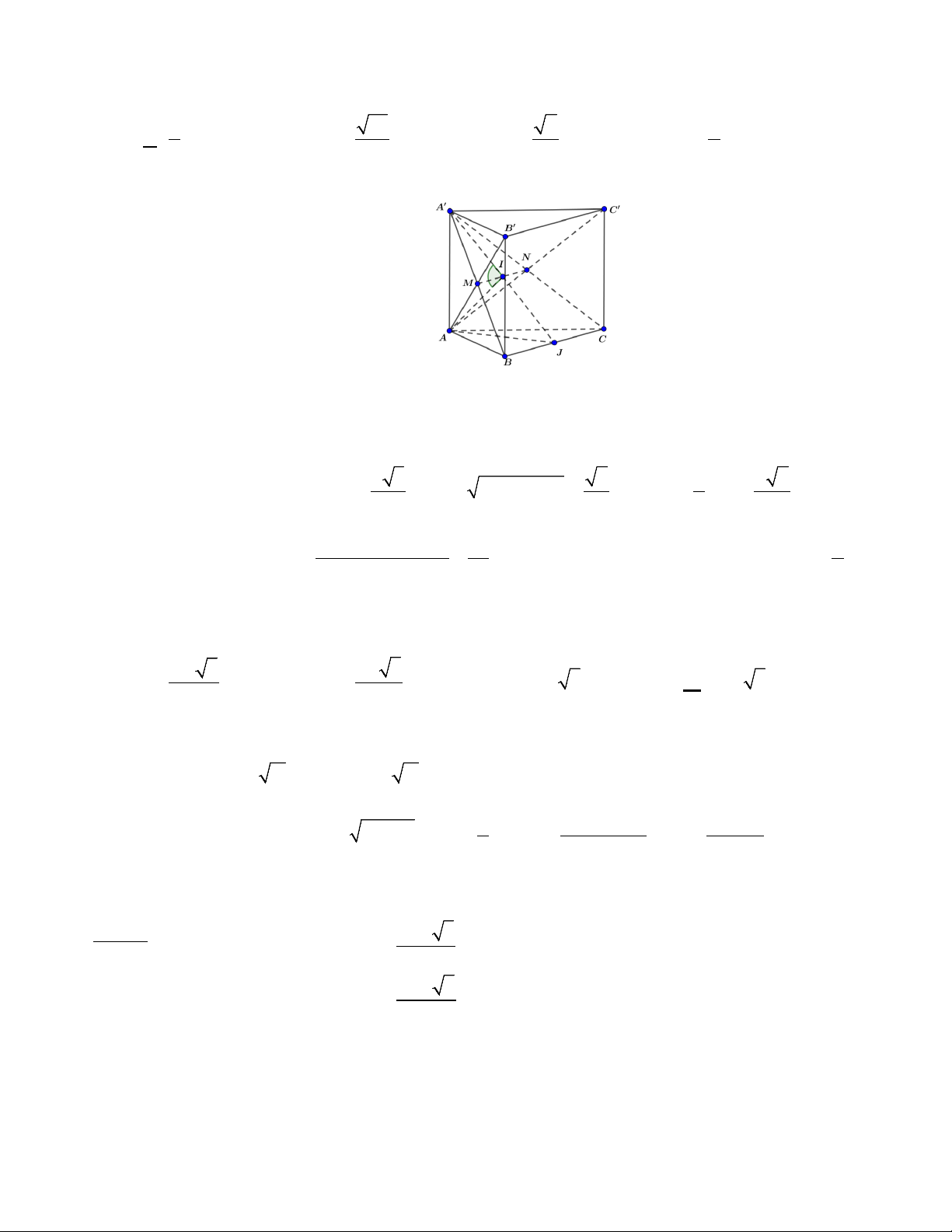
Câu 49: Cho lăng trụ ABC.A′B C
′ ′. Gọi M , N , Q , R lần lượt là trung điểm của các cạnh AB , A′B′ , BC , B C
′ ′ và P , S lần lượt là trọng tâm của các tam giác AA′B , CC B
′ . Tỉ số thể tích khối đa diện MNRQPS và khối
lăng trụ ABC.A′B C ′ ′ là A. 1 . B. 5 . C. 1 . D. 2 . 9 54 10 27 Lời giải 1 2
Đặt: V = V ; V = ′ ′ ′ = ′ ′ ′ S ′ ′ B AA C C V B AA C C AA C C .d , . ( ( ))
ABC.A′B C ′ ′ 3 3 1 1 1 1 V = ′ = ′ ′ ′ ′ S B MNRQ S ′ ′ B AA C C B MNRQ . MNRQ.d , AA C C . d , . ( ( )) ( ( )) 3 3 2 2 1 = S ′ ′ ′ = = ′ ′ B AA C C V V AA C C ( ( )) 1 1 2 1 . .d , . . 3 4 4 3 6 1 1 1 1 1 V = V = = = ′ V ′ V V P MNRQ . A MNRQ . B MNRQ . . . . 3 3 3 6 18 1 2 V = ′ ′ = ′ ′ S ′ ′ A BB C C V A BB C C BB C C .d , . ( ( )) 3 3 1 1 S = = ; 1 1 1 1 S = S = = ′ S ′ ′ S QRS QRC . ′ S ′ S QRC
2 QRC C 4 BBC′ C′ 3
3 4 BBC C 12 BBC′ C′ 1 1 1 V = S A QRS = S ′ ′ ′ ′ A BB C C A QRS QRS .d , BB C C . d , . ( ( )) ( ( ( ))) 3 3 12 1 PB′ 2 1 1 = S ′ ′ = = , V = V = V = V P QRS . AQRS . ′ ′ A BB C C V V BB C C ( ( )) 1 1 2 1 . .d , . . 3 12 12 3 18 . . AB′ 3 18 27 1 1 5 VMNRQPS 5 V = V +V = V + V = V , Vậy: = . MNRQPS P.MNRQ P.QRS 18 27 54
VABC A′BC′′ 54 .
Câu 50: Cho hình chóp S.ABC có SA = x, BC = y, AB = AC = SB = SC =1. Thể tích khối chóp S.ABC đạt giá
trị lớn nhất khi tổng (x + y) bằng A. 2 . B. 3 . C. 4 . D. 4 3 . 3 3 Lời giải: S x 1 K 1 1 C y A H I 1 B
Gọi I, K lần lượt là trung điểm của S ,
A BC và H là hình chiếu của S lên (ABC) .
Ta có: BC ⊥ (SAI) và H ∈ AI, S
∆ AI cân tại I . 2 2 y 4 − y 2 2 − x − y 2 2
SI = AI = SC − IC = 1− = , 2 2 4
IK = AI − AK = 2 2 2 2 2 1 1 S . A IK
.x 4 − x − y
S = SH AI = SA IK ⇒ SH = = SAI . . 2 2 2 AI 4 − y 2 1 y 4 − y S = BC AI = ABC . 2 4
Theo bất đẳng thức trong tam giác ta có: 0 < x, y < 2
Thể tích của khối chóp S.ABC là 1 1 V = S SH = xy − x + y ≤ xy − xy S ABC ABC ( 2 2 1 . . 4 4 2 . ) (vì 3 12 12 2 2
x + y ≥ 2xy ) 3 Suy ra 1 1
1 xy xy 4 2xy 32 3 V ≤ xy − xy = xy xy − xy + + − ≤ = S ABC 4 2 . . 4 2 . ( ) 12 12 12 3 3 x = y V 32 3 2 4 ⇔ V = ⇔ x = y = ⇒ x + y =
S.ABC lớn nhất S.ABC khi và chỉ khi . 3
xy = 4 − 2xy 3 3
Document Outline
- TOAN LẦN 3 NĂM 2022-2023
- ĐÁP ÁN TOAN LẦN 3 NĂM 22-23