Đề học sinh giỏi Toán 12 năm 2022 – 2023 trường THPT Yên Định 1 – Thanh Hóa

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 12 đề thi giao lưu học sinh giỏi môn Toán 12 THPT năm học 2022 – 2023 trường THPT Yên Định 1, tỉnh Thanh Hóa; đề thi hình thức trắc nghiệm với 50 câu hỏi và bài toán

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 12

Môn: Toán 12

Thông tin:

21 trang 8 tháng trước

Tác giả:

Profile Nguyễn Vân
Trang 1/6 - Mã đề 101
TRƯỜNG THPT YÊN ĐỊNH 1
ĐỀ CHÍNH THỨC
MÃ ĐỀ 101
KỲ THI GIAO LƯU HỌC SINH GIỎI LỚP 12 THPT
NĂM HỌC 2022-2023
Môn: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian giao đề)
Ngày thi: / /2022
Câu 1. Cho hàm số
( )
2
2
khi 1
1
3 khi 1
xx
x
fx
x
mx
+−
≠
=
−
=
. Tìm tất cả các giá trị thực của tham số m để hàm số gián
đoạn tại
1.x =
A.
1.m ≠
B.
2.
m
≠
C.
3.m ≠
D.
2.m ≠
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Bất kì một hình chóp nào cũng có một mặt cầu ngoại tiếp.
B. Bất kì một hình lăng trụ nào cũng có một mặt cầu ngoại tiếp.
C. Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp.
D. Bất kì một hình tứ diện nào cũng có một mặt cầu ngoại tiếp.
Câu 3. Chu kỳ của hàm số
3sin
2
x
y
=
là số nào sau đây?
A.
. B.
π
. C.
0
. D.
.
Câu 4. Cho hai tích phân
( )
5
2
d8fx x
−
=
∫
và
(
)
2
5
d3
gx x
−
=
∫
. Tính
( ) ( )
5
2
4 1dI f x gx x
−
= −−


∫
.
A.
13I =
. B.
27
I =
. C.
3I
=
. D.
11I = −
.
Câu 5. Một hình trụ có bán kính đáy
4 c mr =
và độ dài đường sinh
3 c ml =
. Diện tích toàn phần của
hình trụ đó bằng
A.
2
24 cm
π
. B.
2
40 cm
π
C.
2
56 cm
π
D.
2
36 cm
π
Câu 6. Cho hình lăng trụ tứ giác đều
..ABCD EFGH
Tính tỉ số
k
giữa thể tích khối trụ ngoại tiếp và thể tích
khối trụ nội tiếp hình lăng trụ trên.
A.
2 2.k =
B. C.
2.k
=
D.
2.k =
Câu 7. Cho hình lăng trụ đứng
.' ' '
ABC A B C
có đáy
ABC
là tam giác vuông cân tại
A
,
2,BC a
'AB
tạo
với đáy một góc bằng
0
60
. Thể tích của khối lăng trụ bằng
A.
3
3
2
a
. B.
3
3
4
a
. C.
3
3
2
a
. D.
3
2
a
Câu 8. Hình vẽ bên dưới có bao nhiêu mặt
A.
4
. B.
10
. C.
7
. D.
9
.
Câu 9. Giá trị nhỏ nhất của hàm số
21
1
x
y
x
+
=
−
trên đoạn
[ ]
2;3
bằng
A.
3−
. B.
3
4
. C.
5−
. D.
7
2
−
.
Câu 10. Cho dãy số
( )
n
u
với
( )
1
n
n
un= −
. Mệnh đề nào sau đây đúng?
Trang 2/6 - Mã đề 101
A. Dãy số
( )
n
u
là dãy số không bị chặn. B. Dãy số
( )
n
u
là dãy số giảm.
C. Dãy số
( )
n
u
là dãy số tăng. D. Dãy số
( )
n
u
là dãy số bị chặn.
Câu 11. Có bao nhiêu số chẵn mà mỗi số có
4
chữ số đôi một khác nhau?
A.
50000
. B.
4500
. C.
2296
. D.
2520
.
Câu 12. Trên giá sách có
4
quyển sách toán, 3 quyển sách lý,
2
quyển sách hóa. Lấy ngẫu nhiên
3
quyển
sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán.
A.
2
.
7
B.
3
.
4
C.
37
.
42
D.
10
.
21
Câu 13. Cho
0, 1>≠aa
. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Tập giá trị của hàm số
log=
a
yx
là tập
.
B. Tập giá trị của hàm số
=
x
ya
là tập
.
C. Tập xác định của hàm số
log=
a
yx
là tập
.
D. Tập xác định của hàm số
=
x
ya
là khoảng
( )
0; +∞
.
Câu 14. Hình vẽ bên là đồ thị các hàm số
=
a
yx
,
=
b
yx
,
c
yx=
trên miền
( )
0; +∞
. Hỏi trong các số
a
,
b
,
c
số nào nhận giá trị trong khoảng
( )
0; 1
?
A. Số
.b
B. Số
.c
C. Số
a
. D. Số
a
và số
.c
Câu 15. Tích phân
(
)
2
1
2
0
1
d ln
1
x
I x a bc
x
−
= = +
+
∫
, trong đó
a
,
b
,
c
là các số nguyên. Tính giá trị của biểu thức
abc++
?
A.
3
. B.
0
. C.
1
. D.
2
.
Câu 16. Tổng tất cả các cạnh của khối lăng trụ không thể bằng số nào sau đây?
A.
2025
. B.
2019
. C.
2020
. D.
2022
.
Câu 17. Cho
9 9 23
−
+=
xx
. Khi đó biểu thức
53 3
13 3
−
−
++
= =
−−
xx
xx
a
A
b
với
a
b
tối giản và
, ∈ab
. Tích
có giá
trị bằng:
A.
10
. B.
8−
. C.
8
. D.
10−
.
Câu 18. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
4mx
y
xm
+
=
+
giảm trên khoảng
( )
;1−∞
?
A. Vô số. B.
1
. C.
0
. D.
2
.
Câu 19. Tìm giá trị thực của tham số
m
để hàm số
32
3y x x mx=−+
đạt cực tiểu tại
2x =
.
A.
0m =
. B.
2m = −
. C.
1m =
. D.
2m =
.
Câu 20. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào?
O
x
y
1
2
2
2−
1−
O
x
y
a
yx=
b
yx=
c
yx=
Trang 3/6 - Mã đề 101
A.
32
31
yx x=−+
. B.
32
32
yx x=−+
.
C.
32
32
yx x
=++
. D.
32
32
yxx
=−+ +
.
Câu 21. Tập nghiệm của bất phương trình
7 10 3x≥−
x
chứa bao nhiêu số nguyên dương nhỏ hơn
10
?
A.
11
. B.
9
. C.
8
. D.
10
.
Câu 22. Cho tứ diện
OABC
có
,
OA
,
OB
OC
đôi một vuông góc và đều bằng
.a
Khoảng cách giữa hai đường
thẳng
OA
và
bằng
A.
3
.
2
a
B.
.a
C.
2.a
D.
2
.
2
a
Câu 23. Kết quả của
d
x
I xe x=
∫
là
A.
xx
IxeeC= −+
. B.
xx
I e xe C
=++
.
C.
2
2
x
x
I eC= +
. D.
2
2
xx
x
I eeC= ++
.
Câu 24. Cho hàm số
(
)
fx
liên tục trên đoạn
[ ]
0;10
và
( )
10
0
d7fx x=
∫
và
(
)
6
2
d3fx x
=
∫
. Tính
( ) ( )
2 10
06
ddP fx x fx x= +
∫∫
.
A.
4P = −
. B.
4P =
. C.
10P =
. D.
7P =
.
Câu 25. Cho tứ diện
SABC
có
, 2, 3SA a SB a SC a= = =
. Giá trị lớn nhất của thể tích tứ diện bằng
A.
3
6a
. B.
3
a
. C.
3
3
a
. D.
3
6
a
.
Câu 26. Cho hình hộp chữ nhật
ABCDA B C D
′′′′
. Khoảng cách giữa
AB
và
BC
′
là
25
5
a
, giữa
BC
và
AB
′
là
25
5
a
, giữa
AC
và
BD
′
là
3
3
a
. Thể tích của khối hộp đó là:
A.
3
4a
. B.
3
2
a
. C.
3
a
. D.
3
8a
.
Câu 27. Cho đa giác lồi
n
cạnh (
*, 6∈≥nn
) nội tiếp đường tròn
( )
O
sao cho không có ba đường chéo
nào đồng quy. Các cạnh và các đường chéo của đa giác giao nhau tạo thành các tam giác. Gọi
X
là tập hợp
các tam giác như thế. Lấy ngẫu nhiên một tam giác trong tập
X
. Tìm
n
để xác suất lấy được tam giác không
có đỉnh nào là đỉnh của đa giác bằng
4
15
.
A.
23=n
. B.
19=n
. C.
15=n
. D.
11=n
.
Câu 28. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác đều cạnh
a
. Hình chiếu vuông góc của
S
trên đáy là điểm
H
trên cạnh
AC
sao cho
2
3
AH AC=
; mặt phẳng
( )
SBC
tạo với đáy một
góc
60
o
. Thể tích khối chóp
.S ABC
là?
A.
3
3
48
a
B.
3
3
36
a
C.
3
3
24
a
D.
3
3
12
a
Câu 29. Cho hình chóp
.S ABCD
có đáy là hình thoi cạnh
2AB BD= =
, hai đường chéo cắt nhau tại
O
.
Hình chiếu vuông góc của
S
trên mặt phẳng
( )
ABCD
là trung điểm
H
của
BO
. Gọi
G
là trọng tâm tam giác
ADC
. Biết
SC
tạo với mặt phẳng đáy góc
45°
, tính khoảng cách giữa hai đường thẳng
SA
và
CG
.
A.
6 2373
113
. B.
2373
113
. C.
2 14313
367
. D.
4 14313
367
.
Câu 30. Có bao nhiêu giá trị nguyên của
m
thuộc đoạn
0;18
để phương trình
4
2 log 1x xm x 
có
đúng một nghiệm dương?
A.
16
. B.
17
. C.
19
. D.
18
.
Trang 4/6 - Mã đề 101
Câu 31. Cho hàm số
( )
fx
có
( )
49
3
2
f =
và
( )
fx
′
=
3
22
,0
16 4 16
x
x
xx
∀≠
+− +
. Khi đó
(
)
3
0
.dxf x x
∫
bằng
A.
2915
24
. B.
2195
24
. C.
2195
8
. D.
2915
3
.
Câu 32. Cho hình chóp
.S ABC
có đáy
ABC
là tam giác vuông cân tại
B
,
2
AC a=
, tam giác
SAB
và tam
giác
SCB
lần lượt vuông tại
A
và
C
. Khoảng cách từ
S
đến mặt phẳng
(
)
ABC
bằng
a
. Cosin của góc giữa
hai mặt phẳng
(
)
SAB
và
(
)
SCB
bằng
A.
5
3
. B.
22
3
. C.
1
3
. D.
2
3
.
Câu 33. Có tất cả bao nhiêu giá trị nguyên của
y
sao cho tương ứng mỗi
y
luôn tồn tại không quá
63
số
nguyên
x
thỏa mãn điều kiện
( ) ( )
( )
22
2020 2021 4
64log x y log y y log x y+ + ++ ≥ −
A.
602
B.
2
. C.
301
. D.
302
.
Câu 34. Nghiệm của phương trình
sin 3 .cot cot
xx x=
có các điểm biểu diễn trên đường tròn lượng giác tạo
thành đa giác có diện tích bằng
A.
23
đvdt. B.
3
2
đvdt. C.
3
đvdt. D.
3
4
đvdt.
Câu 35. Cho hàm số
()fx
liên tục trên đoạn
−

4;4
và có bản biến thiên như hình vẽ bên dưới
Có tất cả bao nhiêu giá trị thực của tham số
∈−

4;4m
để hàm số
= ++
3
() ( 2) 3( )gx f x x f m
có giá trị
lớn nhất trên đoạn
−

1;1
bằng
8
?
A.
11
. B.
9
. C.
10
. D.
12
.
Câu 36. Cho hai số thực
x
,
y
thoả mãn:
( ) (
)
22
3
log 3 3 .
2
xy
x x y y xy
x y xy
+
= −+ −+
+++
Tìm giá trị lớn nhất của biểu thức
23
6
xy
P
xy
++
=
++
.
A.
59 259
95
+
B.
33 233
94
+
. C.
3 103
49
+
D.
69 249
94
+
Câu 37. Cho hàm số
( )
y fx
=
có đạo hàm liên tục trên
và
( )
11f =
. Đồ thị hàm số
( )
y fx
′
=
như hình
bên.
Có bao nhiêu số nguyên dương
a
để hàm số
( )
4 sin cos 2y f x xa= +−
nghịch biến trên
0;
2
π



.
Trang 5/6 - Mã đề 101
A. Vô số. B.
5.
C.
2.
D.
3
.
Câu 38. Cho hàm số
=− + −−
3 22 3
3 3( 1)y x mx m x m
với
m
là tham số, gọi
(
)
C
là đồ thị của hàm số đã cho.
Biết rằng, khi
m
thay đổi, điểm cực đại của đồ thị
( )
C
luôn nằm trên một đường thẳng
d
cố định. Xác định
hệ số góc
k
của đường thẳng
d
.
A.
= −
1
3
k
. B.
= −3k
. C.
=
1
3
k
. D.
= 3k
.
Câu 39. Có bao nhiêu giá trị nguyên của tham số
m
để hàm số
( )
=−+ −−
52
55 18yx x m x
nghịch biến trên
khoảng
( )
−∞
;1 ?
A.
1.
B.
0.
C.
4.
D.
2.
Câu 40. Cho hàm số
(
)
fx
có đạo hàm liên tục trên đoạn
[1; 4]
thỏa mãn
( ) ( )
1 1, 4 8ff=−=−
và
( )
2
33
() () 9 3, [1;4]x f x fx x x x x− = −− ∈
′
∀
.Tích phân
( )
4
1
fx x
∫
d
bằng
A.
89
.
6
−
B.
79
.
6
−
C.
8.−
D.
7.−
Câu 41. Cho hàm số
( )
2 2 2019
xx
fx x
−
=−+
. Gọi
S
là tập hợp các giá trị nguyên của
m
thỏa mãn điều kiện
( )
( )
( )
32 2
2 3 2 2 5 0, 0;1fx x xm f x x x−+−+ −−<∀∈
. Số phần tử của
S
là?
A.
5
. B.
7
. C.
3
. D.
9
.
Câu 42. Một chiếc ly dạng hình nón ( như hình vẽ với chiều cao ly là
h
). Người ta đổ một lượng nước
vào ly sao cho chiều cao của lượng nước trong ly bằng
1
4
chiều cao của ly. Hỏi nếu bịt kín miệng ly rồi
úp ngược ly lại thì tỷ lệ chiều cao của mực nước và chiều cao của ly nước bây giờ bằng bao nhiêu?
A.
4 63
4
−
. B.
3
4
. C.
3
4 63
4
−
. D.
3
63
4
.
Câu 43. Cho hình nón đỉnh
S
, đường cao SO,
A
và
B
là hai điểm thuộc đường tròn đáy sao cho
khoảng cách từ
O
đến
( )
SAB
bằng
3
3
a
và
00
30 , 60SAO SAB= =
. Độ dài đường sinh của
hình nón theo
a
bằng
A.
5a
B.
3a
C.
23a
D.
2a
Câu 44. Biết rằng
,xy
là các số thực dương sao cho 3 số
2
log
1
8
xy
u
+
=
,
2
log
2
2
xy
u
−
=
,
3
5uy=
theo thứ tự lập
thành một cấp số cộng và một cấp số nhân. Khi đó, tích
2
2.
x
y
có giá trị bằng:
A. 1. B. 5. C.
. D. 10.
Câu 45. Cho hàm số
()fx
,
()gx
có đồ thị như hình vẽ. Biết hai hàm số
(2 1)y fx= −
,
()y g ax b= +
có cùng
khoảng nghịch biến lớn nhất. Khi đó giá trị của biểu thức
( )
4ab+
bằng:
Trang 6/6 - Mã đề 101
A.
2−
. B.
4
−
. C.
3
. D.
0
.
Câu 46. Cho hàmsố
( )
+
=
−
21
2
t
ft
t
và
,xy
là các số thực thỏa mãn
22
522 9x xy y
++=
.
Giátrịlớnnhấtcủa

−

−−

66
49
x
f
xy
bằng
A.
−1
3
. B.
1
3
. C.
2
3
. D.
−
3
.
Câu 47. Đồ thị hàm số
2
51 1
2
xx
y
xx

có tất cả bao nhiêu đường tiệm cận?
A.
0
B.
2
C.
1
D.
3
Câu 48. Cho hàm số
( ).fx
Hàm số
'( )
y fx
có đồ thị như hình vẽ bên.
Gọi
S
là tập hợp các giá trị nguyên của tham số
[ 5; 5]m
để hàm số
22
( 2 1) y f x mx m
nghịch
biến trên khoảng
1
0; .
2


Tổng giá trị các phần tử của
S
bằng
A.
15.
B.
12.
C.
14.
D.
10.
Câu 49. Có bao nhiêu giá trị nguyên dương của tham số
m
để bất phương trình
2
33
log 3log 2
0
2
x
xx
m
−+
<
−
có
không quá 3 nghiệm nguyên dương?
A.
63
. B.
64
. C.
127
. D.
128
.
Câu 50. Cho hình chóp
.S ABCD
có đáy
ABCD
là hình bình hành và có thể tích là
V
. Điểm
P
là trung
điểm của
SC
. Mặt phẳng
( )
α
qua
AP
cắt hai cạnh
SB
và
SD
lần lượt tại
M
và
N
. Gọi
1
V
là thể tích
của khối chóp
.S AMPN
. Tìm giá trị nhỏ nhất của tỷ số
1
V
V
?
A.
3
8
. B.
2
3
. C.
1
8
. D.
1
3
.
------------- HẾT -------------
Mã đề [101]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
A
D
A
A
C
D
A
D
C
A
C
C
A
B
D
C
D
B
A
B
B
D
A
B
B
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
B
B
C
C
B
B
D
A
C
A
D
D
B
A
B
D
C
D
A
A
B
C
C
C
D
Câu 26.
Lời giải
Chọn B
Đặt
AB x
,
AD y
,
AA z
.
Gọi
H
là hình chiếu vuông góc của
B
trên
BC
, ta có
BH
là đoạn vuông góc chung của
AB
và
BC
nên
222 2
25 1 1 1 5
,
54
a
d AB B C BH
BH z y a

. (1)
Gọi
I
là hình chiếu vuông góc của
B
trên
AB
, ta có
BI
là đoạn vuông góc chung của
BC
và
AB
nên
2 22 2
1 11 5
,
4
d BC AB BI
BI x z a

. (2)
Gọi
M
là trung điểm của
DD
,
O
là giao điểm của
AC
và
BD
, ta có mặt phẳng
ACM
chứa
AC
và song
song với
BD
nên
,, ,d AC BD d BD ACM d D ACM


.
Gọi
J
là hình chiếu vuông góc của
D
trên
AC
,
K
là hình chiếu vuông góc của
D
trên
MJ
, ta có
2 2 22 2
1 1143
,,d D ACM d D ACM DK
DK x y z a

. (3)
Từ (1), (2) và (3) ta có
22
21
2
2
z a xya
za
 
.Thể tích khối hộp là
3
2V xyz a
.
Câu 27.
Lời giải
Chọn B Đếm số phần tử của tập
X
.
TH1: Tam giác có 3 đỉnh là 3 đỉnh của đa giác: Số tam giác loại này là
3
n
C
.
A
B
C
TH2: Tam giác có đúng 2 đỉnh là đỉnh của đa giác:
Chọn hai đỉnh của đa giác và một đỉnh nằm trong đa giác là giao điểm của hai đường chéo. Để có một giao
điểm như vậy ta cần phải có hai đường chéo, hay cần 4 đỉnh của đa giác. Mỗi cách chọn 4 đỉnh của đa giác
cho ta 4 tam giác có đúng hai đỉnh là đỉnh của đa giác.
Vậy số tam giác loại này là
4
4
n
C
.
I
A
B
C
D
TH3: Tam giác có đúng một đỉnh là đỉnh của đa giác:
Mỗi cách chọn 5 đỉnh của đa giác sinh ra 5 tam giác loại này.
Vậy có
5
5
n
C
tam giác trong TH này.
TH4: Tam giác không có đỉnh nào là đỉnh của đa giác:
Mỗi cách chọn 6 đỉnh của đa giác sinh ra một tam giác loại này.
Vậy số tam giác trong TH này là
6
n
C
.
Vậy có tất cả:
3 4 56
45
n n nn
C C CC+++
tam giác sịnh ra do các cạnh và đường chéo của đa giác tạo ra.
Lấy ngẫu nhiên một tam giác từ tập
X
, suy ra
( )
3 4 56
45
n n nn
n C C CCΩ= + + +
Gọi A là biến cố lấy được tam giác không có đỉnh nào là đỉnh của đa giác .
Ta có
( )
6
n
nA C=
.
Vậy xác suất của biến cố
A
là
( )
( )
( )
6
32
3 4 56 3 2
12 47 60
4 5 18 43 60
n
n n nn
nA
C
nn n
PA
n
C C CC n n n
− +−
= = =
Ω
+ ++ + −+
( )
32
32
32
4 12 47 60 4
11 252 877 1140 0
15 15
18 43 60
nn n
PA n n n
nn n
− +−
=⇔ =⇔− + −=
+ −+
( )
( )
2
19 11 43 60 0 19n nn n⇔ − − + =⇔=
Câu 28.
Lời giải
Chọn C
Gọi
M
là trung điểm của
BC
.
1
:
3
CN CH
N CM
CM CA
∈==
//
HN AM⇒
. Mà
ABC∆
đều nên
( )
AM BC HN BC BC SHN⊥⇒ ⊥⇒⊥
.
( )
( )
; ( ; ) 60
o
SBC ABC SN HN SNH= = =
.
Do
ABC
∆
đều nên
313
2 36
aa
AM HN AM= ⇒= =
.
SHN∆
vuông tại
H
có
3
.tan .tan 60
62
o
aa
SH HN SNH
= = =
.
23
.
1 1 33
. ..
3 3 2 4 24
S ABC ABC
aa a
V SH S= = =
.
Câu 29.
Lời giải
Chọn C
N
G
M
H
O
C
A
D
B
S
Kéo dài
CG
cắt
AD
tại trung điểm
M
của
AD
, gọi
N
là trung điểm
SD
.
Hình thoi
ABCD
có
2AB BD
= =
nên tam giác
BCD
đều và
22
13
3
2
CO CH CO OH=⇒= + =
.
Tam giác
SHC
vuông cân vì
13
90 , 45
2
SHC SCH SH CH= ° = °⇒ = =
.
Dễ thấy
( )
// //SA MN SA CMN⇒
nên
( ) ( )
( )
( )
( )
( )
( )
,, , ,d SA CG d SA CMN d A CMN d D CMN= = =
.
..
1 1 3 7 39 39
. . .4.
3 32 2 3 6
S ABCD ABCD S ADC
V S SH V= = =⇒=
1 39
.
4 24
NMDC
NMDC
SADC
V
DM DN
V
V DA DS
= =⇒=
Có
26 1 26
2
2 24
SHA SHC SA SC HC MN SA∆ =∆ ⇒== = ⇒ = =
Tam giác
ACD
có
( )
22 2
2
2, 2 3 7
4
AC DC AD
AD CD AC CM
+−
== =⇒= =
Tam giác
SCD
có
22
13 9 22 26
, 2,
44 2 2
SD SH HD CD SC= + = += = =
suy ra trung tuyến
( )
22 2
2
62
44
CS CD SD
CN
+−
= =
Tam giác
CMN
có
62 26 37 434 637112
, 7, cos sin
4 4 868 1736
CN CM MN MCN MCN= ==⇒ =⇒=
.
Suy ra
1 367
. . .sin
2 16
CMN
S CM CN MCN
∆
= =
.
( )
( )
( )
( )
3
1 1 2 14313
. . ., ,
3 3 367
NMDC
NMDC CMN
CMN
V
V Bh S d D CMN d D CMN
S
∆
∆
== ⇒==
.
Vậy
( )
2 14313
,
367
d SA CM =
.
Câu 30.
Lời giải
Bài yêu cầu
0;18m
và
0x
, khi đó
0xm
. Xét
2x
không phải nghiệm của phương trình nên với
2x
ta có:
11
22
44
1
2 log 1 log 4 4 1
2
xx
xx
x
x xm x xm xm m x
x


 
Đặt
1
2
4
x
x
fx x

, ta chỉ quan tâm nghiệm dương nên xét
fx
trên
0; \ 2
.
Ta có
1
2
2
1
4 . .ln 4 1 0, 0; \ 2
2
x
x
fx x
x

.
Bảng biến thiên của
fx
2
-2
+
∞
-
∞
+
∞
f(x)
2
0
f'(x)
x
Từ bảng biến thiên suy ra phương trình đã cho có đúng một nghiệm dương khi
2m
hoặc
2m 
.
Do
m
nguyên thuộc đoạn
0;18
nên tập các giá trị của
m
là
2;3;4;...;18
, có
17
giá trị.
Câu 31.
Lời giải
Chọn B Ta có
(
)
fx
′
=
3
22
16 4 16
x
xx+− +
(
)
3
22
16 16 4
x
xx
=
+ +−
(
)
(
)
(
)
32
22 2
16 4
16 16 4 16 4
xx
xx x
++
=
+ +− ++
(
)
2
22
16 4
4
16 16
xx
x
x
xx
++
= = +
++
( )
fx⇒
2
4
d
16
x
xx
x

= +

+

∫
( )
2
2
4
d + d 16
2 16
xx x
x
= +
+
∫∫
=
2
2
4 16
2
x
xC+ ++
Mà
( )
49
3
2
f =
0C⇒=
( )
fx⇒=
2
2
4 16
2
x
x++
Vậy
( )
3
0
.dxf x x=
∫
3
3
2
0
4 16 d
2
x
xx x

++


∫
(
)
33
3
22
00
81 244 2195
d 2 16d 16
2 8 3 24
x
xx x
= + + +=+ =
∫∫
Câu 32.
Lời giải
Chọn D
Dựng hình vuông
ABCD
.
Ta có
( )
AB SA
AB SAD SD AB
AB AD
⊥
⇒⊥ ⇒⊥
⊥
.
Và
( )
BC SC
BC SCD SD BC
BC CD
⊥
⇒⊥ ⇒⊥
⊥
.
Khi đó
( ) ( )
( )
;
SD AB
SD ABCD SD d S ABCD a
SD BC
⊥
⇒⊥ ⇒= =
⊥
.
Kẻ
DH SA⊥
và
DK SC⊥
Ta có
( )
( )
( )
DH SA
DH SAB
DH AB do AB SAD
⊥
⇒⊥
⊥⊥
Tương tự,
( )
( )
( )
DK SC
DK SBC
DK BC do BC SCD
⊥
⇒⊥
⊥⊥
.
Do đó
( ) ( )
( )
( )
;,SAB SBC DH DK HDK= =
.
Mà
2
2
AC
AD a= =
,
22
3SA SD AD a= +=
và
22
2
.6
3
SD AD a
DH DK
SA
= = =
22
3
3
a
SK SH SD DK⇒== − =
//
2
1
3
3
HK AC
a
HK
HK SH
AC SA
⇒ ⇒=
= =
.
Vậy
222
2
cos
2. 3
DH DK HK
HDK
DH DK
+−
= =
.
Câu 33.
Lời giải
Chọn A Đặt
( )
( )
(
)
( )
22
2020 2021 4
64f x log x y log y y log x y= + + ++ − −
(coi
y
là tham số).
Điều kiện xác định của
( )
fy
là :
2
2
0
64 0
0
xy
yy
xy
+>
++ >
−>
.
Do
x,y
nguyên nên
2
xy y> ≥−
. Cũng vì
x,y
nguyên nên ta chỉ cần xét
( )
fy
trên nửa khoảng
[
)
1y;+ +∞
.
Ta có
( )
( )
( )
2
11
0, 1.
4
2020
fx xy
x y ln
x y ln
′
= − < ∀≥ +
−
+
Ta có bảng biến thiên của hàm số
( )
fx
Yêu cầu bài toán trở thành:
( )
( ) ( )
22
2020 2021 4
64 0 64 64 64f y log y y log y y log+ <⇔ ++ + ++ <
(
)
( )
2
2021 2020
64 . 2021 1 3log y y log
⇔ ++ + <
2020
3
2021 1
2
64 2021 0
log
yy
+
⇔ ++ − <
301,76 300,76
y⇒− < <
Mà
y
nguyên nên
{ }
301; 300;...;299;300y ∈− −
. Vậy có
602
giá trị nguyên của
y
thỏa mãn yêu cầu.
Câu 34.
Lời giải
Chọn C
sin 3 .cot cotxx x=
( )
1
. ĐK:
sin 0x xk
π
≠⇔≠
( )
22
sin 3 1
32
63 63
1
2
cot 0
cos 0
22
kk
xx
x
xk
x
x
xk xk
ππ ππ
π
π
ππ
ππ

=+=+

=
= +
⇔⇔ ⇔ ⇔

=

=
=+=+


Biểu diễn nghiệm lên đường tròn lượng giác và đối chiếu với điều kiện ta được các nghiệm của phương trình
( )
1
là:
2
xk
π
π
= +
;
2
63
k
ππ
+
;
k ∈
.
Các điểm biểu diễn trên đường tròn lượng giác của tập nghiệm này tạo thành hình tứ giác
''BCB C
:
C'
-
π
2
C
5
π
6
π
6
π
2
B
B'
O
y
x
Tứ giác
''BCB C
có 2 đường chéo vuông góc, diện tích của nó là:
3
2. .2
'. '
2
3
22
CC BB
S = = =
.
Câu 35.
Chọn A
Đặt
= = +
3
() 2
t ux x x
ta có
′′
= = +> ∀
2
( ) 3 2 0,
t ux x x
do đó
= +
3
2tx x
là một hàm số tăng vì vậy
∈−

1;1x
thì
∈−

3;3t
.
Dựa vào bảng biến thiên của hàm số
()
fx
trên đoạn
−

3;3
ta có
−


=
3;3
max ( ) 5ft
và
−


= −
3;3
min ( ) 6ft
.
Từ đây ta có
−−


= +
1;1 3;3
max ( ) max ( ) 3 ( )gx ft f m
hoặc
−

−



= +
3;3
1;1
max ( ) min ( ) 3 ( )gx ft f m
Trường hợp 1:
−


−

−



+=
+=

⇔

+ ≥− +

+≥ +
3;3
3;3
3;3
max ( ) 3 ( ) 8
5 3( ) 8
5 3( ) 6 3( )
max ( ) 3 ( ) min ( ) 3 ( )
ft fm
fm
fm fm
ft fm ft fm
=
= −
⇔ ⇔=
≥
() 1
13
()
() 1
3
1
()
2
fm
fm
fm
fm
Từ bảng biến thiên phương trình
=() 1fm
có
5
nghiệm, như vậy trường hợp này có
5
giá trị thực của
m
thỏa mãn.
Trường hợp 2:
−


−




+=
−+ =

⇔

−+ > +

+> +
3;3
3;3
-3;3
min ( ) 3 ( ) 8
6 3( ) 8
6 3( ) 5 3( )
min ( ) 3 ( ) max ( ) 3 ( )
ft fm
fm
fm fm
ft fm ft fm
= −
⇔ ⇔=−
=
<
2
()
3
2
14
()
()
3
3
1
()
2
fm
fm
fm
fm
Từ bảng biến thiên phương trình
= −
2
()
3
fm
có
6
nghiệm, như vậy trường hợp này có
6
giá trị thực của
m
thỏa mãn.
Vậy có tất cả là
11
giá trị thực của
m
thỏa mãn yêu cầu bài toán.
Câu 36.
Lời giải
Điều kiện:
22
0 0.
2
xy
xy
x y xy
+
>⇔+>
+++
Ta có :
(
) ( )
22
3
log 3 3
2
xy
x x y y xy
x y xy
+
= −+ −+
+++
(
)
( )
22 22
33
2log 2log 2 3 3
x y x y xy x y xy x y⇔ +− +++=++−−
( ) ( )
( ) ( )
22 22
33
2log 2 3 3 2log 2 2x y x y x y xy x y xy⇔ +++ + = ++++ +++
( )
( )
( ) ( )
22 22
33
2log 3 3 3 3 2log 2 2 (*).x y x y x y xy x y xy
⇔ + + + = ++++ +++
Xét hàm số:
( )
3
2logft t t= +
với
0.t >
Ta có
(
)
2
' 10
.ln 3
ft
t
= +>
với mọi
0.t >
Suy ra hàm số
()y ft=
đồng biến trên khoảng
( )
0;+∞
.
Khi đó ta có:
( )
( )
( )
22 22
* 3 3 2 3 3 2 (**).f x y f x y xy x y x y xy⇔ + = +++ ⇔+=+++
Đặt
x ab
y ab
= +
= −
. Suy ra
33
26
ab
P
a
−+
=
+
và
( ) ( )
2
2
** 3 1 1.ab⇔ −+=
Đặt
( )
cos 3
3 1 cos
3
sin
sin
t
at
a
bt
bt
+
−=
=

⇔

=
=
với
[0;2 ).t
π
∈
Khi đó
( )
3cos 3sin 6 3
2 3 cos 3sin 6 3 8 3
2cos 8 3
tt
P Pt t P
t
−+
= ⇔− + =−
+
.
Phương trình trên có nghiệm khi :
( )
( )
2
2
2 3 3 63 83PP− +≥ −
2
47 69 24 0PP⇔ − +≤
69 249 69 249
(***).
94 94
P
−+
⇔ ≤≤
Vì luôn tồn tại
[0;2 )t
π
∈
để dấu bằng ở (***) xảy ra. Do đó, ta luôn tìm được
a
,
b
từ đó tìm được
,
xy
để
P
đạt giá trị lớn nhất. Vậy giá trị lớn nhất của
P
là
69 249
94
+
.
Câu 37.
Lời giải
Chọn D
( ) ( )
2
4 sin cos2 4 sin 2sin 1yfx xafx x a= + − = − +−
.
Đặt
sin cos 0, 0;
2
t xt x x
π

′
= ⇒= > ∈


nên khi
x
tăng trên
0;
2
π



thì
t
tăng trên
( )
0;1
.
Do đó hàm số
( )
2
4 sin 2sin 1yf x x a= − +−
nghịch biến trên
0;
2
π



khi và chỉ khi hàm số
(
)
2
4 21y ft t a= − +−
nghịch biến trên
( )
0;1
.
Dễ thấy, điều kiện cần để hàm số
( )
2
4 21
y ft t a= − +−
nghịch biến trên
( )
0;1
là phương trình
( )
2
4 21 0ft t a
− +− =
vô nghiệm trên
(
)
0;1
.
Với điều kiện
,
( )
2
4 21y ft t a= − +−
nghịch biến trên
( )
0;1
khi và chỉ khi
( )
0, 0;1yt
′
≤ ∀∈
( )
( )
( )
( )
( )
( )
2
2
4 44 2 1
0, 0;1
4 21
fttftt a
t
ft t a
′
− − +−
⇔ ≤ ∀∈
− +−
.
( )
**
Dựa vào đồ thị trên ta có
( ) ( )
0, 0;1ft t
′
< ∀∈
, do đó
( ) ( )
4 4 0, 0;1ft t t
′
− < ∀∈
.
Khi đó:
( ) ( ) (
)
( ) ( )
22
** 4 2 1 0, 0;1 4 2 1, 0;1ft t a t a ft t t⇔ − + − > ∀∈ ⇔ < − + ∀∈
.
(điều kiện này luôn đảm bảo thỏa mãn (*))
Hay
(
)
[ ]
2
4 2 1, 0 ;1
a ft t t≤ − + ∀∈
[ ]
(
)
{ }
2
0;1
min 4 2 1a ft t⇔≤ − +
.
Xét hàm số
( )
(
)
2
4 21gt f t t
= −+
trên
[ ]
0;1
có
(
) (
)
[ ]
4 4 0, 0;1gt f t t t
′′
= − < ∀∈
,
nên
( )
gt
nghịch biến trên
[ ]
0;1
.
[ ]
( ) ( )
0;1
min 1 3gt g⇒==
.Vậy
[ ]
( )
0;1
min 3a gt≤=
.
Vì
a
nguyên dương nên
03a<≤
{ }
1; 2; 3a⇒∈
.
Câu 38.
Lời giải
ChọnA
Ta có:
′
= − + −= − + −
2 22 2
3 6 3( 1) 3( 2 1)y x mx m x mx m
= −
′
= ⇔ − + −⇔
= +
22
1
02 1
1
xm
y x mx m
xm
Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy điểm cực đại của đồ thị
(
)
C
là điểm
( )
−− +1; 3 2Mm m
.
Nhận xét:
( )
=− + =− − −=− −⇒ ∈ =− − ∀3 2 3( 1) 1 3 1 : 3 1, .
MM
y m m x M dy x m
Vậy: khi
m
thay đổi, điểm cực đại của đồ thị
(
)
C
luôn nằm trên một đường thẳng
d
cố định có phương
trình:
=−−
31yx
. Vậy đường thẳng
d
có hệ số góc
= −3
k
.
Câu 39.
Lời giải
Chọn A Xét hàm số
( ) ( )
=−+ −−
52
5 5 1 8.fx x x m x
Trường hợp 1:
(
)
=
0fx
có nghiệm
(
)
∈ −∞
0
;1
x
thì hàm số
( )
=y fx
không thể nghịch biến trên khoảng
( )
−∞;1 .
Trường hợp 2:
( )
=
0fx
không có nghiệm
( )
∈ −∞
0
;1
x
.
Ta có:
( ) ( )
′
=−+ −
4
5 10 5 1 .
fx x x m
Khi đó
( ) ( ) ( )
= − + − −= =
52 2
55 18
y x x m x fx f x
nên
′
′
=
2
().()
()
f x fx
y
fx
.
Hàm số nghịch biến trên
( )
−∞
;1
khi và chỉ khi
′
≤
0y
với
( )
∀ ∈ −∞;1x
( )
( )
′
≤
⇔ ∀ ∈ −∞
≠
().() 0
, ;1
0
f x fx
x
fx
( )
<
⇔ ∀ ∈ −∞
′
≥
() 0
, ;1
() 0
fx
x
fx
( vì
( )
→−∞
= −∞
lim
x
fx
)
( ) (
) ( )
( )
′
= − + − ≥ ∀ ∈ −∞
⇔
= −≤
4
5 10 5 1 0, ;1
1 5 17 0
fx x x m x
fm
( )
( )
( )
−∞
≥ −+ += +
≥ − + + ∀ ∈ −∞

⇔⇔

≤

≤
4
4
3
;1
3
max 2 1 1
2 1, ;1
2. 2
17
17
5
5
m xx
mx x x
m
m
∈
⇔ + ≤ ≤ → =
3
3 17
1 3.
5
2. 2
m
mm
Câu 40.
Lời giải
Chọn B Đẳng thức đã cho tương đương với:
( )
( )
( )
2
3
13
9.
fx
fx
x
x
x
− =−−
′
Lấy tích phân hai vế trên đoạn
[1; 4]
ta được:
(
)
4 44
2
3
1 11
() 1 3
( ) 9 21 2 ln 2.
fx
fx x x x
x
x
x

− = −− = −

′

∫ ∫∫
dd d
Tích phân từng phần có
( )
( )
(
)
( )
( )
44 4 4
3
11 1 1
4
22 2 1
6 6 6 36 2 3 .
1
fx
x fx fx f x f x x
xx x x
x
 
′′
= − + = − − − =−+ −
 
 
∫∫ ∫ ∫
dd d
Vậy có
đẳng thức:
( )
( )
( )
44
2
11
1
36 2 3 21 2ln 2fx x fxx
x

+− − =−


′′
∫∫
dd
.
( ) ( )
( )
2
4
1
11
3 0 3, [1; 4] 2 3 .fx x fx x fx x x
xx

⇔ − + = ⇔ ≡ − ∀∈ ⇒ = −


′′
∫
d
Vì vậy
( )
( )
44
11
79
23 .
6
fx x x x x= −=−
∫∫
dd
Câu 41.
Lời giải
Chọn D Ta có
( )
2 ln 2 2 ln 2 2019 0
xx
fx x
−
′
= + + > ∀∈
( )
fx⇒
đồng biến trên
.
Từ giả thiết suy ra
( )
( )
32 2
2 3 22 5fx x xm f x x−+−<− −−
( )
( )
32 2
2 3 2 25fx x xm f x x⇔ − +− < −+
(do
( )
2 2 2019
xx
fx x
−
=−+
là hàm số lẻ)
32 2
32 2
32 2
2 3 2 25
2 3 2 25
2 3 2 25
− + −< − +
⇔ − + − < − +⇔
− + − >− + −
x x xm x x
x x xm x x
x x xm x x
32
3
4 55
5
xxx m
xx m
− + −<
⇔
++>
Xét
( )
32
4 55gx x x x=− +−
và
( )
3
5
hx x x= ++
trên
( )
0;1
có bảng biến thiên là
Từ bảng biến thiên suy ra
( )
( )
( )
32 2
2 3 2 2 5 0, 0;1fx x xm f x x x−+−+ −−<∀∈
khi và chỉ khi
3
35
5
m
m
m
≥−
⇒− ≤ ≤
≤
. Vậy tập
S
có 9 phần tử.
Câu 42.
Lời giải
Chọn C
r
h
/4
r
h'
x
khoảng không
nước
h
Giả sử ly có chiều cao
h
và đáy là đường tròn có bán kính
r
, nên có thể tích
2
1
3
V hr
π
=
.
Khối nước trong ly có chiều cao bằng
1
4
chiều cao của ly nên khối nước tạo thành khối nón có chiều cao
bằng
4
h
và bán kính đáy
4
r
thể tích nước bằng
2
2
1 11 1
..
3 4 4 64 3 64
hr
hr V
ππ

= =


.
Do đó thể tích khoảng không bằng
1 63
64 64
VV V−=
.
Nên khi úp ngược ly lại thì ta có các tỉ lệ :
' .'x h rh
x
rh h
= ⇒=
.
Suy ra: thể tích khoảng không bằng:
2 33
22
1 1 .' 1 ' '
'. . '. . . .
33 3
rh h h
h x h hr V
h hh
ππ π
 
= = =
 
 
.
33
33
3
63 ' ' 63 ' 63 63 63
'
64 64 64 4 4
hh h
V V hh
hh h
 
⇒ = ⇒ = ⇒ = = ⇒=
 
 
.
Nên chiều cao mực nước bằng:
33
63 4 63
'
44
hh h h h
−
−=− =
.
Vậy tỷ lệ chiều cao của mực nước và chiều cao của ly nước bây giờ bằng
3
4 63
4
−
.
Câu 43.
Lời giải
Chọn D
Gọi
K
là trung điểm của
AB
ta có
OK AB
⊥
vì tam giác
OAB
cân tại
O
Mà
SO AB⊥
nên
( )
AB SOK⊥
( )
( )
SOK SAB
⇒⊥
mà
( ) ( )
SOK SAB SK⇒ ∩=
nên từ
O
dựng
OH SK⊥
thì
( )
( )
( )
,OH SAB OH d O SAB⊥ ⇒=
Xét tam giác
SAO
ta có:
sin
2
SO SA
SAO SO
SA
=⇒=
Xét tam giác
SAB
ta có:
3
sin
2
SK SA
SAB SK
SA
=⇒=
Xét tam giác
SOK
ta có:
2 2 2 22 2
1 11 1 1
OH OK OS SK SO SO
= += +
−
2 22
2 22
1 1 1 42
3
4 44
SA SA SA
OH SA SA
⇒=+ =+
−
2
22
63
22SA a SA a
SA a
⇒ =⇒= ⇒=
Câu 44.
Lời giải
Chọn A Điều kiện:
0y >
;
Theo đề bài, ta có:
( )
( )
( )
2
2
2
2
log
log
2 log
log
2.2 8 5 1
2 8 .5
xy
xy
xy
xy
y
y
−
+
−
+
= +
=
( )
( )
2
22 2
2
log
2
log log log
85
8 .5 8 5 0 8 5
4
xy
xy xy xy
y
yy y
+
++ +
+
⇒ = ⇔ −=⇔ =
(2)
( )
( )
( )
2
log
2 2 22 22
222 22 2
2
log 8 log 5 log .log 8 log 5 log
5
3 3log log 5 log 3 2 log log 5 3 log 3
xy
yx y y
x y yx y x
y
+
⇒ = ⇔+ = +
⇔+ = + ⇔+ = ⇔=
Thay
( )
2
vào
( )
1
ta được:
( ) ( )
( )
22
log log
2
22 2
2.2 5 5 2 5 log log 5 log 5 4
xy xy
yy yx y yx y
−−
= + ⇔ = ⇔− = ⇔=
Từ
và
( )
4
( )
3
2 28
22
22
4
5 5 11
log 3.log 5 5
25
5
y yy y
yy
⇒ = ⇒ = ⇔ = ⇒=
2
22
log 5
2
22
44
1 11
log 5. log 5 2 . 2 . 5. 1
5 55
x
xy
 
⇒= = ⇒ = = =
 
 
Câu 45.
Chọn A
Xét hàm số
(
)
(2 1) (2 1) ' 2 '(2 1)
y fx fx f x= −⇒ − = −
nghịch biến khi
(
)
0fx
′
<
(
)
(21)'2.'(21)0 '(21)012131 2
fx fx fx x x
⇔ − = −<⇔ − <⇔< −<⇔<<
.
Xét hàm số
(
)
()()'.'()y g ax b g ax b a g ax b
= +⇒ + = +
nghịch biến khi xảy ra hai trường hợp
0
0
0
0
'( ) 0
2
2
0
0
0
'( ) 0
02
2
a
b
a
x
a
a
ax b
g ax b
b
ax b
x
a
a
a
a
g ax b
ax b
bb
x
aa
>
−
>
<
>
+<

+<
−
+>
⇔⇔
>

<
<
<
+>
< +<
−
− < <−
Nếu
0a >
thì hàm số
()y g ax b= +
nghịch biến trên
2
;; ;
bb
aa
−  −
−∞ +∞


không thỏa mãn điều kiện có khoảng
nghịch biến là
( )
1; 2
.
Nếu
0a <
thì hàm số
()y g ax b= +
nghịch biến trên
2
;
bb
aa
− −
−


Yêu cầu bài toán là hai hàm số
(2 1)y fx= −
,
()y g ax b= +
có cùng khoảng nghịch biến lớn nhất
nên
2
1
2
44
4
2
b
a
a
ab
bb
a
−
−=
= −
⇔ ⇒ +=−

−=
=
.
Câu 46.
Lời giải
Chọn B
Ta có:
( ) (
)
+ + =⇔ + +− =
22
22
522 92 9x xy y x y x y
.
Đặt
+= −=
2 3sin , 3cosx y tx y t
với
ππ
∈−

2 ;2
t
.
⇒= +sin cosxtt
và
= −sin 2cosyt t
.
− +− +−
= = =
−− + − + − + −
6 6 6sin 6cos 6 6sin 6cos 6
4 9 4(sin cos ) sin 2 cos 9 3sin 6cos 9
x tt tt
K
xy t t t t t t
.
( ) ( )
⇒− +− =−3 6sin 6 6cos 9 6K t K tK
.
Điều kiện để phương trình trên có nghiệm là
( ) ( ) ( )
− + − ≥ − ⇔− ≤ ≤
22 2
36 66 96 1 1KKK K
Xét hàm số
+
=
−
21
()
2
t
ft
t
trên
−

1;1
Ta có:
(
)
−
= < ∀≠
−
2
5
'( ) 0, 2
2
ft t
t
. Suy ra
−


= −=
1;1
1
( ) ( 1)
3
Max f t f
.
Câu 47.
Lời giải
Chọn C Tập xác định:
1; \ 0D 
.
•
lim
x
y

2
51 1
lim
2
x
xx
xx


2 34
51 1 1
lim
2
1
x
x
x xx
x


0
0
y
là đường tiệm cận ngang của đồ thị
hàm số.
•
0
lim
x
y
2
0
51 1
lim
2
x
xx
xx

2
2
0
51 1
lim
25 1 1
x
xx
x xx x


2
2
0
25 9
lim
25 1 1
x
xx
x xx x

0
25 9
lim
25 1 1
x
x
xx x

9
4
0
x
không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả
1
đường tiệm cận.
Câu 48.
Lời giải
Chọn C . Dựa vào đồ thị ta thấy
'( ) 0 2fx x
và
'( ) 0 2.
fx x
Ta có
22
'( ) 2( ) '( 2 1). g x x m f x mx m
22
22
22
0
'( 2 1) 0
'()0 2( )'( 2 1)0
0
'( 2 1) 0


 


xm
f x mx m
g x x m f x mx m
xm
f x mx m
22
22
11
2 12
1
.
1
1
2 12
1








xm
xm
m xm
x mx m
mxm
xm
xm
xm
xm
x mx m
xm
Hàm số
()y gx
nghịch biến trên
1
0;
2


0
1
0
1
2
.
2
3
3
2
2



m
m
m
m
m
Kết hợp với
m
và
[ 5; 5]m
suy ra
{0;2;3;4;5}.m
Vậy tổng tất cả các phần tử của
S
bằng
14.
Câu 49.
Lời giải
Chọn C Điều kiện
0
20
x
x
m
>
−>
21
x
mm⇒> ⇒>
.
Ta có
2
33
log 3log 2
0
2
x
xx
m
−+
<
−
2
33
log 3log 2 0
0
20
x
x
x
m
x
⇔
−
>
−
+<
>
( )(
)
33
log 1 log 2 0
0
20
x
x
m
xx
⇔
−
>
−
−<
>
3
1 log
0
20
2
x
x
m
x
>
−>⇔
<
<
2
39
0
x
x
m
x
⇔
<
>
<
>
2
39
x
x
m
<
⇔
<
>
(I).
Để bất phương trình có không quá 3 nghiệm nguyên dương khi và chỉ bất phương trình
2
x
m >
có không quá
3 nghiệm nguyên dương
( )
3; 9x∈
.
Xét hàm số
(
)
2
x
y fx= =
với
( )
3; 9x∈
có
( )
2 .ln 2 0,
x
fx x
′
= >∀
.
Bảng biến thiên
Từ bảng biến thiên suy ra
7
2 128m ≤=
.
Mà
1m
>
và
m
nguyên dương nên
{
}
2,3,...,128m ∈
.
Vậy có 127 giá trị nguyên dương của tham số
m
thoả mãn.
Câu 50.
Hướng dẫn giải
Chọn D
Cách 1
I
P
N
M
S
O
C
D
A
B
Đặt
SM
a
SB
=
,
SN
b
SD
=
,
(
)
0;1
ab<≤
.
Ta có
..
1
S AMP S ANP
VV
V
VV
+
=
..
..
22
S AMP S ANP
S ABC S ADC
VV
VV
= +
1
..
2
SM SP SN SP
SB SC SD SC

= +


=
( )
1
4
ab+
(1)
Lại có
..
1
S AMN S PMN
VV
V
VV
+
=
..
..
22
S AMN S PMN
S ABD S CBD
VV
VV
= +
1
. ..
2
SM SN SM SN SP
SB SD SB SD SC

= +


=
3
4
ab
(2).
Suy ra
(
)
13
3a
4 4 3a 1
a
ab ab ab b b
+ = ⇔+= ⇒=
−
. Từ điều kiện
( )
01b<≤
, ta có
1
3a 1
a
≤
−
, hay
1
2
a
≥
. Thay
vào (2) ta được tỉ số thể tích
2
1
3
.
4 3a 1
V
a
V
=
−
.
Đặt
( )
2
31
. ; ;1
4 3a 1 2
a
fa a

= ∈

−

, ta có
( )
(
)
2
2
0
3 3 2a
'. 0
2
4 (3a 1)
3
aL
a
fa
a
=
−
= = ⇔
−
=
.
( )
1 3 21
1;
2 8 33
ff f
 
= = =
 
 
, do đó
( )
1
1
;1
2
21
.
33
a
V
Min Min f a f
V

∈



= = =


| 1/21
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

TRƯỜNG THPT YÊN ĐỊNH 1
KỲ THI GIAO LƯU HỌC SINH GIỎI LỚP 12 THPT NĂM HỌC 2022-2023 ĐỀ CHÍNH THỨC Môn: TOÁN
Thời gian làm bài: 90 phút (không kể thời gian giao đề) MÃ ĐỀ 101
Ngày thi: / /2022 2  x + x − 2 Câu 1. Cho hàm số  ≠ f (x) khi x 1 =  x −1
. Tìm tất cả các giá trị thực của tham số m để hàm số gián 3
 m khi x =1
đoạn tại x =1.
A. m ≠ 1.
B. m ≠ 2.
C. m ≠ 3.
D. m ≠ 2.
Câu 2. Trong các mệnh đề sau, mệnh đề nào đúng ?
A. Bất kì một hình chóp nào cũng có một mặt cầu ngoại tiếp.
B. Bất kì một hình lăng trụ nào cũng có một mặt cầu ngoại tiếp.
C. Bất kì một hình hộp nào cũng có một mặt cầu ngoại tiếp.
D. Bất kì một hình tứ diện nào cũng có một mặt cầu ngoại tiếp.
Câu 3. Chu kỳ của hàm số 3sin x y =
là số nào sau đây? 2 A. 4π . B. π . C. 0 . D. 2π . 5 2 − 5
Câu 4. Cho hai tích phân f
∫ (x)dx = 8 và g
∫ (x)dx = 3. Tính I =  f
∫  (x)−4g(x)−1dx  . 2 − 5 2 −
A. I =13 .
B. I = 27 .
C. I = 3 . D. I = 11 − .
Câu 5. Một hình trụ có bán kính đáy r = 4 cm và độ dài đường sinh l = 3 cm . Diện tích toàn phần của
hình trụ đó bằng A. 2 24πcm . B. 2 40πcm C. 2 56πcm D. 2 36πcm
Câu 6. Cho hình lăng trụ tứ giác đều ABC .
D EFGH. Tính tỉ số k giữa thể tích khối trụ ngoại tiếp và thể tích
khối trụ nội tiếp hình lăng trụ trên.
A. k = 2 2. B.
C. k = 2.
D. k = 2.
Câu 7. Cho hình lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác vuông cân tại A , BC a 2, A'B tạo
với đáy một góc bằng 0
60 . Thể tích của khối lăng trụ bằng 3 3 3 3 A. 3a . B. 3a . C. 3a . D. a 2 4 2 2
Câu 8. Hình vẽ bên dưới có bao nhiêu mặt A. 4 . B. 10. C. 7 . D. 9.
Câu 9. Giá trị nhỏ nhất của hàm số 2x +1 y = trên đoạn [2; ] 3 bằng 1− x A. 3 − . B. 3 . C. 5 − . D. 7 − . 4 2
Câu 10. Cho dãy số (u với u = −
n . Mệnh đề nào sau đây đúng? n ( ) 1 n n )
Trang 1/6 - Mã đề 101
A. Dãy số (u là dãy số không bị chặn.
B. Dãy số (u là dãy số giảm. n ) n )
C. Dãy số (u là dãy số tăng.
D. Dãy số (u là dãy số bị chặn. n ) n )
Câu 11. Có bao nhiêu số chẵn mà mỗi số có 4 chữ số đôi một khác nhau? A. 50000. B. 4500 . C. 2296 . D. 2520 .
Câu 12. Trên giá sách có 4 quyển sách toán, 3 quyển sách lý, 2 quyển sách hóa. Lấy ngẫu nhiên 3 quyển
sách. Tính xác suất để trong ba quyển sách lấy ra có ít nhất một quyển là toán. A. 2 . B. 3 . C. 37 . D. 10 . 7 4 42 21
Câu 13. Cho a > 0,
a ≠ 1. Tìm mệnh đề đúng trong các mệnh đề sau:
A. Tập giá trị của hàm số y = log x là tập a  .
B. Tập giá trị của hàm số = x
y a là tập  .
C. Tập xác định của hàm số y = log x là tập a  .
D. Tập xác định của hàm số = x
y a là khoảng (0;+∞).
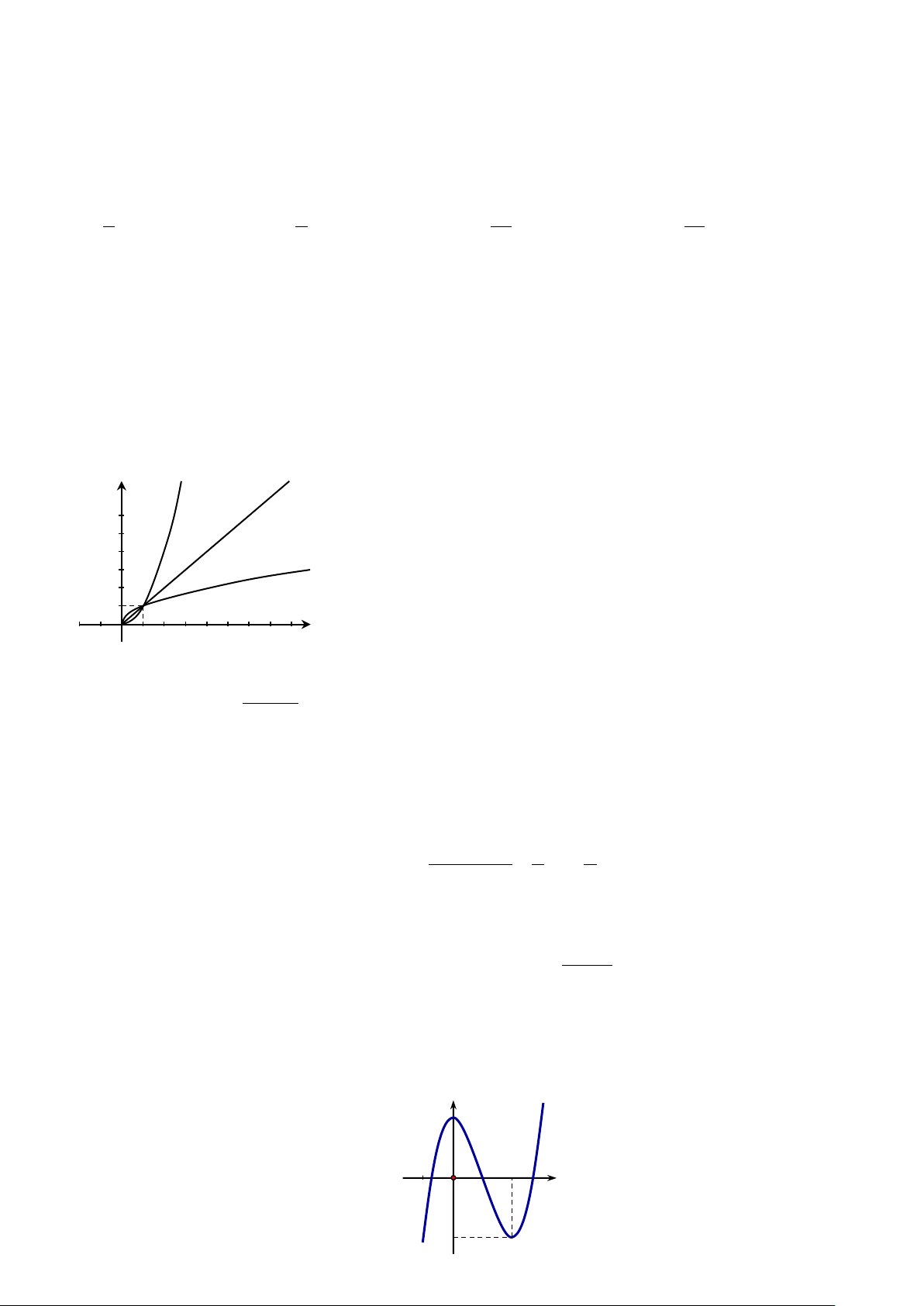
Câu 14. Hình vẽ bên là đồ thị các hàm số = a y x , = b y x , c
y = x trên miền (0;+∞). Hỏi trong các số a , b ,
c số nào nhận giá trị trong khoảng (0; ) 1 ? y a y = x b y = x c y = x O x A. Số . b B. Số . c
C. Số a .
D. Số a và số . c (x − )2 1 1
Câu 15. Tích phân I =
dx = a ln b + c ∫
, trong đó a , b , c là các số nguyên. Tính giá trị của biểu thức 2 x +1 0
a + b + c ? A. 3. B. 0 . C. 1. D. 2 .
Câu 16. Tổng tất cả các cạnh của khối lăng trụ không thể bằng số nào sau đây? A. 2025 . B. 2019 . C. 2020 . D. 2022 . x − x
Câu 17. Cho 9x 9−
+ x = 23. Khi đó biểu thức 5 + 3 + 3 = = a A
với a tối giản và a,b∈ . Tích . a b có giá
1− 3x − 3−x b b trị bằng: A. 10. B. 8 − . C. 8 . D. 10 − .
Câu 18. Có bao nhiêu giá trị nguyên của tham số m để hàm số mx + 4 y = giảm trên khoảng ( ) ;1 −∞ ? x + m A. Vô số. B. 1. C. 0 . D. 2 .
Câu 19. Tìm giá trị thực của tham số m để hàm số 3 2
y = x − 3x + mx đạt cực tiểu tại x = 2 .
A. m = 0. B. m = 2 − . C. m =1.
D. m = 2 .
Câu 20. Đường cong ở hình bên là đồ thị của một trong bốn hàm số dưới đây. Hàm số đó là hàm số nào? y 2 2 1 − O 1 x 2 −
Trang 2/6 - Mã đề 101 A. 3 2
y = x − 3x +1. B. 3 2
y = x − 3x + 2. C. 3 2
y = x + 3x + 2 . D. 3 2
y = −x + 3x + 2 .
Câu 21. Tập nghiệm của bất phương trình 7x ≥10 − 3x chứa bao nhiêu số nguyên dương nhỏ hơn 10? A. 11. B. 9. C. 8 . D. 10.
Câu 22. Cho tứ diện OABC có O ,
A OB, OC đôi một vuông góc và đều bằng .
a Khoảng cách giữa hai đường
thẳng OA và BC bằng A. a 3 a . B. .a C. a 2. D. 2 . 2 2
Câu 23. Kết quả của x I = xe dx ∫ là A. x x
I = xe − e + C . B. x x
I = e + xe + C . 2 2 C. x x I = e + C . D. x x x I =
e + e + C . 2 2 10 6
Câu 24. Cho hàm số f (x) liên tục trên đoạn [0;10] và f
∫ (x)dx = 7 và f
∫ (x)dx = 3. Tính 0 2 2 10 P = f
∫ (x)dx+ f
∫ (x)dx. 0 6 A. P = 4 − .
B. P = 4 .
C. P =10.
D. P = 7 .
Câu 25. Cho tứ diện SABC có SA = a, SB = 2a, SC = 3a . Giá trị lớn nhất của thể tích tứ diện bằng 3 3 A. 3 6a . B. 3 a . C. a . D. a . 3 6
Câu 26. Cho hình hộp chữ nhật a ABCDA′B C ′ D
′ ′ . Khoảng cách giữa AB và B C
′ là 2 5 , giữa BC và AB′ 5 là 2a 5 , giữa a
AC và BD′ là
3 . Thể tích của khối hộp đó là: 5 3 A. 3 4a . B. 3 2a . C. 3 a . D. 3 8a .
Câu 27. Cho đa giác lồi n cạnh ( n∈ *,
n ≥ 6 ) nội tiếp đường tròn (O) sao cho không có ba đường chéo
nào đồng quy. Các cạnh và các đường chéo của đa giác giao nhau tạo thành các tam giác. Gọi X là tập hợp
các tam giác như thế. Lấy ngẫu nhiên một tam giác trong tập X . Tìm n để xác suất lấy được tam giác không
có đỉnh nào là đỉnh của đa giác bằng 4 . 15
A. n = 23.
B. n = 19 .
C. n =15.
D. n =11.
Câu 28. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a . Hình chiếu vuông góc của S
trên đáy là điểm H trên cạnh AC sao cho 2
AH = AC ; mặt phẳng (SBC) tạo với đáy một 3
góc 60o . Thể tích khối chóp S.ABC là? 3 3 3 3 A. a 3 B. a 3 C. a 3 D. a 3 48 36 24 12
Câu 29. Cho hình chóp S.ABCD có đáy là hình thoi cạnh AB = BD = 2, hai đường chéo cắt nhau tại O .
Hình chiếu vuông góc của S trên mặt phẳng ( ABCD) là trung điểm H của BO . Gọi G là trọng tâm tam giác
ADC . Biết SC tạo với mặt phẳng đáy góc 45°, tính khoảng cách giữa hai đường thẳng SA và CG . A. 6 2373 . B. 2373 . C. 2 14313 . D. 4 14313 . 113 113 367 367
Câu 30. Có bao nhiêu giá trị nguyên của m thuộc đoạn 0;18 để phương trình x2log x m x1 có 4  
đúng một nghiệm dương? A. 16. B. 17 . C. 19. D. 18.
Trang 3/6 - Mã đề 101 3 3
Câu 31. Cho hàm số f (x) có f ( ) 49 3 = và f ′(x) = x
, ∀ x ≠ 0 . Khi đó x. f
∫ (x)dx bằng 2 2 2
x +16 − 4 x +16 0 A. 2915 . B. 2195 . C. 2195 . D. 2915 . 24 24 8 3
Câu 32. Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B , AC = 2a , tam giác SAB và tam
giác SCB lần lượt vuông tại A và C . Khoảng cách từ S đến mặt phẳng ( ABC) bằng a . Cosin của góc giữa
hai mặt phẳng (SAB) và (SCB) bằng A. 5 . B. 2 2 . C. 1 . D. 2 . 3 3 3 3
Câu 33. Có tất cả bao nhiêu giá trị nguyên của y sao cho tương ứng mỗi y luôn tồn tại không quá 63 số
nguyên x thỏa mãn điều kiện log ( 2
x + y ) + log ( 2
y + y + 64 ≥ log x − y 2020 2021 ) 4 ( ) A. 602 B. 2 . C. 301. D. 302.
Câu 34. Nghiệm của phương trình sin 3 .xcot x = cot x có các điểm biểu diễn trên đường tròn lượng giác tạo
thành đa giác có diện tích bằng 3 A. 2 3 đvdt. B. 3 đvdt. C. 3 đvdt. D. đvdt. 2 4
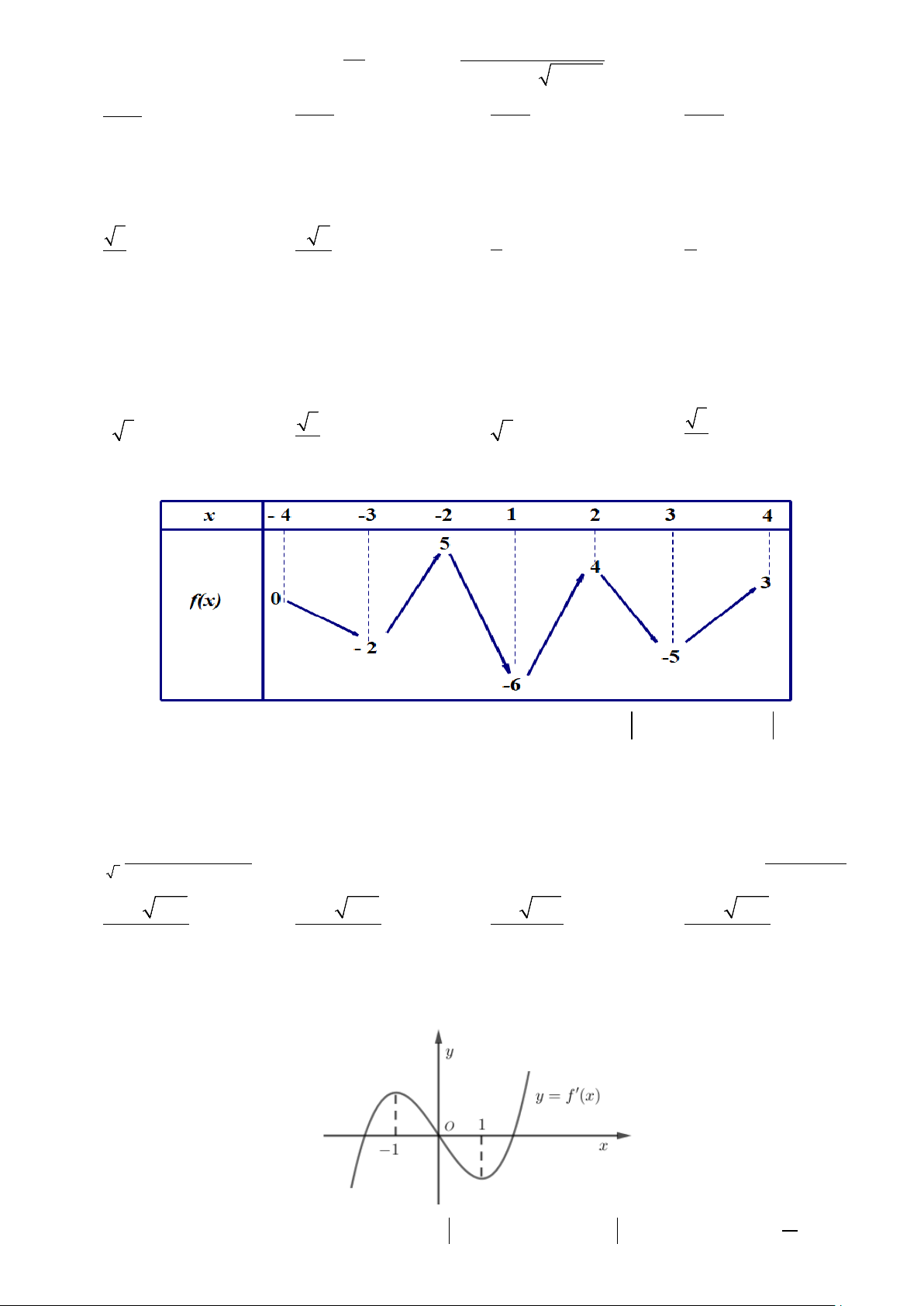
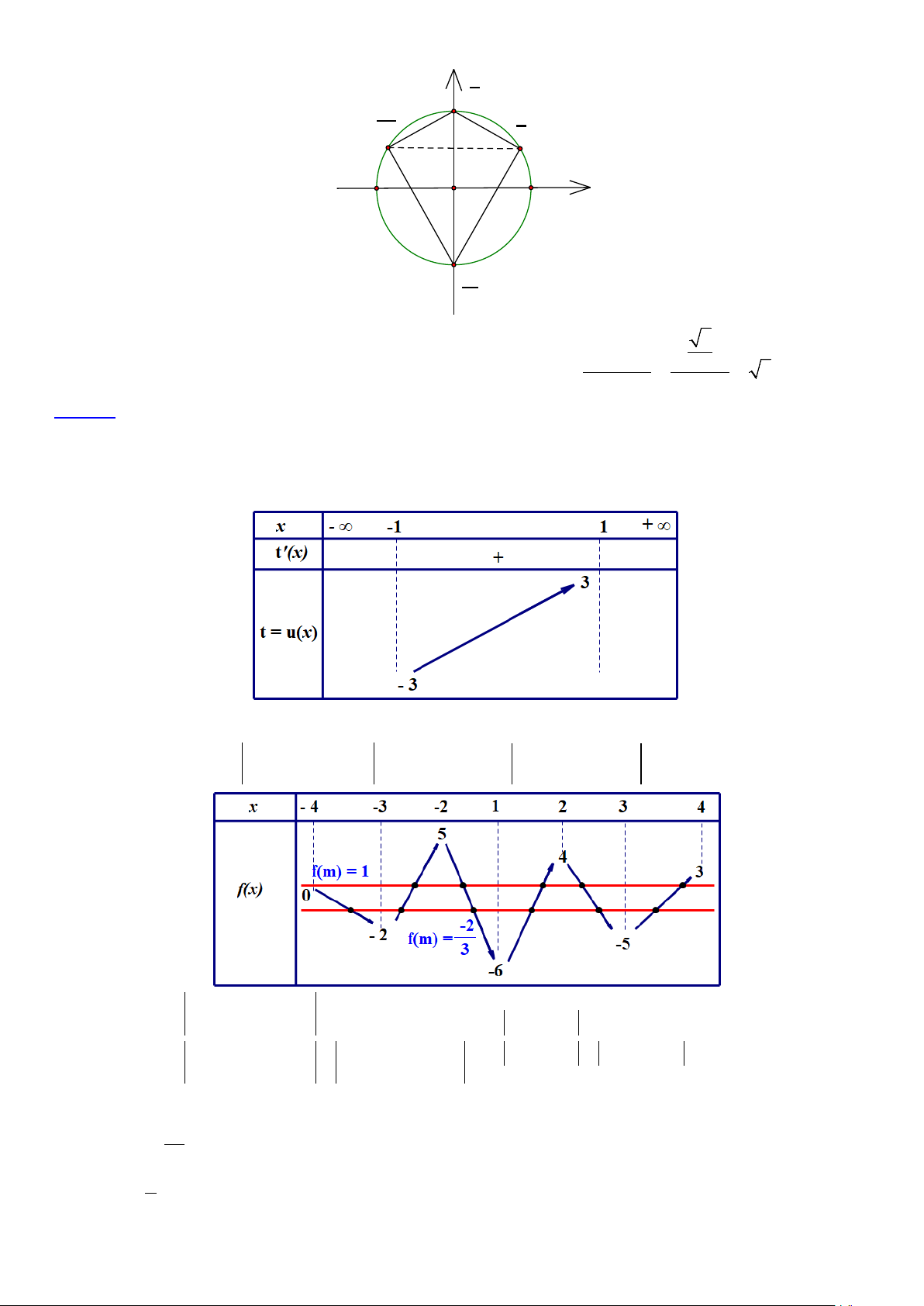
Câu 35. Cho hàm số f (x) liên tục trên đoạn −4;4 
 và có bản biến thiên như hình vẽ bên dưới
Có tất cả bao nhiêu giá trị thực của tham số m∈ −4;4 3   để hàm số (
g x) = f (x + 2x) + 3 f (m) có giá trị
lớn nhất trên đoạn −1;    1 bằng 8 ? A. 11. B. 9 . C. 10 . D. 12 .
Câu 36. Cho hai số thực x , y thoả mãn: log x + y + +
= x x − 3 + y y − 3 + x . y x 2y 3
Tìm giá trị lớn nhất của biểu thức P = . 3 2 2 ( ) ( )
x + y + xy + 2 x + y + 6 59 + 259 33 + 233 3+ 103 69 + 249 A. B. . C. D. 95 94 49 94
Câu 37. Cho hàm số y = f (x) có đạo hàm liên tục trên  và f ( )
1 =1 . Đồ thị hàm số y = f ′(x) như hình bên.  π
Có bao nhiêu số nguyên dương a để hàm số y = 4 f (sin x) + cos2x − a nghịch biến trên 0;   . 2   
Trang 4/6 - Mã đề 101 A. Vô số. B. 5. C. 2. D. 3.
Câu 38. Cho hàm số y = 3 x − 2 mx + 2 m − x − 3 3 3( 1)
m với m là tham số, gọi (C) là đồ thị của hàm số đã cho.
Biết rằng, khi m thay đổi, điểm cực đại của đồ thị (C) luôn nằm trên một đường thẳng d cố định. Xác định
hệ số góc k của đường thẳng d . A. 1 k 1 = − .
B. k = −3. C. k = .
D. k = 3 . 3 3
Câu 39. Có bao nhiêu giá trị nguyên của tham số m để hàm số y = 5 x − 2
5x + 5(m −1)x − 8 nghịch biến trên khoảng (−∞;1)? A. 1. B. 0. C. 4. D. 2.
Câu 40. Cho hàm số f (x) có đạo hàm liên tục trên đoạn [1;4] thỏa mãn f ( ) 1 = 1, − f (4) = 8 − và 4 3
x ( f ′ x )2 3
( ) − f (x) = 9 x − x − 3x, x
∀ ∈[1;4] .Tích phân f (x) x ∫ d bằng 1 A. 89 − . B. 79 − . C. 8. − D. 7. − 6 6
Câu 41. Cho hàm số ( ) = 2x − 2−x f x
+ 2019x . Gọi S là tập hợp các giá trị nguyên của m thỏa mãn điều kiện f ( 3 2
x − x + x − m )+ f ( 2 2 3
2x − 2x −5) < 0, x ∀ ∈(0; )
1 . Số phần tử của S là? A. 5. B. 7 . C. 3. D. 9.
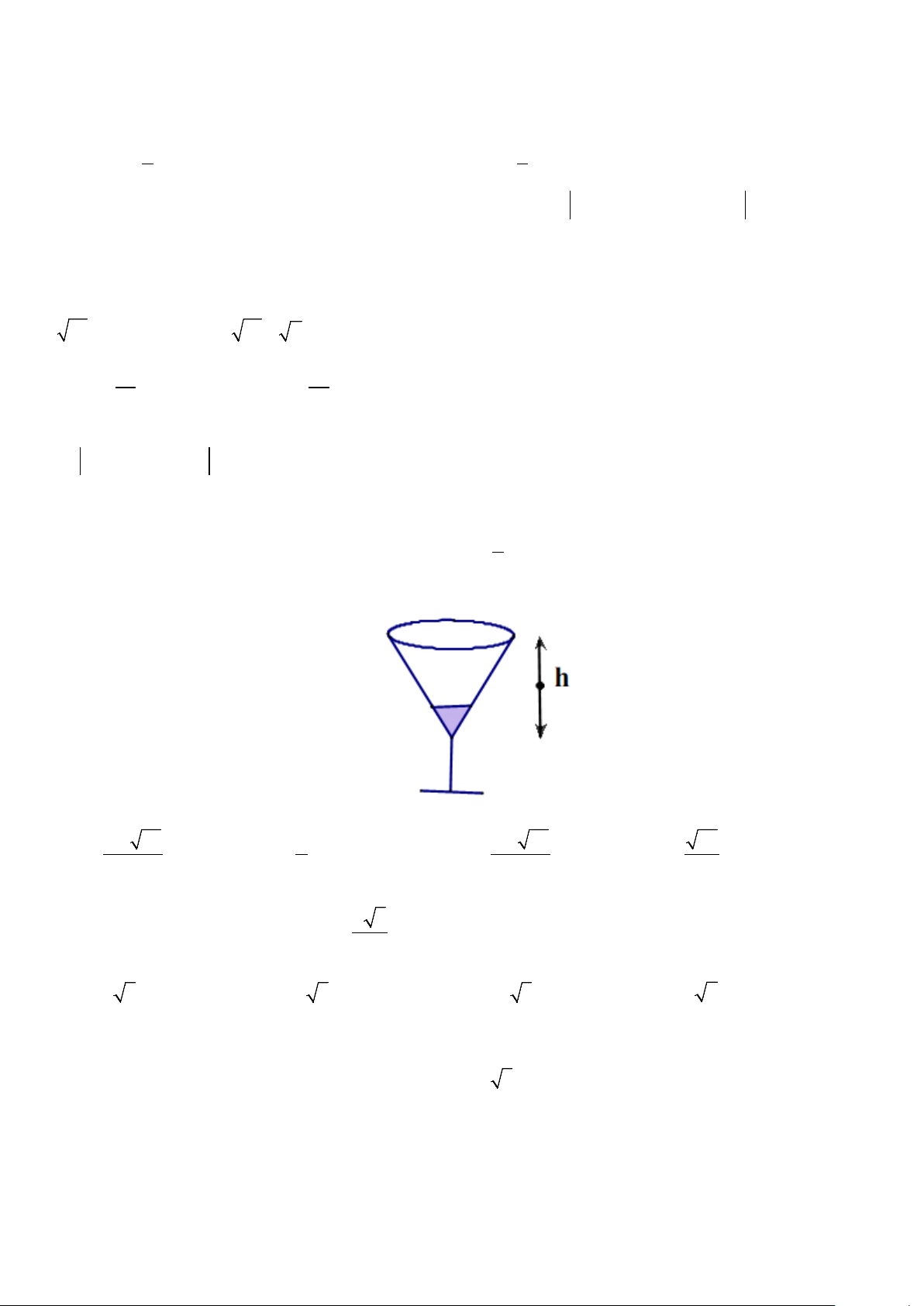
Câu 42. Một chiếc ly dạng hình nón ( như hình vẽ với chiều cao ly là h ). Người ta đổ một lượng nước
vào ly sao cho chiều cao của lượng nước trong ly bằng 1 chiều cao của ly. Hỏi nếu bịt kín miệng ly rồi 4
úp ngược ly lại thì tỷ lệ chiều cao của mực nước và chiều cao của ly nước bây giờ bằng bao nhiêu? 3 3 A. 4 − 63 . B. 3 . C. 4 − 63 . D. 63 . 4 4 4 4
Câu 43. Cho hình nón đỉnh S , đường cao SO, A và B là hai điểm thuộc đường tròn đáy sao cho
khoảng cách từ O đến (SAB) bằng a 3 và  0 =  0
SAO 30 , SAB = 60 . Độ dài đường sinh của 3
hình nón theo a bằng A. a 5 B. a 3 C. 2a 3 D. a 2
Câu 44. Biết rằng x, y là các số thực dương sao cho 3 số log2 8x y u + = , log2 2x y u − =
, u = 5 theo thứ tự lập 1 2 y 3
thành một cấp số cộng và một cấp số nhân. Khi đó, tích x 2
2 .y có giá trị bằng: A. 1. B. 5. C. 5 . D. 10.
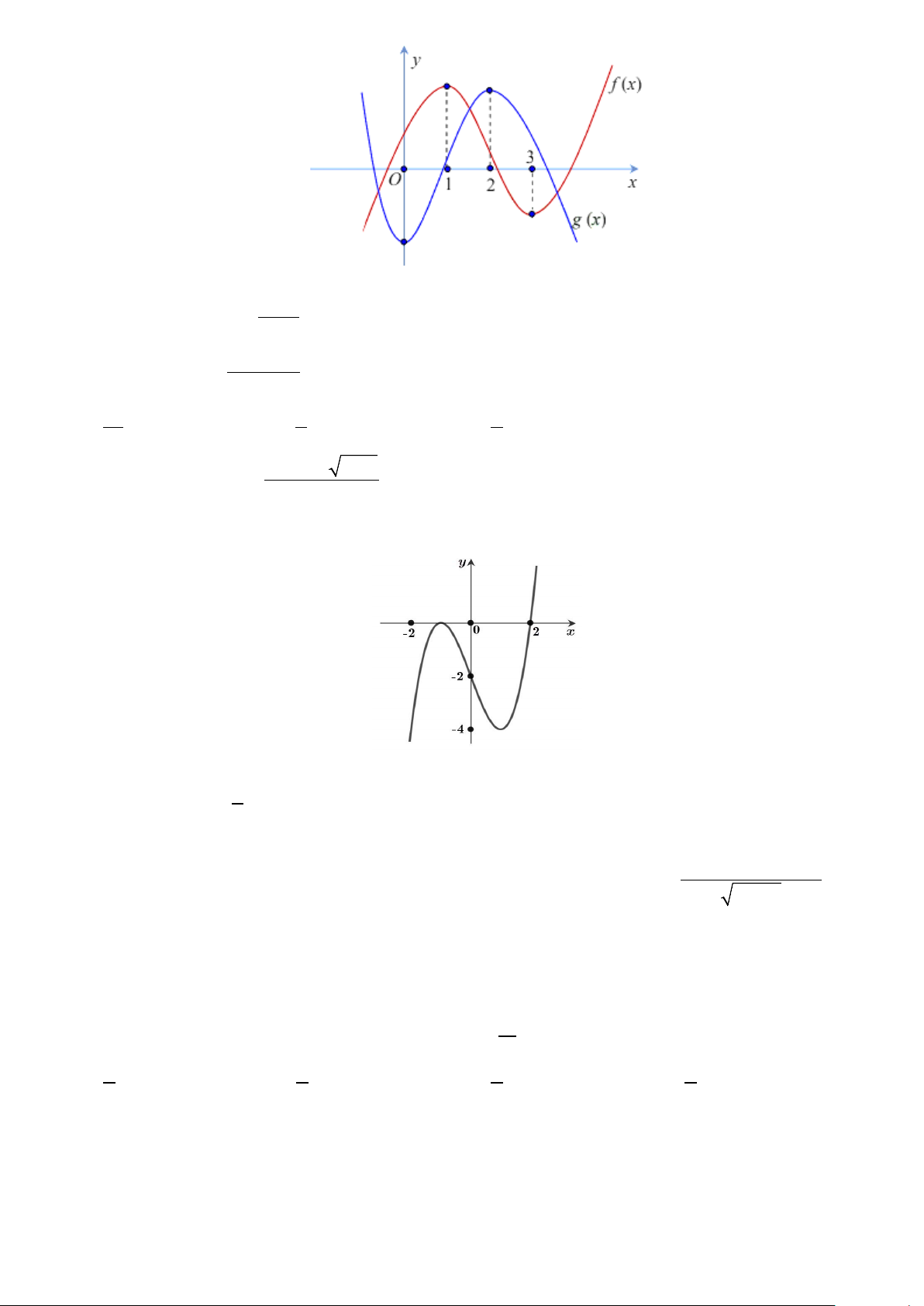
Câu 45. Cho hàm số f (x) , (
g x) có đồ thị như hình vẽ. Biết hai hàm số y = f (2x −1) , y = g(ax + b) có cùng
khoảng nghịch biến lớn nhất. Khi đó giá trị của biểu thức (4a + b) bằng:
Trang 5/6 - Mã đề 101 A. 2 − . B. 4 − . C. 3 . D. 0 .
Câu 46. Cho hàmsố f (t) 2t +1 =
và x,y là các số thực thỏa mãn 2 2
5x + 2xy + 2y = 9 . t − 2  6x − 6 
Giátrịlớnnhấtcủa f   bằng 4x − y −  9  A. −1 . B. 1 . C. 2 . D. −3 . 3 3 3
Câu 47. Đồ thị hàm số
5x 1 x 1 y
có tất cả bao nhiêu đường tiệm cận? 2 x  2x A. 0 B. 2 C. 1 D. 3
Câu 48. Cho hàm số f (x).Hàm số y f '(x) có đồ thị như hình vẽ bên.
Gọi S là tập hợp các giá trị nguyên của tham số m [5;5] để hàm số 2 2
y f (x 2mx m 1) nghịch   biến trên khoảng 1 0; . 
Tổng giá trị các phần tử của S bằng  2 A. 15. B. 12. C. 14. D. 10. 2 − + Câu 49. log x 3log x 2
Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình 3 3 < 0 có m − 2x
không quá 3 nghiệm nguyên dương? A. 63. B. 64 . C. 127 . D. 128.
Câu 50. Cho hình chóp S.ABCD có đáy ABCD là hình bình hành và có thể tích là V . Điểm P là trung
điểm của SC . Mặt phẳng (α ) qua AP cắt hai cạnh SB và SD lần lượt tại M và N . Gọi V là thể tích 1
của khối chóp S.AMPN . Tìm giá trị nhỏ nhất của tỷ số V1 ? V A. 3 . B. 2 . C. 1 . D. 1 . 8 3 8 3
------------- HẾT -------------
Trang 6/6 - Mã đề 101 Mã đề [101]
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
A D A A C D A D C A C C A B D C D B A B B D A B B
26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50
B B C C B B D A C A D D B A B D C D A A B C C C D Câu 26. Lời giải Chọn B
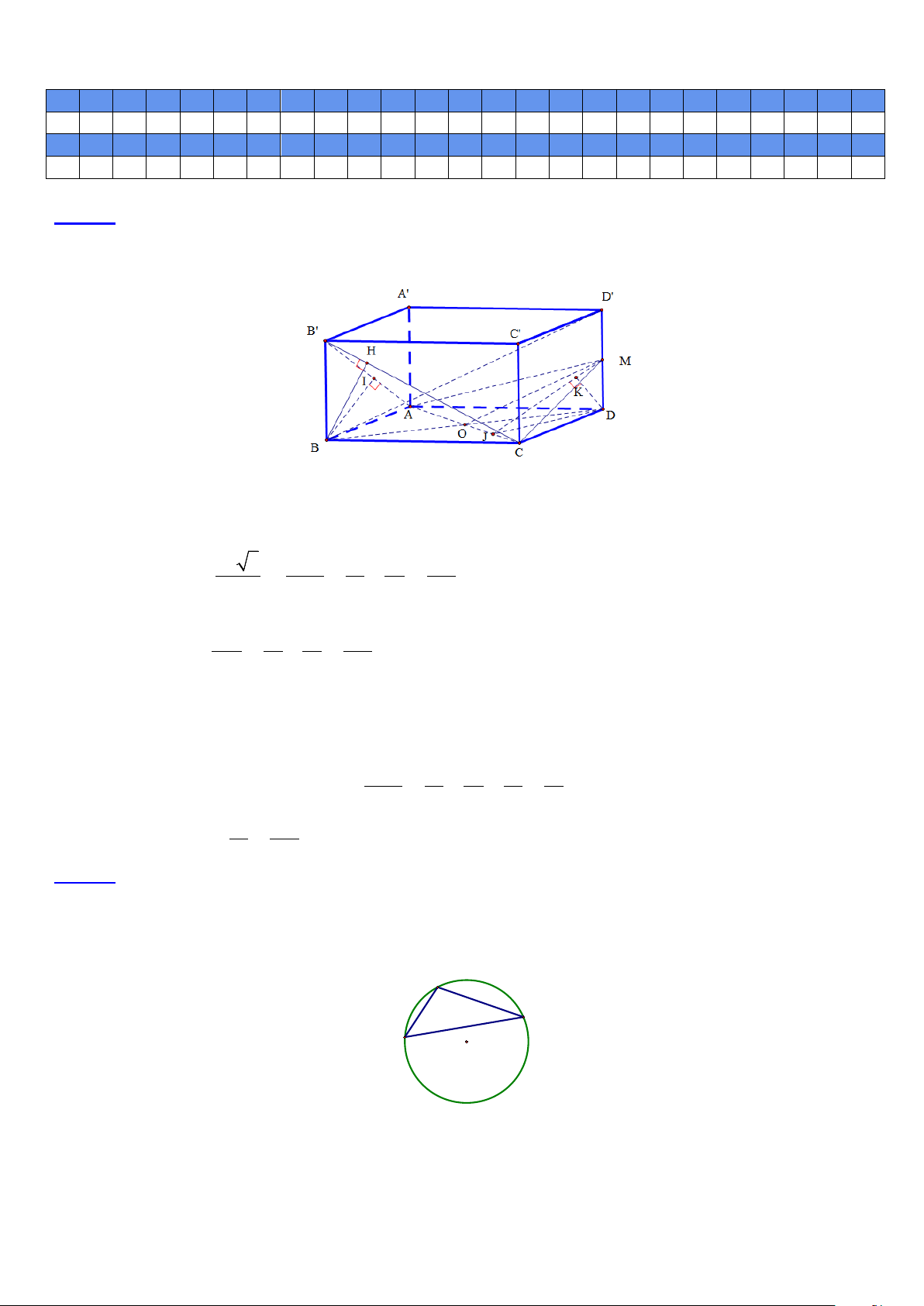
Đặt AB x , AD y , AA  z .
Gọi H là hình chiếu vuông góc của B trên B C
 , ta có BH là đoạn vuông góc chung của AB và B C  nên d AB B C   2a 5 1 1 1 5 ,  BH      . (1) 2 2 2 2 5 BH z y 4a
Gọi I là hình chiếu vuông góc của B trên AB , ta có BI là đoạn vuông góc chung của BC và AB nên d BC AB 1 1 1 5 ,  BI     . (2) 2 2 2 2 BI x z 4a
Gọi M là trung điểm của DD , O là giao điểm của AC và BD , ta có mặt phẳng ACM  chứa AC và song
song với BD nên d AC,BD dBD,ACM  dD,ACM .
Gọi J là hình chiếu vuông góc của D trên AC , K là hình chiếu vuông góc của D trên MJ , ta có
d D ACM  dD ACM  1 1 1 4 3 , ,  DK      . (3) 2 2 2 2 2 DK x y z a Từ (1), (2) và (3) ta có 2 1 
z  2a x y a .Thể tích khối hộp là 3
V xyz  2a . 2 2 z 2a Câu 27. Lời giải
Chọn B Đếm số phần tử của tập X .
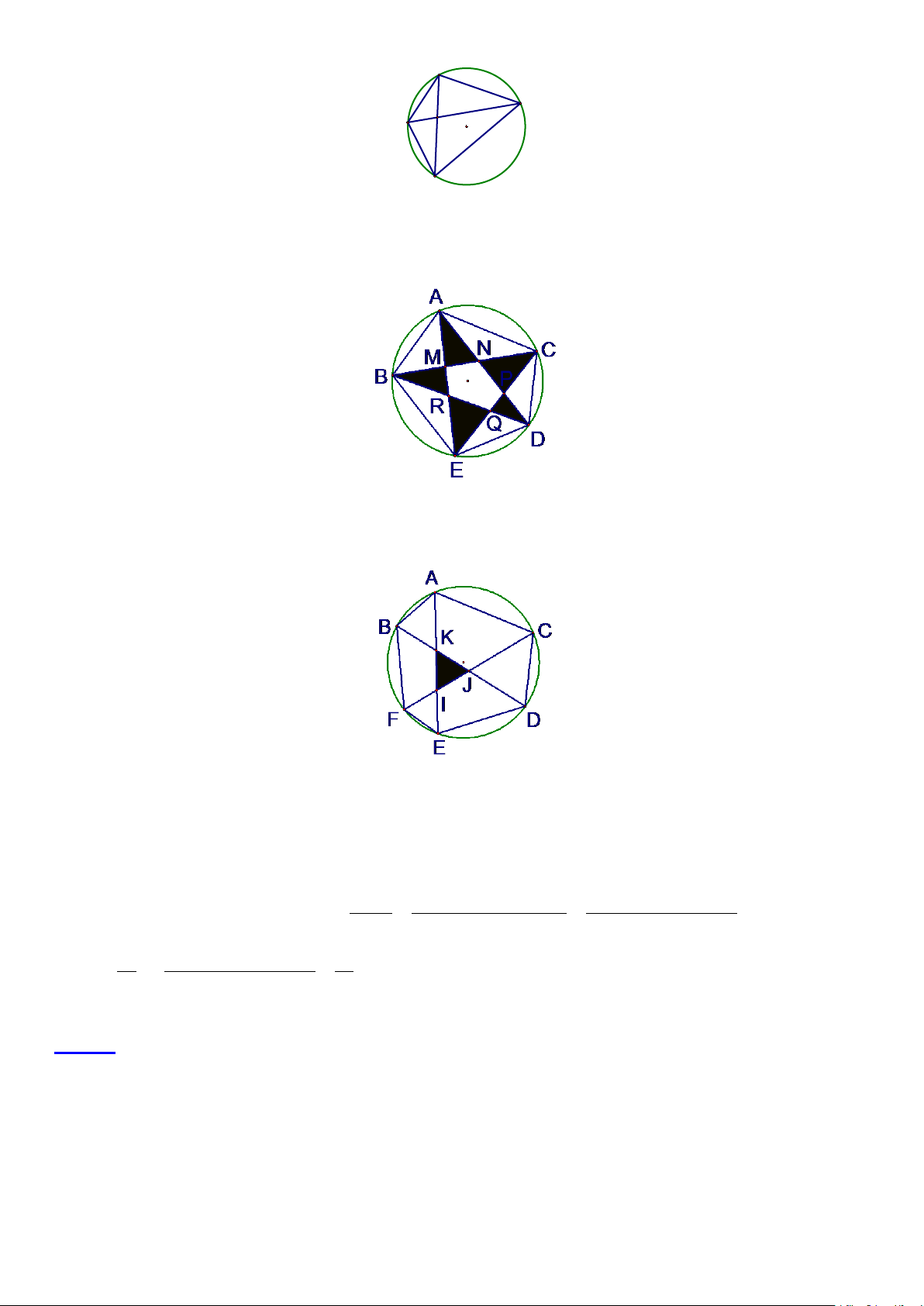
TH1: Tam giác có 3 đỉnh là 3 đỉnh của đa giác: Số tam giác loại này là 3 Cn . A C B
TH2: Tam giác có đúng 2 đỉnh là đỉnh của đa giác:
Chọn hai đỉnh của đa giác và một đỉnh nằm trong đa giác là giao điểm của hai đường chéo. Để có một giao
điểm như vậy ta cần phải có hai đường chéo, hay cần 4 đỉnh của đa giác. Mỗi cách chọn 4 đỉnh của đa giác
cho ta 4 tam giác có đúng hai đỉnh là đỉnh của đa giác.
Vậy số tam giác loại này là 4 4Cn . A I C B D
TH3: Tam giác có đúng một đỉnh là đỉnh của đa giác:
Mỗi cách chọn 5 đỉnh của đa giác sinh ra 5 tam giác loại này. Vậy có 5
5Cn tam giác trong TH này.
TH4: Tam giác không có đỉnh nào là đỉnh của đa giác:
Mỗi cách chọn 6 đỉnh của đa giác sinh ra một tam giác loại này.
Vậy số tam giác trong TH này là 6 Cn . Vậy có tất cả: 3 4 5 6
Cn + 4Cn + 5Cn + Cn tam giác sịnh ra do các cạnh và đường chéo của đa giác tạo ra.
Lấy ngẫu nhiên một tam giác từ tập X , suy ra n(Ω) 3 4 5 6
= Cn + 4Cn + 5Cn + Cn
Gọi A là biến cố lấy được tam giác không có đỉnh nào là đỉnh của đa giác . Ta có n( A) 6 = Cn . 6 3 2 n A − + −
Vậy xác suất của biến cố Cn n 12n 47n 60
A là P( A) ( ) = = = n(Ω) 3 4 5 6 3 2
Cn + 4Cn + 5Cn + Cn n +18n − 43n + 60 3 2 P( A) 4
n −12n + 47n − 60 4 3 2 = ⇔ =
⇔ 11n − 252n + 877n −1140 = 0 3 2 15
n +18n − 43n + 60 15 ⇔ (n − )( 2
19 11n − 43n + 60) = 0 ⇔ n =19 Câu 28. Lời giải Chọn C
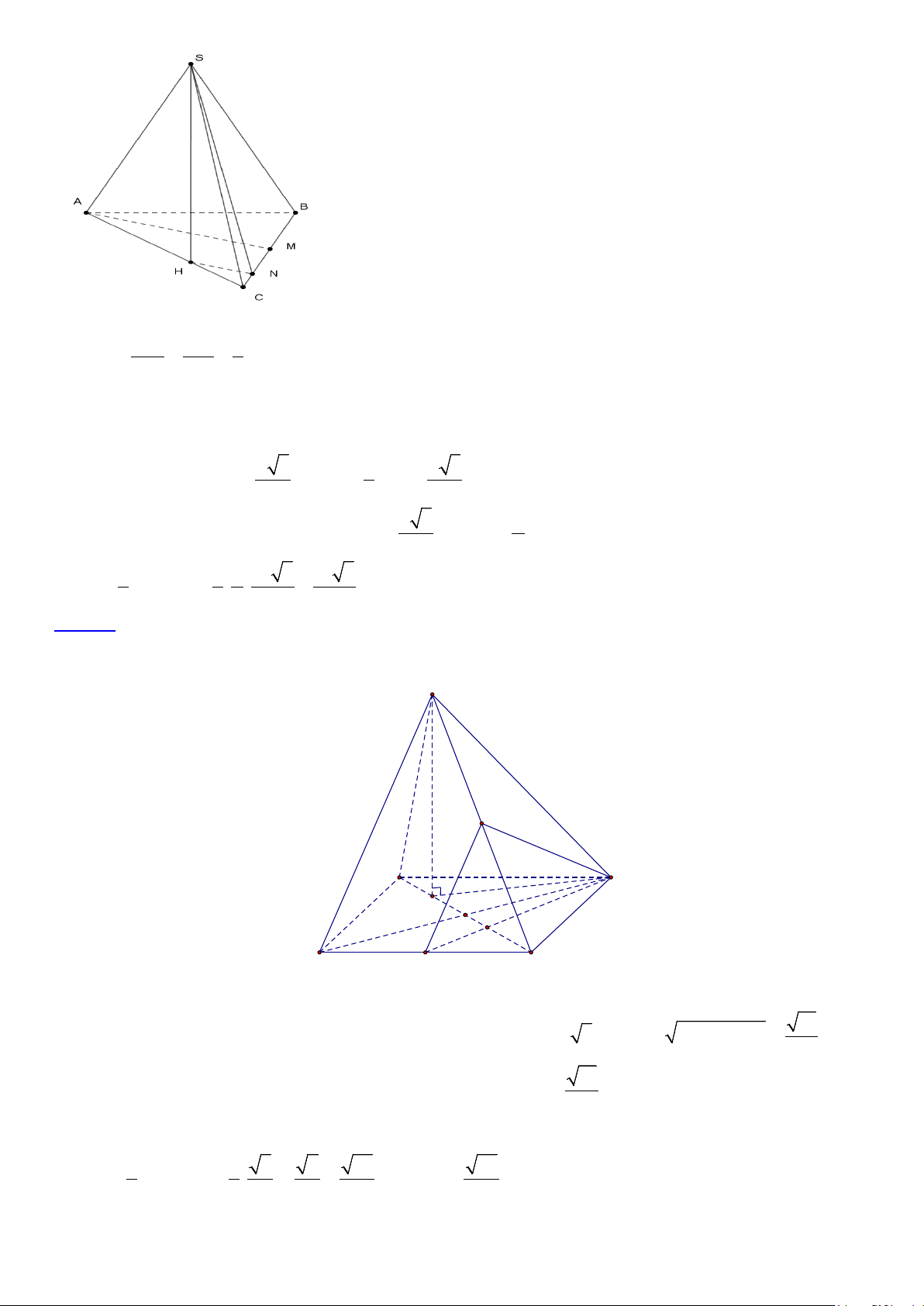
Gọi M là trung điểm của BC . CN CH 1 N ∈CM : = = CM
CA 3 ⇒ HN//AM . Mà A
∆ BC đều nên AM ⊥ BC ⇒ HN ⊥ BC ⇒ BC ⊥ (SHN ) . ( ) ( )  =  =  ; ( ; ) = 60o SBC ABC SN HN SNH . Do a a A ∆ BC đều nên 3 1 3 AM = ⇒ HN = AM = . 2 3 6 a a S
∆ HN vuông tại H có =  3 SH HN.tan SNH = .tan 60o = . 6 2 2 3 1 1 a a 3 a 3 V = SH S = = . S ABC . ABC . . . 3 3 2 4 24 Câu 29. Lời giải Chọn C S N B C H O G A M D
Kéo dài CG cắt AD tại trung điểm M của AD , gọi N là trung điểm SD .
Hình thoi ABCD có AB = BD = 2 nên tam giác BCD đều và 2 2 13
CO = 3 ⇒ CH = CO + OH = . 2
Tam giác SHC vuông cân vì  = °  13
SHC 90 , SCH = 45° ⇒ SH = CH = . 2
Dễ thấy SA / /MN ⇒ SA / / (CMN ) nên d (S ,
A CG) = d (S ,
A (CMN )) = d ( ,
A (CMN )) = d (D,(CMN )) . 1 1 3 7 39 39 V = S SH = = ⇒ V = S ABCD ABCD . . .4. . S. 3 3 2 2 3 ADC 6 V DM DN NMDC 1 39 = . = ⇒ V = V DA DS 4 NMDC SADC 24 Có 26 1 26 SH ∆ A = SH
∆ C ⇒ SA = SC = 2HC = ⇒ MN = SA = 2 2 4 ( 2 2 AC + DC ) 2 2 − AD
Tam giác ACD có AD = CD = 2, AC = 2 3 ⇒ CM = = 7 4 Tam giác SCD có 2 2 13 9 22 26
SD = SH + HD = + = ,CD = 2, SC = suy ra trung tuyến 4 4 2 2 ( 2 2 CS + CD ) 2 2 − SD 62 CN = = 4 4 Tam giác 62 26 37 434 637112 CMN có = = = ⇒  = ⇒  CN ,CM 7, MN cos MCN sin MCN = . 4 4 868 1736 Suy ra 1 =  367 S = . ∆ CM CN MCN CMN . . .sin 2 16 1 1 V V = Bh = S ⇒ = = . ∆ d D CMN d D CMN NMDC CMN ( ( )) ( ( )) 3 NMDC 2 14313 . . . , , 3 3 S C ∆ MN 367
Vậy d (SA CM ) 2 14313 , = . 367 Câu 30. Lời giải
Bài yêu cầu m 0;18 và x  0 , khi đó x m  0. Xét x  2 không phải nghiệm của phương trình nên với x  2 ta có: x 1  x 1 
x2log x m x1 log x mx1 x2 x2 
x m  4  m  4  x 1 4 4   x2 x 1  Đặt f xx2  4
x , ta chỉ quan tâm nghiệm dương nên xét f x trên 0;\   2 . x 1    1
Ta có f xx2  4 .
.ln 41 0, x  0; \ 2 . 2     x2
Bảng biến thiên của f x x 0 2 +∞ f'(x) 2 +∞ f(x) -2 -∞
Từ bảng biến thiên suy ra phương trình đã cho có đúng một nghiệm dương khi m  2 hoặc m 2.
Do m nguyên thuộc đoạn 0;18 nên tập các giá trị của m là 2;3;4;...; 
18 , có 17 giá trị. Câu 31. Lời giải Chọn B Ta có 3 2 3 3 x ( x +16 + 4) f ′(x) = x x = = 2 2
x +16 − 4 x +16 2 x + ( 2 16 x +16 − 4) 2
x +16 ( 2x +16 −4)( 2x +16 + 4) x( 2x +16 + 4) 4x = = x + 2 2 x +16 x +16   2 ⇒ f (x) 4x = ∫ 4 xx + d  x = d x x+ d ∫ ∫ ( 2x +16) = 2 + 4 x +16 + C 2  x +16  2 2 x +16 2 2 Mà f ( ) 49 3 = x
⇒ C = 0 ⇒ f ( x) = 2 + 4 x +16 2 2 3 3 3   3 3 3
Vậy x. f (x)dx x = ∫ 2 ∫ x 81 244 2195  + 4x x +16 dx 2 = dx + 2 x +16d( 2 x +16) = + = ∫ ∫  2 2 8 3 24 0 0  0 0 Câu 32. Lời giải Chọn D
Dựng hình vuông ABCD . AB ⊥ SA Ta có 
⇒ AB ⊥ (SAD) ⇒ SD ⊥ AB . AB ⊥ ADBC ⊥ SC Và 
⇒ BC ⊥ (SCD) ⇒ SD ⊥ BC . BC ⊥ CDSD ⊥ AB Khi đó 
⇒ SD ⊥ ( ABCD) ⇒ SD = d (S;( ABCD)) = a . SD ⊥ BC
Kẻ DH ⊥ SA và DK ⊥ SC DH ⊥ SA Ta có  ⇒ ⊥ DH ⊥ AB  (do AB ⊥ 
(SAD)) DH (SAB) DK ⊥ SC Tương tự,  ⇒ ⊥ . DK ⊥ BC  (do BC ⊥ 
(SCD)) DK (SBC)
Do đó ((SAB) (SBC))  = (DH DK)  =  ; , HDK . 2 2 Mà AC AD = = a 2 , SD .AD a 6 2 2
SA = SD + AD = a 3 và DH = DK = = 2 2 SA 3 HK / / AC  2a 2 2 a 3
⇒ SK = SH = SD − DK = ⇒ HK SH ⇒ HK = . 3 1 = = 3  AC SA 3 Vậy  2 2 2
DH + DK − HK 2 cos HDK = = . 2DH.DK 3 Câu 33. Lời giải
Chọn A Đặt f (x) = log ( 2
x + y ) + log ( 2
y + y + 64 − log x − y (coi y là tham số). 2020 2021 ) 4 ( ) 2 x + y > 0 
Điều kiện xác định của f ( y) là : 2
y + y + 64 > 0 .
x − y > 0  Do x ,y nguyên nên 2
x > y ≥ −y . Cũng vì x , y nguyên nên ta chỉ cần xét f ( y) trên nửa khoảng [ y +1;+ ∞). Ta có f ′(x) 1 1 = ( − < 0, x ∀ ≥ y +1. 2
x + y )ln2020 (x − y)ln4
Ta có bảng biến thiên của hàm số f (x)
Yêu cầu bài toán trở thành:
f ( y + 64) < 0 ⇔ log
( 2y + y +64)+log ( 2y + y +64 < log 64 2020 2021 ) 4 3 ⇔ log
( 2y + y +64 . log 2021+1 < 3 2 log2020 2021 1 y y 64 2021 + ⇔ + + − < 0 2021 ) ( 2020 )
⇒ − 301,76 < y < 300,76
Mà y nguyên nên y ∈{ 301; − − 300;...;299; }
300 . Vậy có 602 giá trị nguyên của y thỏa mãn yêu cầu. Câu 34. Lời giải
Chọn C sin 3 .xcot x = cot x ( )
1 . ĐK: sin x ≠ 0 ⇔ x ≠ kπ  π k2π  π k2π  π x = + x = +  = = +   ( ) sin 3x 1 3x k2π  6 3 6 3 1 ⇔ ⇔  2 ⇔  ⇔  cot x = 0  cos x = 0  π  π x = + kπ x = + kπ  2  2
Biểu diễn nghiệm lên đường tròn lượng giác và đối chiếu với điều kiện ta được các nghiệm của phương trình ( ) π π π
1 là: x = + kπ ; k2 + ; k ∈ . 2 6 3
Các điểm biểu diễn trên đường tròn lượng giác của tập nghiệm này tạo thành hình tứ giác BCB 'C ': y π 5π B 2 π 6 C' 6 C x O -π B' 2 3 2. .2
Tứ giác BCB 'C ' có 2 đường chéo vuông góc, diện tích của nó là: CC '.BB ' 2 S = = = 3 . 2 2 Câu 35. Chọn A
Đặt t = u x = 3
( ) x + 2x ta có t′ = ′ u x = 2
( ) 3x + 2 > 0,∀x do đó t = 3
x + 2x là một hàm số tăng vì vậy x∈ −1;    1 thì t ∈ −3;3   .
Dựa vào bảng biến thiên của hàm số f (x) trên đoạn −3;3 
 ta có max f (t) = 5 và min f (t) = −6 . −3;3   −3;3   Từ đây ta có max (
g x) = max f (t) + 3 f (m) hoặc max g(x) = min f (t) + 3 f (m) −1;  1 −3;3     −1;  1 −3;3    
 max f(t)+ 3f(m) =  8 3;3
 5 + 3 f (m) = 8
Trường hợp 1: −       ⇔ 
5 + 3 f (m) ≥ −6 +  f t + f m ≥ f t +  f m  3 f (m) max ( ) 3 ( ) min ( ) 3 ( )  −3;3 −3;3       f (m) = 1   13 f (m) = − ⇔  ⇔ f (m) =  1 3   1 f (m) ≥  2
Từ bảng biến thiên phương trình f (m) = 1 có 5 nghiệm, như vậy trường hợp này có 5 giá trị thực của m thỏa mãn.
 min f(t)+ 3f(m) =  8 3;3
 −6 + 3 f (m) = 8
Trường hợp 2: −       ⇔ 
−6 + 3 f (m) > 5 +  f t + f m > f t +  f m  3 f (m) min ( ) 3 ( ) max ( ) 3 ( )  −3;3 -3;3       2  f (m) = −   3  14 2 ⇔  f (m) = ⇔ f (m) = −   3 3  1  f (m) <  2
Từ bảng biến thiên phương trình 2
f (m) = − có 6 nghiệm, như vậy trường hợp này có 6 giá trị thực của m 3 thỏa mãn.
Vậy có tất cả là 11 giá trị thực của m thỏa mãn yêu cầu bài toán. Câu 36. Lời giải x + y Điều kiện:
> 0 ⇔ x + y > 0. 2 2
x + y + xy + 2 x + y Ta có : log
= x x − 3 + y y − 3 + xy 3 2 2 ( ) ( )
x + y + xy + 2
⇔ 2log (x + y) − 2log ( 2 2
x + y + xy + 2) 2 2
= x + y + xy − 3x − 3y 3 3
⇔ 2log (x + y) + 2 + (3x + 3y) = 2log ( 2 2
x + y + xy + 2) + ( 2 2
x + y + xy + 2 3 3 )
⇔ 2log (3x + 3y) + (3x + 3y) = 2log ( 2 2
x + y + xy + 2) + ( 2 2
x + y + xy + 2 (*). 3 3 )
Xét hàm số: f (t) = 2log t + t t > 3 với 0. Ta có f (t) 2 ' =
+1 > 0 với mọi t > 0. Suy ra hàm số y = f (t) đồng biến trên khoảng (0;+∞) . t.ln3
Khi đó ta có: ( ) ⇔ f ( x + y) = f ( 2 2
x + y + xy + ) 2 2 * 3 3
2 ⇔ 3x + 3y = x + y + xy + 2 (**).
x = a + b 3a − b + 3 Đặt  . Suy ra P = và ( ) ⇔ (a − )2 2 ** 3 1 + b =1.
y = a − b 2a + 6  (  a − ) cost + 3 3 1 = costa = Đặt  ⇔  3 với t ∈[0;2π ). b  = sint b   = sin t
3cost − 3sint + 6 3 Khi đó P =
⇔ (2P − 3)cost + 3sint = 6 3 −8 3P . 2cost + 8 3
Phương trình trên có nghiệm khi : ( P − ) + ≥ ( − P)2 2 2 3 3 6 3 8 3 2 69 − 249 69 + 249
⇔ 47P − 69P + 24 ≤ 0 ⇔ ≤ P ≤ (***). 94 94
Vì luôn tồn tại t ∈[0;2π ) để dấu bằng ở (***) xảy ra. Do đó, ta luôn tìm được a , b từ đó tìm được x, y để 69 + 249
P đạt giá trị lớn nhất. Vậy giá trị lớn nhất của P là . 94 Câu 37. Lời giải Chọn D y = f ( x) +
x − a = f ( x) 2 4 sin cos2
4 sin − 2sin x +1− a .  π  π
Đặt t = sin x ⇒ t = cos x > 0, x ∈  0;  ′
nên khi x tăng trên 0;
thì t tăng trên (0 ) ;1 . 2      2   π
Do đó hàm số y = f ( x) 2
4 sin − 2sin x +1− a nghịch biến trên 0;   khi và chỉ khi hàm số 2    y = f (t) 2 4
− 2t +1− a nghịch biến trên (0 ) ;1 .
Dễ thấy, điều kiện cần để hàm số y = f (t) 2 4
− 2t +1− a nghịch biến trên (0 ) ;1 là phương trình f (t) 2 4
− 2t +1− a = 0 vô nghiệm trên (0 ) ;1 . ( ) * Với điều kiện ( )
* , y = f (t) 2 4
− 2t +1− a nghịch biến trên (0 ) ;1 khi và chỉ khi
(4 f ′(t) − 4t)(4 f (t) 2 − 2t +1− a)
y′ ≤ 0,∀t ∈(0; ) 1 ⇔
≤ 0, ∀t ∈(0; ) .( ) ** 4 f (t) 1 2 − 2t +1− a
Dựa vào đồ thị trên ta có f ′(t) < 0, ∀t ∈(0; )
1 , do đó 4 f ′(t) − 4t < 0, t ∀ ∈(0; ) 1 .
Khi đó: ( ) ⇔ f (t) 2
− t + − a > ∀t ∈( ) ⇔ a < f (t) 2 ** 4 2 1 0, 0;1 4
− 2t +1,∀t ∈(0 ) ;1 .
(điều kiện này luôn đảm bảo thỏa mãn (*))
Hay a ≤ f (t) 2 4
− 2t +1,∀t ∈[0; ]
1 ⇔ a ≤ min{4 f (t) 2 − 2t + } 1 . [0; ]1
Xét hàm số g (t) = f (t) 2 4 − 2t +1 trên [0 ]
;1 có g′(t) = 4 f ′(t) − 4t < 0, ∀t ∈[0; ] 1 ,
nên g (t) nghịch biến trên [0 ]
;1 . ⇒ min g (t) = g ( )
1 = 3.Vậy a ≤ min g (t) = 3. [0; ]1 [0; ]1
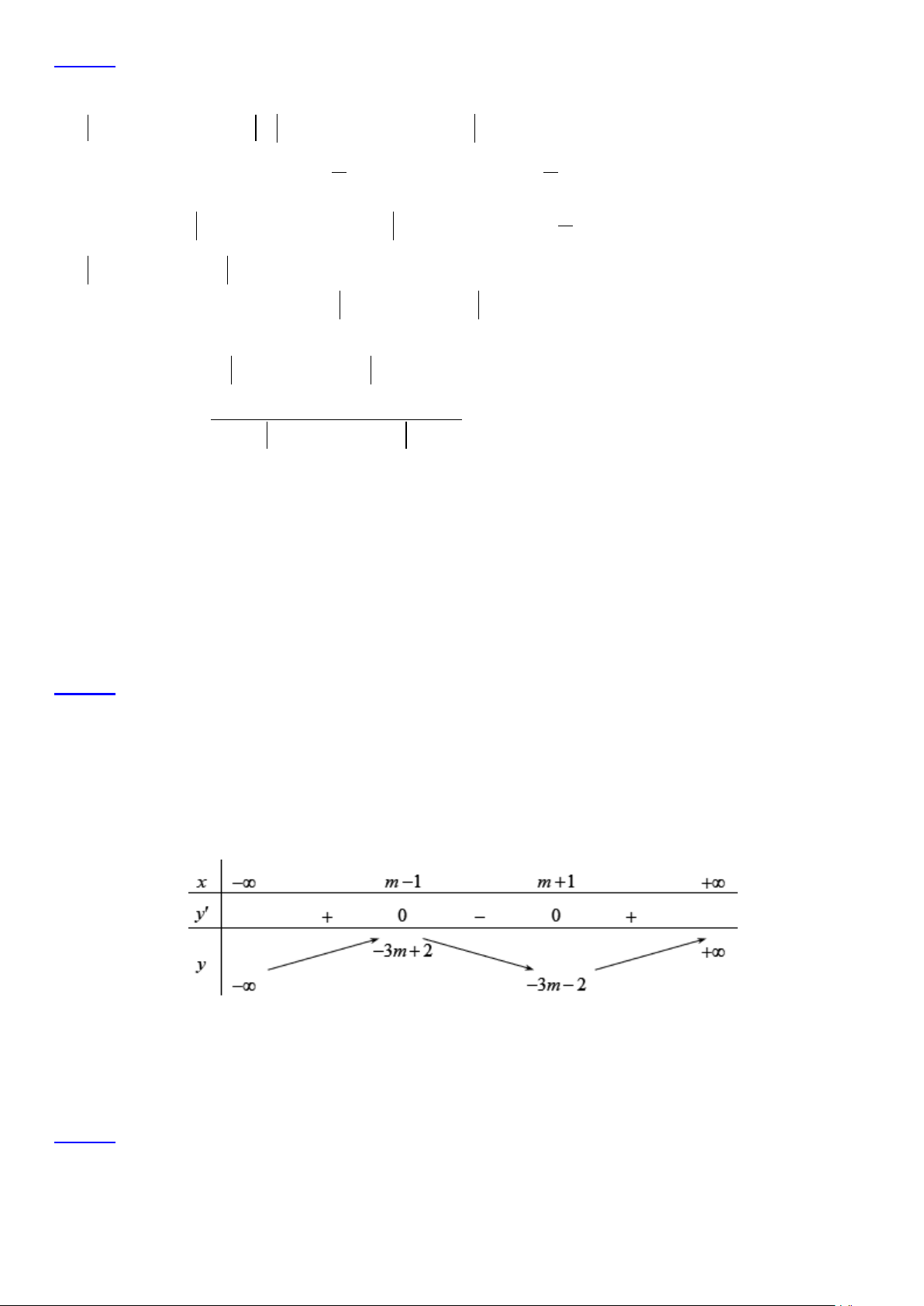
Vì a nguyên dương nên 0 < a ≤ 3 ⇒ a ∈{1;2; } 3 . Câu 38. Lời giải ChọnA Ta có: y′ = 2 x − mx + 2 m − = 2 x − mx + 2 3 6 3( 1) 3( 2 m −1) x = m −1 y′ = 0 ⇔ 2 x − 2mx + 2 m −1 ⇔  x = m +  1 Bảng biến thiên:
Dựa vào bảng biến thiên ta thấy điểm cực đại của đồ thị (C) là điểm M( m −1;−3m + 2 ) .
Nhận xét: y = −3m + 2 = −3(m −1) −1 = −3x −1 ⇒ M ∈(d) : y = −3x −1,∀ . m M M
Vậy: khi m thay đổi, điểm cực đại của đồ thị (C) luôn nằm trên một đường thẳng d cố định có phương
trình: y = −3x −1. Vậy đường thẳng d có hệ số góc k = −3. Câu 39. Lời giải
Chọn A Xét hàm số f (x) = 5 x − 2
5x + 5(m −1)x − 8.
Trường hợp 1: f (x) = 0 có nghiệm x ∈(−∞;1 thì hàm số y = f (x) không thể nghịch biến trên khoảng 0 ) (−∞;1).
Trường hợp 2: f (x) = 0 không có nghiệm x ∈(−∞;1 . 0 )
Ta có: f ′(x) = 4
5x −10x + 5(m −1). f ′ Khi đó
(x). f (x) y = 5 x − 2
x + (m − )x − = f (x) = 2 5 5 1 8
f (x) nên y′ = . 2 f (x)
Hàm số nghịch biến trên (−∞;1) khi và chỉ khi y′ ≤ 0 với
f ′(x). f (x) ≤  0  f (x) < 0
∀x ∈(−∞;1) ⇔  ⇔ 
, ∀x∈(−∞;1) ( vì lim f (x) = −∞ ) f (x) , ∀x∈(−∞;1) ≠  0 f ′(x) ≥  0 x→−∞  f ′(x) = 4
5x −10x + 5(m −1) ≥ 0, ∀x∈(−∞  ;1) ⇔ 
f (1) = 5m −17 ≤  0 3 m ≥ − 4
x + 2x + 1, ∀x ∈(−∞;1)   m ≥  max(− 4 x + 2x + 1) = + 1   (−∞ ) ;1 3 ⇔  ⇔  2. 2 17 m ≤  17  m ≤ 5  5 3 17 ∈ ⇔ + 1 ≤ ≤  m m  →m = 3. 3 2. 2 5 Câu 40. Lời giải f x Chọn B 1 3
Đẳng thức đã cho tương đương với: ( f ′(x))2 ( ) − = 9 − − . 3 x x x
Lấy tích phân hai vế trên đoạn [1;4] ta được: 4 4 4 ∫( f ′ x )2 f (x)  1 3 ( ) dx dx 9  − = − − dx = 21− ∫ ∫  2ln 2. 3 xx 1 1 1 x  Tích phân từng phần có 4 f (x) 4 4 4 dx = f ∫ ∫ (x)  2   2  d − + = − f (x) 4  2  − − f ∫ (x)  1 6 6 6 = 36 − + 2 −       ∫ 3 ′  f ′( x)d . x Vậy có 3 xx   x  1 1 1 1  x  1  x  đẳng thức: 4 ( 4 f ′(x))2  1 dx 36 2 3 + − − f ′ ∫ ∫ (x)dx = 21−   2ln 2. 1 1  x  4 2
f ′(x) 1  ⇔ − + x = ⇔ f ′ ∫ d (x) 1 3 0 ≡ − 3, x
∀ ∈[1;4] ⇒ f (x) = 2 x −   3 .x 1  xx 4 4 79 Vì vậy f
∫ (x)dx = ∫(2 x −3x)dx = − . 6 1 1 Câu 41. Lời giải
Chọn D Ta có ′( ) = 2x ln 2 + 2−x f x ln 2 + 2019 > 0 x
∀ ∈  ⇒ f (x) đồng biến trên  .
Từ giả thiết suy ra f ( 3 2
x − x + x − m ) < − f ( 2 2 3 2x − 2x −5) ⇔ f ( 3 2
x − x + x − m ) < f ( 2 2 3
2x − 2x + 5) (do ( ) = 2x − 2−x f x
+ 2019x là hàm số lẻ) 3 2 2
x − x + x − m < x − x + 3 2 2 2 3 2 2 5
⇔ x − 2x + 3x − m < 2x − 2x + 5 ⇔  3 2 2
x − 2x + 3x − m > 2 − x + 2x − 5 3 2
x − 4x + 5x − 5 < m ⇔  3 
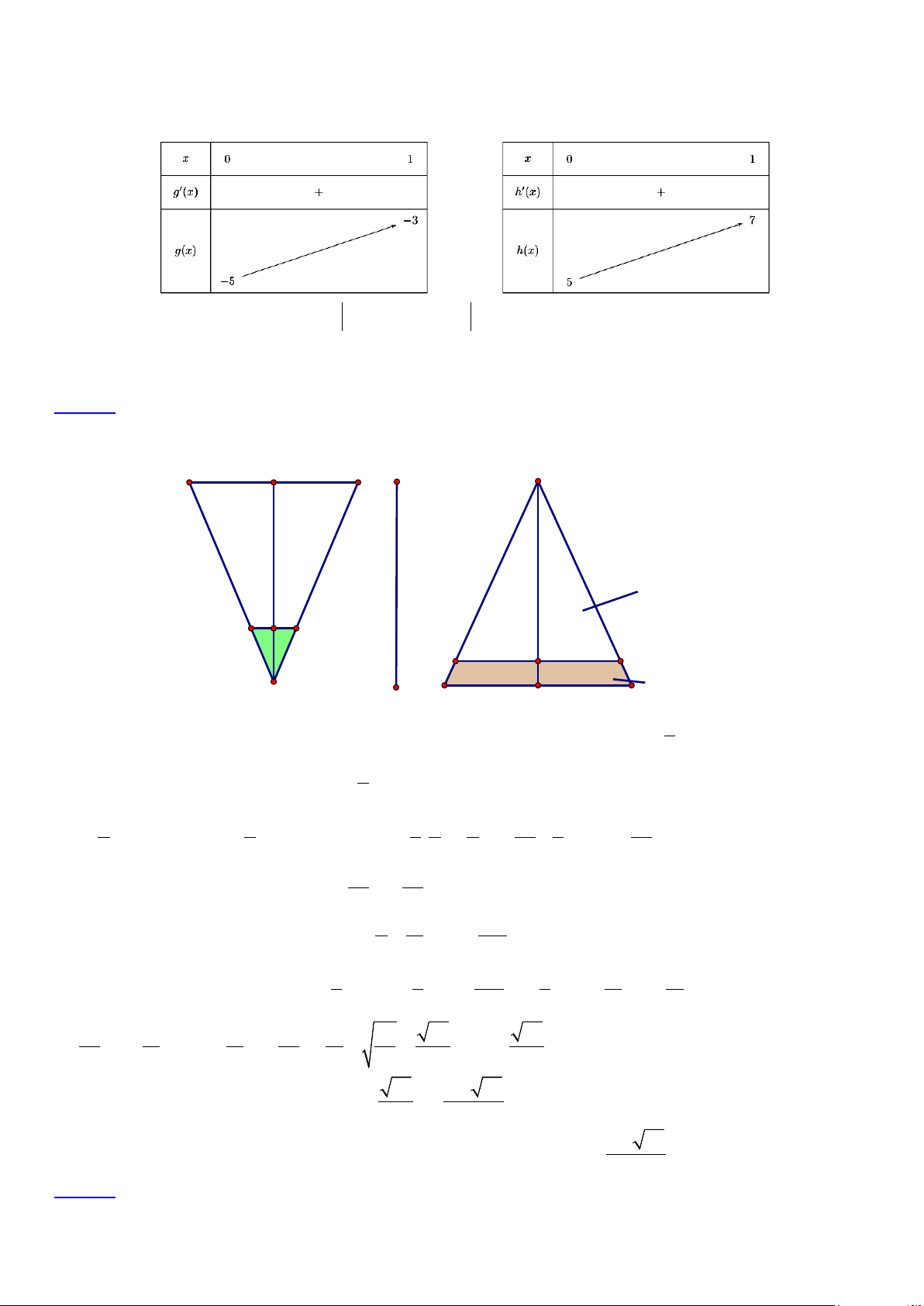
x + x + 5 > m Xét g (x) 3 2
= x − 4x + 5x − 5 và h(x) 3
= x + x + 5 trên (0; )
1 có bảng biến thiên là
Từ bảng biến thiên suy ra f ( 3 2
x − x + x − m )+ f ( 2 2 3
2x − 2x −5) < 0, x ∀ ∈(0; ) 1 khi và chỉ khi m ≥ 3 −  ⇒ 3
− ≤ m ≤ 5 . Vậy tập S có 9 phần tử. m ≤ 5 Câu 42. Lời giải Chọn C r h' khoảng không h h/4 x nước r Giả sử ly có chiều cao 1
h và đáy là đường tròn có bán kính r , nên có thể tích 2 V = π hr . 3
Khối nước trong ly có chiều cao bằng 1 chiều cao của ly nên khối nước tạo thành khối nón có chiều cao 4 2
bằng h và bán kính đáy r thể tích nước bằng 1 h r  1  1 2  1 . π = . π hr =     V . 4 4 3 4  4  64  3  64
Do đó thể tích khoảng không bằng 1 63 V − V = V . 64 64
Nên khi úp ngược ly lại thì ta có các tỉ lệ : x h' r.h' = ⇒ x = . r h h 2 3 3
Suy ra: thể tích khoảng không bằng: 1 2 1  r.h '  1 2  h '   h ' h'.π x .h'.π. π hr .  = = =       .V . 3 3  h  3  h   h  3 3 3 3 63  h '   h '  63 h' 63 63 63 ⇒ = ⇒ = ⇒ = 3 V V = ⇒ h' =     h . 64  h   h  64 h 64 4 4 3 3
Nên chiều cao mực nước bằng: 63 4 − 63
h − h' = h − h = h . 4 4 3
Vậy tỷ lệ chiều cao của mực nước và chiều cao của ly nước bây giờ bằng 4 − 63 . 4 Câu 43. Lời giải Chọn D
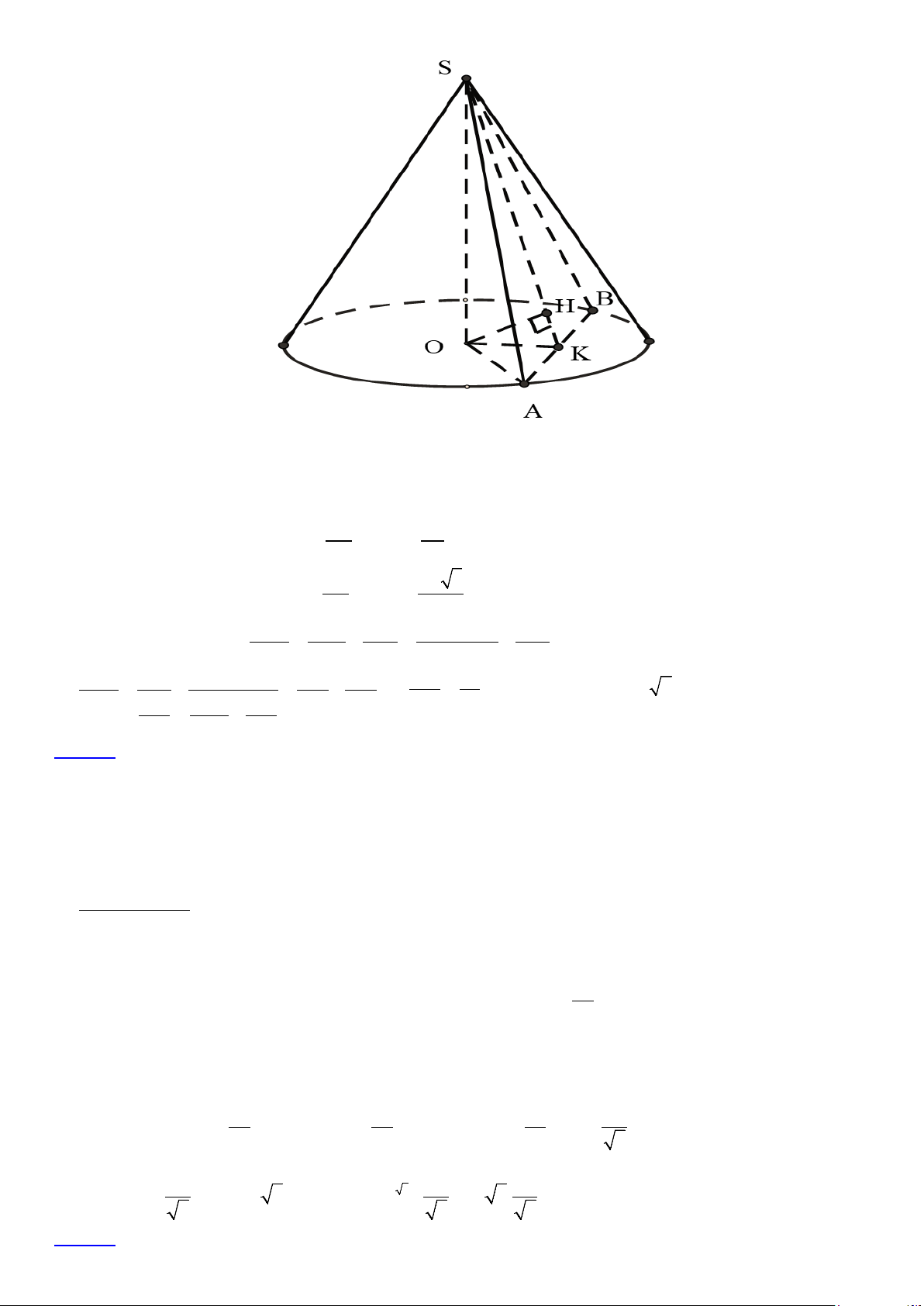
Gọi K là trung điểm của AB ta có OK ⊥ AB vì tam giác OAB cân tại O
Mà SO ⊥ AB nên AB ⊥ (SOK ) ⇒ (SOK ) ⊥ (SAB) mà ⇒ (SOK ) ∩(SAB) = SK nên từ O dựng OH ⊥ SK
thì OH ⊥ (SAB) ⇒ OH = d (O,(SAB))
Xét tam giác SAO ta có:  sin SO SA SAO = ⇒ SO = SA 2
Xét tam giác SAB ta có:  SK SA 3 sin SAB = ⇒ SK = SA 2
Xét tam giác SOK ta có: 1 1 1 1 1 = + = + 2 2 2 2 2 2 OH OK OS SK − SO SO 1 1 1 4 2 6 3 ⇒ = + = + 2 ⇒ =
⇒ SA = 2a ⇒ SA = a 2 2 2 2 2 2 2 OH SA 3SA SA SA SA 2 2 − SA a 4 4 4 Câu 44. Lời giải
Chọn A Điều kiện: y > 0; (x−log2 y) x+log2 2.2 = 8 y + 5y ( ) 1 Theo đề bài, ta có:  2(x−log2 y) x+log2 2 = 8 y.5y ( 2 x+log2 8 y + 5y) 2 x+log2 ⇒ = 8
y.5y ⇔ ( x+log2 8 y − 5y) x+log2 = 0 ⇔ 8 y = 5y 4 (2)
⇒ log 8x+ y = log 5y ⇔ x + log y .log 8 = log 5 + log y 2 ( log2 ) 2 ( 2 ) 2 2 2 5
⇔ 3x + 3log y = log 5 + log y ⇔ 3x + 2log y = log 5 ⇔ 3x = log 3 2 2 2 2 2 2 2 ( ) y Thay (2) vào ( ) 1 ta được: (x−log2 y) (x−log2 y) 2 2.2 = 5y + 5y ⇔ 2
= 5y ⇔ x − log y = log 5y ⇔ x = log 5y 4 2 2 2 ( ) Từ ( 5 5 1 1 3) và (4) ⇒ log = 3.log 5y ⇒ = 5y ⇔ y = ⇒ y = 2 2 ( )3 2 2 8 2 2 4 y y 25 5 2 2  1  x 2 log  1  1 2 5 ⇒ x = log 5. = log 5 ⇒ 2 .y = 2 . = 5. =     1 2 2 4 4  5   5  5 Câu 45. Chọn A
Xét hàm số y = f (2x −1) ⇒ ( f(2x −1))' = 2 f '(2x −1)nghịch biến khi f ′(x) < 0
⇔ ( f (2x −1))' = 2. f '(2x −1) < 0 ⇔ f '(2x −1) < 0 ⇔ 1 < 2x −1 < 3 ⇔ 1 < x < 2 .
Xét hàm số y = g(ax + b) ⇒ (g(ax + b))' = .ag'(ax + b)nghịch biến khi xảy ra hai trường hợp a > 0  a > 0  −  b  > 0  x a <     0   + < a ax b
g'(ax + b) < 0     2 ⇔ + >   2 − b ax b ⇔  x > a < 0    a  a < 0
g'(ax + b) > 0   a < 0 
0 < ax + b < 2   b − 2 b − < x < −   a a
Nếu a > 0 thì hàm số 
−b   − b
y = g(ax + b) nghịch biến trên 2 −∞; ; ;+∞ 
không thỏa mãn điều kiện có khoảng a a      nghịch biến là(1;2).
Nếu a < 0 thì hàm số  b − −b
y = g(ax + b) nghịch biến trên 2 −  ; a a   
Yêu cầu bài toán là hai hàm số y = f (2x −1) , y = (
g ax + b) có cùng khoảng nghịch biến lớn nhất  b − 2 − = 1  a = 2 − nên a  ⇔  ⇒ 4a + b = 4 − . −b b =   4 = 2  a Câu 46. Lời giải Chọn B
Ta có: x + xy + y = ⇔ ( x + y)2 + (x − y)2 2 2 5 2 2 9 2 = 9 .
Đặt 2x + y = 3sint, x − y = 3cost với t ∈ − π 2 π ;2    .
⇒ x = sint + cost và y = sint − 2cost . 6x − 6
6sint + 6cost − 6
6sint + 6cost − 6 K = = = .
4x − y − 9 4(sint + cost) − sint + 2cost − 9 3sint + 6cost − 9
⇒ (3K − 6)sint + (6K − 6)cost = 9K − 6 .
Điều kiện để phương trình trên có nghiệm là ( K − )2 + ( K − )2 ≥ ( K − )2 3 6 6 6 9 6 ⇔ −1 ≤ K ≤ 1 Xét hàm số 2t + 1 f (t) = trên −1;  1 t − 2   Ta có: −5 f '(t) =
< 0,∀t ≠ 2 . Suy ra 1
Max f (t) = f (−1) = . (t −2)2 −1;    1 3 Câu 47. Lời giải
Chọn C Tập xác định: D 1;\ 0 . 5 1 1 1    2 3 4 • lim y
5x 1 x 1  lim  lim x x x
x  0  y  0 là đường tiệm cận ngang của đồ thị x 2 x x  2x x 2 1 x hàm số. 5x  2 1  x 1 2 • lim y
5x 1 x 1 25x 9x  lim  lim  lim x0 2 x0 x  2x x0  2
x  2x5x 1 x 1 x0 2
x  2x5x 1 x 1 25x 9 9  lim 
x0 x  25x 1 x 1 4
x  0 không là đường tiệm cận đứng của đồ thị hàm số.
Vậy đồ thị hàm số có tất cả 1 đường tiệm cận. Câu 48. Lời giải
Chọn C . Dựa vào đồ thị ta thấy f '(x)  0  x  2 và f '(x)  0  x  2. Ta có 2 2
g '(x)  2(xm) f '(x 2mx m 1).
xm  0   2 2
f '(x 2mx m 1)   0 2 2 g '(x) 0
2(x m) f '(x 2mx m 1) 0           
xm  0   2 2 
f '(x 2mx m 1)   0   x    m x m      m  
1 x m 1 2 2 x  
2mx m 1 2    
m x m    1      x m   .      x m  x m1   
x m 1  2 2   x  
2mx m 1 2      
x m1    m  0     1     1   m  0  Hàm số  y m  
g(x) nghịch biến trên 1   2 0;     2   .  2   3  3 m  m   2  2
Kết hợp với m   và m [5;5] suy ra m {0;2;3;4;5}. Vậy tổng tất cả các phần tử của S bằng 14. Câu 49. Lời giải x > 0
Chọn C Điều kiện  ⇒ > 2x m ⇒ m >1.
m − 2x > 0 x > 0 x > 0 2
log x − 3log x + 2 Ta có 3 3 < 0 
⇔ m − 2x > 0
⇔ m − 2x > 0 m − 2x  2 
log x − 3log x + 2 < 0
(log x −1 log x − 2 < 0  3 )( 3 ) 3 3 x > 0 x > 0  m > 2x ⇔ 
m − 2x > 0
⇔ m > 2x ⇔  (I). 3  < x < 9 1
 < log x < 2   3 < x < 9 3 
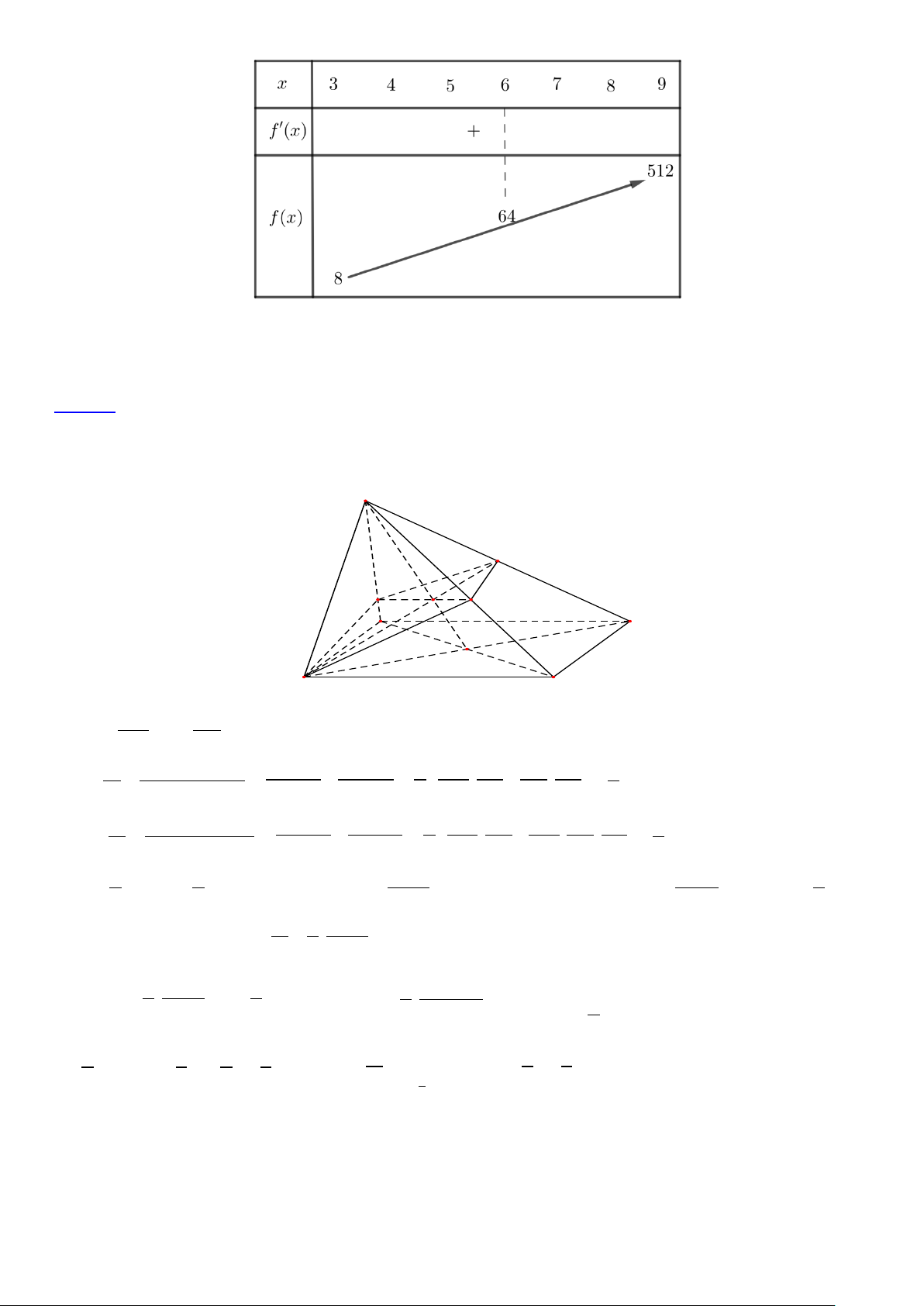
Để bất phương trình có không quá 3 nghiệm nguyên dương khi và chỉ bất phương trình 2x m > có không quá
3 nghiệm nguyên dương x∈(3;9) .
Xét hàm số = ( ) = 2x y f x
với x∈(3;9) có ′( ) = 2x f x .ln 2 > 0, x ∀ . Bảng biến thiên
Từ bảng biến thiên suy ra 7 m ≤ 2 =128 .
Mà m >1 và m nguyên dương nên m∈{2,3,..., } 128 .
Vậy có 127 giá trị nguyên dương của tham số m thoả mãn. Câu 50. Hướng dẫn giải Chọn D Cách 1 S P I M N C B O A D Đặt SM a = , SN b =
, (0 < a;b ≤ ) 1 . SB SD V V Ta có V V +VSM SP SN SP  1 1 S.AMP S.ANP = S.AMP S.ANP = + 1 = . +  . = (a + b) (1) V V 2V V 2  SB SC SD SC S ABC 2 . S.ADC  4 V V Lại có V V +VSM SN SM SN SP  1 S.AMN S.PMN = S.AMN S.PMN = + 1 = . +  . . = 3 ab (2). V V 2V V
2  SB SD SB SD SC S ABD 2 . S.CBD  4 Suy ra 1 ( + ) 3 = ⇔ + = 3a a a b ab a b b ⇒ b =
. Từ điều kiện (0 < b ≤ ) 1 , ta có a ≤1, hay 1 a ≥ . Thay 4 4 3a −1 3a −1 2 2
vào (2) ta được tỉ số thể tích V 3 a 1 = . . V 4 3a −1  = 2 a 0(L) 2
Đặt f (a) 3 a 1 . ;a  ;1 = ∈
, ta có f (a) 3 3a − 2a ' . 0  = = ⇔ . 4 3a 1 2  − 2   2 4 (3a −1)  a =  3  1 V  2  1 f  =  f ( ) 3  2  1 1 = ; f =  , do đó 1
Min = Min f (a) = f =   . 2 8  3      3 1 V a ;1 ∈  3  3 2   
Document Outline

  • Made 101
  • Made 101_HDG