Đề học sinh giỏi Toán 12 năm 2023 – 2024 trường THPT Bình Chiểu – TP HCM

SỞ GIÁO DỤC VÀ ĐÀO TẠO TP.HCM
KÌ THI HỌC SINH GIỎI CẤP TRƯỜNG TRƯỜNG THPT BÌNH CHIỂU NĂM HỌC 2023 - 2024 TỔ TOÁN –TIN Môn: TOÁN - Lớp 12 ĐỀ CHÍNH THỨC
Thời gian: 120 phút (Không kể thời gian phát đề) 2 4x 4x1
Câu 1. (3,0 điểm) Giải phương trình: 2 log    4x 1 6x 7  2x 
Câu 2. (3,0 điểm) Một người vay tiền ở một ngân hàng theo hình thức lãi kép với lãi suất 0, 7% / tháng
với tổng số tiền vay là 1 tỉ đồng. Mỗi tháng người đó đều trả cho ngân hàng một số tiền như nhau
để trừ vào tiền gốc và lãi. Biết rằng đúng 25 tháng thì người đó trả hết gốc và lãi cho ngân hàng.
Hỏi số tiền của người đó trả cho ngân hàng ở mỗi tháng là bao nhiêu?
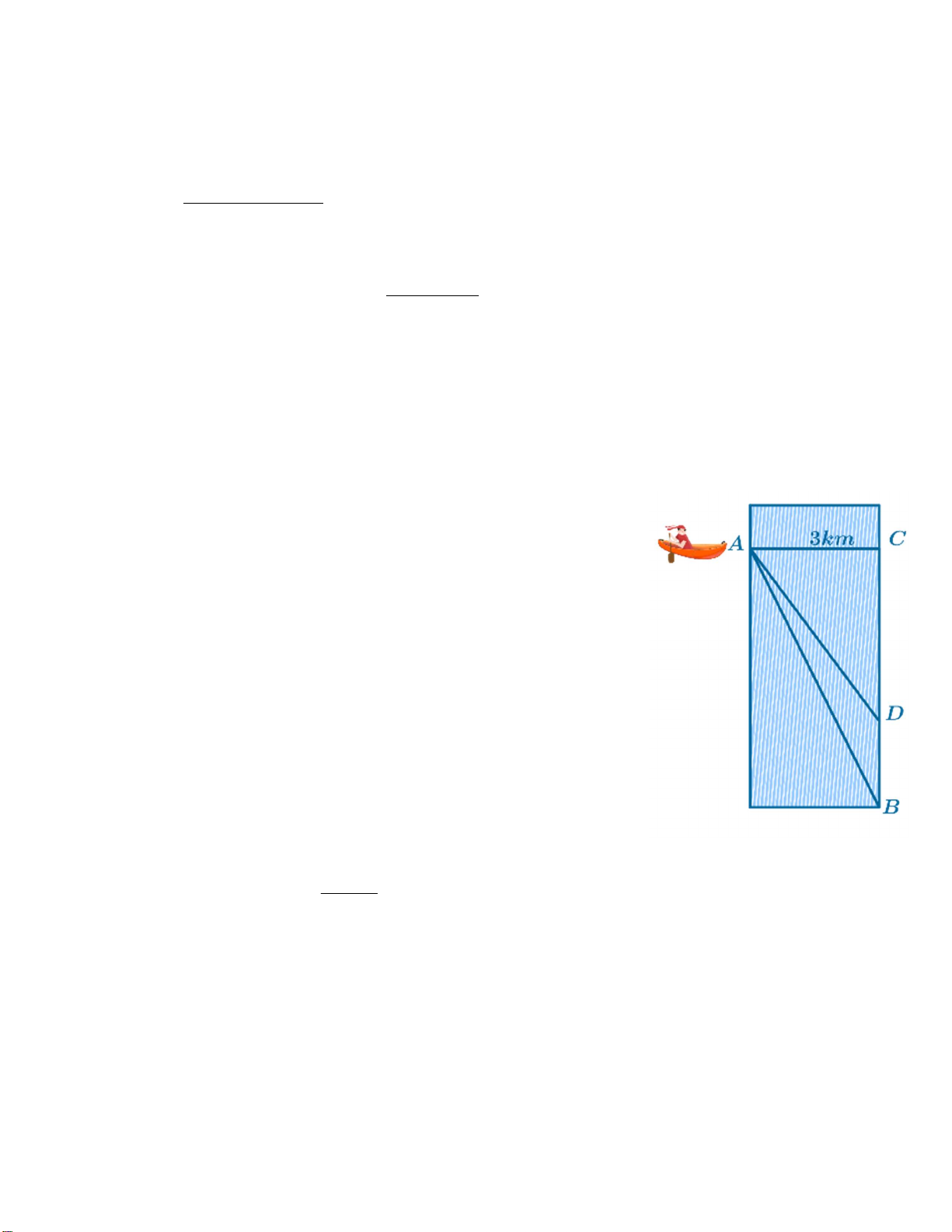
Câu 3. (3,0 điểm) Một người đàn ông muốn chèo thuyền từ vị trí A tới
điểm B về phía hạ lưu bờ đối diện càng nhanh càng tốt trên một
bờ sông thẳng rộng 3km (như hình vẽ). Anh có thể chèo thuyền của
mình trực tiếp qua sông để đến C và sau đó chạy đến B, hay có thể
chèo trực tiếp đến B, hoặc anh ta có thể chèo thuyền đến một điểm
D giữa B và C và sau đó chạy đến B. Biết anh ấy có thể chèo thuyền
6km/h, chạy bộ 8km/h và quãng đường BC=8km. Biết tốc độ dòng
nước là không đáng kể so với tốc độ chèo thuyền của người đàn
ông. Tính khoảng thời gian ngắn nhất (đơn vị: giờ) để người đàn ông đến B.  x 
Câu 4.(3,0 điểm) Cho hàm số 2 3 y 
có đồ thị (C) . Viết phương trình tiếp tuyến của đồ thị (C) , biết x 1
tiếp tuyến này cắt hai trục Ox, Oy lần lượt tại hai điểm A, B khác O và 5OA  4OB .
Câu 5. (2,0 điểm) Cho hình chóp S.ABC có AB  4 , AC  2 và 
BAC  120 , SA vuông góc với mặt đáy.
Gọi M , N lần lượt là hình chiếu vuông góc của A trên SB,SC . Góc giữa mặt phẳng  ABC và
AMN bằng 60 . Thể tích của khối chóp đã cho bằng bao nhiêu ? 1
Câu 6. (3,0 điểm) Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng 2a. Mặt phẳng qua AB và trung
điểm M của SC cắt hình chóp theo thiết diện có chu vi bằng 7a. Tính thể tích của khối nón có đỉnh
là S và đường tròn đáy ngoại tiếp tứ giác ABCD .
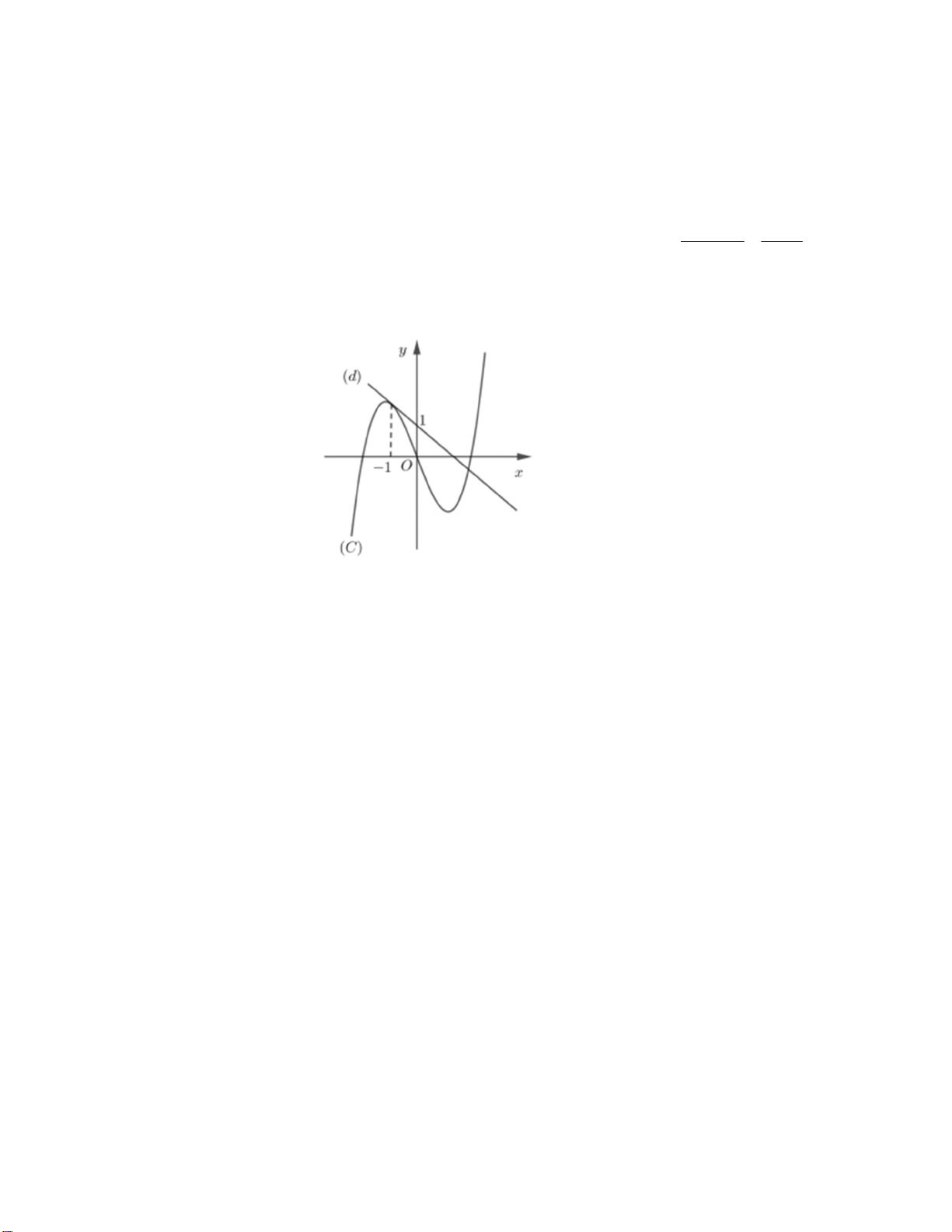
Câu 7. (3,0 điểm) Cho hàm số   3 2
f x  ax  bx  cx có đồ thị C như hình vẽ. Đường thẳng d : y  g  x f  x 1 g  x
là tiếp tuyến của C tại điểm có hoành độ x  1  . Hỏi phương trình   có bao g  x  f  x 0 1 nhiêu nghiệm? ------ HẾT -----
Học sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
Họ tên thí sinh: ……………………………. . . . .……. Số báo danh:………………. …….……
Chữ kí của giám thị 1: ……………………. . . . .……. .Chữ kí của giám thị 2:……. …….…… 2
ĐÁP ÁN ĐỀ HỌC SINH GIỎI CẤP TRƯỜNG KHỐI 12 Câu Đáp án Điểm 1 Điều kiện: x 0, x . 2 Ta có: 2 4x 4x 1 2 2 2 log 4x 1 6x log 4x 4x 1 4x 4x 1 log 2x 2x 7 7 7 2x 3,0 . 1 điểm 1 Xét hàm số f t log t t có f t 1 0 t 0 nên là hàm số đồng 7 (1,0X3) t ln 7 biến trên 0; . 3 5 Do đó ta có 2 2 4x 4x 1 2x 4x 6x 1 0 x . 4
Gọi M là số tiền vay ban đầu.
Gọi A là số tiền mà hàng tháng người đó trả cho ngân hàng.
Sau tháng 1 dư nợ còn lại là: M.1,007 − A
Sau tháng 2 dư nợ còn lại là: (M − ) 2
.1,007 A .1,007 − A = M.1,007 − . A 1,007 − A
Sau tháng 3 dư nợ còn lại là: (M − A − A) − A = M − A (  )2 2 3 .1, 007 .1, 007 .1, 007 .1, 007 . 1, 007 +1,007 +1   . n− − 3,0 2
Sau tháng thứ n dư nợ còn lại là: n M − A (  ) 1 n 2 .1, 007 . 1, 007 +1,007 +...+1,007 +1   điểm
Vì đúng 25 tháng thì trả hết nợ nên: − A (  )24 25 23 1.1, 007 . 1, 007 +1,007 +...+1,007 +1 = 0   −  1,007 = . A (1, 007) 25 24 1, 007 1 25 23 25
+1,007 +...+1,007 +1  1,007 = . A   . 0, 007 25 1, 007 .0, 007  A =
 0,04374151341 tỉ đồng  43.741.513 đồng 25 1, 007 −1  43.740.000 đồng Gọi CD = x 2 x + 9 8 − x Thời gian đi ADB: + 6 8 ( ) 2 x + 9 8 − x f x = + (0  x  8) 6 8 x 1 9 3,0 3
Xét hàm số f '( x) = − = 0  x = 2 + 8 6 x 9 7 điểm   f ( ) 3 = f ( ) 73 9 7 0 , 8 = , f =1+   2 6  7  8 7
Vậy thời gian ngắn nhất là 1+ 8 4 5 −
Tập xác định D = R \ −  1 ; y ' =  0, x   1 − . 2 (x +1) (3,0
điểm) Suy ra mọi tiếp tuyến của (C) có hệ số góc âm. 1
Gọi M(x0;y0) là tiếp điểm của (C) và tiếp tuyến  thỏa đề. −5
Hệ số góc tiếp tuyến  là: k = y '( = 0 x ) . 2 ( + 0 x 1) OB 5
Từ giả thiết suy ra  có hệ số góc k = − tan OAB = − = − . OA 4 1 5 5 − 5 x =1 Do đó: 0 y '( = −  = −  0 x )  2 4 (x +1) 4 = −  0 x 3 0 1 5 1 5 7 + Với = − − + = − + 0 x = 1 thì 0 y =  PTTT  là: y (x 1) hay y x . 0,5 2 4 2 4 4 9 5 9 5 33 + Với − = − + − = − − 0
x = 3 thì y = − 0  PTTT  là: y (x 3) hay y x . 0,5 2 4 2 4 4 Cách khác:
+ Gọi  là tiếp tuyến thỏa đề.
Phương trình tiếp tuyến  của đồ thị (C) tại M (x ; y ) có dạng: 0 0 5 − 2 − x + 3 y = y '( − + 0  = − + 0 x )(x 0 x ) 0 y y (x 0 x ) (d). 2 1 (x +1) + 0 x 1 0 2  2
− x + 6x + 3  1 + 0 0   Ox = A  A ;0  5   2  2
− x + 6x + 3  + 0 0   Oy= B  B0;  2 (x +1)  0  2 2 2 2  2
− x + 6x + 3  ( 2 − x + 6x + 3) + 0 0 0 0 5OA=4OB  25  =16. (*) 4 5 (x +1)   0
+ vì A và B không trùng với O nên 2 2
− x + 6x +3  0 0 0 x =1 Do đó (*) 4 0  (x +1) =16  0 x = 3 −  0 1 5 1 5 7 + Với = − − + = − + 0 x = 1 thì 0 y =  PTTT () là: y (x 1) hay y x . 0,5 2 4 2 4 4 9 5 9 5 33 + Với − = − + − = − − 0
x = 3 thì y = − 0  PTTT () là: y (x 3) hay y x . 2 4 2 4 4 0,5
* Nếu học sinh giải ra 4 tiếp tuyến thì trừ 0,25 điểm. 5 Đáp án Điểm (2,0 điểm) 0,5
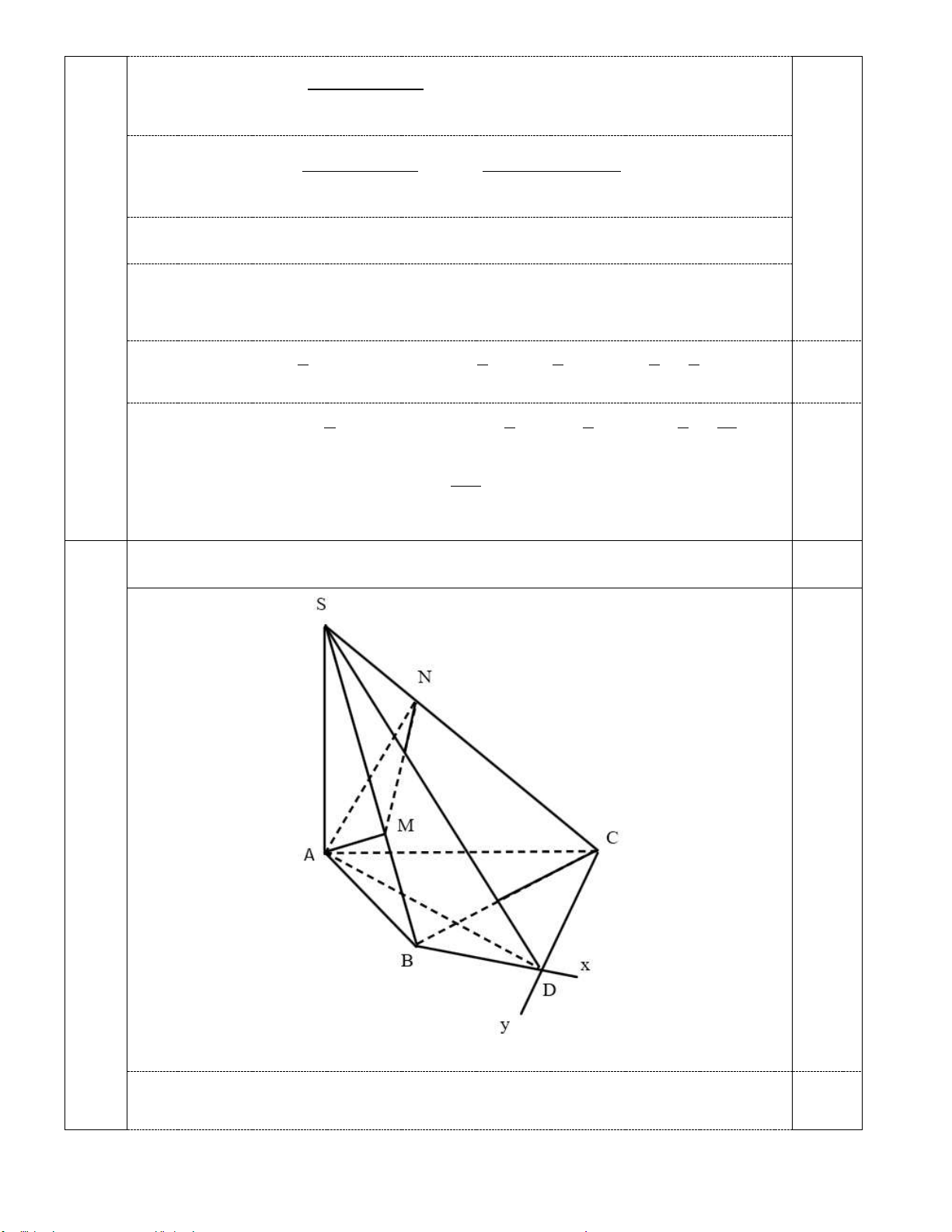
Trong ( ABC) gọi D là điểm thỏa mãn ABD = ACD = 90 . 0,5 Xét ABC có: 2 2 2
BC = AB + AC − 2.A . B A . C cos A
Với AD là đường kính của đường tròn ngoại tiếp tứ giác ABDC hay là đường tròn
ngoại tiếp ABC . BC 2 7 4 21
Theo định lý sin trong ABC ta có: AD = = = . sin120 3 3 2
Ta có: BD ⊥ (SAB)  BD ⊥ AM  AM ⊥ (SBD)  AM ⊥ SD .
Tương tự: AN ⊥ SD  SD ⊥ ( AMN ) . SA ⊥ ABC AMN ABC 0,5 Mặt khác: (
). Do đó góc giữa hai mặt phẳng ( ) và ( ) là góc giữa
hai đường thẳng SA và AD .
 Góc giữa SA và AD là(S ,
A SD) = ASD = 60 . AD 4 21 4 7
Trong SAD : SA = = : tan 60 = . tan ASD 3 3 1 1 Ta có: S = . . AB AC.sinA = .4.2.sin120 = 2 3  . ABC 0,5 2 2 1 1 4 7 8 21
Vậy thể tích của khối chóp S.ABC là: V = .S . A S = . .2 3 = . S . ABC  3 ABC 3 3 9 Câu Đáp án Điểm 6 3,0 điểm 0,5
Gọi E là trung điểm SD  ME / / AB suy ra ( ABM ) cắt hình chóp S.ABCD theo
thiết diện là hình thang ABME .
Gọi độ dài cạnh bên của hình chóp là x . Do chóp S.ABCD là chóp đều nên SAD  = SBC   AE BM . 1 2 2 2 SB + BC SC 2 2 x + 8a
Áp dụng hệ thức trung tuyến ta có: 2 BM = − = . 2 4 4 2 2 x + 8a Suy ra AE = BM = 4
Mặt khác dễ thấy EM = a , AB = 2a mà chu vi thiết diện bằng 7a nên ta có: 2 2 x + 8a 1 a + 2a + 2
= 7a  x = 2a 2 . 4 2 AC
Suy ra chiều cao của hình chóp: 2 2 SH = SA − 2
= 6a  SH = a 6 . 4
Khối nón có đỉnh là S và đường tròn đáy ngoại tiếp tứ giác ABCD chiều cao là 0,5 AC
SH = a 6 và bán kính đường tròn đáy là
= a 2 nên thể tích khối nón là: 2 3 2 a 6 V =  (a )2 1 2 a 6 = . 3 3 7 Đáp án Điểm (3
f ( x) −1 g ( x) Xét phương trình −
= 0 ( f x  0; g x  ) 1 điểm) g ( x) −1 f ( x) ( ) ( ) 2
 f (x) − f (x) 2
= g (x) − g (x) 2  f (x) 2
− g (x) = f (x) − g (x)   f
 (x) − g (x)  f
  (x) + g (x) = f 
(x)− g(x) 1,0
 f ( x) = g (x) (1)    f
 ( x) = − g ( x) . 1 (2) x = −1
- Xét phương trình (1) : Từ đồ thị suy ra (1) có đúng 2 nghiệm phân biệt  0,5 x =   0.
- Xét phương trình (2) : Xét hàm số y = f (x) có đồ thị là đường cong (C ) như hình
vẽ và hàm số y = −g(x) +1 có đồ thị là đường thẳng d  được xác định như sau:
+ Lấy đối xứng phần đồ thị đường thẳng d qua trục Ox . 0,5
+ Sau đó tịnh tiến đường thẳng trên theo phương Oy lên trên 1 đơn vị.
Khi đó số nghiệm của (2) bằng số giao điểm của (C ) với d . Từ đồ thị suy ra có 3 0,5
giao điểm, trong đó 1 giao điểm là gốc tọa độ O.
Do đó (2) có 3 nghiệm phân biệt trong đó có 1 nghiệm x = 0 (loại). 0,5
Vậy phương trình đã cho có 4 nghiệm