Đề học sinh giỏi Toán 12 THPT cấp tỉnh năm 2023 – 2024 sở GD&ĐT Hải Dương

SỞ GIÁO DỤC VÀ ĐÀO TẠO
KỲ THI CHỌN HỌC SINH GIỎI HẢI DƯƠNG
LỚP 12 THPT CẤP TỈNH NĂM HỌC 2023 - 2024 Môn thi: TOÁN ĐỀ CHÍNH THỨC Ngày thi: 25/10/2023
Thời gian làm bài: 180 phút, không tính thời gian phát đề
Đề thi gồm 05 câu, 01 trang Câu 1 (2,0 điểm)
a) Tìm các giá trị của m để hàm số 4 3
y = x − 4x + (m + 25) x − m đồng biến trên khoảng (1;+∞). b) Cho hàm số 3 2
y = 2x − 3mx + (m −1)x +1, với m là tham số thực. Tìm các giá trị của m để hàm
số có hai điểm cực trị x , x thỏa mãn x − x ≥1. 1 2 1 2 Câu 2 (2,0 điểm)
a) Gọi S là tập hợp các số tự nhiên có năm chữ số đôi một khác nhau được lập từ các chữ số 0, 1, 2,
3, 4, 5, 7, 8, 9. Chọn ngẫu nhiên một số thuộc tập S. Tính xác suất để số được chọn chia hết cho 5.
b) Giải phương trình: ( 2 x − x − ) 2 3
1 2x + 3 + 5x = 2x + x + 3. Câu 3 (2,0 điểm)
 x + 2 + y + 2 = 7y −3x +8
a) Giải hệ phương trình:  . 6 3
27x = x + 4y + 2
b) Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD và đường thẳng ∆ có phương
trình x − 2y + 6 = 0 . Điểm C thuộc đường thẳng ∆ , điểm M (6; 4) thuộc cạnh BC. Đường tròn
đường kính AM cắt đoạn BD tại điểm N (1; 5). Tìm tọa độ các đỉnh của hình vuông ABCD , biết
rằng đỉnh C có tọa độ nguyên và đỉnh A có hoành độ nhỏ hơn 1.
Câu 4 (3,0 điểm)
a) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và SC = 2a 5 . Hình chiếu của S
trên mặt phẳng ( ABC) là trung điểm M của AB. Góc giữa đường thẳng SC và mặt phẳng ( ABC) bằng 0
60 . Tính theo a khoảng cách từ B đến mặt phẳng (SAC).
b) Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại ,
A cạnh BC = 2a và  0
ABC = 60 . Biết tứ giác BCC B ′ ′ là hình thoi có  B B
′ C nhọn. Biết mặt phẳng (BCC B ′ ′) vuông góc với
mặt phẳng ( ABC) và mặt phẳng ( ABB A
′ ′) tạo với mặt phẳng ( ABC) một góc 0
45 . Tính theo a thể
tích khối lăng trụ ABC.A′B C ′ ′.
c) Cho tứ diện ABC .
D Gọi K là điểm thuộc cạnh CD sao cho 2KD = 3KC và I là điểm thuộc
đoạn thẳng BK sao cho IK = 2 .
IB Mặt phẳng (α ) đi qua I và luôn cắt các tia AB, AC, AD lần lượt
tại các điểm M , N, P (khác đỉnh A). Tìm giá trị nhỏ nhất của biểu thức: 2 2 2
= 4. AB + 9. AC +16. AD T 2 2 2 AM AN AP Câu 5 (1,0 điểm)
Cho x, y, z ∈[1;4] và thỏa mãn x ≥ y; x ≥ z. Tìm giá trị nhỏ nhất của biểu thức: x y z P = + +
2x + 3y y + z z + x --- HẾT ---
Họ và tên thí sinh: ..............................................................…......; Số báo danh: ......................................
Chữ kí cán bộ coi thi số 1: ................................ Chữ kí cán bộ coi thi số 2: ......…...................................
SỞ GIÁO DỤC VÀ ĐÀOTẠO
KỲ THI CHỌN HỌC SINH GIỎI CẤP TỈNH HẢI DƯƠNG
LỚP 12 THPT NĂM HỌC 2023 – 2024 Ngày thi: 25/10/2023 HƯỚNG DẪN CHẤM Môn thi: TOÁN
(Hướng dẫn chấm gồm có 07 trang) Câu Đáp án Điểm
a) Tìm m để hàm số 4 3
y = x − 4x + (m + 25) x − m đồng biến trên khoảng (1;+∞) . 1,0
Tập xác định D = .  Ta có 3 2
y′ = 4x −12x + m + 25. 0,25
Hàm số đồng biến trên khoảng (1;+∞) ⇔ y′ ≥ 0, x ∀ ∈(1;+∞) 3 2
⇔ 4x −12x + m + 25 ≥ 0 , x ∀ ∈(1;+∞) 3 2 ⇔ m ≥ 4
− x +12x − 25, x ∀ ∈(1;+∞). 0,25
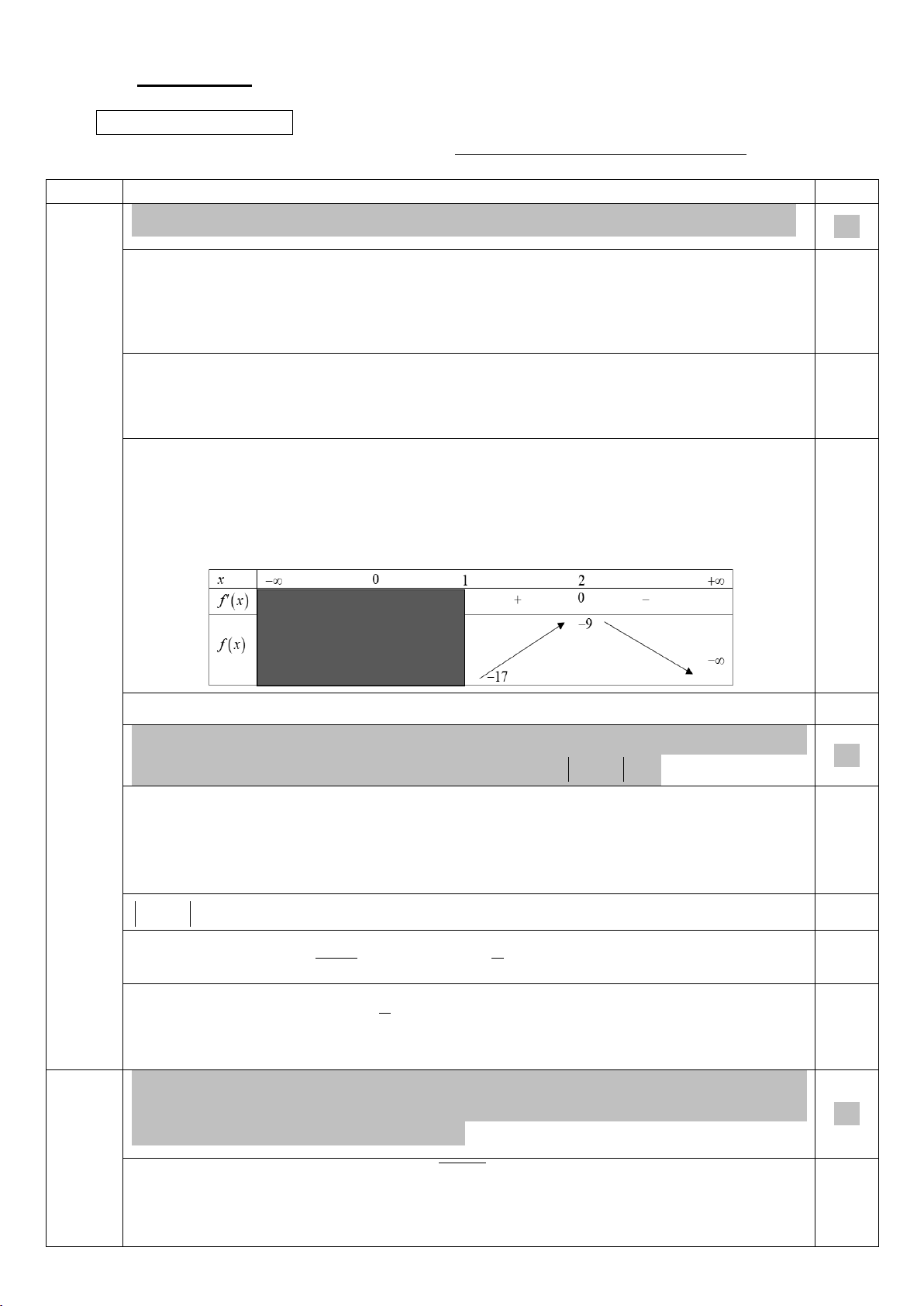
Xét hàm số f (x) 3 2 = 4
− x +12x − 25 trên (1;+∞) . f ′(x) 2 = 12 − x + 24x . 1 x = 0 f ′(x) 2 = 0 ⇔ 12
− x + 24x = 0 ⇔
. Ta có bảng biến thiên sau: (2,0 đ)  x = 2 0,25
Dựa vào bảng biến thiên ta có: 3 2 m ≥ 4
− x +12x − 25, x ∀ > 1 ⇔ m ≥ 9 − . 0,25 b) Cho hàm số 3 2
y = 2x − 3mx + (m −1)x +1,với m là tham số thực. Tìm các giá trị
của m để hàm số có hai điểm cực trị x , x thỏa mãn x − x ≥1. 1,0 1 2 1 2
Tập xác định D = .  Ta có 2
y′ = 6x − 6mx + m −1 0,25 2
∆ ' = 9m − 6m + 6 > 0, m
∀ ⇒ y ' = 0 có hai nghiệm phân biệt và y ' đổi dấu hai lần.
Vậy hàm số có 2 điểm cực trị với mọi m.
x − x ≥1 ⇔ (x − x )2 ≥1 ⇔ (x + x )2 − 4x x ≥1 0,25 1 2 1 2 1 2 1 2 Do m 1 x x m; x x − + = = nên ta có 2 2 m − (m − ) 1 ≥1 1 2 1 2 0,25 6 3  1 m ≤ − 2 3m 2m 1 0  ⇔ − − ≥ ⇔ 3  0,25 m ≥ 1
a) Gọi S là tập hợp các số tự nhiên có năm chữ số đôi một khác nhau được lập từ
các chữ số 0,1,2,3, 4, 5, 7, 8, 9. Chọn ngẫu nhiên một số thuộc tập S. Tính xác 1,0
suất để chọn được một số chia hết cho 5 .
Mỗi số tự nhiên thuộc tập S có dạng abcde
Số phần tử của không gian mẫu là 4 n(Ω) = 8A 0,25 8
Gọi A là biến cố chọn được số chia hết cho 5 0,25
TH1: Chọn được một số có dạng abcd0 , trường hợp này có 4 A cách 8
TH2: Chọn được một số có dạng abcd5, trường hợp này có 3 7A cách 0,25 7 4 3 n A
Vậy xác suất cần tìm là + P( A) ( ) A 7.A  5 8 7  = = =  . 0,25 2 n(Ω) 4 8A  512 8 
(2,0 đ) b) Giải phương trình: ( 2x − x − ) 2 3
1 2x + 3 + 5x = 2x + x + 3 ( ) 1 1,0 Điều kiện: 3 x ≥ − 2 0,25
Phương trình tương đương với ( 2
x − x − ) x + = ( 2 1 2 3 x − x − ) 1 (2x − 3) 2 ⇔ (
x − x −1 = 0 1a 2 x − x − )
1 ( 2x + 3 − 2x + 3) ( ) = 0 ⇔  0,25
 2x + 3 = 2x − 3  (1b) ( a) 1± 5 1 ⇔ x = (t / m) 2  3 3 x ≥ 3    2 ≥ 0,25 ( x x ≥  1b) ⇔  2 ⇔  2
⇔ x = 3 ⇔ x = 3 (t / m) 2x + 3 =  (2x −3)2  2
2x − 7x + 3 = 0  1 x =  2  ± 
Vậy phương trình đã cho có tập nghiệm là 1 5 S 3;  =  0,25  2   
 x + 2 + y + 2 = 7y −3x +8
a) Giải hệ phương trình:  . 1,0 6 3
27x = x + 4y + 2 x ≥ 2 −
Điều kiện: y ≥ 2 −
7y −3x +8 ≥  0 0,25 Do x = 2
− không là nghiệm của hệ. Suy ra x > 2. − y +  y +  3
Biến đổi phương trình thứ nhất: 2 2 1+ = 7 −   3 . (2,0 đ) x + 2  x + 2  Đặt y + 2 t =
(t ≥ 0) ta có phương trình1+ t = 7t −3 ⇔ t =1⇒ y = x . 0,25 x + 2
Thế vào phương trình thứ hai ta được: 6 3 2 3 3
27x = x + 4x + 2 ⇔ 3x = x + 4x + 2 0,25 3 2 3 3 3
⇔ x + 3x + 4x + 2 = x + 4x + 2 + x + 4x + 2 ⇔ (x + )3 1 + (x + ) 3 3 3
1 = x + 4x + 2 + x + 4x + 2 (*) Hàm số ( ) 3
f u = u + u có f ′(u) 2
= 3u +1 > 0, u
∀ ∈  nên đồng biến trên .  0,25 Khi đó
(*) ⇔ f (x + )1 = f (3 3x + 4x+ 2) 3 3
⇔ x +1 = x + 4x + 2 ⇔ (x + )3 3 1 = x + 4x + 2  1+ 13 1+ 13 x =
(t / m) ⇒ y = (t / m) 2 6 6
⇔ 3x − x −1 = 0 ⇔  1− 13 x = (t m) 1− 13 / ⇒ y = (t / m)  6 6  + +   − − 
Vậy nghiệm của hệ đã cho là 1 13 1 13 1 13 1 13  ; ;  ; 6 6 6 6     
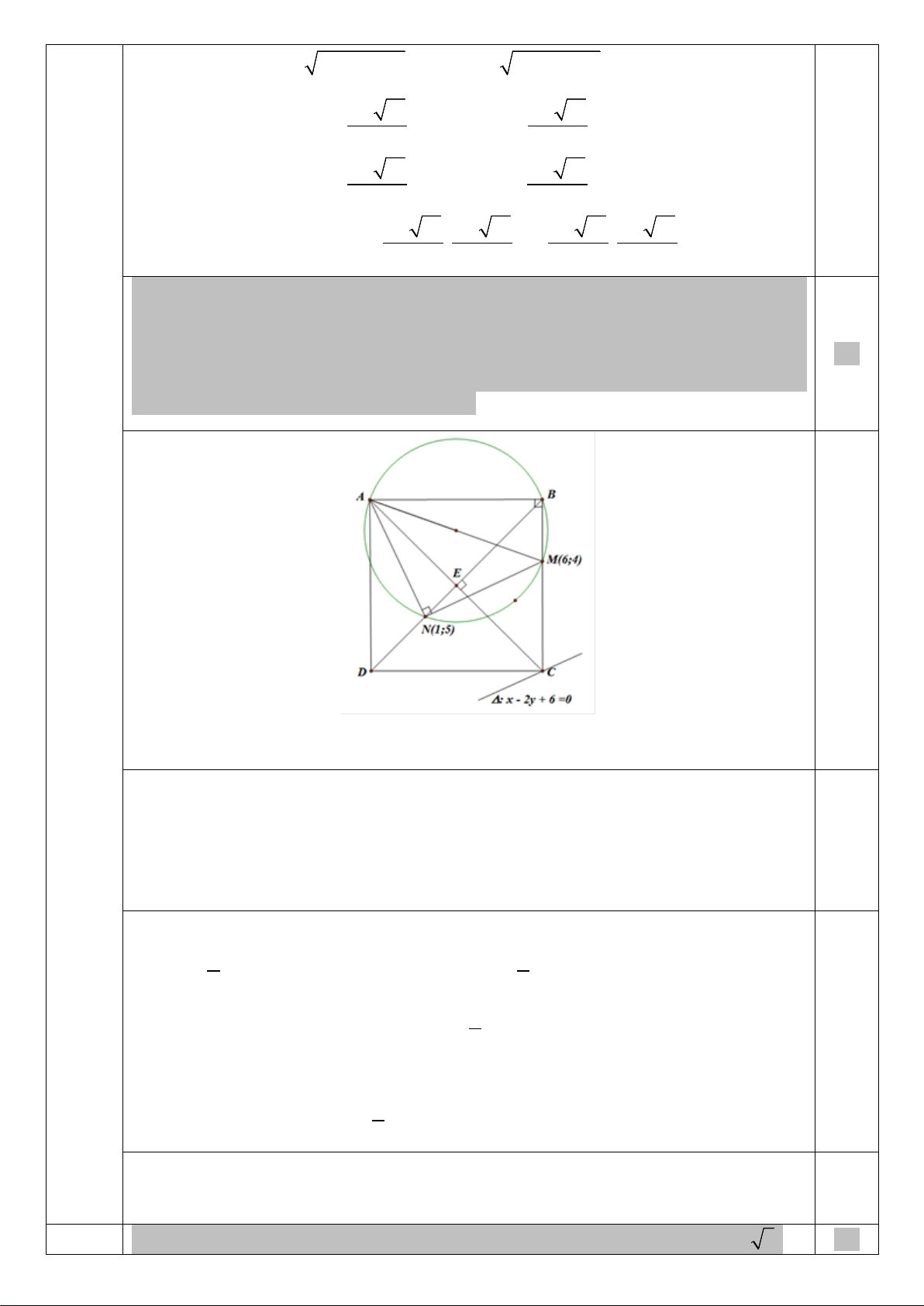
b) Trong mặt phẳng với hệ trục tọa độ Oxy, cho hình vuông ABCD và đường
thẳng ∆ có phương trình x − 2y + 6 = 0 . Điểm C thuộc đường thẳng ∆ , điểm
M (6; 4) thuộc cạnh BC. Đường tròn đường kính AM cắt đoạn BD tại điểm 1,0
N (1; 5). Tìm tọa độ các đỉnh của hình vuông ABCD , biết rằng đỉnh C có tọa độ
nguyên và đỉnh A có hoành độ nhỏ hơn 1. 0,25
Ta có tam giác AMN vuông tại N và  =  0
NMA NBA = 45 nên tam giác AMN vuông cân tại N.
Do đó, ta có phương trình đường thẳng AN là 5x − y = 0.
Gọi A(t;5t)∈ AN , ta có 2 2
AN = MN ⇔ (t − )2 1 + 25(t − )2 1 = 26 0,25 t = 2 A 2; 10 2 ( ) ⇔ (t − ) 1 =1 ⇔ ⇔  
Vì A có hoành độ nhỏ hơn 1 nên A(0; 0). t = A  ( ) . 0 0; 0
Vì C ∈ ∆ : x − 2y + 6 = 0 ⇒ C (2c − 6; c). Gọi E là tâm của hình vuông. Khi đó    3; c E c  −  c  
. Suy ra AC (2c − 6; c), NE c − 4; −  5.  2   2    Ta có: . 0 (2 6)( 4) c AC NE c c c 5 = ⇔ − − + − =   0 0,25  2  c = 6 2 5c 38c 48 0  ⇔ − + = ⇔
8 Vì C có tọa độ nguyên nên C (6; 6). c =  5
⇒ E (3; 3). Do đó MC : x = 6, NE : x + y − 6 = 0 ⇒ B(6;0) ⇒ D(0;6) .
Vậy A(0;0),B(6;0),C (6;6),D(0;6). 0,25 4
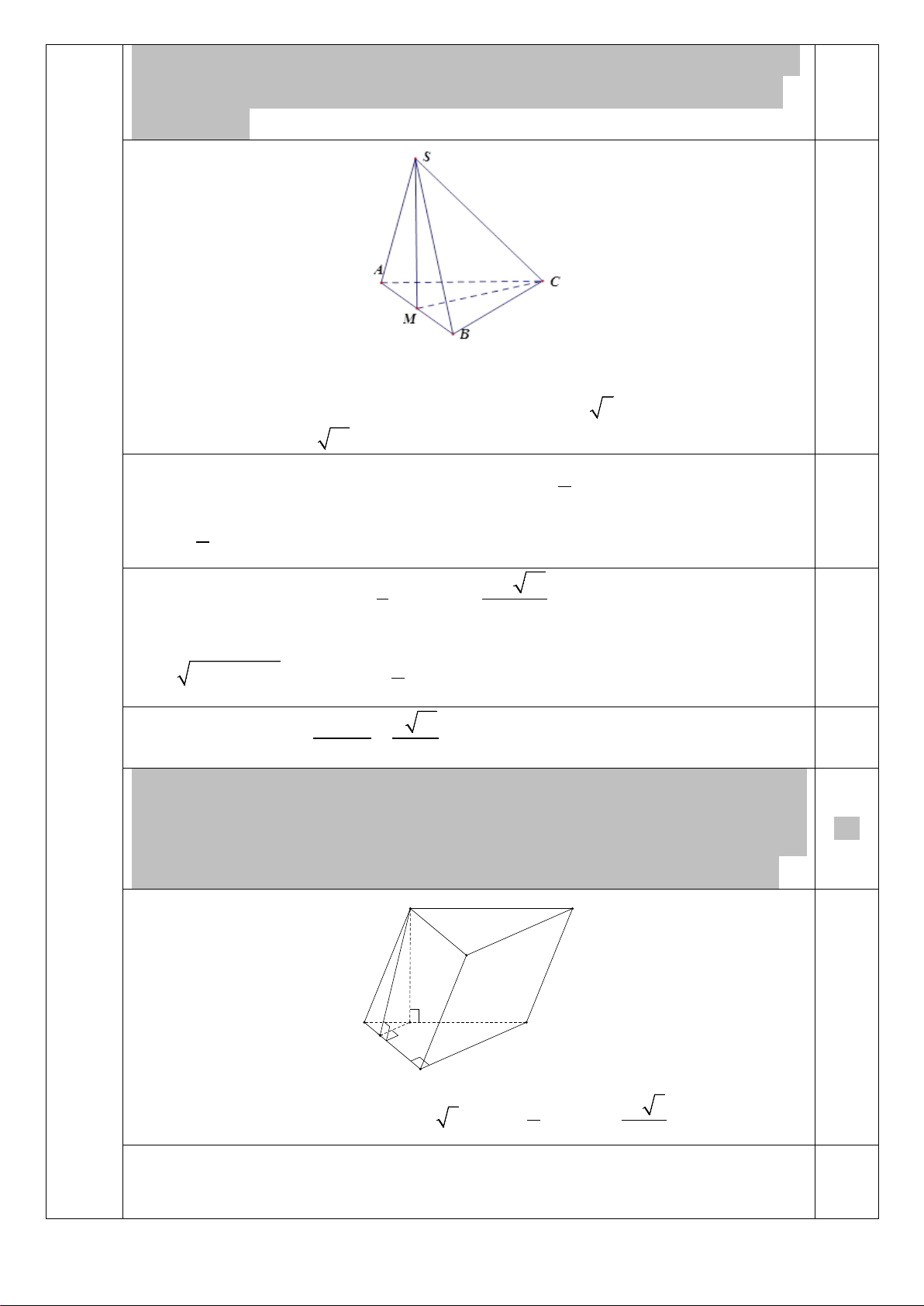
a) Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A và SC = 2a 5 . 1,0
(2,0 đ) Hình chiếu của S trên mặt phẳng ( ABC) là trung điểm M của AB. Góc giữa đường
thẳng SC và mặt phẳng ( ABC) bằng 0
60 . Tính theo a khoảng cách từ B đến mặt phẳng (SAC). 0,25 ⊥ ( ) ⇒  = ( )  ,( ) = 60o SM ABC SCM SC ABC
Tam giác SMC vuông tại M nên: = 
MC SC.cos SCM = a 5 = 
SM SC.sin SCM = a 15 2
Đặt AC = x, vì tam giác AMC vuông tại A nên 2  x  2 x + = 5a ⇒ x =   2a ;  2  0,25 1 2 2 S = AC = a ABC 2 2 3
Thể tích khối S.ABC: 1 2a 15 V = S SM = S ABC ABC . . 3 3
Ta có AC ⊥ AB, AC ⊥ SM ⇒ AC ⊥ SA nên tam giác SAC vuông tại A, do đó 0,25 2 2 1 2
SA = SC − AC = 4a; S = SA AC = a SAC . 4 . 2
Suy ra d (B,(SAC)) 3V a S ABC 15 . = = 0,25 SSAC 2
b) Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại , A cạnh BC = 2a và  0
ABC = 60 . Biết tứ giác BCC B ′ ′ là hình thoi có  B BC ′ nhọn. Biết mặt phẳng (BCC B
′ ′) vuông góc với mặt phẳng ( ABC) và mặt phẳng ( ABB A
′ ′) tạo với 1,0
mặt phẳng ( ABC) một góc 0
45 . Tính theo a thể tích khối lăng trụ ABC.A′B C ′ ′ . B' C' A' 2a H 0,25 B C K A 2 Ta có  1 a 3
AB  BC.sin30  a  AC  a 3, S  AB AC  ABC . . 2 2 Kẻ B H
  BC, H  BC. Ta có BCC B
  ABC nên B H   ABC.  0,25 ABB A
 ABC AB AB  B H 
Kẻ HK  AB, K  A . B Ta có   B K   A . B AB   HK 
Do đó góc giữa ABB A
  và ABC bằng góc giữa B K  và HK bằng  B KH 45 .    Ta có B H  HK HK B H  HK, 2 2 BH   BH   . sin 60 3 3 0,25 2  2a 3 2 2 2 2 2 4      4 B H BB B H HB a  B H    B H   3 7 2 3
2a 3 a 3 3a
Thể tích khối lăng trụ ABC.AB C   là V        B H.S ABC A B C ABC . . . 0,25 7 2 7
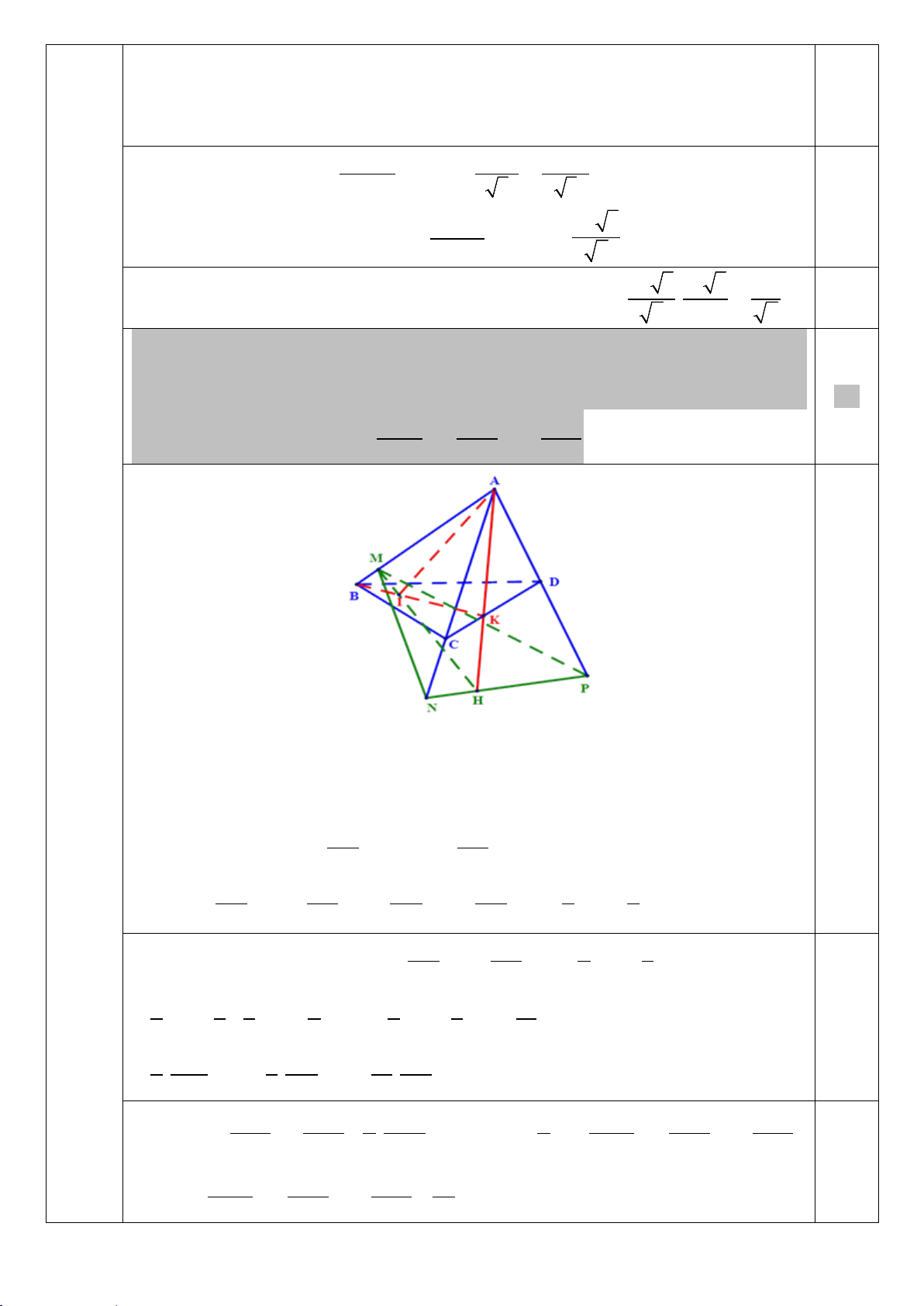
c) Cho tứ diện ABC .
D Gọi K là điểm thuộc cạnh CD sao cho 2KD = 3KC và I
là điểm thuộc đoạn thẳng BK sao cho IK = 2 .
IB Mặt phẳng (α ) đi qua I và luôn
cắt các tia AB, AC, AD lần lượt tại các điểm M , N, P (khác đỉnh A). Tìm giá trị 1,0 2 2 2
nhỏ nhất của biểu thức = 4. AB + 9. AC +16. AD T 2 2 2 AM AN AP 0,25
Lấy điểm M thuộc tia AB, trong mp( ABK ) : MI ∩ AK = H
Trong mp( ACD) : đường thẳng qua H cắt các tia AC, AD lần lượt tại N và . P
Trong tam giác ACD ta có:
    CK   CK  
AK = AC + CK = AC + CD = AC + (AD− AC) CD CD 
CK  CK  KD  KC  3  2  = 1− AC + AD = .AC + .AD = .AC +   .AD  CD  CD CD CD 5 5     
Trong tam giác ABK ta có: IK IB 2 1 AI = .AB +
.AK = .AB + .AK BK BK 3 3
2  1  3  2     .AB . 2 1 2  .AC .AD = + +
= .AB + .AC + .AD 0,25 3 3 5 5    3 5 15
2 AB  1 AC  2  = . . + . . + . AD AM AN .AP . 3 AM 5 AN 15 AP 2 2 2 2      2 2AB 3AC 1 4AD 1 ⇒ 15 = 5. +1. + . ≤ 
 25 +1+  4. AB + 9. AC +16. AD 2 2 2  AM AN 2 AP   4  AM AN AP  0,25 2 2 2 AB AC AD 60 ⇒ T = 4. + 9. +16. ≥ 2 2 2 AM AN AP 7  2AB 3AC 4AD  AB 10 =  AM AN AP  AM 7  = =   5 1 1 Dấu " = " có khi:  AC 4  ⇔  = 2 AN 21    AB AC AD  AD 1 10. + 3. + 2. = 15 =  AM AN AP    AP 14  AB 10 =  AM 7 0,25 
Vậy, giá trị nhỏ nhất của biểu thức T bằng 60 khi  AC 4  = . 7 AN 21   AD 1 =  AP 14   
*(Nếu chỉ đưa ra công thức KD = . KC AK AC +
.AD mà không chứng minh thì trừ CD CD 0,25 đ)
Cho x, y, z ∈[1;4] và thỏa mãn x ≥ y; x ≥ z. Tìm giá trị nhỏ nhất của biểu thức: x y z 1,0 P = + +
2x + 3y y + z z + x Ta có 1 1 1 P = + + . Đặt y z x 1 a ; b ; c a ;1 = = = ⇒ ∈ ; c ∈   [1;4] ; 2 + 3 y 1 z + 1 x + x y z  4  x y z 0,25 abc =1. Khi đó 1 1 1 P = + +
2 + 3a 1+ b 1+ c Vì 1 a  ;1 ∈ 
và abc =1 nên bc ≥1. 4    Ta có + ≥
⇔ ( bc − )( b − c)2 1 1 2 1
≥ 0 (luôn đúng với bc ≥1)
1+ b 1+ c 1+ bc 5 0,25
(1,0 đ) Áp dụng bất đẳng thức trên ta có 1 2 1 2 a P ≥ + = +
2 + 3a 1+ bc 2 + 3a 1+ a Đặt 1 t a t  ;1 = ⇒ ∈ 1 2t  và P ≥ + = f t 2 ( ) 2    2 + 3t t +1 4 3 2 f ′(t) 6 − t 2
9t − 3t + 6t − 3t + 4 = ( + = 2. 2
2 + 3t )2 (t + )2 1 ( 2
2 + 3t )2 .(t + )2 1 3 3 0,25 t (3t − ) 1 + 3t (2t − ) 1 + 4 1 2.  =   ( > 0, t ∀ ∈
;1 . Suy ra f (t) đồng biến trên 1 ;1 2 2   + 3t )2 .(t + )2 1  2     2  f (t) 1 34 f   ⇒ ≥ =  . Dấu “=” xảy ra khi 1
a = ; b = c = 2 ⇒ x = 4; y =1; z = 2. 2    33 4 0,25 Vậy 34 min P =
khi x = 4; y =1; z = 2. 33
Chú ý: Thí sinh làm theo cách khác đúng vẫn cho điểm tối đa.
Document Outline

• TOÁN - CHÍNH THỨC
• TOÁN - HƯỚNG DẪN CHẤM