PHÒNG GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ THI CHỌN HSG LỚP 8 THCS HUYỆN GIA VIỄN NĂM HỌC 2022-2023 Môn: Toán Ngày thi: 30/3/2023
ĐỀ THI CHÍNH THỨC
Thời gian làm bài:150 phút (không kể thời gian giao đề)
Họ và tên thí sinh :..............................................................Số báo danh .......................................
Họ và tên, chữ ký: Giám thị thứ nhất: ............................................................................................
Giám thị thứ hai:.................. ................ ...........................................................
Câu 1 (4,5 điểm) 2 2        Cho biểu thức 2x x 6 1 2   x 6 A    :    x  2    với x ≠ 2. ± 2  x 4
x2 x  2    2 x 
a) Rút gọn biểu thức A.
b) Tìm giá trị của x để A nhận giá trị âm.
c) Tìm giá trị nguyên của x để biểu thức A nhận giá trị nguyên.
Câu 2 (4,0 điểm)
a) Phân tích đa thức sau thành nhân tử: (x − y − z)2 2 2
− y + 2yz − z .
b) Cho 3 số nguyên dương a ;a ;a có tổng bằng 2023 2022 . Chứng minh rằng: 1 2 3 3 3 3
a + a + a chia hết cho 3. 1 2 3
Câu 3 (4,5 điểm)
a) Giải các phương trình sau: 1 1 1 3 − + + = . 2 2 2
x + 7x +12 x + 9x + 20 x +11x + 30 2
b) Tính giá trị của biểu thức: y 5y − 4 B x = +
. Biết 2x − y = 6. x − 3 x − 5
c) Tìm tất cả các cặp số nguyên (x;y) thoả mãn: 2 2
x + 5y + 4xy = 2023.
Câu 4 (5,0 điểm)
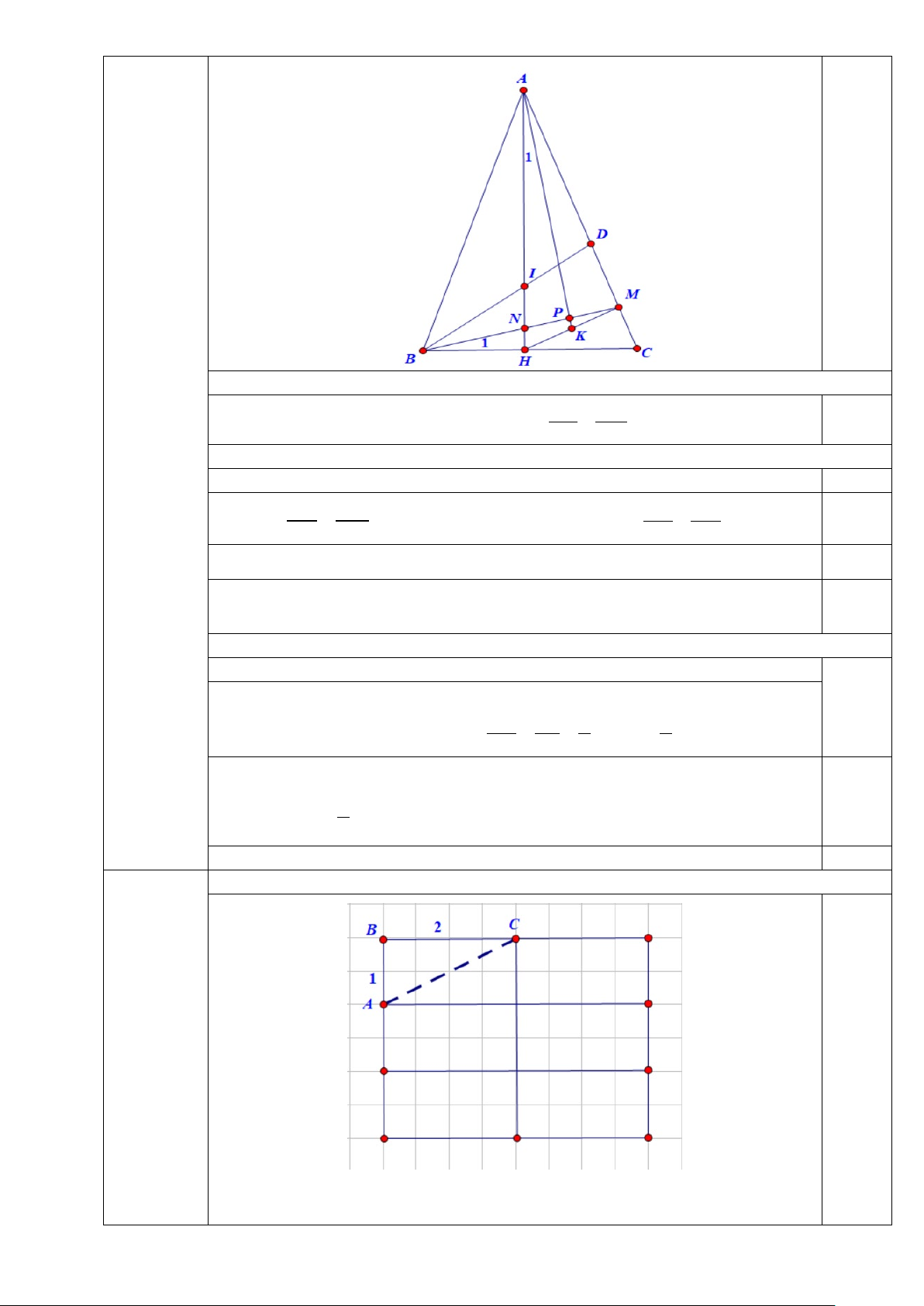
Cho tam giác ABC cân tại A (góc A nhọn), đường cao AH cắt tia phân giác BD tại
điểm I. Gọi M là hình chiếu của điểm H trên cạnh AC, K là trung điểm của HM. a) Chứng minh AH HM = . HC CM
b) Chứng minh AK vuông góc với BM.
c) Biết AI = 5cm, HI = 4cm. Tính độ dài cạnh BC.
Câu 5 (2,0 điểm)
a) Xét hình chữ nhật kích thước 3cm x 4 cm. Chứng minh rằng với 7 điểm bất kì
nằm trong hình chữ nhật, luôn có thể chọn ra hai điểm có khoảng cách nhỏ hơn 3.
b) Cho hai số thực x, y thỏa mãn x > 1;
− y > 1 và x + y = 1. Tìm giá trị nhỏ nhất 2 2 của biểu thức  1   1  P x1     y 1    .   x 1  y1 --------Hết.--------
Thí sinh không được sử dụng tài liệu. Giám thị không giải thích gì thêm.
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM HUYỆN GIA VIỄN
ĐỀ THI CHỌN HSG LỚP 8 THCS NĂM HỌC 2022-2023 Môn: Toán Ngày thi 30/3/2023
(Hướng dẫn chấm này gồm 04 trang) Câu Đáp án Điểm
a) (2,0 điểm) 2 2 2x  x6 1 2   x    6 A    :    x  2    với x ≠ 2. ±        2 x 4
x 2 x 2  2 x   2  2x  x6 x  2 x   2 2 2 2 
 x 4 x 6 A     0,5  :    
x2x  2 x2x  2 x2x  2    x2 x2  2 2x 2 A  : 0,75
x2x 2 x2 2 2 2x x2 A  . x  x 0,75 2x  2 2 x  2 b) (1,5 điểm) Câu 1 2 x 2 x
4,5 điểm) Ta có: A  ( x ≠ 2) ±  0 x  2
nhận giá trị âm thì A < 0 nên x2 0,5
⇔ x + 2 < 0 (vì x2 ≥ 0 với mọi x ≠ 2 ± ) ⇔ x < 2 − (thỏa mãn đk) 0,75 Vậy x < 2
− thì A nhận giá trị âm. 0,25 c) (1,5 điểm) 2 2 0,5 Ta có: x x 4 4 4 A     x2
với x ∈ Z, x ≠ 2. ± x  2 x  2 x  2 x  2 4
Để A nhận giá trị là số nguyên thì
 Z  x  2  Ư(4) 0,25 x  2
 x 2 1;1;2;2;4; 
4  x 1;3;0;4;2;  6 0,5
x ∈ Z, x ≠ 2 ± ⇒ x ∈{ 1 − ; 3 − ;0; 4 − ;− } 6 0,25 Vậy x ∈{ 1 − ; 3 − ;0; 4 − ;− }
6 thì A nhận giá trị là số nguyên. a) (2,0 điểm)
(x − y − z)2 2 2
− y + 2yz − z 1,0
= (x − y − z)2 − ( 2 2
y − 2yz + z ) = (x − y − z)2 −( y − z)2
= (x − y − z + y − z)(x − y − z − y + z) 0,5
= (x − 2z)(x − 2y) 0,5 Câu 2 b) (2,0 điểm)
(4,0 điểm) Ta có: 2023 2022 3; 2023
a + a + a = 2022
nên a + a + a 3.  0,5 1 2 3 1 2 3 Với n ∈  thì 3
n − n = n( 2
n − ) = (n − )n(n + ) 3 1 1 1 3
 ⇒ n − n 3  0,5
(vì n – 1; n; n + 1 là ba số nguyên liên tiếp nên tích chia hết cho 3).
Do đó: ( 3a − a ) 3  ; ( 3 a − a ) 3  ; ( 3 3 a − a 1 1 2 2 3 3 ) ⇒ ( 3 a − a )+( 3 a − a )+( 3 a − a 3. 3 3 3
⇒ a + a + a − a + a + a 3 1 1 2 2 3 3 ) ( 1 2 3 ) ( 1 2 3) 0,5
Mà a + a + a 3
a + a + a 3. 1 2 3  nên 3 3 3 1 2 3  0,5 a) (1,5 điểm) 1 1 1 3 + + = − . (1) 2 2 2
x + 7x +12 x + 9x + 20 x +11x + 30 2 0,25 ĐK: x ≠ 3 − ; x ≠ 4 − ; x ≠ 5 − ; x ≠ 6 − (1) 0,25 1 1 1 1 1 1 3 ⇔ − + − + − = − .
x + 3 x + 4 x + 4 x + 5 x + 5 x + 6 2 1 1 3 3 3 0,5 ⇔ − = − ⇔ = − x + 3 x + 6 2 (x +3)(x + 6) 2 ⇒ (x + )(x + ) 2 3 6 = 2
− ⇔ x + 9x + 20 = 0 ⇔ (x + 4)(x + 5) = 0 0,25 x = 4 − ⇔ 
(không tmđk). Vậy phương trình đã cho vô nghiệm. 0,25 x = 5 − b) (1,5 điểm) Ta có: y 5y − 4 B x = +
. ( x ≠ 3; x ≠ 5); 2x − y = 6 ⇒ y = 2x − 6 . Câu 3 x − 3 x − 5 0,5 (4,5 điểm)
2x − 6 5.(2x − 6) − 4x Khi đó: B = + . x − 3 x − 5
2(x −3) 6x −30 6(x − 5) B = + = 2 + = 2 + 6 = 8. 1,0 x − 3 x − 5 x − 5 c) (1,5 điểm) Ta có: 2 2
x + 5y + 4xy = 2023. (1) (x,y ∈ ) ⇔ (x + y)2 2 2 + y = 2023. 0,25 Với n ∈  thì 2
n ≡ 0;1;2;3 (mod 4) ⇒ n ≡ 0;1(mod 4)
Vậy x,y∈  thì (x + y)2 2 ≡ 0;1 (mod 4) và 2 y ≡ 0;1 (mod 4) 0,5 nên (x + y)2 2 2
+ y ≡ 0;1;2 (mod 4) mà 2023 ≡ 3 (mod 4) 0,5
Do đó, phương trình (x + y)2 2 2
+ y = 2023, không có nghiệm nguyên. 0,25
Vậy không có số nguyên x, y nào thỏa mãn yêu cầu đề bài. a) (2,0 điểm) Chứng minh A ∆ HM ∽ HC ∆ M (g-g) AH HM ⇒ = 2,0 HC CM b) 1,5 điểm)
Gọi N, P lần lượt là giao điểm của BM và AH, AK. Câu 4:
(5,0 điểm) - Ta có: AH HM =
mà HM = 2HK, BC = 2CH nên AH HK = 0,5 HC CM BC CM - Chứng minh A ∆ HK ∽ BM ∆ C (c-g-c)   ⇒ A = B 0,5 1 1 - Chứng minh NA ∆ P ∽ N ∆ BH (g-g)   0,5
⇒ APN = BHN , mà  0  0
BHN = 90 ⇒ APN = 90 ⇒ AK ⊥ BM c) (1,5 điểm)
Ta có: AH = AI + HI = 5 + 4 = 9 (cm)
Vì BD là tia phân giác của A ∆ BC nên 0,5 BI là tia phân giác của BH HI A ∆ BH 4 5 ⇒ = = ⇒ AB = .BH AB AI 5 4 Xét A
∆ BH vuông tại H, có: 2 2 2
AH + BH = AB 2 2 2  5 
⇒ 9 + BH =  .BH ⇒ BH =12 (cm) 0,5 4    A
∆ BC cân tại A, có BC = 2.BH = 2.12 = 24 (cm) 0,5
a) (1,0 điểm) Câu 5 (2,0 điểm) 0,25
Chia hình chữ nhật kích thước 3cm x4 cm thành 6 hình chữ nhật nhật
kích thước 1 cm x 2 cm (hình vẽ).
Theo nguyên lý Dirichlet, trong 7 điểm bất kì nằm trong hình chữ nhật
kích thước 3cm x4 cm (hay nằm trong 6 hình chữ nhật nhật kích thước 1
cm x 2 cm) thì luôn tồn tại 2 điểm cùng thuộc một chữ nhật nhật kích 0,5
thước 1 cm x 2 cm và khoảng cách giữa hai điểm này luôn nhỏ hơn độ dài đường chéo AC = 2 2 1 + 2 = 5 < 3.
Vậy với 7 điểm bất kì nằm trong hình chữ nhật kích thước 3cm x4 cm,
luôn có thể chọn ra hai điểm có khoảng cách nhỏ hơn 3. 0,25 b) (1,0 điểm) x > 1;
− y > 1 thì x +1 > 0 ;
y - 1 > 0 ; x + y = 1 ⇔ (x + ) 1 + (y − ) 1 = 1 Đặt (x + ) 1 = a ( ; y − )
1 = b ( ,ab > 0) ⇒ a + b =1 0,25 2 2 2 2  1   1        1  1 P x1  y 1           a     b           x 1 y 1  a  b
Áp dụng bất đẳng thức Bunhiacopxki, có: 0,25 2 2 2  1 1        a     b               2 2   1 1
. 1 1 a b     a  b  a b   Mà ,
a b > 0, a + b = 1, 1 1 4  
 4 nên  P   2 25 2. 1 4  P  0,25 a b a b 2 Dấu “=” xảy ra khi 1 a   b  1 3  x  ; y  . 2 2 2 Vậy 25 P   khi 1 3 x  ; y  . 0,25 min 2 2 2 Lưu ý:
- Lời giải chỉ trình bày tóm tắt, học sinh trình bày hoàn chỉnh, lý luận chặt chẽ mới cho điểm tối đa.
- Học sinh có thể trình bày nhiều cách giải khác nhau nếu đúng thì cho điểm tương ứng./.