PHÒNG GIÁO DỤC VÀ ĐÀO
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH GIỎI
TẠO THÀNH PHỐ VINH NĂM HỌC 2022- 2023 ĐỀ TH I CHÍNH THỨC
Môn thi: Toán lớp 8
(Đề thi gồm có 01 trang)
Thời gian: 120 phút ( không kể thời gian giao đề)
Câu 1. (4,0 điểm) 2ab a, Cho 2 2
3a  b  4ab và 3a  2b  0 . Hãy tính giá trị biểu thức A  2 3a  5ab 2 x  3 8x 3x 1 b, Cho P  1 : (   ) 2 3 2 2 x  5x  6 4x  8x 3x 12 x  2 x 1
Tìm các giá trị x nguyên dương để P  2
Câu 2. (3,0 điểm)
Giải các phương trình sau: a, 4 4 4 (1 ) x  (2  ) x  (3 2 ) x x 1 x  6 x  2 x  5 b,    2 2 2 x(x  2) x 12x  35 x  4x  3 x 10x  24
Câu 3. (3,0 điểm)
a, Cho các số nguyên a, ,
b c thoả mãn ab  bc  ca  1 . Chứng minh rằng 2 2 2
A  (1 a )(1 b )(1 c ) là số chính phương
b, Gọi S(n) là tổng các chữ số của số nguyên dương n khi biểu diễn nó trong hệ thập
phân. Biết rằng với bất kỳ số nguyên dương n ta có 0  S( )
n  n . Tìm số nguyên dương n thỏa mãn 2
S (n)  n  2023n  7
Câu 4. (3,0 điểm)
a, Tìm các hệ số a, , b c để đa thức 3 2 f ( )
x  x  ax  bx  c chia hết cho đa thức x  2 và chia cho đa thức 2 x 1 thì dư 3 b, Cho , a , b ,
c d,elà các số thực dương thỏa mãn a  b  c  d  e  4 . Tìm giá trị nhỏ
(a  b  c  d )(a  b  c)(a  b)
nhất của biểu thức P  abcde
Câu 5. (7,0 điểm)
1, Cho tam giác ABC có ba góc nhọn (AB  AC) , trung tuyến AM . Kẻ BE vuông
góc với AM . Trên đoạn MC lấy điểm F sao cho ˆ ˆ
MFA  MEC . Gọi N , I lần lượt là trung
điểm của đoạn thẳng AF, EC ; AF cắt CE ở O .
a, Chứng minh rằng O
 EF đồng dạng với O  AC AM 1 MN b, Biết tỷ số  , tính tỷ số BC 2 MI
c, Chứng minh rằng NB  NC
2, Cho hình thang cân ABCD (AB / /C )
D . Gọi M , N lần lượt là trung điểm của AB
và CD . Trên tia đối của tia DA lấy điểm E , tia EN cắt đoạn thẳng AC tại F . Chứng
minh rằng MN là tia phân giác của góc EMF .
........................ Hết .......................... 1
HƯỚNG DẪN CHẤM – BIỂU ĐIỂM CÂU NỘI DUNG ĐIỂM
Câu 1. (4,0 điểm) 2ab a, Cho 2 2
3a  b  4ab và 3a  2b  0 . Hãy tính giá trị biểu thức A  2 3a  5ab 2 x  3 8x 3x 1 b, Cho P  1 : (   ) 2 3 2 2 x  5x  6 4x  8x 3x 12 x  2 x 1
Tìm các giá trị x nguyên dương để P  2 1.a 2 2 2 2
3a  b  4ab  3a  4ab  b  0 0,5
2,0đ  (3a  ) b (a  ) b  0 0,25
3a  b  0 0,25   (1) a  b  0
Do 3a  2b  0  3a  b  0 0,25
nên (1)  a  b  0  a  b 0,25 2 2aa 2a 0,5
Thay vào biểu thức A ta có A    1  2 2 3a  5aa 2  a 1.b ĐKXĐ: x  2  ; 3  ;0 0,25 2,0đ 2 x  3 8x 3x 1 0,25 P  1 : (   ) 2 3 2 2 x  5x  6 4x  8x 3x 12 x  2 2 x  3  8x 3x 1  P  1  :     2
(x  2)(x  3)  4x (x  2) 3(x  2)(x  2) x  2  1  2 x 1  0,25 P  1  :    
(x  2) (x  2) (x  2)(x  2) x  2  1
2(x  2)  x  (x  2) 0,25 P  1  : (x  2)
(x  2)(x  2) 1 6 P  1  :
(x  2) (x  2)(x  2) 1
(x  2)(x  2) 0,25 P  1  . (x  2) 6 x  2 x  4 P  1   6 6 x 1 x  4 x 1 0,25 P    2 6 2
 x  4  3(x 1)  2  x  7  0,25 7  x  2  7  0,25
Vậy x  Z x    2 
Câu 2. (3,0 điểm) Giải các phương trình sau: a, 4 4 4 (1 ) x  (2  ) x  (3 2 ) x 2 x 1 x  6 x  2 x  5 b,    2 2 2 x(x  2) x 12x  35 x  4x  3 x 10x  24 2.a Đặt 1 x  ;
a 2  x  b  3  2x  a  b 0,25 1,5đ 4 Ta có 4 4
a  b  a  b 4 4 4 4
 a  b  a  b  ab 2 2 2
2a  3ab  2b  0,25  ab 2 2 2
2a  3ab  2b   0 (1) 1 0,25
Do 2a  3ab  2b 
4a  3b2 2 2 2
 7b   0, a  ,b 8  
4a  3b  0 0,25
Dấu ‘’=’’ xảy ra 
 a  b  0 b   0 1   x  0 x 1 0,25 Suy ra    (vô lí)  2  x  0 x  2 a  0 1   x  0 x  1 0,25 Nên (1)       b  0 2  x  0 x  2
Vậy tập nghiệm của phương trình là S  1;  2 2.b * ĐKXĐ: x  0; 1  ; 2  ; 3  ; 4  ; 5  ; 6  ; 7  0,25 1,5đ * Ta có 0,25 x 1 x  6 x  2 x  5    (1) 2 2 2 x(x  2) x 12x  35 x  4x  3 x 10x  24 x 1 x  6 x  2 x  5     x(x  2)
(x  5)(x  7)
(x 1)(x  3)
(x  4)(x  6) x  1 1 1 (x  6) 1 1  (  )  (  ) 2 x x  2 2 x  5 x  7 x  2 1 1 x  5 1 1  (  )  (  ) 2 x  1 x  3 2 x  4 x  6 1 1 1 1  0,25 1  1 1 1 ) x x  2 x  5 x  7 1 1 1 1  1 1 1 1 x  1 x  3 x  4 x  6 1 1 1 1 1 1 1 1         x x  2 x  5 x  7 x 1 x  3 x  4 x  6 1 1 1 1 1 1 1 1  (  )  (  )  (  )  (  ) x x  7 x  2 x  5 x  1 x  6 x  3 x  4  1 1 1 1   (2x  7)     0   2 2 2 2
 x  7x x  7x 10 x  7x  6 x  7x 12  2x  7  0 (2) 0,25   1 1 1 1      0 (3) 2 2 2 2
 x  7x x  7x 10 x  7x  6 x  7x 12 0,25 Đặ 1 1 1 1 t 2
t  x  7x ta có (3)      0 t t  10 t  6 t  12 2
 t 14t  60  0 3 2
 (t  7) 11 0 (Vô nghiệm) 7 (2)  x  2   0,25
Vậy tập nghiệm của phương trình (1) là 7 S     2  Câu 3. (3,0 điểm)
a, Cho các số nguyên a, ,
b c thoả mãn ab  bc  ca  1 . Chứng minh rằng 2 2 2
A  (1 a )(1 b )(1 c ) là số chính phương
b, Gọi S(n) là tổng các chữ số của số nguyên dương n khi biểu diễn nó trong hệ thập phân.
Biết rằng với bất kỳ số nguyên dương n ta có 0  S( )
n  n . Tìm số nguyên dương n thỏa mãn 2
S (n)  n  2003n  7 3.a 2 2
ab  bc  ca  11 a  a  ab  bc  ca  (a  ) b (a  ) c 0,25
1,5đ Tương tự ta có 2
1  b  (b  c)(b  a) 0,25 2
1  c  (c  a)(c  b) 0,25 Suy ra 2 2 2 2 2 2
A  (1 a )(1 b )(1 c )  (a  ) b (b  ) c (c  ) a 0,25 Do , a ,
b c  Z  (a  )
b ,(b  c)(c  a)  Z 0,25 Nên 2 2 2 2 2 2
A  (1 a )(1 b )(1 c )  (a  ) b (b  ) c (c  )
a là một số chính phương 0,25 3.b 0  S( ) n  n và 2
S (n)  n  2003n  7 0,25 1,5đ Mặt khác: 2 2
n  2003n  7  0  n  2003n  2022  0 0,25
 (n 1)(n  2022)  0 . Mà n  2  n  2022  0  n  2022 (1) 0,25 Ta có: 2 S( )
n  n  n  2004n  7  0 0,25 2
 n  2024n  0  (
n n  2024) . Mà n  0  n  2024  0  n  2024 (2) 0,25
Từ (1) và (2) suy ra n  2023 0,25 Câu 4. (3,0 điểm)
a, Tìm các hệ số a, , b c để đa thức 3 2 f ( )
x  x  ax  bx  c chia hết cho đa thức x  2 và chia cho đa thức 2 x 1 thì dư 3 b, Cho , a , b ,
c d,elà các số thực dương thỏa mãn a  b  c  d  e  4 . Tìm giá trị nhỏ nhất
(a  b  c  d )(a  b  c)(a  b)
của biểu thức P  abcde 4.a 3 2 f ( )
x  x  ax  bx  c x  2  f ( 2  )  0 0,25 1,5đ 3 2  ( 2  )  ( a 2  )  ( b 2  )  c  0 0,25
 4a  2b  c  8 3 2 2
(x  ax  bx  )
c : (x 1) dư 3, ta có: 3 2
x  ax  bx  c  (x 1)(x 1)g( )
x  3 với g(x) là một đa thức
Tại x 1ta có a  b  c  2 0,25 Tại x  1
 ta có a b  c  4
4a  2b  c  8 (1) 
Suy ra a  b  c  2 (2)
a b  c  4 (3) 
Từ (2) và (3) suy ra 2b  2   b  1  0,25 4
4a  c  6 (1) 3  a  3 a 1 0,25
Thay vào (1) và (2) được      
a  c  3 (2) a  c  3 c  2
Vậy a  1;b  1  ;c  2 0,25 4.2 Áp dụng bđt : ( 2
x  y)  4xy 0,25 1,5đ Áp dụng bđt : ( 2
x  y)  4xy 0,25 Ta có 2
(a  b  c  d  ) e
 4(a  b  c  d)e 2
(a  b  c  d)  4(a  b  ) c d 2 (a  b  ) c  4(a  ) b c 2 (a  ) b  4ab
Do a, b,c, d là các số dương, nhân theo vế các bđt trên ta được: 0,25
Mà a  b  c  d  e  4 0,25 Suy ra 2 4
4 (a  b  c  d)(a  b  ) c (a  ) b  4 abcde
(a  b  c  d )(a  b  c)(a  b) Hay : P   16 abcde  1  0,25
a  b  c  d  e a  b    4
a  b  c  d    1
Dấu bằng có khi: a  b  c  c   2   a  b  d  1
a  b  c  d  e  4   e  2 1 1 0,25 Vậy P       min = 16 a b , c , d 1, e 2 4 2
Câu 5. (7,0 điểm)
1, Cho tam giác ABC có ba góc nhọn (AB  AC) , trung tuyến AM . Kẻ BE vuông góc
với AM . Trên đoạn MC lấy điểm F sao cho ˆ ˆ
MFA  MEC . Gọi N , I lần lượt là trung điểm của
đoạn thẳng AF, EC ; AF cắt CE ở O .
a, Chứng minh rằng O
 EF đồng dạng với O  AC AM 1 MN b, Biết tỷ số  , tính tỷ số BC 2 MI
c, Chứng minh rằng NB  NC
2, Cho hình thang cân ABCD (AB / /C )
D . Gọi M , N lần lượt là trung điểm của AB và
CD . Trên tia đối của tia DA lấy điểm E , tia EN cắt đoạn thẳng AC tại F . Chứng minh rằng
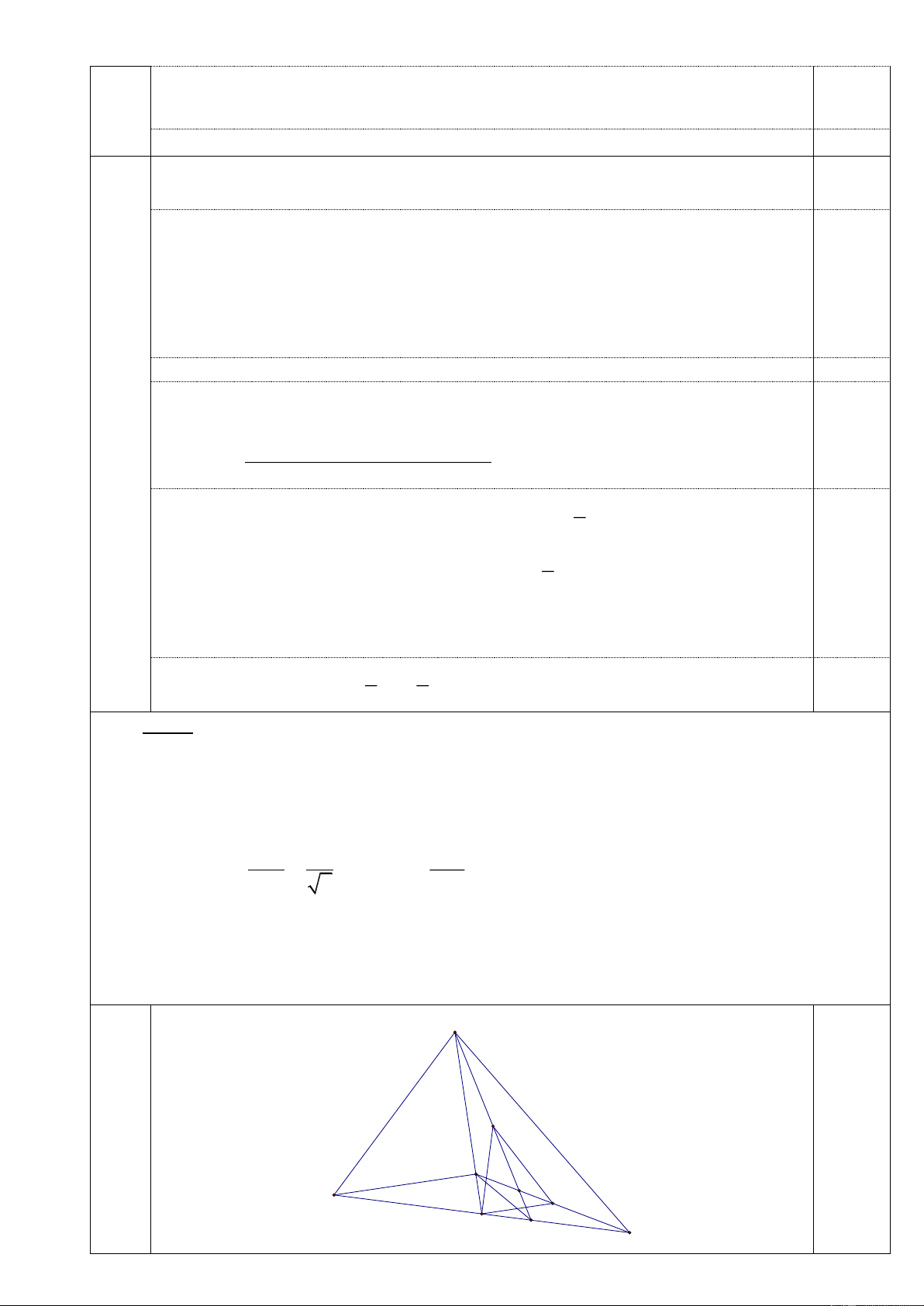
MN là tia phân giác của góc EMF . A M E O I B M 0,25 F C 5 5.1.a Ta có 0,25 2,0đ M  FA  M
 EC(gt), F  MA  E  MC  M  EC M  F ( A g  g) 0,25  M  CE  M  AF 0,25  F  CO  E  AO Mà A  OE  C
 OF (đối đỉnh) 0,25  A  OE C
 OF(g  g) 0,25 OE OA   0,25 OF CO Mà A  OC  E
 OF (đối đỉnh) 0,25  O  EF O
 AC(c  g  ) c 0,25 5.1.b AM 1 AM 0,25 1,5đ  ; BC  2MC   2 (1) BC 2 MC 1 0,25 AF AF AM 2 AM M  EC M  FA     CE MC 1 MC CE 2 AN AM   0,25 CI MC Mà M  AN  M  CI nên A  MN C  MI (c-g-c) 0,25 MN AM  0,25 (2) MI MC MN 0,25 Từ (1) và (2) suy ra  2 MI
5.1.c M là trung điểm của BC, I là trung điểm của EC suy ra 0,25
1,5đ MI//BE  B   M  1 1 A  MN C  MI  M   M  0,25 1 3 A  MN C  MI  M   M  0,25 1 3 Suy ra  B   M  0,25 1 3 Mà 0 B   M   90 nên 0 M   M   90 0,25 1 4 3 4
Suy ra NM  BC
Lại có M là trung điểm của BC nên IM là đường trung trực của BC 0,25
Vậy NB  NC 5.2 M 2,0đ A B K F D H N I C E 6
EM cắt CD tại H, EN cắt AB tại K, MF cắt CD tại I 0,5 HN DN EN 0,5 DN / / AK   ( ) MK AK EK NI NC NF NC / / AK   ( ) MK AK FK 1 DN NC 0,5
Mà DN  NC  CD   2 AK AK HN NI 0,25 Suy ra   HN  NI MK MK H
 MI có MN  HI; HN  NI ( vì M là trung điểm AB, N là trung điểm của 0,25
DC nên MN là trục đối xứng của hình thang cân) suy ra MN là tia phân giác của H  MI
Hay MN là tia phân giác của E  MF
(Học sinh giải các cách khác đúng vẫn đánh giá điểm tối đa) 7