PHÒNG GD&ĐT THỊ XÃ BA ĐỒN ĐỀ THI CHỌN HỌC SINH GIỎI
TRƯỜNG THCS BA ĐỒN MÔN TOÁN LỚP 8-NĂM HỌC 2022-2023
Thời gian: 150 phút (không kể thời gian giao đề) ĐỀ RA:
Câu 1 (2,0 điểm): Cho biểu thức 2 x +1 x x −1
x − x x + x −1 P = + +
với x  0; x 1 x x − x x − x x
a) Rút gọn biểu thức P
b) Chứng minh rằng P  4 với x  0; x 1.
Câu 2 (2,0 điểm): a b c b a c a) Cho ba số a, ,
b c  0 thỏa mãn + + = + + b c a a c b
Tính giá trị của biểu thức A = (a − b)(b − c)(c − a)(a + b + c)2022 2 3 + 2023 2 2  x −1   2x + 4  x −1 b) Giải phương trình: − + 3. = 0      x + 2   x − 3  x − 3
Câu 3 (1,5 điểm): Cho x,y là các số dương thỏa mãn điều kiện x + y  6 . Tìm giá 6 8
trị nhỏ nhất của biểu thức M = 3x + 2y + + x y
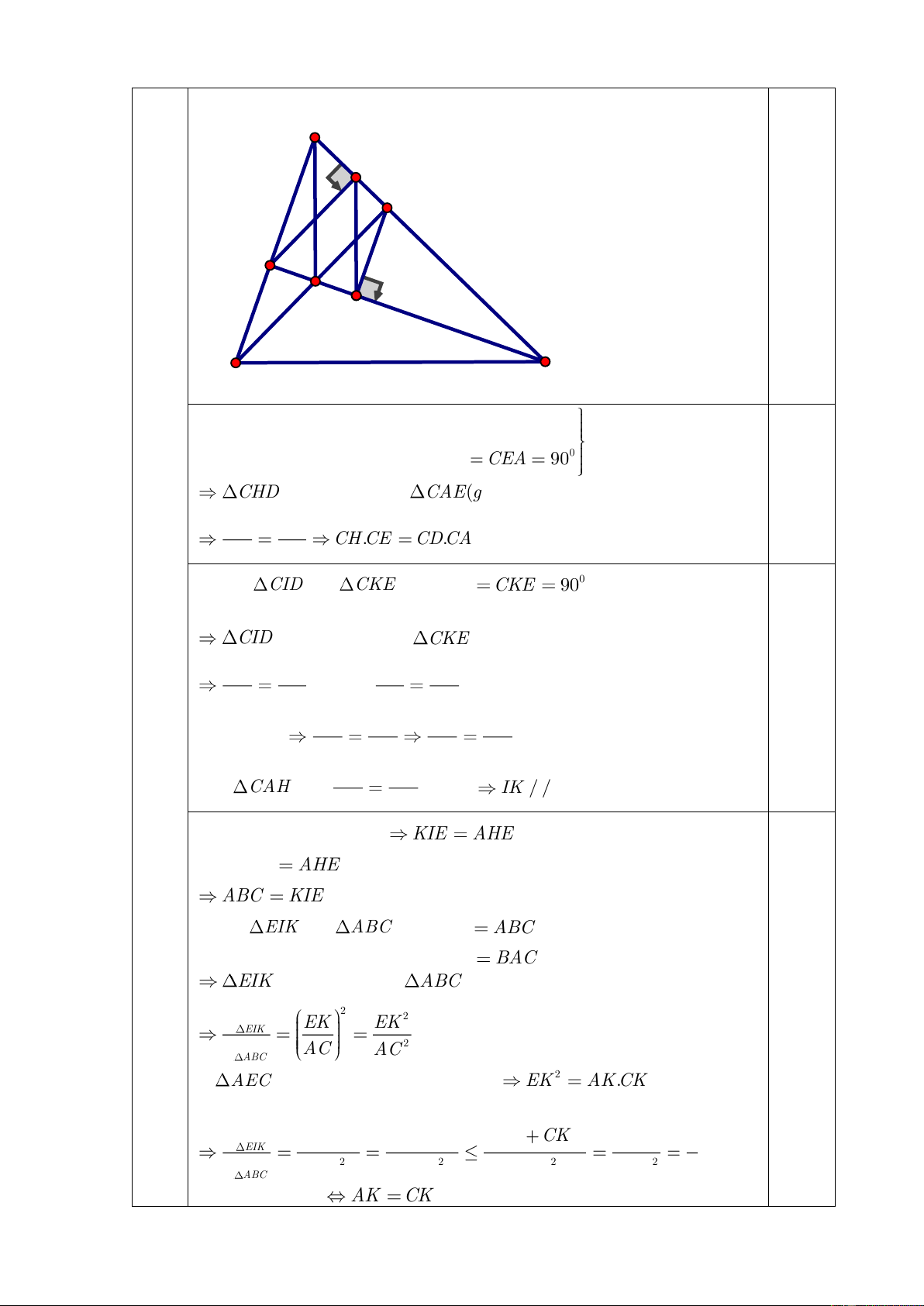
Câu 4 (3,5 điểm): Cho tam giác ABC có ba góc nhọn, các đường cao BD, CE cắt nhau tại H.
a) Chứng minh CH.CE = CD.CA
b) Kẻ EK ⊥ AC tại K, kẻ DI ⊥ EC tại I. Chứng minh AH // IK 1 c) Chứng minh S  S EIK  4 ABC 
Câu 5 (1,0 điểm): Chứng minh tích của bốn số tự nhiên liên tiếp cộng với 1 luôn
là một số chính phương. Ghi chú:
- Học sinh không được sử dụng tài liệu, máy tính cầm tay.
- Cán bộ coi thi không giải thích gì thêm.
PHÒNG GD&ĐT THỊ XÃ BA ĐỒN HDC ĐỀ THI CHỌN HỌC SINH GIỎI
TRƯỜNG THCS BA ĐỒN MÔN TOÁN LỚP 8-NĂM HỌC 2022-2023 Câu Đáp án Điểm Câu 2 x +1 x x −1
x − x x + x −1 a) P = + + 1 x x − x x − x x x +1 ( x − ) 1 ( x + x + ) 1
( x − )1(x x + )1 = + − 0,25 x x ( x − ) 1 x ( x − ) 1 x +1 + +
( x − )1( x + )1(x− x + x x )1 1 = + − 0,25 x x x ( x − ) 1 ( x + ) 1 x +1 x + x +1 x − x +1 = + − x x x 0,25 x +1+ x + x +1− x + x −1 = x x + 2 x +1 = x 0,25 1 1 0,25
b) Ta có P = x + + 2  2 x. + 2 = 4 (Theo BĐT Côsi) x x 0,25 1 P = 4  x =
 x = 1(loại do x 1) 0,25 x Vậy P  4 x   0, x  1. 0,25 Câu a b c b a c a) Với a, , b c  0 , ta có + + = + + 2 b c a a c b a c a c b b  − − + + − = 0 0,25 b b c a c a a − c
(a + c)(a −c) b(a −c)  − + = 0 b ac ac  +  0,25  ( − ) 1 a c b a c − + = 0    b ac ac   (a − c)( 2
ac − ab − bc + b ) = 0
 (a − c)(c − b)(a −b) = 0
 (a − b)(b − c)(c − a) = 0 0,25
A = (a − b)(b − c)(c − a)(a + b + c)2022 2 3 + 2023 0,25 = 0 + 2023 = 2023 2 2  x −1   2x + 4  x −1 b) − + 3. = 0     x  − x   x + 2   x − 3  x − ĐKXĐ: 2; 3 3 2 2  x −1   x + 2  x −1  − 4. + 3. = 0      x + 2   x − 3  x − (1) 3 Đặ x −1 x + 2 x −1 t a = ; b =  ab = x + 2 x − 3 x − 3 0,25
Phương trình (1) trở thành 2 2
a − 4b + 3ab = 0 2 2 2
 a − b + 3ab − 3b = 0
 (a − b)(a + 4b) = 0  a = b   0,25 a = 4 − b + Trườ x −1 x + 2
ng hợp a = b  = x + 2 x − 3
 (x − )(x − ) = (x + )2 1 3 2  8x +1 = 0 1  x = − (TM ) 8 x −1 4 − (x + 2) + Trườ 0,25 ng hợp a = 4 − b  = x + 2 x − 3  (x − ) 1 ( x − 3) = 4 − (x + 2)2 2
 5x +12x +19 = 0 2  6  59  5 x + + = 0 (PTVN)    5  5 1
Vậy phưởng trình đã cho có một nghiệm x = − 8 0,25 Câu 6 8
M = 3x + 2y + + 3 x y 6 8 12 16 2M 2 3x 2y 3 x y 3x y x y x y 0,25
Từ giả thiết và theo BĐT Cô – si, ta có: 3 x y 3.6 18 12 12 3x 2 3x. 12 0,25 x x 16 16 y 2 y. 8 y y Do đó, 2M 18 12 8 38 M 19 0,5
Vậy minM = 19. Dấu “=” xảy ra khi x = 2; y = 4. 0,5 Câu 0,5 A 4 K D E H I B C ECA chung 0,25
a) Xét  CHD và  CAE có 0 CDH CEA 90 0,25
CHD đồng dạng với CAE(g.g) CH CD 0,25 CH.CE CD.CA CA CE 0,25
b) Xét CID và CKE có: 0 CID CKE 90 ICD chung CID 0,25 đồng dạng với CKE (g-g) CI CD CD CH (1) mà (c/m a) (2) 0,25 CK CE CE CA CI CH CI CK Từ (1), (2) 0,25 CK CA CH CA CI CK 0,25 Xét CAH có: (cmt)
IK / /AH ( ĐL Ta-lét đảo) CH CA
c) Có IK // AH (cm b) KIE AHE (đồng vị) Mà ABC
AHE (cùng phụ với EAH ) ABC KIE
+ Xét EIK và ABC có: KIE ABC (cmt) 0,25 IEK
BAC (cùng phụ với ACE )
EIK đồng dạng với ABC (g-g) 2 2 S EK EK EIK 0,25 2 S AC AC ABC
+ AEC vuông tại E, đường cao EK 2 EK
AK.CK (hệ thức 0,25 lượng) 2 2 S AK.CK 4AK. AK CK CK AC 1 EIK 0,25 2 2 2 2 S AC 4AC 4AC 4AC 4 ABC Dấu “=” xảy ra AK CK .
Câu Gọi 4 số tự nhiên, liên tiêp đó là: ,
n n +1, n + 2, n + 3 (n  N ). 0,25 5 Ta có : n(n + )
1 (n + 2)(n + 3) + 1 = .
n (n + 3(n + ) 1 (n + 2) + 1 = ( 2 n + 3n)( 2
n + 3n + 2) + 1 ( *) 0,25 Đặ t 2
n + 3n = t (t  N ) thì 2 2
(*) =t(t + 2) +1=t + 2t +1=(t +1) . 0,25  n(n + )
1 (n + 2)(n + 3) + 1 = ( 2 2 n + 3n + ) 1 .
Vì n  N nên 2
n + 3n +1 N. 0,25 Vậy n(n + )
1 (n + 2)(n + 3) + 1 là số chính phương.