UBND HUYỆN AN DƯƠNG
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022 -2023 MÔN: TOÁN 8 ĐỀ CHÍNH THỨC
Thời gian: 150 phút (không kể thời gian giao đề)
(Đề thi gồm có 01 trang) Bài 1. (2,0 điểm)
1. Cho hai số a,b thỏa mãn a  b  9; ab  14. Chứng minh rằng: 2 2 3 3
a  b  2(a  b )  755.
2. Tìm một đa thức bậc ba P(x) , biết P(x) chia cho các đa thức x  
1 ,  x  2,  x  3 đều được dư là 6 và P  1  1  8 . Bài 2. (2,0 điểm)
1. Giả sử p và q là các số nguyên tố thỏa mãn đẳng thức 2
p( p 1)  q(q 1). Chứng minh rằng tồn tại số nguyên dương k sao cho 2 p 1  kq; q 1  k . p
2. Giải phương trình nghiệm nguyên: 2 2 2x  4x 19  3y . Bài 3. (2,0 điểm) 5 1. Giải phương trình: 2  x  4x 1  0. 2 x  4x  5 2. Cho a, ,
b c là các số thực dương. Chứng minh rằng: 2 2 2 a b c 1    (a  b  c) 2 2 2 2 2 2 3a  8b 14ab 3b  8c 14bc 3c  8a 14ca 5 Bài 4. (3,0 điểm)
Cho hình vuông ABCD, trên cạnh AB lấy điểm E và trên cạnh AD lấy điểm
F sao cho AE  AF . Vẽ AH vuông góc với BF ( H thuộc BF ), đường thẳng
AH cắt các đường thẳng DC và BC lần lượt tại hai điểm M và N.
1. Chứng minh rằng tứ giác AEMD là hình chữ nhật.
2. Biết diện tích tam giác BCH gấp bốn lần diện tích tam giác AEH.
Chứng minh rằng : AC  2EF. 1 1 1 3. Chứng minh rằng :   . 2 2 2 AD AM AN Bài 5. (1,0 điểm)
Một giải bóng chuyền có 9 đội bóng tham gia thi đấu vòng tròn 1 lượt (hai đội
bất kỳ chỉ thi đấu với nhau 1 trận). Biết đội thứ nhất thắng a trận và thua b trận, 1 1
đội thứ 2 thắng a trận và thua b a trận và thua b trận. 2
2 trận, …., đội thứ 9 thắng 9 9 Chứng minh rằng 2 2 2 2 2 2 2 2
a  a  a  ...  a  b  b  b  ...  b 1 2 3 9 1 2 3 9
---------------------------------Hết----------------------------
Họ và tên thí sinh: .................................................Số báo danh..................................... UBND HUYỆN AN DƯƠNG
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP HUYỆN
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO NĂM HỌC 2022 -2023 MÔN: TOÁN 8 HƯỚNG DẪN CHẤM
Thời gian: 150 phút (không kể thời gian giao đề) Bài Nội dung cần đạt Điểm 1
1. Cho hai số a,b thỏa mãn a  b  9; ab  14 . Chứng minh rằng: (2,0đ) 2 2 3 3
a  b  2(a  b )  755. Ta có: 0,25 2 2 2 2
a  b  (a  b)  2ab  9  2.14  53. 3 3 3 3
a  b  (a  b)  3ab(a  b)  9  3.14.9  351 0,25 3 3
 2(a  b )  2.351  702. 0,25 Vậy: 2 2 3 3
a  b  2(a  b )  53  702  755. 0,25
2. Tìm một đa thức bậc ba, biết P(x) chia cho  x  
1 ,  x  2,  x  3 đều được dư 6 và P  1  1  8 .
Theo định lí Bézout ta có: P 
1  P2  P3  6. 0,25 Do đó ta đặt
P x  d  c x   1  bx  
1  x  2  a x  
1  x  2 x  3
Cho x 1 ta được P  1  d , suy ra d  6
P x  6  c x   1  b x  
1  x  2  a x  
1  x  2 x  3
Cho x  2 ta được P2  6  c , suy ra c  0 0,25
P x  6  0 x   1  b x  
1  x  2  a x  
1  x  2 x  3
Cho x  3 ta được P3  6  2b , suy ra b  0 0,25
P x  6  0 x   1  0 x  
1  x  2  ax   1  x  2x  3
Do đó P x  6  a x  
1  x  2 x  3
Cho x  1 ta được P 
1  6  24a , do đó 18  6  24a suy ra 0,25 a 1.
Vậy P x  6 1. x  
1  x  2 x  3
Rút gọn ta được: P x 3 2  x  6x 11x .
1. Giả sử p và q là các số nguyên tố thỏa mãn đẳng thức 2 p( p 1)  q(q 1).
Chứng minh rằng tồn tại số nguyên dương k sao cho 2 p 1  k ; q q 1  k . p  p  q  0 0,25 Nếu p  q thì ta có 2 p 1  q 1
, điều này vô lí vì p,q   p  q 1 là các số nguyên tố.
Do đó p  q , khi đó do p,q là các số nguyên tố nên 0,25 2    ( p 1) q; (q 1) . p
Như vậy tồn tại các số nguyên dương , m n thỏa mãn 0,25 2 p 1  m ; q q 1  n . p
Thay vào đẳng thức đã cho ta được . p mq  . q np  m  n  p 1  kq 0,25 2
Vậy tồn tại số nguyên dương k( m  n) sao cho  . 2 (2,0đ) q 1  kp
Giải phương trình nghiệm nguyên: 2 2 2x  4x 19  3y .
Biến đổi phương trình đã cho ta được : 0,25 2 2 2 2
2x  4x 19  3y  2(x 1)  3y  21 Suy ra : 2 2 2
3y  21 y  7  y 0;1;  4 . 0,25 Với 2 2
y  0  2(x 1)  21.PT không có nghiệm nguyên. 0,25 x 1 3 x  4 Với 2 2 2
y 1 2(x 1) 18  (x 1)  9    x 1 3      y  2  x  4  y  1; x  2   y  1  Ta được ( ; x y)( 2
 ;1);(2;1);(4;1);(4; 1   ) . Với 2 2
y  4  2(x 1)  9.PT không có nghiệm nguyên. 0,25
Vậy PT đã cho có các nghiệm nguyên ( ; x y) là: ( 2  ;1);(2; 1  );(4;1);(4; 1  ) 5 2 Giải phương trình:  x  4x 1  0. 2 x  4x  5
ĐKXĐ: x   do x  x    x  2 2 4 5 2 1  0 x   . 0,25 Đặt 2
x  4x  5  y thì y 1 và 2
x  4x 1  y  4. 0,25
Phương trình đã cho trở thành: 0,25 5  y  5 2
 y  4  0  5  y  4y  0   y  5 y   1  0   y y     1 loaïi 3 (2,0đ) x  0 0,25 Với y  5 ta có 2
x  4x  5  5  x x  4  0   x  4
Vậy PT đã cho có tập nghiệm là: S  0;  4 .
Cho a,b,c là các số thực dương. Chứng minh rằng: 2 2 2 a b c 1    (a  b  c) 2 2 2 2 2 2 3a  8b 14ab 3b  8c 14bc 3c  8a 14ca 5
Áp dụng bất đẳng thức AM-GM ta có: 0,25 2 2 1
3a  8b 14ab  (a  4b)(3a  2b)  (4a  6b)  2a  3b 2 Tương tự ta có: 0,25 2 2 2 2
3b  8c 14bc  2b  3 ; c
3c  8a 14ca  2c  3 . a Do đó: 0,25 2 2 2 a b c   2 2 2 2 2 2 3a  8b 14ab 3b  8c 14bc 3c  8a 14ca 2 2 2 a b c    (1) 2a  3b 2b  3c 2c  3a
Áp dụng bất đẳng thức Cauchy – Schwarz ta có: 0,25 2 2 2 2 a b c (a  b  c) 1     (a  b  c) (2) 2a  3b 2b  3c 2c  3a
2a  3b  2b  3c  2c  3a 5
Từ (1) và (2) ta có điều phải chứng minh.
Đẳng thức xảy ra khi và chỉ khi: a  b  . c
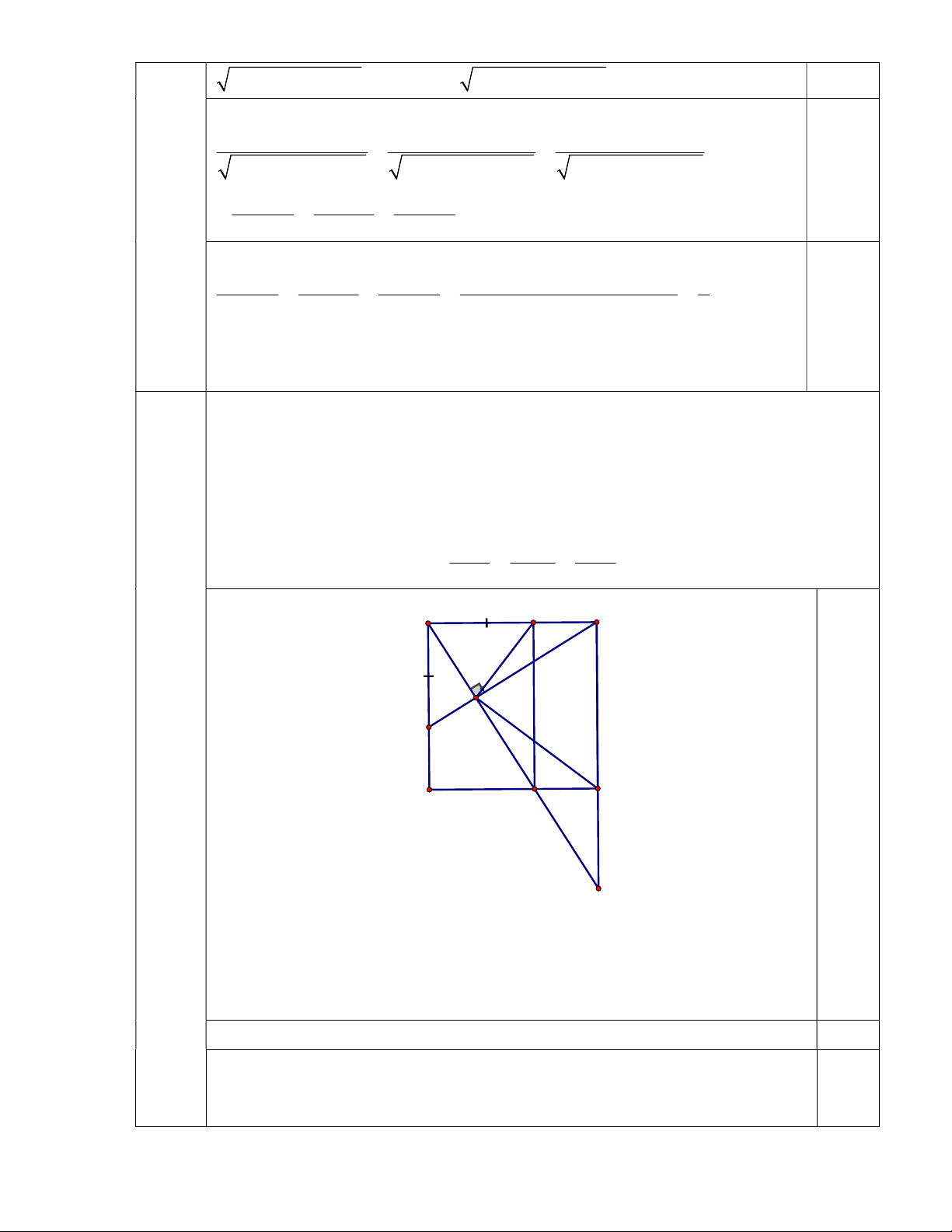
Cho hình vuông ABCD, trên cạnh AB lấy điểm E và trên cạnh AD lấy điểm
F sao cho AE  AF . Vẽ AH vuông góc với BF ( H thuộc BF ), đường thẳng
AH cắt các đường thẳng DC và BC lần lượt tại hai điểm M và N.
1. Chứng minh rằng tứ giác AEMD là hình chữ nhật.
2. Biết diện tích tam giác BCH gấp bốn lần diện tích tam giác
AEH.Chứng minh rằng : AC  2EF. 1 1 1 3. Chứng minh rằng :   . 2 2 2 AD AM AN A E B H F D M C 4 (3,0đ) N a) Ta có:  
MAD  ABF (cùng phụ với  BAH )   0 AB  AD
(gt); BAF  ADM  90 (ABCD là hình vuông) 0,25  A
 DM  BAF g. .cg 
 DM  AF,mà AF  AE(gt) nên AE  DM 0,25
Lại có: AE / /DM (vì AB / /DC) 0,25
Suy ra tứ giác AEMD là hình bình hành . Mặt khác  0 DAE  90 (gt) 0,25
Vậy tứ giác AEMD là hình chữ nhật
b) Ta có ABH # FAH (g.g) 0,25 AB BH   BC BH hay  AB  BC; AE  AF  AF AH AE AH Lại có:  
HAB  HBC (cùng phụ với  ABH ) 0,25  C  BH # AEH ( . c g.c) 2 S  BC  2 S  BC  0,25 CBH   , 2   mà CBH 2  4(gt)   4  BC    2AE S  AE  S  AE  EAH EAH
 BC  2AE  E là trung điểm của AB, F là trung điểm của AD 0,25
Do đó: BD  2EF hay AC  2EF.
c) Do AD / /CN(gt).Áp dụng hệ quả của định lí Ta-let ta có: 0,25 AD AM AD CN     CN MN AM MN
Lại có: MC / / AB gt.Áp dụng hệ quả của định lí Ta-let ta có: 0,25 MN MC AB MC    AD MC hay  AN AB AN MN AN MN 2 2 2 2 2 2 2  AD   AD   CN   CM  CN  CM MN 0,25       1         2 2  AM   AN   MN   MN  MN MN 2 2  AD   AD  1 1 1 0,25   1   (dfcm)     2 2 2  AM   AN  AM AN AD
Một giải bóng chuyền có 9 đội bóng tham gia thi đấu vòng tròn 1 lượt (hai đội
bất kỳ chỉ thi đấu với nhau 1 trận). Biết đội thứ nhất thắng a trận và thuab 1 1
trận, đội thứ 2 thắng a trận và thua b trận, …., đội thứ 9 thắng a trận và thua 2 2 9 b trận. 9 5 Chứng minh rằng 2 2 2 2 2 2 2 2
a  a  a  ...  a  b  b  b  ...  b . 1 2 3 9 1 2 3 9
(1,0đ) Mỗi đội bóng thi đấu với 8 đội bóng khác và hai đội bất kỳ chỉ gặp nhau 0,25
1 trận nên mỗi đôi sẽ thi đấu 8 trận  a  b  8 (với i = 1;2;3;...;8) i i
Đẳng thức cần chứng minh tương đương với: 0,25
a  a  a  ...  a  8  a 2  8  a 2  8  a 2  8  a 2 2 2 2 2 1 2 3 9 1 2 3 9
 16a  a  a  ... a  576 (1) 1 2 3 9 
Mặt khác, tổng số trận thắng của các đội bằng tổng số trận đấu nên : 0,25 9.8
a  a  a  ...  a   36 (2) 1 2 3 9 2
Từ (1) và (2) suy ra đẳng thức cần chứng minh luôn đúng. 0,25 Vậy 2 2 2 2 2 2 2 2
a  a  a  ...  a  b  b  b  ...  b . 1 2 3 9 1 2 3 9 * Chú ý:
+ Học sinh làm cách khác đúng vẫn cho điểm tối đa.
+ Điểm toàn bài làm tròn đến 0,25 điểm.