Đề HSG Toán 11 cấp trường năm 2019 – 2020 trường Nguyễn Đăng Đạo – Bắc Ninh

SỞ GIÁO DỤC & ĐÀO TẠO BẮC NINH
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
TRƯỜNG THPT NGUYỄN ĐĂNG ĐẠO Năm học: 2019 – 2020
MÔN THI: TOÁN, LỚP 11
Thời gian làm bài: 150 phút (không kể thời gian phát đề)
Câu 1. (2,0 điểm) Cho parabol (P) 2
: y = x − 2x và đường thẳng d : y = 2x + m . Tìm m để d cắt (P) tại hai điểm phân biệt ,
A B sao cho tam giác OAB vuông tại O (O là gốc tọa độ). Câu 2. (4,0 điểm)
1) Giải phương trình: 3 sin 2x − cos 2x + 3sin x − 3 cos x −1 = 0 2cos x + 3  x(x − ) 1 + x = y +1  (1+ y y+1) ( )1
2) Giải hệ phương trình:  3  (x − ) 2
1 = 2 4 + y − 4 2 − y + 9 − x (2) Câu 3. (4,0 điểm)
1) Chứng minh rằng phương trình 2 4 3 2
m x − x − 2m + 2m = 0 luôn có nghiệm với mọi m∈ .  1 u =  1
2) Cho dãy số (u thỏa mãn  4
. Tính giới hạn lim(u . n ) n )  4 *  u = ∀ ∈ + n n , 1   4 − un Câu 4. (2,0 điểm)
Trong mặt phẳng tọa độ Oxy , cho tam giác ABC có A(2;3) . Các điểm I (6;6) , J (4;5) lần lượt là
tâm đường tròn ngoại tiếp và tâm đường tròn nội tiếp tam giác ABC . Tìm tọa độ các đỉnh B và C biết
hoành độ điểm B lớn hơn hoành độ điểm C. Câu 5. (5,0 điểm)
1) Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, AB = a, AD = b , cạnh bên SA vuông góc với đáy.
a) Gọi I, J lần lượt là trung điểm của SB và CD. Biết đường thẳng IJ tạo với mặt phẳng ( ABCD) một góc 0
60 . Tính độ dài đoạn thẳng SA .
b) (α ) là mặt phẳng thay đổi qua AB và cắt các cạnh SC, SD lần lượt tại M và N. Gọi K là giao điểm
của hai đường thẳng AN và BM. Chứng minh rằng biểu thức AB BC T = −
có giá trị không đổi. MN SK
2) Cho tứ diện ABCD có AD = BC = 2a, AC = BD = 2b , 2 A .
B CD = 4c . Gọi M là điểm di động trong
không gian. Chứng minh rằng biểu thức H = (MA+ MB + MC + MD)2 ≥ ( 2 2 2
8 a + b + c ) . Câu 6. (3,0 điểm)
1) Có hai cái hộp đựng tất cả 15 viên bi, các viên bi chỉ có 2 màu đen và trắng. Lấy ngẫu nhiên từ mỗi
hộp 1 viên bi. Biết số bi ở hộp 1 nhiều hơn hộp 2, số bi đen ở hộp 1 nhiều hơn số bi đen ở hộp 2 và
xác suất để lấy được 2 viên đen là 5 . Tính xác suất để lấy được 2 viên trắng. 28
2) Cho các số thực x, y, z thỏa mãn x, y, z ≥1 và (x + y + z) 2 2 2 3
= x + y + z + 2xy . 2
Tìm giá trị nhỏ nhất của biểu thức: x x P = + . (x + y)2 2 + x z + x
………….. Hết…………..
(Chú ý: Giám thị coi thi không giải thích gì thêm)
SỞ GIÁO DỤC & ĐÀO TẠO BẮC NINH
ĐÁP ÁN ĐỀ THI HSG CẤP TRƯỜNG
TRƯỜNG THPT NGUYỄN ĐĂNG ĐẠO Năm học: 2019 – 2020
MÔN THI: TOÁN, LỚP 11 Câu Nội dung Điểm Câu 1 2,0
Phương trình hoành độ giáo điểm: 2 2
x − 2x = 2x + m ⇔ x − 4x − m = 0( ) 1 Đường thẳng
d cắt (P) tại hai điểm phân biệt A, B khi và chỉ khi pt(1) có 2 nghiệm phân
biệt ⇔ ∆′ = m + 4 > 0 ⇔ m > 4 − 0,25
Gọi A(x ;2x + m , B x ;2x + m ( x , x là các nghiệm của pt(1)) 1 1 ) ( 2 2 ) 1 2  x + x = 4 Theo Định lý Vi-et: 1 2  x x = −  m 0,5 1 2   Vì OA ∆
B vuông tại O ⇒ .
OAOB = 0 ⇒ x x + 2x + m 2x + m = 0 1 2 ( 1 )( 2 ) m = 0
⇒ 5x x + 2m(x + x ) 2 + m = 0 2
⇒ m + 3m = 0 ⇒ 1 2 1 2  m = 3 − 0,5 x = 0
+) Với m = 0, phương trình (1) trở thành: 2 x − 4x = 0 ⇔ ⇒ A(0;0) ≡  O (Loại) x = 4
x =1⇒ A 1; 1 − 2 ( ) +) Với m = 3
− , phương trình (1) trở thành: x − 4x + 3 = 0 ⇔  (t/m) x = 3 ⇒ B  (3;3) 0,5
Kết luận: Vậy m = 3 − 0,25 Câu 2.1 2,0 π Điều kiện: 3 5 cos x = − ⇔ x ≠ ± + k2π 2 6 0,25
Phương trình tương đương: x( x − ) + ( 2 3 cos 2sin 1
2sin x + 3sin x − 2) = 0
⇔ 3 cos x(2sin x − ) 1 + (2sin x − ) 1 (sin x + 2) = 0 ⇔ (2sin x − )
1 ( 3cos x +sin x + 2) = 0 0,75  π x = + k2π  1  sin x = 6   2 π ⇔   5 ⇔ x =
+ k2π (k ∈)   π  0,5 cos x  − = 6  1 −      6  7π x = + k2π  6 π
Kết hợp điều kiện suy ra nghiệm của phương trình là: x = + k2π (k ∈) 6 0,5 Câu 2.2 2.0  0 ≤ x ≤ 3 Điều kiện:   1 − ≤ y ≤ 2
Ta thấy x = 0, y = 1
− không phải là nghiệm của hệ. Từ đó suy ra x + y > 1 − . Do đó phương
trình (1) của hệ tương đương ( 2 2
x − y ) −(x + y) + ( x − y +1) = 0 0,5  1 
⇔ (x − y − ) 1  x + y +  = 0(*)  x y 1  + +   ( x + y+ )2 1
Ta có: x + y = x + ( y + ) 1 −1≥ −1 2 ( x + y + )2 1 1 1 ⇒ x + y + ≥ + −1 x + y +1 2 x + y +1 Lại có: ( x + y+1)2 1 + −1 2 x + y +1 ( x + y +1)2 1 1 = + ( + − x + y + ) ( x + y+ ) 1 2 2 1 2 1 ( x + y +1)2 3 1 ≥ 33 ( − = − = . x + y + ) 1 1 2 2 2 8 1
Do đó, phương trình (*) tương đương x − y −1= 0 ⇔ y = x −1 0,5
Thế vào pt(2), ta được: (x − ) 2 3
3 = 2 3+ x − 4 3− x + 9 − x
 3+ x = u,u ≥ 0 Đặt:  ⇒ 3(x − ) 2 2 1 = u − 2v
 3− x = v,v ≥ 0 Suy ra: 2 2
u − 2v = 2u − 4v + uv 2 ⇔ u − ( + v) 2 2
u − 2v + 4v = 0 2
∆ = 9v −12v + 4 = (3v − 2)2 u = 2 − v ⇒   u = 2v 0,5
+) u = 2 − v ⇒ 3+ x = 2 − 3− x (Vô nghiệm)
+) u = 2v ⇔ 3+ x = 2 3− x 9 4 ⇔ x = ⇒ y = 5 5 0,5
Vậy hệ cho có nghiệm (x y)  9 4 ; ;  =  . 5 5    Câu 3.1 2,0
Xét hàm số f (x) 2 4 3 2
= m x − x − 2m + 2m Ta thấy 0,5
f (x) liên tục trên  f ( ) 2
1 = −m + 2m −1 = −(m − )2 1 ≤ 0, m ∀ ∈  0,5 f (− ) 2 2
2 =14m + 2m + 8 =13m + (m + )2 1 + 7 > 0, m ∀ ∈ 
+) Nếu m =1⇒ f ( )
1 = 0 ⇒ phương trình có nghiệm x =1 +) Nếu 0,5 m ≠ 1⇒ f ( 2 − ). f ( )
1 < 0 ⇒ Phương trình có nghiệm x∈( 2; − ) 1
Vậy phương trình đã cho luôn có nghiệm với mọi m. 0,5 Câu 3.2 2,0 Ta có: 4 2u − n 4 u − = − ⇔ − = + u n 2 2 n+ 2 1 1 4 − u − u n 4 n 0,5 1 4 − un 1 1 1 ⇒ = ⇔ = − + u − − − − + u u + u n 2 2 n 2 n 2 2 n 2 1 ( ) 1 0,5  4 v = −  1 Đặt: 1  7 v = ⇒ n u  − n 2 1  * v = − + ∀ ∈ + v n n n , 1    2 4 1 n v n − − ⇒ = − − − = n ( ) 7 1 1 7 2 14 1 7 − n −1 14 0,5 ⇒ = ⇒ u = − n 2 u − n + n 2 14 7 1 ( 0,5 u   ⇒ = − = n ) 14 lim lim2  2  7n +1 Câu 4 2,0
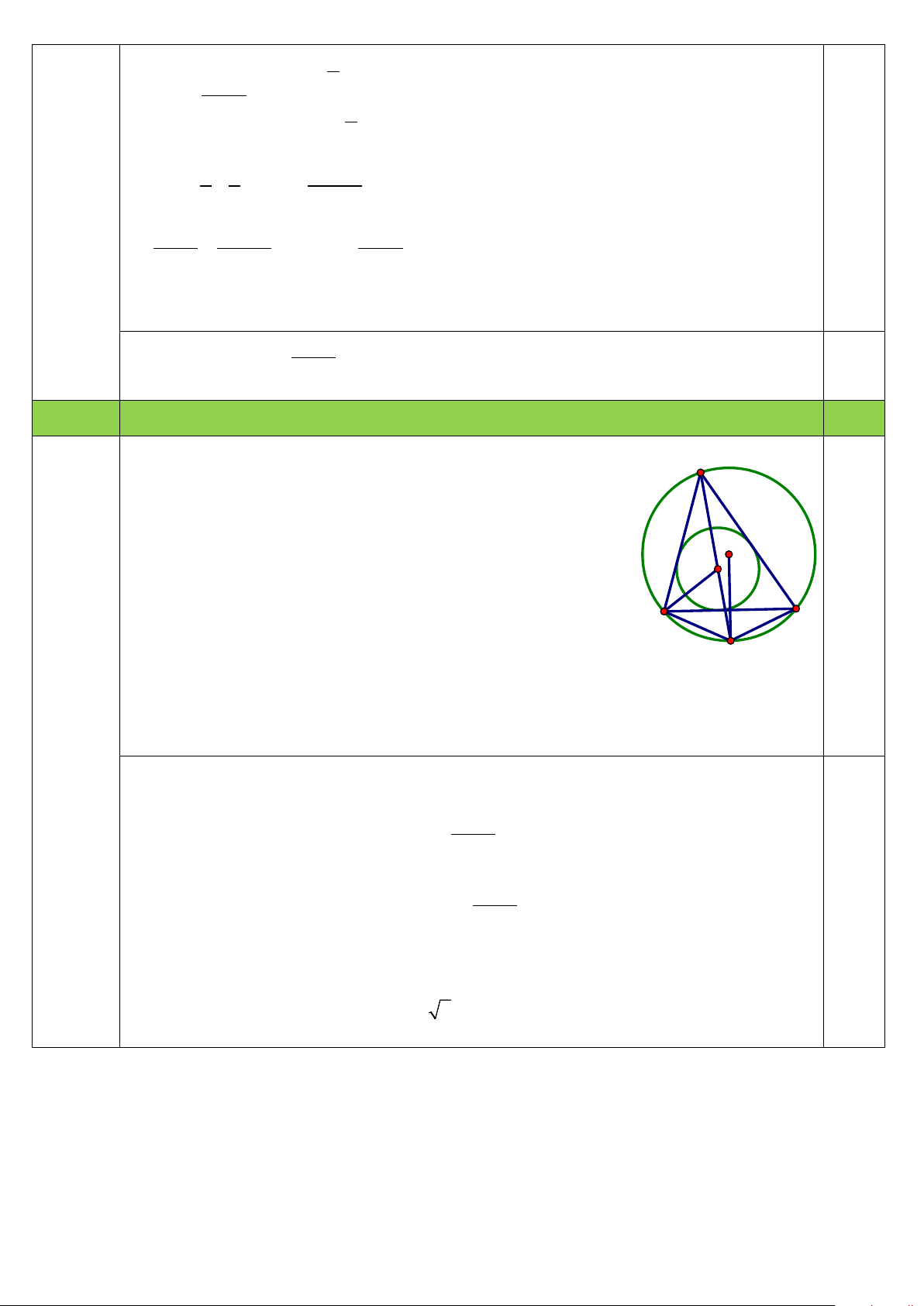
Đường tròn (C) ngoại tiếp tam giác ABC có tâm I (6;6) , bán A
kính R = IA = 5 có phương trình: (x − )2 + ( y − )2 6 6 = 25 .
Phương trình đường thẳng AJ: x − y +1 = 0 . I
Gọi D là giao điểm thứ hai của đường thẳng AJ với đường J tròn (C). B C 2 2 
⇒ Tọa độ D là nghiệm của hệ: (
 x − 2) + ( y − 3) = 25  D
 x − y +1 = 0
⇒ D(9;10) (Do A ≠ D ) 0,5 Vì  = 
BAD CAD ⇒ D là điểm chính giữa cung 
BC ⇒ DB = DC ( ) 1 
BJD là góc ngoài tam giác    A B JAB BJD + ⇒ = (2) 2  =  +  JBD JBC CBD  +  B A  ⇒  =  +  JBD JBC CAD = (3)  =  CBD CAD  2
Từ (2) và (3) suy ra  =  BJD JBD ⇒ D
∆ BJ cân tại D (4)
Từ (1) và (4) suy ra DB = DC = DJ = 5 2 0,75
⇒ B,C thuộc đường tròn (C′) tâm D, bán kính R′ = 5 2
Phương trình (C′) (x − )2 + ( y − )2 : 9 10 = 50
B, C là các giao điểm của (C) và (C′) nên tọa độ của B và C là các nghiệm của hệ:
 (x −6)2 +( y −6)2 = 25 ⇒ B(10;3),C(2;9) (Do x > x ) (  B C  x − 9  )2 +( y −10)2 = 50 0,5
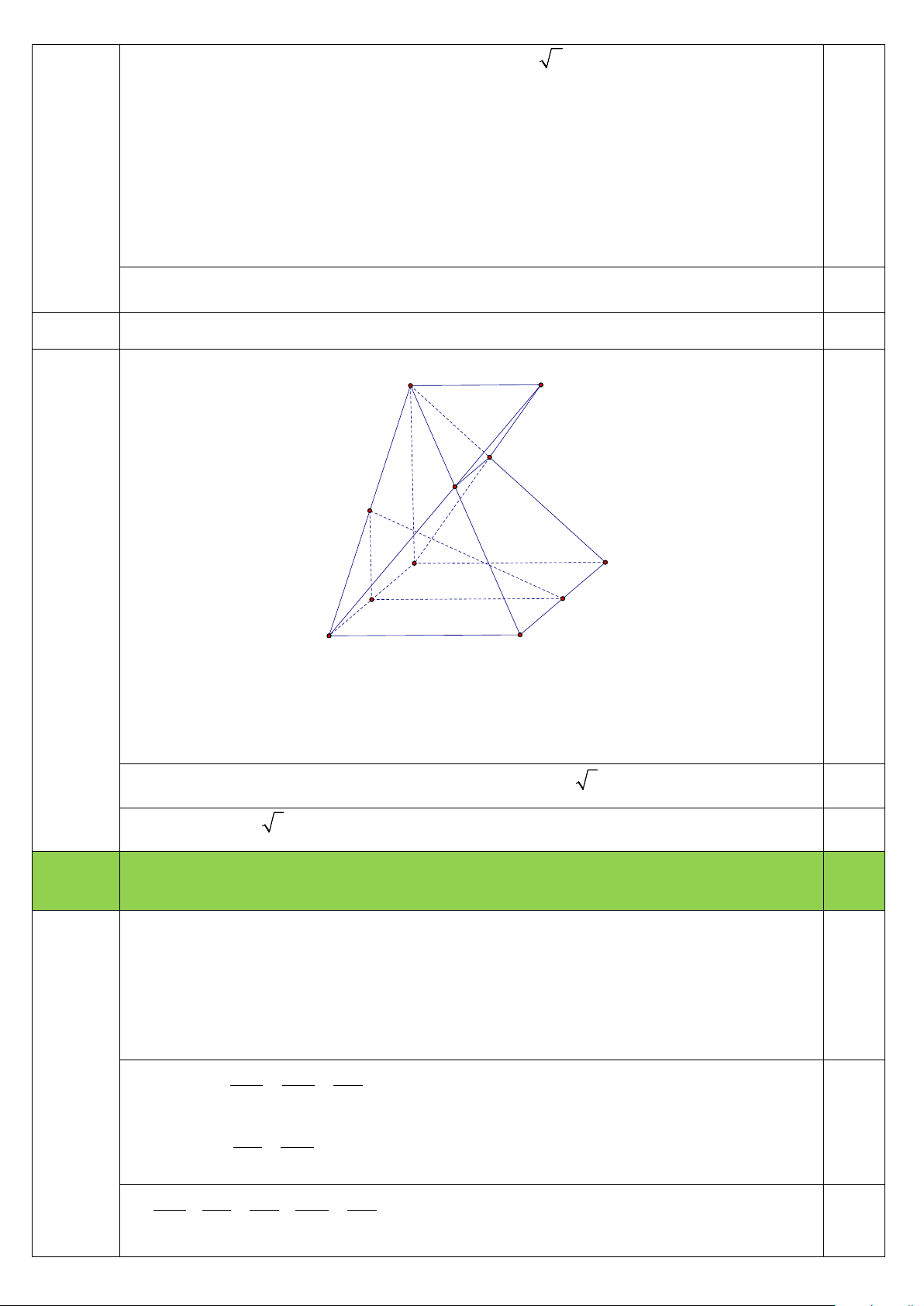
Vậy B(10;3),C (2;9) 0,25 Câu 5.1a 1,5 S K N M I A D H J B C
Gọi H là trung điểm của AB ⇒ IH / /SA ⇒ IH ⊥ ( ABCD) ⇒ góc giữa IJ với ( ABCD) là 0,75 góc  ⇒  0 IJH IJH = 60
Trong tam giác IHJ vuông tại H ta có: = 
IH HJ.tan IJH = b 3 0,5
⇒ SA = 2IH = 2b 3 0,25 Câu 1,5 5.1b
MN = (α ) ∩(SCD) Ta có :
 ⇒ MN / / AB / /CD AB / /CD 
SK = (SAD) ∩(SBC)
 ⇒ SK / / AD / /BC AD / /BC  0,5 Từ đó suy ra AB CD CS = = MN MN MS BC CM = 0,5 SK SM AB BC CS CM MS ⇒ − = − = = 1 (đpcm) MN SK MS SM MS 0,5 Câu 5.2 2,0 A P M I B D Q N C Đặt 2 AB = ,
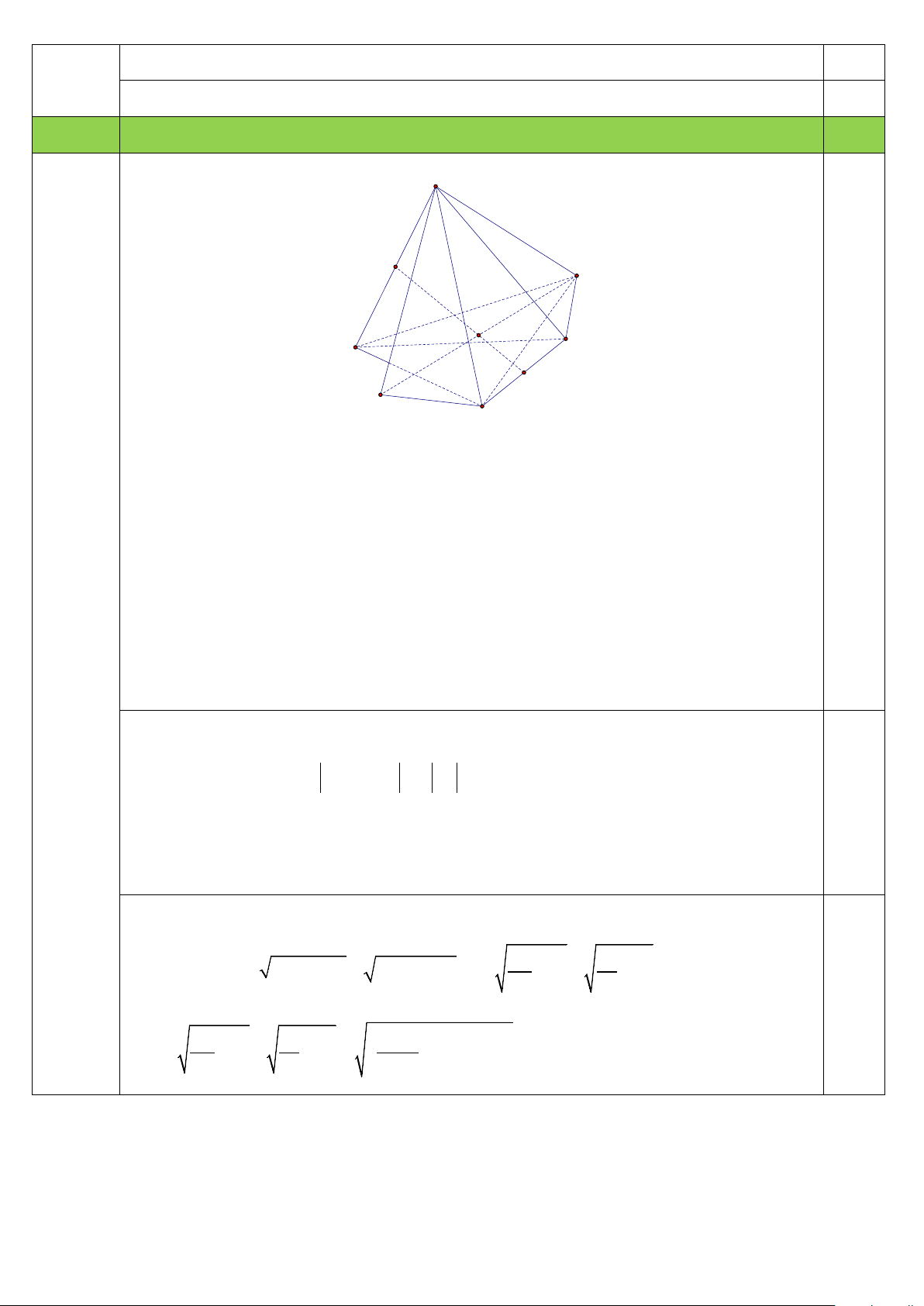
m CD = n ⇒ mn = 4c
Gọi P, Q lần lượt là trung điểm của AB và CD . Ta có B ∆ CD = A
∆ DC ⇒ BQ = AQ ⇒ QA ∆
B cân tại Q ⇒ QP ⊥ AB
Tương tự ta có QP ⊥ CD
⇒ B đối xứng A qua PQ và D đối xứng C qua PQ
Gọi N là điểm đối xứng của M qua PQ và I là giao điểm của MN với 0,5
PQ⇒ MB = N ; A MD = NC 2 2
Ta có: H = (MA+ MB + MC + MD) = (MA+ NA+ MC + NC)   
Trong tam giác AMN có AM + AN = 2 AI ⇒ AM + AN ≥ 2AI
Tương tự ta có: CM + CN ≥ 2CI 2 2
⇒ H ≥ (2AI + 2CI ) = 4( AI + CI ) 0,5
Đặt: IP = x, IQ = y 2  2 2  2 2 2 2 2 m 2 n 2
⇒ ( AI + CI ) = ( IP + PA + IQ +QC ) = + x + + y   4 4    2 2 2  + Ta có m 2 n 2 m n x y  + + + ≥ + (x +   y)2 0,5 4 4  2  2 2 2 2 2
m + n + 2mn 2
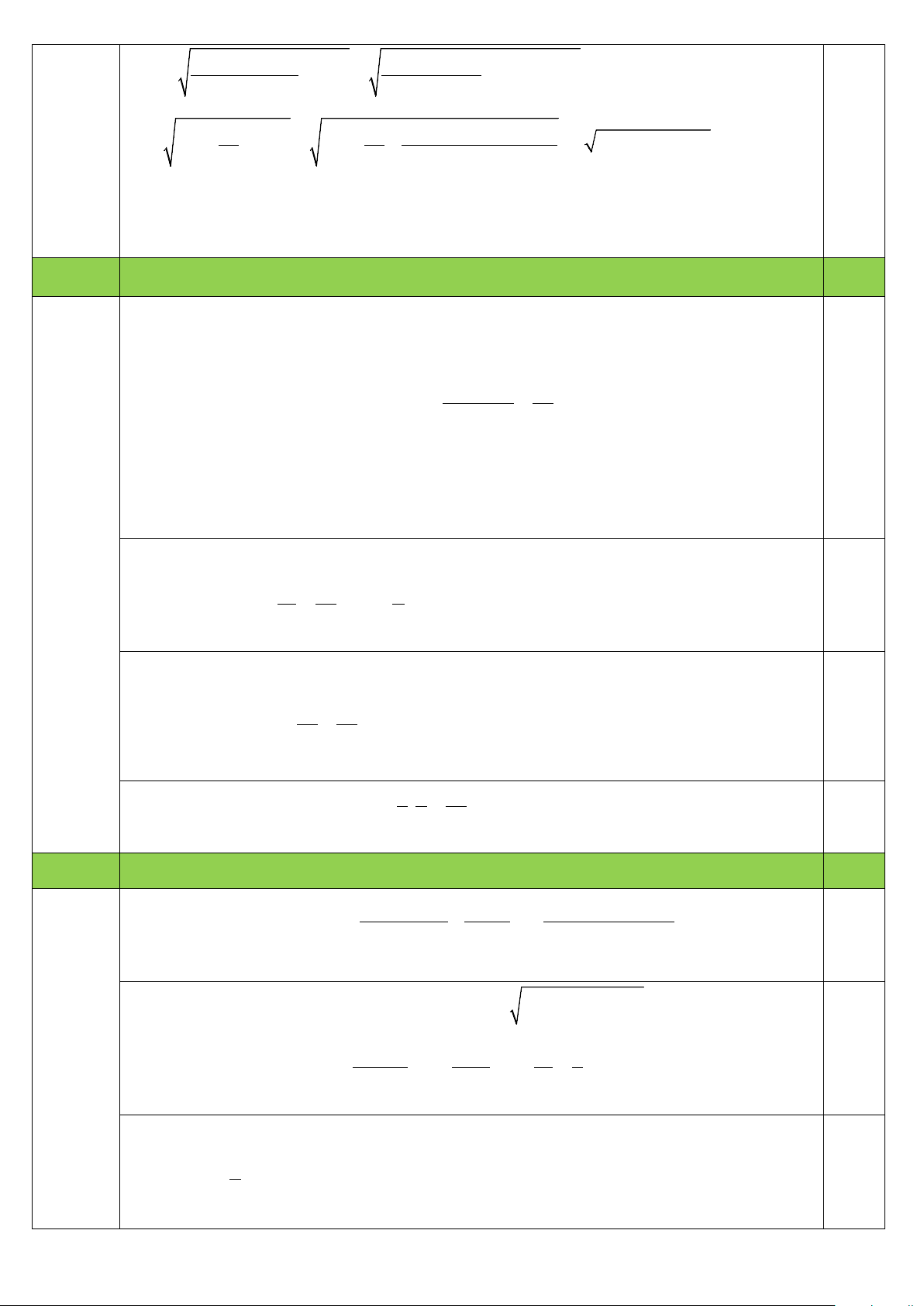
m + n + 8c 2 2 = + PQ = + BQ − PB 4 4 2 2 2 2 2 2 n 2 2 n 2BC 2 2 2 BD CD c BQ c + − + + = + + 2 2 2
= 2a + 2b + 2c 4 4 4 ⇒ H ≥ ( 2 2 2
a + b + c ) = ( 2 2 2 4 2 2 2
8 a + b + c ) (đpcm). 0,5 Câu 6.1 1,5
Gọi số bi trong hộp 1 là n ( 7 < n <15 , n∈ ).
Gọi x, y lần lượt là số bi đen ở hộp 1 và hộp 2 (n ≥ x > y > 0, x, y ∈) .
Suy ra xác suất lấy được 2 viên bi đen là: xy 5 = ( ) 1 n(15 − n) 28  n7
⇒ 28xy = 5n(15 − n) ⇒  (15 − n)7 0,5
+) Nếu n7 , do 7 < n <15 ⇒ n =14 ⇒ số bi ở hộp 2 là 1 viên ⇒ y =1. Thay vào (1) ta có: x 5 = 5 ⇒ x = (Loại). 14 28 2 0,25
+) Nếu (15− n)7 , do 7 < n <15 ⇒ n = 8  x = 5
Thay vào (1) ta được: xy 5 = ⇒ xy =10 ⇒ 56 28  y = 2 0,5
⇒ Xác suất lấy được 2 bi trắng là: 3 5 15 . = . 0,25 8 7 56 Câu 6.2 1,5   Ta có 2 1 1
x ≥1⇒ x ≥ x ⇒ P ≥ x 4x  +  ≥ . ( x + y)2 2 + x z + x    (x + y)2 2 + z + 2x 0,5
Theo giả thiết ta có: (x + y)2 2
+ z = (x + y + z) ≤ (x + y)2 2 3 3 2 + z    ⇒ (x + y)2 2 + z ≤18 4x 18 18 1 ⇒ P ≥ = 2 − ≥ 2 − = 0,5 2x +18 x + 9 10 5
Dấu “=” xảy ra khi x =1, y = 2, z = 3. Vậy 1 min P = 5 0,5
...................... Hết…………….
Document Outline

• Đề thi hsg 11 cấp trường (2019-2020)