Đề HSG Toán 11 năm 2023 – 2024 cụm trường THPT Gia Lâm & Long Biên – Hà Nội

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 11 đề thi chọn học sinh giỏi cấp cụm môn Toán 11 năm học 2023 – 2024 cụm trường THPT Gia Lâm & Long Biên, thành phố Hà Nội; đề thi gồm 1 trang với 5 bài tập tự luận có đáp án và hướng dẫn chấm điểm. Mời bạn đọc đón xem!

58 29 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

5 trang 6 tháng trước

Tác giả:

Profile M. Hậu
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
CỤM TRƯỜNG THPT GL - LB
ĐỀ CHÍNH THỨC
KỲ THI CHỌN HỌC SINH GIỎI CỤM LỚP 11
NĂM HỌC 2023 - 2024
Môn thi: TOÁN
Thời gian làm bài: 150 phút
Bài I (4,0 điểm) Cho phương trình
sin cos 2 cos sin 0.
x x x x
1) Giải phương trình đã cho.
2) Tính tổng các nghiệm của phương trình trong khoảng
0;20 .
Bài II (4,0 điểm)
1) Tính các giới hạn sau:
a)
2
1 1 1
3 3 3
n
n
b)
3
2
1
7 3 1
.
lim
1
x
x x
x
2) Cho hàm số
2
2
khi 1
1
4 khi 1
ax bx
x
f x
x
x
.
Tìm tất cả các cặp số
,
a b
để hàm số
f x
liên tục tại
1.
x
Bài III (2,0 điểm) Giải bất phương trình
2
1 8
2
2
log 1 log 3 log 3 0.
x x x
Bài IV (7,0 điểm) Cho hình chóp
.
S ABCD
có đáy
ABCD
là hình vuông tâm
,
O
cạnh
.
a
Đường
thẳng
SA
vuông góc với mặt phẳng
, 2.
ABCD SA a
1) Tính góc giữa hai đường thẳng
AD
và
.
SC
2) Mặt phẳng đi qua
A
và vuông góc với
SC
cắt các cạnh
, ,
SB SC SD
lần lượt tại các điểm
, , .
E F I
Chứng minh đường thẳng
IE
song song với đường thẳng
.
BD
3) Gọi
H
là giao điểm của hai đường thẳng
AF
và
.
IE
Tính tỉ số
.
AH
AF
4) Gọi
M
là một điểm thay đổi trên cạnh
,(
CD M
khác
C
và
).
D
Mặt phẳng qua
M
và vuông
góc với
CD
cắt các cạnh
,
SC SB
lần lượt tại
N
và
.
P
Tìm giá trị lớn nhất của diện tích tam giác
.
MNP
Bài V (3,0 điểm) Cho dãy số
n
u
được xác định như sau:
1
1
1
3 2 , 1,2,3,...
n
n n
u
u u n
1) Đặt
2 , 1,2,3,...
n
n n
v u n Chứng minh
n
v
là một cấp số nhân.
2) Tìm
1 2
...
lim .
3
n
n
n
u u u

- - - - - - - - - - Hết - - - - - - - - - -
Họ và tên thí sinh:...............................................Số báo danh:..............................................
Chữ kí CBCT 1: .............................................. Chữ kí CBCT 2: ..........................................
S
Ở GIÁO DỤC V
À ĐÀO
T
ẠO H
À N
ỘI
CỤM TRƯỜNG THPT GL - LB
HƯỚNG DẪN CHẤM
KỲ THI CHỌN HỌC SINH GIỎI CỤM LỚP 11
NĂM HỌC 2023 - 2024
Môn thi: TOÁN
Bài Nội dung
Điểm
Bài I
(4,0 đ)
1)
Giải phương trình
sin cos 2 cos sin 0.
x x x x
2,0
Ta có:
sin cos 2 cos sin 0
x x x x
2
sin 2cos 1 cos sin 0
x x x x
2
2sin cos cos 0
x x x
0,5
cos 0
cos 2sin cos 1 0
sin2 1
x
x x x
x
1,0
2
.
4
x k
k
x k
0,5
2) Tính tổng các nghiệm của phương trình trong khoảng
0;2 .
2,0
Xét họ nghiệm
,
2
x k k
có
0;20 0 19
x k
0,5
Tương tự họ nghiệm
,
4
x k k
có
0;20 0 19
x k
0,5
Do đó tổng các nghiệm của phương trình trong khoảng
0;20
là:
19 19
0 0
2 4
k k
S k k
0,5
19 .20 19 .20
2 2 4 4
395 .
2 2
0,5
Bài II
(4,0 đ)
1)
Tính các giới hạn sau:
a)
2
1 1 1
lim 1 ...
3 3 3
n
n
b)
3
2
1
7 3 1
lim
1
x
x x
x
2,0
a) Ta có
1
2 1
1
1
1 1 1 3 1
3
1 ... 1
1
3 3 3 2 3
1
3
n
n n
0,5
Do đó
2 1
1 1 1 3 1 3
lim 1 ... lim 1
3 3 3 2 3 2
n n
n n
 
0,5
b) Ta có
3 3
2 2
1 1
7 3 1 7 2 2 3 1
lim lim
1 1
x x
x x x x
x x
0,25
2
1
3 3
1 3
lim
1 2 3 1
1 7 2 7 4
x
x x
x x x
0,5
1 3 1
24 8 3
0,25
2) Tìm
,
a b
để hàm số
f x
liên tục tại
1.
x
2,0
Để hàm số
f x
liên tục tại
1
x
thì
f x
phải có giới hạn tại
1.
x
Do đó
2 0 4.
a b b a
0,5
Khi đó
2
1 1
4 2
lim lim
1
x x
ax ax x
f x
x
2
2
1 1
2
1 4
4 4 2
.
lim lim
2
4 2
1 4 2
x x
a x
ax ax x a
ax ax x
x ax ax x
1,0
Hàm số
f x
có giới hạn tại
1
x
1
2
lim 1 4 6 2.
2
x
a
f x f a b
0,5
Bài III
(2,0 đ)
Giải phương trình
2
1 8
2
2
log 1 log 3 log 3 0.
x x x
2,0
Điều kiện:
1 3.
x
0,5
2
1 8 2 2 2
2
2
log 1 log 3 log 3 0 log 1 log 3 log 3
x x x x x x
0,5
2
1 3 3 2 3 3
x x x x x x
2
1
.
0
0
x
x x
x
0,5
Kết hợp điều kiện ta được tập nghiệm của bất phương trình là:
1;0 1;3 .
S
0,5
Bài IV
(7,0 đ)
1)
Tính góc giữa hai đường thẳng
AD
và
.
SC
2,0
Do
, ,
AD BC SC AD SC CB
∥
.
0,5
Chứng minh
SBC
vuông tại
B
,
SC CB SCB
0,5
3
tan 3 60
SB a
SCB SCB
BC a
Vậy góc giữa
SC
và
AD
là
60
.
1,0
2)
Mặt phẳng đi qua
A
và vuông góc với
SC
…
1,0
D
C
A
B
S
Chứng minh
BD SC BD AEI
∥
0,5
Do
.
BD AEI
BD EI
AEI SBD EI
∥
∥
0,5
3)
Gọi
H
là giao điểm của hai đường thẳng
AF
và
.
IE
..
2,0
Chứng minh ba điểm
, ,
S H O
thẳng hàng.
0,5
Do
2
SA AC a SAC
vuông cân tại
A F
là trung điểm
SC
.
0,5
Xét
SAC
có
SO AF H H
là
trọng tâm
2
.
3
AH
SAC
AF
1,0
4) Gọi
M
là một điểm thay đổi trên cạnh
,(
CD M
khác
C
và
).
D
..
2,0
Gọi
Q
là giao điểm của
và
AB
.
Chứng minh
MNPQ
là hình thang vuông tại
P
và
Q
.
1
.
2
MNP
S NP PQ
.
1,0
Đặt
0 1
SP
x x
SB
ta có:
.
2 1
NP SP
NP x a
BC SB
PQ BP
PQ a x
SA BS
0,5
Suy ra
2
2 2 2
2 2 1 2
. 1
2 2 2 8
MNP
a a x x a
S x x
Vậy
2
2
Max
8
MNP
a
S
khi
M
là trung điểm
CD
.
0,5
Bài V
1) Chứng minh
n
v
là một cấp số nhân.
1,0
D
C
A
B
S
F
E
H
O
I
D
C
A
B
S
F
E
Q
N
D
C
A
B
S
M
P
(3,0 đ)
Ta có:
1
1 1
3 2 2 3 2
n n n
n n n n
u u u u
0.5
1
1
3
3 , 1,2,3...
n n
v
v v n
Suy ra
n
v
là một cấp số nhân.
0,5
2) Tìm
1 2
...
lim .
3
n
n
n
u u u

2,0
Ta có
3 , 1,2,3...
n
n
v n
3 2 , 1,2,3...
n n
n
u n
0,5
Do đó
1 1 2 2
1 2
... 3 2 3 2 ... 3 2
n n
n
u u u
0,5
2 2
1 1 2
1 *
1 3 3 ... 3 1 2 2 ... 2
3 1 3 2 1
2 1 ,
2 2
n n
n n n
n
n
0,5
Suy ra
1 2
1 2
...
3 2 1 3
.
lim lim
3 2.3 2
n n
n
n n
n n
u u u
 
0,5
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CỤM LỚP 11
CỤM TRƯỜNG THPT GL - LB
NĂM HỌC 2023 - 2024 Môn thi: TOÁN ĐỀ CHÍNH THỨC
Thời gian làm bài: 150 phút
Bài I (4,0 điểm) Cho phương trình sin x cos 2x  cos x  sin x  0.
1) Giải phương trình đã cho.
2) Tính tổng các nghiệm của phương trình trong khoảng 0;20.
Bài II (4,0 điểm)
1) Tính các giới hạn sau:  1 1 1  a) lim 1   ...  .  2   3 3 3n n 
3 x  7  3x 1 b) . lim 2 x 1  x 1 2
ax bx  2  khi x  1
2) Cho hàm số f x   x 1 . 4 khi x  1 
Tìm tất cả các cặp số  ,
a b để hàm số f x liên tục tại x  1.
Bài III (2,0 điểm) Giải bất phương trình log
x  1  log 3  x  log  x  32  0. 1 8 2 2
Bài IV (7,0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, cạnh . a Đường
thẳng SA vuông góc với mặt phẳng  ABCD, SA a 2.
1) Tính góc giữa hai đường thẳng AD và SC.
2) Mặt phẳng đi qua A và vuông góc với SC cắt các cạnh S ,
B SC, SD lần lượt tại các điểm
E, F, I. Chứng minh đường thẳng IE song song với đường thẳng B . D AH
3) Gọi H là giao điểm của hai đường thẳng AF và IE. Tính tỉ số . AF
4) Gọi M là một điểm thay đổi trên cạnh CD, (M khác C và D). Mặt phẳng qua M và vuông
góc với CD cắt các cạnh SC, SB lần lượt tại N và .
P Tìm giá trị lớn nhất của diện tích tam giác MNP. u   1 1
Bài V (3,0 điểm) Cho dãy số u được xác định như sau: n
u  3u  2n, n   1, 2, 3,...  n 1  n
1) Đặt v u  2n , n
  1, 2, 3,... Chứng minh v là một cấp số nhân. n n n
u u  ...  u 2) Tìm 1 2 lim n .  3n n
- - - - - - - - - - Hết - - - - - - - - - -
Họ và tên thí sinh:...............................................Số báo danh:..............................................
Chữ kí CBCT 1: .............................................. Chữ kí CBCT 2: ..........................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO HÀ NỘI
KỲ THI CHỌN HỌC SINH GIỎI CỤM LỚP 11
CỤM TRƯỜNG THPT GL - LB
NĂM HỌC 2023 - 2024
Môn thi: TOÁN HƯỚNG DẪN CHẤM Bài Nội dung Điểm
1) Giải phương trình sin x cos 2x  cos x  sin x  0. 2,0
Ta có: sin x cos 2x  cos x  sin x  0  x  2 sin 2 cos x  
1  cos x  sin x  0 0,5 2
 2sin x cos x  cos x  0 cos x  0
 cos x 2sin x cos x   1  0   1,0 sin 2x  1    x   k  2   k . 0,5 
x   k  4 Bài I
2) Tính tổng các nghiệm của phương trình trong khoảng 0; 2. (4,0 đ) 2,0
Xét họ nghiệm x   k ,
 k   có x 0; 20  0  k  19 0,5 2 
Tương tự họ nghiệm x   k ,
 k   có x 0; 20  0  k  19 0,5 4
Do đó tổng các nghiệm của phương trình trong khoảng 0; 20 là: 19 19       0,5 S   k   k      k 0  2  k 0  4           19 .20  19 .20      2 2   4 4  0,5    395 .  2 2
1) Tính các giới hạn sau:  1 1 1 
3 x  7  3x 1 a) lim 1   ...   b) lim 2,0 2  2  3 3 3n n  x 1  x 1 n 1   1  1   1 1 1  3  3  1  a) Ta có 1   ...    1 0,5 Bài II 2 nn 1  3 3 3 1 2  3   (4,0 đ) 1 3  1 1 1  3  1  3 Do đó lim 1   ...   lim 1   0,5 2 n   n 1  n  3 3 3 n  2  3     2 3 3
x  7  3x 1
x  7  2  2  3x  1 b) Ta có lim  lim 0,25 2 2 x 1  x 1 x 1  x 1    1 3  0,5  lim   2  x 1 
  x   3 x   3  x    x   1 2  3x 1 1 7 2 7 4    1 3 1     0,25 24 8 3 2) Tìm  ,
a b để hàm số f x liên tục tại x  1. 2,0
Để hàm số f x liên tục tại x  1 thì f x phải có giới hạn tại x  1. 0,5
Do đó a b  2  0  b  a  4. 2
ax ax  4x  2
Khi đó lim f x  lim x 1  x 1  x 1 2
ax ax  4x  4 a x   1  4 a  2 1,0    . lim lim x 1   x   1  2
ax ax  4x  2 x 1  2 2
ax ax  4x  2
Hàm số f x có giới hạn tại x  1 a  2 0,5
 lim f x  f   1 
 4  a  6  b  2  . x 1  2 Giải phương trình log
x  1  log 3  x  log  x  32  0. 1 8 2 2,0 2
Điều kiện: 1  x  3. 0,5 log
x  1  log 3  x  log  x  32  0  log x 1  log 3  x  log x  3 1 8 2   2   2   Bài III 2 0,5 2 (2,0 đ)
  x     x   x   2 1 3
3  x  2x  3  x  3 x  1 0,5 2
x x  0  .  x  0 
Kết hợp điều kiện ta được tập nghiệm của bất phương trình là: S  1;0  1;3. 0,5
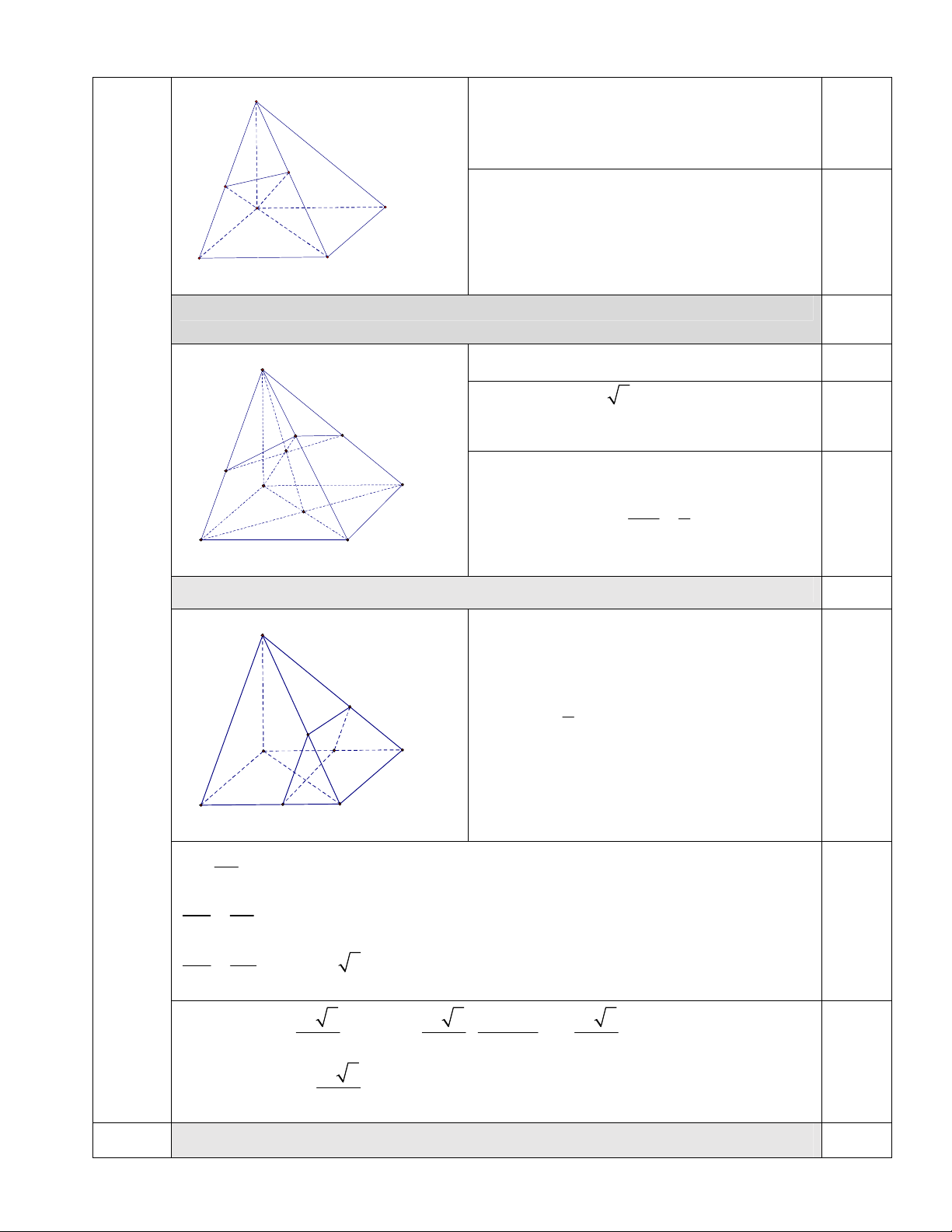
1) Tính góc giữa hai đường thẳng AD và SC. 2,0 S 0,5
Do AD∥ BC  SC, AD   SC,CB .
Chứng minh SBC vuông tại B Bài IV   SC CB  ,  SCB 0,5 (7,0 đ) A BSB a 3   tan SCB    3  SCB  60 BC a 1,0 D C
Vậy góc giữa SC và AD là 60 .
2) Mặt phẳng đi qua A và vuông góc với SC … 1,0 S
Chứng minh BD SC BD∥ AEI  0,5 F EBD∥ AEI  Do   BD∥ EI. A BAEI
 SBD  EI  0,5 D C
3) Gọi H là giao điểm của hai đường thẳng AF và IE. .. 2,0 S
Chứng minh ba điểm S, H , O thẳng hàng. 0,5
Do SA AC a 2  S
AC vuông cân tại 0,5 F E
A F là trung điểm SC . H I
Xét SAC có SO AF  H  H là A B AH 2 trọng tâm SAC   . 1,0 O AF 3 D C
4) Gọi M là một điểm thay đổi trên cạnh CD, (M khác C và D)... 2,0 S
Gọi Q là giao điểm của  và AB .
Chứng minh MNPQ là hình thang vuông tại P và Q . P 1  SN . P PQ . MNP 2 1,0 N A B Q D M C SP Đặt
x 0  x   1 ta có: SB NP SP   NP  . x a BC SB 0,5 PQ BP
PQ a 2 1 xSA BS 2 2 2 2 a 2 a
2  x 1 x a 2 Suy ra S  . xx   MNP 1    2 2  2  8 0,5 2 a 2 Vậy Max S
khi M là trung điểm CD . MNP 8 Bài V
1) Chứng minh v là một cấp số nhân. n 1,0 (3,0 đ) Ta có: n n 1 u
 3u  2  u
 2   3 u  2n n 1  n n 1   n  0.5 v  3 1   v  3v , n   1, 2,3...  n 1  n 0,5
Suy ra v là một cấp số nhân. n
u u  ...  u 2) Tìm 1 2 lim n . 2,0  3n n
Ta có v  3n , n
  1, 2, 3...  u  3n  2n , n   1, 2, 3... 0,5 n n
Do đó u u  ...  u        n  1 1 3 2   2 2 3 2 ... 3n 2n 1 2    0,5   2
1 3  3  ...  3n    2
1 2  2  ...  2n n 1  n 1  n 2 3 1 0,5      n 3 2 1 1 2   * 1  , n    2 2 n 1  n2
u u  ... u 3  2 1 3 Suy ra 1 2 n . lim  lim  0,5  3n  2.3n n n 2
Lưu ý: Học sinh làm theo cách khác đúng vẫn cho điểm tối đa.