Đề HSG Toán 7 năm 2022 – 2023 cụm chuyên môn 3T-H-G Bình Xuyên – Vĩnh Phúc

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 7 đề thi chọn học sinh giỏi cấp trường môn Toán 7 năm học 2022 – 2023 cụm chuyên môn 3T-H-G trực thuộc phòng GD&ĐT huyện Bình Xuyên, tỉnh Vĩnh Phúc

25 13 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 7

Môn: Toán 7

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
PHÒNG GD&ĐT BÌNH XUYÊN
CỤM CHUYÊN MÔN 3T-H-G
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
NĂM HỌC 2022 – 2023
ĐỀ THI MÔN: TOÁN, LỚP 7
Thời gian làm bài: 120 phút, không kể thời gian giao đề.
Họ và tên thí sinh:............................................................................. SBD:.....................
Câu 1. (2 điểm) Tính hp l
4 2 2 3 3 3
:.
7 5 3 7 5 2
−−
+ + +
Câu 2. (2 điểm) Rút gọn biểu thức sau:
( )
34
2023
23
23
. . 1
34
71
5
25
.
5 12
A
−−
=−
−
.
Câu 3. (2 điểm) Tìm
x
biết:
9 19 2 4
3 2 : 1 1
10 10 5 5
x
− − + − − + =
Câu 4. (2 điểm) Tìm 3 số x, y, z biết rằng:
;
yz
25
=
và x + y + z = -110.
Câu 5. (2 điểm) Cho n l số t nhiên, chứng minh rằng
9.10 18
n
+
chia hết cho 27
Câu 6. (2 điểm) Tìm số t nhiên n nhỏ nhất để số
2023
2 23n+
l mt bi số ca 31
Câu 7. (2 điểm) Ba lớp 7A, 7B, 7C cùng tham gia trng cây trong vưn trưng, lúc đầu thầy
ph trch d định giao số cây trng cho ba lớp tỉ lệ với 5:6:7 nhưng sau đó thầy giao theo tỉ
lệ 4:5:6 nên có mt lớp trng nhiều hơn d định 4 cây. Tnh tổng số cây m ba lớp đã trng.
Câu 8. (4 điểm) Cho tam gic ABC có ba góc nhọn (AB
AC). Vẽ về pha ngoi tam gic
ABC các tam giác đều ABD v ACE.
a) Chứng minh rằng DC = BE.
b) Gọi M v N lần lưt l trung điểm ca CD v BE. Chứng minh rằng AMN đều.
Câu 9. (1 điểm) Cho tam gic ABC cân tại A, gọi D l trung điểm ca AC. Trên đoạn BD
lấy điểm E sao cho
DAE ABD=
. Chứng minh rằng
DAE ECB=
.
Câu 10. (1 điểm) Cho x l số thc. Tìm gi trị nhỏ nhất ca biểu thức:
2 1 2 2 2 10A x x x= − + − + + −
==== HẾT ====
Cán bộ coi thi không giải thích gì thêm.
HƯỚNG DẪN CHẤM
MÔN Toán LỚP 7
HDC này gồm 04 trang
A. Hướng dẫn chung:
- Đề thi và đáp án tính theo thang điểm 20.
- Hướng dẫn chấm chỉ là một cách giải. HS có thể giải theo cách khác, nếu đúng logic,
khoa học giám khảo căn cứ vào bài làm cụ thể của HS để cho điểm; điểm cho không
được vượt quá thang điểm phần đó.
- Câu hình học nếu học sinh không vẽ hình hoặc vẽ sai thì không chấm điểm.
B. Đáp án và thang điểm:
Câu
Ý
Nội dung
Điểm
1
4 2 2 3 3 2
::
7 5 3 7 5 3
−−
= + + +
=
4 2 3 3 2
:
7 5 7 5 3
−−

+ + +


4 3 2 3 2
:
7 7 5 5 3
− −
= + + +


2
0: 0
3
==
Vậy: A = 0
0,5
0,5
0,5
0,5
2
( )
34
2023
9 5 2
23
6 3 3
23
. . 1
34
71 2 .3 .5 71
5 2 .3 .5 5
25
.
5 12
A
−−
= − = −
−
72 71 1
;
5 5 5
AA= − =
1
1
3
Ta có
0 ;4
2 ;22
2
10
1
10
21
2
10
1
10
5
.
5
1
2
10
21
5
1
10
5
:2
10
21
5
4
1
10
4
10
10
10
19
:2
10
9
10
30
1
5
4
5
2
1
10
19
:2
10
9
3
−=
−=+
=−=+
==+−
=
+−
−=
−−
+−−
=+
−−
+−−
x
x
x
x
x
x
x
Vậy x = 0; -4
0,5
0,5
0,5
0,5
4
Từ
x y x y
3 7 6 14
= =
;
y z y z
2 5 14 35
= =
.
0,5
0,25
Suy ra
x y z
6 14 35
==
Áp dng tnh chất ca dãy tỉ số bằng nhau, ta có:
x y z
6 14 35
==
x y z 110
6 14 35 55
+ + −
==
++
= -2
Suy ra x = -2.6 = -12; y = -2.14 = -28; z = -2.35 = - 70.
Vậy x = -12; y = -28; z = - 70.
0,5
0,5
0,25
5
Ta có:
9.10 18
n
+
=
( )
9 10 2
n
+
9
(1)
Mt khc
10
n
l số có tổng cc ch số l 1
Nên
10 2
n
+
l số có tổng cc ch số l 3
Suy ra:
10 2
n
+
3
(2)
Từ (1) v (2) suy ra:
( )
9 10 2
n
+
27
hay
9.10 18
n
+
27
0,5
0,5
0,5
0,5
6
Ta có
5
2 32 1( d 31)mo=
và 2023=5.404+3
nên:
2022 5 404
2 (2 ) .8 8(mod31)=
.
Suy ra
2023
2 23 8 23 ( d 31)n n mo+ +
Vì n l số t nhiên nhỏ nhất thỏa mãn
2023
2 23 31n+
nên 8+23n =31
n=1
Vậy: n=1 l số t nhiên nhỏ nhất thỏa mãn.
0,5
0,5
0,5
0,5
7
Gọi tổng số cây 3 lớp đã trng l x (x l số t nhiên khc 0)
Số cây d định chia cho 3 lớp 7A, 7B, 7C lúc đầu lần lưt l: a, b, c
Ta có:
5 6 7
;;
5 6 7 18 18 18 18 3 18
a b c a b c x x x x x
a b c
++
= = = = = = = =
(1)
Số cây sau đó chia cho 3 lớp lần lưt l a’, b’, c’, ta có:
, , , , , ,
, , ,
4 5 6
;;
4 5 6 15 15 15 15 3 15
a b c a b c x x x x x
a b c
++
= = = = = = = =
(2)
So snh (1) v (2) ta có: a > a’; b=b’; c < c’ nên lớp 7C nhận nhiều hơn lúc
đầu
Vây: c’ – c = 4 hay
67
4 4 360
15 18 90
x x x
x− = = =
Vậy số cây 3 lớp đã trng là 360 cây.
0,25
0,5
0,5
0,25
0,25
0,25
8
a
Ta có: AD = AB;
DAC BAE=
và AC = AE
Suy ra ADC = ABE (c.g.c) Suy ra DC=BE
1
1
N
M
E
D
B
C
A
b
Từ ADC = ABE (câu a) CM = EN và
ACM AEN=
ACM = AEN (c.g.c) AM = AN (1)
và
CAM EAN=
MAN CAE=
= 60
0
. (2)
Từ (1) v (2) suy ra AMN đều.
0,5
0,5
0,5
0,5
9
Vẽ AF vuông góc BD, CG vuông góc BD, CH vuông góc với AE.
Ta có
ABF CAH =
(cạnh huyền – góc nhon).
Suy ra: AF = CH.
()ADF CDG ch gn = −
suy ra AF = CG.
Từ đó ta có CH = CG.
( ) ;CEH CEG ch cgv CEH CEG = − =
Mà
;;CEG EBC ECB CEH EAC ECA= + = +
Do đó:
;EBC ECB EAC ECA+ = +
(1)
Măt khc:
;EBA EBC ECB ECA+ = +
(2)
lấy (1) trừ (2) theo vế ta có:
ECB EBA EAC ECB EBA ECB
EBA ECB
− = − = −
=
Mà
DAE ABD=
nên
DAE ECB=
.
0,25
0,25
0,25
0,25
10
Ta có:
2 1 2 2 2 10A x x x= − + − + −
( 2 1 2 10) ( 2 2 2 9) ( 2 5 2 6)A x x x x x x= − + − + − + − + + − + −
( 2 1 10 2 ) ( 2 2 9 2 ) ( 2 5 6 2 )A x x x x x x= − + − + − + − + + − + −
2 1 10 2 2 2 9 2 2 5 6 2A x x x x x x − + − + − + − + + − + −
9 7 5 3 1 25= + + + + =
0,25
0,25
D
G
E
H
B
C
F
A
Dấu bằng khi:
1
5
2
(2 1)(10 2 ) 0
9
(2 2)(9 2 ) 0
1
5
3
2
...............................
2
...............
(2 5)(6 2 ) 0
5
3
2
x
xx
xx
x
x
xx
x

− −
− −





− −

Vậy GTNN ca A l 25 khi
5
3
2
x
0,25
0,25
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GD&ĐT BÌNH XUYÊN
ĐỀ THI CHỌN HỌC SINH GIỎI CẤP TRƯỜNG
CỤM CHUYÊN MÔN 3T-H-G
NĂM HỌC 2022 – 2023
ĐỀ THI MÔN: TOÁN, LỚP 7
Thời gian làm bài: 120 phút, không kể thời gian giao đề.
Họ và tên thí sinh:............................................................................. SBD:.....................  4 − 2  2  3 − 3  3
Câu 1. (2 điểm) Tính hợp lí + : + + .      7 5  3  7 5  2 3 4  2   3  . − .(−     )2023 1
Câu 2. (2 điểm) Rút gọn biểu thức sau:  3   4  71 A = − . 2 3  2   5 −  5 .      5   12   9  19 2  4
Câu 3. (2 điểm) Tìm x biết: 3 − − x + 2 : −1− + = 1      10  10 5  5 y z
Câu 4. (2 điểm) Tìm 3 số x, y, z biết rằng: x y = ; = và x + y + z = -110. 3 7 2 5
Câu 5. (2 điểm) Cho n là số tự nhiên, chứng minh rằng 9.10n +18 chia hết cho 27
Câu 6. (2 điểm) Tìm số tự nhiên n nhỏ nhất để số 2023 2
+ 23n là một bội số của 31
Câu 7. (2 điểm) Ba lớp 7A, 7B, 7C cùng tham gia trồng cây trong vườn trường, lúc đầu thầy
phụ trách dự định giao số cây trồng cho ba lớp tỉ lệ với 5:6:7 nhưng sau đó thầy giao theo tỉ
lệ 4:5:6 nên có một lớp trồng nhiều hơn dự định 4 cây. Tính tổng số cây mà ba lớp đã trồng.
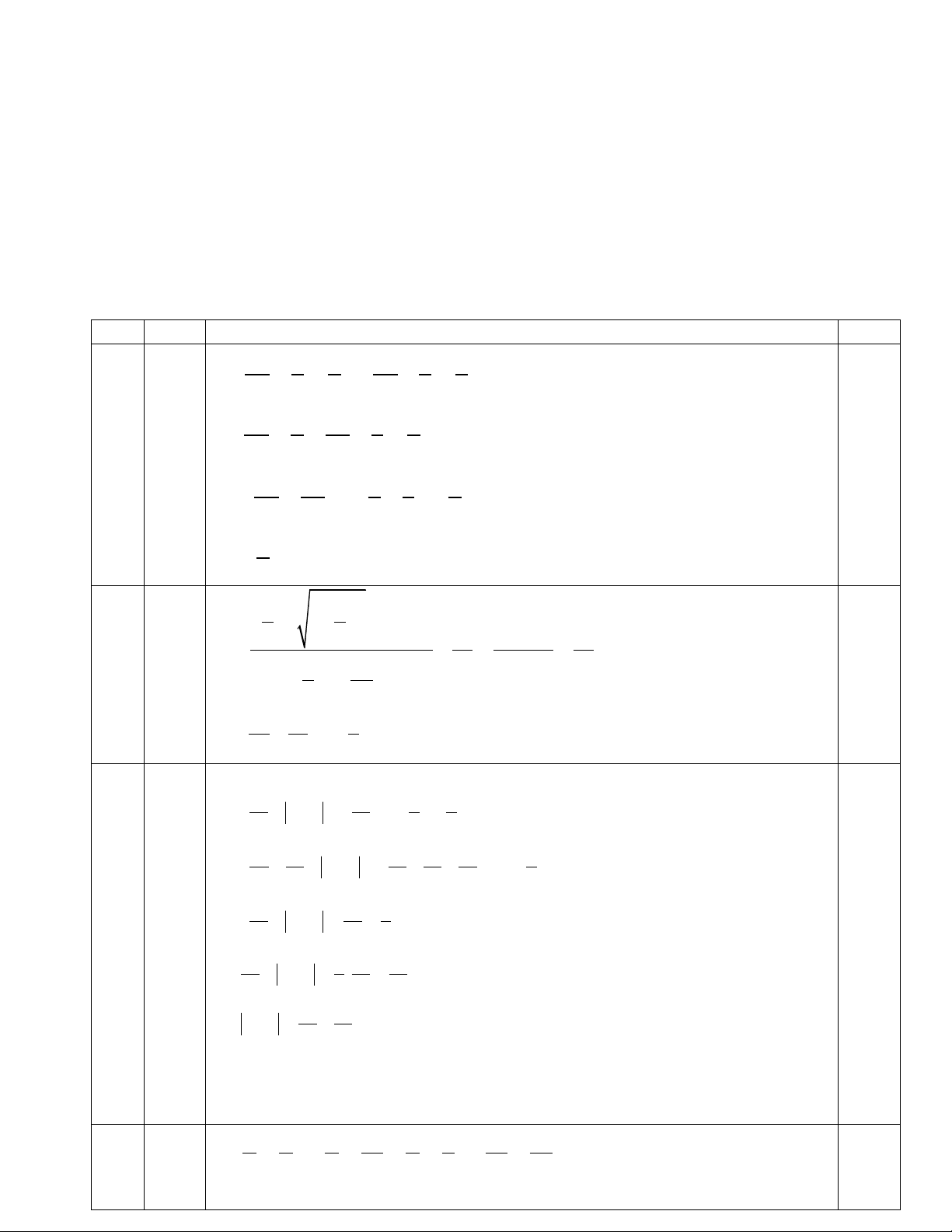
Câu 8. (4 điểm) Cho tam giác ABC có ba góc nhọn (AB  AC). Vẽ về phía ngoài tam giác
ABC các tam giác đều ABD và ACE.
a) Chứng minh rằng DC = BE.
b) Gọi M và N lần lượt là trung điểm của CD và BE. Chứng minh rằng AMN đều.
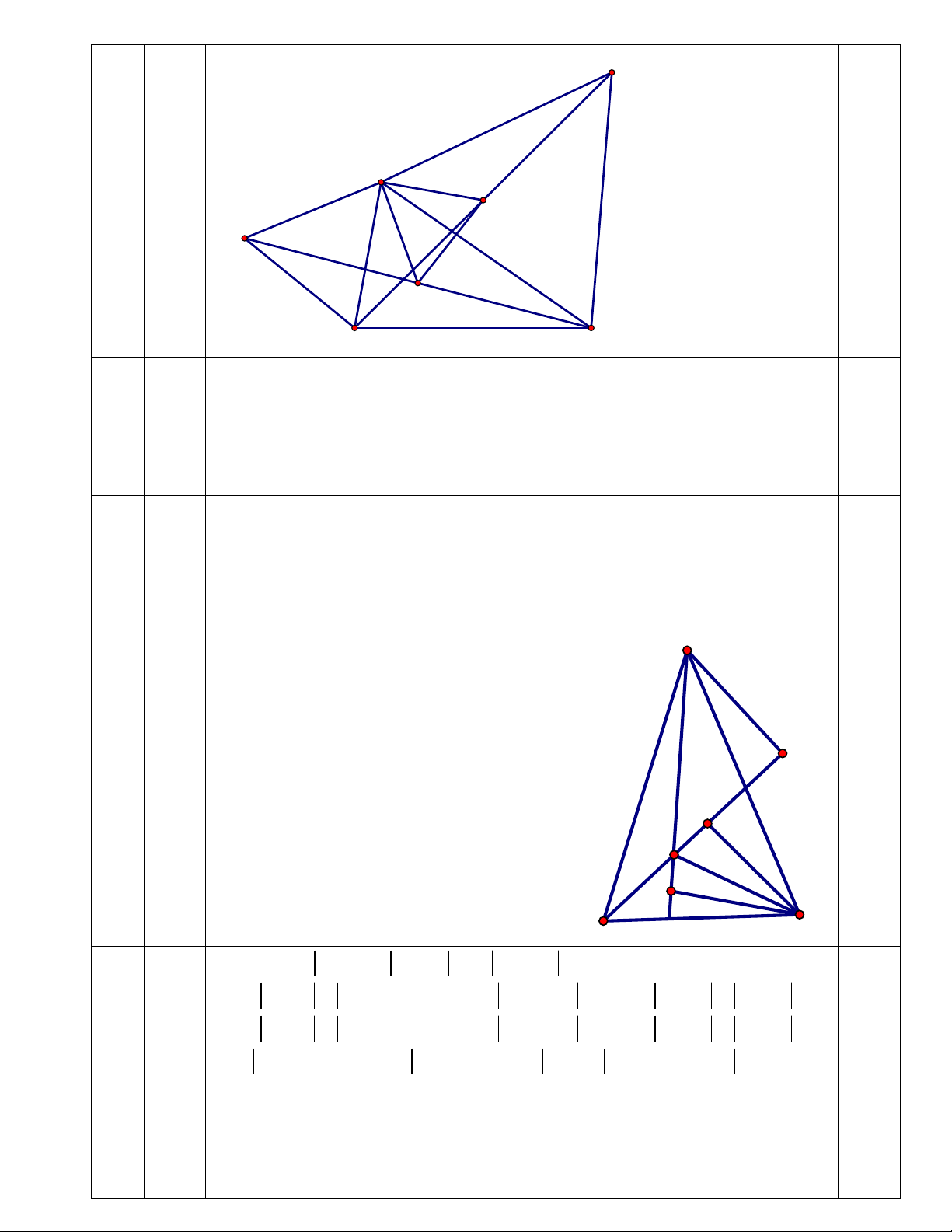
Câu 9. (1 điểm) Cho tam giác ABC cân tại A, gọi D là trung điểm của AC. Trên đoạn BD
lấy điểm E sao cho DAE = ABD . Chứng minh rằng DAE = ECB .
Câu 10. (1 điểm) Cho x là số thực. Tìm giá trị nhỏ nhất của biểu thức:
A = 2x −1 + 2x − 2 +    + 2x −10 ==== HẾT ====
Cán bộ coi thi không giải thích gì thêm. HƯỚNG DẪN CHẤM MÔN Toán LỚP 7
HDC này gồm 04 trang
A. Hướng dẫn chung:
- Đề thi và đáp án tính theo thang điểm 20.
- Hướng dẫn chấm chỉ là một cách giải. HS có thể giải theo cách khác, nếu đúng logic,
khoa học giám khảo căn cứ vào bài làm cụ thể của HS để cho điểm; điểm cho không
được vượt quá thang điểm phần đó.
- Câu hình học nếu học sinh không vẽ hình hoặc vẽ sai thì không chấm điểm.
B. Đáp án và thang điểm: Câu Ý Nội dung Điểm  4 − 2  2  3 − 3  2 = + : + + :      0,5 7 5  3  7 5  3  4 − 2 3 − 3  2 = + + + :   0,5  7 5 7 5  3 1  4 − 3 −   2 3  2 = + + + :     0,5  7 7   5 5  3 2 = 0 : = 0 Vậy: A = 0 3 0,5 3 4  2   3  . − .(−     )2023 1 9 5 2  3   4  71 2 .3 .5 71 A = − = − 1 2 3 6 3 3  2   5 −  5 2 .3 .5 5 2 .      5   12  72 71 1 A = − ; A = 1 5 5 5 Ta có  9  19 2  4 3 − − x + 2  : −1−  + =1  10  10 5  5  30 9  19 10 4  4   − − x + 2  :  − −  =1−  10 10  10 10 10  5 0,5  21  5 1   − x + 2  : = 10  10 5 3 21 1 5 1  − x + 2 = . = 0,5 10 5 10 10 21 1  x + 2 = − = 2 10 10 0,5  x + 2 = − 2 ; 2  x = − 0 ; 4 Vậy x = 0; -4 0,5 x y x y y z y z Từ =  = ; =  = . 0,5 4 3 7 6 14 2 5 14 35 0,25 x y z Suy ra = = 6 14 35
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có: 0,5 x y z + + − = = x y z 110 = = 0,5 6 14 35 6 +14 + = -2 35 55
Suy ra x = -2.6 = -12; y = -2.14 = -28; z = -2.35 = - 70. 0,25
Vậy x = -12; y = -28; z = - 70.
Ta có: 9.10n +18 = 9(10n + 2) 9 (1) 0,5 Mặt khác
10n là số có tổng các chữ số là 1 0,5 5
Nên 10n + 2 là số có tổng các chữ số là 3 Suy ra: 10n + 2 3 (2) 0,5
Từ (1) và (2) suy ra: 9(10n + 2) 27 hay 9.10n +18 27 0,5 Ta có 5 2 = 32  1( d
mo 31) và 2023=5.404+3 0,5 nên: 2022 5 404 2 = (2 ) .8  8(mod31) . 0,5 Suy ra 2023 2
+ 23n  8 + 23n(m d o 31) 6
Vì n là số tự nhiên nhỏ nhất thỏa mãn 2023 2 + 23n 31 0,5
nên 8+23n =31 n=1
Vậy: n=1 là số tự nhiên nhỏ nhất thỏa mãn. 0,5
Gọi tổng số cây 3 lớp đã trồng là x (x là số tự nhiên khác 0) 0,25
Số cây dự định chia cho 3 lớp 7A, 7B, 7C lúc đầu lần lượt là: a, b, c a b c a + b + c x 5x 6x x 7x Ta có: = = = =  a = ;b = = ;c = (1) 0,5 5 6 7 18 18 18 18 3 18
Số cây sau đó chia cho 3 lớp lần lượt là a’, b’, c’, ta có: , , , , , , a b c a + b + c x 4x 5x x 6x 7 , , , = = = =  a = ;b = = ;c = (2) 0,5 4 5 6 15 15 15 15 3 15
So sánh (1) và (2) ta có: a > a’; b=b’; c < c’ nên lớp 7C nhận nhiều hơn lúc 0,25 đầu Vây: c’ – 6x 7x x c = 4 hay − = 4  = 4  x = 360 0,25 15 18 90 Vậy số 0,25
cây 3 lớp đã trồng là 360 cây.
Ta có: AD = AB; DAC = BAE và AC = AE 1
Suy ra ADC = ABE (c.g.c) Suy ra DC=BE 1 8 a E A N D M B C
Từ ADC = ABE (câu a)  CM = EN và ACM = AEN 0,5
ACM = AEN (c.g.c)  AM = AN (1) 0,5 b
và CAM = EAN  MAN = CAE = 600. (2) 0,5
Từ (1) và (2) suy ra AMN đều. 0,5
Vẽ AF vuông góc BD, CG vuông góc BD, CH vuông góc với AE. Ta có ABF = C
AH (cạnh huyền – góc nhon). Suy ra: AF = CH. 0,25 ADF = C
DG (ch − g ) n suy ra AF = CG. Từ đó ta có CH = CG. A C
EH = CEG(ch − cgv)  CEH = CEG; Mà 9
CEG = EBC + ECB;CEH = EAC + EC ; A 0,25 Do đó: F
EBC + ECB = EAC + EC ; A (1) Măt khác:
EBA + EBC = ECB + EC ; A (2) D G
lấy (1) trừ (2) theo vế ta có: E 0,25
ECB − EBA = EAC − ECB = EBA − ECB EBA = ECB H
Mà DAE = ABD nên DAE = ECB . B C 0,25
Ta có: A = 2x −1 + 2x − 2 +    2x − 10
A = ( 2x −1 + 2x −10 ) + ( 2x − 2 + 2x − 9 ) +    + ( 2x − 5 + 2x − 6 )
A = ( 2x −1 + 10 − 2x ) + ( 2x − 2 + 9 − 2x ) +    + ( 2x − 5 + 6 − 2x ) 0,25
A  2x −1 + 10 − 2x + 2x − 2 + 9 − 2x +    + 2x − 5 + 6 − 2x 10 = 9 + 7 + 5 + 3+1= 25 0,25 1  x  5 2 
(2x −1)(10 − 2x)  0   9
(2x 2)(9 2x) 0  − −  1   x  5 Dấu bằng khi:    2   x  3
............................... 2  0,25 ...............  
(2x − 5)(6 − 2x)  0  5  x  3 2 5
Vậy GTNN của A là 25 khi  x  3 0,25 2