Đề HSG Toán 8 năm 2017 – 2018 phòng GD&ĐT Duy Xuyên – Quảng Nam

Xin giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 8 đề HSG Toán 8 năm 2017 – 2018 phòng GD&ĐT Duy Xuyên – Quảng Nam; đề thi có đáp án, lời giải chi tiết và hướng dẫn chấm điểm.

12 6 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 8

Môn: Toán 8

Thông tin:

3 trang 4 tháng trước

Tác giả:

Profile Mai Nguyệt
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI HỌC SINH GIỎI
DUY XUYÊN NĂM HỌC 2017-2018
Môn : TOÁN - Lớp 8
Thời gian làm bài : 120 phút
Bài 1(3,5đ)
a) Chứng minh chia hết cho 6 với mọi
b) Rút gọn biểu thức
Bài 2(4,5đ)
a) Một vật thể chuyển động từ A đến B theo cách sau: đi được 4 m thì dừng lại
1 giây, rồi đi tiếp 8m dừng lại 2 giây, rồi đi tiếp 12m dừng lại 3 giây, … Cứ như vậy đi
từ A đến B kể cả dừng hết tất cả 155 giây. Biết rằng khi đi vật thể luôn có vận tốc
2 m/giây. Tính khoảng cách từ A đến B.
b) Biết và Tính M =
Bài 3(4đ)
a) Giải phương trình
b) Tìm giá trị nhỏ nhất của P =
Bài 4(4,5đ)
Cho tam giác ABC vuông tại A, phân giác BD. Gọi P, Q, R lần lượt là trung điểm
của BD, BC, DC.
a) Chứng minh APQR là hình thang cân.
b) Biết AB = 6cm, AC = 8cm Tính độ dài của AR.
Bài 5(2,5đ)
Cho hình bình hành ABCD. Một đường thẳng qua B cắt cạnh CD tại M, cắt đường
chéo AC tại N và cắt đường thẳng AD tại K. Chứng minh
Bài 6(1đ)
Biết là độ dài ba cạnh của một tam giác. Chứng minh rằng :
------ Hết------
BK
BM
BN
111
nn 17
3
Zn
1)1)((
1)1)((
222
222
xaaax
xaaax
53
23
aba
103
23
bab
2018
22
ba
12)2)(1(
22
xxxx
2010)(4
22
yxyx
cba ,,
04)(
222222
bacba
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM
DUY XUYÊN THI HỌC SINH GIỎI
NĂM HỌC 2017-2018 Môn : TOÁN - Lớp 8
Bài 1:
(3,5đ)
a) =
là tích 3 số nguyên liên tiếp nên chia hết cho 2
và 3, (2,3) =1 nên chia hết cho 6
chia hết cho 6
Suy ra Điều chứng minh
b)
)1)(1(
)1)(1(
22
22
aax
aax
=
2
2
1
1
a
a
aa
0,5
0,5
0,5
0
0,5
0,5
1.0
Bài 2:
( 4,5đ)
a) Gọi x là số lần đi , số lần dừng là x-1
Thời gian đi
= 2+4+6+…+2x = 2(1+2+3+…+x) = x(x+1)
Thời gian dừng 1+2+3+….+(x-1)
Lập được pt
Biến đổi được
Giải tìm đúng x= 10 (chọn), x= -31/3 (loại)
Khoảng cách AB là 10(10+1).2 = 220 (m)
b)
0,25
0,5
0.5
0,25
0.25
0.5
0.25
0.5
0.5
0.5
0.5
Bài 3
(4đ)
a)
Đặt có
Vô nghiệm
0,25
0,25
0,5
0,5
0,5
1
1
1)1)((
1)1)((
22222
22222
222
222
xaaaaxx
xaaaaxx
xaaax
xaaax
)1()1(
)1()1(
1
1
222
222
22222
22222
aaaax
aaaax
aaxaaxx
aaxaaxx
nn 17
3
nnnnnnn 18)1)(1(18
3
)1)(1(
nnn
n18
)0,(
xNx
2
4
.......
2
12
2
8
2
4 x
2
)1(
2
)1)(11(
xxxx
155)1(
2
)1(
xx
xx
03103
2
xx
53
23
aba
2596
42246
babaa
103
23
bab
10096
24426
babab
12533
642246
bbabaa
2018
5
2018
5)(
22
3322
ba
ba
12)2)(1(
22
xxxx
Xxx 1
2
012
2
XX
0)3)(4(01234
2
XXXXX
3;4
XX
0
4
19
)
2
1
(054
22
xxxX
0)2()2(023
22
xxxxxX
2;10)2)(1(
xxxx
0,5
b)P =
=
=
P
m
in
=
-
201
8
khi x
=y =
2
0,5
0,5
0,5
Bài 4
(4,5đ)
a) PQ là đường trung bình tam giác BDC, suy ra PQ// AR nên
APQR là hình thang.
AQ= ½ BC (trung tuyến tam giác vuông ABC)
PR = ½ BC ( đường trung bình tam giác DBC)
Suy ra AQ = PR
Kết luận APQR là hình thang cân
b)Tính đư
ợc BC= 10 cm
Tính chất đường phân giáctrong của Tg ABC
Suy ra
Thay số tính đúng AD= 3cm; DC=5cm; DR=2,5 cm
Kết quả AR= 5,5 cm
https://nguyenthienhuongvp77.violet.vn/
0,5
0,5
0,5
0,5
0,25
0,5
0,5
0,5
0,5
0,25
Bài 5
(2,5đ)
AB//AC (hai cạnh đối hình bình hành). Theo định lí Talét có :
Từ (1) và (2)
Mà MC+MD= CD=AB nên
Suy ra điều cần chứng minh
0,5
0,5
0,75
0,25
0.5
Bài 6(1đ)
Tổng 2 cạnh tam giác lớn hơn cạnh thứ ba nên cả 4 thừa số của tích
đều dương, suy ra điều chứng minh
https://nguyenthienhuongvp77.violet.vn/
0,25
0,25
0,25
0,25
Học sinh giải cách khác , phân biểu điểm tương tự./.
BC
BA
DC
DA
.
BC
BC
BA
AC
DA
.
)1(
.
BN
BM
BN
NBMN
AB
ABMC
NB
MN
AN
NC
AB
MC
)2(
.
AB
MDAB
BK
BM
AB
MDAB
BK
KMBK
AB
MD
KA
KD
BK
KM
AB
MDMC
AB
MDAB
AB
MCAB
BK
BM
BN
BM
1
.
BK
BM
BN
BM
20184444
22
yyxx
20182018)2()2(
22
yx
2010)(4
22
yxyx
)2)(2(4)(
222222222222
abcbaabcbabacba
2222
)()( cbacba
))()()(( acbbcacbacba
| 1/3
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

PHÒNG GIÁO DỤC VÀ ĐÀO TẠO ĐỀ THI HỌC SINH GIỎI
DUY XUYÊN NĂM HỌC 2017-2018 Môn : TOÁN - Lớp 8
Thời gian làm bài : 120 phút Bài 1(3,5đ) a) Chứng minh n 3
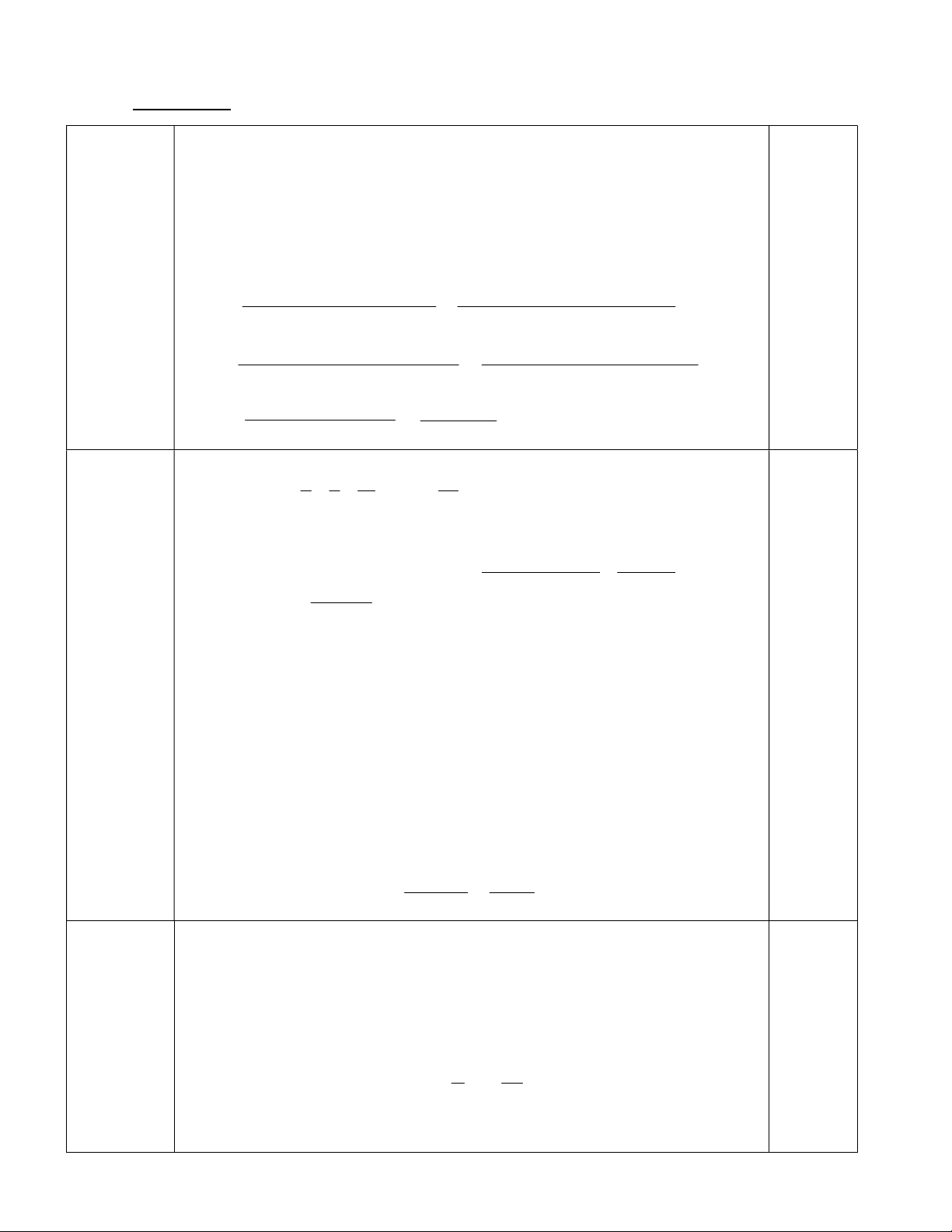
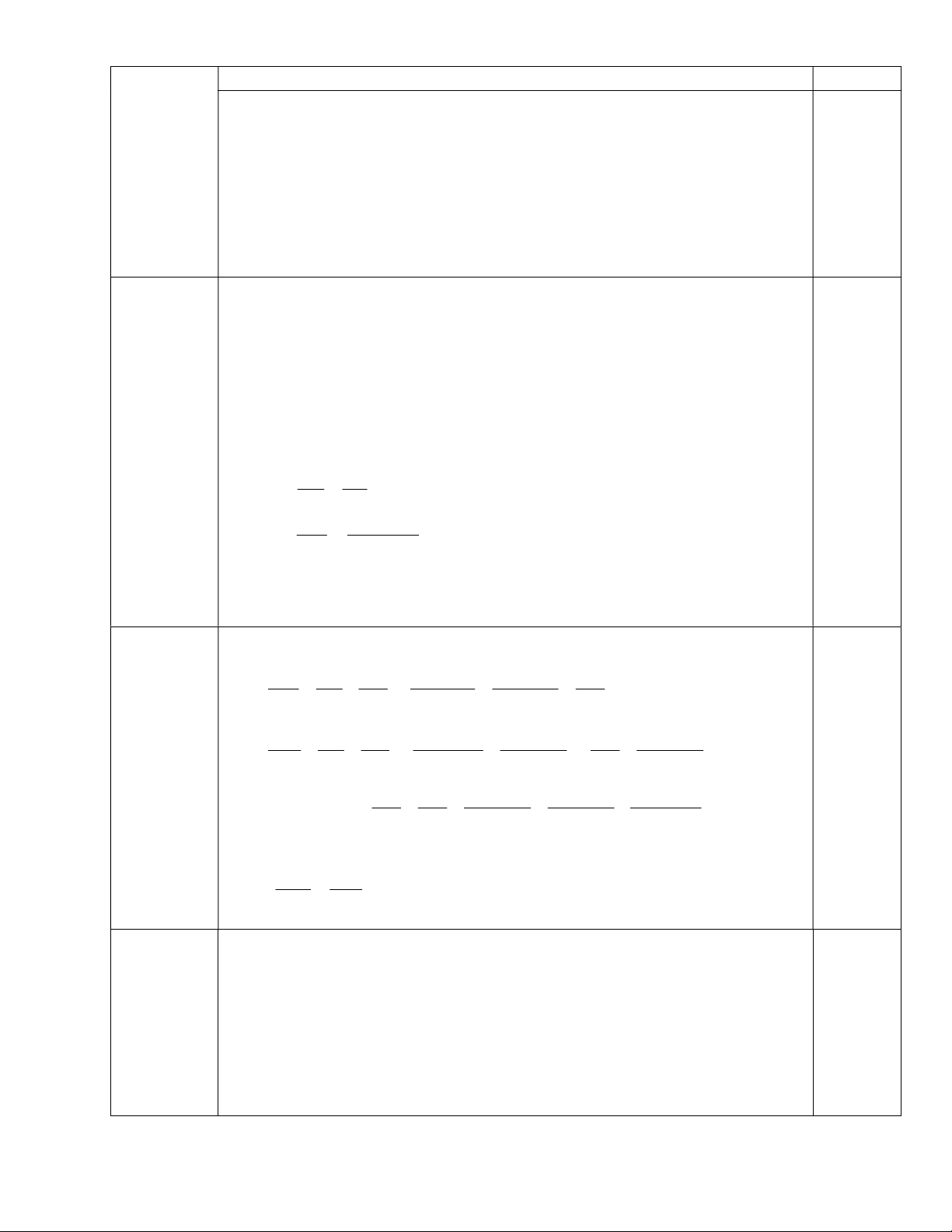
 1 7 n chia hết cho 6 với mọi n  Z b) Rút gọn biểu thức ( 2 x  a) 1 (  a) 2 2  a x 1 2 2 2 Bài 2(4,5đ) (x  a) 1 (  a)  a x  1
a) Một vật thể chuyển động từ A đến B theo cách sau: đi được 4 m thì dừng lại
1 giây, rồi đi tiếp 8m dừng lại 2 giây, rồi đi tiếp 12m dừng lại 3 giây, … Cứ như vậy đi
từ A đến B kể cả dừng hết tất cả 155 giây. Biết rằng khi đi vật thể luôn có vận tốc
2 m/giây. Tính khoảng cách từ A đến B. 2 2 a  b b) Biết a 3  3 a b 2  5 và b 3  3 a 2 b  1 0 Tính M = 2018 Bài 3(4đ) a) Giải phương trình ( 2 x  x  ) 1 ( 2 x  x  2)  12
b) Tìm giá trị nhỏ nhất của P = x 2  y 2  4 ( x  y)  2010 Bài 4(4,5đ)
Cho tam giác ABC vuông tại A, phân giác BD. Gọi P, Q, R lần lượt là trung điểm của BD, BC, DC.
a) Chứng minh APQR là hình thang cân.
b) Biết AB = 6cm, AC = 8cm Tính độ dài của AR. Bài 5(2,5đ)
Cho hình bình hành ABCD. Một đường thẳng qua B cắt cạnh CD tại M, cắt đường 1 1 1
chéo AC tại N và cắt đường thẳng AD tại K. Chứng minh   BN BM BK Bài 6(1đ) Biết
a , b , clà độ dài ba cạnh của một tam giác. Chứng minh rằng : ( 2 2 2 a  b  c )2  4 2 2 a b  0 ------ Hết------
PHÒNG GIÁO DỤC VÀ ĐÀO TẠO HƯỚNG DẪN CHẤM
DUY XUYÊN THI HỌC SINH GIỎI
NĂM HỌC 2017-2018 Môn : TOÁN - Lớp 8 Bài 1: 3 3 (3,5đ) a) n  1 7
n = n  n18n  n(n  ) 1 (n  ) 1 18n 0,5 n ( n
 1 ) ( n  )1 là tích 3 số nguyên liên tiếp nên chia hết cho 2
và 3, (2,3) =1 nên chia hết cho 6 0,5 1 8 n chia hết cho 6 0,5 0 Suy ra Điều chứng minh 2 2 2 2 2 2 2 2 b) (x  a) 1 (  a)  a x 1
x  x a  a  a  a x 1  2 2 2 2 2 2 2 2 0,5 (x  a) 1 (  a)  a x 1
x  x a  a  a  a x 1 2 2 2 2 2 2 2 2
x  x a  a x 1 a  a x 1 (  a  a )  1 (  a  a )   0,5 2 2 2 2 x  x a  a x 1 2 2  a  a x 1 ( 2  a  a )  1 ( 2  a  a ) ( 2 x  ) 1 1 ( 2  a  a ) 2 1  a  a  = ( 2 x  ) 1 1 ( 2  a  a ) 2 1  a  a 1.0
a) Gọi x là số lần đi ( x  N , x  ) 0 , số lần dừng là x-1 0,25 Bài 2: Thời gian đi 4 8 12 4x    .......  ( 4,5đ) 2 2 2 2
= 2+4+6+…+2x = 2(1+2+3+…+x) = x(x+1) 0,5
Thời gian dừng 1+2+3+….+(x-1) (x 1  ) 1 (x  ) 1 x(x  ) 1   0.5 Lập được pt x(x  ) 1 2 2  x(x  ) 1 155 0,25 2 Biến đổi được 3 2 x  x  310  0 0.25
Giải tìm đúng x= 10 (chọn), x= -31/3 (loại) 0.5
Khoảng cách AB là 10(10+1).2 = 220 (m) 0.25 b) a 3  3 a b 2  5 6  a  6 4 2 a b  9 2 4 a b  25 0.5 3 b  3 2 a b  10 6 2 4 4 2  b  a b  a b  6 9 100 0.5 6  a  3 4 2 a b  3 2 4 6 a b  b  125 0.5 2 2 a  2 2 3 3 5  b (a  b )  5   0.5 2018 2018 Bài 3 a) 2 2 (x  x  ) 1 (x  x  2)  12 (4đ) 2 2 Đặt x  x  1  X có X  X 12  0 0,25 2
X  4X  3X 12  0 (X  ) 4 (X  ) 3  0 0,25  X   ; 4 X  3 0,5 2 1 19
X    x  x    x    4 2 5 0 ( ) 0 Vô nghiệm 0,5 2 4 X  3 2
 x  x  2  0  ( 2 x  2x)  (x  2)  0 0,5
 (x )1(x2)  0  x   ;1x  2 0,5 2 2
b)P = x  y  4(x  y)  2010 2 2
x  4x  4  y  4 y  4  2018 = 0,5
= (x  2)2  ( y  2)2  2018  2  018 0,5 Pmin = -2018 khi x=y =2 0,5 Bài 4
a) PQ là đường trung bình tam giác BDC, suy ra PQ// AR nên (4,5đ) APQR là hình thang. 0,5
AQ= ½ BC (trung tuyến tam giác vuông ABC) 0,5
PR = ½ BC ( đường trung bình tam giác DBC) 0,5 Suy ra AQ = PR 0,5
Kết luận APQR là hình thang cân 0,25 b)Tính được BC= 10 cm 0,5
Tính chất đường phân giáctrong của Tg ABC D . A BA  DC BC 0,5 Suy ra .DA BA 0,5  AC BC  BC
Thay số tính đúng AD= 3cm; DC=5cm; DR=2,5 cm 0,5 Kết quả AR= 5,5 cm 0,25
https://nguyenthienhuongvp77.violet.vn/ Bài 5
AB//AC (hai cạnh đối hình bình hành). Theo định lí Talét có : (2,5đ) .MC NC MN MC  AB MN  NB BM      ) 1 ( 0,5 AB AN NB AB BN BN 0,5 .KM KD MD BK  KM AB  MD BM AB  MD       ( ) 2 BK KA AB BK AB BK AB Từ (1) và (2) BM BM AB  MC AB  MD MC  MD      0,75 BN BK AB AB AB Mà MC+MD= CD=AB nên 0,25 .BM BM
  1 Suy ra điều cần chứng minh 0.5 BN BK Bài 6(1đ) ( 2 2 2 a  b  c )2  4 2 2 a b  ( 2 2 2 a  b  c  2ab)( 2 2 2 a  b  c  2ab) 0,25   2 2 (a  b)  c  2 2 (a  b)  c  0,25           (a b c)(a b c)(a c b)(b c a) 0,25
Tổng 2 cạnh tam giác lớn hơn cạnh thứ ba nên cả 4 thừa số của tích
đều dương, suy ra điều chứng minh 0,25
https://nguyenthienhuongvp77.violet.vn/
Học sinh giải cách khác , phân biểu điểm tương tự./.