PGD&ĐT TP THANH HOÁ
TRƯỜNG THCS TRẦN MAI NINH ĐỀ KHẢO SÁT CHỌN ĐỘI TUYỂN
TOÁN 8 NĂM HỌC 2023 – 2024 (VÒNG I)
ĐỀ THI CHÍNH THỨC
Ngày thi 02 tháng 12 năm 2023 Đề thi có 01 trang
Thời gian làm bài 120 phút, không kể thời gian giao đề
Bài 1: (4,0 điểm)
a) Cho x – y = 2. Tính giá trị của biểu thức: M = 2( x3 – y3) – 3( x + y)2 1 1 1 1 1 1 1 1 1
b) Cho + + = 2; a + b + c = . abc + + = + + . a b c Chứng minh: 2 2 2 a b c a b c
Bài 2: (4,0 điểm)
a) Tìm x biết: (x – 3)3 + (2x – 1)3 = (3x – 4)3
b) Tìm a, b để đa thức f(x) = ax3 + bx2 + 5x – 50 chia hết cho đa thức g(x) = x2 + 3x – 10.
Bài 3: (4,0 điểm)
a) Tìm số tự nhiên n để B = n3 – n2 – 7n + 10 là số nguyên tố.
b) Tìm n nguyên để C = n4 + 2n3 + 2n2 + n +7 là số chính phương
Bài 4: (6,0 điểm)
1) Cho tam giác ABC vuông tại A, O là trung điểm của BC. Vẽ tia Bx vuông góc
với BC (Bx cùng phía với điểm A đối với đường thẳng BC). Qua A vẽ đường thẳng
vuông góc với AO cắt Bx ở M. Đường thẳng qua O và song song với AB cắt AM ở D,
AC ở F. Đường thẳng MO cắt AB ở E.
a) Chứng minh rằng: EF = AO.
b) BD cắt CM ở I Chứng minh rằng: Ba điểm E, I, F thẳng hàng.
2) Cho tam giác MNP có MN = 5cm, MP = 6cm, NP = 7cm. Gọi I là giao điểm
của ba đường phân giác, G là trọng tâm của tam giác MNP. Chứng minh rằng: IG//MP
Bài 5: (2,0 điểm)
Cho các số thực a, b, c thỏa mãn 0 ≤ a,b,c ≤ 1. Chứng minh rằng: 2 2 2 a + b + c ≤ 1+ ab + bc + ac
---------------Hết----------------
Cán bộ coi thi không giải thích gì thêm. 1 PGD&ĐT TP THANH HOÁ
TRƯỜNG THCS TRẦN MAI NINH HƯỚNG DẪN VÀ BIỂU CHẤM
Biểu chấm gồm 02 trang
KHẢO SÁT CHỌN ĐỘI TUYỂN TOÁN 8 - VÒNG I
NĂM HỌC 2023 – 2024 Bài
Nội dung cần đạt Điểm
a) Cho x – y = 2. Tính giá trị của biểu thức: M = 2( x3 – y3) – 3( x + y)2 2,0 Ta có:
M = 2(x3 – y3) – 3(x + y)2 = 2(x – y)(x2 + xy + y2) – 3(x2 + 2xy+ y2) 0,5 M = (x – y)2 0,5
Mà x – y = 2 nên M = (x – y)2 = 4. 0,5
Vậy với x – y = 2 thì M = 4. 0,5 1 1 1
b) Cho + + = 2; a + b + c = .
abc Chứng minh: Bài 1 a b c 4,0đ 2,0 1 1 1 1 1 1 + + = + + . 2 2 2 a b c a b c 2 1 1 1  1 1 1  1 1 1 2 2 2 Vì + + = 2 ⇒ + + = 4 ⇒ + + + + + =   4 2 2 2 a b c  a b c  a b c ab bc ca 0,75 1 1
1 2(a + b + c) ⇒ + + + = 4 2 2 2 a b c abc 0,5
Mà a + b + c = abc 1 1 1 1 1 1 1 1 1 + + = 2 ⇒ + + = + + 2 2 2 2 2 2 a b c a b c a b c 0,75
a) Tìm x biết: (x – 3)3 + (2x – 1)3 = (3x – 4)3 2,0
Đặt x – 3 = a; 2x – 1 = b thì 3x – 4 = a + b. Ta có:  x = 3 a = 0 x − 3 = 0  3 3 3   1  + = + ⇒ + = ⇒ = ⇒ − = ⇒ =
Bài 2 a b (a b) 3ab(a b) 0 b 0 2x 1 0 x    2 1,5 4.0đ
a + b = 0 3x − 4 = 0  4 x =  3  1 4 Vậy x ∈ 3  ; ; 2 3   0,5
b) Tìm a, b để đa thức f(x) = ax3 + bx2 + 5x – 50 chia hết cho đa thức g(x) = x2 + 3x – 10. 2,0 2
Ta có: g(x) = (x +5)(x – 2) 0,25
f(x) chia hết cho g(x) nên f(x) = (x +5)(x – 2).k(x) => f(2) = 0 và f(-5) = 0 0,75
Từ f(2) = 0 => 8a + 4b + 10 – 50 = 0 => 2a + b = 10 (1) 0,25
Từ f(-5) = 0 => -125a + 25b – 25 – 50 = 0 => – 5a + b = 3 (2) 0,25
Từ (1) và (2) suy ra a = 1; b = 8 0,25
Vậy a = 1; b = 8 thì f(x) chia hết cho g(x). 0,25
a) Tìm số tự nhiên n để B = n3 – n2 – 7n + 10 là số nguyên tố. 2,0
Ta có: B = (n – 2)(n2 + n – 5)
B là số nguyên tố nên (n – 2) và (n2 + n – 5) là ước của 1 0,5
+ Nếu (n – 2) = 1 thì n = 3 khi đó B = 7 (chọn)
Nếu (n – 2) = -1 thì n = 1 khi đó B = 3 (chọn) 0,5
Nếu n2 + n – 5 = 1 thì (n + 3)(n – 2) = 0 0,5
Với n là số tự nhiên nên n = 2 khi đó B = 0 (loại)
Vậy n = 3 và n = 1 thì B là số nguyên tố. 0,5
b) Tìm n nguyên để C = n4 + 2n3 + 2n2 + n +7 là số chính phương 2,0 Ta có: 4 3 2 4 3 2 2
C = n + 2n + 2n + n + 7 = n + 2n + n + n + n + 7 2 2
= n (n +1) + n(n +1) + 7. Đặt n(n+1) = y ta có C = y2 + y + 7
Bài 3 Vì C là số chính phương nên 0,25 4,0đ 2 2 2 2 2 2
Ta có : y + y + 7 = k (k ∈ N) ⇔ 4k = 4y + 4y + 28 ⇔ 4k − (2y +1) = 27
⇔ (2k − 2y −1)(2k + 2y +1) = 27 0,5
Vì 2k − 2y −1< 2k + 2y +1; 2k − 2y −1+ 2k + 2y +1 = 4k
 2k − 2y −1 = 1 k = 7 *)  ⇒ 2k 2y 1 27  + + = y = 6 0,5
Khi y = 6 ta có n(n +1) = 6 (n∈ Z) ⇒ n = 2; n = − 3
 2k − 2y −1 = 1 − k = 7 − *)  ⇒  (loai)
2k + 2y +1 = 27 −  y = 6
 2k − 2y −1 = 9 k = 3 *)  ⇒ 
⇒ n(n +1) =1 (loai)
2k + 2y +1 = 3  y = 1 0,5
 2k − 2y −1 = 3 − k = 3 − *)  ⇒  (loai)
2k + 2y +1 = 9 − y = 1
Vậy n = 2; n = - 3 thì C là số chính phương. 0,25
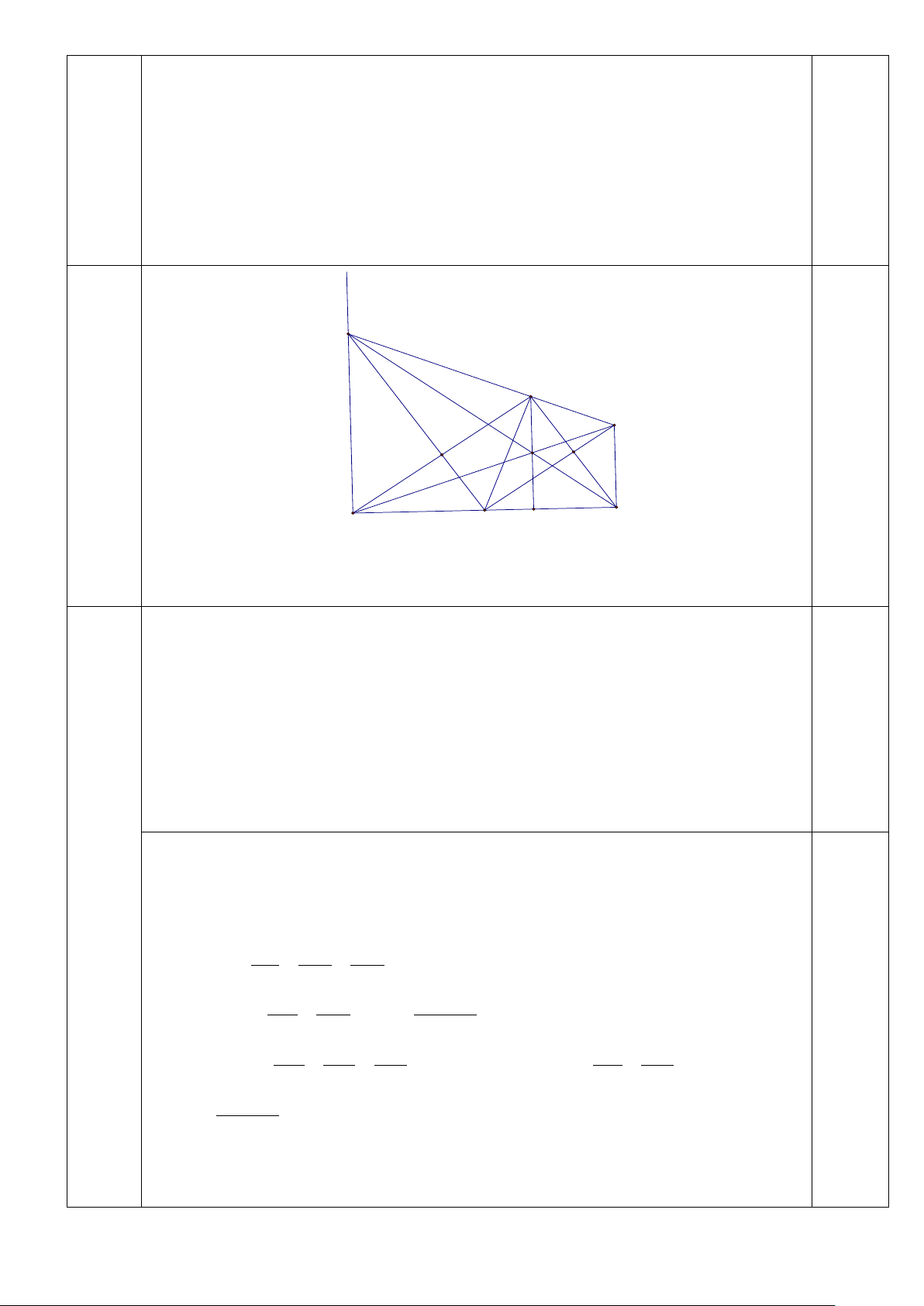
1) Cho tam giác ABC vuông tại A, O là trung điểm của BC. Vẽ tia Bx 3
vuông góc với BC (Bx cùng phía với điểm A đối với đường thẳng BC). 4,0
Bài 4.1 Qua A vẽ đường thẳng vuông góc với AO cắt Bx ở M. Đường thẳng
4,0đ qua O và song song với AB cắt AM ở D, AC ở F. Đường thẳng MO cắt AB ở E.
a) Chứng minh rằng: EF = AO.
b) BD cắt CM ở I Chứng minh rằng: Ba điểm E, I, F thẳng hàng. M A D E F I B O H C 1. a) Ta có:
Mà OA=OB nên OM là trung trực của AB => OM⊥ AB tại E và EA= EB. 0,5 =>  0 BEO = 90 OD // AB; AB 0,5
⊥ AC=>OD ⊥ AC tại F=>  0 AFO = 90 Mà  0 BAC = 90 (GT)
=> AEOF là hình chữ nhật => AO = FE 1,0 1. b) Ta có A
∆ OC cân ở O nên đường cao OD đồng thời là phân giác Câu 1 =>∆ = ∆ ⇒  0 AOD COD
OCD = 90 ⇒ DC ⊥ BC ⇒ BM / /CD và AD = CD. 0,5
4,0đ Gọi giao điểm của AI và BC là H. / / IM BM AM MB CD ⇒ = =
⇒ IA / /CD ⇒ IH / /CD / /BM IC CD AD IA AM AM. 0,5 / / CD Do IA CD ⇒ = ⇒ IA = DC MD MD / / IH IC AD ⇒ = = ; = ; IH CD Do IH MB
MA MB CD = AD ⇒ = MB MC MD MA MD 0,5 AM.CD ⇒ IH = ⇒ IH = ;
IA EA = EB ⇒ IE / /BC. MD 0,5
Từ IE//BC; EF//BC=> E, I, F thẳng hàng. 4
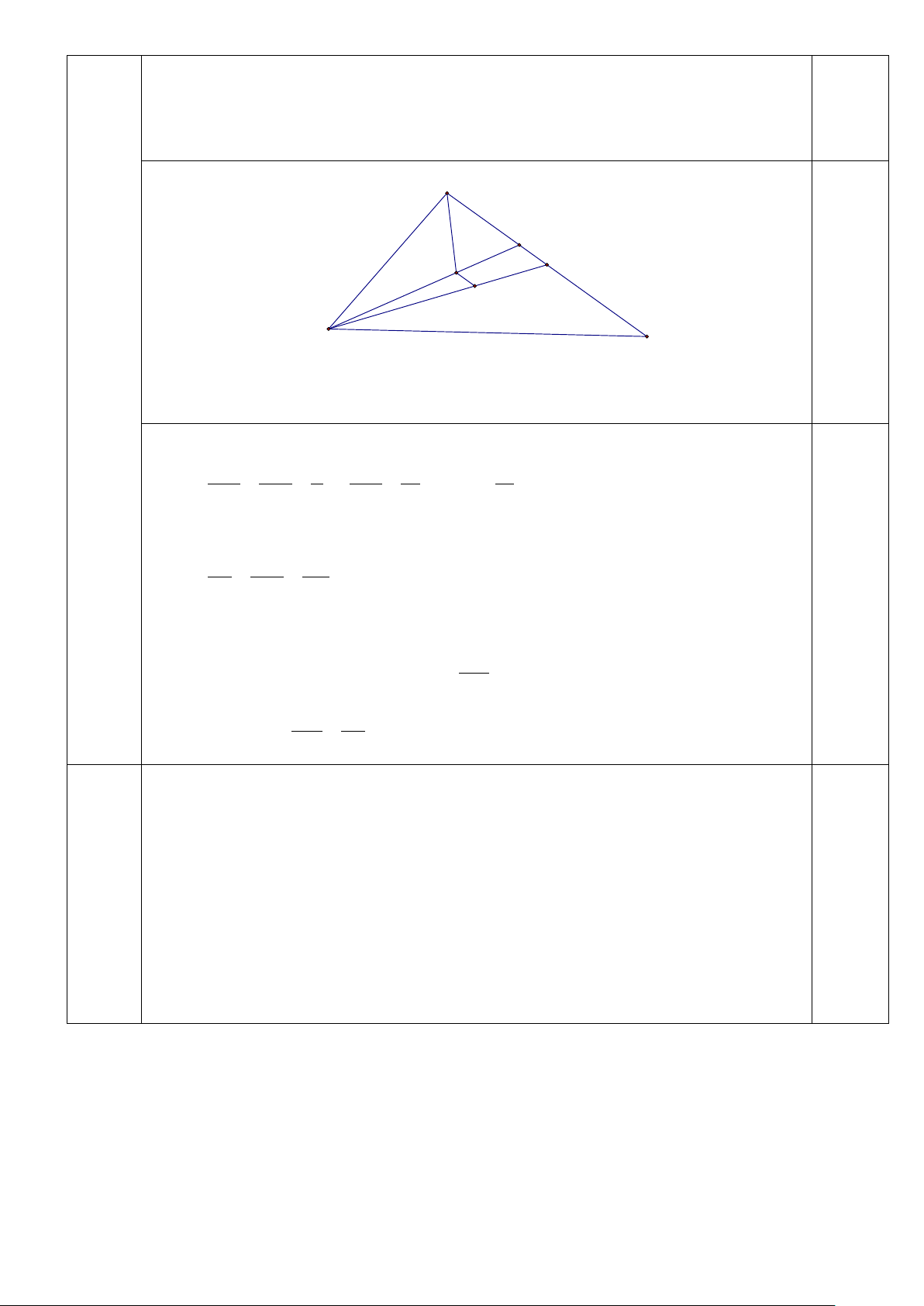
2) Cho tam giác MNP có MN = 5cm, MP = 6cm, NP = 7cm. Gọi I là 2,0
giao điểm của ba đường phân giác, G là trọng tâm của tam giác MNP.
Chứng minh rằng: IG//MP M D K I G N P Bài 4.2
2,0đ 2. Ta có: ND là phân giác của tam giác MNP MD MN 5 MD 5 5 Ta có : = = ⇒ = ⇒ MD = MP = 2,5 (cm) DP NP 7 MP 12 12 0,5
MI là phân giác của tam giác MND IN MN 5 Ta có : = = = 2 (1) ID MD 2,5 0,5
Gọi K là trung điểm của MP.
Vì G là trọng tâm của ∆ MNP nên GN = 2 (2) NK 1,0 Tù (1) và (2) GN IN ⇒ =
⇒ IG / /DK Hay IG// MP NK ID
Do: 0 ≤ a,b,c ≤1
(a −1);(b −1);(c −1) ≤ 0 ⇒ (a −1)(b −1)(c −1) ≤ 0 0,5
Do (a −1)(b −1)(c −1) = a + b + c + abc − ab − ac − bc −1 0,5
Bài 5 ⇒ a + b + c + abc − ab − ac −bc −1≤ 0 ⇒ a + b + c + abc − ab − ac −bc ≤1
2,0đ ⇒ a + b + c ≤1+ ab + ac + bc − abc ≤1+ ab + ac + bc 0,5
⇒ a + b + c ≤1+ ab + ac + bc 2 2 2 Do0 ≤ a, ,
b c ≤1⇒ a ≤ a; b ≤ ; b c ≤ c 0,5 2 2 ⇒ a + b 2
+ c ≤1+ ab + ac + bc 5