Đề khảo sát chất lượng môn Toán 11 trường Đoàn Thượng – Hải Dương lần 2

Đề khảo sát chất lượng môn Toán 11 trường Đoàn Thượng – Hải Dương lần 2 gồm 5 câu hỏi tự luận, có lời giải chi tiết.

16 8 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Đề thi Toán 11

Môn: Toán 11

Thông tin:

5 trang 8 tháng trước

Tác giả:

Profile Kim Oanh
SỞ GD&ĐT HẢI DƯƠNG
TRƯỜNG THPT ĐOÀN THƯỢNG
ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN 2
NĂM HỌC 2016 – 2017 MÔN TOÁN 11
Thời gian làm bài: 120 phút
Câu 1 (3,0 điểm).
a) Tính giá trị biểu thức:
0 0 00
0
cos65 .cos40 sin40 .sin65
sin65
+
b) Giải phương trình:
12cos2sin3 =− xx
c) Giải phương trình:
2
1 cos2
1 cot2
sin 2
x
x
x
−
+=
Câu 2 (3,0 điểm).
a) Từ 4 chữ số 0, 1, 2, 3 lập được bao nhiêu số tự nhiên có 3 chữ số phân
biệt. Tính tổng các số được thành lập.
b) Một thầy giáo có 12 cuốn sách khác nhau, bao gồm 5 cuốn sách văn, 4
cuốn sách toán, 3 cuốn sách tiếng anh. Ông muốn lấy 6 cuốn để tặng cho
6 học sinh, mỗi em một cuốn. Tính xác suất để sau khi thầy giáo tặng
xong, mỗi loại toán, văn, tiếng anh còn lại ít nhất 1 cuốn.
c) Tính tổng:
0 2015 1 2014 2015 2015 0
2016 2016 2016 2015 2016 2016 2016 1
kk
k
SCC CC CC CC
−
−
= + ++ ++
Câu 3 (1,0 điểm). Cho đường tròn
(
)
( )
(
)
22
: 2 3 25Cx y
− ++ =
. Tìm phương
trình đường tròn
(
)
'C
là ảnh của đường tròn
qua phép vị tự tâm
( )
3;1I
tỉ số
3k = −
Câu 4 (2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M
là điểm thuộc cạnh SC (M không trùng điểm S và C),N, P lần lượt là trung điểm
AB, AD.
a) Tìm giao điểm của SD với mặt phẳng (ABM)
b) Xác định thiết diện của hình chóp với mặt phẳng (MNP).
Câu 5 (1,0 điểm). Cho
,, 0xyz>
thoả mãn
1xy yz zx++=
. Tính giá trị biểu
thức:
( )
( ) (
)( )
( )( )
22 22 2 2
2 22
11 11 11
111
yz zx xy
Sx y z
xyz
++ ++ ++
=++
+++
……………Hết……………
Họ và tên thí sinh: ……………………………Số báo danh: ……………………
SỞ GD&ĐT HẢI DƯƠNG
TRƯỜNG THPT ĐOÀN THƯỢNG
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN 2
NĂM HỌC 2016 – 2017 MÔN TOÁN 11
Câu
Ý
Nội dung
Điểm
1
a
Tính
0 0 00
0
cos65 cos40 sin40 .sin65
sin65
+
1,00
( )
00
0 0 00 0
0 00
cos 65 40
cos65 cos40 sin40 .sin65 cos25
sin65 sin65 sin65
−
+
= =
0,5
( )
00
0
00
cos 90 65
sin65
1
sin65 sin65
−
= = =
0,5
1
b
Giải phương trình:
12cos2sin3 =− xx
1,25
31 1 1
sin 2 cos2 sin 2 cos cos2 sin
2 2 2 6 62
pt x x x x
ππ
⇔ −=⇔ − =
0,25
sin 2 sin
66
x
ππ

⇔ −=


0,5
22
66
6
22
66
2
xk
xk
xk
xk
ππ
π
π
π
ππ
π
ππ
π
−=+
= +
⇔⇔
−=−+
= +
0,25
0,25
1
c
Giải phương trình:
2
1 cos2
1 cot2
sin 2
x
x
x
−
+=
0,75
Điều kiện:
sin2 0
2
x xk
π
≠⇔≠
0,25
2
1 cos2
1 cot2
1 cos 2
x
pt x
x
−
⇔+ =
−
1
1 cot2
1 cos2
x
x
⇔+ =
+
cos2 1
1
sin 2 1 cos2
x
xx
⇔+ =
+
sin2(1 cos2) cos2(1 cos2) sin2xxxxx⇔ ++ +=
sin 2 cos2 cos2 (1 cos2 ) 0xx x x
⇔ + +=
cos2 (sin2 cos2 1) 0xx x⇔ + +=
cos2 0
sin 2 cos2 1
x
xx
=
⇔
+=−
0,25
cos2 0
42
x xk
ππ
+ =⇔= +
(tm)
0,25
sin 2 cos2 1
xx++ =−
sin(2 ) sin( )
44
x
ππ
⇔ += −
( )
( )
4
2
x k tm
x kL
π
π
π
π
=−+
⇔
= +
Vậy,phương trình có nghiệm:
42
xk
ππ
= +
2
a
Từ 4 chữ số 0, 1, 2, 3 lập được bao nhiêu số tự nhiên có 3 chữ số phân
biệt. Tính tổng các số được thành lập.
1,25
Gọi số cần tìm là
abc
(
0a ≠
, a, b, c đôi một khác nhau).
Chọn số a có 3 cách.
Chọn 2 chữ số b, c còn lại có
2
3
6A =
cách
0,5
Theo quy tắc nhân có 3.6 = 18 số tm yêu cầu bài toán.
0,5
+ Xét số A có 3 chữ số phân biệt và chữ số hàng trăm có thể là 0.
Từ
3
4
A 24
số A ta lập được 12 cặp số có tổng là 333. Ví dụ 012 + 321
= 333.
Suy ra tổng các số A là 12.333 = 3996.
+ Xét số B có 3 chữ số phân biệt và chữ số hàng trăm là 0.
Từ
2
3
A6
số B ta lập được 3 cặp số có tổng là 44. Ví dụ 032 + 012 =
44.
Suy ra tổng các số B là 3.44 = 132.
Vậy tổng các số thỏa yêu cầu là 3996 – 132 = 3864.
0,25
2
b
Một thầy giáo có 12 cuốn sách khác nhau, bao gồm 5 cuốn sách văn, 4
cuốn sách toán, 3 cuốn sách tiếng anh. Ông muốn lấy 6 cuốn để tặng
cho 6 học sinh, mỗi em một cuốn.
Tính xác suất để sau khi thầy giáo
tặng xong, mỗi loại toán, văn, tiếng anh còn lại ít nhất 1 cuốn.
1,0
Ta thấy không thể chọn sao cho cùng hết 2 loại sách.
Chọn 6 cuốn sách bất kì tặng cho 6 học sinh có
6
12
665280A =
cách.
0,25
Số cách chọn sao cho không còn sách văn:
1
7
1. .6! 5040C
=
Số cách chọn sao cho không còn sách toán:
2
8
1. .6! 20160C =
0,25
Số cách chọn sao cho không còn sách tiếng anh:
3
9
1. .6! 60480C =
( )
665280 5040 20160 60480 579600nA= −− − =
0,25
( )
579600
0,8712
665280
PA= =
0,25
2
c
Tính tổng:
0,75
0 2015 1 2014 2015 2015 0
2016 2016 2016 2015 2016 2016 2016 1
kk
k
SCC CC CC CC
−
−
= + ++ ++
Ta có:
( ) ( )
2015
2016 2016 2015
2016! 2015!
2016 2016.
! 2015 ! ! 2015 !
kk k
k
CC C
kk kk
−
−
==⋅=
−−
0,5
( )
( )
2015
0 1 2015 2015
2015 2015 2015
2016. 2016 1 1 2016.2S CC C⇒= + + + = + =
0,25
3
Cho đường tròn
(
) (
) ( )
22
: 2 3 25Cx y
− ++ =
. Tìm phương trình đường
tròn
( )
'C
là ảnh của đường tròn
qua phép vị tự tâm
( )
3;1I
tỉ số
3k = −
1,00
Đường tròn (C) có tâm
( )
2; 3A −
, bán kính
5R =
0,25
phép vị tự tâm
( )
3;1
I
tỉ số
3k = −
biến điểm A thành A’. Tìm được
'(7;13)A
0,25
đường tròn
( )
'
C
là ảnh của đường tròn
qua phép vị tự tâm
( )
3;1I
tỉ
số
3k = −
có bán kính
' 3.5 15R =−=
0,25
Vậy pt đường tròn
(
) (
) (
)
22
' : 7 13 225Cx y
− +− =
0,25
4
4
a
Tìm giao điểm của SD với mặt phẳng (ABM)
1,0
AC BD O∩=
Trên (SAC) có:
AM SO I∩=
0,5
Trên (SBD) có:
BI SD J∩=
Vậy J là giao điểm của SD với mặt phẳng (ABM)
0,5
4
b
Xác định thiết diện của hình chóp với mặt phẳng (MNP).
1,0
( ) ( )
MNP ABCD NP∩=
11
;NP BC M NP CD N∩= ∩=
0,25
(
) ( )
11 2
;MNP SCD MN MN SD N
∩ = ∩=
( ) ( )
11 2
;MNP SBC MM MM SB M∩ = ∩=
(
) ( )
(
) (
)
22
;
MNP SAD PN MNP SAB NM∩= ∩=
Vậy thiết diện là ngũ giác
22
MM NPN
0,25
5
Cho
,, 0xyz>
thoả mãn
1xy yz zx++=
. Tính giá trị biểu thức:
(
)(
)
(
)(
)
(
)(
)
22 22 2 2
2 22
11 11 11
111
yz zx xy
Sx y z
xyz
++ ++ ++
=++
+++
1,00
ĐÆt
γβα
tan;tan;tan
===
zyx
víi
0
<
γ
β
α
;
;
<
2
π
(*)
(
)
tan tan tan tan tan tan 1
tan tan tan 1 tan tan
gt
αβ βγ γα
αβ γ βγ
⇒ ⋅ + ⋅+⋅ =
⇔ + =−⋅
( ) ( )
1
tan cot , *
tan 2 2
k do
ππ
βγ α αβγ π αβγ
α
⇔ + = = ⇔++= + ⇒++=
0,25
( )( )
2
22
1
11
x
zy
x
+
++
γβ
α
γ
β
α
α
γβ
α
α
coscos
sin
coscos
cos
tan
coscos
cos
tan
22
2
⋅
=
⋅
=
⋅
=
( )
yz
−
=⋅
−=
⋅
⋅−⋅
=
⋅
+
=
1
tantan
1
coscos
sinsincos
cos
coscos
cos
γβ
γ
β
γβγ
β
γ
β
γβ
0,5
Tương tự
.213111 =−=−+−
+−=⇒ xyxzyz
S
0,25
| 1/5
| | Tải xuống

Có thể bạn quan tâm:

Preview text:

SỞ GD&ĐT HẢI DƯƠNG
ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN 2
TRƯỜNG THPT ĐOÀN THƯỢNG
NĂM HỌC 2016 – 2017 MÔN TOÁN 11
Thời gian làm bài: 120 phút Câu 1 (3,0 điểm). 0 0 0 0
cos 65 .cos 40 + sin 40 .sin 65
a) Tính giá trị biểu thức: 0 sin 65
b) Giải phương trình: 3 sin 2x − cos 2x = 1 1 − cos 2x
c) Giải phương trình: 1 + cot 2x = 2 sin 2x Câu 2 (3,0 điểm).
a) Từ 4 chữ số 0, 1, 2, 3 lập được bao nhiêu số tự nhiên có 3 chữ số phân
biệt. Tính tổng các số được thành lập.
b) Một thầy giáo có 12 cuốn sách khác nhau, bao gồm 5 cuốn sách văn, 4
cuốn sách toán, 3 cuốn sách tiếng anh. Ông muốn lấy 6 cuốn để tặng cho
6 học sinh, mỗi em một cuốn. Tính xác suất để sau khi thầy giáo tặng
xong, mỗi loại toán, văn, tiếng anh còn lại ít nhất 1 cuốn. c) Tính tổng: 0 2015 1 2014 k 2015−k 2015 0 S = C C + C C ++ C C ++ C C 2016 2016 2016 2015 2016 2016−k 2016 1 2 2
Câu 3 (1,0 điểm). Cho đường tròn (C ) : ( x − 2) + ( y + 3) = 25. Tìm phương
trình đường tròn (C ') là ảnh của đường tròn (C) qua phép vị tự tâm I (3; ) 1 tỉ số k = 3 −
Câu 4 (2,0 điểm). Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. M
là điểm thuộc cạnh SC (M không trùng điểm S và C),N, P lần lượt là trung điểm AB, AD.
a) Tìm giao điểm của SD với mặt phẳng (ABM)
b) Xác định thiết diện của hình chóp với mặt phẳng (MNP).
Câu 5 (1,0 điểm). Cho x, y, z > 0 thoả mãn xy + yz + zx = 1. Tính giá trị biểu ( 2 1 + y )( 2 1 + z ) ( 2 1 + z )( 2 1 + x ) ( 2 1 + x )( 2 1 + y ) thức: S = x + y + z 2 2 2 1 + x 1 + y 1 + z
……………Hết……………
Họ và tên thí sinh: ……………………………Số báo danh: …………………… SỞ GD&ĐT HẢI DƯƠNG
ĐÁP ÁN VÀ HƯỚNG DẪN CHẤM
TRƯỜNG THPT ĐOÀN THƯỢNG
ĐỀ KHẢO SÁT CHẤT LƯỢNG LẦN 2
NĂM HỌC 2016 – 2017 MÔN TOÁN 11 Câu Ý Nội dung Điểm 1 a 0 0 0 0 cos 65 cos 40 + sin 40 .sin 65 Tính 1,00 0 sin 65 + cos( 0 0 0 0 0 0 65 − 40 cos 65 cos 40 sin 40 .sin 65 ) 0 cos 25 = = 0,5 0 0 0 sin 65 sin 65 sin 65 cos( 0 0 90 − 65 ) 0 sin 65 = = =1 0,5 0 0 sin 65 sin 65 1
b Giải phương trình: 3 sin 2x − cos 2x = 1 1,25 3 1 1 π π 1 pt ⇔ sin 2x − cos 2x =
⇔ sin 2xcos − cos2xsin = 0,25 2 2 2 6 6 2  π  π ⇔ sin 2x − = sin   0,5  6  6  π π  π 0,25 2x − = + k2π x = + kπ   6 6 6 ⇔  ⇔ π π  π   2x − = π − + k2π x = + kπ  0,25  6 6  2 1 c − Giải phương trình 1 cos 2x : 1 + cot 2x = 0,75 2 sin 2x π
Điều kiện: sin 2x ≠ 0 ⇔ x ≠ k 0,25 2 1 − cos 2x
pt ⇔ 1 + cot 2x = 2 1 − cos 2x 1 ⇔ cos 2x 1 1 + cot 2x = ⇔ 1+ = 1 + cos 2x sin 2x 1 + cos 2x
⇔ sin 2x(1+ cos2x) + cos2x(1+ cos2x) = sin 2x 0,25
⇔ sin 2xcos2x + cos2x(1+ cos2x) = 0 ⇔ cos2x(sin 2x + cos2x +1) = 0 cos2x = 0 ⇔ 
sin 2x + cos2x = 1 − π π
+cos2x = 0 ⇔ x = + k (tm) 0,25 4 2  π x = − + kπ (tm) π π  + 4
sin 2x + cos 2x = 1
− ⇔ sin(2x + ) = sin(− ) ⇔  4 4 π
x = + kπ (L)  2 π π
Vậy,phương trình có nghiệm: x = + k 4 2 2
a Từ 4 chữ số 0, 1, 2, 3 lập được bao nhiêu số tự nhiên có 3 chữ số phân
biệt. Tính tổng các số được thành lập. 1,25
Gọi số cần tìm là abc ( a ≠ 0 , a, b, c đôi một khác nhau). Chọn số a có 3 cách. 0,5
Chọn 2 chữ số b, c còn lại có 2 A = 6 cách 3
Theo quy tắc nhân có 3.6 = 18 số tm yêu cầu bài toán. 0,5
+ Xét số A có 3 chữ số phân biệt và chữ số hàng trăm có thể là 0. Từ 3 A  24 4
số A ta lập được 12 cặp số có tổng là 333. Ví dụ 012 + 321 = 333.
Suy ra tổng các số A là 12.333 = 3996.
+ Xét số B có 3 chữ số phân biệt và chữ số hàng trăm là 0. Từ 0,25 2 A  6 3
số B ta lập được 3 cặp số có tổng là 44. Ví dụ 032 + 012 = 44.
Suy ra tổng các số B là 3.44 = 132.
Vậy tổng các số thỏa yêu cầu là 3996 – 132 = 3864. 2
b Một thầy giáo có 12 cuốn sách khác nhau, bao gồm 5 cuốn sách văn, 4
cuốn sách toán, 3 cuốn sách tiếng anh. Ông muốn lấy 6 cuốn để tặng
cho 6 học sinh, mỗi em một cuốn. Tính xác suất để sau khi thầy giáo 1,0
tặng xong, mỗi loại toán, văn, tiếng anh còn lại ít nhất 1 cuốn.
Ta thấy không thể chọn sao cho cùng hết 2 loại sách.
Chọn 6 cuốn sách bất kì tặng cho 6 học sinh có 6 0,25 A = 665280 cách. 12
Số cách chọn sao cho không còn sách văn: 1 1.C .6! = 5040 7
Số cách chọn sao cho không còn sách toán: 2 1.C .6! = 20160 0,25 8
Số cách chọn sao cho không còn sách tiếng anh: 3 1.C .6! = 60480 9 0,25
n( A) = 665280 − 5040 − 20160 − 60480 = 579600 P ( A) 579600 = = 0,8712 0,25 665280 2 c Tính tổng: 0,75 0 2015 1 2014 k 2015−k 2015 0 S = C C + C C ++ C C ++ C C 2016 2016 2016 2015 2016 2016−k 2016 1 Ta có: k −k 2016! 2015! 2015 C C = = 2016 ⋅ = 2016. k C 2016 2016−k k ( ! 2015 − k )! k ( ! 2015 − k ) 2015 ! 0,5
⇒ S = 2016.(C + C ++ C ) = 2016(1+ )2015 0 1 2015 2015 1 = 2016.2 0,25 2015 2015 2015 3 Cho đường tr 2 2
òn (C ) : ( x − 2) + ( y + 3) = 25. Tìm phương trình đường
tròn (C ') là ảnh của đường tròn (C ) qua phép vị tự tâm I (3; ) 1 tỉ số 1,00 k = 3 −
Đường tròn (C) có tâm A(2; 3
− ), bán kính R = 5 0,25
phép vị tự tâm I (3; ) 1 tỉ số k = 3
− biến điểm A thành A’. Tìm được 0,25 A'(7;13)
đường tròn (C ') là ảnh của đường tròn (C) qua phép vị tự tâm I (3; ) 1 tỉ số 0,25 k = 3
− có bán kính R' = 3 − .5 =15
Vậy pt đường tròn (C ) (x − )2 + ( y − )2 ' : 7 13 = 225 0,25 4 4
a Tìm giao điểm của SD với mặt phẳng (ABM) 1,0
AC ∩ BD = O 0,5
Trên (SAC) có: AM ∩ SO = I
Trên (SBD) có: BI ∩ SD = J Vậy 0,5
J là giao điểm của SD với mặt phẳng (ABM) 4
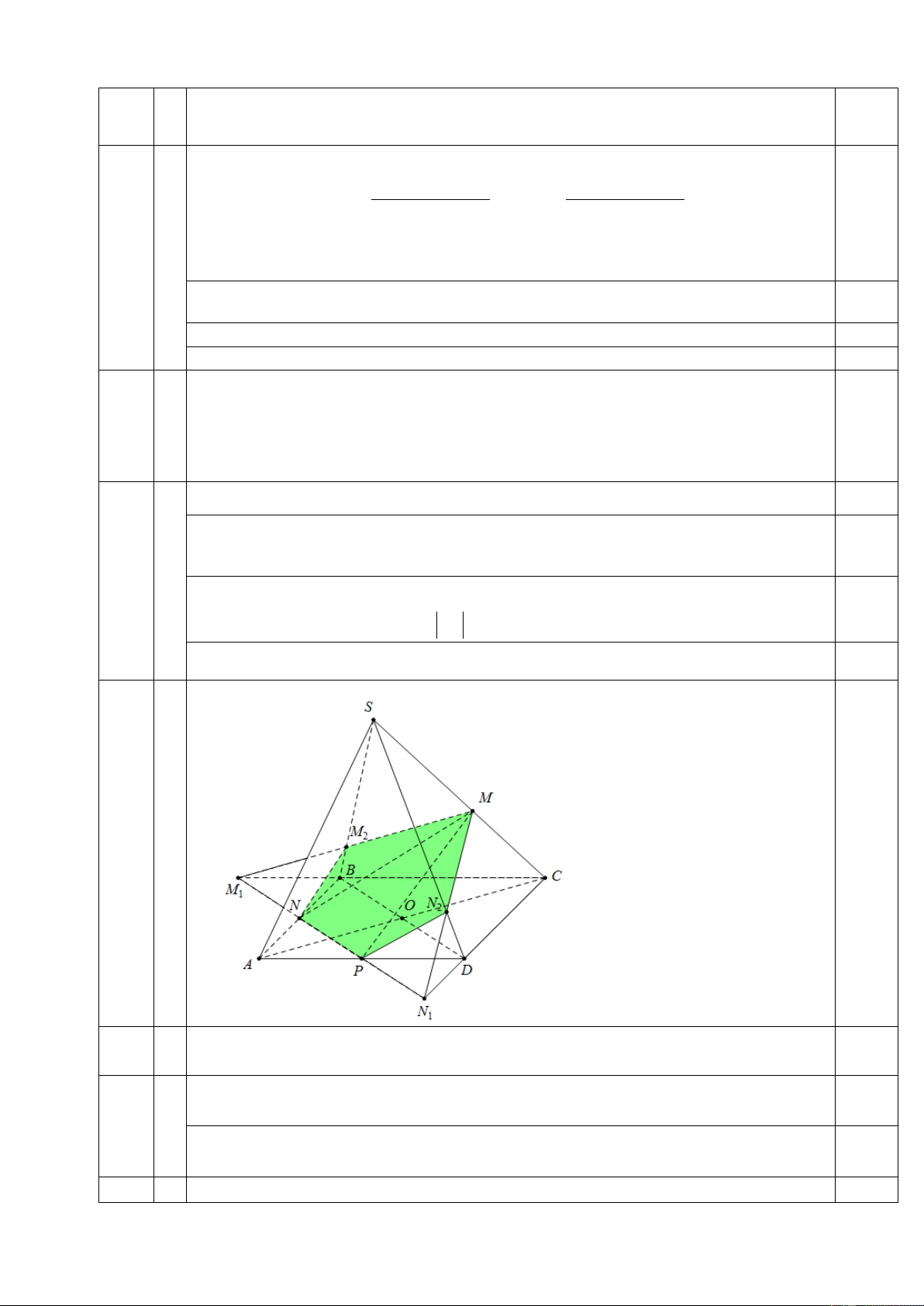
b Xác định thiết diện của hình chóp với mặt phẳng (MNP). 1,0
(MNP) ∩( ABCD) = NP 0,25
NP ∩ BC = M ; NP ∩ CD = N 1 1
(MNP) ∩(SCD) = MN ;MN ∩ SD = N 1 1 2
(MNP) ∩(SBC) = MM ;MM ∩ SB = M 1 1 2
(MNP) ∩(SAD) = PN ; MNP ∩ SAB = NM 2 ( ) ( ) 2
Vậy thiết diện là ngũ giác 0,25 MM NPN 2 2 5
Cho x, y, z > 0 thoả mãn xy + yz + zx = 1. Tính giá trị biểu thức: ( 2 1 + y )( 2 1 + z ) ( 2 1 + z )( 2 1 + x ) ( 2 1 + x )( 2 1 + y ) 1,00 S = x + y + z 2 2 2 1 + x 1 + y 1 + z ĐÆt π
x = tan α; y = tan β ; z = tan γ víi 0 < α; β ;γ < (*) 2
gt ⇒ tanα ⋅ tan β + tan β ⋅ tan γ + tan γ ⋅ tanα = 1
⇔ tanα (tan β + tanγ ) =1− tan β ⋅ tanγ 0,25 ⇔ (β + γ ) 1 π π tan =
= cotα ⇔ α + β + γ = + kπ ,do(*) ⇒ α + β + γ = tanα 2 2 ( 2 1 + y )( 2 1 + z ) cos2 α cosα sin α x = tanα = tanα = 2 1 + x cos2 β ⋅ cos2 γ cos β ⋅ cosγ cos β ⋅ cosγ 0,5 cos(β + γ ) β γ β γ cos ⋅ cos − sin ⋅ = = sin
= 1− tan β ⋅ tan γ = 1− yz cos β ⋅ cosγ cos β ⋅ cosγ
Tương tự ⇒ S = 1− yz +1− xz +1− xy = 3 −1 = . 2 0,25