Đề khảo sát chất lượng môn Toán lớp 10 trường chuyên Vĩnh Phúc lần 1

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KSCL CÁC MÔN THI THPT LẦN 1
Trường THPT Chuyên Vĩnh Phúc
NĂM HỌC 2016 -2017. Môn : TOÁN 10
(Đề thi gồm 01 trang)
Thời gian làm bài: 180 phút, không kể thời gian phát đề
Câu 1 (1,0 điểm). Cho 2 tập hợp: A   2
x  R | 2x  3x 1   0 và B   2
x  R | (2x 1)   1 Tìm A , B A , B A \ B
Câu 2 (1,0 điểm). Cho hàm số 3
y  f (x)  x  3x
a. Xét tính chẵn, lẻ của hàm số .
b. Xét tính đồng biến, nghịch biến của hàm số trên đoạn  1  ;  1
Câu 3 (1,0 điểm). Tìm tập xác định của các hàm số sau: x  1  2x a. y  x  2 x  1 b. y  1  x  1
Câu 4 (2,0 điểm). Cho hàm số y  ax2  bx  c có đồ thị (P), xác định các hệ số a, b, c trong các trường hợp sau:
a) (P) có đỉnh I ( 1  ; 4  ) và đi qua ( A 2;5)
b) Khảo sát vẽ đồ thị hàm số tìm được ở phần a)
Câu 5 (2,0 điểm). Cho hình bình hành ABCD . Trên cạnh AB,CD lần lượt lấy hai điểm M , N sao cho 6 3AM  A ,
B 2NC  CD . Gọi I là điểm trên cạnh BC thỏa mãn BI 
BC , G là trọng tâm 11 B  MN . a)
Biểu diễn các véctơ AN, AG theo AB và AD b) Chứng minh rằng ,
A G, I thẳng hàng.
Câu 6 ( 1 điểm) Cho hình chữ nhật ABCD có độ dài AB  3c ,
m AD  4cm . Lấy điểm M bất kì.
Tính độ dài các véctơ u  MA MB  MC  3MD và v  MA 3MB  4MC  2MD 2 2
2y(x  y )  3x
Câu 7 (1,0 điểm).Giải hệ phương trình:  2 2
x(x  y ) 10y
Câu 8 (1,0 điểm). Cho a,b là các số thực dương thỏa mãn:  2 2
2 a  b   ab  a  bab  2 . 2 2  a b   a b 
Tìm giá trị nhỏ nhất của biểu thức P    4  .     2 2  b a   b a 
.............HẾT............
Thí sinh không được sử dụng tài liệu. Cán bộ coi thi không giải thích gì thêm.
Họvà tên thí sinh ......................................................... ; Sốbáo danh....................................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
HƯỚNG DẪN CHẤM KHẢO SÁT CHẤT LƯỢNG
Trường THPT Chuyên Vĩnh Phúc LẦN 1
NĂM HỌC 2016 – 2017 (Đề có 01 trang) Môn :Toán 10 Câu ý Nội dung Điểm 1
Cho 2 tập hợp: A   2
x  R | 2x  3x  1   0 và B   2
x  R | (2x  1)   1 1.0 Tìm A , B A , B A \ B 1 
A   ;1 , B  0;  1 .  0.25 2 
A  B    1 0.25  1 
A  B  0; ;1 0,25  2  1 
A \ B    0,25 2  2
Xét tính chẵn, lẻ của hàm số 3
y  x  3x . 1.0
Tập xác định của hàm số là D  R . Với mọi xD , ta có x D 0.25 a f x 3
 x  3x   f (x) 0,25
suy ra f  x là hàm số lẻ.
b Xét tính đồng biến, nghịch biến của hàm số 3
y  x  3x trên đoạn  1  ;  1
Với mọi x , x  D  1  ;1 ta có: 1 2   3 3
f (x )  f (x )
x  x  3(x  x ) 0,25 1 2 1 2 1 2 2 2 T  
 x  x  x x  3 1 2 1 2 x  x x  x 1 2 1 2 Do x , x  1  ;1 nên 2 2
x  x  x x  3  T  0 1 2   1 2 1 2 0,25 Vậy hàm số 3
y  x  3x nghịch biến trên đoạn  1  ;  1 3 a x  1 2x
Tìm tập xác định của các hàm số sau: a. y  1.0 x  2 x  2  0 1
Hàm số xác định với những giá trị x thỏa mãn:   2   x  0,25 1   2x  0 2  1 
Vậy tập xác định của hàm số là: D  2;   0,25  2  b x  1 y  1  x  1 x 1  0 
Hàm số xác định với những giá trị x thỏa mãn:  x  1  x  1 0,25  0 1 x 1
Vậy tập xác định của hàm số là: D  1; 0,25 4
Cho hàm số y  ax2  bx  c có đồ thị (P). 2 a (P) có đỉnh I( 1  ; 4  ) và đi qua ( A 2;5) 1,0  b   1 
Từ giả thiết suy ra a, b, c thỏa mãn hệ 2a 
a  b  c  4 0,25
4a  2b  c  5   b  2a 
 3a  3b  9
c  4  a  b  a  1   b  2 0,25 c  3  Vậy (P): 2
y  x  2x  3 0,25 b
Khảo sát vẽ đồ thị hàm số 2
y  x  2x  3 1,0
Tập xác định D  R 0,25
Tọa độ đỉnh I( 1  ; 4  )
Trục đối xứng x  1 0,25
Hàm số nghịch biến trên khoảng ( ;  1
 ) , đồng biến trên khoảng ( 1  ; ;  ) Bảng biến thiên x  -1  y + ¥  0,25 -4
Đồ thị :Đồ thị hàm số 2
y = x + 2x - 3 là một Parabol có bề lõm quay lên trên , đồ thị cắt 0,25
Ox tại 1;0 và  3
 ;0, cắt Oy tại 0; 3   y f(x)=x*x+2x-3 6 5 4 3 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6 5
Cho hình bình hành ABCD. Trên cạnh AB,CD lần lượt lấy hai điểm M , N sao cho
3AM  AB, 2NC  CD . Gọi I là điểm trên cạnh BC thỏa mãn 6 BI 
BC , G là trọng tâm 11 1,0 B  MN . a B I C G M N D A A
Biểu diễn AN, AG theo AB và AD AN  AD  DN 0,25 1  AB  AD 0,25 2 1
AG   AB  AM  AN  0,25 3 1  1 1   11 1 AB  AB  AB  AD    AB  AD (1) 3  3 2  18 3 0,25 b Chứng minh rằng ,
A G, I thẳng hàng 1,0
AI  AB  BI 0,25 6 6  AB  BC  AB  AD (2) 0,25 11 11 11
Từ (1) và (2) suy ra AG  AI 0,25 18
 AG, AI cùng phương hay ,
A G, I thẳng hàng 0,25
Cho hình chữ nhật ABCD có độ dài AB  3c ,
m AD  4cm . M là điểm bất kì. Tính độ dài 1,0 6
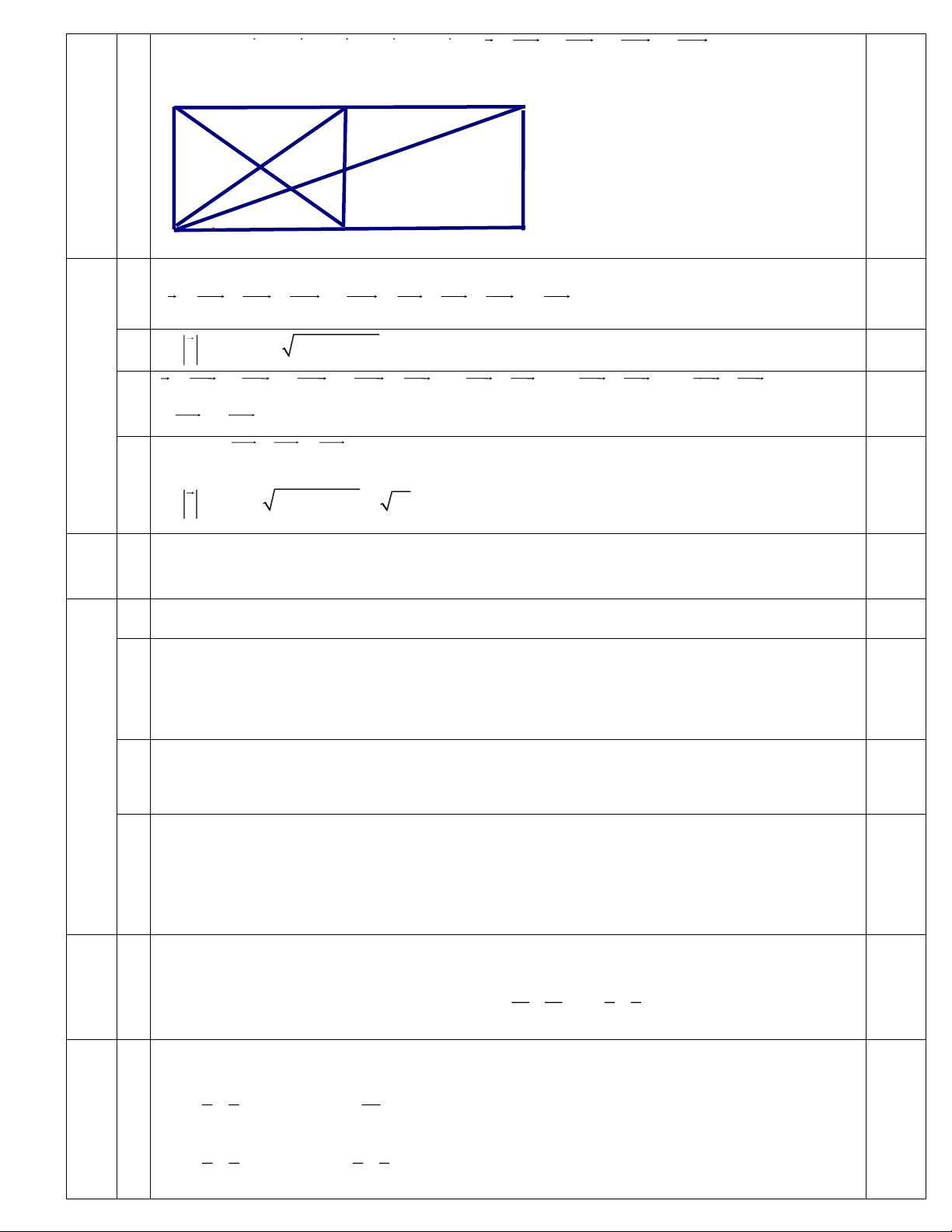
các véctơ u  MA MB  MC 3MD và v  MA 3MB  4MC  2MD B C F M. E A D 0,25
u  MA  MB  MC  3MD  DA  DB  DC  2DB 2 2
 u  2BD  2 AB  AD  10cm 0,25
v  MA  3MB  4MC  2MD  MA  3MA  AB  4MA AC  2MA AD 0,25  AB  2AD
 AB  AE  AF với AE  2AD  8(cm) 0,25 2 2
 v  AF  AB  AF  73(cm) 7 2 2
2y(x  y )  3x (1)
Giải hệ phương trình  . 1,0 2 2
x(x  y ) 10y (2)
Với x  0  y  0 (tm ) 0,25
Với x  0  y  0 . Từ (2)  xy  0 Hpt 2 2 2 2 2 2
 20y (x  y )  3x (x  y ) 0,25 4 2 2 4
 3x 17x y  20y  0 2 2 2 2
 (x  4y )(3x  5y )  0  0,25
x  2 y (Do xy  0 ) x  2y  x  2
Thay x  2 y vào hệ ta được 2 2
x  y  5   (thử lại tm)   y  1 0,25 x  0 
Vậy hệ đã cho có nghiệm: (2;1),(0;0).
Cho a, b là các số thực dương thỏa mãn:  2 2
2 a  b   ab  a  bab  2 . 8 2 2 1,0
Tìm giá trị nhỏ nhất của biểu thức  a b   a b  P      4  .   2 2  b a   b a 
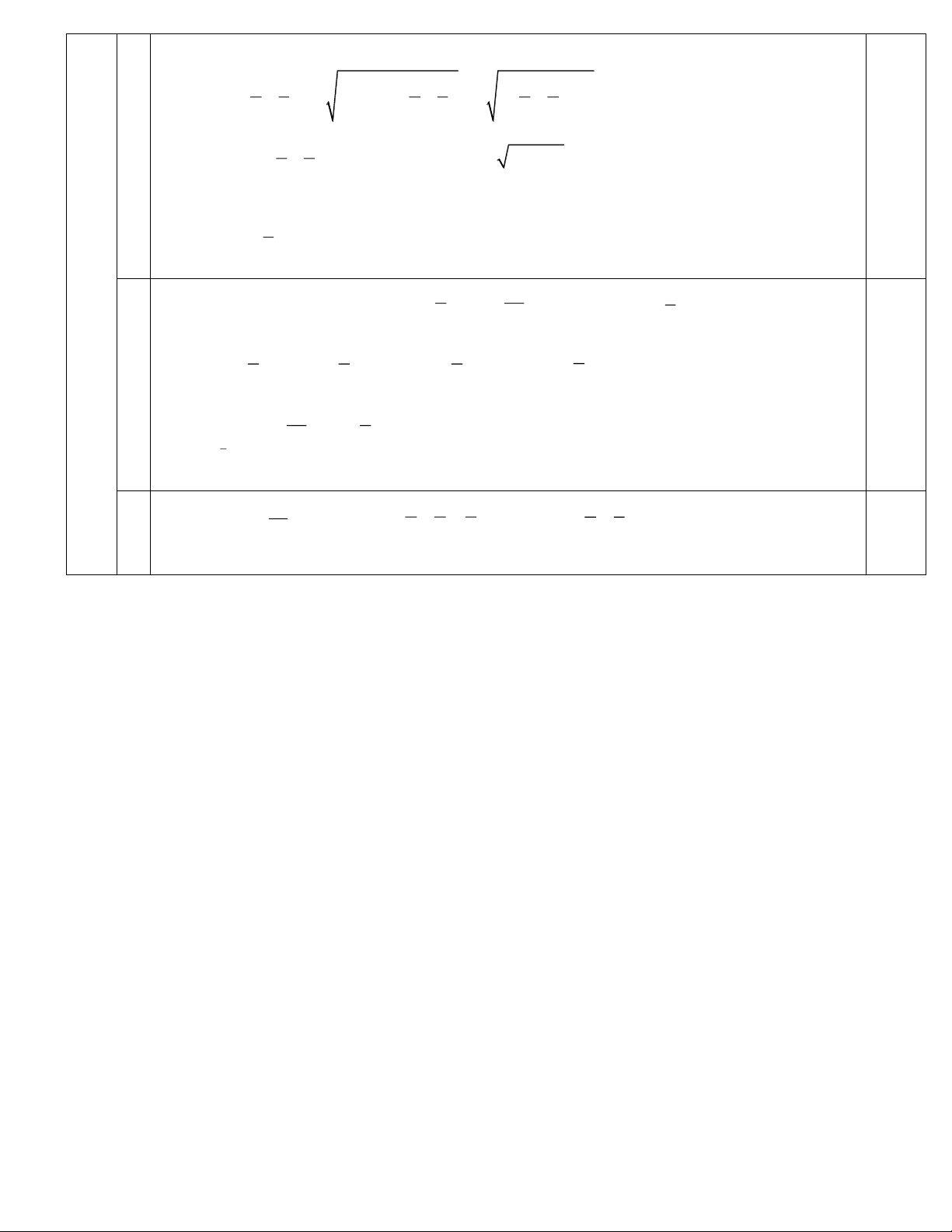
Với a, b dương, ta có:  2 2
2 a  b   ab  a  bab  2  a b      
  a  b 2 2 1 1      b a   ab  0,25  a b   1 1   2 
1  a  b  2       b a   a b 
Áp dụng bất đẳng thức Cauchy ta được  1 1   1 1   a b 
a  b  2   2 2  
a b   2 2   2      a b   a b   b a  Đặ a b t t 
 ,t  0 ta được: 2t 1 2 2(t  2) 0,25 b a 2
4t  4t 15  0  (2t  5)(2t  3)  0 1
 t  (Do t  0) 2 Khi đó 5
P  t  4t  2  t  22 1 23 2  6   6  
, dấu bằng khi t  4 4 2 5 1 5  t 
 t  2   t  22 1    ( Do : với mọi t ;   ) 2 2 4  2  0,25 23 5 suy ra min P    t  . 5  4 2 ;   2    Vậy 23 a b 1 1 min P   khi và chỉ khi 5
  và a  b  2    khi và chỉ khi 4 b a 2  a b  0,25
 ;ab  2; 1 ;ab  1;2 Lưu ý khi chấm bài:
-Đáp án chỉ trình bày một cách, nếu học sinh bỏ qua bước nào thì không cho điểm bước đó.
-Nếu học sinh giải cách khác, giám khảo căn cứ các ý trong đáp án để cho điểm.
-Trong bài làm, nếu ở một bước nào đó bị sai thì các phần sau có sử dụng kết quả sai đó không được điểm.
-Học sinh được sử dụng kết quả phần trước để làm phần sau.
-Điểm toàn bài tính đến 0,25 và không làm tròn.
----------------Hết----------------