












Preview text:
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 12 THANH HÓA
(LẦN 1) NĂM HỌC 2023 - 2024 ĐỀ CHÍNH THỨC Môn thi: TOÁN
Câu 1: Cho cấp số cộng (u với u = 4
− và công sai d = 3. Tính u . n ) 1 4 A. u = 1 − .
B. u = 5 .
C. u = 500 .
D. u = 500 − . 4 4 4 4 Lời giải Chọn B
Ta có u = u + 3d = 5. 4 1
Câu 2: Có bao nhiêu cách xếp 4 học sinh vào một bàn dài? A. 24 . B. 6 . C. 1. D. 4 . Lời giải Chọn A
Mỗi cách xếp là một hoán vị của bốn phần tử nên số cách xếp là 4!= 24.
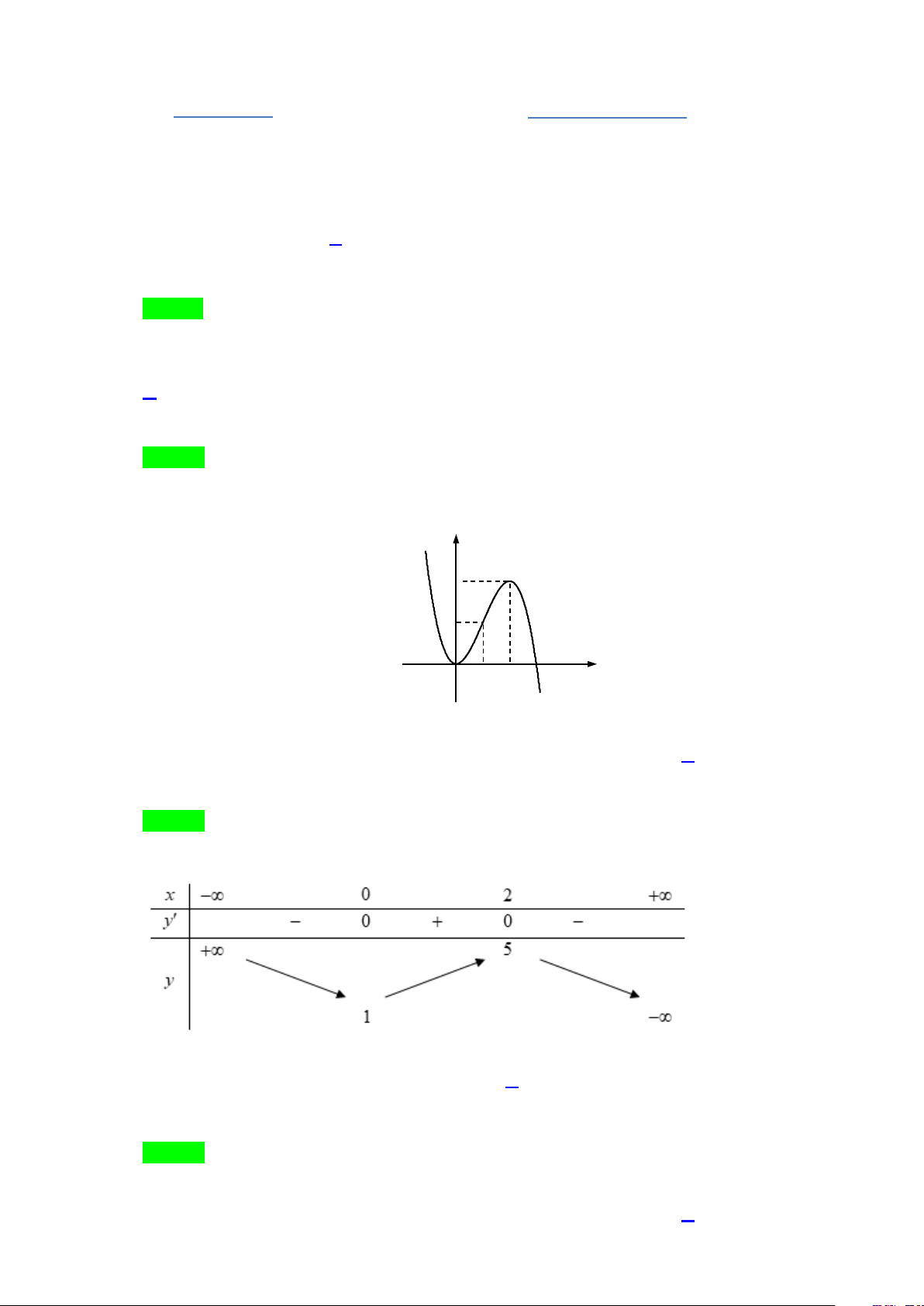
Câu 3: Cho hàm số y = f (x) có đồ thị như hình vẽ. y 4 2 O 1 2 3 x
Giá trị lớn nhất của hàm số trên đoạn [0;2] bằng A. 0 . B. 2 . C. 3. D. 4 . Lời giải Chọn D
Câu 4: Cho hàm số y = f (x) có bảng biến thiên như sau
Điểm cực tiểu của đồ thị hàm số là A. x = 0 .
B. x = 2 . C. (0; ) 1 . D. (2;5) . Lời giải Chọn C
Câu 5: Tìm giá trị lớn nhất M của hàm số 3
y = x + 3x trên đoạn [0;2].
A. M = 4 . B. M = 2 − .
C. M = 0 .
D. M =14 . Trang 1 Lời giải Chọn D Ta có 3 2
y = x + 3x ⇒ y ' = 3x + 3 > 0, x ∀ ∈ nên hàm số 3
y = x + 3x đồng biến trên tập số thực,
nên giá trị lớn nhất trên đoạn [0;2]bằng y(2) =14. Câu 6: − +
Tiệm cận đứng của đồ thị hàm số x 1 y =
là đường thẳng có phương trình : x + 2 A. y = 2 − . B. x = 1 − .
C. x = 2 . D. x = 2 − . Lời giải Chọn D Vì lim y = . +∞ x 2+ →−
Câu 7: Số giao điểm của đồ thị hàm số 2x + 2 y =
với trục hoành là x − 4 A. 1. B. 2. C. 0. D. 1. − Lời giải Chọn A + Với 2x 2 y = 0 ⇔ = 0 ⇔ x = 1.
− Nên đồ thị cắt trục hoành tại một điểm. x − 4
Câu 8: Đạo hàm của hàm số y = log x trên (0;+∞) là A. 1 y′ = . B. x y′ = . C. 1 y′ = . D. 1 y′ = . xln10 ln10 x x log e Lời giải Chọn A 1
y = log x ⇒ y ' = . x ln10
Câu 9: Nghiệm của phương trình x−2 3 = 9 là A. x = 1 − .
B. x = 4 . C. x =1.
D. x = 5. Lời giải Chọn B x−2 x−2 2
3 = 9 ⇔ 3 = 3 ⇔ x − 2 = 2 ⇔ x = 4.
Câu 10: Tập xác định của hàm số y (x ) 3 1 − = + là A. [ 1; − +∞). B. \{ } 1 − . C. ( 1; − +∞) . D. (0;+∞). Lời giải Chọn B
Điều kiện xác định của hàm số y (x ) 3 1 − = +
là x +1 ≠ 0 ⇔ x ≠ 1
− nên tập xác định là \{− } 1 .
Câu 11: Tìm tập nghiệm S của phương trình log ( 2 x −1 = 3 . 2 )
A. S = { } 3 .
B. S = {± } 3 .
C. S = {− } 3 .
D. S = { } 2 . Lời giải Chọn B Trang 2 log ( 2 x − ) 2 3 2
1 = 3 ⇔ x −1 = 2 ⇔ x = 9 ⇔ x = 3. ± 2
Câu 12: Cho hàm số f (x) 4 2
= 5x + 3x +1. Khẳng định nào dưới đây đúng? A. ∫ ( ) 5 3 f x dx x
= + x + x + C . B. f ∫ (x) 5 3
dx =20x +12x + x + C . C. ∫ ( ) 5 3 f x dx x 1 = + x + C . D. f ∫ (x) 5 3 2 dx x
= + x + x + C . 2 Lời giải Chọn A Ta có f
∫ (x)dx = ∫( 4 2 x + x + ) 5 3 5 3
1 dx = x + x + x + C. 3 3 3
Câu 13: Biết f
∫ (x)dx = 2; g
∫ (x)dx = 3. Tính ∫( f (x)+ g(x)) . dx 1 1 1 A. 6. B. 5. C. 4. D. 2. Lời giải Chọn B 3 3 3
Ta có ∫( f (x)+ g(x))dx = f
∫ (x)dx+ g
∫ (x)dx =2+3 = 5. 1 1 1
Câu 14: Cho hàm số f (x) 2x 1 x e + = +
. Khẳng định nào dưới đây đúng? 2 2x 1 + 2 A. ∫ ( ) x e f x dx = + + C . B. f ∫ (x) x 2x 1 dx e + = + + C . 2 2 2 C. ∫ ( ) 2 1 2 x f x dx e + = + C . D. f ∫ (x) 2 2x 1 dx x e + = + + C . Lời giải Chọn A x+ ∫ ( ) ∫( x+ = + ) 2 2 1 2 1 x e f x dx x e dx = + + C. 2 2
Câu 15: Cho hàm số y = f (x) xác định và liên tục trên đoạn [ ;
a b]. Thể tích vật thể tròn xoay được sinh
ra khi quay hình phẳng giới hạn bởi đồ thị hàm số y = f (x) , trục hoành và hai đường thẳng
x = a, x = b quanh trục hoành được tính theo công thức b b b a
A. V = f ∫ (x) dx . B. 2 V = π f
∫ (x)dx. C. 2 V = f
∫ (x)dx. D. 2 V = π f ∫ (x)dx. a a a b Lời giải Chọn B
Câu 16: Khối lăng trụ có thể tích bằng 12, diện tích đáy bằng 4 thì chiều cao của khối lăng trụ bằng A. 3. B. 9. C. 48 . D. 4 . Lời giải Chọn A Ta có = . V
V B h ⇒ h = = 3. B
Câu 17: Cho hình nón có bán kính đáy r = 8 và độ dài đường sinh l = 3 . Diện tích xung quanh của hình nón bằng: Trang 3 A. 24π . B. 192π . C. 48π . D. 64π . Lời giải Chọn A
Ta có S = rl π = π xq 24 .
Câu 18: Trong không gian Oxyz , cho mặt cầu có phương trình: (x − )2 + ( y − )2 + (z − )2 1 4 3 = 9. Tìm tọa
độ tâm I và bán kính r của mặt cầu.
A. I (1;4;3),r = 3.
B. I (1;4;3),r = 9. C. I ( 1 − ; 4 − ; 3
− ),r = 3. D. I ( 1 − ; 4 − ; 3 − ),r = 9. Lời giải Chọn A
Câu 19: Trong không gian Oxyz , cho hai điểm A(0;1;−1 ), B(2;3;5) . Tọa độ trung điểm M của đoạn thẳng AB là
A. M (1;2;2) .
B. M (1;2;− 2) .
C. M (2;2;6) .
D. M (2;4;4). Lời giải Chọn A x + x A B x = = M 1 2 Ta có y + y A B y = = M 2. 2 z + z A B z = = M 2 2
Câu 20: Tính diện tích toàn phần của khối bát diện đều có cạnh bằng 2. A. 4 3 . B. 8 3 . C. 16 3 . D. 3 . Lời giải Chọn B
Hình bát diện đều có tám mặt, mỗi mặt là một tam giác đều, vì mỗi cạnh bằng 2 nên diện tích một mặt là 2 3 2 .
= 3. Vậy diện tích toàn phần bằng 8 3. 4
Câu 21: Trong hộp có 4 viên bi xanh, 5 viên bi đỏ, 6 viên bi vàng. Lấy ngẫu nhiên từ hộp 3 viên bi. Số cách lấy là A. 9. B. 3 C . C. 3 A . D. 3 3 3
C + C + C . 15 15 4 5 6 Lời giải Chọn B
Tổng số bi trong hộp là 15 viên nên số cách lấy 3 viên từ hộp là 3 C . 15
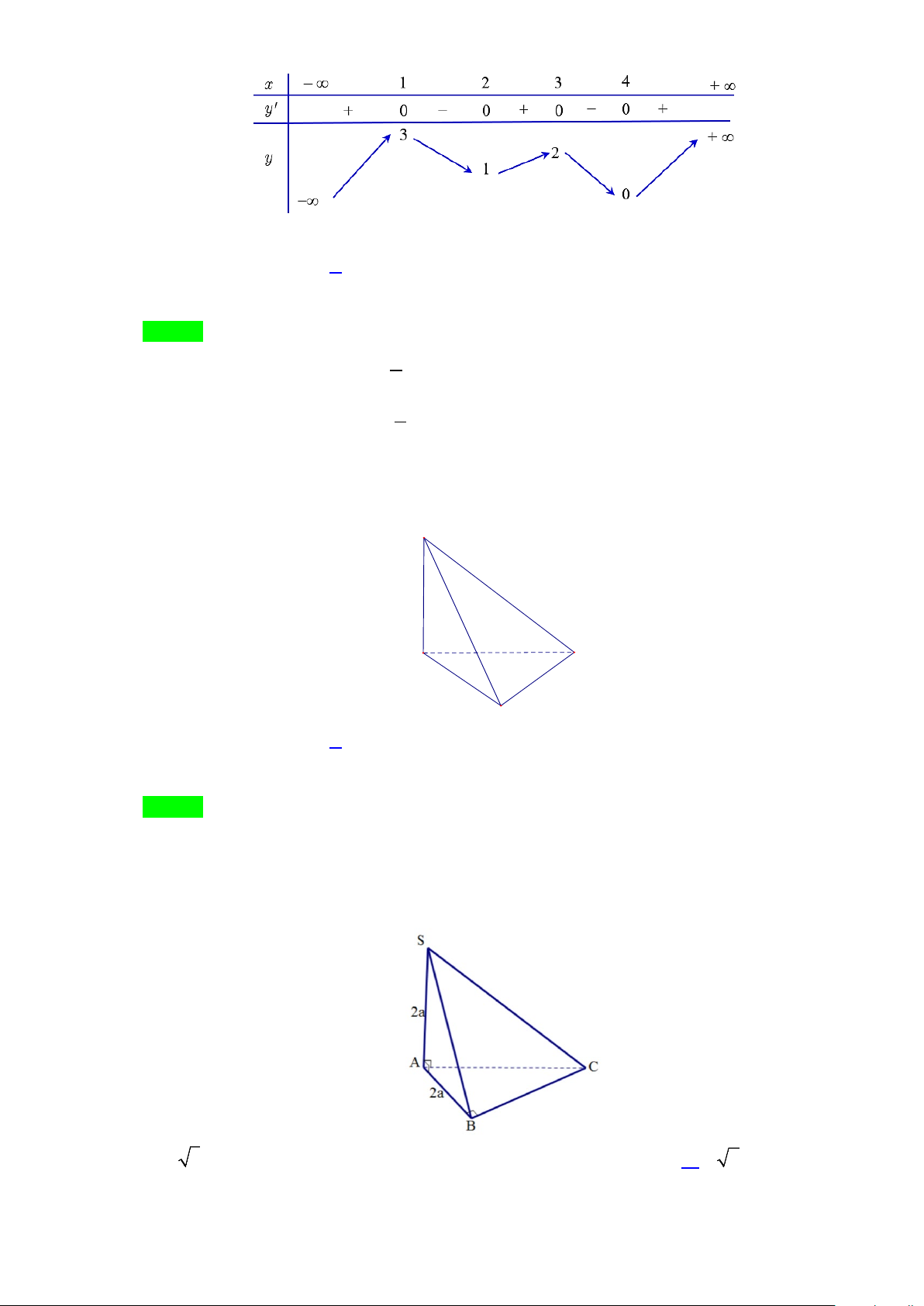
Câu 22: Cho hàm số y = f (x) liên tục trên và có bảng biến thiên như sau Trang 4
Số nghiệm của phương trình 2. f (x) −3 = 0 là A. 3. B. 5. C. 2. D. 4. Lời giải Chọn B
Ta có: f (x) − = ⇔ f (x) 3 2. 3 0
= nên số nghiệm của phương trình bằng số giao điểm của đồ 2
thị y = f (x) và đường thẳng 3 y = . 2
Câu 23: Cho hình chóp S.ABC có SA ⊥ ( ABC) ; tam giác ABC đều cạnh a và SA = a (tham khảo hình
vẽ). Tính góc giữa đường thẳng SC và mặt phẳng ( ABC). S A C B A. o 60 . B. o 45 . C. o 135 . D. o 90 . Lời giải Chọn B Ta có S
∆ AC vuông cân tại A , SC ( ABC) = 0 ; SCA = 45 .
Câu 24: Cho hình chóp S.ABC có SA ⊥ ( ABC) , SA = AB = 2a , tam giác ABC vuông tại B (tham khảo
hình vẽ). Khoảng cách từ A đến mặt phẳng (SBC) bằng A. a 3 . B. a . C. 2a . D. a 2 . Lời giải Trang 5 Chọn D
Gọi H là trung điểm của SB , do tam giác SAB cân tại A nên AH ⊥ SB , mặt khác theo giả thiết
BC ⊥ (SAB) ⇒ BC ⊥ AH suy ra AH ⊥ (SBC) ⇒ d ( ;
A (SBC)) = AH = a 2.
Câu 25: Biết rằng đường thẳng y = 2
− x + 2 cắt đồ thị hàm số 3
y = x + x + 2 tại điểm duy nhất; kí hiệu
(x ; y là tọa độ của điểm đó. Tìm (x + y ). 0 0 ) 0 0
A. x + y =1.
B. x + y = 3.
C. x + y = 2 .
D. x + y = 4 . 0 0 0 0 0 0 0 0 Lời giải Chọn C
Phương trình hoành độ giao điểm là: 3 3 x + x + 2 = 2
− x + 2 ⇔ x + 3x = 0 ⇔ x = 0 ⇒ y = 2 ⇒ x + y = 2. 0 0
Câu 26: Cho hàm số f (x) có đạo hàm f (x) = x( − x)2 ( − x)3 (x − )4 ' 1 3
2 với mọi x∈ . Điểm cực đại
của hàm số đã cho là
A. x = 2 .
B. x = 0 .
C. x = 3. D. x =1. Lời giải Chọn C x = 0 =
f (x) = x( − x)2 ( − x)3 (x − )4 ⇒ f (x) x 1 ' 1 3 2 ' = 0 ⇔ . x = 2 x = 3
Bảng xét dấu đạo hàm.
Suy ra hàm số f (x) đạt cực đại tại x = 3.
Câu 27: Gọi S là tập hợp các giá trị nguyên của tham số m để đồ thị 3
y = x − 3x cắt đường thẳng y = m
tại ba điểm phân biệt. Số phần tử của tập S bằng A. 4 . B. 2 . C. 5. D. 3 . Lời giải Chọn D x =1 Ta có 3 2
y = x − 3x ⇒ y ' = 3x − 3 = 0 ⇔ ⇒ y = 2, y = 2 −
. Để đường thẳng y = mcắt x = 1 CÐ CT − đồ thị 3
y = x − 3x thì y < m < y ⇔ − < m < , vì m nguyên nên m∈{ 1; − 0; } 1 . CT CÐ 2 2
Câu 28: Tính tổng tất cả các nghiệm nguyên của bất phương trình ( 2
log x + 2x + 3) ≤ log6. A. 5 − . B. 5 . C. 4 . D. 7 . Lời giải Chọn A Trang 6
x + x + ≤ log(x + 2x + 3) 2 2 3 6 2 2 ≤ log 6 ⇔
⇔ x + 2x − 3 ≤ 0 ⇔ 3
− ≤ x ≤1.Vậy tổng tất cả các 2
x + 2x + 3 > 0
nghiệm nguyên của x bằng: 3 − − 2 −1+ 0 +1 = 5. −
Câu 29: Tìm tập xác định D của hàm số y = ( 2
ln −x − 3x + 4).
A. D = ( ; −∞ 4 − ) ∪(1;+∞).
B. D = ( 4; − ) 1 . C. D = [ 4; − ] 1 .
D. D = ( 1; − 4). Lời giải Chọn B
Điều kiện xác định là 2
−x − 3x + 4 > 0 ⇔ 4
− < x <1.Vậy tập xác định D = ( 4; − ) 1 .
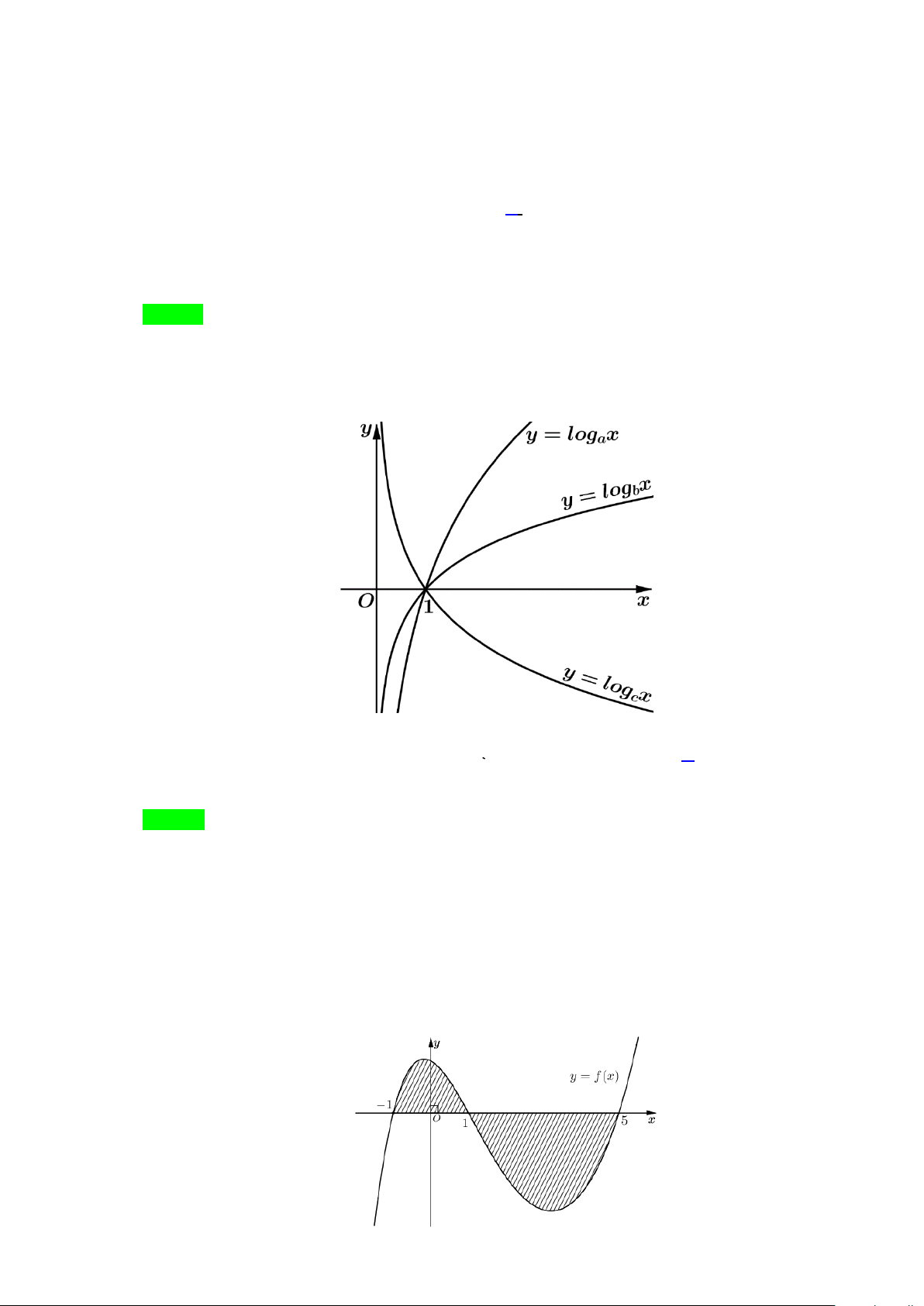
Câu 30: Cho a,b,c là các số thực dương khác 1. Hình vẽ bên là đồ thị của ba hàm số y = log x y = x y = x .
a , logb , logc
Khẳng định nào sau đây là đúng?
A. a < c < b .
B. a < b < c .
C. c < b < a .
D. c < a < b . Lời giải Chọn D
Nhìn đồ thị ta có y = log x y =
x là các hàm số đồng biến nên a >1;b >1 và hàm số a , logb lo
y = g x nghịch biến nên 0 < c <1. c
Kẻ đường thẳng y =1 trên cùng hệ trục đã cho thì đường thẳng y =1cắt đồ thị y = log x y =
x lần lượt tại các điểm có hoành độ là a,b , nhận thấy a < b ⇒ c < a < . b a , logb
Câu 31: Cho hàm số y = f (x) liên tục trên có đồ thị như hình vẽ dưới. Gọi S là diện tích hình phẳng
giới hạn bởi đồ thị y = f (x), trục hoành và các đường thẳng x = 1, − x = 5. Trang 7
Mệnh đề nào sau đây đúng? 1 5 1 5
A. S = − f (x)dx − f (x)dx ∫ ∫ .
B. S = f (x)dx + f (x)dx ∫ ∫ . 1 − 1 1 − 1 1 5 1 5
C. S = f (x)dx − f (x)dx ∫ ∫ .
D. S = − f (x)dx + f (x)dx ∫ ∫ . 1 − 1 1 − 1 Lời giải Chọn C 5 1 5 1 5 Ta có S = f
∫ (x)dx = f
∫ (x)dx+ f
∫ (x)dx = f
∫ (x)dx− f ∫ (x) . dx 1 − 1 − 1 1 − 1
Vì: f (x) ≥ 0, x ∀ ∈[ 1; − ]
1 ; f (x) ≤ 0, x ∀ ∈[1;5].
Câu 32: Biết F (x) x 2
= e + x là một nguyên hàm của hàm số f (x) trên . Khi đó f (2x)dx ∫ bằng A. 1 1 x 2
2e + 2x + C. B. 2x 2
e + x + C. C. 2x 2
e + 2x + C. D. 2x 2
e + 4x + C. 2 2 Lời giải Chọn C Ta có f ∫ ( x) 1 dx = f ∫ ( x) 1 d x = f ∫ (t) 1 2 2 (2 ) dt = ( t 2
e + t ) + C với t = 2 .x 2 2 2 Vậy f ∫ (2x) 1 2x 2
dx = e + 2x + C. 2 2 x
Câu 33: Hàm số f (x) = (t − ) 1 dt, x∈ ∫
có bao nhiêu điểm cực trị? 1 A. 1. B. 0 . C. 2 . D. 3. Lời giải Chọn D x = 0 2 x 4
Ta có f (x) ∫ (t ) x 2 1 1 dt x
f '(x) 2x( 2 x )1 0 = − = − + ⇒ =
− = ⇔ x =1 do 3 nghiệm này 2 2 1 x = 1 −
phân biệt nên hàm số đã cho có 3 điểm cực trị.
Câu 34: Trong không gian Oxyz , cho mặt cầu 2 2 2
x + y + z + 4x − 4y + 2z = 0.Biết rằng mặt cầu cắt mặt
phẳng (Oxy) theo giao tuyến là đường tròn tâm H. Tìm tọa độ điểm H. A. H ( 2; − 2;0). B. H ( 2; − 2;− ) 1 .
C. H (0;0;− ) 1 .
D. H (2; 2; − 0). Lời giải Chọn A
Ta có tâm mặt cầu là I ( 2; − 2;− )
1 nên H chính là hình chiếu của I trên (Oxy) , hay H ( 2; − 2;0).
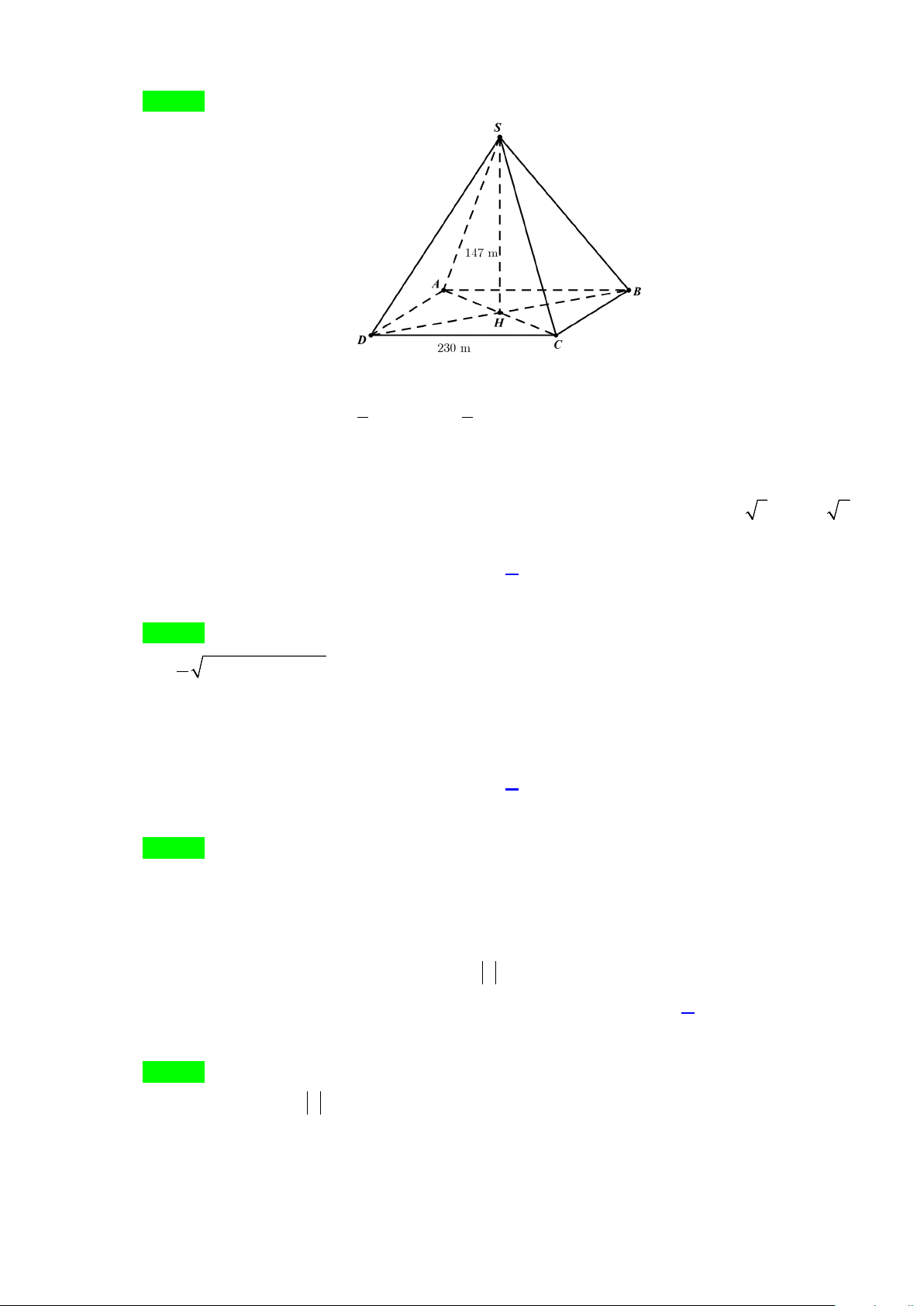
Câu 35: Kim tự tháp Kê - ốp ở Ai Cập được xây dựng vào khoảng 2500 năm trước Công nguyên. Kim tự
tháp này là một khối chóp tứ giác đều có chiều cao là 147 m , cạnh đáy là 230 m . Thể tích của nó là A. 3 2592100 m . B. 3 2952100 m . C. 3 2529100 m . D. 3 2591200 m . Trang 8 Lời giải Chọn A
Gọi khối chóp tứ giác đều là S.ABCD có đáy là hình vuông cạnh 230 m ; chiều cao SH =147 m. Thể tích của nó là: 1 1 V = S SH = = . S ABCD . ABCD. .( 2 230 .147 2592100 . ) 3 3
Vậy thể tích Kim tự tháp là 3 2592100 m .
Câu 36: Cho khối chóp S.ABC,có ,
SA SB, SC đôi một vuông góc nhau, SA = 2a, SB = a 5, SC = a 7.
Tính bán kính R của mặt cầu ngoại tiếp khối chóp S.ABC.
A. R = 4a .
B. R = a .
C. R = 2a .
D. R = 8a . Lời giải Chọn C 1 2 2 2 R =
SA + SB + SC = 2 . a 2
Câu 37: Trong không gian Oxyz , gọi S là tập các giá trị của m để điểm A( 2
1;2;m − 2m) nằm trên mặt
phẳng (Oxy).Số phần tử của tập S là A. 1. B. 0 . C. 2 . D. 3. Lời giải Chọn C = A( m 0 2
1;2;m − 2m)∈(Oxy) 2
⇔ z = ⇔ m − m = ⇔ A 0 2 0 . m = 2
Câu 38: Cho hàm số y = f (x) có đạo hàm f (x) 2 2 '
= x − 2x + m − m , x
∀ ∈ . Có tất cả bao nhiêu giá trị
nguyên của tham số m để hàm số g (x) = f ( x ) có 5 điểm cực trị? A. 3. B. 2. C. 1. D. 0. Lời giải Chọn D
Để hàm số g (x) = f ( x ) có 5 điểm cực trị thì hàm số y = f (x) có 2 cực trị dương, hay phương trình f (x) 2 2 '
= x − 2x + m − m = 0 có hai nghiệm dương phân biệt, điều kiện cần và đủ là: Trang 9 2
∆ = m − m +1 > 0
x + x = 2 > 0 ⇔ 0 < m <1. 1 2 2
x .x = m − m > 0 1 2
Vậy không có giá trị nguyên của tham số m thỏa mãn yêu cầu bài toán.
Câu 39: Cho hàm số ( ) = ( 2 ln + ) 1 + 3 m f x x x x + .
Gọi S là tập hợp tất cả các giá trị nguyên của tham x
số m với 0 < m < 68 sao cho hàm số f (x) nghịch biến trên khoảng (0; 2). Có tất cả bao nhiêu
phần tử thuộc S ? A. 50. B. 49 . C. 48 . D. 47 . Lời giải Chọn A
Tập xác định của hàm số f (x) là D = (0; + ∞) . 2 ′( ) 3x +1 m f x = + − . x( 3 2 x + ) 2 1 x
Hàm số f (x) nghịch biến trên khoảng (0; 2) khi và chỉ khi f ′(x) ≤ 0, x ∀ ∈(0; 2) (do phương trình f ′(x) = 0
tại hữu hạn nghiệm thuộc khoảng (0; 2)) 2 3 3x +1 m 3x + x 2 ⇔ + ≤ ⇔ + ≤ ( ) 1 , x ∀ ∈(0; 2). x( 3 3x m 2 x + ) 2 2 1 x x +1 3 4 2 + +
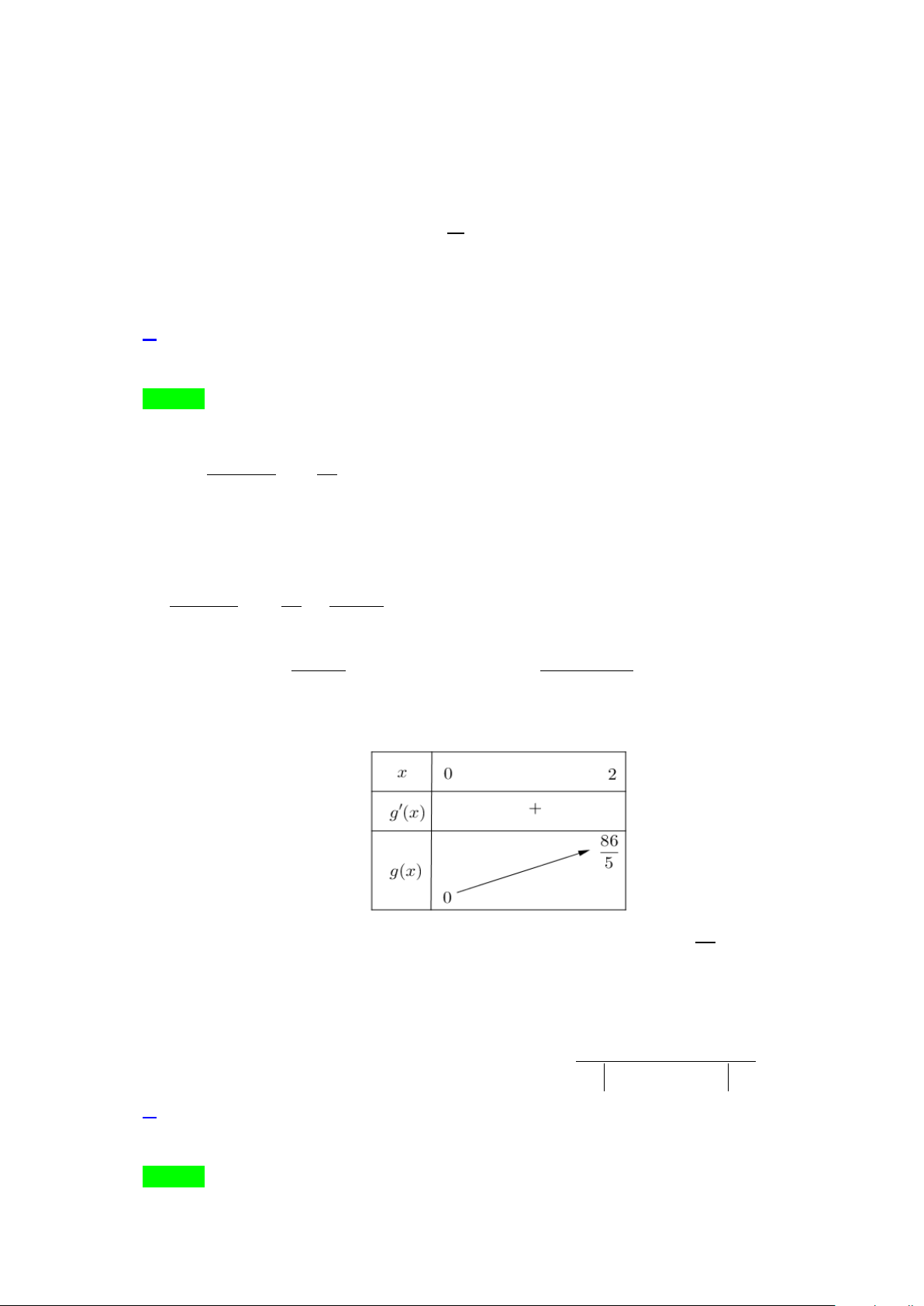
Xét hàm số g (x) 3x + x 2 3x 8x 1 =
+ 3x , x ∈ 0; 2 . g′(x) = + 6x > 0, x ∀ ∈ 0; 2 . 2 ( ) 2 ( ) x +1 ( 2x + )1
Ta có bảng biến thiên của hàm số g (x)
Từ bảng biến thiên ta thấy ( )
1 đúng với mọi x∈(0;2) khi và chỉ khi 86 m ≥ . 5
Do m∈(0; 68) và m là số nguyên nên m∈ S = {18;19;...; } 67 .
Vậy số phần tử thuộc S là 50.
log ( 3x − log (2x) +13 2 ) 2
Câu 40: Tính tổng tất cả các nghiệm nguyên của bất phương trình 2 ≥ 0. 3 2
x − 4x + 5x − 2 A. 133. B. 136. C. 153. D. 135. Lời giải Chọn A Trang 10 x > 0 x > 0 Điều kiện ⇔ . 3 2
x 4x + 5x − 2 ≠ 0 −
x ≠ 1; x ≠ 2 3
log x − log (2x) +13 2 ( ) 2
Với điều kiện suy ra bất phương trình: 2 ≥ 0 3 2
x − 4x + 5x − 2 ⇔ x − ( + x)2 + ≥ ⇔ −( x)2 1 3log 1 log 13 0 log + log x +12 ≥ 0 ⇔ 3
− ≤ log x ≤ 4 ⇔ ≤ x ≤16 2 2 2 2 2 8 (thoả mãn).
Với điều kiện trên và x∈ ⇒ x∈{3;4;5; ; … 16}.
Do đó tổng các nghiệm nguyên của bất phương trình là 3+ 4 + 5 +…+16 =133. 4 x Câu 41: Biết 1 x + e +
dx = a + eb − ec ∫
với a,b,c là các số nguyên. Tính T = a − b − .c 2 4 x x 1 xe A. T = 3. −
B. T = 3.
C. T = 6. D. T = 5. − Lời giải Chọn C 2 x Vì 1 x + e 1 1 + = + nên 2 4x xe x 2 x ex 4 1 x + ex 4 1 1 + dx ∫ = + ∫ dx ( e x x − = − )4 1 − 4 1 e e− = + − . 2 4 x x 2 x ex 1 xe 1 1
Suy ra a =1, b = 1 − , c = 4 − . Vậy T = 6 .
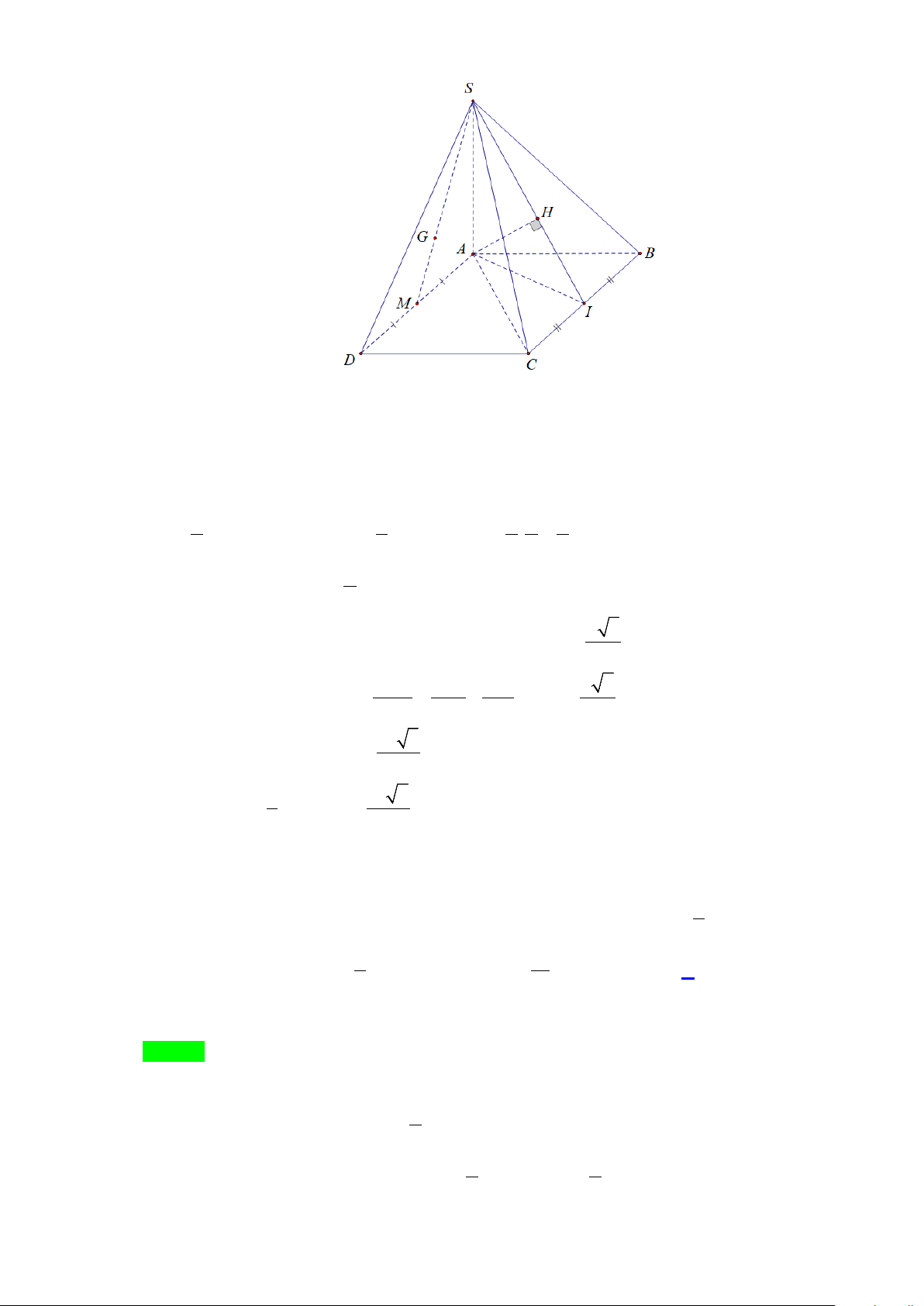
Câu 42: Cho hình chóp S.ABCD có đáy là hình thoi cạnh a , góc 0
ABC = 60 và SA vuông góc với mặt
phẳng đáy. Gọi G là trọng tâm tam giác SAD . Biết khoảng cách từ G đến mặt phẳng (SBC)
bằng a . Thể tích khối chóp S.ABCD là 3 3 3 3 3 A. a 2 . B. a 2 . C. a 3 . D. a 3 . 8 6 18 12 Lời giải Chọn A Trang 11
Gọi I, H lần lượt là hình chiếu vuông góc của A lên BC và SI , ta có BC ⊥ SA
BC ⊥ (SAI ) AH ⊥ BC ⇒ ⇒
⇒ AH ⊥ (SBC) ⇒ d ( ,
A (SBC)) = AH ( ) BC ⊥ AI AH ⊂ (SAI ) 1 AH ⊥ SI
Gọi M là trung điểm AD, G là trọng tâm S ∆ AD , ta có: 3 = ⇒ ( ( )) 3 = ( ( )) 3 , , = . a a MS GS d M SBC d G SBC = = d ( ,
A (SBC)) (2) (do AD (SBC)) 2 2 2 3 2 Từ (1) và (2) suy ra a AH = . 2
Mặt khác tam giác ABC là tam giác đều cạnh a nên a 3 AI = 2
Trong tam giác vuông SAI có 1 1 1 a 6 = + ⇒ SA = . 2 2 2 AH AS AI 4 2 Diện tích đáy a 3 S = S = . ABCD 2. ABC 2 3 Suy ra 1 a 2 V = SA S = . S ABCD . . . 3 ABCD 8
Câu 43: Trong không gian Oxyz , cho A(1; 2 ; 0) ; B(3; −1; 2) ; C (1; 2 ; 2); D(3; −1; ) 1 và điểm M 1
∈(Oxy) . Tìm giá trị lớn nhất của biểu thức 2 2 2 4
T = MA + 2MB − MC − MD . 4 A. 1. B. 7 . C. 15 . D. 6 . 4 4 Lời giải Chọn D +) Gọi I (x y
là điểm thỏa mãn IA + 2IB − IC = 0 ⇔ I (3; −1; )
1 . Suy ra I ≡ D .
I ; I ; zI ) +) Ta có 2 2 2 1 4
T = MA + 2MB − MC − MD 4
= (MI + IA)2 + 2(MI + IB)2 −(MI + IC)2 1 4 − MI = 2 1 4 2MI − MI + ( 2 2 2
IA + 2IB − IC ). 4 4 Trang 12 +) IA = ( 2 − ; 3 ; − ) 1 ; IB = (0 ; 0 ; ) 1 ; IC = ( 2 − ; 3 ; ) 1 . Suy ra 2 2 2
IA + 2IB − IC =14 + 2 −14 = 2 ) Đặt 2 1 MI = x . Ta có 2
T = 2x − x + 2. 4
+) Gọi H là hình chiếu của I trên (Oxy) . Ta có MI ≥ IH =1, M ∀ ∈(Oxy) . +) Xét hàm số 1 2
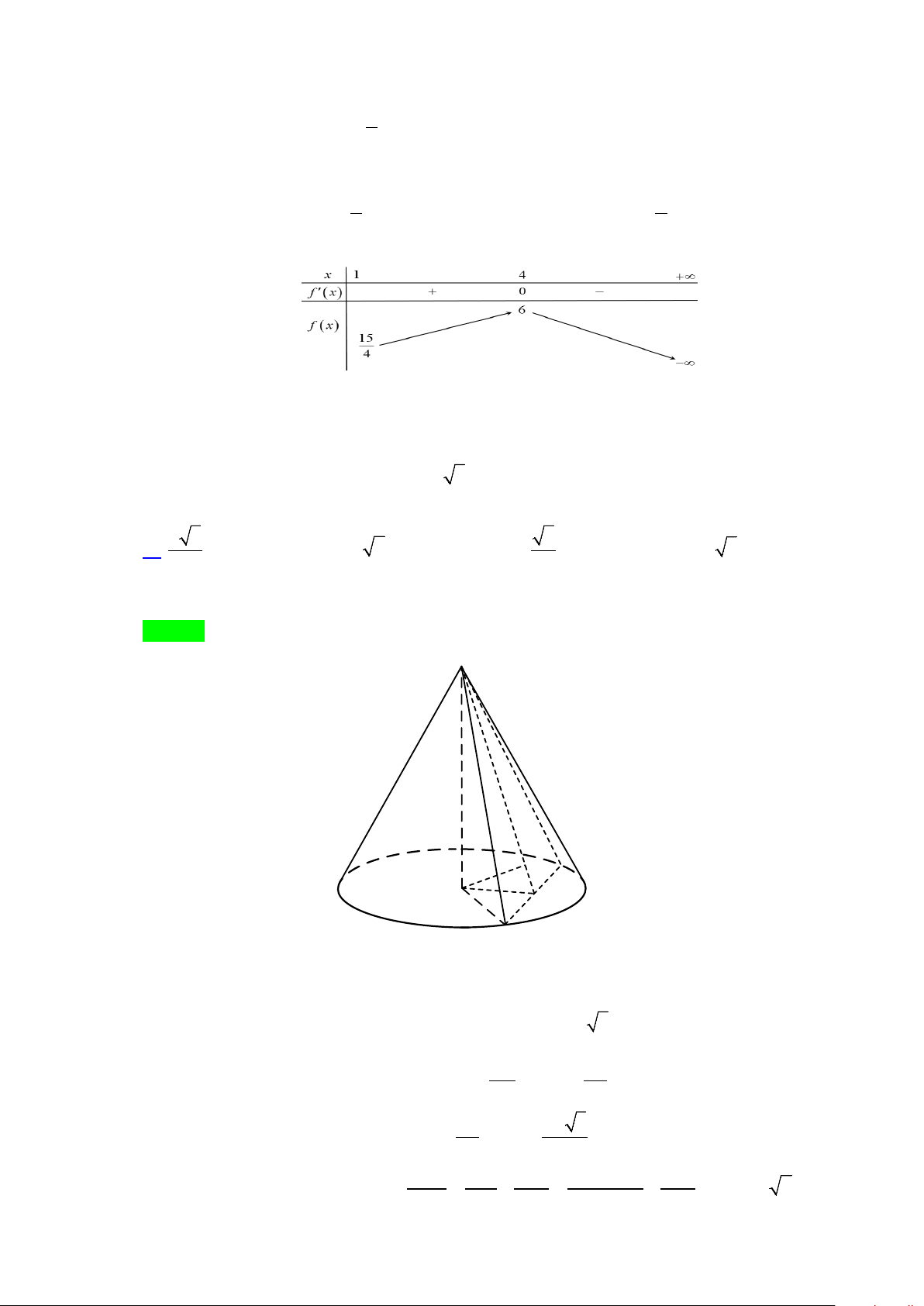
y = f (x) = − x + 2x + 2, với x∈[1; + ∞) . 1
f '(x) = − x + 2 ; f '(x) = 0 ⇔ x = 4 4 2 Bảng biến thiên:
Vậy maxT = 6 , khi x = 4 , hay MI = 2 và M ∈(Oxy) .
Câu 44: Cho hình nón đỉnh S , đường cao SO , A và B là hai điểm thuộc đường tròn đáy sao cho khoảng
cách từ O đến mặt phẳng (SAB) bằng 3 và 0 = 0
SAO 30 , SAB = 60 . Diện tích tam giác SAB bằng: A. 9 3 . B. 3 2 . C. 3 . D. 3 5 . 2 2 Lời giải Chọn A S H B O I A
Gọi I là trung điểm của AB ⇒ OI ⊥ AB .
Gọi H là hình chiếu của O lên SI ⇒ OH ⊥ SI . OI ⊥ AB Ta có:
⇒ OH ⊥ (SAB) ⇒ d ( ;
O (SAB)) = OH = 3 OS ⊥ AB
Xét tam giác SAO vuông tại O có: sin SO SA SAO = ⇒ SO = SA 2 Xét tam giác SI SA
SAI vuông I có: 3 sin SAI = ⇒ SI = SA 2 Xét tam giác 1 1 1 1 1
SOI vuông tại O có: = + = + ⇒ SA = 3 2 2 2 2 2 2 2 OH OI OS SI − SO OS Trang 13 2 Diện tích tam giác đều SA . 3 9 3 SAB là: S = = . ABC 4 2
Câu 45: Cho hai hàm số f (x), g (x) có đạo hàm trên tập số thực và thỏa mãn ln 4 f (x) 2
− 4x +12x +1 + f (x) 2 − x + 3x = 0 , x
∀ ∈ . Tìm tổng tất cả các giá trị nguyên g ( x) 3 2
= x − x + f (x) + log m
dương của tham số m để phương trình: g(3.g(x)) + 8g (x) = 3x có 3 nghiệm phân biệt? A. 24090 . B. 23871. C. 24310 . D. 24531. Lời giải Chọn C
Viết lại giả thiết thứ nhất: { f (x) 2
− x + x + } + f (x) 2 ln 4 3 1 − x + 3x = 0 Nếu f (x) 2
− x + 3x > 0 thì vế trái dương nên không thỏa mãn Nếu f (x) 2
− x + 3x < 0 thì vế trái âm nên không thỏa mãn Nếu f (x) 2
− x + 3x = 0 thì vế trái bằng không nên thỏa mãn
Vậy từ giả thiết thứ nhất ta tìm được f (x) 2 = x − 3 . x Với f (x) 2
= x − x ⇒ g (x) 3 3 + 3x = x + log . m Xét hàm số 3 2
y = x + log m ⇒ y ' = 3x ≥ 0, x ∀ ∈ .
Hay hàm số y = g (x) + 3x đồng biến trên tập số thực. Ta có:
g g x + g (x) = x ⇔ g ( g (x)) + g (x) = g (x) + x ⇔ g (x) = x ⇔ ( 3 (3 ( )) 8 3 3 3.3 3 3
3 x − 3x + log m) = .x 3
⇔ 3x −10x = 3 − log ,
m xét hàm h(x) 3
= 3x −10x, để phương trình có 3 nghiệm phân biệt thì
điều kiện cần và đủ là: h < −
m < h ⇔ ≤ m ≤ vì * m∈ N . CT 3log CÐ 1 220,
Ta có 1+ 2 + 3+...+ 220 = 24310.
Vậy tổng các giá trị của tham số cần tìm là 24310.
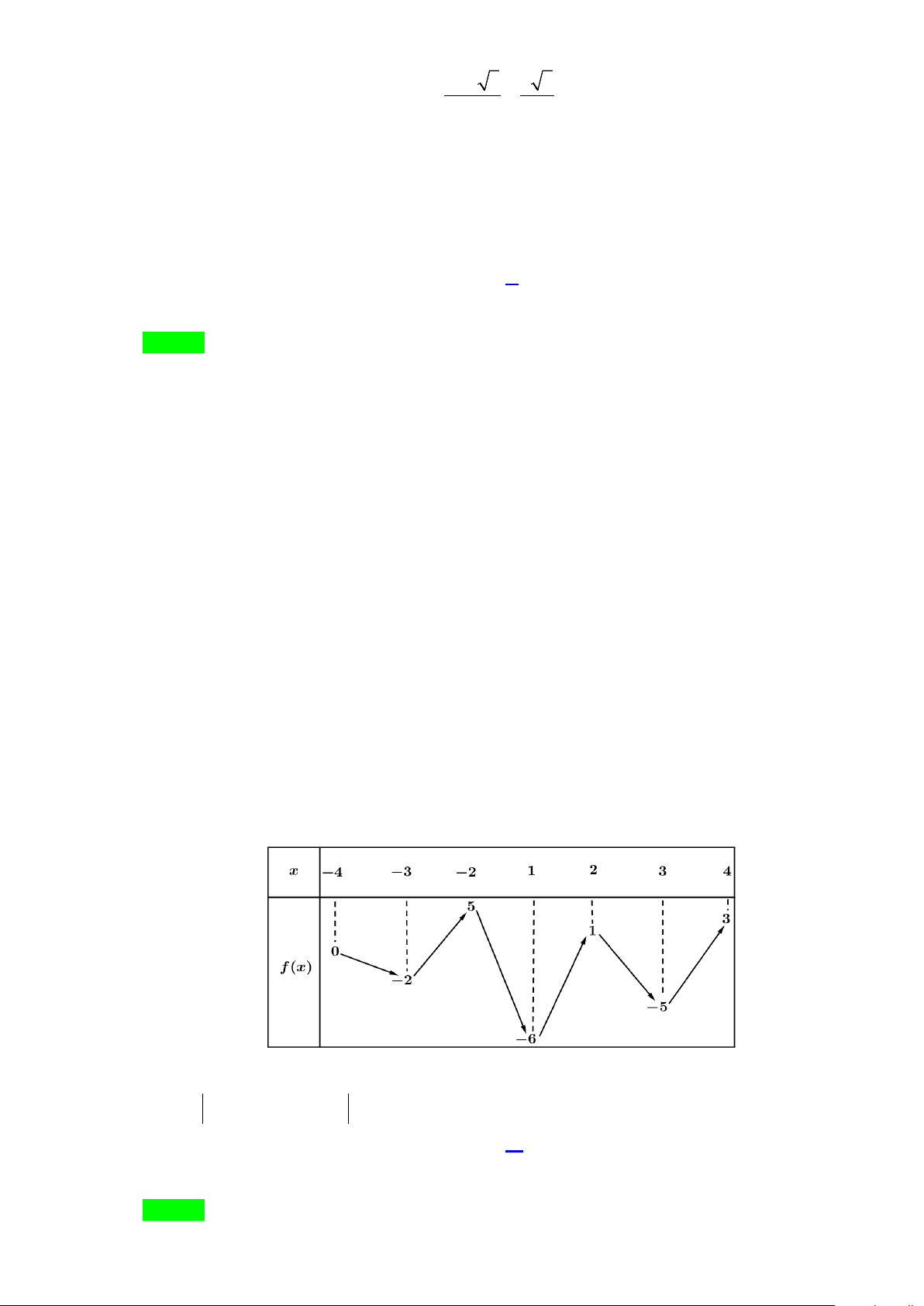
Câu 46: Cho hàm số y = f (x) liên tục trên đoạn [ 4;
− 4] và có bảng biến thiên như hình vẽ bên dưới
Có tất cả bao nhiêu giá trị thực của tham số m thuộc đoạn [ 4; − 4] để hàm số
g (x) = f ( 3
x + 2x) + f (m) có giá trị lớn nhất trên đoạn [ 1; − ] 1 bằng 8 ? A. 10. B. 9. C. 8 . D. 7 . Lời giải Chọn C Trang 14 Đặt 3 2
t = x + 2x ⇒ t′ = 3x + 2 > 0 x ∀ ∈ . Hàm số 3
t = x + 2x luôn đồng biến trên . Do đó x ∈[ 1; − ] 1 ⇒ t ∈[ 3 − ; ] 3 f ( 3
x + 2x) = f (t) với t ∈[ 3 − ; ] 3 .
Ta có max[ f (t) + f (m)] = 5 + f (m); min [ f (t) + f (m)] = 6 − + f (m) t [ ∈ 3 − ; ] 3 t [ ∈ 3 − ; ] 3 5 + f (m) = 8 6 − + f (m) ≥ 8 − f (m) = Nên g (x) =
f (t) + f (m) 3 max max = 8 ⇔ ⇔ x [ ∈ 1 − ] ;1 t [ ∈ 3 − ; ] 3 5 + f (m) ≤ 8 f (m) = 2 − 6 − + f (m) = 8 −
Dựa vào bảng biến thiên với m∈[ 4; − 4] ta có:
Với f (m) = 3 phương trình có 3 nghiệm. Với f (m) = 2
− phương trình có 5 nghiệm.
Vậy có tất cả 8 giá trị của m thoả mãn. 2 x y 1 + 2
2 − 4 = 2y + 2 − x
Câu 47: Cho hệ phương trình 3
4x + 2(2y + 2) = ( 4 x + ) 4
1 x +16(2y + 2) +8x +1
Biết hệ có một nghiệm (x ; y , x a b c 2 > 0, với x + − + = trong đó a,b, 0 0 ) 0 0 c là các số 2
nguyên dương. Khi đó giá trị của N = b + c − a bằng A. 4 . B. 2 . C. 6 . D. 8 . Lời giải Chọn A 2 2 x y 1 + 2 x 2 2 y+2 2
2 − 4 = 2y + 2 − x ⇔ 2 + x = 2
+ (2y + 2) ⇔ x = 2y + 2. Thế 2
x = 2y + 2 vào phương trình còn lại ta được phương trình: 2 x ( x + ) 2 4 4
4 1 + x = x +1. x + (4x + )2 1 ( ) 1 . u = ( 2x ) ;1 Đặt 2 2 4 4 2 ⇒ = + + = + + + v = ( .
u v x 4x 1 x ; u . v x 1. x 4x 1 . 2 4x +1; x ) ( ) ( ) Mà ta luôn có: 2
u v ≤ u v ⇒ x ( x + ) 2 4 4 .
4 1 + x ≤ x +1. x + (4x + )2 1 (2) Trang 15
Từ (1) và (2) suy ra u và v cùng hướng hay: x 1
x + 2x +1+ 2 = 0 VN 4 =
⇒ x − 4x −1 = 0 ⇔ ( 2
x +1 = 2 x +1 ⇔ 2 ) 2 2 2 ( )2 ( ) + 2 4x 1 x
x − 2x +1− 2 = 0
Từ đây ta tìm được nghiệm dương là 2 + 2 − + 4 2 x =
⇒ a = b = 2;c = 4. 2
Vậy N = c + b − a = 4.
Câu 48: Cho hai số thực dương a , 1 1 b thỏa mãn log a = log
. Giá trị nhỏ nhất của biểu thức 2024 2024 2 b 2
P = 4a + b − 3log ( 2
4a + b được viết dưới dạng x − y log z , với 3 ) 3
x, y, z là các số nguyên
dương lớn hơn 2. Khi đó, tổng 2
(x + 2y + z) có giá trị bằng A. 225 . B. 144. C. 196. D. 121. Lời giải Chọn C Ta có: 1 1 1 1 1 log a = log ⇔ log a = 2log ⇔ log a = log ⇔ a = . 2024 2024 2024 2024 2024 2024 2 2 2 b b b b Đặt 2 4 4
t = 4a + b . Áp dụng bất đẳng thức AM – GM ta có: 2 2 2
t = 4a + b = + b ≥ 2 .b = 4 . 2 2 b b
Đẳng thức xảy ra khi b = 2 và 1 a = . 2 Khi đó: 2
P = 4a + b − 3log ( 2
4a + b = t − 3log t , với t ≥ 4 . 3 ) 3
Xét hàm số: f (t) = t −3log t liên tục trên nửa khoảng [4;+∞) . 3 Có f ′(t) 3 t ln 3− 3 =1− = > 0 , t ∀ > 4 t ln 3 t ln 3
Suy ra hàm số f (t) đồng biến trên [4;+∞) .
⇒ P = f (t) ≥ f (4) = 4 − 3log 4 . Suy ra: P = 4 − 3log 4 khi 1 a = và . 3 min 3 b = 2 2 Vậy 2
x = 4; y = 3; z = 4 ⇒ (x + 2y + z) =196 .
Câu 49: Cho hàm số f (x) có đạo hàm trên tập số thực và thỏa mãn f (x) 2 f (x) 8 6 4 2 ' 3
+1 = 9x + 21x +15x + 6x +1, x ∀ ∈ , f (0) = 0. Tính 1 f (x) 2023 − f x x x ∫ + e + e f x + . dx 4 ( ) 2 ( ) ( ) + + − x 1 x e 1 1 A. 92 . B. 73 . C. 77 . D. 0. 105 105 105 Lời giải Chọn A Ta có f (x) 2 f (x) 8 6 4 2 ' 3
+1 = 9x + 21x +15x + 6x +1,
lấy nguyên hàm hai vế kết hợp với điều
kiện f (0) = 0 ta được f (x) + f (x) = (x + x)3 3 3 + ( 3
x + x) ⇒ f (x) 3 = x + . x Trang 16 a
Ta chứng minh được nếu f (x) là hàm số lẻ thì f
∫ (x)dx = 0và nếu f (x)là hàm số chẵn thì −a a f (x) a dx = f x dx ∫ x ∫ ( ) . + − e 1 a 0 f (x) 2023 Với ( ) 3
f x = x + x suy ra các hàm số y = ; x − x y = e + e
f x là các hàm số lẻ còn 4 ( ) ( ) x + 1 hàm số 2
y = f (x) là hàm số chẵn. Khi đó: 1 f (x) 2023 − f x x x ∫ + e + e f x + dx 4 ( ) 2 ( ) ( ) + + − x 1 x e 1 1 . 1 f (x) 2023 1 = ∫ dx + ∫ ( − f x f x x x e + e ) 1 2 1 2 1 f (x) ( ) ( ) dx + dx =
dx = x + x dx = ∫ x ∫ x ∫( )2 3 92 . 4 + + + − x 1 − − e 1 − e 1 105 1 1 1 1 0
Câu 50: Cho lăng trụ ABC.A′B C
′ ′có chiều cao bằng 6 và đáy là tam giác đều cạnh bằng 4. Gọi M , N, P
lần lượt là tâm các mặt bên ABB A ′ ,′ ACC A ′ ,′ BCC B
′ ′ . Thể tích khối đa diện lồi có các đỉnh là các điểm ,
A B,C, M , N, P bằng A. 9 3 . B. 10 3 . C. 7 3 . D. 12 3 . Lời giải Chọn A A' C' B' N D F M P E A C B
Gọi DEF là thiết diện của lăng trụ cắt bởi mặt phẳng (MNP) .
Dễ chứng minh được (DEF ) / / ( ABC) và D, E, F lần lượt là trung điểm của các đoạn thẳng 1
AA ,′ BB ,′CC′ suy ra V = V = . ABC DEF ABC A′B C ′ ′ 12 3 . . 2 Ta có V = V −V −V −V . ABCPNM ABC.DEF ADMN BMPE CPMF Mặt khác 1 3 V = V = V = V ⇒ V = V = . ADMN BMPE CPMF ABC DEF ABCPNM ABC DEF 9 3 . . 12 4 -------- Hết ------ Trang 17
Document Outline
- de-khao-sat-chat-luong-toan-12-lan-1-nam-2023-2024-so-gddt-thanh-hoa
- LỜI GIẢI CHI TIẾT KHẢO SÁT LẦN 1-2023-2024 GỬI PHẢN BIỆN LẦN 1




