11 trang 6 lượt tải

Đề khảo sát chất lượng Toán 9 năm 2024 – 2025 sở GD&ĐT Hà Tĩnh

12

Giới thiệu đến quý thầy, cô giáo và các em học sinh lớp 9 đề thi khảo sát chất lượng học sinh môn Toán 9 năm học 2024 – 2025 sở Giáo dục và Đào tạo tỉnh Hà Tĩnh. Đề thi cấu trúc 20% trắc nghiệm kết hợp 80% tự luận, thời gian làm bài 90 phút, có đáp án chi tiết và hướng dẫn chấm điểm. Kỳ thi được diễn ra vào ngày 04 tháng 05 năm 2025.

Chủ đề: Đề thi Toán 9 415 tài liệu

Môn: Toán 9 3.4 K tài liệu

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/11
SỞ GD&ĐT HÀ TĨNH
ĐỀ THI CHÍNH THỨC
(Đề thi gồm 02 trang, 14 câu)
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9
NĂM HỌC 2024 - 2025
Môn thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
(Trong mỗi câu hỏi từ câu 1 đến câu 8, viết vào tờ giấy thi đáp án đúng mà em chọn. Ví dụ: Câu 1 nếu
chọn A là đúng thì viết Câu 1: A).
Câu 1. Kết quả rút gọn biểu thức
18 32A = +
là:
A.
32
.
B.
3
.
C.
72
. D.
52
.
Câu 2. Nghiệm của phương trình
là:
A. 2.
B.
5−
.
C. 3.
D.
1
−
.
Câu 3. Đồ thị của hàm số
2
1
2
yx= −
đi qua điểm nào sau đây:
A.
( )
1; 2
. B.
(
)
1; 2−
. C.
( )
2; 2
−−
.
D.
( )
2; 2
.
Câu 4. Gieo một con xúc xắc cân đối và đồng chất hai lần liên tiếp. Số phần tử của không gian mẫu là:
A.
6
.
B. 12.
C. 36.
D. 35.
Câu 5. Cho tam giác
ABC
vuông tại
A
. Biết
3
AB =
cm,
4AC
=
cm,
cosC
bằng
A.
3
5
. B.
4
3
. C.
3
4
D.
4
5
Câu 6. Thể tích của một hình nón có bán kính đáy
5 cm
và chiều cao
9 cm
là:
A.
3
75 cm
π
.
B.
3
225 cm
π
.
C.
3
15 cm
π
. D.
3
150 cm
π
.
Câu 7. Nghiệm của bất phương trình
2 60x− −≥
là:
A.
3.x >−
B.
3.x ≤−
C.
3.x ≥
D.
3.
x ≤
Câu 8. Cho bảng tần số điểm kiểm tra giữa học kỳ II môn Toán của 35 học sinh lớp 9, trường THCS X
như sau:
Điểm 4 5 6 7 8 9 10
Tần số 1 2 5 7 11 7 2
Tần số tương đối của điểm số 9 là:
A. 2%.
B. 20%.
C. 8%.
D. 9%.
II. PHẦN TỰ LUẬN (8,0 điểm) (Thí sinh trình bày lời giải vào tờ giấy thi)
Câu 9 (1,0 điểm). Rút gọn biểu thức
:
4
22
xx x
A
x
xx

= −


−
+−

,với
0, 4>≠xx
Câu 10 (1,0 điểm). Biết phương trình
2
2 70xx− −=
có hai nghiệm
12
,xx
. Không giải phương trình,
tính giá trị của biểu thức
22
1 2 12
3T x x xx=+−
.
MÃ ĐỀ 01
Câu 11 (1,0 điểm). Giải hệ phương trình
21
34 6
xy
xy
+=
+=−
.
Câu 12 (2,0 điểm).
a) Trong một hộp có 6 quả bóng bàn kích thước và chất liệu như nhau gồm 2 quả màu đỏ, 2 quả
màu xanh, 2 quả màu trắng. Lấy ngẫu nhiên đồng thời 2 quả bóng bàn từ hộp. Tính xác suất của biến
cố A: “Trong 2 quả bóng bàn lấy ra có ít nhất một quả bóng bàn màu đỏ”.
b) Một xí nghiệp đặt kế hoạch sản xuất 3000 sản phẩm trong một thời gian. Trong 5 ngày đầu
xí nghiệp thực hiện đúng kế hoạch, những ngày sau đó mỗi ngày xí nghiệp sản xuất vượt 10 sản phẩm
nên đã hoàn thành sớm được một ngày so với dự định và còn vượt mức 55 sản phẩm so với kế hoạch
ban đầu. Tính số sản phẩm xí nghiệp dự định làm trong một ngày theo kế hoạch ?
Câu 13 (2,0 điểm).
Từ một điểm
M
ở bên ngoài đường tròn
( )
O
, vẽ hai tiếp tuyến
, MA MB
với đường tròn
(
, AB
là hai tiếp điểm). Tia
MO
cắt đường tròn
( )
O
tại hai điểm phân biệt
C
và
D
(C nằm giữa
M
và O) và cắt đoạn
AB
tại
F
.
a) Chứng minh bốn điểm
,,,AOBM
cùng thuộc một đường tròn.
b) Vẽ đường kính
AK
của đường tròn
(
)
O
. Gọi
H
là chân đường vuông góc kẻ từ
B
đến
, AK I
là giao điểm của
MK
và
BH
. Chứng minh
..MC MD MF MO=
và tính tỉ số
FI
AH
.
Câu 14 (1,0 điểm).
a) Một nhà máy sản xuất cần thiết kế một thùng sơn dạng hình trụ bằng nhựa Polypropylen có
nắp đậy với dung tích
3
1000cm
. Tìm bán kính nắp đậy của thùng sơn để nhà sản xuất tiết kiệm nguyên
vật liệu nhất.
b) Cho
, , abc
là các số thực dương và thỏa mãn điều kiện
3abc++=
.
Tìm giá trị nhỏ nhất của biểu thức
22 2
111
.
111
ab
P
bca
c +++
=++
+++
--------Hết--------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh: …………………………......…; Số báo danh: ............................
Đáp án
HƯỚNG DẪN CHẤM
I- PHẦN GHI KẾT QUẢ (Mỗi câu có kết quả đúng cho 0,25 điểm)
Câu
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Đáp án
C
A
C
C
D
A
B
B
II- PHẦN TỰ LUẬN (8 điểm)
CÂU
ĐÁP ÁN
ĐIỂM
9
(1 điểm)
( )
( )
:
22
22
x xx
A
xx
xx


= −

+−
+−

( )( )
( )
( )
( )
2
:
2
22 22
xx
xx
x
xx xx

−

= −

−
+− +−

( )
( )( )
2
:
2
22
x xx
x
x
xx

−−

=

−
+−

( )
( )
2 22
.
2
22
xx
xx
xx
−
= =
+
+−
.
0,25
0,25
0,25
0,25
10
(1 điểm)
Vì phương trình đã cho luôn có hai nghiệm nên
Theo định lý Viete ta có
12
12
7
2
xx
x x
+=
= −
.
Ta có
( )
12 1 2 12
2
22
12
3 5 4 35 39T xxx xxxxx+=+− = − =+=
.
0,5
0,5
Câu 11
(1 điểm)
Hệ đã cho có dạng
8 4 4 (1)
3 4 6 (2)
xy
xy
+=
+=−
Trừ từng vế hai phương trình (1) và (2) ta được phương trình
5 10x =
khi đó
2x
=
.
Thế giá trị
2x =
vào phương trình
21xy+=
ta được phương trình
2.2 1y+=
hay
3y
= −
.
Vậy hệ phương trình có nghiệm duy nhất
( ) ( )
; 2; 3xy = −
.
0,5
0,5
12.a
(1 điểm)
Kí hiệu các quả bóng bàn đỏ, xanh, trắng lần lượt là Đ
1
, Đ
2
, X
1
, X
2
, T
1
, T
2
.
Không gian mẫu:
Ω = { Đ
1
Đ
2
, X
1
X
2
, T
1
T
2
, Đ
1
X
1,
Đ
1
X
2
, Đ
2
X
1
, Đ
2
X
2
, Đ
1
T
1
, Đ
1
T
2
, Đ
2
T
1
, Đ
2
T
2
, X
1
T
1
, X
1
T
2
,
X
2
T
1
, X
2
T
2
}
Có 9 kết quả thuận lợi cho biến cố A là: Đ
1
Đ
2
, Đ
1
X
1,
Đ
1
X
2
, Đ
2
X
1
, Đ
2
X
2
, Đ
1
T
1
, Đ
1
T
2
, Đ
2
T
1
,
Đ
2
T
2
Xác suất của biến cố A là:
( )
9
15
PA=
.
0,5
0,5
12.b
(1 điểm)
Gọi số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là x (sản phẩm)
Thời gian hoàn thành công việc theo dự định là
3000
x
(ngày)
Số sản phẩm làm trong 5 ngày đầu là 5x (sản phẩm)
Những ngày sau, mỗi ngày xí nghiệp làm được số sản phẩm là x + 10 (sản phẩm)
0,25
Thời gian làm số sản phẩm còn lại và làm vượt mức 55 sản phẩm là
3000 5 55 3055 5
10 10
xx
xx
−+ −
=
++
(ngày)
0,25
Vì xí nghiệp hoàn thành công việc sớm hơn 1 ngày nên ta có phương trình:
3000 3055 5
51
10
x
xx
−

−+ =

+

2
115 30000 0
xx⇔+ − =
1
125x⇔=
(thỏa mãn),
2
240x = −
(loại)
0,25
Vậy số sản phẩm xí nghiệp dự định làm trong 1 ngày theo kế hoạch là 125 (sản phẩm)
0,25
13. a
(1 điểm)
a) Ta có
,MA MB
lần lượt là tiếp tuyến của
đường tròn (O) nên
0
90MAO MBO= =
.
0,5
0,5
Gọi J là trung điểm MO, vì tam giác MAO
vuông tại A, nên ta có
JA JM JO= =
vì tam giác MBO vuông tại B, nên ta có
JB JM JO= =
, suy ra bốn điểm A, O, B,
M cùng thuộc một đường tròn. Đpcm.
13. b
(1 điểm)
b) Ta có hai tam giác MAC và MDA đồng dạng (học sinh phải chứng minh), nên ta có
2
.MC MD MA=
0,25
Ta có hai tam giác MFA và MAO đồng dạng (học sinh phải chứng minh), nên ta có
2
.MF MO MA=
do đó
..MF MO MC MD=
0,25
- Gọi N là giao điểm của AM và KB
Ta có
0
90ABK =
(Vì
( )
,
B O AK∈
đường kính), suy ra
NK AB
⊥
Theo tính chất tiếp tuyến, ta có
MO AB⊥
, do đó ta có
//MO NK
Xét ∆ANK , ta có O là trung điểm AK , suy ra M là trung điểm AN ⇒
AM NM=
.
Ta có
NA AK⊥
và
BH AK⊥
⇒
//AN BH
Xét ∆KAM, ta có
//IH AM
⇒
KI IH
KM MA
=
(1)
0,25
Xét ∆KNM, ta có
//
KI BI
BI MN
KM MN
⇒=
(2)
Từ (1) và (2), ta có
(vì )
IH BI
IH BI MA MN
MA MN
= ⇒= =
, suy ra
I
là trung điểm
BH
Ta có
F
là trung điểm
AB
, suy ra
1
2
FI
AH
=
.
0,25
14. a
(0,5 điểm)
Gọi
( )
0rr>
là bán kính nắp đậy của thùng sơn. Thể tích thùng sơn là
2
2
V
V
rh h
r
π
π
⇒= =
.
Diện tích toàn phần của thùng sơn:
3
2 2 2 22 2
3
2
2
2 2 2 2 2 2 3 2 300 2
V V VV
S rh r r r r r V cm
r r rr
πππ π π π π π
π
=+= +=+=++≥ =
Diện tích toàn phần của thùng sơn nhỏ nhất bằng
2
3
300 2 cm
π
khi
2
3
3
10
2
2
2
VV
r r cm
r
π
π
π
= ⇔= =
0,25
0,25
14. b
(0,5 điểm)
Ta có:
( ) ( ) ( )
(
) ( ) ( )
222
22 2 2 2 2
111
11
111
111 1 1 1
111
()
3( ) 3
222 2
1
ab bc ca
ab
P abc
bca b c a
abbcca
a b c ab bc ca
abc
c
+++
++
= + + = +− + +− + +−
+++ + + +
+++
++− + +
≥+++− + + =+
+
Mặt khác có:
( )
2
222
2223( )
33
33 3
2
a b c a b c ab bc ca ab bc ca
ab bc ca P
++ = + + + + + ≥ + +
−
⇒ + + ≤⇒ ≥+ =
Dấu bằng xảy ra khi a = b = c = 1; Vậy giá trị nhỏ nhất bằng 3.
0,25
0,25
SỞ GD&ĐT HÀ TĨNH
ĐỀ THI CHÍNH THỨC
(Đề thi gồm 02 trang, 14 câu)
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9
NĂM HỌC 2024 - 2025
Môn thi: TOÁN
Thời gian làm bài: 90 phút, không kể thời gian phát đề
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
(Trong mỗi câu hỏi từ câu 1 đến câu 8, viết vào tờ giấy thi đáp án đúng mà em chọn. Ví dụ: Câu 1 nếu
chọn A là đúng thì viết Câu 1: A).
Câu 1. Kết quả rút gọn biểu thức
12 48
A
= +
là:
A.
9
.
B.
63
. C.
43
. D.
23
.
Câu 2. Nghiệm của phương trình
(
)
2 14
x +=
là:
A.
5
.
B. 1.
C. 2.
D.
1−
.
Câu 3. Đồ thị của hàm số
2
1
3
yx= −
đi qua điểm nào sau đây:
A.
( )
1; 3
. B.
( )
1; 3−
. C.
( )
3; 3−−
.
D.
( )
3; 3
.
Câu 4. Gieo 1 đồng xu cân đối và đồng chất hai lần liên tiếp. Số phần tử không gian mẫu là:
A. 4.
B. 2.
C. 1.
D. 6.
Câu 5. Cho tam giác
ABC
vuông tại
A
. Biết
3AB =
cm,
4AC =
cm,
sinC
bằng
A.
3
5
. B.
4
3
. C.
3
4
. D.
4
5
.
Câu 6. Thể tích của một hình nón có bán kính đáy
3 cm
và chiều cao
6 cm
là:
A.
3
54 cm
π
.
B.
3
6 cm
π
.
C.
3
18 cm
π
.
D.
3
12 cm
π
.
Câu 7. Nghiệm của bất phương trình
2 80x− −≥
là:
A.
4.
x ≤−
B.
4.>−x
C.
4.
x ≥
D.
4.x ≤
Câu 8. Cho bảng tần số điểm kiểm tra giữa học kỳ II môn Toán của 40 học sinh lớp 9, trường THCS X
như sau:
Điểm 4 5 6 7 8 9 10
Tần số 1 2 5 7 15 8 2
Tần số tương đối của điểm số 8 là:
A. 15%.
B. 8%.
C. 3,75%.
D. 37,5%.
II. PHẦN TỰ LUẬN (8,0 điểm) (Thí sinh trình bày lời giải vào tờ giấy thi)
Câu 9 (1,0 điểm). Rút gọn biểu thức
:
4
22
xx x
A
x
xx

= −


−
++

, với
0, 4>≠
xx
Câu 10 (1,0 điểm). Biết phương trình
2
2 10 0xx−−=
có hai nghiệm
12
,xx
. Không giải phương trình,
tính giá trị của biểu thức
22
1 2 12
5T x x xx=+−
.
MÃ ĐỀ 02
Câu 11 (1,0 điểm). Giải hệ phương trình
231
34 2
xy
xy
−=
−=
.
Câu 12 (2,0 điểm).
a) Trong một hộp có 6 quả bóng bàn kích thước và chất liệu như nhau gồm 2 quả màu đỏ, 2 quả
màu xanh, 2 quả màu trắng Lấy ngẫu nhiên đồng thời 2 quả bóng bàn từ hộp. Tính xác suất của biến cố
A: “Trong 2 quả bóng bàn lấy ra có ít nhất một quả bóng bàn màu xanh”.
b) Một xí nghiệp đặt kế hoạch sản xuất 3000 sản phẩm trong một thời gian. Trong 6 ngày đầu
xí nghiệp thực hiện đúng kế hoạch, những ngày sau đó mỗi ngày xí nghiệp sản xuất vượt 10 sản phẩm
nên đã hoàn thành sớm được một ngày so với dự định và còn vượt mức 60 sản phẩm so với kế hoạch
ban đầu. Tính số sản phẩm xí nghiệp dự định làm trong một ngày theo kế hoạch ?
Câu 13 (2,0 điểm).
Từ một điểm
M
ở bên ngoài đường tròn
( )
O
, vẽ hai tiếp tuyến
, MC MD
với đường tròn
(
, CD
là hai tiếp điểm). Tia
MO
cắt đường tròn
( )
O
tại hai điểm phân biệt
A
và
B
(
A
nằm giữa
M
và
O
) và cắt đoạn
CD
tại
F
.
a) Chứng minh bốn điểm
,,,CODM
cùng thuộc một đường tròn.
b) Vẽ đường kính
CK
của đường tròn
( )
O
. Gọi
H
là chân đường vuông góc kẻ từ
D
đến
, CK I
là giao điểm của
MK
và
DH
. Chứng minh
..MA MB MF MO
=
và tính tỉ số
FI
CH
.
Câu 14 (1,0 điểm).
a) Một nhà máy sản xuất cần thiết kế một thùng sơn dạng hình trụ bằng nhựa Polypropylen có
nắp đậy với dung tích
3
800cm
. Tìm bán kính nắp đậy của thùng sơn để nhà sản xuất tiết kiệm nguyên
vật liệu nhất.
b) Cho
, ,
abc
là các số thực dương và thỏa mãn điều kiện
6abc
++=
.
Tìm giá trị nhỏ nhất của biểu thức
22 2
444
.
444
ab
P
bca
c +++
=++
+++
--------Hết--------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh: …………………………......…; Số báo danh: ............................
IV. Đáp án
HƯỚNG DẪN CHẤM
I- PHẦN GHI KẾT QUẢ (Mỗi câu có kết quả đúng cho 0,25 điểm)
Câu
Câu 1
Câu 2
Câu 3
Câu 4
Câu 5
Câu 6
Câu 7
Câu 8
Đáp
án
B B C A A C
A
D
II- PHẦN TỰ LUẬN (8 điểm)
CÂU ĐÁP ÁN
ĐIỂ
M
9
(1 điểm)
( )
(
)
:
22
22
x xx
A
xx
xx


= −

++
+−

(
)
( )
(
)
(
)
(
)
2
:
2
22 22
xx
xx
x
xx xx

−

= −

+
+− +−

( )
( )( )
2
:
2
22
x xx
x
x
xx

−−

=

+
+−

( )( )
2 22
.
2
22
xx
xx
xx
+
= =
−
+−
.
0,25
0,25
0,25
0,25
10
(1 điểm)
Do phương trình đã cho luôn có hai nghiệm nên
Theo định lý Viete ta có
12
12
10
2x
x
x
x = −
+=
.
Ta có
( )
12 1 2 12
2
22
12
5 7 4 70 74T xxx xxxxx+=+− = − =+=
.
0,5
0,5
Câu 11
(1 điểm)
Hệ đã cho có dạng
6 9 3 (1)
6 8 4 (2)
xy
xy
−=
−=
Trừ từng vế hai phương trình (1) và (2) ta được phương trình
1y−=−
khi đó
1y =
.
Thế giá trị
1y =
vào phương trình
231xy−=
ta được phương trình
2 31x −=
hay
2x
=
.
Vậy hệ phương trình có nghiệm duy nhất
( )
( )
; 2;1xy =
.
0,5
0,5
12.a
(1 điểm)
Kí hiệu các quả bóng bàn đỏ, xanh, trắng lần lượt là Đ
1
, Đ
2
, X
1
, X
2
, T
1
, T
2
.
Không gian mẫu:
Ω = { Đ
1
Đ
2
, X
1
X
2
, T
1
T
2
, Đ
1
X
1,
Đ
1
X
2
, Đ
2
X
1
, Đ
2
X
2
, Đ
1
T
1
, Đ
1
T
2
, Đ
2
T
1
, Đ
2
T
2
, X
1
T
1
, X
1
T
2
,
X
2
T
1
, X
2
T
2
}
Có 9 kết quả thuận lợi cho biến cố A là: X
1
X
2
, X
1
Đ
1
, X
1
Đ
2
, X
1
T
1
, X
1
T
2
, X
2
Đ
1
, X
2
Đ
2
, X
2
T
1
,
0,5
X
2
T
2
.
Xác suất của biến cố A là:
(
)
9
15
PA
=
.
0,5
12.b
(1 điểm)
Gọi số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là x (sản phẩm)
Thời gian hoàn thành công việc theo dự định là
3000
x
(ngày)
Số sản phẩm làm trong 6 ngày đầu là 6x (sản phẩm)
Những ngày sau, mỗi ngày xí nghiệp làm được số sản phẩm là x + 10 (sản phẩm)
0,25
Thời gian làm số sản phẩm còn lại và làm vượt mức 60 sản phẩm là
3000 6 60 3060 6
10 10
xx
xx
−+ −
=
++
(ngày)
0,25
Vì xí nghiệp hoàn thành công việc sớm hơn 1 ngày, nên ta có phương trình:
3000 3060 6
61
10
x
xx
−

−+ =

+

2
130 30000 0xx⇔+ − =
1
120x⇔=
(thỏa mãn),
2
250x = −
(loại)
0,25
Vậy số sản phẩm xí nghiệp dự định làm trong 1 ngày theo kế hoạch là 120 (sản phẩm)
0,25
13. a)
(1 điểm)
a) Ta có
,MC MD
lần lượt là tiếp tuyến
của đường tròn (O)
nên
0
90MCO MDO= =
.
0,5
Gọi J là trung điểm MO, vì tam giác
MCO vuông tại C, nên ta có
JC JM JO= =
,
vì tam giác MDO vuông tại D, nên ta có
JD JM JO= =
, suy ra bốn điểm C, O,
D, M cùng thuộc một đườ
ng tròn.
Đpcm.
0,5
13. b)
(1 điểm)
b) Ta có hai tam giác MCA và MBC đồng dạng (học sinh phải chứng minh), nên ta có
2
.MA MB MC=
0,25
Ta có hai tam giác MFC và MCO đồng dạng (học sinh phải chứng minh), nên ta có
2
.MF MO MC=
do đó
..MF MO MA MB=
0,25
- Gọi N là giao điểm của CM và KD
Ta có
0
90CDK =
(Vì
(
)
,D O AK∈
đường kính), suy ra
NK CD⊥
Theo tính chất tiếp tuyến, ta có
MO CD⊥
Do đó
//MO NK
Xét ∆CNK, ta có O là trung điểm CK , suy ra M là trung điểm CN ⇒
CM NM=
.
Ta có
NC CK⊥
và
DH CK⊥
⇒
//CN DH
Xét ∆KCM, ta có
//IH CM
⇒
(1)
0,25
Xét ∆KNM, ta có
//
KI DI
DI MN
KM MN
⇒=
(2)
Từ (1) và (2), ta có
(vì )
IH DI
IH DI MC MN
MC MN
= ⇒= =
, suy ra
I
là trung điểm
DH
Ta có
F
là trung điểm
CD
, suy ra
1
2
FI
CH
=
.
0,25
14. a
(0,5 điểm)
Gọi
( )
0rr>
là bán kính nắp đậy của thùng sơn. Thể tích thùng sơn là
2
2
V
V
rh h
r
π
π
⇒= =
.
Diện tích toàn phần của thùng sơn:
3
2 2 2 22 2
3
2
2
2 2 2 2 2 2 3 2 120 20
V V VV
S rh r r r r r V cm
r r rr
πππ π π π π π
π
=+= +=+=++≥ =
Diện tích toàn phần của thùng sơn nhỏ nhất bằng
2
3
120 20
cm
π
khi
2
33
800 50
22
2
V
r r cm
r
π
ππ
= ⇔= =
0,25
0,25
14. b
(0,5 điểm)
Ta có:
( ) ( ) ( )
222
222
444
1
444
44 4 4

+++
= +− ++− ++−

+++

ab bc ca
Pa b c
bca
( ) ( ) (
)
444
1
12 ( ) 3
4 4 4 4 16
abbcca
ab bc ca
abc
+++

++
≥ +++ − + + =−


Mặt khác có:
( )
2
222
2223( )
12 9
12 3
16 4
a b c a b c ab bc ca ab bc ca
ab bc ca P
++ = + + + + + ≥ + +
⇒ + + ≤ ⇒ ≥− =
Dấu bằng xảy ra khi a = b = c = 2;
Vậy GTNN của P bằng
9
4
0,25
0,25
Xem thêm: KHẢO SÁT CHẤT LƯỢNG TOÁN 9
https://thcs.toanmath.com/khao-sat-chat-luong-toan-9

Tài liệu khác của Toán 9

Preview text:

SỞ GD&ĐT HÀ TĨNH
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 NĂM HỌC 2024 - 2025
ĐỀ THI CHÍNH THỨC Môn thi: TOÁN
(Đề thi gồm 02 trang, 14 câu)
Thời gian làm bài: 90 phút, không kể thời gian phát đề MÃ ĐỀ 01
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
(Trong mỗi câu hỏi từ câu 1 đến câu 8, viết vào tờ giấy thi đáp án đúng mà em chọn. Ví dụ: Câu 1 nếu
chọn A là đúng thì viết Câu 1: A).
Câu 1. Kết quả rút gọn biểu thức A = 18 + 32 là: A. 3 2 . B. 3.
C. 7 2 . D. 5 2 .
Câu 2. Nghiệm của phương trình 2(x + ) 1 = 6 là: A. 2. B. 5 − . C. 3. D. 1 − .
Câu 3. Đồ thị của hàm số 1 2
y = − x đi qua điểm nào sau đây: 2 A. (1; 2) . B. (1; 2 − ) . C. ( 2; − 2 − ).
D. (2;2) .
Câu 4. Gieo một con xúc xắc cân đối và đồng chất hai lần liên tiếp. Số phần tử của không gian mẫu là: A. 6 . B. 12. C. 36.
D. 35.
Câu 5. Cho tam giác ABC vuông tại A . Biết AB = 3cm, AC = 4 cm, cosC bằng A. 3 . B. 4 . C. 3 D. 4 5 3 4 5
Câu 6. Thể tích của một hình nón có bán kính đáy 5 cm và chiều cao 9 cm là: A. 3 75π cm . B. 3 225π cm . C. 3 15π cm . D. 3 150π cm .
Câu 7. Nghiệm của bất phương trình 2 − x − 6 ≥ 0 là: A. x > 3. − B. x ≤ 3. −
C. x ≥ 3.
D. x ≤ 3.
Câu 8. Cho bảng tần số điểm kiểm tra giữa học kỳ II môn Toán của 35 học sinh lớp 9, trường THCS X như sau: Điểm 4 5 6 7 8 9 10 Tần số 1 2 5 7 11 7 2
Tần số tương đối của điểm số 9 là: A. 2%. B. 20%. C. 8%.
D. 9%.
II. PHẦN TỰ LUẬN (8,0 điểm) (Thí sinh trình bày lời giải vào tờ giấy thi)  
Câu 9 (1,0 điểm). Rút gọn biểu thức x x =  −  : x A
,với x > 0, x ≠ 4 x 4 x 2  − + x −   2
Câu 10 (1,0 điểm). Biết phương trình 2
x − 2x − 7 = 0 có hai nghiệm x , x . Không giải phương trình, 1 2
tính giá trị của biểu thức 2 2
T = x + x − 3x x . 1 2 1 2 2x + y = 1
Câu 11 (1,0 điểm). Giải hệ phương trình . 3   x + 4y = 6 − Câu 12 (2,0 điểm).
a) Trong một hộp có 6 quả bóng bàn kích thước và chất liệu như nhau gồm 2 quả màu đỏ, 2 quả
màu xanh, 2 quả màu trắng. Lấy ngẫu nhiên đồng thời 2 quả bóng bàn từ hộp. Tính xác suất của biến
cố A: “Trong 2 quả bóng bàn lấy ra có ít nhất một quả bóng bàn màu đỏ”.
b) Một xí nghiệp đặt kế hoạch sản xuất 3000 sản phẩm trong một thời gian. Trong 5 ngày đầu
xí nghiệp thực hiện đúng kế hoạch, những ngày sau đó mỗi ngày xí nghiệp sản xuất vượt 10 sản phẩm
nên đã hoàn thành sớm được một ngày so với dự định và còn vượt mức 55 sản phẩm so với kế hoạch
ban đầu. Tính số sản phẩm xí nghiệp dự định làm trong một ngày theo kế hoạch ? Câu 13 (2,0 điểm).
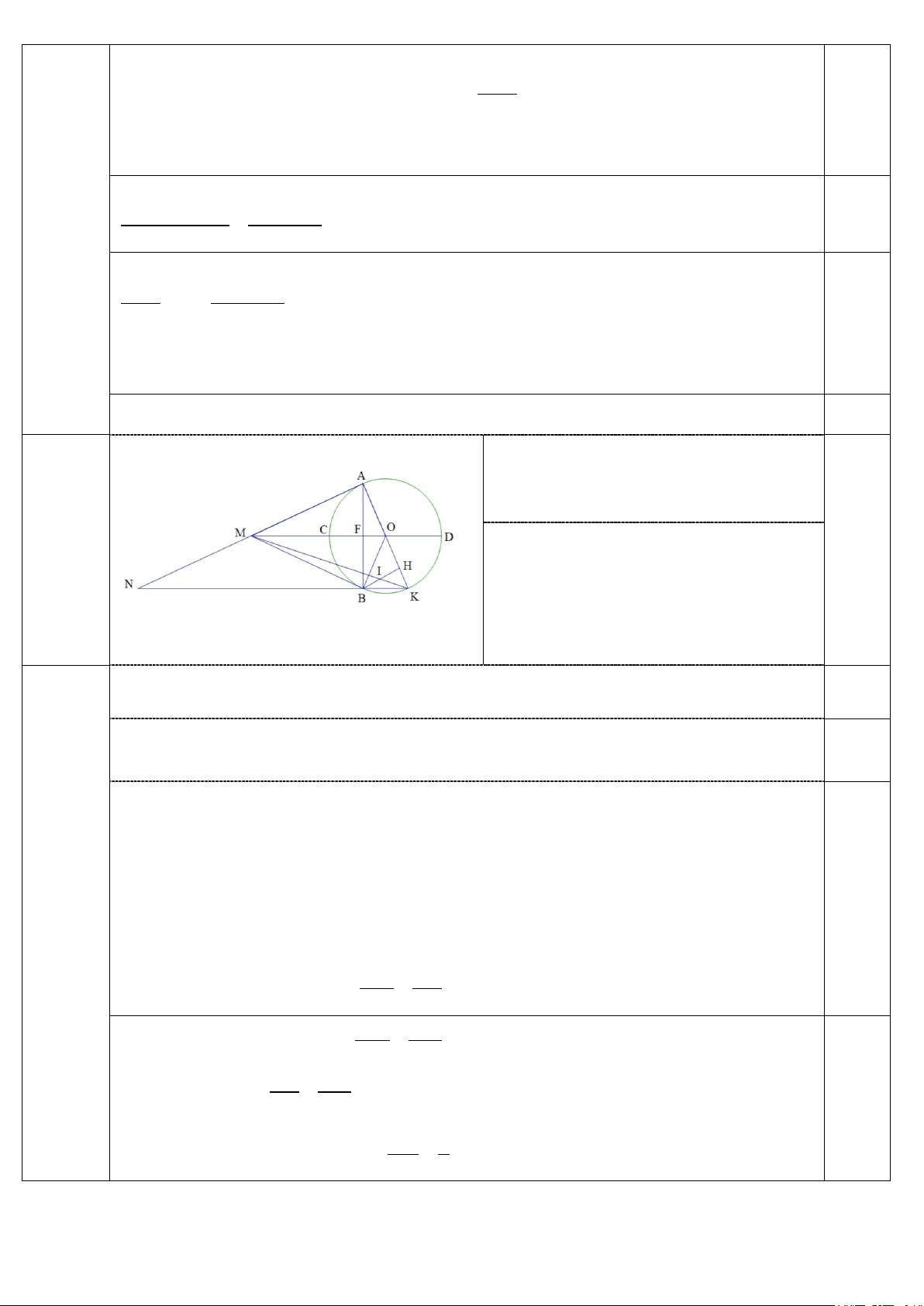
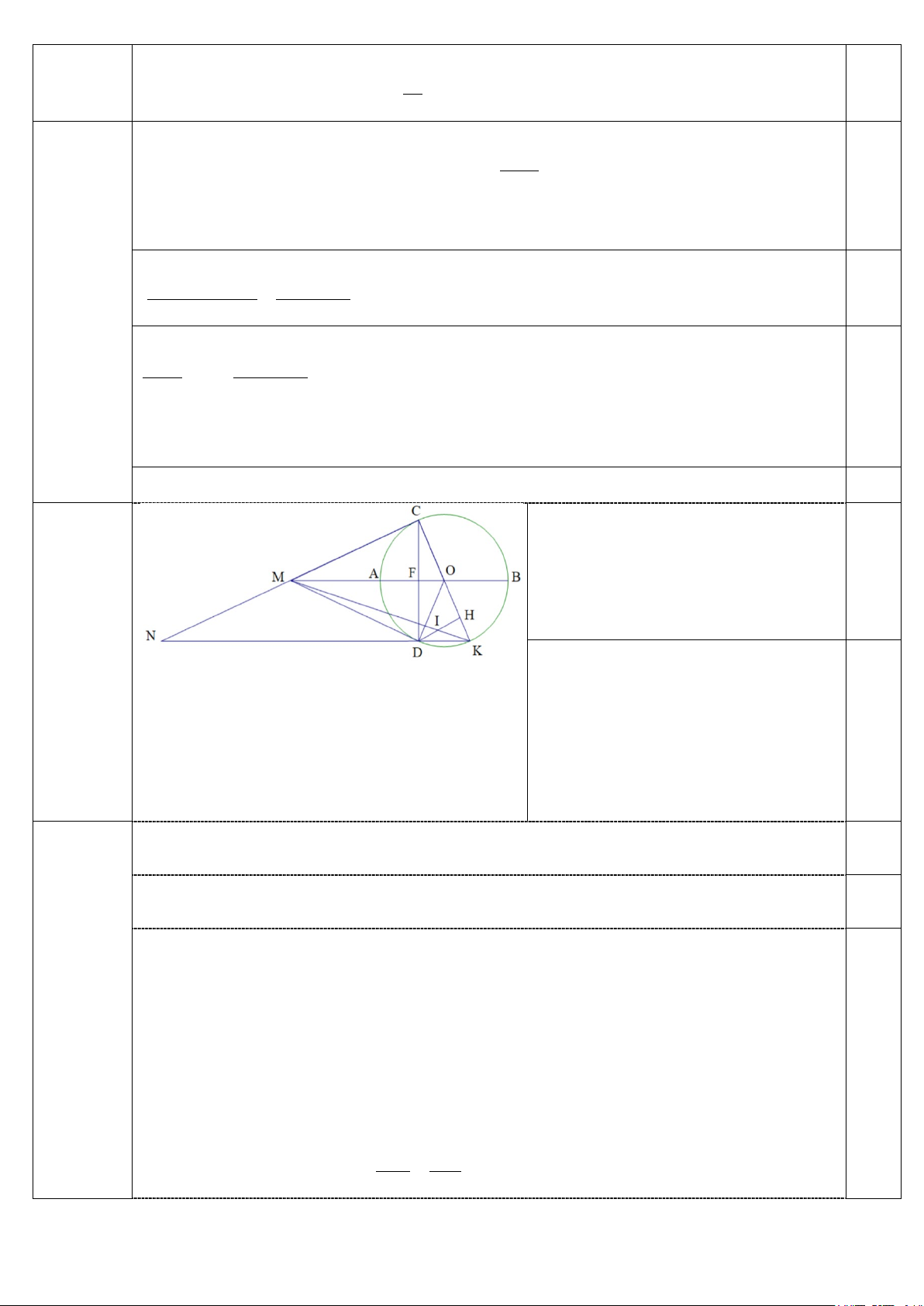
Từ một điểm M ở bên ngoài đường tròn (O) , vẽ hai tiếp tuyến ,
MA MB với đường tròn ( ,
A B là hai tiếp điểm). Tia MO cắt đường tròn (O) tại hai điểm phân biệt C và D (C nằm giữa M
và O) và cắt đoạn AB tại F .
a) Chứng minh bốn điểm ,
A O, B, M cùng thuộc một đường tròn.
b) Vẽ đường kính AK của đường tròn (O) . Gọi H là chân đường vuông góc kẻ từ B đến
AK, I là giao điểm của MK và BH . Chứng minh MC.MD = MF.MO và tính tỉ số FI . AH
Câu 14 (1,0 điểm).
a) Một nhà máy sản xuất cần thiết kế một thùng sơn dạng hình trụ bằng nhựa Polypropylen có nắp đậy với dung tích 3
1000cm . Tìm bán kính nắp đậy của thùng sơn để nhà sản xuất tiết kiệm nguyên vật liệu nhất.
b) Cho a, b, c là các số thực dương và thỏa mãn điều kiện a + b + c = 3.
Tìm giá trị nhỏ nhất của biểu thức a +1 b +1 c +1 P = + + . 2 2 2
b +1 c +1 a +1
--------Hết--------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh: …………………………......…; Số báo danh: ............................ Đáp án HƯỚNG DẪN CHẤM
I- PHẦN GHI KẾT QUẢ (Mỗi câu có kết quả đúng cho 0,25 điểm) Câu Câu 1
Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Đáp án C A C C D A B B
II- PHẦN TỰ LUẬN (8 điểm) CÂU ĐÁP ÁN ĐIỂM x x x A =  0,25  ( −  x + 2)( x − 2) : x + 2 x − 2   x x ( x −2)  =  −  : x 0,25 9
( x + 2)( x − 2) ( x + 2)( x − 2) x − 2  (1 điểm)
x − x ( x −2)  x 0,25 =  ( 
x + 2)( x − 2) :  x − 2  2 x x − 2 2 0,25 = ( = .
x + 2)( x − 2). x x + 2
Vì phương trình đã cho luôn có hai nghiệm nên 0,5 10 x + x = 2
Theo định lý Viete ta có 1 2  . (1 điểm) x x = 7 − 1 2 0,5 Ta có 2 2 2
T = x + x − 3x x = x + x
− 5x x = 4 + 35 = 39. 1 2 1 2 ( 1 2) 1 2 Hệ đã cho có dạng 8  x + 4y = 4 (1)
Trừ từng vế hai phương trình (1) và (2) ta được phương trình 5x =10 3   x + 4y = 6 − (2) 0,5
Câu 11 khi đó x = 2 .
(1 điểm) Thế giá trị x = 2 vào phương trình 2x + y =1 ta được phương trình
2.2 + y =1 hay y = 3 − . 0,5
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (2; 3 − ) .
Kí hiệu các quả bóng bàn đỏ, xanh, trắng lần lượt là Đ1, Đ2, X1, X2, T1, T2. Không gian mẫu:
Ω = { Đ1Đ2, X1X2, T1T2, Đ1X1, Đ1X2, Đ2X1, Đ2X2, Đ1T1, Đ1T2, Đ2T1, Đ2T2, X1T1, X1T2, 0,5 12.a X2T1, X2T2}
(1 điểm) Có 9 kết quả thuận lợi cho biến cố A là: Đ1Đ2, Đ1X1, Đ1X2, Đ2X1, Đ2X2, Đ1T1, Đ1T2, Đ2T1, Đ2T2
Xác suất của biến cố A là: 0,5 P( A) 9 = . 15
Gọi số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là x (sản phẩm)
Thời gian hoàn thành công việc theo dự định là 3000 (ngày) x 0,25
Số sản phẩm làm trong 5 ngày đầu là 5x (sản phẩm)
Những ngày sau, mỗi ngày xí nghiệp làm được số sản phẩm là x + 10 (sản phẩm)
Thời gian làm số sản phẩm còn lại và làm vượt mức 55 sản phẩm là
3000 − 5x + 55 3055 − 5x 0,25 12.b = (ngày) (1 điểm) x +10 x +10
Vì xí nghiệp hoàn thành công việc sớm hơn 1 ngày nên ta có phương trình: 3000  3055 − 5 0,25 5 x  − + =   1 xx +10  2
⇔ x +115x − 30000 = 0
⇔ x =125 (thỏa mãn), x = 240 − (loại) 1 2
Vậy số sản phẩm xí nghiệp dự định làm trong 1 ngày theo kế hoạch là 125 (sản phẩm) 0,25 a) Ta có ,
MA MB lần lượt là tiếp tuyến của
đường tròn (O) nên  =  0 MAO MBO = 90 . 13. a
Gọi J là trung điểm MO, vì tam giác MAO 0,5 (1 điểm)
vuông tại A, nên ta có JA = JM = JO
vì tam giác MBO vuông tại B, nên ta có
JB = JM = JO , suy ra bốn điểm A, O, B,
M cùng thuộc một đường tròn. Đpcm. 0,5
b) Ta có hai tam giác MAC và MDA đồng dạng (học sinh phải chứng minh), nên ta có 0,25 2
MC.MD = MA
Ta có hai tam giác MFA và MAO đồng dạng (học sinh phải chứng minh), nên ta có 2
MF.MO = MA do đó MF.MO = MC.MD 0,25
- Gọi N là giao điểm của AM và KB Ta có  0
ABK = 90 (Vì B ∈(O), AK đường kính), suy ra NK ⊥ AB
Theo tính chất tiếp tuyến, ta có MO ⊥ AB , do đó ta có MO / /NK 13. b 0,25
Xét ∆ANK , ta có O là trung điểm AK , suy ra M là trung điểm AN ⇒ AM = NM . (1 điểm)
Ta có NA ⊥ AK và BH ⊥ AK ⇒ AN / /BH
Xét ∆KAM, ta có IH / / AM ⇒ KI IH = (1) KM MA Xét ∆KNM, ta có / / KI BI BI MN ⇒ = (2) KM MN
Từ (1) và (2), ta có IH BI =
⇒ IH = BI (vì MA = MN) , suy ra I là trung điểm BH 0,25 MA MN
Ta có F là trung điểm AB , suy ra FI 1 = . AH 2
Gọi r (r > 0) là bán kính nắp đậy của thùng sơn. Thể tích thùng sơn là 2 V V = π r h ⇒ h = . 2 π r 0,25
Diện tích toàn phần của thùng sơn: 14. a 2 V 2 2V 2 V V 2 3 2 3 2
S = 2π rh + 2π r = 2π r + 2π r =
+ 2π r = + + 2π r ≥ 3 2πV = 300 2π cm (0,5 điểm) 2 π r r r r
Diện tích toàn phần của thùng sơn nhỏ nhất bằng 3 2 300 2π cm khi 0,25 V 2 V 10 = π ⇔ = 3 2 r r = cm 3 r 2π 2π Ta có: a +1 b +1 c +1 (a + ) 2 1 b (b + ) 2 1 c (c + ) 2 1 a P = + + = a +1− + b +1− + c +1− 0,25 2 2 2 2 2 2
b +1 c +1 a +1 b +1 c +1 a +1
(a + )1b (b + )1c (c + )1a
a + b + c − (ab + bc + ca)
≥ a + b + c + 3− ( + + ) = 3+ Mặt khác có: 2 2 2 2 14. b
(0,5 điểm) (a + b + c)2 2 2 2
= a + b + c + 2ab + 2bc + 2ca ≥ 3(ab + bc + ca) 3− 3
⇒ ab + bc + ca ≤ 3 ⇒ P ≥ 3+ = 3 2 0,25
Dấu bằng xảy ra khi a = b = c = 1; Vậy giá trị nhỏ nhất bằng 3.
SỞ GD&ĐT HÀ TĨNH
KỲ THI KHẢO SÁT CHẤT LƯỢNG HỌC SINH LỚP 9 NĂM HỌC 2024 - 2025
ĐỀ THI CHÍNH THỨC Môn thi: TOÁN
(Đề thi gồm 02 trang, 14 câu)
Thời gian làm bài: 90 phút, không kể thời gian phát đề MÃ ĐỀ 02
I. PHẦN TRẮC NGHIỆM (2,0 điểm)
(Trong mỗi câu hỏi từ câu 1 đến câu 8, viết vào tờ giấy thi đáp án đúng mà em chọn. Ví dụ: Câu 1 nếu
chọn A là đúng thì viết Câu 1: A).
Câu 1. Kết quả rút gọn biểu thức A = 12 + 48 là: A. 9. B. 6 3 .
C. 4 3 . D. 2 3 .
Câu 2. Nghiệm của phương trình 2(x + ) 1 = 4 là: A. 5. B. 1. C. 2. D. 1 − .
Câu 3. Đồ thị của hàm số 1 2
y = − x đi qua điểm nào sau đây: 3 A. (1; 3) . B. (1; 3 − ) . C. ( 3 − ; 3
− ) . D. (3;3) .
Câu 4. Gieo 1 đồng xu cân đối và đồng chất hai lần liên tiếp. Số phần tử không gian mẫu là: A. 4. B. 2. C. 1. D. 6.
Câu 5. Cho tam giác ABC vuông tại A . Biết AB = 3cm, AC = 4 cm, sinC bằng A. 3 . B. 4 . C. 3 4 . D. . 5 3 4 5
Câu 6. Thể tích của một hình nón có bán kính đáy 3 cm và chiều cao 6 cm là: A. 3 54π cm . B. 3 6π cm . C. 3 18π cm . D. 3 12π cm .
Câu 7. Nghiệm của bất phương trình 2 − x −8 ≥ 0 là: A. x ≤ 4. − B. x > 4. −
C. x ≥ 4. D. x ≤ 4.
Câu 8. Cho bảng tần số điểm kiểm tra giữa học kỳ II môn Toán của 40 học sinh lớp 9, trường THCS X như sau: Điểm 4 5 6 7 8 9 10 Tần số 1 2 5 7 15 8 2
Tần số tương đối của điểm số 8 là: A. 15%. B. 8%.
C. 3,75%. D. 37,5%.
II. PHẦN TỰ LUẬN (8,0 điểm) (Thí sinh trình bày lời giải vào tờ giấy thi)  
Câu 9 (1,0 điểm). Rút gọn biểu thức x x =  −  : x A
, với x > 0, x ≠ 4 x 4 x 2  − + x +   2
Câu 10 (1,0 điểm). Biết phương trình 2
x − 2x −10 = 0 có hai nghiệm x , x . Không giải phương trình, 1 2
tính giá trị của biểu thức 2 2
T = x + x − 5x x . 1 2 1 2 2x − 3y =1
Câu 11 (1,0 điểm). Giải hệ phương trình . 3   x − 4y = 2 Câu 12 (2,0 điểm).
a) Trong một hộp có 6 quả bóng bàn kích thước và chất liệu như nhau gồm 2 quả màu đỏ, 2 quả
màu xanh, 2 quả màu trắng Lấy ngẫu nhiên đồng thời 2 quả bóng bàn từ hộp. Tính xác suất của biến cố
A: “Trong 2 quả bóng bàn lấy ra có ít nhất một quả bóng bàn màu xanh”.
b) Một xí nghiệp đặt kế hoạch sản xuất 3000 sản phẩm trong một thời gian. Trong 6 ngày đầu
xí nghiệp thực hiện đúng kế hoạch, những ngày sau đó mỗi ngày xí nghiệp sản xuất vượt 10 sản phẩm
nên đã hoàn thành sớm được một ngày so với dự định và còn vượt mức 60 sản phẩm so với kế hoạch
ban đầu. Tính số sản phẩm xí nghiệp dự định làm trong một ngày theo kế hoạch ? Câu 13 (2,0 điểm).
Từ một điểm M ở bên ngoài đường tròn (O) , vẽ hai tiếp tuyến MC, MD với đường tròn
(C, D là hai tiếp điểm). Tia MO cắt đường tròn (O) tại hai điểm phân biệt A và B ( A nằm giữa
M và O ) và cắt đoạn CD tại F .
a) Chứng minh bốn điểm C,O, D, M cùng thuộc một đường tròn.
b) Vẽ đường kính CK của đường tròn (O) . Gọi H là chân đường vuông góc kẻ từ D đến
CK, I là giao điểm của MK và DH . Chứng minh .
MA MB = MF.MO và tính tỉ số FI . CH
Câu 14 (1,0 điểm).
a) Một nhà máy sản xuất cần thiết kế một thùng sơn dạng hình trụ bằng nhựa Polypropylen có nắp đậy với dung tích 3
800cm . Tìm bán kính nắp đậy của thùng sơn để nhà sản xuất tiết kiệm nguyên vật liệu nhất.
b) Cho a, b, c là các số thực dương và thỏa mãn điều kiện a + b + c = 6 .
Tìm giá trị nhỏ nhất của biểu thức a + 4 b + 4 c + 4 P = + + . 2 2 2
b + 4 c + 4 a + 4
--------Hết--------
- Thí sinh không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.
Họ tên thí sinh: …………………………......…; Số báo danh: ............................ IV. Đáp án HƯỚNG DẪN CHẤM
I- PHẦN GHI KẾT QUẢ (Mỗi câu có kết quả đúng cho 0,25 điểm) Câu Câu 1
Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Đáp án B B C A A C A D
II- PHẦN TỰ LUẬN (8 điểm) CÂU ĐÁP ÁN ĐIỂ M  0,25 x x x A =   ( −  x + 2)( x − 2) : x + 2 x + 2  0,25  x x ( x −2)  x =  −  9
( x + 2)( x − 2) ( x + 2)( x − 2) :  x + 2 (1 điểm)  0,25
x − x ( x −2)  x =  ( 
x + 2)( x − 2) :  x + 2  0,25 2 x x + 2 2 = ( = .
x + 2)( x − 2). x x − 2
Do phương trình đã cho luôn có hai nghiệm nên 0,5 10 x + x = 2
Theo định lý Viete ta có 1 2  . (1 điểm) x x = 10 − 1 2 0,5 Ta có 2 2 2
T = x + x − 5x x = x + x
− 7x x = 4 + 70 = 74 . 1 2 1 2 ( 1 2) 1 2 Hệ đã cho có dạng 6x − 9y = 3 (1) 
Trừ từng vế hai phương trình (1) và (2) ta được phương trình −y = 1 − 6x − 8y = 4 (2) 0,5
Câu 11 khi đó y =1. (1 điểm)
Thế giá trị y =1 vào phương trình 2x − 3y =1 ta được phương trình
2x − 3 =1 hay x = 2 . 0,5
Vậy hệ phương trình có nghiệm duy nhất ( ; x y) = (2; ) 1 .
Kí hiệu các quả bóng bàn đỏ, xanh, trắng lần lượt là Đ1, Đ2, X1, X2, T1, T2. 12.a Không gian mẫu:
(1 điểm) Ω = { Đ1Đ2, X1X2, T1T2, Đ1X1, Đ1X2, Đ2X1, Đ2X2, Đ1T1, Đ1T2, Đ2T1, Đ2T2, X1T1, X1T2, 0,5 X2T1, X2T2}
Có 9 kết quả thuận lợi cho biến cố A là: X1X2, X1Đ1, X1Đ2, X1T1, X1T2, X2Đ1, X2Đ2, X2T1, X2T2.
Xác suất của biến cố A là: P( A) 9 0,5 = . 15
Gọi số sản phẩm xí nghiệp làm trong 1 ngày theo dự định là x (sản phẩm)
Thời gian hoàn thành công việc theo dự định là 3000 (ngày) x
Số sản phẩm làm trong 6 ngày đầu là 6x (sản phẩm) 0,25
Những ngày sau, mỗi ngày xí nghiệp làm được số sản phẩm là x + 10 (sản phẩm)
Thời gian làm số sản phẩm còn lại và làm vượt mức 60 sản phẩm là − + − 0,25 12.b
3000 6x 60 3060 6x = (ngày) (1 điểm) x +10 x +10
Vì xí nghiệp hoàn thành công việc sớm hơn 1 ngày, nên ta có phương trình: 3000  3060 − 6 0,25 6 x  − + =   1 xx +10  2
⇔ x +130x − 30000 = 0
⇔ x =120 (thỏa mãn), x = 250 − (loại) 1 2
Vậy số sản phẩm xí nghiệp dự định làm trong 1 ngày theo kế hoạch là 120 (sản phẩm) 0,25
a) Ta có MC, MD lần lượt là tiếp tuyến của đường tròn (O) nên  =  0 MCO MDO = 90 . 0,5 13. a)
Gọi J là trung điểm MO, vì tam giác (1 điểm)
MCO vuông tại C, nên ta có
JC = JM = JO ,
vì tam giác MDO vuông tại D, nên ta có 0,5
JD = JM = JO , suy ra bốn điểm C, O,
D, M cùng thuộc một đường tròn. Đpcm.
b) Ta có hai tam giác MCA và MBC đồng dạng (học sinh phải chứng minh), nên ta có 0,25 2 . MA MB = MC
Ta có hai tam giác MFC và MCO đồng dạng (học sinh phải chứng minh), nên ta có 0,25 2
MF.MO = MC do đó MF.MO = . MA MB
- Gọi N là giao điểm của CM và KD Ta có  0
CDK = 90 (Vì D ∈(O), AK đường kính), suy ra NK ⊥ CD 13. b)
(1 điểm) Theo tính chất tiếp tuyến, ta có MO ⊥ CD
Do đó MO / /NK 0,25
Xét ∆CNK, ta có O là trung điểm CK , suy ra M là trung điểm CN ⇒CM = NM .
Ta có NC ⊥ CK và DH ⊥ CK ⇒ CN / /DH
Xét ∆KCM, ta có IH / /CM ⇒ KI IH = (1) KM MC Xét ∆KNM, ta có / / KI DI DI MN ⇒ = (2) KM MN 0,25
Từ (1) và (2), ta có IH DI =
⇒ IH = DI (vì MC = MN) , suy ra I là trung điểm DH MC MN
Ta có F là trung điểm CD , suy ra FI 1 = . CH 2 Gọi r (r
> 0) là bán kính nắp đậy của thùng sơn. Thể tích thùng sơn là 2 V V = π r h ⇒ h = . 2 π r 0,25
Diện tích toàn phần của thùng sơn: 14. a 2 V 2 2V 2 V V 2 3 2 3 2
S = 2π rh + 2π r = 2π r + 2π r =
+ 2π r = + + 2π r ≥ 3 2πV =120 20π cm (0,5 điểm) 2 π r r r r
Diện tích toàn phần của thùng sơn nhỏ nhất bằng 3 2 120 20π cm khi 0,25 V 2 800 50 = π ⇔ = 3 = 3 2 r r 2 cm r 2π π Ta có: 0,25 1  (a + 4) 2 b (b + 4) 2c (c + 4) 2 a P =  a + 4 − + b + 4 − + c + 4 − 2 2 2 4 b 4 c 4 a 4  + + +   1 
(a + 4)b (b + 4)c (c + 4)a + +  ≥  + + +12 − ( + + ) = 3 ab bc ca a b c − 4 4 4 4 16    14. b 0,25
(0,5 điểm) Mặt khác có:
(a +b + c)2 2 2 2
= a + b + c + 2ab + 2bc + 2ca ≥ 3(ab + bc + ca) 12 9
⇒ ab + bc + ca ≤12 ⇒ P ≥ 3− = 16 4
Dấu bằng xảy ra khi a = b = c = 2;
Vậy GTNN của P bằng 94
Xem thêm: KHẢO SÁT CHẤT LƯỢNG TOÁN 9
https://thcs.toanmath.com/khao-sat-chat-luong-toan-9
Document Outline

  • Mã đề 01_04.5
  • Mã đề 02_04.5
  • KS 9

Tài liệu liên quan: