Đề khảo sát chất lượng Toán 9 năm 2024 – 2025 sở GD&ĐT Thái Bình

SỞ GIÁO DỤC VÀ ĐÀO TẠO
ĐỀ KHẢO SÁT CHẤT LƯỢNG NĂM HỌC 2024 - 2025 THÁI BÌNH Môn: TOÁN 9
Thời gian làm bài: 120 phút, không kể thời gian phát đề
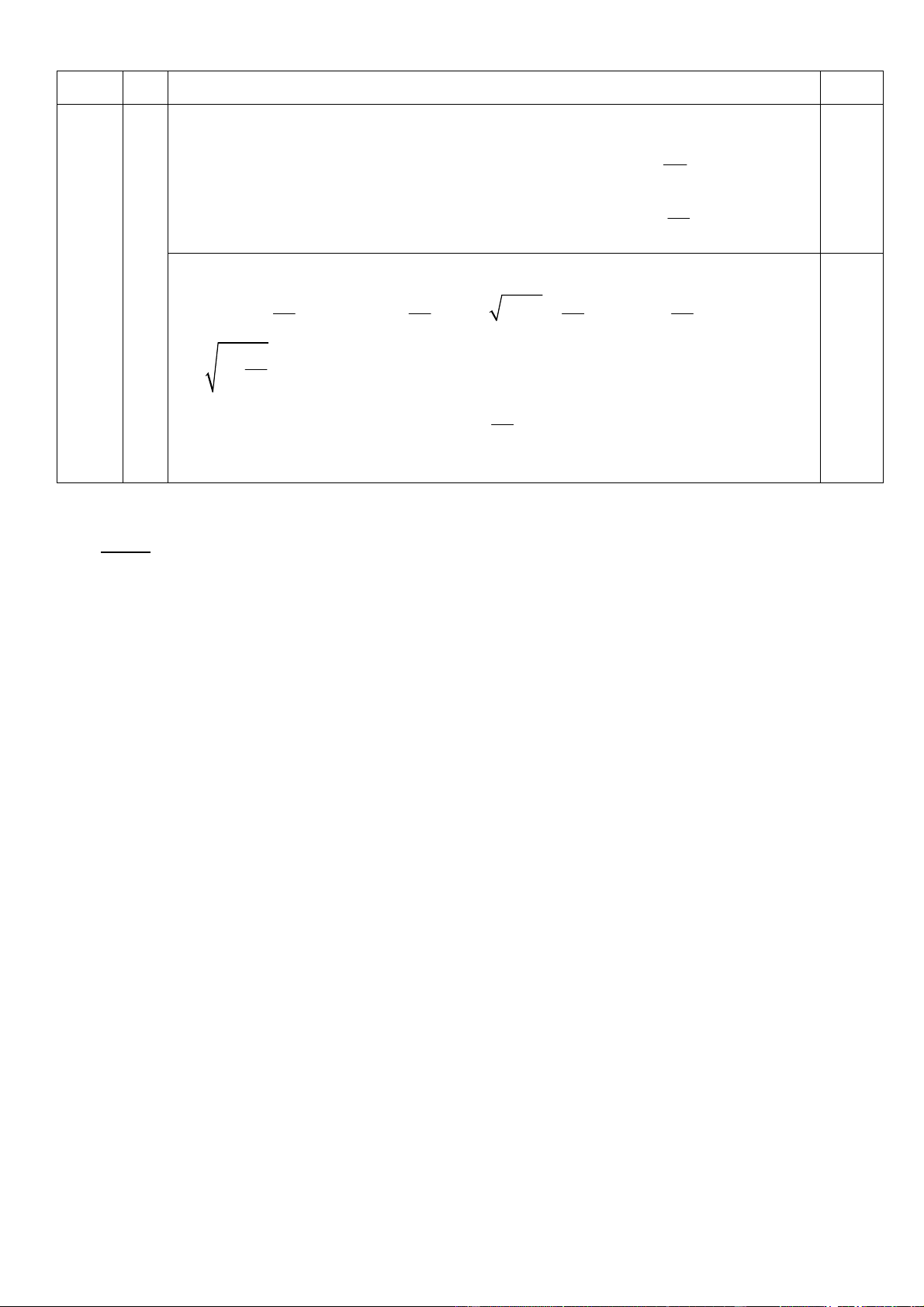
Câu 1. (2,0 điểm) x  2 x 1 x 1 3 x  1 1 Cho hai biểu thức A  và B    với x  0, x  , x  1. 2 x 1 x 1 x 1 x 1 4
a) Tính giá trị của biểu thức A khi x = 16.
b) Rút gọn biểu thức B.
c) Tìm tất cả các giá trị của x để A.B  0.
Câu 2. (2,5 điểm)
a) Cho bảng tần số thể hiện ngành nghề yêu thích của các em học sinh lớp 12A: Ngành nghề Công an Bác sĩ Ca sĩ Diễn viên Giáo viên Cộng Tần số 8 9 4 10 9 40
Hãy lập bảng tần số tương đối của mẫu số liệu thống kê trên.
b) Gieo đồng thời hai đồng xu cân đối, đồng chất I và II. Tính xác suất để có ít nhất một đồng xu xuất hiện mặt sấp.
c) Một cái ly thuỷ tinh dạng hình trụ có đường kính đáy là 6 cm và chiều cao là 15 cm được để
trên một mặt phẳng nằm ngang và đang chứa đầy nước. Một chiếc bát sứ được coi là có dạng nửa
hình cầu đường kính là 12 cm. Hỏi chiếc bát sứ đó có đựng được toàn bộ lượng nước mà cái ly
đang chứa hay không? (Giả thiết độ dày thành ly, đáy ly và độ dày thành bát là không đáng kể).
Câu 3. (2,0 điểm)
a) Một cửa hàng thời trang đang có chương trình khuyến mại cho một loại quần áo. Tổng giá
tiền niêm yết của một chiếc quần và một chiếc áo loại đó là 1,2 triệu đồng. Nhưng nếu khách hàng
mua loại quần áo đó với số lượng từ 5 chiếc trở lên thì mỗi chiếc quần được giảm giá 10% và mỗi
chiếc áo được giảm giá 15%. Mẹ Ngọc mua tặng Ngọc 2 chiếc quần và 3 chiếc áo loại đó phải thanh
toán 2,685 triệu đồng. Hỏi giá niêm yết của mỗi chiếc quần và mỗi chiếc áo loại đó là bao nhiêu?
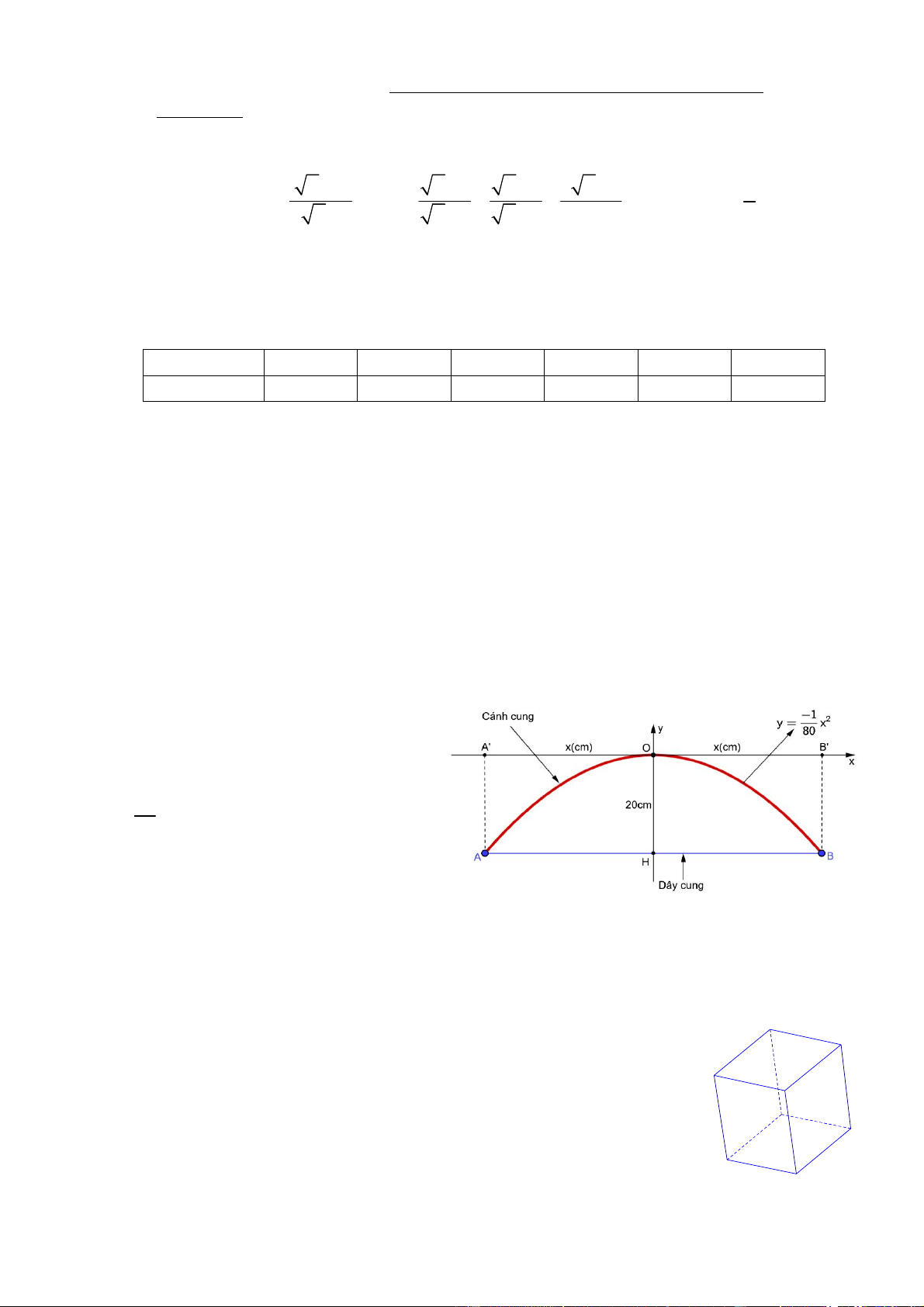
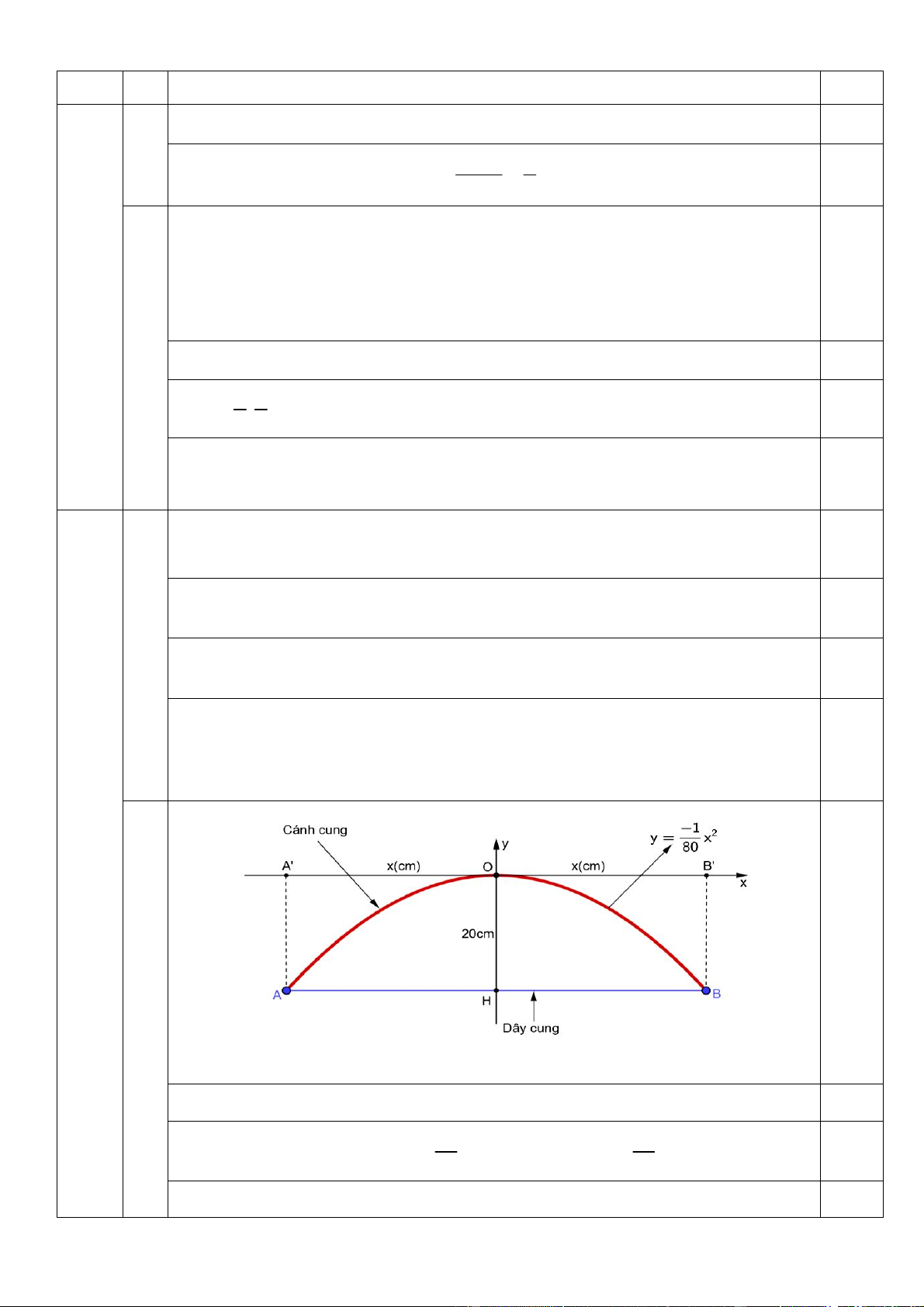
b) Trong mặt phẳng tọa độ Oxy, cánh cung
của một cung thủ có dạng như hình vẽ bên.
Biết rằng khi ở trạng thái dây cung không
kéo, cánh cung có hình dạng của parabol 1 2 y  
x và khoảng cách từ đỉnh O của 80
cánh cung đến dây cung AB là OH = 20 cm.
Tính độ dài của dây cung AB.
Câu 4. (3,0 điểm)
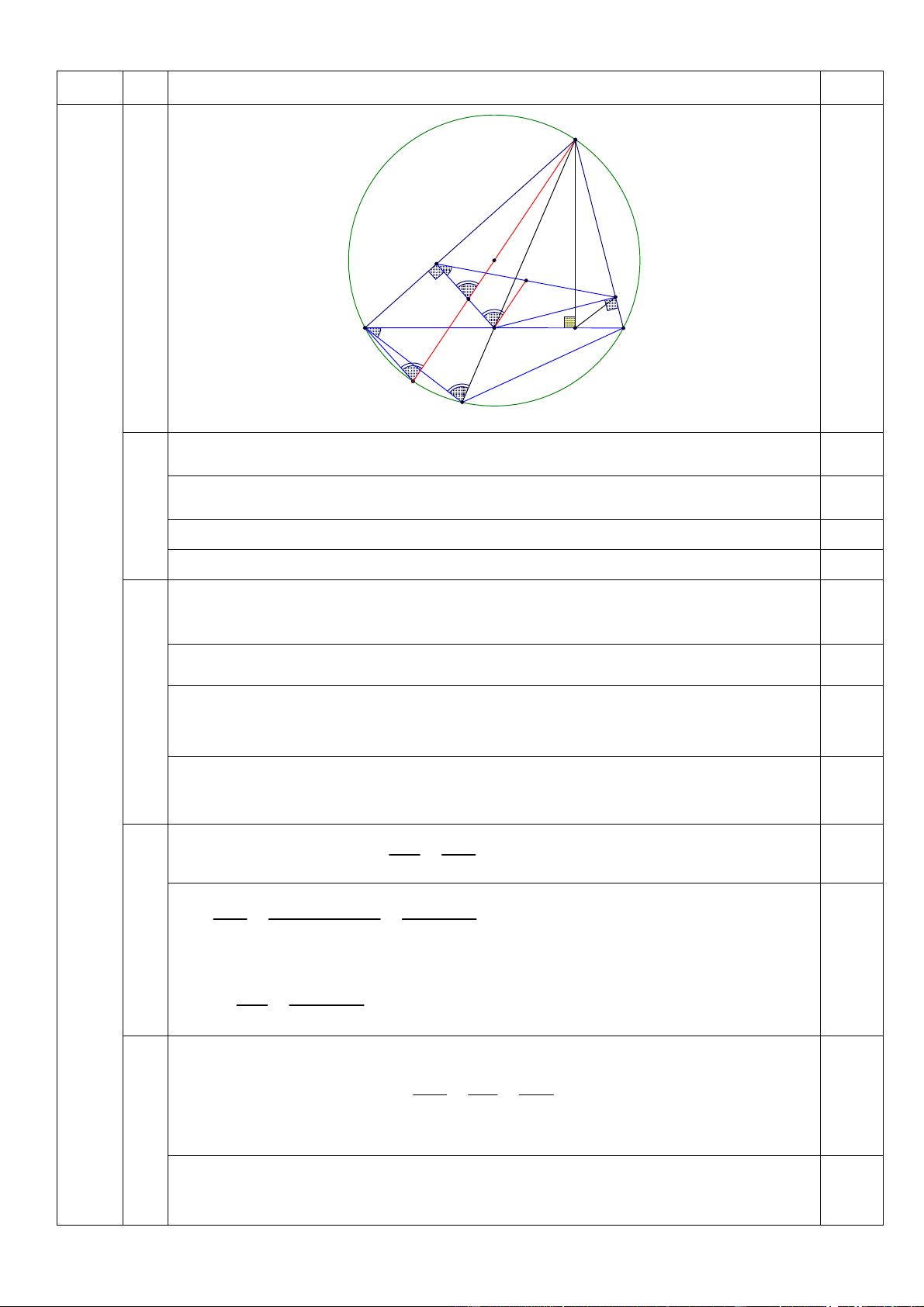
Cho tam giác nhọn ABC (AB > AC) nội tiếp đường tròn (O). Gọi M là trung điểm của BC; E và F
lần lượt là chân đường vuông góc kẻ từ M đến AB và AC.
a) Chứng minh A, E, M, F cùng thuộc một đường tròn.
b) Gọi K là giao điểm thứ hai của AM với đường tròn (O). Chứng minh KBC ᔕ MEF. c) Chứng minh   KB.Sin BCA  KC.Sin ABC .
d) Gọi J là trung điểm của EF. Chứng minh JM // AO.
Câu 5. (0,5 điểm)
Một công ty muốn thiết kế một loại hộp nhôm có dạng hình hộp chữ nhật
(như hình vẽ bên); có đáy là hình vuông độ dài cạnh là x dm và thể tích hộp
là 8 dm3. Để tiết kiệm vật liệu nhôm làm hộp, người ta cần thiết kế sao cho
diện tích toàn phần nhỏ nhất. Hỏi x có giá trị bằng bao nhiêu đềximet? ----- HẾT -----
Họ và tên: ................................................................ Số báo danh: ................
SỞ GIÁO DỤC VÀ ĐÀO TẠO
KHẢO SÁT CHẤT LƯỢNG NĂM HỌC 2024- 2025 THÁI BÌNH
HƯỚNG DẪN CHẤM VÀ BIỂU ĐIỂM MÔN TOÁN 9 (Gồm 04 trang) Câu Ý Nội dung Điểm Câu 1 a) 1
Thay x  16 (thoả mãn điều kiện x  0, x 
, x  1 ) vào biểu thức A. 0,25 (2,0) (0,5) 4 16  2 A  2 16 1 4  2 2 2 A  
. Vậy khi x  16 thì A  . 0,25 2.4 1 7 7 b) Ta có: 0,25 (1,0)   2    2 x 1 x 1  3 x     1 x 1 x 1 3 x 1 B     x 1 x 1  x  1 x  1  x  1 x  1
x  2 x 1  x  2 x 1 3 x 1 2x  3 x 1 0,25   .  x  1 x  1  x  1 x  1  0,25 2 x   1  x   1 2 x 1   .  x  1 x   1 x 1 2 x 1 0,25 Vậy B  . x 1 c) x  2 2 x 1 x  2 0,25 (0,5) Ta có A.B  .  . 2 x 1 x 1 x 1 x  2 0,25 A.B  0 khi
 0 , suy ra x  2  0 (vì x 1>0) hay x  4 . x 1 1 1
Kết hợp với điều kiện x  0, x 
, x  1 , ta được 0  x  4 , x  , x  1 4 4 Câu 2 a)
Bảng tần số tương đối của mẫu số liệu thống kê trên là: (2,5) (0,5) Công Diễn Giáo Ngành nghề Bác sĩ Ca sĩ Cộng an viên viên 0,5 Tần số 20% 22, 5% 10% 25% 22, 5% 100% tương đối
b) Không gian mẫu của phép thử là   
 S,S;S, N;N,S;N, N . 0,25
(1,0) Vì các đồng xu cân đối và đồng chất nên 4 kết quả trên là đồng khả năng
Suy ra số phần tử của không gian mẫu là n   4 .
Gọi biến cố A: “Có ít nhất một đồng xu xuất hiện mặt sấp”. 0,25
Các kết quả thuận lợi cho biến cố A là A  
 S,S; S,N; N,S . 1 Câu Ý Nội dung Điểm
Số phần tử của A là n A  3 . 0,25 n A 3 0,25
Xác suất của biến cố A là P A    0, 75 . n  4 c)
Vì độ dày thành ly, đáy ly và độ dày thành bát là không đáng kể nên thể tích 0,25
(1,0) lượng nước trong ly bằng thể tích của hình trụ có đường kính đáy là 6 cm và
chiều cao là 15 cm; thể tích phần không gian bên trong chiếc bát bằng nửa thể
tích hình cầu đường kính 12 cm. Do vậy thể tích nước và thể tính phần không
gian bên trong chiếc bát là: 2
V   .3 .15  135 (cm3). 0,25 n 1 4 0,25 3 V 
.  .6  144 (cm3). kgb 2 3 Ta thấy V  V
nên chiếc bát sứ đó dựng được toàn bộ lượng nước mà chiếc 0,25 n kgb ly đang chứa. Câu 3 a)
Gọi giá niêm yết của một chiếc quần và một chiếc áo loại đó lần lượt là x; y 0,25
(2,0) (1,0) triệu đồng x; y  0 .
Vì tổng giá tiền niêm yết của một chiếc quần và một chiếc áo loại đó là 1, 2 0,25
triệu đồng nên ta có phương trình x  y  1, 2
Vì mẹ Ngọc phải trả 2, 685 triệu đồng cho 2 chiếc quần và 3 chiếc áo loại đó 0,25
nên ta có phương trình 2x.90%  3y.85%  2, 685 hay 1,8x  2,55y  2, 685 x  y  1, 2 x  0,5 0,25 Ta có hệ  . Giải hệ ta được  (thỏa mãn). 1,8x  2,55y  2, 685  y  0, 7 
KL: Giá niêm yết 1 chiếc quần là 500 (nghìn đồng), 1 chiếc áo là 700 (nghìn đồng). b) 0,25 (1,0)
Đặt OB '  x cm, x  0 .
Khi đó điểm B có tọa độ x; 20 . 0,25 1 1 0,25 Vì điểm B thuộc parabol 2 y   x nên ta có 2 20   x suy ra x  40 80 80
Vậy độ dài dây cung AB  2x  80cm . 0,25 2 Câu Ý Nội dung Điểm Câu 4 A (3,0) E O J F N B M H C P K a)
Vì ME  AB nên AEM vuông ở E. 0,25
(1,0) Suy ra tam giác AEM nội tiếp đường tròn đường kính AM. 0,25
Tương tự tam giác AFM cũng nội tiếp đường tròn đường kính AM. 0,25
Suy ra các điểm A, E, M, F cùng thuộc đường tròn đường kính AM. 0,25 b) Trong đườ  
ng tròn đường kính AM ta có MEF  MAF (Hai góc nội tiếp cùng 0,25 (1,0) chắn cung  MF ).   
Trong đường tròn (O) ta có MAF  KBC (Hai góc nội tiếp cùng chắn cung KC ). 0,25   Suy ra MEF  KBC . 0,25  
Chứng minh tương tự được MFE  KCB.     K  BC và M
 EF có: MEF  KBC , MFE  KCB. 0,25 Suy ra K  BC ᔕ M  EF (g – g). c) KB ME 0,25 Vì K  BC ᔕ M  EF nên  . (0,5) KC MF   ME MB.Sin ABC Sin ABC 0,25 Mà     (Do B  EM , C  FM là những tam giác MF MC.Sin BCA Sin BCA vuông và MB  MC ).  KB Sin ABC   Suy ra 
 hay KB.Sin BCA  KC.Sin ABC (đpcm). KC Sin BCA
d) Kẻ đường kính AP của đường tròn (O). 0,25 (0,5) BK BC BM Do K  BC ᔕ M  EF suy ra   . EM EF EJ Do đó KBM ᔕ M  EJ (c – g – c).    
Suy ra EMJ  BKM  BPA  ENA . 0,25
Từ đó suy ra JM // AO (đpcm). 3 Câu Ý Nội dung Điểm Câu 5
Gọi chiều cao của khối hộp là h (dm), điều kiện h  0 . 0.25 (0,5) 8
Do thể tích khối hộp bằng 8 (dm3) nên ta có 2 x .h  8  h  . 2 x 32
Diện tích toàn phần của khối hộp là 2 2 S  2x  4xh  2x  . tp x
Theo bất đẳng thức AM-GM cho hai số dương ta có 0,25 2 32     2   32 2 32 32 S 2x 2x 8   8  2 16x   8  8x   8 tp x x x x 32  2 8x.  8  32  8  24 . x 32 Đẳng thức xảy ra khi 2 2x  8 và 8x  , suy ra x  2 . x
Vậy khi cạnh đáy bằng 2 (dm) thì diện tích toàn phần của khối hộp nhỏ nhất. Chú ý:
- Trên đây là hướng dẫn chấm. Giám khảo căn cứ vào nội dung và điểm số tương ứng
trong hướng dẫn để thống nhất cho điểm bài thi một cách hợp lý;
- Điểm thành phần và điểm toàn bài không làm tròn;
- Các phương án đúng khác giám khảo căn cứ hướng dẫn, thống nhất cho điểm tương ứng. -----HẾT----- 4
Xem thêm: KHẢO SÁT CHẤT LƯỢNG TOÁN 9
https://thcs.toanmath.com/khao-sat-chat-luong-toan-9
Document Outline

• De_Toan9_KS24-25
• HDC_DA_Toan9_KS24_25
• KS 9