Đề Khảo Sát Chọn HSG Toán 8 Phòng GD&ĐT Hải Hậu 2025-2026 Có Đáp Án

PHÒNG GD&ĐT HẢI HẬU
ĐỀ KHẢO SÁT CHỌN HỌC SINH GIỎI MÔN TOÁN - LỚP 8 Năm học 2025-2026 ĐỀ CHÍNH THỨC
Thời gian làm bài: 120 phút (Không kể thời gian giao đề) Đề bài
Bài 1: (4,0 điểm) 2 3 2
y − y − 2 x −10x + 25x Cho biểu thức: P = : 2 y − 2 x − 25 1. Rút gọn P.
2. Tính giá trị của P với các giá trị của x và y thỏa mãn đẳng thức: 2 2
x + x − 2 + 4 y − 4xy = 0. Bài 2: (4,0 điểm)
1. Tìm a và b để đa thức 4 3 2
f (x) = x − 3x + 3x + ax + b chia hết cho đa thức 2
g(x) = x + 4 − 3 . x
2. Chứng minh rằng tích của 4 số nguyên dương liên tiếp không thể là một số chính phương. Bài 3: (3,0 điểm)
x − b − c
x − c − a x − a − 1. Cho b
abc (ab + bc + ca)  0, giải phương trình ẩn x: + + = 3. a b c
2. Tìm các cặp số nguyên (x;y) thoả mãn 3 3
x + y +1 = 6x . y Bài 4: (7,0 điểm)
Cho tam giác ABC vuông cân tại A có D là trung điểm của BC. Trên AD lấy điểm M bất kì, Gọi
E và F là hình chiếu của M trên AB, AC.
1. Chứng minh EF//BC.
2. Kẻ EN vuông góc với FD. a. Tính góc ANM.
b. Chứng minh NE là phân giác của góc ANM.
3. Chứng minh ba điểm B, M, N thẳng hàng. Bài 5: (2,0 điểm)
1. Cho ba số dương x, y, z thoả mãn xyz = 1 1 1 1
Tìm giá trị lớn nhất của biểu thức P = + + 3 3 3 3 3 3
x + y +1 y + z +1 z + x +1
2. Trên 6 đỉnh của một lục giác lồi có ghi 6 số chẵn liên tiếp theo chiều kim đồng hồ. Ta
thay đổi các số như sau: Mỗi lần chọn một cạnh bất kì rồi cộng mỗi số ở hai đỉnh thộc cạnh đó
với cùng một số nguyên nào đó. Hỏi sau một số lần thay đổi như thế thì 6 số mới ở các đỉnh lục
giác có thể bằng nhau không? Vì sao? ------- Hết ------
Họ và tên thí sinh: ......................................
Họ tên, chữ kí GT số 1: ..........................................
Số BD: ................. Phòng thi số: …………
Họ tên, chữ kí GT số 2: ……………...................... Trang 1
PHÒNG GD&ĐT HẢI HẬU
HƯỚNG DẪN CHẤM KHẢO SÁT CHỌN HSG
MÔN TOÁN LỚP 8 Năm học 2025-2026 Câu Nội dung Điểm 2 3 2
y − y − 2 x −10x + 25x Cho biểu thức: P = : 2 y − 2 x − 25 1 1. Rút gọn P 4.0
2. Tính giá trị của P với các giá trị của x và y thỏa mãn đẳng thức: 2 2
x + x − 2 + 4 y − 4xy = 0. 1.1
ĐKXĐ: y  2, x  0, x  5 0.5
y + y − y − x ( 2 2 x −10x + 25 2 2 ) Khi đó: P = : 0.5 y − 2
(x − 5)(x + 5)
y ( y + ) − ( y + ) x (x − )2 1 2 1 5 = : y − 2 (x −5)(x + 5) 0.5 ( y + )
1 ( y − 2) (x + 5)(x − 5) ( y + ) 1 (x + 5) = . = y − 2 x(x − 5)2 x(x − 5) 0.5 1.2 Vì 2 2
x + x − 2 + 4 y − 4xy = 0 2 2
 x − 4xy + 4y + x − 2 = 0 0.5  (x − y)2 2 + x − 2 = 0 0.5 (
 x − 2y)2 = 0 x = 2     (TM ) 0.5  x − 2 = 0   y = 1 (1+1)(2 + 5) 7 −  P = = 2(2 − 5) 3 0.5 2 1.
Tìm a và b để đa thức : 4 3 2
f (x) = x − 3x + 3x + ax + b chia hết cho đa thức 2
g(x) = x + 4 − 3x. 4.0 2.
Chứng minh rằng tích của 4 số nguyên dương liên tiếp không
thể là một số chính phương. 2.1 Ta có : 4 3 2 2
x − 3x + 3x +ax + b : x − 3x + 4 1.0 2
= x +1dư (a − 3)x + b + 4
f(x) chia hết cho g(x) khi và chỉ khi số dư bằng 0. a − 3 = 0  a = 3     b + 4 = 0 b = 4 − 1.0 Kết luận 2.2
Giả sử có 4 số nguyên dương liên tiếp là n, n + 1, n + 2, n + 3 0.5
Xét tích: P = n(n + ) 1 (n + 2)(n + 3) = ( 2 n + 3n)( 2 n + 3n + 2) = (n + 3n)2 2 + 2( 2 n + 3n) 0.5
Dễ dàng nhận thấy: (n + n)2  P  (n + n + )2 2 2 3 3 1 0.5 Trang 2
Vậy P không thể là số chính phương 0.5 3
1. Cho abc(ab + bc + ca)  0, giải phương trình ẩn x: 3.0
x − b − c x − c − a
x − a − b + + = 3 a b c
2. Tìm các cặp số nguyên (x;y) thoả mãn 3 3
x + y +1 = 6xy 3.1 − − − − − − Với x b c x c a x a b
abc(ab + bc + ca)  0, ta có: + + = 3 a b c
x − b − c − a
x − c − a − b x − a − b − c 0.25  + + = 0 a b c  1 1 1 
 (x − a − b − c) + + = 0    a b c  
x − a − b − c = 0 
x = a + b + c  0.25 1 1 1  
 ab + bc + ca  + + = 0  = 0(*)  a b c  abc
Ta thấy (*) không xảy ra vì abc(ab + bc + ca)  0. 0.25
Vậy nghiệm của phương trình là x = a + b + c 0.25 3.2 Ta có: 3 3 3 2 2 2
a + b + c − 3abc = (a + b + c)(a + b + c −ab − bc − ca) 0.25 3 3
 x + y +1 = 6xy 3 3 3
 x + y + 2 − 3. . x . y 2 = 7 2 2
 (x + y + 2)(x + y + 4 − xy − 2x − 2y) = 7 0.25 Lại có: 2 2 2 2 2 2(x + y 4
+ − xy − 2x − 2y) = (x − y) + (x − 2) + (y − 2)  0 0.25
Nên ta có 2 trường hợp sau: 2
(x + y) − 3xy − 2(x + y) + 4 = 7 x + y = 1 − 0.25 +)    x + y + 2 =1 xy = 0  ( ; x y) = (0; 1 − );( 1 − ;0) 2
(x + y) − 3xy − 2(x + y) + 4 =1 x + y = 5 y = 5 − x 0.25 +)      x + y + 2 = 7 xy = 6
x(5 − x) = 6  ( ; x y) = (2;3);(3;2)
Vậy nghiệm nguyên của phương trình là 0.25 ( ; x y) = (0; 1 − );( 1 − ;0);(2;3);(3;2) 4
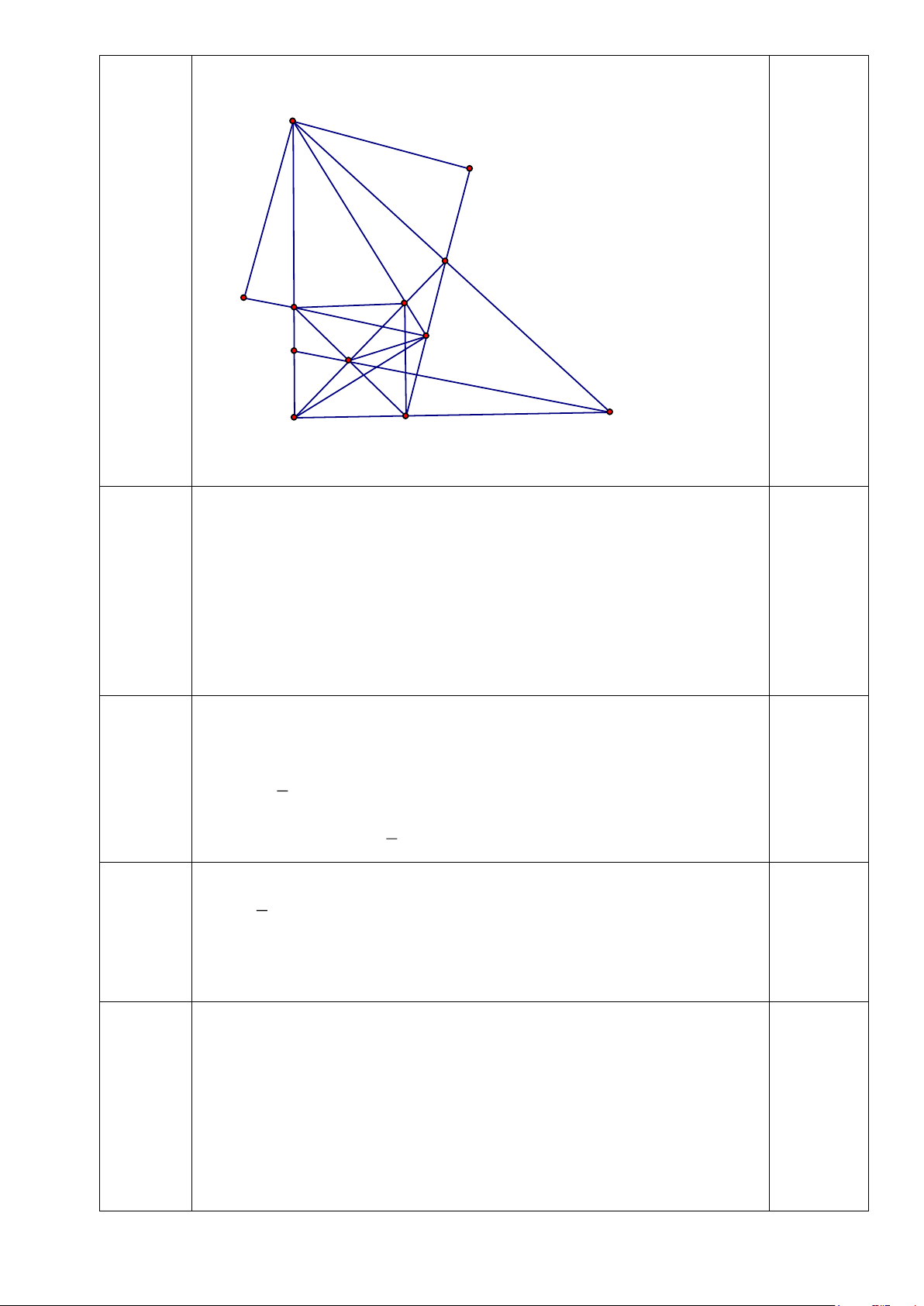
Cho tam giác ABC vuông cân tại A có D là trung điểm của BC. Trên 7.0
AD lấy điểm M bất kì, Gọi E và F là hình chiếu của M trên AB, AC.
1. Chứng minh EF song song với BC.
2. Kẻ EN vuông góc với FD. a. Tính góc ANM .
b. Chứng minh NE là phân giác của ANM .
3. Chứng minh ba điểm B, M, N thẳng hàng. Trang 3 B P M D Q E K O N j I C A F 4.1 Ta có 
ABC vuông cân ở A, có AD là đường trung tuyến 0.5
 AD đồng thời là đường cao, đường phân giác của ABC
Xét tứ giác AEMF có 0
EAF = AEM = AFM = 90 0.5
 tứ giác AEMF là hình chữ nhật (dhnb).
Lại có AD là phân giác của EAF
 tứ giác AEMF là hình vuông AM ⊥ EF 0.5
Mà AM ⊥ BC  EF / /BC 0.5 4.2a
Gọi O là giao điểm của AM và EF. Tứ giác AEMF là hình vuông 0.5
 OA = OE = OM = OF và EF = AM (t/c)
Xét ENF vuông tại N có NO là trung tuyến ứng với cạnh huyền EF nên 1 0.5 NO = EF (t/c). 2 Mà EF = AM 1
 NO = AM  AMN  vuông tại N 0  ANM = 90 2 0.5 4.2b
Theo tính chất góc ngoài của hai tam giác cân ENO và ANO ta có 1 0 0.5 ENA = EOA = 45 2 0  ENM = 45 0.5  0
ENA = ENM (= 45 )  NE là phân giác của ANM 0.5 4.3
Từ C kẻ tia Cx vuông góc với FD tại I và cắt AB tại K.
Gọi P và Q theo thứ tự là hình chiếu của B trên FD và EN ta c/m
được tứ giác BPNQ là hình chữ nhật. 0.5
Ta có BP / /CK(⊥ FD)  PBK = CKA (đồng vị) Mà 0 QBK + PBK = 90 , 0
KCA + CKA = 90  QBK = KCA
Lại có AB = AC(gt); AE = AF(cmt)  BE = CF  BQ  E = C
 IF (cạnh huyền- góc nhọn)  BQ = CI 0.5
Chứng minh BPD = CID (cạnh huyền- góc nhọn) Trang 4
 BP = CI  BP = BQ  Tứ giác BPNQ là hình vuông 0.5 nên NE là phân giác của 0 PNQ  BNQ = 45 0.5 Mà 0
QNM = 45 (cmt)  B, M , N thẳng hàng 5
1. Cho ba số dương x,y,z thoả mãn xyz = 1.Tìm giá trị lớn nhất của biểu thức 1 1 1 P = + + 3 3 3 3 3 3
x + y +1 y + z +1 z + x +1
2. Trên 6 đỉnh của một lục giác lồi có ghi 6 số chẵn liên tiếp theo 2.0
chiều kim đồng hồ. Ta thay đổi các số như sau: Mỗi lần chọn một
cạnh bất kì rồi cộng mỗi số ở hai đỉnh thộc cạnh đó với cùng một số
nguyên nào đó. Hỏi sau một số lần thay đổi như thế thì 6 số mới ở
các đỉnh lục giác có thể bằng nhau không? Vì sao? 5.1 Ta có: 3 3 2 2 3 2 2 3
x + y  x y + xy  x − xy − x y + y  0 2 2 2 2 2 2
 x(x − y ) − y(x − y )  0  (x − y)(x − y )  0 2  0.25
(x − y) (x + y)  0 (luôn đúng với mọi x, y  0 ) Do đó 1 1 1  = 3 3 2 2 2 2
x + y +1 x y + xy +1 x y + xy + xyz 1 z z 0.25 = = =
xy(x + y + z)
xyz(x + y + z)
x + y + z Tương tự 1 x  1 y ;  3 3
y + z +1 x + y + z 3 3
z + x +1 x + y + z 1 1 1 z y x  + +  + + 3 3 3 3 3 3
x + y +1 y + z +1 z + x +1 x + y + z x + y + z
x + y + z 0.25 
P  1. Dấu “=” xảy ra  x = y = z = 1
Vậy GTLN của P là 1  x = y = z =1 0.25 5.2
Gọi các số chẵn ghi ở 6 đỉnh của lục giác lồi lúc đầu theo thứ tự từ
nhỏ đến lớn là a ;a ;a ;a ;a ;a . 0.25 1 2 3 4 5 6
Vì đó là các số chẵn liên tiếp nên ta có
a − a + a − a + a − a = 2 + 2 + 2 = 6 2 1 4 3 6 5
 (a + a + a ) − (a + a + a ) = 6 0.25 2 4 6 1 3 5
Mỗi lần thay đổi thì hai số ở hai đỉnh kề nhau (theo thứ tự trên, coi a 6 kề với a
1 ) đều cộng thêm cùng một số nên hiệu trên luôn không đổi và luôn bằng 6. 0.25
Nếu 6 số mới ở các đỉnh lục giác lồi đều bằng nhau thì hiệu trên
bằng 0 nên sau một số lần thay đổi như thế thì 6 số mới ở các đỉnh
lục giác không thể bằng nhau. 0.25 Lưu ý: 1. Trong từng câu:
+ Học sinh giải cách khác hợp lý, đúng cho điểm tương ứng.
+ Các bước tính hoặc chứng minh độc lập cho điểm độc lập, các bước liên quan với nhau đúng
đến đâu cho điểm đến đó.
2. Điểm toàn bài là tổng điểm các phần đạt được không làm tròn. Trang 5