


Preview text:
UBND HUYỆN THƯỜNG XUÂN
KÌ THI KHẢO SÁT ĐỘI TUYỂN LẦN 5
TRƯỜNG THCS XUÂN LẸ NĂM HỌC 2023-2024
Môn thi: Toán - Lớp 7 Số báo danh
Thời gian: 120 phút (không kể thời gian giao đề) Ngày thi 13/3/2024
(Đề thi có 01 trang, gồm 5 câu)
Câu 1: (4.0 điểm). Tính giá trị các biểu thức sau: 1. A = 5 1 4 3 3 1 3 2 − − 2. B = 1 5 1 5 15 : − − 25 : − 6 3 15 5 4 7 4 7 2018 2018 2018 2018 5 4 9 + + + ... + 3. C = 4 9. − 6. 2 4. 2 3 4 2019 D = 210 3 . 8 + 68 20 . 2018 2017 2016 1 + + + ... + 1 2 3 2018
Câu 2: (4.0 điểm). 1. Tìm x, biết : a. ( x + ) = ( − )2 2 2 19 2.5 :14 13 8 − 4
b. 2x +1 + x +8 = 4x
2. Tìm x, y, z biết x y ; y z =
= và x − 2y + z = 48 − 2 3 5 4
Câu 3: (4.0 điểm).
1. Tìm số tự nhiên x, y biết: (x − )2 2 5. 2019 = 24 − y
2. Cho 3 số x , y , z khác 0 thỏa mãn điều kiện : y + z − x z + x − y x + y − z = = x y z
Hãy tính giá trị của biểu thức : B = 1 x 1 y 1 z + + + y z x
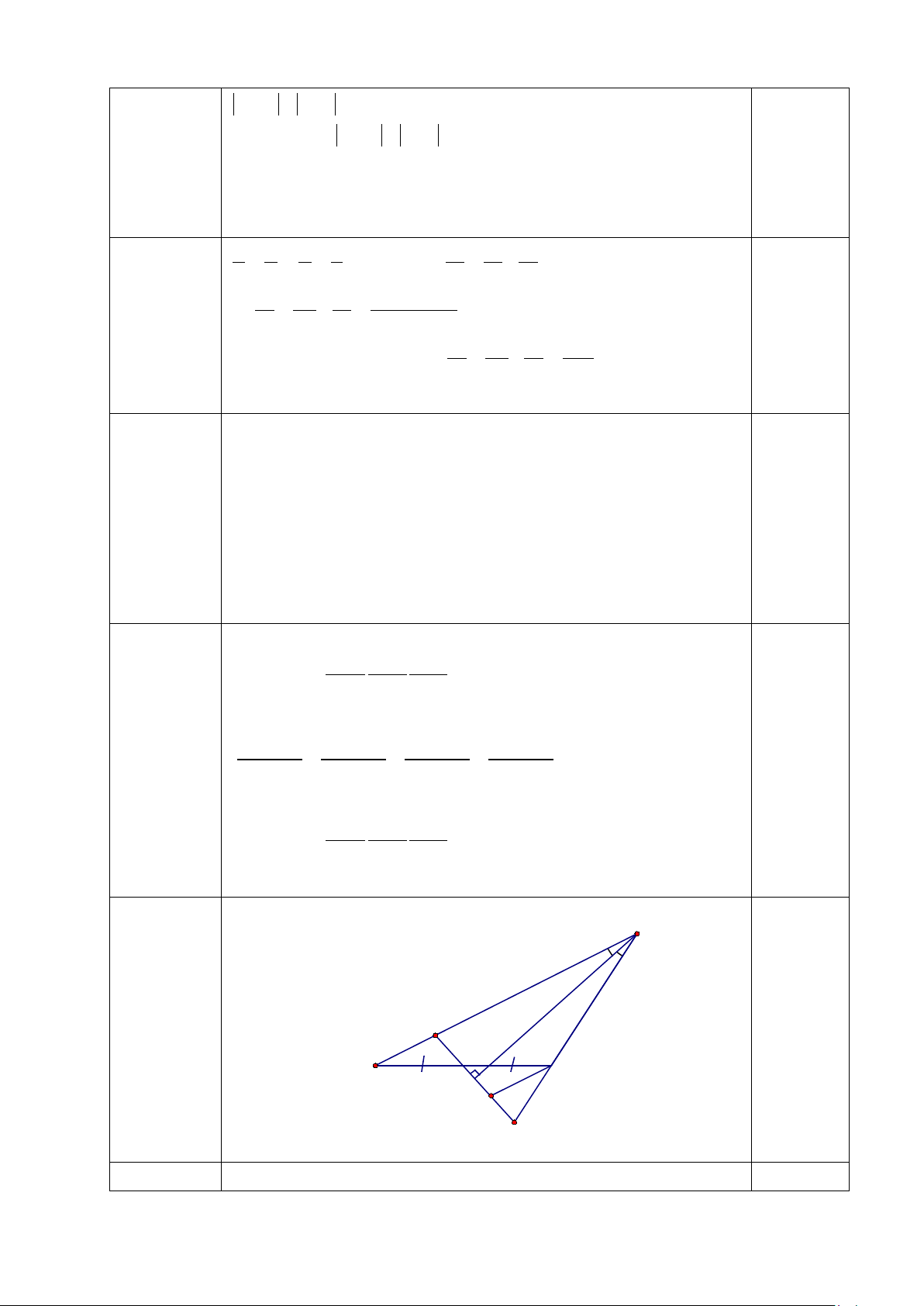
Câu 4:(6.0 điểm). Cho tam giác ABC (AB > AC), M là trung điểm của BC. Đường
thẳng qua M vuông góc với tia phân giác của góc A tại H cắt các đường thẳng AB,
AC lần lượt tại E và F. Chứng minh : 1. EH = HF 2. = − 2BME ACB B . 3. BE = CF .
Câu 5: (2.0 điểm). Tìm các chữ số a, b, c biết rằng: 1 1 1 11 + + = . ab bc . bc ca c . a ab 3321 Hết
Cán bộ coi thi không giải thích gì thêm!
HƯỚNG DẪN CHẤM TOÁN 7 LẦN 5 Câu
Nội dung cần đạt Điểm A = 5 1 4 3 3 1 3 2 − − 6 3 15 5 Câu 1.1 5 1 4 3 3 1 3 2 = + − − + − − 6 3 15 5 (1,0 điểm) 0,5 điểm 1 1 5 2 5 = 2 + 0,5 điểm 1− = ⋅ = 2 3 2 3 3
Nếu hs đổi ra phân số rồi quy đồng vẫn cho điểm tối đa B = 1 5 1 5 15 : 25 : − − − 4 7 4 7 Câu 1.2 1 1 5 = 15 − 25 : − 4 4 7 0,5 điểm (1,0 điểm) 1 1 5 15 25 : = + − − − 4 4 7 7 10 = − ⋅ − = 14 0,5 điểm 5 10 8 10 9 C = 2 .3 − 2 .3 Câu 1.3 0,5 điểm 10 8 10 8 2 .3 + 2 .3 .5 (1,0 điểm) 10 8 2 .3 (1−3) 1 − = = 0,5 điểm 10 8 2 .3 (1+ 5) 3 2018 2018 2018 2018 + + + ... + 2 3 4 2019 D = 2018 2017 2016 1 + + + ... + 1 2 3 2018 1 1 1 1 2018. ... + + + + 2 3 4 2019 = 0,25 điểm 2017 2016 1 1 1 ... + 1 + + + + + + 1 Câu 1.4 2 3 2018 (1,0 điểm) 1 1 1 1 2018. ... + + + + 2 3 4 2019 = 0,25 điểm 2019 2019 2019 2019 + + + ... + 2 3 4 2019 1 1 1 1 2018. ... + + + + 2 3 4 2019 2018 = = 1 1 1 1 2019 0,5 điểm 2019. + + + ... + 2 3 4 2019 ( 2 + ) =( − )2 2 19x 2.5 :14 13 8 − 4 0,25 điểm
Câu 2.1a (19x + 50):14 = 9 0,25 điểm
(1,0 điểm) 19x + 50 =126 0,25 điểm 19x = 76 0,25 điểm x = 4
2x +1 + x + 8 = 4x (1)
Câu 2.1b Nếu x < 0 thì 2x +1 + x +8 > 0 và 4x < 0 nên không có giá trị của x 0,5 điểm
(1,0 điểm) thỏa mãn (1)
Nếu x ≥ 0 thì 2x + 1 > 0, x + 8 > 0 nên từ (1) suy ra: 2x + 1 + x + 8 = 4x
x = 9 (t/m khoảng đang xét) 0,5 điểm x y ; y z = = suy ra được x y = z = 0,5 điểm 2 3 5 4 10 15 12 Câu 2.2 x 2y z x − 2 ⇒ = = y + z = 0,5 điểm 10 30 12 10 − 30 +12 (2,0 điểm) mà x − − 2y + z = 48 − nên x 2y z 48 ⇒ = = = = 6 0,5 điểm 10 30 12 8 −
Suy ra: x = 60; y = 90; z = 72 0,5 điểm (x − )2 2 5. 2019 = 24 − y (1) Do (x − )2 5. 2019 ≥ 0 và (x − )2 5. 2019 5 Câu 3.1 nên 2 24 − y ≥ 0 và 2
24 − y 5 suy ra y = 2 hoặc y = 3 (Do y ∈ N ) 0,5 điểm
(2,0 điểm) Với y = 2 thay vào (1) ta được: (x − )2 2019 = 4 1,0 điểm
Tìm được x = 2021; x = 2017
Với y = 3, thay vào (1) ta được (x − )2
2019 = 3 không có giá trị của x. 0,5 điểm Vậy ...............
Nếu x + y + z = 0 thì x + y = -z, x + z = -y, y + z = -x
Khi đó: B = x + y y + z x + z = 1 − y z x 1,0 điểm
Nếu x + y + z ≠ 0 thì Câu 3.2
y + z − x z + x − y x + y − z x + y + z = = = = 1 (2,0 điểm) x y z x + y + z
suy ra: x + y = 2z, x + z = 2y, y + z = 2x
Khi đó: B = x + y y + z x + z = 8 y z x 1,0 điểm Vậy: ......... A Câu 4 E (6,0 điểm) 1 B M C H D F Câu 4.1 C/m được A ∆ EH = A
∆ FH (g-c-g) Suy ra EH = HF (2,0 điểm) 2,0 điểm Từ A ∆ EH = A
∆ FH Suy ra = E F 0,5 điểm 1 Câu 4.2 Xét C ∆ MF có
ACB là góc ngoài suy ra = − CMF ACB F 0,5 điểm
(2,0 điểm) B ∆ ME có
E là góc ngoài suy ra = − BME E B 1 1 0,5 điểm
vậy + = − + −
CMF BME (ACB F) (E B) 1 hay = − 2BME ACB B 0,5 điểm C/m A ∆ HE = A
∆ HF(g − c − g) Suy ra AE = AF và = E F 1
Từ C vẽ CD // AB ( D ∈ EF ) 0,25 điểm C/m được B ∆ ME = C
∆ MD(g − c − g) ⇒ BE = CD (1) 0,25 điểm Câu 4.3 và có =
E CDF (cặp góc đồng vị) 1 (2,0 điểm) do đó = CDF F
Vẽ đường cao CK của tam giác CDF. 0,25 điểm C/m được CH ∆ D = CH ∆
F(cgv − gn) ⇒ CF = CD (2) 0,25 điểm
Từ (1) và (2) suy ra BE = CF
Quy đồng ta được: 81.41(ab +bc + ca) =11. . ab . bc ca (1)
Do 41 là số nguyên tố và . ab .
bc ca41 nên có một số trong tích chia hết cho 41. 0,5 điểm
Giả sử: ab41 (do vai trò các số như nhau)
suy ra: ab = 41 hoặc ab = 82
+ Với ab = 41 suy ra a = 4, b = 1, thay vào (1) ta được:
81(41+1c + c4) =11.1 .cc4 Câu 5
Do (81,11) = 1 nên 1 .cc481. Mà 1c không chia hết cho 27 nên c4 chia hết cho 9 suy ra c = 5
(2,0 điểm) Thay vào ta thấy thỏa mãn. 0,75 điểm
+ Với ab = 82 suy ra a = 8, b = 2, thay vào (1) ta được: 81(82+ 2c + 8 c ) = 22.2 .c 8 c (2)
Từ (2) ta thấy c chẵn, do (81,22) = 1 nên 2 .c 8
c 81. Mà 2c không chia hết cho 81 nên 8
c chia hết cho 3 suy ra c = 4. Khi đó 24.48
không chia hết cho 81 (loại). 0,5 điểm
Lập luận tương tự với ca41,bc41
Vậy bộ số (a,b,c) cần tìm là: (4,1,5); (4,5,1); (1,4,5); (1,5,4); (5,1,4); 0,25 điểm (5,4,1)
1. Học sinh làm cách khác đúng thì chấm điểm tối đa tương ứng.
2. Bài hình học sinh không vẽ hình hoặc vẽ hình sai cơ bản thì không cho điểm.




