Đề khảo sát học sinh giỏi Toán 11 năm 2020 – 2021 trường THPT Quế Võ 1 – Bắc Ninh

TRƯỜNG THPT QUẾ VÕ SỐ 1
KÌ THI KHẢO SÁT HỌC SINH GIỎI NĂM HỌC 2020-2021 ĐỀ CHÍNH THỨC
Môn thi: TOÁN - Lớp 11 THPT
Thời gian: 150 phút (không kể thời gian giao đề)
Câu 1 (2 điểm). Cho  P  2 2 : y  x  2mx  m  m P m . Biết rằng 
luôn cắt đường phân giác góc phần tư thứ nhất m 
tại hai điểm A , B . Gọi A , B lần lượt là hình chiếu của A , B
A , B lần lượt là hình chiếu của A , B 1 1 lên Ox , 2 2
lên Oy . Tìm m để tam giác OB B có diện tích gấp 4 lần diện tích tam giác OA A . 1 2 1 2 Câu 2 (4 điểm).
2sin 2x  cos 2x  7sin x  4  3 1. Giải phương trình  1. 2 cos x  3 3 2 y  4y  4y  x 1   2y 5y4 x1  1
2.Giải hệ phương trình  .
2 x  3x  3  6x  7  y x  2 2 2 1    2y  1 3x2 2 Câu 3 (4 điểm). 2 2 2 2 2 1. Chứng minh rằng  1 C   2 C   3 C  ... 2021 C   2022 C  1011  C 1. 2022 2022 2022 2022 2022 2022
2.Cho đa giác đều A A ...A
nội tiếp đường tròn tâm O , chọn ngẫu nhiên 4 đỉnh bất kỳ của đa giác đó. Tính 1 2 2020
xác suất để nhận được một tứ giác có đúng một cạnh là cạnh của đa giác.
Câu 4 (2 điểm). Nhà anh A muốn khoan một cái giếng sâu 20 mét dùng để lấy nước cho sinh hoạt gia đình.
Có hai cơ sở khoan giếng tính chi phí như sau:
Cơ sở I: Mét thứ nhất 200 nghìn đồng và kể từ mét thứ hai trở đi, giá của mỗi mét tăng thêm 60 nghìn đồng so
với giá của mỗi mét trước đó.
Cơ sở II: Mét thứ nhất 10 nghìn đồng và kể từ mét thứ hai trở đi, giá của mỗi mét gấp 2 lần so với giá của mỗi mét trước đó.
Hỏi gia đình anh A để tiết kiệm tiền thì nên chọn cơ sở nào để thuê, biết rằng hai cơ sở trên có chất lượng khoan là như nhau. Câu 5 (6 điểm).
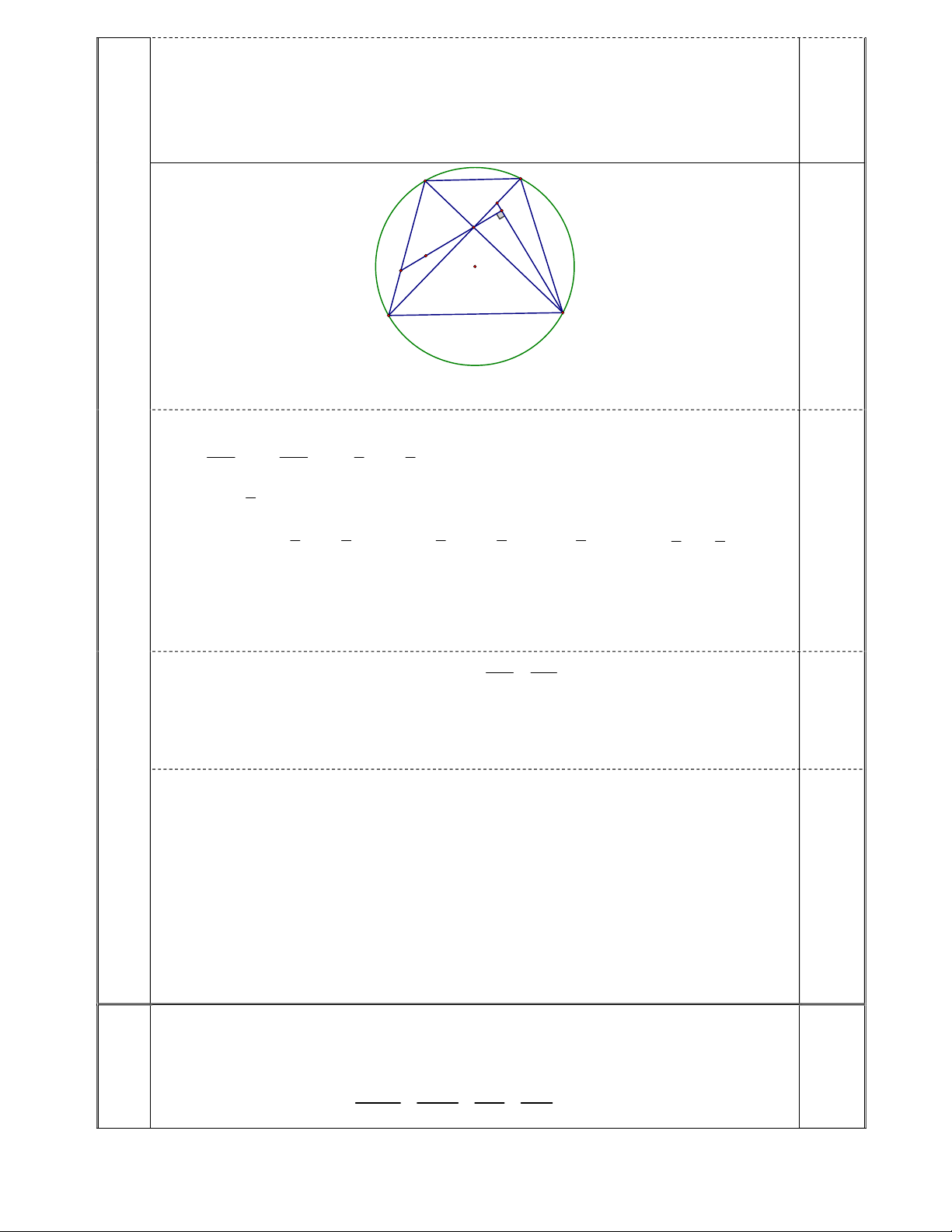
1.Trong mặt phẳng hệ tọa độ Oxy cho hình thang cân ABCD có hai đường chéo BD và AC vuông góc với
nhau tại H và AD  2BC . Gọi M là điểm nằm trên cạnh AB sao cho AB  3AM , N là trung điểm HC . Biết B  1
 ; 3 , đường thẳng HM đi qua điểm T 2;3 , đường thẳng DN có phương trình x  2y  2  0 . Tìm
tọa độ các điểm A , C và D .
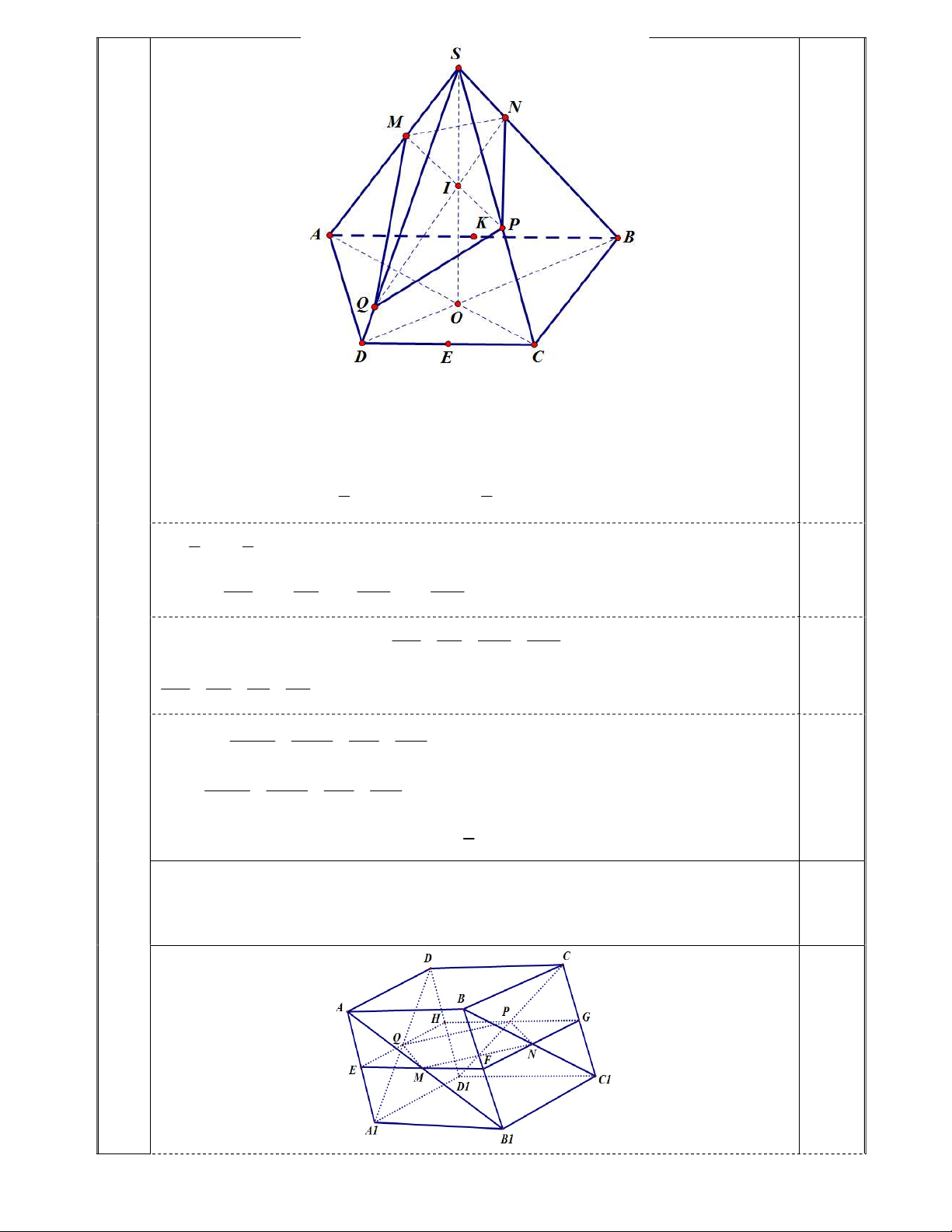
2. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB // CD, AB  2CD . Các cạnh bên có độ dài
bằng 1. Gọi O là giao điểm của AC và BD. I là trung điểm của SO. Mặt phẳng   thay đổi đi qua I và cắt S ,
A SB, SC, SD lần lượt tại M , N, P, Q . Tìm giá trị nhỏ nhất của biểu thức 1 1 1 1 T     . 2 2 2 2 2SM 2SN SP SQ
3. Cho hình lăng trụ tứ giác ABC . D A B C D  1 1 1 1 , mặt phẳng 
 thay đổi và song song với hai đáy của lăng trụ
lần lượt cắt các đoạn thẳng AB , BC , CD , DA tại M , N , P, Q . Hãy xác định vị trí của mặt phẳng   để tứ 1 1 1 1
giác MNPQ có diện tích nhỏ nhất. Câu 6 (2 điểm).
1. Cho a,b, c là các số thực dương thoả mãn abc  1. Chứng minh bất đẳng thức ab bc ca 9 3 3 3 a  b  c     . 2 2 2 2 2 2 a  b b  c c  a 2
2. Giải phương trình 1 2020x  1 2020x  1 2021x 1 2021x  1 2021x 1 2021x . ---------- Hết ------------ 1
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM (Gồm có 06 trang) Câu NỘI DUNG Điểm I Cho  P y  x  mx  m  m P m  2 2 : 2 . Biết rằng 
luôn cắt đường phân giác góc phần tư m  2,0
điểm thứ nhất tại hai điểm A , B . Gọi A , B lần lượt là hình chiếu của A , B A , B 1 1 lên Ox , 2 2 2,0
lần lượt là hình chiếu của A , B lên Oy . Tìm m để tam giác OB B có diện tích gấp 4 lần 1 2 diện tích tam giác OA A . 1 2 x  m     
Xét phương trình hoành độ giao điểm: 2 2 x 2mx m m x  . 0,5 x  m 1 *TH1: Am;m  A m;0 A 0;m 1  ; . 2   B m 1;m  
1  B m 1;0 ; B 0; m 1 . 2   1   0,75 m 1 1 2 1 2  Khi đó S  4S  m   m  . OB B OA A  1 4. . 1  1 2 1 2  2 2 m   3 *TH2: Bm;m  B m;0 B 0;m 0,75 1  ; . 2   Am 1;m  
1  A m 1;0 ; A 0;m 1 . 2   1   m  2  1 1 2 Khi đó 2 S 4S m 4. m       . OB B OA A  1 2  1 2 1 2 2 2 m   3
Vậy có 4 giá trị của m thỏa mãn yêu cầu đề bài. II
2sin 2x  cos 2x  7sin x  4  3 4,0 1. Giải phương trình  1. điểm 2 cos x  3 2,0 5 Điều kiện: x    k2 (*). 6 0,5
Phương trình tương đương 2sin 2x  cos 2x  7sin x  4  3  2cos x  3
 2sin 2x  cos 2x  7sin x  2cos x  4  0   x  x   2 2sin 2 2cos
1 2sin x  7sin x  4  0 0,5  2cos x2sin x   1  2sin x   1 sin x  3  0 2  x     x   x  x   2sin 1 0 2sin 1 sin 2cos 3  0  . 
sin x  2cos x  3  0  Giải (1) :   0,5 x   k2  1 6 sin x    2 5  x   k2  6
 Giải (2): sin x  2cos x  3 vô nghiệm vì 2 2 2 1  2  3 . 
Đối chiếu điều kiện (*) phương trình có họ nghiệm x   k2 k  . 0,5 6
2. Giải hệ phương trình 3 2 y  4y  4y  x 1   2y 5y4 x1   1  . 2,0
2 x  3x  3  6x  7  y x  2 2 2 1    2y  1 3x2 2 2 x  (*) Điều kiện: 0,25 3 2 2
Phương trình (1)  y  y  2  x 1  y  2  y  x 1  
  y  x   y  2 1
2  x 1  0  y  x    1 0,5 2 vì x 
  y  22  x 1  0. 3
Thế y  x 1 vào phương trình (2) ta có:
x  x   x    x  x  2 2 2 3 3 6 7 1 1  x 3x  2 2 3 2
 2 x  3x  3  6x  7  x  x  x 1 x 3x  2 0,5  2 2x 3x 3   3
1  x 3x 2  x  x 7x  6 2 2 x  3x  2 3x  2  x  2  x   2 x  3x  2x  3 2 x  3x  3 1 3x  2  x    2 x  2
x  3x  2 x  3    0 2  x  3x  3 1 3x  2  x  2 x  3x  2  0 3 0,25   2 x  x  3    0 4 .  2  x  3x  3 1 3x  2  x
 Giải (3) ta được x  1; x  2 2 x
 Giải (4): phương trình x  3    0 2 x  3x  3 1 3x  2  x  2   x   x  2    1  0   2  x  3x  3 1  3x  2  x  0,5 2 2 x  3x  3 3x  2  2 x  
 0 vô nghiệm vì vế trái luôn dương với x  . 2      3 x 3x 3 1 3x 2 x
Đối chiếu điều kiện (*) suy ra tập nghiệm hệ là S    1; 2,2; 3. III 2 2 2 2 2 1 2 3 2021 2022 1011        4,0 1. Chứng minh rằng C C C ... C C C 1. 2022   2022  2022  2022   2022  2022 2,0 điểm Ta có 0,25 3
C 2 C 2 C 2 ...C 2 C 2 1 2 3 2021 2022 1011  C 1 2022 2022 2022 2022 2022 2022
 C 2 C 2  C 2 C 2 ...C 2  C 2 0 1 2 3 2021 2022 1011  C 2022 2022 2022 2022 2022 2022 2022 . 1 x2022 0 1 2 2 3 3 2022 2022  C  xC  x C  x C ... x C 2022 2022 2022 2022 2022 x  2022 2022 0 2021 1 2020 2 2019 3 2021 2022 1  x C  x C  x C  x C  ... xC  C 2022 2022 2022 2022 2022 2022 0,75 2022 2020 Hệ số 2022 x
trong khai triển 1 x x  1 là
C 2 C 2 C 2 C 2 ...C 2 C 2 0 1 2 3 2021 2022 . 2022 2022 2022 2022 2022 2022 2022 2022 2022 2020 Mà 1 x x   1   2 1 x    C   2 1 k k k x . 2022 0,5 k 0 Hệ số của 2022 x
trong khai triển   2022 2 1 x là 1011 C . 2022 0,5
Vậy có điều phải chứng minh.
2. Cho đa giác đều A A ...A
nội tiếp đường tròn tâm O , chọn ngẫu nhiên 4 đỉnh bất kỳ 1 2 2020
của đa giác đó. Tính xác suất để nhận được một tứ giác có đúng một cạnh là cạnh của đa 2,0 giác.
Xác định được không gian mẫu và tính số phần tử của không gian mẫu n  4  C 2020 0,5
Xác định được biến cố, chỉ ra ứng vỡi mỗi cạnh có 2 C
(chia 2016 cái kẹo cho 3 bạn mà bạn 2019
nào cũng có kẹo) tứ giác thỏa mãn bài toán. 0,5 n  A 2  2020.C 2019 0,5 Xác suất cần tìm là 0,5 P  A n A 12   n  2017 IV
1. Nhà anh A muốn khoan một cái giếng sâu 20 mét dùng để lấy nước cho sinh hoạt gia 2,0
đình. Có hai cơ sở khoan giếng tính chi phí như sau:
điểm Cơ sở I: mét thứ nhất 200 nghìn đồng và kể từ mét thứ hai trở đi, giá của mỗi mét tăng
thêm 60 nghìn đồng so với giá của mỗi mét trước đó. 2,0
Cơ sở II: mét thứ nhất 10 nghìn đồng và kể từ mét thứ hai trở đi, giá của mỗi mét gấp 2
lần so với giá của mỗi mét trước đó.
Hỏi gia đình anh A để tiết kiệm tiền thì nên chọn cơ sở nào để thuê, biết rằng hai cơ sở
trên có chất lượng khoan là như nhau.
Cơ sở I: Gọi u (nghìn đồng) là số tiền chi phí khoan giếng ở mét thứ n . n
Theo giả thiết ta có u  200 và u  u  60 1 n 1  n 0,5
Chứng minh dãy số u là một cấp số cộng có công sai d  60 . n
Vậy số tiền thanh toán cho cơ sở I khoan giếng khi khoan giếng sâu 20 mét là: 20.19
S  u  u  ...  u  20u  d  15400 (nghìn đồng). 0,5 20 1 2 20 1 2
Cơ sở II: Gọi v (nghìn đồng) là số tiền chi phí khoan giếng ở mét thứ n . n
Theo giả thiết ta có v  10 và v  v 2 0,5 1 n 1  n
Chứng minh dãy số v là một cấp số nhân có công bội q  2 . n
Vậy số tiền thanh toán cho cơ sở II khoan giếng khi khoan giếng sâu 20 mét là: 20 q 1
S  v  v  ... v  v .  24697 (nghìn đồng). 0,5 20 1 2 20 1 q 1
Vậy gia đình anh A nên thuê cơ sở I. 4
1. Trong mặt phẳng hệ tọa độ Oxy cho hình thang cân ABCD có hai đường chéo BD và
AC vuông góc với nhau tại H và AD  2BC . Gọi M là điểm nằm trên cạnh AB sao cho
AB  3AM , N là trung điểm HC . Biết B  1
 ; 3 , đường thẳng HM đi qua điểm 2,0
T 2; 3 , đường thẳng DN có phương trình x  2y  2  0 . Tìm tọa độ các điểm A , C và D . B C N L H T M A D
Ta có ABCD là hình thang cân nên có hai đường chéo BD và AC vuông góc với nhau tại 0,5 H nên HB  HC, HA  HD . Ta đặt HB  HC  , a HA  HD  b  , a b  0 , khi đó:
 MB  MA  2  1  HM  .HA  .HB  HA  HB AB AB 3 3 V
  1  DN  DH  HC 6,0 2 điểm
   2  1  1  1   1   1 1 0,5 Suy ra HM.DN  HA  HB DH  HC  H . A HC  DH.HB      ab  ab  0 .  3 3  2  3 3 3 3 Do đó HM  DN
Đường thẳng HM đi qua T 2;3 và vuông góc với DN nên có phương trình là: 2x  y  7  0 . HD AD
 
Gọi H  ;t2t  7  HM . Theo định lí Talet ta có:   2 và H , D HB ngược hướng HB BC  
nên HD  2HB , suy ra D 3t  2;6t 15 . 0,5
Mặt khác D  DN nên 3t  2  26t 15  2  0  t  2  H 2;  3  D8; 3 . .
Nhận xét rằng H  T , đường thẳng BD : y  3 .
Đường thẳng AC đi qua H và vuông góc với BD có phương trình : x  2  0 . x  2 x  2
Tọa độ điểm N là nghiệm của hệ phương trình:     N 2;0. x  2y  2  0 y  0
Vì N là trung điểm của HC nên C 2;3 . 0,5   x  2  0    A x 2 Mặt khác HA  4 A HN      A  .  y  3  4   y    A 0 3 2; 15 15  A
Vậy tọa độ ba điểm cần tìm là A2;15, C 2;3, D8; 3 .
2. Cho hình chóp S.ABCD có đáy ABCD là hình thang cân, AB // CD, AB  2CD . Các
cạnh bên có độ dài bằng 1. Gọi O là giao điểm của AC và BD. I là trung điểm của SO. Mặt
phẳng   thay đổi đi qua I và cắt S ,
A SB, SC, SD lần lượt tại M , N, P, Q . Tìm giá trị 2,0 1 1 1 1
nhỏ nhất của biểu thức T     . 2 2 2 2 2SM 2SN SP SQ 5 0,5
Gọi K là trung điểm của AB, E là trung điểm của CD Ta có    SA  SB  2SK    SC  SD  2SE C  D / / AB  3 
  3   Do: 
 EK  OK  SK  SE  (SK  SO) AB  2CD 2 2 3  1          
SO  SK  SE  SA  SB  2SC  2SD  2SK  4SE  6SO 2 2       0,5  SA SB 2SC 2SD SM  SN  SP  SQ  6SO  12SI SM SN SP SQ SA SB 2SC 2SD
Do M , N , P, Q đồng phẳng nên     12 . Suy ra SM SN SP SQ 0,5 1 1 2 2     12 . SM SN SP SQ   1 1 1 1 2  12       2 2 2  2  2  2 2 2 2 2   2SM 2SN SP SQ   1 1 1 1 T=     12 0,5 2 2 2 2 2SM 2SN SP SQ 1
Vậy min T  12 khi SM  SN  SP  SQ  . 2
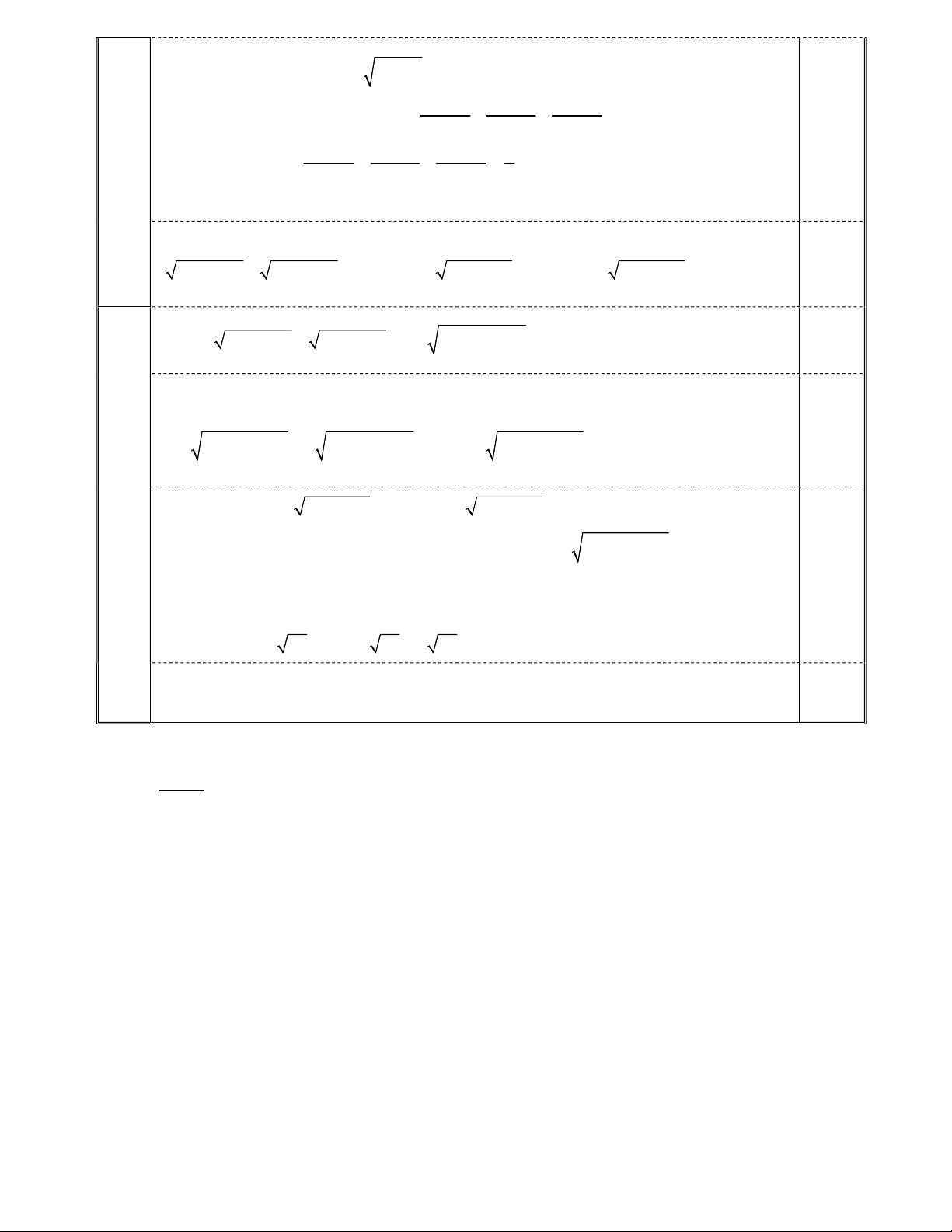
3. Cho hình lăng trụ tứ giác ABC .
D A B C D , mặt phẳng   thay đổi và song song với 1 1 1 1
hai đáy của lăng trụ lần lượt cắt các đoạn thẳng AB , BC , CD , DA tại M , N , P, Q . Hãy 1 1 1 1 2,0 
xác định vị trí của mặt phẳng   để tứ giác MNPQ có diện tích nhỏ nhất. 6
Giả sử mặt phẳng   cắt các cạnh AA , BB ,CC , DD lần lượt tại E, F,G, H . 1 1 1 1 AE BF CG DH 0,5
Do mặt phẳng   //  ABCD nên ta có:    . AA BB CC DD 1 1 1 1 AE Đặt  x,0  x   1 ; S  S S  S 
với S là hằng số. Ta có ABCD AA  . EHGF 1 0,5 EM AM AE EQ A Q A E Suy ra    x 1 1     1 x . EF AB AA EH A D A A 1 1 1 1 S E  MQ EQ EM   .  x1 x  S  x  x S . E  MQ 1  EFH S EH EF E  FH
Chứng minh tương tự ta có: S  x      0,5  1 xS ; S x   1 xS ; S x   1 x S . HPQ HGE PGN HGF NFM  GFE Ta có S  S  S  S  S  S  MNPQ
 EMQ PGH PGN NFM   S  x   xS  S  S  S       .     S x x S S  2 1 1 2 1 2x 2x EFH HEG HGF GFE  2   S Ta có 2 1 1 1 1 2x  2x  2 x     S     2  2 2  . MNPQ 2 S 1 Khi đó S 0,5 
đạt giá trị nhỏ nhất là khi x  . MNPQ 2 2
Vậy mặt phẳng   đi qua trung điểm các cạnh AA , BB ,CC , DD . 1 1 1 1
1. Cho a,b, c là các số thực dương thoả mãn abc  1. Chứng minh bất đẳng thức ab bc ca 9 3 3 3 a  b  c     . 1,0 2 2 2 2 2 2 a  b b  c c  a 2 Ta có 0  a  b4 4 3 2 2 3 4 4 4 2 2
 a  4a b  6a b  4ab  b  a  b  2a b  4ab 2 2 a  ab  b      a  ab  b a  b ab  a b   a b  4ab a  ab  b  2 2 2 2 2 1 2 2 2 2    1   0,5 2 2 2 2   a  b 4ab a  b 4  b a  VI bc 1  b c  ca 1  c a  2,0 Tương tự có 1   ; 1   . 2 2   2 2   điểm b  c 4  c b  c  a 4  a c 
Do đó, cộng theo vế các bất đẳng thức trên và sử dụng bất đẳng thức Schur cùng giả thiết abc 1 ta được  ab bc
ca  1  b  c c  a a  b  3        2 2 2 2 2 2     a  b b  c c  a  4  a b c 
bc b  c  cac  a  aba  b bcb  c  cac  a  aba  b   0,25 4abc 4 1   1 3 3 3
a  b  c  3abc   3 3 3 a  b  c  3 4 4  ab bc ca  Hay 3 3 3 a  b  c  4    9 1  2 2 2 2 2 2     a  b b  c c  a  7 3 Mặt khác  3 3 3 a  b  c  3 3
 3.3 abc  9 2  ab bc ca  Từ   1 và 2 suy ra 3 3 3 4 a  b  c     18  2 2 2 2 2 2  a b b c c a      0,25 ab bc ca 9 Do vậy 3 3 3 a  b  c     2 2 2 2 2 2 a  b b  c c  a 2
Dấu đẳng thức xảy ra khi và chỉ khi a  b  c  1. 2. Giải phương trình 1,0
1 2020x  1 2020x  1 2021x 1 2021x  1 2021x 1 2021x . VT    x   x 2    x2 2 1 2020 1 2020 4 1 2020 0,25
x  0  2021x2  2020x2  1 2021x2 1 2020x2 2 0,25
 4 1 2021x2  4 12020x2 VT  4 12021x2
VP  1 2021x 1 2021x  1 2021x 2 2   1 2021x  
 2 1 2021x2 1 2021x  1 2021x1 2021x2   4 1 2021x2   0,25 a  1 2021x a  b  2  Thật vậy,    . b   1 2021x 1   ab   2021x2  2 2
2 a b  ab   4 ab  ab  ab  ab 1 ab  0 , luôn đúng.
Vậy phương trình xảy ra  x  0 . 0,25 ---------- Hết ------------ Chú ý:
- Các cách làm khác nếu đúng vẫn cho điểm tối đa, điểm thành phần giám khảo tự phân chia trên
cơ sở tham khảo điểm thành phần của đáp án. 8